阶段空场嗣后充填法具有采充效率高、损失贫化率低、作业安全等优点,同时能够起到控制地压、维护采场稳定性、保证作业安全以及控制地表塌陷等作用[1-3],在国内外矿山得到广泛应用。然而在高阶段两步骤回采过程中,一步骤胶结充填体的强度和稳定性对二步骤矿柱的安全回采具有关键作用[4-5],在矿柱回采工程中需要具有足够强度的胶结充填体来支撑围岩并且处于稳定状态,以安全回采相邻矿柱[6-7]。因此,进行高阶段充填体稳定性风险评价对预防和规避回采过程可能发生的安全风险事件、降低矿石损失贫化意义重大。近年来许多专家学者针对高阶段充填体的稳定性开展了大量研究。魏晓明[7]通过FLAC数值模拟,研究了李楼铁矿不同配比条件下高阶段充填体的应力场、位移场及塑性破坏区,为矿山设计了合理的采场充填配比方案。曾照凯等[8]运用米切尔算法和强度计算经验公式从力学的角度探讨了安庆铜矿充填体强度与自立高度和宽度的关系,揭示了高阶段充填体稳定性的特征。刘志祥等[9]建立高阶段矿柱开采爆破分析模型对胶结充填体动静强度进行了试验,分析了爆破动载下充填体破坏规律,研究成果指导了安庆铜矿5号矿柱的开采,并且取得良好的效果。徐文彬等[10]认为岩体稳固性是影响嗣后充填采场矿柱稳定性的关键因素,研究了不同围压下矿柱失稳的4个阶段,结果表明剪切破坏是高阶段嗣后充填体的主要破坏方式。
以上研究通过数值模拟和理论分析的方法从充填配比、自立高度和宽度、爆破动载和岩体稳固性等角度分析了充填体的强度和稳定性,然而高阶段充填体稳定性是一个定性概念,且评估过程受诸多不确定因素影响与控制,单从某个影响因素分析,往往以偏概全、事倍功半[11],因此综合考虑多种因素的耦合影响,将充填体稳定性进行定量化研究具有重要意义。云模型是由Li等[12]提出的处理定性概念与定量描述的不确定性转换模型,通过运行正向正态云发生器,云模型能够将评估对象的模糊性和随机性转化为确定度这一定量值,从而克服了传统数学方法在模糊性与随机性、定性与定量之间存在的局限[13]。故笔者采用云模型理论研究高阶段充填体的稳定性,同时结合改进CRITIC-G1法确定指标组合权重,得到不同风险等级的综合确定度,以此判定高阶段充填体稳定性风险等级,并用工程实例对该方法的有效性和合理性进行验证。
1 云模型理论 1.1 云模型概念及其数字特征假设C是定量论域U中的一个定性概念,存在某个定量值x属于U,同时也是C的一个随机实现,定量x对定性C的确定度可表示为μ(x)∈[0, 1],且μ(x)的分布满足[14]
| $ \mu: U \rightarrow[0, 1], \forall x \in U \text {, 有 } x \rightarrow \mu(x) \text {, } $ | (1) |
则把每一个x称为云滴,x在U中的分布称为云,云的数字特性由期望Ex、熵En和超熵He表征。其中Ex为云滴所在论域区间的期望,体现了论域空间的中心值;熵En表示定性概念随机性与模糊性的综合度量;超熵He表示论域区间中云滴的厚度。
1.2 正向云发生器云发生器是云模型将评价指标的定性概念与定量描述实现转化的工具,正向云发生器是完成定性到定量的映射,即根据云的数字特征生成云滴的过程。计算步骤如下[15]:
1) 生成以En为期望、He2为方差的一个高斯随机数Eni′=NORM(En, He2)。
2) 生成以Ex为期望值、Eni′2为方差的一个高斯随机数xi=NORM(En, Eni′2)。
3) 计算确定度值:
| $ \mu_{i}=\mathrm{e}^{-\frac{\left(x_{i}-E_{x}\right)^{2}}{2\left(E_{\mathrm{n}}\right)^{2}}} 。$ | (2) |
4) 形成某个区间内的一个云滴(xi, μi)。
5) 重复步骤1)~4),直至产生N个云滴为止。
2 基于改进CRITIC-G1法组合赋权的高阶段充填体稳定性风险评价云模型 2.1 评判指标体系的建立高阶段充填体稳定性评估是一个多因素的复杂系统工程[11],影响充填体稳定性的因素有很多,既包含定量因素,又包含定性因素。参照相关论文和专家意见[16-18],最终选取坍落度(I1)、充填料浆坡度(I2)、骨料中值粒径(I3)、充填间隔时间(I4)、相邻结构面最大强度比(I5)、内聚力(I6)、爆破震动峰值振速(I7)、垂直应力与水平应力比(I8)、侧向暴露面积(I9)、自立高度(I10)、充填体密度(I11)、28 d最低抗压强度(I12)、地下水状况(I13)、接顶效果(I14)、布料均匀性(I15)、围岩稳固性(I16)等16项影响高阶段充填体稳定性因素。其中I1~I12为定量指标,I13~I16为定性指标,各影响指标的说明见表 1。
| 表 1 影响高阶段充填体稳定性评估指标 Table 1 Stability indexes of high stage filling body |
结合工程实际及相关资料[11, 13]得到评价指标的定量分级标准和定性分级赋值,并对高阶段充填体受影响程度划分风险等级,分别为Ⅰ级(风险较小)、Ⅱ级(风险一般)、Ⅲ级(风险较大)、Ⅳ级(风险极大)。对于单边界限的变量,如指标I3中,骨料中值粒径d<40 μm时均匀系数合理、级配良好,为Ⅰ级风险,d不为0是因为矿山充填所采用的骨料多为尾砂、河沙、棒磨砂等[13];d≥100 μm为Ⅳ级风险,因为此时料浆中粗颗粒过多,形成的充填体黏结性差,同时加剧了对管道的磨损。指标I4中,充填间隔时间t<12 h时处于Ⅰ级风险,此时t可取值为0,表示连续充填,因为间隔充填会使充填体内部产生结构面,破坏其稳定性。针对双边界限的变量,如指标I1中风险等级为Ⅰ级时取值范围为18~25 cm,因为坍落度处于这个区间内的料浆满足自流输送的条件,同时也能形成强度较高的充填体;Ⅳ级风险的范围为29~30 cm,因为此时料浆的坍落度大,容易离析,形成的充填体强度低,最大上限值30 cm为坍落度筒高度。各指标取值范围见表 2~3。
| 表 2 充填体稳定性评估定量指标分类标准 Table 2 Classification criteria of quantitative indexes for stability evaluation of backfill body |
| 表 3 充填体稳定性评估定性指标评分标准 Table 3 Scoring standard of qualitative indexes for stability evaluation of filling body |
参照相关文献[19],高阶段充填体稳定性评估指标的云模型数字特征参数可通过下式来计算:
| $ \left\{\begin{array}{l} E_{x}=\left(C_{\min }+C_{\max }\right) / 2, \\ E_{\mathrm{n}}=\left(C_{\max }-C_{\min }\right) / 6, \\ H_{\mathrm{e}}=k, \end{array}\right. $ | (3) |
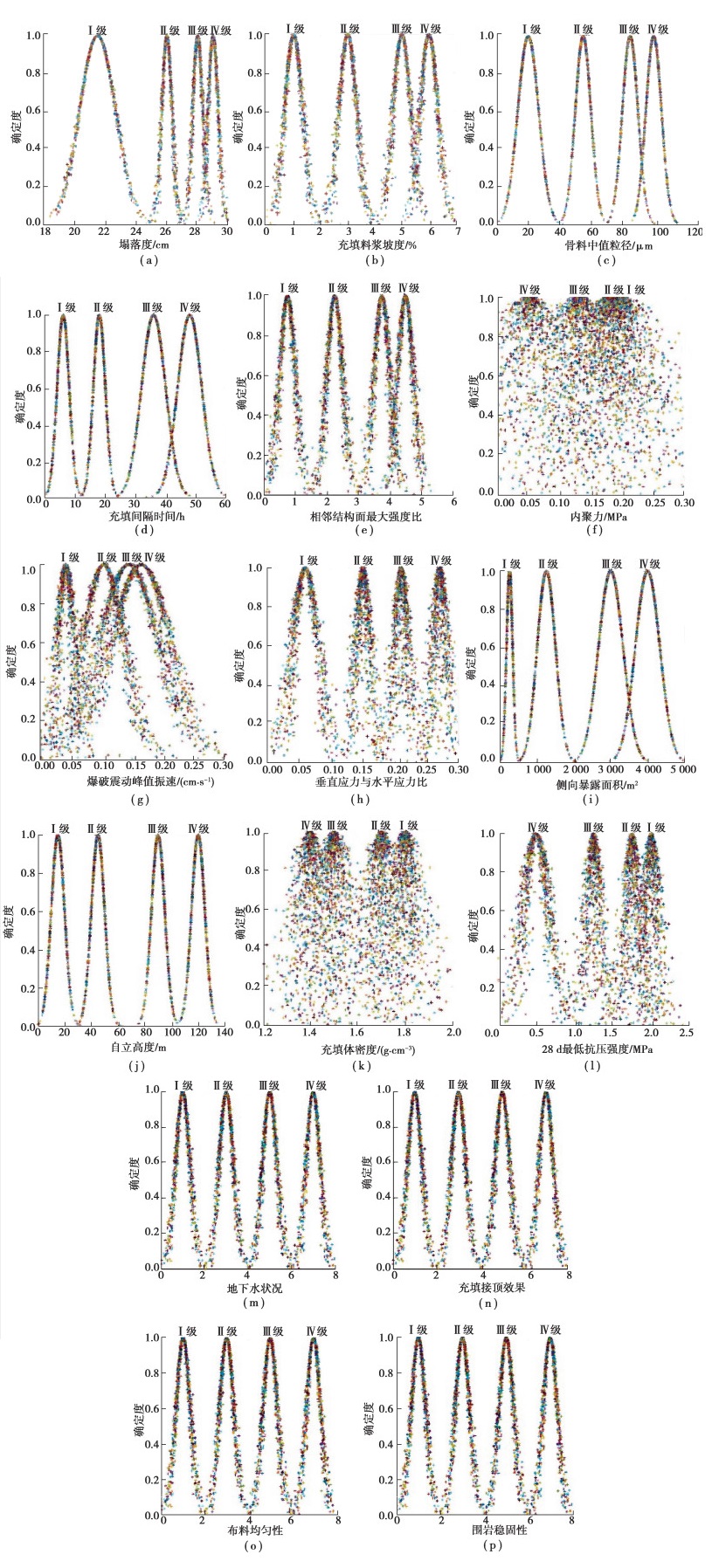
式中:Cmin和Cmax为评估指标某一风险等级标准的上限与下限;k为常数,表示评价指标的模糊程度,根据经验取值0.05。当出现单边界限的变量如[Cmin,+∞]或[-∞,Cmax]时,可通过数据的最大上限或下限求出边界参数,再通过式(3)求出指标的云数字特征[20]。例如评价因子xi的4个评价等级的区间分别为Ⅰ(0,a)、Ⅱ(a,b)、Ⅲ(b,c)和Ⅳ(c,+∞),云数字特征计算方法如表 4所示,高阶段充填体稳定性风险评价指标按上述模型确定3个云数字特征值Ex、En及He,见表 5。选取正向云发生器,根据云的数字特征通过MATLAB编写程序生成指标云图,如图 1所示,其中横坐标为指标等级取值范围,纵坐标代表对应的确定度。图 1(a)(b)(c)(d)(e)(g)(h)(i)(j)(m)(n)(o)(p)展示的云图中风险等级顺序相同,从左至右依次为Ⅰ级、Ⅱ级、Ⅲ级、Ⅳ级,可以明确指标的取值所隶属风险等级的情况。图(c)(d)(f)(g)(i)中数据点有交叉现象,反映了云滴的离散程度较大,同时也说明将指标取值转换为所隶属风险等级确定度时存在的亦此亦彼的模糊性与不确定性。
| 表 4 评价指标云字特征计算方法 Table 4 Calculation rules of cloud model digital characteristics |
| 表 5 高充填体稳定性风险指标的云数字特征 Table 5 Numerical characteristics of cloud model for stability risk index of filling body |
|
图 1 高阶段充填体风险指标评价等级的云模型 Fig. 1 Cloud model of risk index evaluation grade of high stage filling body |
G1法是在AHP法基础上提出的一种改进型主观权重的赋值方法,在确定各指标权重过程中不需要构造矩阵,计算过程比AHP法简便[21]。G1法步骤如下:
1) 确定评价指标的序关系。如果指标{X1,X2,…,Xn}对评估对象影响程度具有关系式
| $ X_{1}>X_{2}>, \cdots, >X_{n}, $ | (4) |
称为在评价指标{X1,X2,…,Xn}之间确立了按“ > ”排序的序关系。
2) 得出各评价指标之间的相对重要程度比。通过邀请专家理性判断评价指标Xk-1与Xk对于评估对象的重要程度,得出重要程度之比:
| $ W_{k-1} / W_{k}=r_{k} \quad(k=n, n-1, \cdots, 3, 2), $ | (5) |
即Wk-1的权重是Wk的rk倍,其中rk的参考值见表 6。
| 表 6 rk赋值表 Table 6 rk assignment table |
3) 计算评价指标权重系数。基于以上2步,求出指标的主观权重:
| $ W_{k}=\left(1+\sum\limits_{k=2}^{n} \prod\limits_{i=k}^{n} r_{i}\right)-1, $ | (6) |
| $ W_{k-1}=r_{k} W_{k} \quad(k=n, n-1, \cdots, 3, 2)。$ | (7) |
CRITIC法在综合考虑评价指标的信息量及指标之间的关联性的基础上确定权重,具有一定的优越性。由于标准差不能很好地衡量指标间量纲、数量级的变异性,本文中采用变异系数改进CRITIC法,其主要步骤如下[22]。
1) m个高阶段充填体评估对象和n个评价指标中第i个对象的第j个指标取值xij构成原始评估矩阵X,X=(xij)m×n。
2) 对评估矩阵X中各指标值标准化:
| $ x_{i j}{ }^{*}=\frac{x_{i j}-\overline{x_{j}}}{s_{j}} \quad(i=1, 2, \cdots, m ; j=1, 2, \cdots, n), $ | (8) |
其中
| $ \overline{x_{j}}=\frac{1}{m} \sum\limits_{i=1}^{m} x_{i j}, \quad s_{j}=\sqrt{\frac{1}{m} \sum\limits_{i=1}^{m}\left(x_{i j}-\overline{x_{j}}\right)^{2}} 。$ | (9) |
式中:xj和sj分别为第j个指标的均值和标准差。
3) 求指标的变异系数:
| $ v_{j}=\frac{s_{j}}{\overline{x_{j}}} \quad(j=1, 2, \cdots, n), $ | (10) |
式中vj为第j个指标的变异系数。
4) 利用步骤2)求得的标准化矩阵X求出相关系数,得到相关系数矩阵:
| $ \boldsymbol{R}=\left(r_{k l}\right) n \times n \quad(k=1, 2, \cdots, n ; l=1, 2, \cdots, n) 。$ | (11) |
5) 求各指标独立性程度的量化系数:
| $ \eta_{j}=\sum\limits_{k=1}^{n}\left(1-r_{k j}\right) \quad(j=1, 2, \cdots, n) 。$ | (12) |
6) 求各评价指标的综合性系数:
| $ C_{j}=v_{j} \sum\limits_{k=1}^{n}\left(1-r_{k j}\right) \quad(j=1, 2, \cdots, n) 。$ | (13) |
7) 确定各指标权重:
| $ w_{j}=\frac{C_{j}}{\sum\limits_{j=1}^{n} C_{j}} \quad(j=1, 2, \cdots, n) 。$ | (14) |
运用G1法和改进CRITIC法得到了指标的主客观权重。由于主客观赋权法各有各的缺陷,高阶段充填体稳定性风险评价指标权重的确立需充分结合主观经验和客观信息的内在规律,所以结合2种方法的优点,定义了由G1法与改进CRITIC法组成的综合赋权法[23]:
| $ W_{j}^{*}=\frac{W_{\mathrm{G} 1 j} W_{\text {CRITIC}_{j}}}{\sum\nolimits_{j=1}^{n} W_{\mathrm{G} 1_{j}} W_{\text {CRITIC}_{j}}}, $ | (15) |
式中:Wj*为第j个评价指标对充填体稳定性的综合权重,WG1j和WCRITICj分别为利用G1法和CRITIC法得到的第j个指标对目标的权重。
2.4 计算综合确定度根据高阶段充填体稳定性评价指标的3个云数字特征,使用MATLAB软件编写程序生成单指标云图以确定该指标取值在不同等级下的确定度,再结合指标权重计算获得综合确定度,基于最大隶属度原则,选择综合确定度最大值所对应的等级作为充填体稳定性评估结果[24]。综合确定度计算公式为
| $ U=\sum\limits_{j=1}^{n} \mu(x) W_{j}^{*}, $ | (16) |
式中μ(x)为单指标确定度。
3 应用实例为了验证本文云模型的有效性并方便与其他方法进行对比,以采用高阶段空场嗣后充填采矿法的安庆铜矿(S1)、李楼铁矿(S2)、冬瓜山铜矿(S3)和司家营铁矿(S4)为例,利用改进CRITIC-G1组合赋权云模型对高阶段充填体的稳定性进行风险评估,通过以往对高阶段充填体的研究[4, 8, 9, 11, 18]和矿山的实际资料得到各指标实测值见表 7。
| 表 7 各矿山充填体稳定性评估指标实测值 Table 7 Measured values of stability evaluation indexes of filling body in various mines |
根据2.3节的计算方法,通过G1法计算主观权重,邀请专家对评价指标的理性判断获得指标之间的序关系和重要程度比,由式(4)~(7)求得各指标主观权重如表 8所示。利用改进CRITIC法进行客观权重计算,由式(8)~(11)计算出各指标的均值、标准差和变异系数,通过各矿山充填体稳定性指标的实测值进行标准化后,求出指标之间的相关系数,再根据式(12)~(14)求出评价指标的客观权重如表 9所示。最后结合2种方法的优点,由式(15)计算出各指标的组合权重见表 10。
| 表 8 G1法确定的指标权重 Table 8 Index weight determined by G1 method |
| 表 9 改进CRITIC法确定的指标权重 Table 9 Index weight determined by CRITIC method |
| 表 10 改进CRITIC-G1法组合权重 Table 10 Comprehensiveindex weight determined by CRITIC-G1 method |
根据表 5得到的高阶段充填体稳定性指标的云数字特征,由(2)式计算求得各评估指标隶属于不同风险等级的确定度,再结合表 10得出的各评估指标综合权重值,用式(16)计算指标的综合确定度,根据最大确定度原则,确定每个矿山的最终风险等级,并与未确知测度理论模型、模糊数学理论模型评估结果对比,结果见表 11。
| 表 11 高阶段充填体稳定性风险等级评估结果及对比 Table 11 Assessment results of stability risk level of high stage filling body |
由表 11可知:4座高阶段嗣后充填的矿山充填体稳定性风险等级分别为安庆铜矿Ⅳ级、李楼铁矿Ⅳ级、冬瓜山铜矿Ⅲ级、司家营铁矿Ⅱ级。且李楼铁矿U(Ⅳ)、冬瓜山铜矿U(Ⅲ)与司家营铁矿U(Ⅱ)远大于另外3个风险等级的确定度,表明这3座矿山充填体稳定性风险等级比较稳定,司家营铁矿的风险等级为Ⅱ级(风险一般),而针对Ⅳ级风险的李楼铁矿和Ⅲ级风险的冬瓜山铜矿则需要大幅调节指标参数来确保其稳定性风险等级降低。此外,安庆铜矿经改进CRITIC-G1云模型对其充填体稳定性风险评估后,综合确定度分别为:U(Ⅰ)=0.056 5,U(Ⅱ)=0.054 4,U(Ⅲ)=0.026 8,U(Ⅳ)=0.060 1,根据最大隶属度原则安庆铜矿的风险等级处于Ⅳ级(极大风险),然而该矿山稳定性风险隶属于Ⅰ级和Ⅱ级的综合确定度与Ⅳ级接近,表明安庆铜矿可通过调节影响稳定性的指标因素,能够较容易地控制矿山充填体稳定性风险等级。与其他2种评价模型对比分析可以发现,该模型利用云数字表征模糊性与随机性从而获得不同评估指标耦合作用下的充填体稳定性等级,实现了等级的可视化,结果与其他2种模型结果吻合,表明应用云模型评价高阶段充填体稳定性是有效可行的。另外,这里采用的改进CRITIC-G1组合赋权法综合考虑了专家对风险指标的理性判断与指标之间的相关性,评估结果更能反映矿山充填体的实际风险状况,可靠性更高。
4 结论1) 通过引入云模型,综合考虑充填体稳定性的影响因素,选取坍落度、侧向暴露面积、充填料浆坡度、充填接顶效果等16项定量与定性指标,将高阶段充填体稳定性划分为风险较小(Ⅰ级)、风险一般(Ⅱ级)、风险较大(Ⅲ级)、风险极大(Ⅳ级)4个等级,建立了高阶段充填体稳定性风险评价模型,基于云模型数字特征与组合权重计算综合确定度,根据最大隶属度原则确定风险等级,结果显示安庆铜矿、李楼铁矿、冬瓜山铜矿和司家营铁矿充填体稳定性风险等级分别为Ⅳ级、Ⅳ级、Ⅲ级和Ⅱ级。
2) 针对高阶段充填体风险评估过程中的模糊性和随机性,建立了基于改进CRITIC-G1组合赋权法与云模型相结合的高阶段充填体稳定性风险评估模型,较好地评估指标的信息量和指标之间的相关性,并综合专家经验和决策者的意见,兼顾主客观因素,使计算结果更为客观合理,解决了风险评估中评估指标存在不确定性的问题。
3) 基于云模型和组合赋权的高阶段充填体稳定性风险评价模型既可以通过最大综合确定度得到充填体稳定性的风险等级,而且能分析每一项指标,确定影响高阶段充填体稳定性的主要因素,对矿山回采工作安全管理及风险防控工作提供了一定参考,为高阶段嗣后充填的矿山有效解决充填体稳定性风险评价问题提供了新思路。
| [1] |
李占金, 郝家旺, 孙文诚, 等. 深部大规模开采岩体稳定性数值模拟研究[J]. 金属矿山, 2018(2): 56-60. Li Z J, Hao J W, Sun W C, et al. Numerical simulation analysis on stability of deep large-scale mining rock mass[J]. Metal Mine, 2018(2): 56-60. (in Chinese) |
| [2] |
Yilmaz E, Belem T, Benzaazoua M. Effects of curing and stress conditions on hydromechanical, geotechnical and geochemical properties of cemented paste backfill[J]. Engineering Geology, 2014, 168: 23-37. DOI:10.1016/j.enggeo.2013.10.024 |
| [3] |
Ghirian A, Fall M. Coupled thermo-hydro-mechanical-chemical behaviour of cemented paste backfill in column experiments: Part Ⅱ: Mechanical, chemical and microstructural processes and characteristics[J]. Engineering Geology, 2014, 170: 11-23. DOI:10.1016/j.enggeo.2013.12.004 |
| [4] |
魏晓明, 郭利杰, 李长洪, 等. 高阶段胶结充填体强度空间变化规律研究[J]. 岩土力学, 2018, 39(S2): 45-52. Wei X M, Guo L J, Li C H, et al. Study of space variation law of strength of high stage cemented backfill[J]. Rock and Soil Mechanics, 2018, 39(S2): 45-52. (in Chinese) |
| [5] |
Cao S, Xue G L, Yilmaz E, et al. Utilizing concrete Pillars as an environmental mining practice in underground mines[J]. Journal of Cleaner Production, 2021, 278: 123433. DOI:10.1016/j.jclepro.2020.123433 |
| [6] |
Cao S, Zheng D, Yilmaz E, et al. Strength development and microstructure characteristics of artificial concrete pillar considering fiber type and content effects[J]. Construction and Building Materials, 2020, 256: 119408. DOI:10.1016/j.conbuildmat.2020.119408 |
| [7] |
魏晓明. 高阶段全尾砂胶结充填体强度特性及充填体配比设计研究[D]. 北京: 北京科技大学, 2017. Wei X M. Study on strength characteristic and ratio design of high stage whole tailing cemented backfill[D]. Beijing: University of Science and Technology Beijing, 2017. (in Chinese) |
| [8] |
曾照凯, 张义平, 王永明. 高阶段采场充填体强度及稳定性研究[J]. 金属矿山, 2010(1): 31-34. Zeng Z K, Zhang Y P, Wang Y M. Research on the strength and stability on fill body of high-bench stope[J]. Metal Mine, 2010(1): 31-34. (in Chinese) |
| [9] |
刘志祥, 李夕兵. 爆破动载下高阶段充填体稳定性研究[J]. 矿冶工程, 2004, 24(3): 21-24. Liu Z X, Li X B. Research on stability of high-level backfill in blasting[J]. Mining and Metallurgical Engineering, 2004, 24(3): 21-24. (in Chinese) DOI:10.3969/j.issn.0253-6099.2004.03.007 |
| [10] |
徐文彬, 宋卫东, 杜建华, 等. 崩落法转阶段嗣后充填法采场稳定性分析[J]. 北京科技大学学报, 2013, 35(4): 415-422. Xu W B, Song W D, Du J H, et al. Stability analysis of a backfill stope due to transforming from block caving to stage backfill[J]. Journal of University of Science and Technology Beijing, 2013, 35(4): 415-422. (in Chinese) |
| [11] |
王新民, 张国庆, 李帅, 等. 高阶段大跨度充填体稳定性评估[J]. 中国安全科学学报, 2015, 25(6): 91-97. Wang X M, Zhang G Q, Li S, et al. Stability evaluation of high stage and large span backfill[J]. China Safety Science Journal, 2015, 25(6): 91-97. (in Chinese) |
| [12] |
Li D Y, Han J W, Shi X M, et al. Knowledge representation and discovery based on linguistic atoms[J]. Knowledge-Based Systems, 1998, 10(7): 431-440. DOI:10.1016/S0950-7051(98)00038-0 |
| [13] |
王石, 宋学朋, 石海天. 基于云模型和改进CRITIC的深井垂直充填管道磨损风险评估[J]. 重庆大学学报, 2020, 43(4): 73-84. Wang S, Song X P, Shi H T. An improved CRITIC and cloud model evaluation method for predicting the wear risk of vertical filling pipes in deep well[J]. Journal of Chongqing University, 2020, 43(4): 73-84. (in Chinese) |
| [14] |
王加闯, 黄明健, 过江. 基于CRITIC-有限区间云模型的边坡稳定性评价[J]. 中国安全生产科学技术, 2019, 15(6): 113-119. Wang J C, Huang M J, Guo J. Evaluation of slope stability based on CRITIC-finite interval cloud model[J]. Journal of Safety Science and Technology, 2019, 15(6): 113-119. (in Chinese) |
| [15] |
涂圣文, 郑克梅, 张尧, 等. 基于改进CRITIC法与云模型相结合的高速公路路堑高边坡工程施工安全总体风险评估模型研究[J]. 安全与环境工程, 2019, 26(3): 127-132. Tu S W, Zheng K M, Zhang Y, et al. Research on overall risk assessment model of construction safety of freeway high cutting slope engineering based on improved CRITIC method and cloud model[J]. Safety and Environmental Engineering, 2019, 26(3): 127-132. (in Chinese) |
| [16] |
Singh R, Mandal P K, Singh A K, et al. Coal pillar extraction at deep cover: with special reference to Indian coalfields[J]. International Journal of Coal Geology, 2011, 86(2/3): 276-288. |
| [17] |
Zhou N, Yan H, Jiang S, et al. Stability analysis of surrounding rock in paste backfill recovery of residual room pillars[J]. Sustainability, 2019, 11(2): 1-13. |
| [18] |
刘志祥, 李夕兵, 张义平. 基于混沌优化的高阶段充填体可靠性分析[J]. 岩土工程学报, 2006, 28(3): 348-352. Liu Z X, Li X B, Zhang Y P. Reliability analysis of high level backfill based on chaotic optimization[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(3): 348-352. (in Chinese) DOI:10.3321/j.issn:1000-4548.2006.03.013 |
| [19] |
李健, 汪明武, 徐鹏, 等. 基于云模型的围岩稳定性分类[J]. 岩土工程学报, 2014, 36(1): 83-87. Li J, Wang M W, Xu P, et al. Classification of stability of surrounding rock using cloud model[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(1): 83-87. (in Chinese) |
| [20] |
崔铁军, 马云东. 基于AHP-云模型的巷道冒顶风险评价[J]. 计算机应用研究, 2016, 33(10): 2973-2976. Cui T J, Ma Y D. Risk evaluation of roadway roof fall based on AHP-cloud model[J]. Application Research of Computers, 2016, 33(10): 2973-2976. (in Chinese) DOI:10.3969/j.issn.1001-3695.2016.10.023 |
| [21] |
王双川, 吕瑞强, 李德权, 等. 基于熵权G1法的飞行保障装备维修合同商模糊综合评价[J]. 兵工自动化, 2016, 35(12): 52-55, 59. Wang S C, Lyu R Q, Li D Q, et al. Fuzzy comprehensive evaluation of flight support equipment maintenance contractor based on entropy weight and G1 method[J]. Ordnance Industry Automation, 2016, 35(12): 52-55, 59. (in Chinese) |
| [22] |
过江, 张为星, 赵岩. 岩爆预测的多维云模型综合评判方法[J]. 岩石力学与工程学报, 2018, 37(5): 1199-1206. Guo J, Zhang W X, Zhao Y. A multidimensional cloud model for rockburst prediction[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(5): 1199-1206. (in Chinese) |
| [23] |
郭春燕, 朱孔来. 城市软实力评价指标体系和测度方法的实证研究: 以山东省17市为例[J]. 西安财经学院学报, 2014, 27(4): 79-85. Guo C Y, Zhu K L. Empirical study of city soft power index system and evaluation method: taking 17 cities in Shandong as an example[J]. Journal of University of Finance and Economics, 2014, 27(4): 79-85. (in Chinese) |
| [24] |
关贤欢, 郑相悦, 荣帅. 地下矿山充填管道堵塞风险评估模型研究[J]. 化工矿物与加工, 2018, 47(07): 51-56. Guan X H, Zheng X Y, Rong S. Study on risk assessment model of filling pipeline blockage in underground metal mines[J]. Industrial Minerals & Processing, 2018, 47(7): 51-56. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45


