2. 重庆嘉陵全域机动车辆有限公司, 重庆 400032
2. Chongqing Jialing Global Motor Vehicles Co., Ltd., Chongqing 400032, P. R. China
全地形车凭借其快速、机动和灵活等特点,在自然条件恶劣的山地崎岖地形等复杂工况具有更好的机动性和通过性,使得其在军事、民用等领域发挥重要作用[1-2]。传统的被动悬架结构参数固定,在面对复杂条件路况时减振效果性能大幅下降[3]。基于磁流变阻尼器的半主动智能悬架系统可通过不同的路面信息和车辆行驶工况改变磁流变阻尼器控制电流实现阻尼力值的调节,可以更好地实现减振效果[4-5],而成为智能悬架研究的热点。由于智能悬架控制策略主要是处理车身的垂向振动,对车辆姿态变化不能实现较好的控制。辨识出全地形车在行驶过程中的行驶工况[6],可以通过控制律对车身姿态进行控制。全地形车行驶在非结构化路面,使得车身不同姿态下振动耦合严重。使用单一传感器信号对车辆行驶工况辨识则误差太大,同时由于外界环境和车辆电气系统的影响,传感器的信号会出现较大的噪声或者异常值,严重影响了辨识结果的准确性。目前车辆行驶工况辨识主要方式可分为:聚类法,神经网络和逻辑门限值法[7]。聚类法首先提取不同行驶工况下的特征数据,然后根据相应的规则将其分类,通过将实时数据与预设数据进行比对后得出车辆的行驶工况;神经网络方法通过使用预先采集到的不同行驶工况下的特征参数值对神经网络进行训练,对采集的特征值进行行驶工况的识别;逻辑门限值方法是最简单的一种分类方法,通过对传感器信号的阈值比较分析就可以快速获取车辆的行驶工况。以上的辨识方法依赖于先验信息和精确的传感器信号,在缺少先验信息和传感器信号噪声较大的情况下则会使辨识结果准确率降低,甚至造成行驶工况误判进而导致控制效果恶化。
信息融合技术通过对不同的传感器信号进行特征提取,并按照一定规则进行融合进而得到对识别对象的最佳辨识[8]。目标识别信息融合方法按照数据类型的不同主要可以分为:数据级融合、特征级融合和决策级融合。数据级融合直接处理传感器原始信号数据,要求传感器信息来自同质传感器且具有较高的精度。特征级融合首先提取不同的传感器的原始数据的特征值,然后按照对应的规则将其融合和分类汇总后由决策层给出与目标状态的最佳一致性估计。但是当传感器信号存在较大噪声或者异常值时,基于数据级融合或特征层融合的辨识方法的辨识精度会严重下降。决策层融合对特征层融合后的辨识结果进行进一步优化选择和融合,具有高鲁棒性、高实时性等优点。常用决策级融合方法主要有:模糊推理, 贝叶斯推理、D-S证据理论等,其中D-S证据理论对不确定性的信息使用“区间估计”的方法进行处理,无需先验信息并且结构灵活高效[9-12],具有可以区分不确定信息和鲁棒性强的优点[13],已经应用在各种目标识别检测中,但是在智能悬架领域还未有深入研究。
基于以上分析,文中第1节选取了可以反映全地形车身整体变化的质心处垂直加速度、俯仰角、横摆角传感器作为行驶工况辨识的信号来源。第2节针对由单一传感器信号对车辆行驶工况辨识困难和传感器存在较大误差影响辨识结果的问题,首先通过改进的距离评估方法对全地形车上的传感器行驶工况的敏感特征值进行了提取和筛选,使用特征级融合方法对选取的传感器的特征值进行融合,完成了对行驶工况的初步辨识。然后将传感器信号的噪声和异常值当做不确定性信息,使用D-S证据理论合成方法对来自特征级融合后识别结果进行最高级别的决策层融合。最后基于可行区间的决策规则实现了车辆行驶工况的准确辨识。在第3节中经过Carsim仿真验证了当传感器信号存在较大误差时,相比特征级融合方法,基于D-S证据理论融合方法具有更高的准确性。
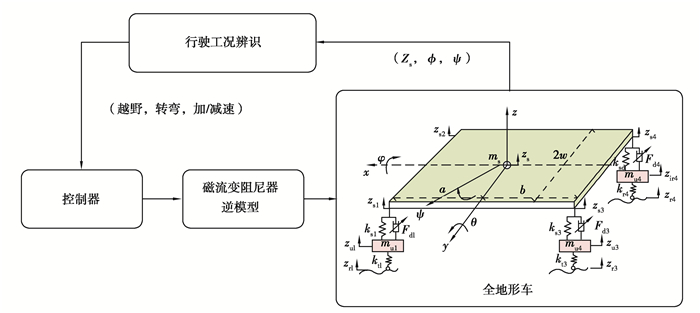
1 全地形车传感器信号选取文中设计的全地形车智能悬架控制策略如图 1所示。控制器通过行驶工况辨识获取当前车辆的行驶状态,经过控制律决策后得到实时阻尼器控制电流,完成阻尼力的调节实现对车辆姿态的控制。在全地形车的悬架阻尼器处分别安装有加速度和位移传感器,车辆中心安装有三轴加速度、俯仰角、横摆角、侧倾角传感器。相较于悬架阻尼器处的簧载加速度和悬架位移传感器,车身质心处的俯仰角φ,横摆角ψ,侧倾角θ,垂直加速度Zs信号更能体现车身整体的变化,因此选择以上传感器信号作为全地形车的行驶工况辨识的信号来源。通过对其特征值进行提取,最后在决策层进行融合处理,实现不同行驶工况(加/减速、越野、转弯)的辨识。
|
图 1 智能悬架控制策略 Fig. 1 Hierarchical humanoid intelligent control strategy |
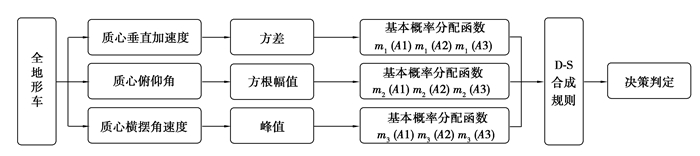
通过第1节中选择了车辆质心处的横摆角,z轴加速度、俯仰角、侧倾角、作为行驶工况辨识传感器信号来源,当某一传感器的值存在较大误差时,会影响辨识结果的准确,而通过对多传感器特征值进行融合和分析,则可以提升系统的辨识准确性。因此文中提出了基于D-S证据理论的决策层融合方法实现对全地形车行驶工况的识别,其框架如图 2所示,首先对不同行驶工况下进行传感器信号的采集与预处理、提取特征信息与融合识别,然后将识别结果当作证据源,对每个证据源进行基本信任分配函数(basic probability assignment, BPA)、似然函数(plausibility function, Pl)和信任函数(belief function, Bel)的赋值。采用D-S合成规则计算后得到新的基本信任分配函数,最后基于可行区间的决策规则实现了车辆行驶工况的决策判定。
|
图 2 全地形车行驶工况辨识总体框图 Fig. 2 Overall block diagram of ATV driving condition identification |
由于传感器的数量和特征值较多,文中选用改进的距离评估方法对行驶工况相关的显著特征值进行选取,获取与行驶工况相关相关性最优的特征值。首先对传感器信号进行时域统计特征参数进行分析,如表 1所示,其中x(n)是对应的传感器信号,(f1, f3-f5)和(f2, f6-f11)分别表示传感器信号在时域上的振动幅值和能量,以及分布时间序列。
| 表 1 传感器信号时域统计特征 Table 1 Time domain statistical characteristics of sensor signal |
在列举了传感器的不同的时域特征参数后,使用改进的距离评估方法进行特征值选取,其步骤为:
首先假设C类特征集可表示为
| $ \left\{q_{m, c, j}, m=1, 2, \cdots M_{c} ; c=1, 2, \cdots C ; j=1, 2, \cdots J\right\}, $ | (1) |
式中:qm, c, j表示C类特征集中的第J个特征对应的第m个样本;Mc表示所有的样本数;J表示样本的特征值。
通过计算同类样本的平均距离,得出平均距离dj(w)
| $ \begin{array}{l} {d_{c, j}} = \frac{1}{{{M_c}\left( {{M_c} - 1} \right)}}\sum\limits_{l, m = 1}^{{M_c}} {\left| {{q_{m, c, j}} - {q_{l, c, j}}} \right|} , l, m = 1, 2, \cdots , {M_c}, l \ne m, \\ {d_j}^{(w)} = \frac{1}{C}\sum\limits_{c = 1}^c {{d_{c, j}}} 。\end{array} $ | (2) |
计算平均距离dj(w)的方差因子
| $ v_{j}^{(w)}=\frac{\max \left(d_{c, j}\right)}{\min \left(d_{c, j}\right)} 。$ | (3) |
计算同类所有样本的平均特征值
| $ u_{c, j}=\frac{1}{M_{c}} \sum\limits_{m=1}^{M_{c}} q_{m, c, j}。$ | (4) |
得到不同类之间的平均距离dj(b)
| $ d_{j}^{(b)}=\frac{1}{C(C-1)} \sum\limits_{c, e=1}^{C}\left|u_{e, j}-u_{c, j}\right|, c, e=1, 2, \cdots, C, c \neq e 。$ | (5) |
定义和计算dj(b)的方差因子为
| $ v_{j}^{(b)}=\frac{\max \left(\left|u_{e, j}-u_{c, j}\right|\right)}{\min \left(\left|u_{e, j}-u_{c, j}\right|\right)} \quad c, e=1, 2, \cdots, C, c \neq e 。$ | (6) |
定义和计算补偿因子为
| $ \lambda_{j}=\frac{1}{\left(v_{j}^{(w)} / \max \left(v_{j}^{(w)}\right)+v_{j}^{(b)} / \max \left(v_{j}^{(b)}\right)\right)}。$ | (7) |
计算dj(b)和dj(w)的比率,修正补偿因子为
| $ \alpha_{j}=\lambda_{j} \frac{d_{j}^{(b)}}{d_{j}^{(w)}}, $ | (8) |
进行归一化处理为
| $ {{\bar \alpha }_j} = \frac{{{\alpha _j}}}{{\max \left( {{\alpha _j}} \right)}} 。$ | (9) |
根据式(9)中距离评估准则αj的值越大,这说明所选择的传感器特征值越能辨识出对应的行驶工况。
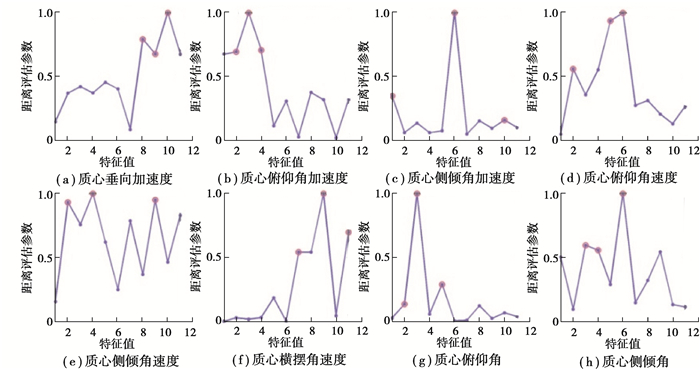
2.2 传感器特征值筛选与信息融合通过使用上述的改进的距离评估方法对全地形车上车身质心处的垂直加速度Zs,俯仰角φ,侧倾角θ,横摆角ψ信号的不同时域特征值进行了提取和筛选。结果如图 3所示,其中与车辆行驶工况敏感度最大的传感器特征值用红圈标出。
|
图 3 特定行驶工况下传感器敏感特征值的选取 Fig. 3 The selection of sensor sensitive characteristic values under specific driving conditions |
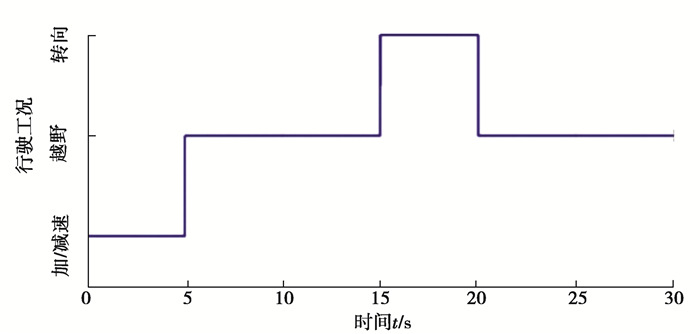
通过改进的距离评估方法对全地形车上的传感器行驶工况的敏感特征值进行了提取,为了实现对车辆特定行驶工况下的识别,需要对选择的传感器信号和对应特征值进行进一步的筛选。为了模拟车辆的行驶工况,选择Carsim仿真平台对全地形车的行驶工况进行仿真实验。验证车辆在转弯、越野道路行驶和加减速的情况下不同传感器的敏感特征值对特定行驶工况的敏感程度。通过对采集的信号进行分析选择特定行驶工况下的传感器特征值。其中Carsim仿真平台实验设定如图 4所示,在0~5 s车辆进行加减速操作,5~15 s表示车辆行驶在越野道路,15~20 s表示车辆进行转向,然后车辆又恢复越野道路行驶工况。通过仿真实验实时采集车辆行驶中的传感器的特征值,其结果如图 5所示。
|
图 4 Carsim仿真工况设置 Fig. 4 Carsim simulation condition setting |
|
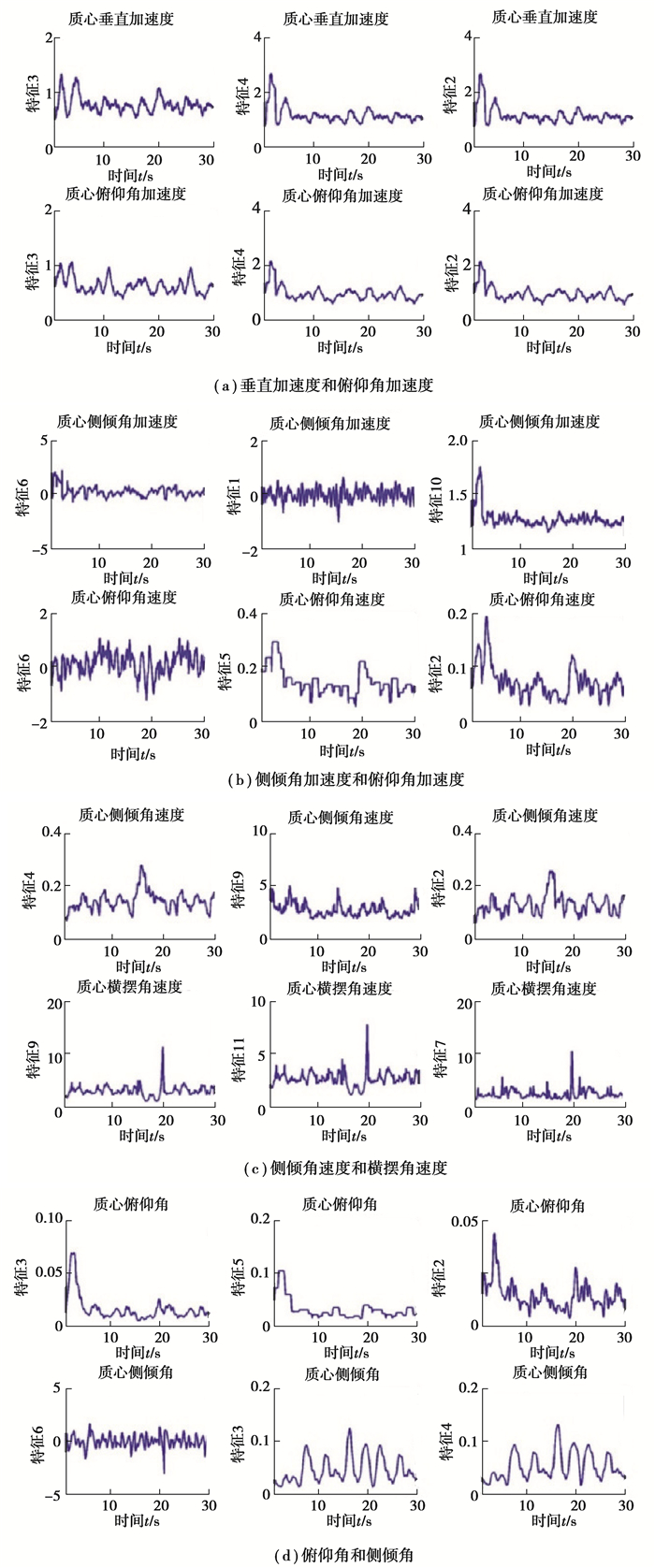
图 5 不同传感器参数的时域统计特性 Fig. 5 Sensitivity of different sensor parameters to driving conditions |
从图 5(a)可以看出, 当车辆处于加减速行驶工况下,车辆质心处的俯仰角和垂直加速度的特征值均能识别,因此选择垂直加速度与俯仰角加速度的方差和方根幅值作为此工况的辨识参数;从图 5(c)中可以得出, 当车辆处于转向行驶中,横摆角速度的峰值可以较好地反映出车辆的行驶工况。由于车辆在越野道路行驶特征不明显,因此结合前2种行驶工况的识别,选择的传感器信号特征值如表 2所示。
| 表 2 越野道路直线行驶工况选择的传感器参数 Table 2 Sensor parameters selected for straight road driving on off-road |
D-S证据理论不需要知道先验概率,能够很好地表示“不确定”,被广泛用来处理不确定数据。其最大的特点就是对不确定性信息的描述采用“区间估计”,在区分不知道和不确定方面以及精确反映证据收集方面显示出很大的灵活性,其定义为:
Θ={θ1, θ2, …, θN}为辨识系统的识别框架,其中θi表示识别对象所有存在的可能子集组成,2Θ为Θ的幂集:
| $ 2^{\Theta}=\left\{\varnothing, \left\{\theta_{1}\right\}, \left\{\theta_{2}\right\}, \cdots\left\{\theta_{N}\right\}, \left\{\theta_{1} \cup \theta_{2}\right\}, \left\{\theta_{1} \cup \theta_{3}\right\}, \cdots, \Theta\right\}, $ | (10) |
式中:Ø代表空集;Θ为全集;θi∪…∪θj, i, j∈[1, n]且i≠j,表示子元素的并集。因此文中根据车辆不同的行驶工况,首先制定了辨识系统的识别框架Θ={A, B, C, D}。A表示车辆处于其他行驶工况,B表示车辆处于直线越野路面行驶,C表示车辆进行转弯操作,D表示车辆进行加减速动。
对于定义的Θ,BPA是Θ的所有的子集到[0, 1]之间的函数映射,即m: 2Θ→[0, 1],该函数映射满足:
| $ \left\{ \begin{array}{l} m\left( \emptyset \right) = 0,\\ \sum\limits_{A \subset \Theta } {m\left( A \right) = 1} 。\end{array} \right. $ | (11) |
BPA函数表征的是初期证据建立的信任度,而Bel函数则表征的是每个命题为真的信任度,可表示为Bel函数(B(·))。B: 2Θ→0, 1,则子命题A的B函数定义为所有满足B⊆A的集合B的BPA函数的和,即
| $ B(A)=\sum\limits_{B \subseteq A} m(B)_{\circ} $ | (12) |
若
当集合Θ中的某一子集A是否成立存在不确定性时,通过似然函数P(·)表达其信任度。其似然函数P(A)为命题A为真和疑似为真的信任程度,即
| $ P(A)=1-B(\bar{A})=\sum\limits_{B \cap A \neq \varnothing} m(B), $ | (13) |
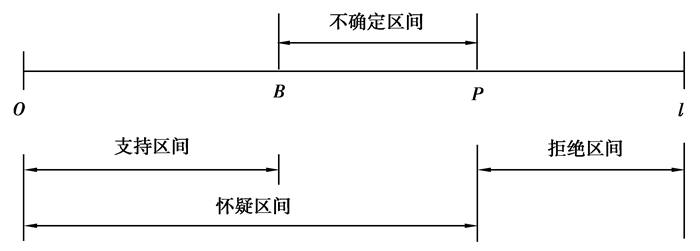
其中B(A)表示命题A为假的信任程度。P(A)和B(A)分别为对命题A信任度的上下限,可表达为B(A), P(A),同时采用P(A)-B(A)表示对A的不确定区间,如图 6所示。
|
图 6 不确定性区间信息划分 Fig. 6 Uncertainty interval information division |
D-S合成规则通过正交和运算对多个BPA函数进行合成,并得到合成后的概率分配函数。当存在多个证据E1, E1, …, En时,其对应焦元的BPA函数分别表示为m1(Ai)和m2(Bj),利用正交和算
| $ \begin{array}{c} m(A) = {m_1} \oplus {m_2} \oplus \cdots {m_n} = \left\{ {\begin{array}{*{20}{c}} {\frac{{\sum\limits_{{A_1} \cap {A_2} \cap \cdots {A_n} = A} {{m_1}} \left( {{A_1}} \right){m_2}\left( {{A_2}} \right) \cdots {m_n}\left( {{A_n}} \right)}}{{1 - K}}}&{A \ne \emptyset , }\\ 0&{A = \emptyset , } \end{array}} \right.\\ K = \sum\limits_{{A_1} \cap {A_2} \cap \cdots {A_n} = \emptyset } {{m_1}} \left( {{A_1}} \right){m_2}\left( {{A_2}} \right) \cdots {m_n}\left( {{A_n}} \right) < 1, \end{array} $ | (14) |
式中,K为各个证据之间的冲突因子,其大小与各个证据之间的冲突程度正相关。
通过D-S规则将各个证据源合成后,需要进行决策辨识,文中利用可行性区间作为决策规则进行辨识,因此定义可用性函数u(B)将信任区间修正为可用性区间,得到其上限和下限分别为:
| $ \begin{aligned} &E^{*}(B)=\sum\limits_{B \cap A \neq \varnothing} u(A) B(A), \\ &E_{*}(B)=\sum\limits_{B \subseteq A \subseteq \Theta} u(A) B(A)。\end{aligned} $ | (15) |
则在B⊆Θ的情况下,平均可用性为
| $ E(B)=E_{*}(B)+\rho\left[E^{*}(B)-E_{*}(B)\right] \text {, } $ | (16) |
式中,ρ为概率估计。对于命题Ai⊆Θ的可用性为
| $ u\left( {{A_i}} \right) = \sum\nolimits_{j = 1}^n {{c_j}{n_j}}。$ | (17) |
nj表示包含命题Ai的命题数,系数cj=1/(10j),当目标较多时,整个的可用性为
| $ u(A) = \mathop {\max }\limits_{{A_j} \in A} u\left( {{A_j}} \right), $ | (18) |
其中平均可用性最大的命题Aj定义为最终的识别结果。
文中对来自特征级融合后识别结果当作D-S证据理论合成的证据源E1, E2, E3,通过每一个证据识别结果的正确的错误时间和正确时间长度确定其BPA函数。在假设车辆质心处的横摆角速度传感器信号值存在较大噪声和异常的情况下,每个证据的BPA函数如表 3所示,最后通过对应的决策层和D-S合成规则辨识出全地形车特定的行驶工况。
| 表 3 证据源E1, E2, E3的概率密度函数 Table 3 Probability density function of evidence source E1, E2, E3 |
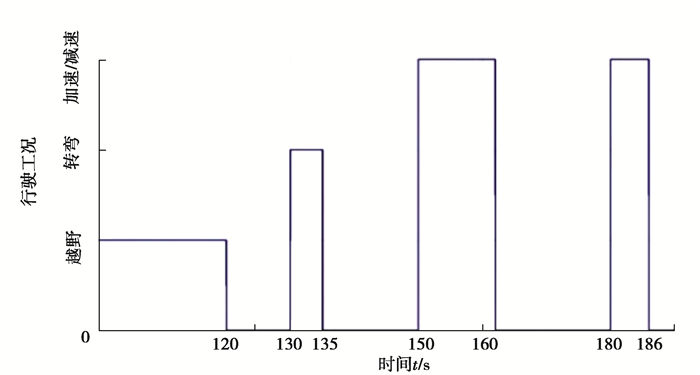
为了验证基于D-S证据理论的辨识方法的准确性,如图 7所示在Carsim仿真软件中设定了全地形车不同的行驶工况。
|
图 7 行驶工况 Fig. 7 Driving conditions |
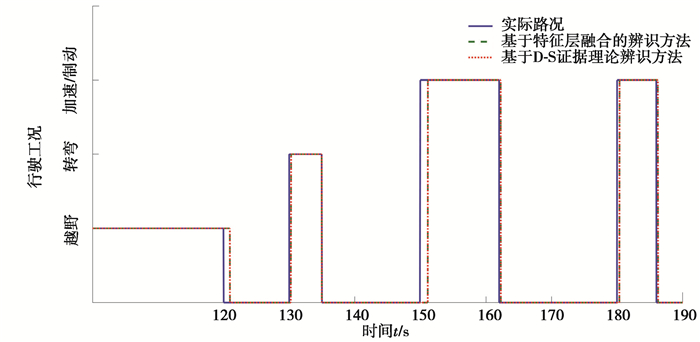
仿真设计当传感器信号获取精确时,分别采用特征级融合和D-S证据理论融合的辨识结果如图 8所示。两者均能实现对全地形车行驶工况的准确辨识。并没有出现误判的现象。行驶工况辨识的结果与所选特征传感器和特征值有很大的关系,因需要对传感器信号特征值进行提取和计算,所以2种辨识方法会存在一定的延时。根据图 8可知,对越野段和加速段的辨识时间在1.3 s左右,对减速段的辨识时间在0.7 s左右,对转弯的辨识时间在0.2 s左右,延迟时间差异与选择的信号特征值有关。
|
图 8 横摆角速度信号正确时不同方法的辨识结果 Fig. 8 Identification results of different methods when yaw velocity signal is correct |
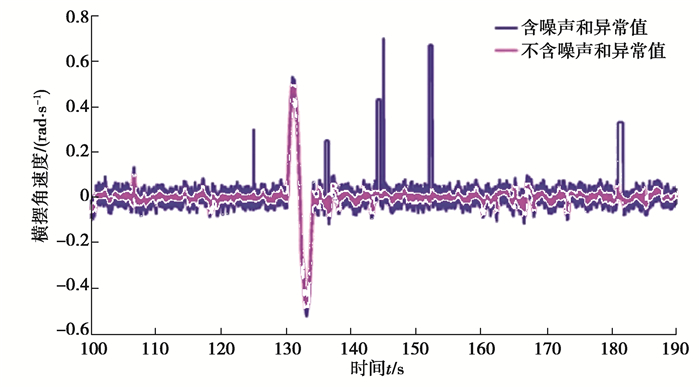
为了更好地模拟车辆的实际行驶环境,如图 9所示,在仿真中给车辆的横摆角速度信号加入了噪声和异常值,即仿真中
|
图 9 横摆角速度原始信号和加入噪声和异常值后的时域信号 Fig. 9 Yaw velocity original signal and time domain signal after adding noise and outliers |
|
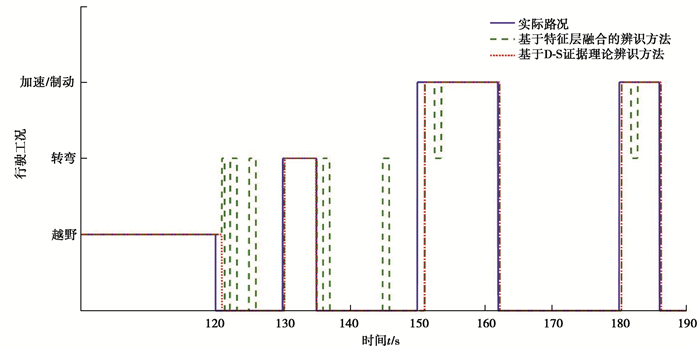
图 10 加入噪声和异常之后不同方法的辨识结果 Fig. 10 Identification results of different methods after adding noise and anomaly |
针对由单一传感器信号对全地形车车辆行驶工况辨识困难和传感器信号存在较大误差影响辨识结果的问题,文章通过改进的距离评估方法对全地形车上的传感器行驶工况的敏感特征值进行了提取和筛选。使用特征级融合方法对选取的传感器的特征值进行了融合,完成了对行驶工况的初步辨识。将传感器信号的噪声和异常值当做不确定性信息,使用D-S证据理论合成方法对来自特征级融合后识别结果进行最高级别的决策层融合。最后基于可行区间的决策规则实现了车辆行驶工况的准确辨识。在Carsim中完成了对全地形车的越野,转弯,加减速行驶工况辨识仿真实验。实验结果表明:当处于传感器信号在理想状态下,特征层融合辨识和基于D-S证据理论的决策层融合辨识均能实现全地形车行驶工况的正确辨识,但是对信号加入噪声和异常值后,特征层融合辨识会出现辨识错误的现象,而基于D-S证据理论的决策层融合方法可以保证正确的辨识结果,说明了其具有较高的辨识精度。
| [1] |
Bouton N, Lenain R, Thuilot B, et al. An active anti-rollover device based on Predictive functional control: application to an all-terrain vehicle[M]. Japan: Kobe International Conference Center Kobe, 2009: 1309-1314.
|
| [2] |
Bouton N, Lenain R, Thuilot B, et al. A rollover indicator based on the prediction of the load transfer in presence of sliding: application to an all-terrain vehicle[M]. Roma, Italy, 2007.
|
| [3] |
Du X M, Yu M, Fu J, et al. Experimental study on shock control of a vehicle semi-active suspension with magneto-rheological damper[J]. Smart Materials and Structures, 2020, 29(7): 074002. DOI:10.1088/1361-665X/ab859e |
| [4] |
Yang J, Ning D, Sun S S, et al. A semi-active suspension using a magnetorheological damper with nonlinear negative-stiffness component[J]. Mechanical Systems and Signal Processing, 2021, 147: 107071. DOI:10.1016/j.ymssp.2020.107071 |
| [5] |
Du X M, Yu M, Fu J, et al. H∞ control for a semi-active scissors linkage seat suspension with magnetorheological damper[J]. Journal of Intelligent Material Systems and Structures, 2019, 30(5): 708-721. DOI:10.1177/1045389X18778340 |
| [6] |
Bhardawaj S, Sharma R C, Sharma S K. Development of multibody dynamical using MR damper based semi-active bio-inspired chaotic fruit fly and fuzzy logic hybrid suspension control for rail vehicle system[J]. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-Body Dynamics, 2020, 234(4): 723-744. DOI:10.1177/1464419320953685 |
| [7] |
董小瑞, 武雅文, 张志文, 等. 基于遗传算法和支持向量机的汽车行驶工况识别[J]. 车用发动机, 2021(2): 13-17. Dong X R, Wu Y W, Zhang Z W, et al. Recognition of vehicle driving conditions based on genetic algorithm and support vector machine[J]. Vehicle Engine, 2021(2): 13-17. (in Chinese) |
| [8] |
姬晓飞, 石宇辰, 王昱, 等. D-S理论多分类器融合的光学遥感图像多目标识别[J]. 电子测量与仪器学报, 2020, 34(5): 127-132. Ji X F, Shi Y C, Wang Y, et al. D-S theory based multi-classifier fusion optical remote sensing image target recognition[J]. Journal of Electronic Measurement and Instrumentation, 2020, 34(5): 127-132. (in Chinese) |
| [9] |
Zhao G Z, Chen A G, Lu G X, et al. Data fusion algorithm based on fuzzy sets and D-S theory of evidence[J]. Tsinghua Science and Technology, 2019, 25(1): 12-19. DOI:10.26599/TST.2018.9010138 |
| [10] |
Jusoh S, Almajali S. A systematic review on fusion techniques and approaches used in applications[J]. IEEE Access, 2020, 8: 14424-14439. DOI:10.1109/ACCESS.2020.2966400 |
| [11] |
Rassafi A A, Ganji S S, Pourkhani H. Road safety assessment under uncertainty using a multi attribute decision analysis based on dempster-shafer theory[J]. KSCE Journal of Civil Engineering, 2018, 22(8): 3137-3152. DOI:10.1007/s12205-017-1854-5 |
| [12] |
Luo L X. Information fusion for wireless sensor network based on mass deep auto-encoder learning and adaptive weighted D-S evidence synthesis[J]. Journal of Ambient Intelligence and Humanized Computing, 2020, 11(2): 519-526. DOI:10.1007/s12652-018-0999-5 |
| [13] |
段中兴, 毕瀚元, 张作伟. 基于D-S证据理论的不完整数据混合分类算法[J]. 信息与控制, 2020, 49(4): 455-463, 471. Duan Z X, Bi H Y, Zhang Z W. A D-S evidence reasoning based hybrid classification algorithm for incomplete data[J]. Information and Control, 2020, 49(4): 455-463, 471. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45


