2. 重庆大学 a.光电工程学院; b.光电技术与系统教育部重点实验室, 重庆 400044;
3. 陆军装备部驻重庆地区第六军事代表室, 重庆 400000
2. College of Optoelectronic Engineering; 2b. Key Laboratory of Optoelectronic Technology and System of Ministry of Education, Chongqing University, Chongqing 400044, P. R. China;
3. The Sixth Military Representative Office of the Army Equipment Department in Chongqing 400000, Chongqing, P. R. China
磁流变阻尼器作为一种阻尼可调的半主动智能减振器件,可以通过控制外加磁场的大小来实现阻尼力的实时动态调节,具有结构简单、可调阻尼力范围宽、响应时间快、可靠性高和能耗低等优点,在军事、航空、建筑等领域,尤其在汽车磁流变悬架中具有广泛应用前景[1-4]。
在实时控制中,磁流变阻尼器的逆模型将控制器计算出的阻尼力转化为控制电流,其模型精度将直接影响控制性能[5-6]。阻尼器建模方法主要分为参数化建模和非参数化建模2种。参数化建模一般是基于弹簧和粘壶的本构模型的组合,常见的有Kelvin模型、Koh-Kelly模型、Bouc-wen模型和Dahl模型等[7-9],可以准确反映磁流变阻尼器的滞回特性,但需辨识的参数多,无法通过求逆获得阻尼器的逆向模型,难以在实际控制系统中应用。非参数化模型是基于实验测试数据,直接记录或分析系统输入输出信号的系统估计方法,无需假设模型结构,灵活性强。常采用的非参数化模型有多项式模型、神经网络模型和模糊系统等模型。祝世兴等[10]采用多项式模型对阻尼器进行建模时,为达到设定的模型精度,发现模型参数较多,阶数选择较为复杂,不利于实际的控制应用。廖英英等[11]采用BP神经网络建立了阻尼器的逆模型,仿真结果表明,其逆模型可以准确地预测所需电流指令,但学习速率慢、容易陷入局部极小。而T-S模糊推理建模方法由Takagi等[12]提出,可以逼近任意的非线性函数,辨识参数较少,模型结构简单,更易于工程控制的实现,已用于磁流变阻尼器的建模中。T-S模糊模型的参数辨识准确性对模型精度会有重要的影响,而常见的参数辨识方法有神经网络、遗传算法、聚类等。姜康等[13]采用自适应神经模糊推理模型来逼近磁流变阻尼器的逆模型,所设计系统能较准确逼近实验结果,但参数辨识时使用基于梯度下降的神经模糊优化技术容易陷入局部最优、泛化能力差。Du等[14]采用基于进化算法的T-S模糊推理模型对磁流变阻尼器进行逆向建模,仿真结果表明,逆向模型能较准确地计算出不同输出阻尼力所对应的激励电流,但进化算法辨识参数需要对数据进行大量的训练,导致计算时间长、代价高。常规的聚类法虽然简单且速度快,但存在投影误差和拟合误差,导致模型精度降低,影响控制精度。改进的Gath-Geva聚类法[15]能同时辨识出T-S模型的局部模型和先验部分,通过后续排序和删除无信息的前因变量和后继变量获得准确的模型,具有辨识参数少、建模精度高的优点。文中基于改进的Gath-Geva聚类法的模糊T-S模型,建立磁流变阻尼器的逆向模型。搭建了MTS测试系统,使用MTS测试了不同工况下流变阻尼器的力学性能,获得了阻尼器的力位移曲线,并进行分析。基于改进Gath-Geva聚类算法建立了磁流变阻尼器的T-S模糊推理逆模型。使用建立的T-S模糊推理逆模型对输出电流进行预测,并将预测结果与实测数据进行了比较,验证了模型的准确性。
1 磁流变阻尼器力学性能测试为了采用T-S模糊方法建立磁流变阻尼器的逆向模型,需要通过力学性能测试获得建模数据。通过MTS试验系统测试了磁流变阻尼器在不同工况下的力学性能,获得了磁流变阻尼器的力位移曲线,并对测试结果进行了分析。
1.1 测试系统搭建磁流变阻尼器力学性能测试装置如图 1所示,主要包含MTS、力传感器、磁流变阻尼器、直流电源、数据采集系统。测试时,磁流变阻尼器在MTS激振平台正弦位移激励的作用下往复运动,同时电源(WYK-603型,EASRT)给磁流变阻尼器施加不同大小的激励电流,整个过程中通过数据采集系统(MDR-80V5-D1型,北京航天南华公司)对力传感器(CYB-601S型, 北京威斯特中航机电技术有限公司)测得的磁流变阻尼器的阻尼力值进行实时采集。通过给MTS激振平台设置不同频率的正弦位移激励,可测得不同频率电流和不同频率位移激励下磁流变阻尼器的输出力值。
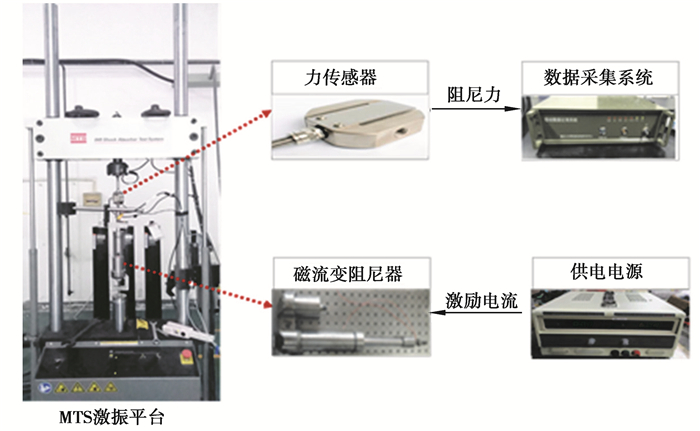
|
图 1 磁流变阻尼器力学特性测试装置图 Fig. 1 Diagram of testing device for mechanical properties of MR damper |
测试时分别采用恒定电流和正弦电流作为激励:通过测试恒定控制电流下的阻尼力变化,验证阻尼器的磁控性能,其中,MTS激励位移幅值为0.05、0.1 m,激励速度幅值分别为0.1、0.3、0.6 m/s,频率范围包含1、2、3、6、12 Hz,分别对应车辆在行驶过程中的低速、中速和高速3种不同的工况,磁流变阻尼器的激励电流为0.0、0.4、0.8、1.2、1.6、2.0、3.0 A;采用时变的正弦电流,目的是模拟实际阻尼器的运行情况,为后面建立阻尼器逆模型提供试验数据,设置幅值为0.05 m、频率为2 Hz的正弦位移信号,以及幅值为2 A、频率为2 Hz的正弦电流信号。
1.2 测试结果分析通过MTS对磁流变阻尼器的力学性能进行测试,得到不同恒定电流、不同速度下的磁流变阻尼器的测试结果,如图 2和图 3所示。由图可知,磁流变阻尼器的压缩力和复原力大小基本一致,符合设计时的对称结构。随着激励速度从0.1 m/s增加至0.6 m/s,压缩力和复原力也在不断增加。同时,随着电流的增大,磁流变阻尼器的力值也相应增大,当电流大于1 A时,由于导磁颗粒磁致饱和的原因,力值的增长率变缓。可以发现,激励速度的变化对阻尼力的影响要小于激励电流对阻尼力的影响。考虑到车辆通常保持中速行驶,高速下阻尼器的示功曲线存在一定的畸变,文中选择的是0.3 m/s的运动速度,以及0.05 m的行程进行分析。通过计算得到磁流变阻尼器在该工况下的压缩阻尼力的可调阻尼比为4.2,复原阻尼力的可调阻尼比为2.97,验证了所设计的阻尼器具有较宽的阻尼力调节范围。
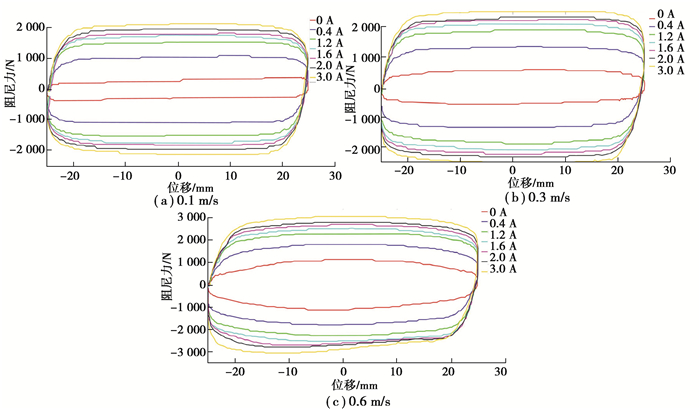
|
图 2 激励位移50 mm,不同激励速度下的磁流变阻尼器(前左)力位移曲线图 Fig. 2 Excitation displacement 50 mm, MR damper (front left) force-displacement curve at different excitation speeds |
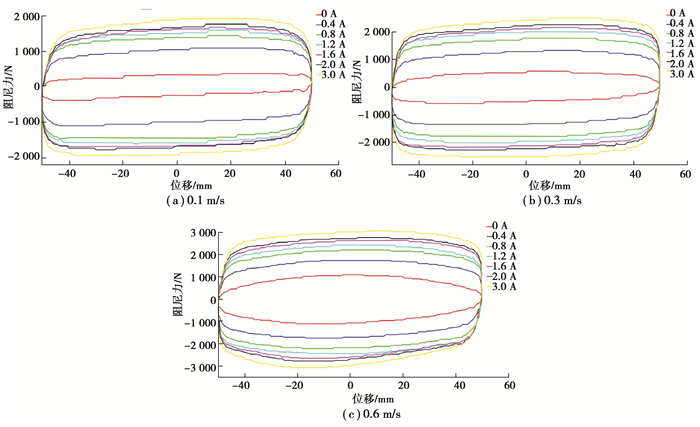
|
图 3 激励位移100 mm,不同激励速度下的磁流变阻尼器(前左)力-位移曲线图 Fig. 3 Excitation displacement 100 mm, MR damper (front left) force-displacement curve at different excitation speeds |
正弦激励电流下的磁流变阻尼器测试结果,如图 4所示。由于阻尼器在交变电流下的力位移特性与直流情况下类似,此处仅给出磁流变阻尼器的位移、速度、电流、力的样本数据。与直流激励下的测试结果不同之处在于,交变电流下的电流和位移存在相位差,使得图 4(d)中的阻尼器的力非正弦信号。
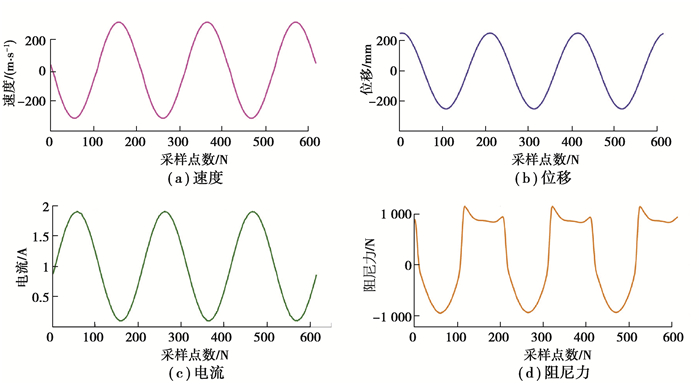
|
图 4 正弦电流激励下磁流变阻尼器的位移、速度、电流、力值样本数据 Fig. 4 Sample data of displacement, velocity, current and force of MR damper excited by sinusoidal current |
通过实验发现,阻尼器在实时控制中的驱动电流为交变电流,为了使模型能更加贴合实际工况,文中采用交流激励下测试所得的数据对阻尼器进行建模。
2 模型建立基于实验数据,采用T-S模糊建模方法建立磁流变阻尼器的逆向模型,并通过改进Gath-Geva聚类算法对参数进行辨识。
T-S型模糊模型为
| $ \begin{array}{c} {R_i}:{\rm{if}}\;{x_{1, k}}\;{\rm{is}}\;{A_{i1}}\;{\rm{and}}\;{x_{2, k}}\;{\rm{is}}\;{A_{i2}}\;{\rm{and}}\;{x_{3, k}}\;{\rm{is}}\;{A_{i3}}, \\ {\rm{then}}\;y_k^i = a_i^{\rm{T}}{X_k} + {b_i} = {p_{i0}} + {p_{i1}}{x_{1, k}} + {p_{i2}}{x_{2, k}} + {p_{i3}}{x_{3, k}}, \end{array} $ | (1) |
其中:Ri表示第i条模糊规则,i=1, 2, …c,c为规则库中的模糊规则数目;xj, k∈Rr (j=1, 2, 3)是系统k时刻的输入变量,即阻尼器的相对运动位移(x1, k)、相对运动速度(x2, k)以及输出阻尼力(x3, k);yki表示第i条规则k时刻的输出,Aij表示输入论域模糊子集,用隶属度函数表示ωiAij(xj), 并且ωi∈[0, 1]表示规则的期望影响的规则权重,其函数参数称为前件前提参数;Pi=(pi0, pi1, pi2, pi3)则为后件结论参数。
其中,规则的隶属度函数为
| $ {\beta _i}\left( {{X_k}} \right) = {\omega _i}{A_i}\left( {{X_k}} \right) = {\omega _i}\prod\limits_{j = 1}^3 {{A_{i, j}}} \left( {{x_{j, k}}} \right) = {\omega _i}\exp \left( { - \frac{1}{2}{{\left( {{X_k} - v_{ij}^x} \right)}^{\rm{T}}}\left( {{H_i}} \right) - 1\left( {{X_k} - v_i^x} \right)} \right), $ | (2) |
得到模糊输出为
| $ y_{k}=\frac{\sum\nolimits_{i=1}^{c} \beta_{i}\left(X_{k}\right) g_{i}}{\sum\nolimits_{i=1}^{c} \beta_{i}\left(X_{k}\right)}, $ | (3) |
以上需要辨识的参数为Θ=[vi, Hi, Pi]。
将实测数据代入模型中,采用改进Gath-Geva聚类原理对以上的隶属度函数中心值νi, 隶属度函数方差矩阵Hi,以及后件参数Pi进行辨识。聚类目标是最小化采样点和聚类原型η的加权平均距离,用隶属度值μi, k作为Di, k2的加权系数。目标函数为
| $ J(Z, \boldsymbol{U}, \eta)=\sum\limits_{i=1}^{c} \sum\limits_{k=1}^{N}\left(\mu_{i, k}\right) D_{i, k}^{2}, $ | (4) |
其中:Z为输入输出数据;U为隶属度矩阵;η为聚类原型参数。同时,为了得到模糊划分空间,隶属度函数必须满足以下条件:
| $ U \in^{c \times N} \mid \mu_{i, k} \in[0, 1], \forall i, k \quad \sum\limits_{i=1}^{c} \mu_{i, k}=1, \forall k \quad 0 <\sum\limits_{k=1}^{N} \mu_{i, k}<N, \forall i 。$ | (5) |
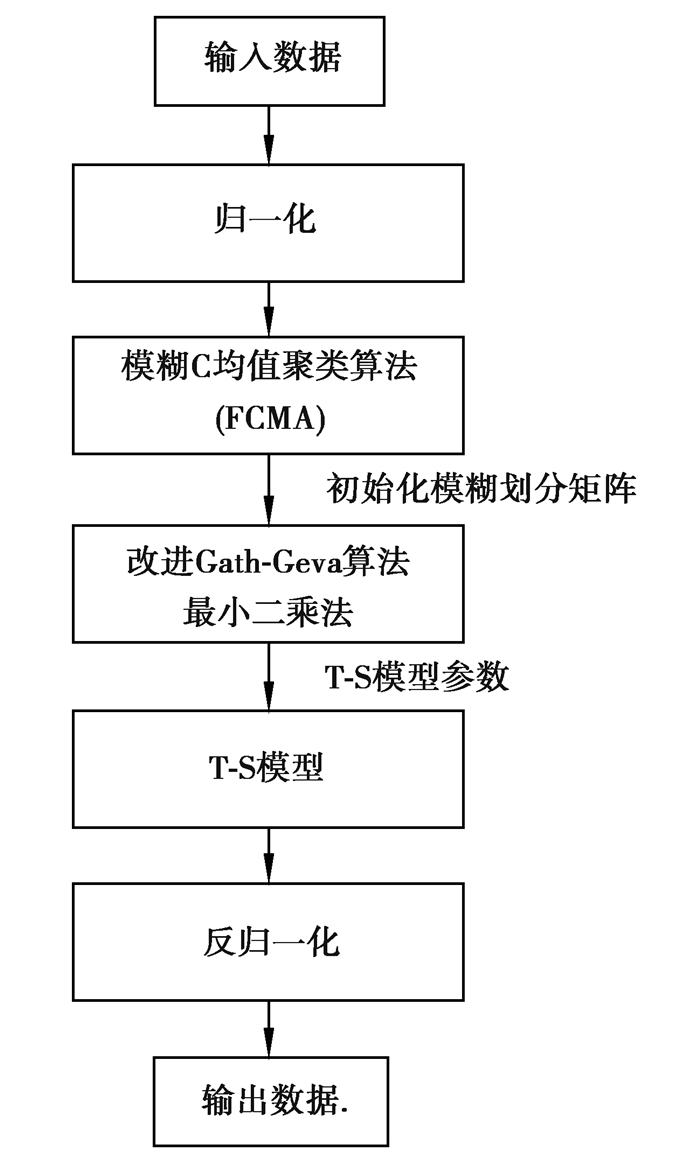
整个模型建立的流程如图 5所示。
|
图 5 基于改进Gath-Geva聚类方法的T-S模糊模型流程图 Fig. 5 T-S fuzzy model flow chart based on improved Gath-Geva clustering method |
基于改进Gath-Geva聚类算法的具体辨识步骤为:
步骤1:初始化
给定簇类数目c,加权因子m,终止误差ε,初始化模糊划分矩阵U=[μi, k]c×N。
步骤2:计算聚类参数
计算聚类的中心和协方差:
| $ v_{i}^{(l)}=\frac{\sum\nolimits_{k=1}^{N} \mu_{i, k}^{l-1} x_{k}}{\sum\nolimits_{k=1}^{N} \mu_{i, k}^{l-1}}, \sigma_{i, j}^{2(l)}=\frac{\sum\nolimits_{k=1}^{N} \mu_{i, k}^{l-1}\left(x_{j, k}-v_{j, k}\right)^{2}}{\sum\nolimits_{k=1}^{N} \mu_{i, k}^{l-1}}, 1 \leqslant i \leqslant c 。$ | (6) |
局部模型的后件参数:
| $ {\theta _i} = \left( {\Phi _e^{\rm{T}}{\beta _i}{\Phi _e}} \right) - 1\Phi _e^{\rm{T}}{\beta _i}y 。$ | (7) |
模型误差:
| $ \sigma _i^2 = \frac{{\sum\nolimits_{k = 1}^N {{{\left( {{y_k} - {f_i}\left( {{X_k}, {\theta _i}} \right)} \right)}^{\rm{T}}}} \left( {{y_k} - {f_i}\left( {{X_k}, {\theta _i}} \right)} \right)\mu _{i, k}^{l - 1}}}{{\sum\nolimits_{k = 1}^N {\mu _{i, k}^{l - 1}} }} 。$ | (8) |
簇的先验概率以及规则的加权因子:
| $ p\left( {{\eta _i}} \right) = \frac{1}{N}\sum\limits_{k = 1}^N {{\mu _{i, k}}} , {\omega _i} = p\left( {{\eta _i}} \right)\prod\limits_{j = 1}^n {\frac{1}{{\sqrt {2\pi \sigma _{i, j}^2} }}}。$ | (9) |
步骤3:计算测量距离
| $ \frac{1}{{D_{i, k}^2\left( {{z_k}, {\eta _i}} \right)}} = {\omega _i}\prod\limits_{j = 1}^n {\exp } \left( { - \frac{1}{2}\frac{{{{\left( {{x_{j, k}} - {v_{j, k}}} \right)}^2}}}{{{\sigma} _{i, j}^2}}} \right)\frac{{\exp \left( {{{\left( {y - \left[ {{\varphi _k}1} \right]\theta _i^{\rm{T}}} \right)}^{\rm{T}}}\left( {y - \left[ {{\varphi _k}1} \right]\theta _i^{\rm{T}}} \right)} \right)}}{{\sqrt {2\pi \sigma _i^2} }} 。$ | (10) |
步骤4:更新划分矩阵
| $ \mu _{i, k}^l = \frac{2}{{\sum\nolimits_{j = 1}^c {\left( {\frac{{{D_{i, k}}\left( {{z_k}, {\eta _i}} \right)}}{{{D_{j, k}}\left( {{z_k}, {\eta _j}} \right)}}} \right)2/(m - 1)} }}, 1 \leqslant i \leqslant c, 1 \leqslant k \leqslant N 。$ | (11) |
步骤5:满足终止条件U(l)-U(l-1) < ε则结束,否则跳回步骤2重新迭代。
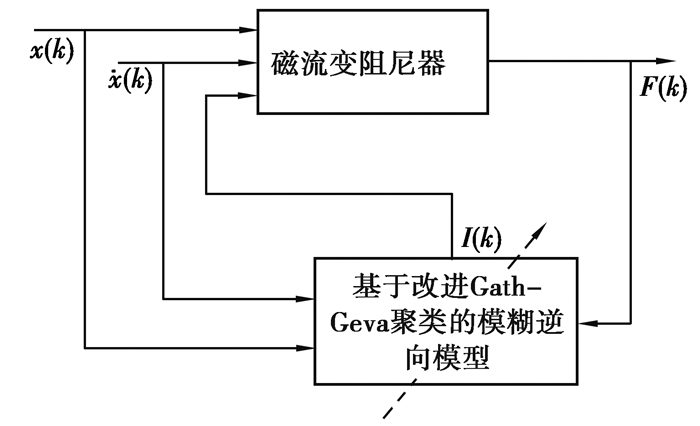
3 结果及分析基于改进Gath-Geva聚类原理的T-S模糊模型,使用实测数据通过Matlab对磁流变阻尼器的逆向模型进行参数辨识,模型框图如图 6所示。逆向模型当前时刻的输入为阻尼器的相对运动位移、速度和输出的阻尼力,输出为控制电流。为了尽可能模拟阻尼器实际运行工况,试验中70%数据作为训练数据,30%数据作为泛化数据,设定聚类中心数目c=2,加权因子m=3,终止误差ε=1×10-8,辨识得到的模型参数为
|
图 6 磁流变阻尼器逆向模型框图 Fig. 6 Block diagram of inverse model of MR damper |
隶属度函数中心 v=[-0.052 2, 1.290 7, 0.836 4;0.000 0, 0.000 0, 0.000 0],
隶属度函数方差 H=[0.126 6, 0.001 8, 0.000 2;0.996 8, 0.996 8, 0.996 8],
后件参数:
| $ P = \left[ { - 0.031\;4, - 1.010\;5, 0.035\;0, - 0.013\;9; - 0.025\;3, - 0.997\;2, - 0.002\;5, 0.000\;0} \right]。$ |
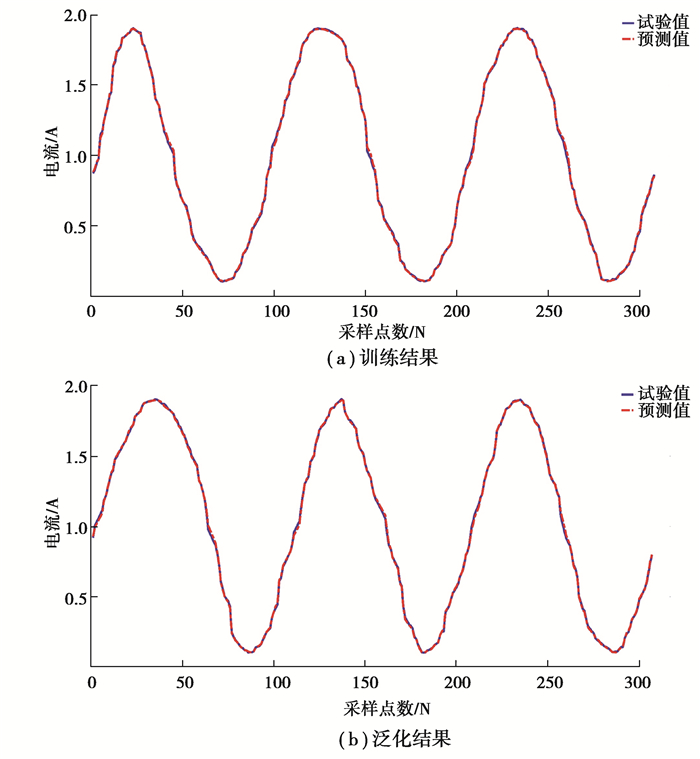
模型训练结果如图 7(a)所示,可以看出训练结果与实验测试数据具有较高的吻合度。使用剩余的30%非建模数据来对文中模型进行泛化,将非建模数据中的位移、速度和阻尼力输入建立的逆模型中,得到电流预测值,再将其与实测电流数据对比,结果如图 7(b)所示,计算预测电流值与实验电流值的均方根误差为0.008 8 A,可以看出,模型预测值与试验值吻合度很好。
|
图 7 磁流变阻尼器逆向模型电流预测结果 Fig. 7 Current prediction results of inverse model of MR dampe |
文中主要对磁流变阻尼器逆模型的建立方法进行研究,基于改进Gath-Geva聚类原理的T-S模糊理论建立了磁流变阻尼器的逆模型。通过搭建MTS测试系统,获得了阻尼器的力位移曲线,验证了磁流变阻尼器具有较好的磁控特性,其在中速工况下阻尼力调节范围达到4倍。同时,使用测试所得的70%数据作为T-S建模数据,在满足目标误差10-8的前提下,通过改进Gath-Geva聚类对模型的隶属度函数中心、隶属度函数方差和后件参数进行辨识。通过另外30%的测试数据对逆模型进行了泛化,发现输出电流的预测值与实际值的误差均方根值为0.008 8 A,所建立的磁流变阻尼器逆向模型可以较为准确地拟合其控制力、激励位移、速度和控制电流之间的非线性关系。
| [1] |
Dong X M, Yu M, Li Z S, et al. Neural network compensation of semi-active control for magneto-rheological suspension with time delay uncertainty[J]. Smart Materials and Structures, 2009, 18(1): 015014. DOI:10.1088/0964-1726/18/1/015014 |
| [2] |
林展, 覃海鹰, 王正峰. 直升机旋翼磁流变阻尼器样件仿真和试验验证[J]. 南京航空航天大学学报, 2021, 53(2): 283-290. Lin Z, Qin H Y, Wang Z F. Simulation and test verification of helicopter rotor magneto-rheological damper[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2021, 53(2): 283-290. (in Chinese) |
| [3] |
Du X M, Yu M, Fu J, et al. H∞ control for a semi-active scissors linkage seat suspension with magnetorheological damper[J]. Journal of Intelligent Material Systems and Structures, 2019, 30(5): 708-721. DOI:10.1177/1045389X18778340 |
| [4] |
Yu M, Dong X M, Choi S B, et al. Human simulated intelligent control of vehicle suspension system with MR dampers[J]. Journal of Sound and Vibration, 2009, 319(3/4/5): 753-767. |
| [5] |
Tudon-Martinez J C, Hernandez-Alcantara D, Amezquita-Brooks L, et al. Magneto-rheological dampers—model influence on the semi-active suspension performance[J]. Smart Materials and Structures, 2019, 28(10): 105030. DOI:10.1088/1361-665X/ab39f2 |
| [6] |
Jeyasenthil R, Yoon D S, Choi S B. Response time effect of magnetorheological dampers in a semi-active vehicle suspension system: performance assessment with quantitative feedback theory[J]. Smart Materials and Structures, 2019, 28(5): 054001. DOI:10.1088/1361-665X/ab0cb4 |
| [7] |
孟小杰, 于海龙, 芮筱亭, 等. 磁流变阻尼器建模及在座椅减振中应用[J]. 噪声与振动控制, 2017, 37(1): 58-62, 81. Meng X J, Yu H L, Rui X T, et al. MRD modeling and its application in seat cushioning[J]. Noise and Vibration Control, 2017, 37(1): 58-62, 81. (in Chinese) |
| [8] |
Weber F. Bouc-Wen model-based real-time force tracking scheme for MR dampers[J]. Smart Materials and Structures, 2013, 22(4): 045012. DOI:10.1088/0964-1726/22/4/045012 |
| [9] |
Zhu H T, Rui X T, Yang F F, et al. An efficient parameters identification method of normalized Bouc-Wen model for MR damper[J]. Journal of Sound and Vibration, 2019, 448: 146-158. DOI:10.1016/j.jsv.2019.02.019 |
| [10] |
祝世兴, 王璐琦, 王博. 磁流变阻尼器力学模型改进与分析[J]. 机床与液压, 2020, 48(17): 88-92, 102. Zhu S X, Wang L Q, Wang B. Improvement and analysis of mechanical model of magnetorheological damper[J]. Machine Tool & Hydraulics, 2020, 48(17): 88-92, 102. (in Chinese) DOI:10.3969/j.issn.1001-3881.2020.17.018 |
| [11] |
廖英英, 刘永强, 刘金喜. 磁流变阻尼器的神经网络建模及在半主动控制中的应用[J]. 北京交通大学学报, 2011, 35(6): 67-71. Liao Y Y, Liu Y Q, Liu J X. Neural network modeling of a magnetorheological damper and application in semi-active control[J]. Journal of Beijing Jiaotong University, 2011, 35(6): 67-71. (in Chinese) DOI:10.3969/j.issn.1673-0291.2011.06.013 |
| [12] |
Takagi T, Sugeno M. Fuzzy identification of systems and its applications to modeling and control[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1985, SMC-15(1): 116-132. DOI:10.1109/TSMC.1985.6313399 |
| [13] |
姜康, 张腾, 冯忠祥, 等. 磁流变阻尼器悬架的一种半主动控制策略[J]. 重庆交通大学学报(自然科学版), 2016, 35(6): 153-157. Jiang K, Zhang T, Feng Z X, et al. A semi-active control strategy of MR damper suspension[J]. Journal of Chongqing Jiaotong University (Natural Science), 2016, 35(6): 153-157. (in Chinese) |
| [14] |
Du H P, Zhang N. Evolutionary Takagi-sugeno fuzzy modelling for MR damper[C]//2006 Sixth International Conference on Hybrid Intelligent Systems (HIS′06). December 13-15, 2006, Rio de Janeiro, Brazil. IEEE, 2006: 69.
|
| [15] |
Liu Y Y, Zhou S L. Modified Gath-Geva Clustering based Linear T-S Fuzzy model Identification for Multi-input Multi-output Chaotic Systems. Proceedings of the 31st Chinese Control Conference, 2012: 1771-1776.
|
 2022, Vol. 45
2022, Vol. 45


