风能作为一种可再生的清洁能源是绿色能源的代表。海上风力发电是一种对风能进行有效开发利用的新技术,已成为风力发电的主流发展趋势[1-2],在全球范围受到越来越多的关注。海上风力机采用新型复合材料后比以前更大更轻,这些大型柔性结构容易受到海洋环境外部振动源影响。为了保证海上风电机组的安全运行,需要对风电机组的动力响应进行振动控制。目前,国内外学者对海上风机塔架/叶片的振动控制主要采用在海上风机塔架顶部(即机舱内)安装被动调谐质量阻尼器(TMD)[3-5],通过抑制塔顶位移最大的塔架基本振型,达到对风机塔架的减振效果,该方法适用于海上风机在风、波浪低频载荷下的振动控制,此时风机塔架的主要激发模态为塔顶位移的第一阶主振型。世界上很多已建或在建海上风电机组位于地震多发地带,在风、波浪、地震多种载荷作用下,海上风机的高阶模态振型被激发,系统呈现多个不同阶次固有频率的振动特征,若仍采用针对常规工况(风/浪载荷)设计的被动TMD对风机减振,效果会大大降低甚至造成抑振失效。
针对此类问题,有学者[6-9]提出了多重调谐质量阻尼器(MTMD),由2个或2个以上质量较小的TMD分别安装在塔筒的不同位置以应对不同的振动特性,结果表明控制效果优于单一TMD;还有学者提出半主动控制方法,通过采用智能材料驱动和自适应控制算法,衰减海上风机在多载荷激励下的振动响应,如:李静等[10]提出了磁流变阻尼器与模糊控制算法结合的半主动控制模型,应用于地震和风载荷作用的海上风机结构,结果表明,采用磁流变阻尼器能够有效减小地震和风载荷作用下的风机结构的加速度和位移响应;闫石等[11]基于形状记忆合金(SMA)的超弹性效应,设计了针对风机塔架结构的耗能减振装置,通过对比塔架位移和加速度响应证明了SMA-TMD的有效性。
文中应用一种基于磁流变弹性体的变刚度调谐质量阻尼器,开展导管架式近海风机在风、波浪和地震多种载荷联合作用下的振动控制研究。对MRE-TMD的结构设计和工作原理进行了分析,提出了针对风机减振需求的关键参数设计;建立了导管架式海上风机-TMD的动力学模型,基于频率跟踪算法,评估了MRE-TMD对海上风机动力学响应的控制效果。
1 MRE-TMD结构和工作原理 1.1 磁流变弹性体材料特性磁流变弹性体的弹性模量可以随着磁场的改变而改变,当磁场撤去后可立即恢复到初始状态。基于这种磁控特性,磁流变弹性体已广泛应用于变刚度智能吸振器及隔振器。
根据偶极子模型[12]可知,MRE中的铁磁颗粒在磁场作用下发生相对运动,导致材料剪切模量变化,磁致剪切模量为[13]
| $ \varDelta G=36 \varphi \mu_{0} \mu_{1} \beta^{2} \vec{H}_{0}^{2}\left(\frac{a}{r_{0}}\right)^{3} \zeta, $ | (1) |
式中,a是铁磁粒子半径;r0是粒子间距离;φ是铁磁颗粒体积分数;
磁流变弹性体材料在零磁场下的剪切模量Gzero为[14]
| $ G_{\text {zero }}=G_{0}\left(1+2.5 \varphi+14.1 \varphi^{2}\right), $ | (2) |
式中,G0为基体弹性模量。
MRE的有效剪切模量为
| $ \begin{gathered} G_{\mathrm{MRE}}=G_{\text {zero }}+\Delta G= \\ G_{0}\left(1+2.5 \varphi+14.1 \varphi^{2}\right)+36 \varphi \mu_{0} \mu_{1} \beta^{2} \vec{H}_{0}^{2}\left(\frac{a}{r_{0}}\right)^{3} \zeta 。\end{gathered} $ | (3) |
海上风机在风、波和地震荷载作用下,塔架结构顶部与机舱将出现明显位移,设计的MRE-TMD在机舱应承受较大的横向应变;此外,TMD与主结构的质量比一般设置在1%~8%之间[7],海上风机主结构的质量以百吨计入,意味着MRE-TMD需要提供足够的竖直承载力。为了满足OWT振动控制要求,文中采用多层MRE变刚度TMD,如图 1所示,其由MRE隔振器[15]连接质量块构成,通过顶端质量块运动提供惯性力来进行风机的振动控制。
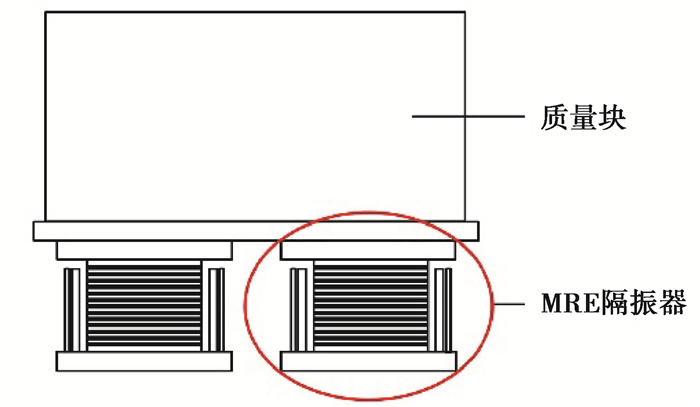
|
图 1 MRE-TMD装置 Fig. 1 MRE-TMD device |
作为MRE-TMD系统的核心部件,MRE在剪切工作模式下的刚度可表示为
| $ k_{\mathrm{MRE}-\mathrm{TMD}}=\frac{G_{\mathrm{MRE}} A}{n h}, $ | (4) |
式中:GMRE为MRE的剪切模量;A为MRE的横截面积;h为橡胶层的厚度;n为该装置中磁流变弹性体层数。
在多载荷联合激励下,海上风机主要被激发一阶和二阶主振型模态,并且模态参与比在80%以上[7]。因此,文中主要针对风机的前两阶主频,设计MRE-TMD的变频范围,[λopt·f1, λopt·f2],其中,
| $ \left\{\begin{array}{l} m_{\mathrm{MRE}-\mathrm{TMD}}=\mu m_{s} \\ f_{i}=\lambda_{\mathrm{opt}} f_{s} \\ K_{\mathrm{MRE}-\mathrm{TMD}}=m_{\mathrm{MRE}-\mathrm{TMD}}\left(2 {\rm{ \mathsf{ π} }} f_{i}\right)^{2} \\ C_{\mathrm{MRE}-\mathrm{TMD}}=4 {\rm{ \mathsf{ π} }} \zeta_{\mathrm{opt}} f_{\mathrm{MRE}-\mathrm{TMD}} m_{\mathrm{MRE}-\mathrm{TMD}} \end{array}\right. $ | (5) |
| 表 1 导管架式海上风机前两阶固有频率 Table 1 First two natural frequencies of jacket supported offshore wind turbine |
式中:μ为质量比,文中取μ=5%;fi为MRE-TMD变频范围内的频率;ζ为阻尼比。
2 海上风机MRE-TMD系统动力学建模 2.1 海上风机模型研究对象为NREL公司5MW导管架式海上风机[7-9],主要参数如表 2所示,导管架式海上风机模型如图 2所示。
| 表 2 NREL 5MW导管架式海上风机参数 Table 2 Parameters of NERL 5MW jacket supported offshore wind turbine |
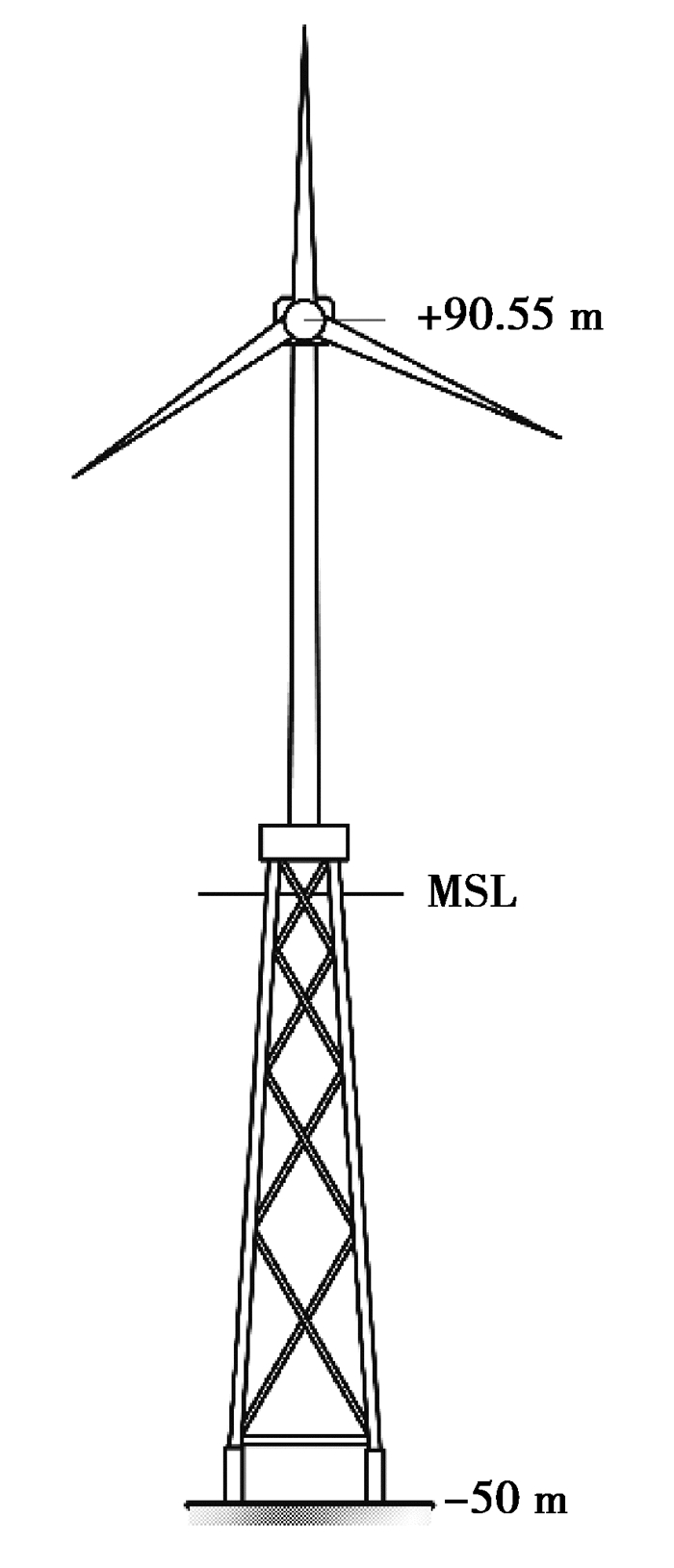
|
图 2 导管架式海上风机示意图 Fig. 2 Schematic diagram of jacket supported offshore wind turbine |
应用有限元软件ANSYS,建立NREL 5MW导管架式海上风机有限元模型。叶片和机舱简化为集中质量,单元类型为MASS21单元,塔筒采用SHELL181单元,连接塔筒和导管架基础的过渡块采用SOLID95单元,导管架结构采用PIPE59单元,泥桩结构采用PIPE16单元。建立的导管架式海上风机有限元模型如图 3所示。

|
图 3 导管架式海上风机有限元模型 Fig. 3 Finite element model of jacket supported offshore wind turbine |
海上风机工作环境复杂,受风、冰、流、波浪和地震等荷载作用。文中主要研究风载荷、波浪载荷和地震3种载荷的联合作用。
2.2.1 风载荷由于将风机模型简化为多自由度集中质量模型,只考虑作用在风机塔筒上的风载荷,不考虑风机叶片上的作用力。作用在风机塔筒上的风载荷为
| $ F_{\text {wind }}=\frac{1}{2} C_{\mathrm{d}} \rho_{\mathrm{a}} A\left(\bar{v}(t)+v^{\prime}(t)\right)^{2}, $ | (6) |
式中: Cd为空气阻力系数;ρa为空气密度;A为塔筒的迎风面积;v(t)为平均风速;v'(t)为脉动风速,采用Davenport脉动风速谱通过谐波叠加法模拟求得;仿真的风载荷工况为机舱位置平均风速25 m/s。
2.2.2 波浪载荷波浪是一个随机过程,组成波浪的能量分布可以用波谱来描述。利用JONSWAP谱模拟波浪高程。JONSWAP谱[17]为
| $ S_{\eta}(\omega)=\alpha^{*} H_{s}{ }^{2} \frac{\omega_{\mathrm{m}}{ }^{4}}{\omega^{5}} \exp \left[-\frac{5}{4}\left(\frac{\omega_{m}}{\omega}\right)^{4}\right] \gamma^{\exp }\left[-\frac{(\omega-\omega m)^{2}}{2 \sigma^{2} \omega_{m}^{2}}\right], $ | (7) |
式中: Hs为波高;γ为峰值系数(文中取γ=3.3);g为重力加速度;σ为峰形因子和α*计算如下:
| $ \left\{\begin{array}{l} \omega \leqslant \omega_{m}, \sigma=0.07, \\ \omega>\omega_{m}, \sigma=0.09 ; \end{array}\right. $ | (8) |
| $ \alpha^{*}=\frac{0.0624}{0.230+0.0336 \gamma-0.185(1.9+\gamma)-1} 。$ | (9) |
根据莫里森方程,单位高度dz上的波浪力为
| $ \mathrm{d} F_{\mathrm{H}}=f_{\mathrm{H}} \mathrm{d} z=\frac{1}{2} C_{\mathrm{D}} \rho_{\mathrm{w}} v_{x}\left|v_{x}\right| \mathrm{d} z+C_{\mathrm{M}} \rho_{\mathrm{w}} \frac{{\rm{ \mathsf{ π} }} D^{2}}{4} a_{x} \mathrm{d} z, $ | (10) |
式中,CD和CM分别为拖曳力系数和惯性力系数,取CD=0.65,CM=2,ρw为海水密度,取1 030kg/m3。波浪工况为,Hs=9.4 m/s,Tp=10.47 s。
2.2.3 地震载荷处于地震带的海上风机,地震荷载是极端工况载荷。以Kobe(1995)为地震波输入,其地震加速度时程和加速度谱如图 4和图 5所示。
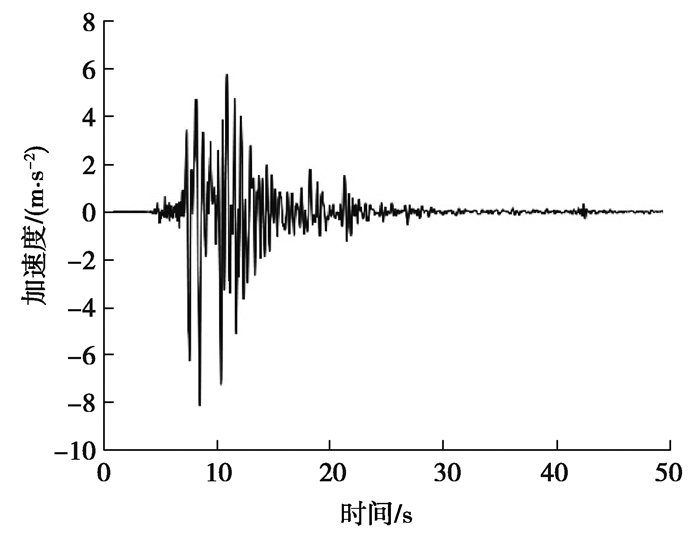
|
图 4 Kobe地震加速度时程 Fig. 4 Acceleration time history of Kobe earthquake |
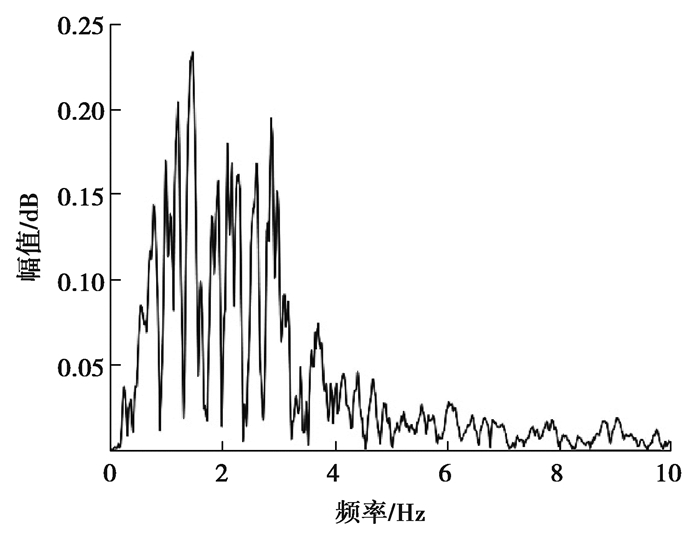
|
图 5 Kobe地震加速度谱 Fig. 5 Acceleration response spectra of Kobe earthquake |
建立风机-MRE-TMD动力学模型,运动方程为
| $ [\boldsymbol{M}]\{\ddot{x}\}+[\boldsymbol{C}]\{\dot{x}\}+[\boldsymbol{K}]\{x\}=\left\{F_{\text {wind }}(t)\right\}+\left\{F_{\text {wave }}(t)\right\}+[M] \ddot{x}_{g}+\left\{F_{\text {MRE-TMD}}\right\}, $ | (11) |
式中:
图 6为MRE-TMD安装在风机机舱内的示意图。
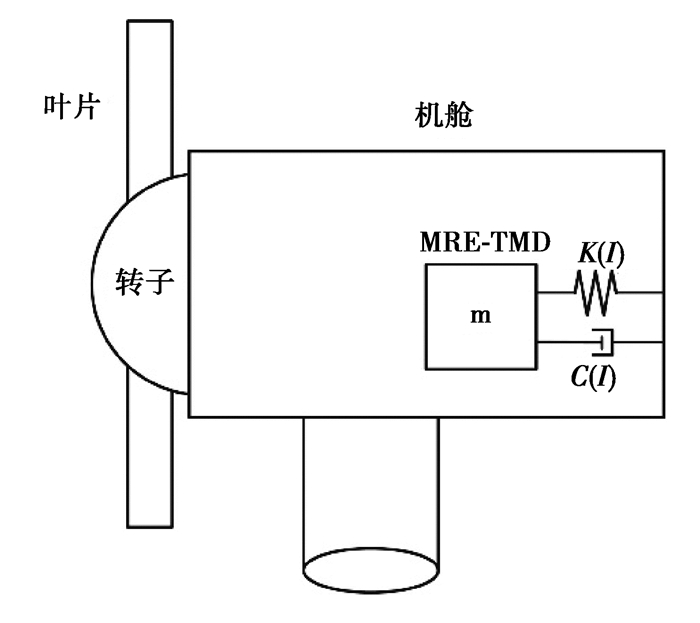
|
图 6 MRE-TMD在机舱的布局示意图 Fig. 6 Schematic diagram of MRE-TMD in the nacelle |
根据结构设计原理和海上风机主要参数,可以确定MRE-TMD的变刚度范围,[kMRE-TMD-min, kMRE-TMD-max]。文中MRE-TMD关键参数如表 3所示。采用多次非线性拟合[18-19],获得刚度、阻尼与电流之间的关系。其中,作为对比的被动TMD是根据系统的一阶主频设计得到的,其各个参数为MRE-TMD在刚度最小时的参数。
| 表 3 MRE-TMD参数 Table 3 Parameters of MRE-TMD |
TMD装置由质量、阻尼器和附在结构上的弹簧组成,MRE-TMD是基于MRE材料的TMD装置,其刚度和阻尼由MRE提供。该装置的主要特点是通过改变外加磁场来改变MRE的刚度进而调节MRE-TMD装置的频率,使其频率跟随风机结构的主频,从而在外部激励作用时通过质量块的振动耗能,达到降低结构振动的目的。
文中基于短时傅里叶变换(short-time fourier transform, STFT)对风机塔筒顶层(机舱位置)响应的频率进行识别,实时计算MRE-TMD所需刚度,根据MRE刚度与电流的对应关系确定控制电流的大小,最后输出时变控制力对风机进行减振。
短时傅里叶变换的基本原理为[20]
| $ X(t, \omega)=\frac{1}{2 {\rm{ \mathsf{ π} }}} \int \mathrm{e}^{-\mathrm{j} \omega t} \hat x=\frac{1}{2 {\rm{ \mathsf{ π} }}} \int \mathrm{e}^{-j \omega t} x(\tau) h(\tau-t), $ | (12) |
式中: x(τ)为源信号;h(τ-t)为窗函数。
t时刻功率谱密度为
| $ P(t, \omega)=|X(t, \omega)|^{2}=X(t, \omega) \cdot \overline{X(t, \omega)}, $ | (13) |
因此,t时刻的瞬时频率为
| $ \omega_{\tau}=\frac{1}{|x(\tau)|^{2}} \int \omega|X(t, \omega)|^{2} \mathrm{~d} \omega 。$ | (14) |
基于短时傅里叶变换半主动控制,尽可能实时识别风机塔筒顶端的响应频率,根据频率实时调节MRE-TMD的刚度。实时控制流程如图 7所示。
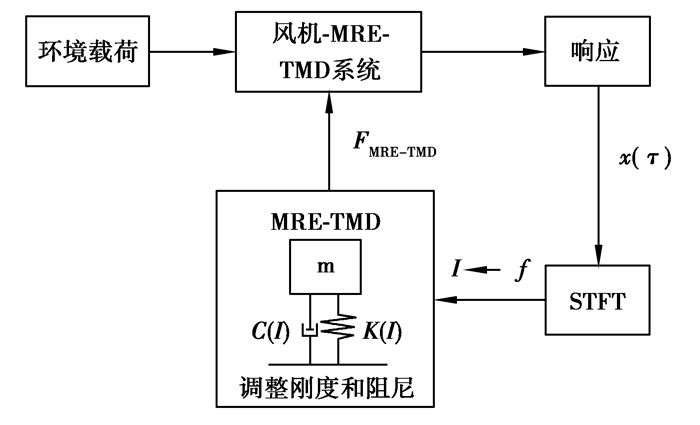
|
图 7 半主动控制流程 Fig. 7 Flowchart of semi-active control |
海上风机工作环境复杂,容易受到风、波浪、地震等载荷的作用,文中研究对象为固定式海上风机,单独的波浪载荷对风机的影响相对风载荷和地震载荷来说较小,因此,仿真了在风、地震单独作用及风浪联合作用的工况下,海上风机在被动和半主动控制下的响应时程结果如图 8~图 11所示。
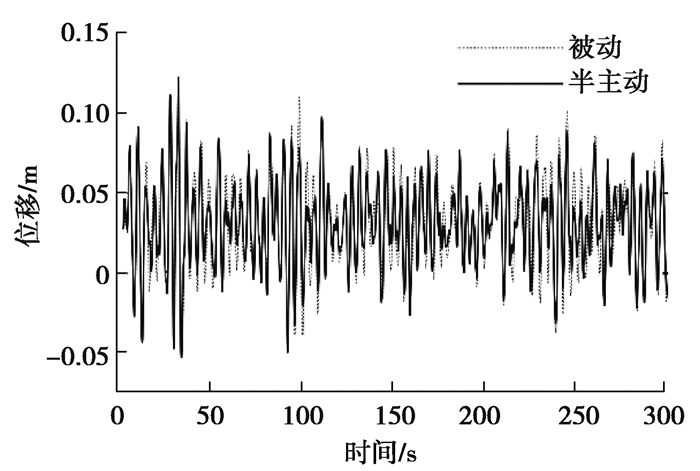
|
图 8 风载荷作用下的塔筒顶层位移响应时程 Fig. 8 Tower top displacement time history under wind loading |
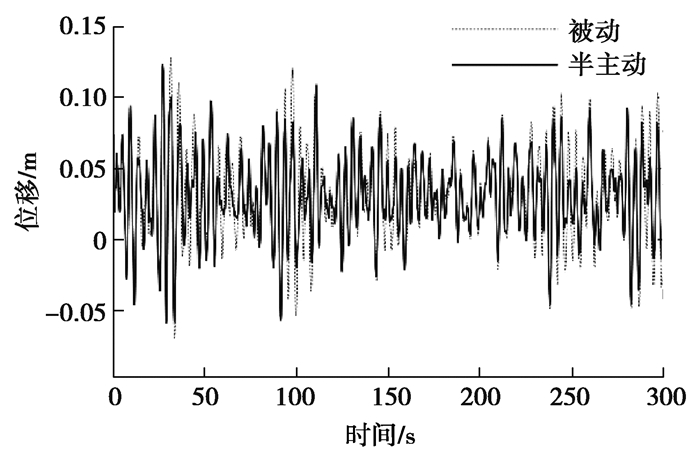
|
图 9 风浪联合载荷作用下的塔筒顶层位移响应时程 Fig. 9 Tower top displacement time history under wind and wave loadings |
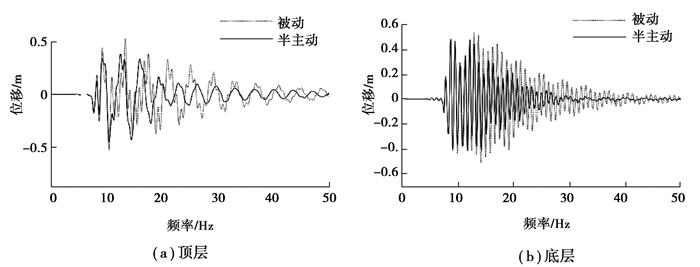
|
图 10 地震作用下位移响应时程 Fig. 10 Displacement time history under earthquake |
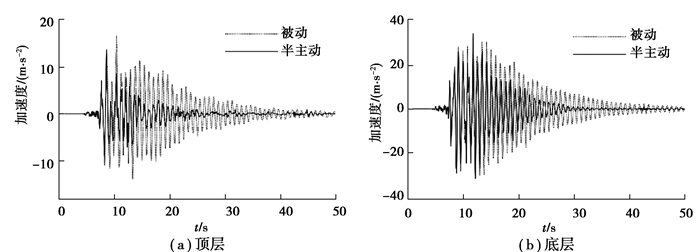
|
图 11 地震作用下加速度响应时程 Fig. 11 Acceleration time history under earthquake |
由图 8和图 9的时程结果可知,风载荷单独作用和风浪作用下,风机塔筒顶层位移半主动控制略优于被动控制,这个结果是合理的,因为风载荷和波浪载荷是低频载荷,只会激起风机的一阶振型,被动TMD就是根据系统的一阶主频设计的,有很好的减振效果。从图 10和图 11的仿真结果可知,在地震单独作用下,半主动控制效果明显优于被动控制,这是由于地震属于宽频载荷,会激起风机的高阶振型,此时,半主动MRE-TMD通过变刚度调节,实时跟踪风机系统的频率,达到了更好的减振效果。为了对海上风机进行详细分析,从时域和频域对海上风机在风、波浪和地震3种载荷联合作用下的被动控制和半主动控制的仿真结果进行了分析,如图 12~图 14所示。
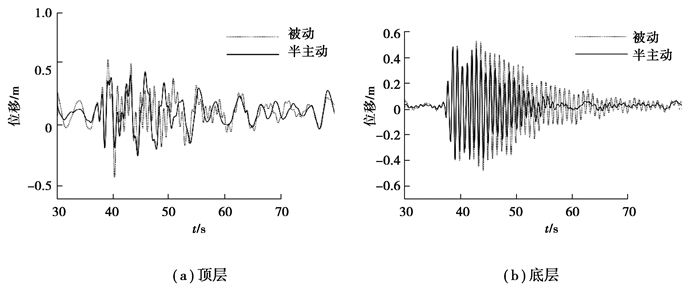
|
图 12 位移响应时程 Fig. 12 Displacement time history |
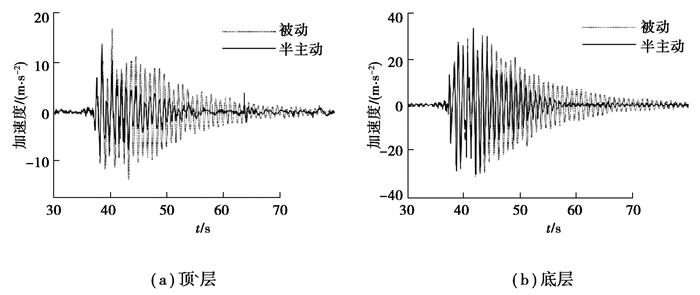
|
图 13 加速度响应时程 Fig. 13 Acceleration time history |
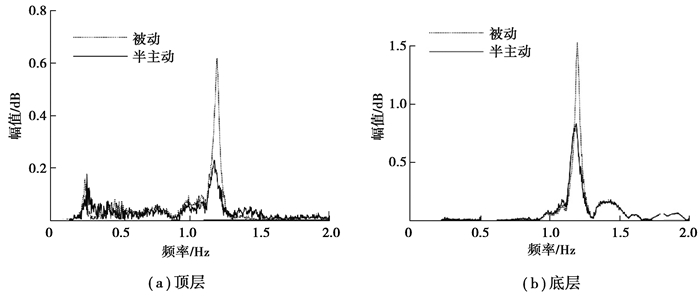
|
图 14 加速度幅值对比 Fig. 14 Comparison of acceleration amplitude |
在3种载荷作用下,风机塔筒顶层和塔筒底层的位移、加速度在被动控制和半主动控制2种方式下的响应时程结果,如图 12和图 13所示。为说明文中风机-MRE-TMD系统的半主动控制效果,以被动控制结果作为参考对比。由图 12和图 13结果可知,半主动控制下的塔筒顶层和底层的位移和加速度响应均小于被动控制下对应的响应结果。由表 4和表 5可知,被动控制对塔筒顶层和底层的位移减振率分别为50.92%和22.35%,对塔筒顶层和底层的加速度减振率分别为24.53%和4.78%。而在半主动控制下,位移减振率为70.4%和35.71%,加速度减振率分别为99.97%和29.43%,半主动控制减振效果明显优于被动控制。
| 表 4 位移均方根(RMS) Table 4 RMS displacement |
| 表 5 加速度均方根 Table 5 RMS acceleration |
为了进一步验证MRE-TMD在地震激起的高阶模态下的响应的减振效果,风机塔筒顶端和底端的加速度幅频响应如图 14所示。当有地震作用时,风机的高阶模态会被激发,因此对于高阶模态响应的抑制至关重要。从图 14可以看出,半主动控制对于抑制风机系统的二阶模态响应效果明显,根据表 6中结果,被动控制和半主动控制对于风机系统一阶模态的控制效果相当,降幅均在80%以上,而对于第二阶模态响应,半主动控制对塔筒顶层和底层的加速度幅值的降幅分别为64.3%和48.81%,而被动控制的效果不明显,分别为3.88%和5.79%。结果表明,MRE-TMD半主动控制能够有效减轻多种载荷作用下风机系统的振动。
| 表 6 加速度幅值 Table 6 Amplitude of acceleration |
通过磁流变弹性体调谐质量阻尼器MRE-TMD对导管架式海上风机进行了半主动控制,对比分析了被动控制和半主动控制2种方式作用下,海上风机在风、波浪和地震3种载荷作用时的位移和加速度响应;结果表明,MRE-TMD半主动控制可有效降低风机的动力学响应振动,塔筒顶层和底层的位移RMS减振率分别为70.4%和35.71%,加速度幅值一阶减振率分别为84.54%和92.38%,二阶减振率分别为64.3%和48.84%,对于地震激发的高阶模态的减振效果较被动TMD效果更好。
| [1] |
荣维栋, 李洪斌. 近海单桩风机在波浪地震联合作用下的动力特性分析[J]. 江苏科技大学学报(自然科学版), 2015, 29(1): 27-32. Rong W D, Li H B. Analysis on the dynamic response of offshore wind turbine under the joint action of wave and seismic[J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2015, 29(1): 27-32. (in Chinese) |
| [2] |
周文杰, 王立忠, 汤旅军, 等. 导管架基础海上风机动力响应数值分析[J]. 浙江大学学报(工学版), 2019, 53(8): 1431-1437, 1447. Zhou W J, Wang L Z, Tang L J, et al. Numerical analysis of dynamic responses of jacket supported offshore wind turbines[J]. Journal of Zhejiang University (Engineering Science), 2019, 53(8): 1431-1437, 1447. (in Chinese) |
| [3] |
杨明亮, 王鹏, 渠晓刚, 等. 基于模糊逻辑推理的风机塔筒半主动控制[J]. 现代制造工程, 2020(1): 118-125. Yang M L, Wang P, Qu X G, et al. Semi-active control of wind turbine tower based on fuzzy logic inference[J]. Modern Manufacturing Engineering, 2020(1): 118-125. (in Chinese) |
| [4] |
贺尔铭, 胡亚琪, 张扬. 基于TMD的海上浮动风力机结构振动控制研究[J]. 西北工业大学学报, 2014, 32(1): 55-61. He E M, Hu Y Q, Zhang Y. Structural vibration control of offshore floating wind turbine based on TMD[J]. Journal of Northwestern Polytechnical University, 2014, 32(1): 55-61. (in Chinese) |
| [5] |
周红杰, 丁勤卫, 李春, 等. 基于多岛遗传算法的漂浮式风力机TMD参数优化[J]. 动力工程学报, 2018, 38(5): 406-411, 417. Zhou H J, Ding Q W, Li C, et al. Optimization of TMD parameters based on MIGA for a floating wind turbine[J]. Journal of Chinese Society of Power Engineering, 2018, 38(5): 406-411, 417. (in Chinese) DOI:10.3969/j.issn.1674-7607.2018.05.011 |
| [6] |
黄致谦, 周蕊, 丁勤卫, 等. 基于MTMD的Barge型漂浮式风力机稳定性控制研究[J]. 热能动力工程, 2018, 33(6): 130-136. Huang Z Q, Zhou R, Ding Q W, et al. Study of the control over the stability of a barge type floating wind turbine based on the multiple tuned mass dampers(MTMD)[J]. Journal of Engineering for Thermal Energy and Power, 2018, 33(6): 130-136. (in Chinese) |
| [7] |
Zuo H R, Bi K M, Hao H. Using multiple tuned mass dampers to control offshore wind turbine vibrations under multiple hazards[J]. Engineering Structures, 2017, 141: 303-315. DOI:10.1016/j.engstruct.2017.03.006 |
| [8] |
Hussan M, Sharmin F, Kim D. Multiple tuned mass damper based vibration mitigation of offshore wind turbine considering soil-structure interaction[J]. China Ocean Engineering, 2017, 31(4): 476-486. DOI:10.1007/s13344-017-0054-x |
| [9] |
Hussan M, Rahman M S, Sharmin F, et al. Multiple tuned mass damper for multi-mode vibration reduction of offshore wind turbine under seismic excitation[J]. Ocean Engineering, 2018, 160: 449-460. DOI:10.1016/j.oceaneng.2018.04.041 |
| [10] |
李静, 陈健云, 柴健, 等. 磁流变阻尼器对近海风机的半主动控制研究[J]. 水利与建筑工程学报, 2013, 11(5): 62-65, 74. Li J, Chen J Y, Chai J, et al. Study on semi-active control of offshore wind turbines by magneto-rheological damper[J]. Journal of Water Resources and Architectural Engineering, 2013, 11(5): 62-65, 74. (in Chinese) |
| [11] |
阎石, 于君元, 牛健, 等. 基于SMA的风机塔架结构风致振动控制研究[J]. 防灾减灾工程学报, 2016, 36(1): 159-164. Yan S, Yu J Y, Niu J, et al. Wind-induced vibration control of wind turbine tower structures based on shape memory alloys[J]. Journal of Disaster Prevention and Mitigation Engineering, 2016, 36(1): 159-164. (in Chinese) |
| [12] |
Shen Y, Golnaraghi M F, Heppler G R. Experimental research and modeling of magnetorheological elastomers[J]. Journal of Intelligent Material Systems and Structures, 2004, 15(1): 27-35. DOI:10.1177/1045389X04039264 |
| [13] |
Sun S S, Yang J, Li W H, et al. Development of an isolator working with magnetorheological elastomers and fluids[J]. Mechanical Systems and Signal Processing, 2017, 83: 371-384. DOI:10.1016/j.ymssp.2016.06.020 |
| [14] |
Davis L C. Model of magnetorheological elastomers[J]. Journal of Applied Physics, 1999, 85(6): 3348-3351. DOI:10.1063/1.369682 |
| [15] |
Gu X Y, Yu Y, Li Y C, et al. Experimental study of semi-active magnetorheological elastomer base isolation system using optimal neuro fuzzy logic control[J]. Mechanical Systems and Signal Processing, 2019, 119: 380-398. DOI:10.1016/j.ymssp.2018.10.001 |
| [16] |
Wang W H, Li X, Pan Z X, et al. Motion control of pentapod offshore wind turbines under earthquakes by tuned mass damper[J]. Journal of Marine Science and Engineering, 2019, 7(7): 224. DOI:10.3390/jmse7070224 |
| [17] |
王树青, 梁丙臣. 海洋工程波浪力学[M]. 青岛: 中国海洋大学出版社, 2013. Wang S Q, Liang B C. Wave mechanics for ocean engineering[M]. Qingdao: China Ocean University Press, 2013. (in Chinese) |
| [18] |
Han Y, Hong W, Faidley L E. Field-stiffening effect of magneto-rheological elastomers[J]. International Journal of Solids and Structures, 2013, 50(14/15): 2281-2288. |
| [19] |
Gu X Y, Li J C, Li Y C, et al. Frequency control of smart base isolation system employing a novel adaptive magneto-rheological elastomer base isolator[J]. Journal of Intelligent Material Systems and Structures, 2016, 27(7): 849-858. DOI:10.1177/1045389X15595291 |
| [20] |
Sun C, Nagarajaiah S. Study on semi-active tuned mass damper with variable damping and stiffness under seismic excitations[J]. Structural Control and Health Monitoring, 2014, 21(6): 890-906. DOI:10.1002/stc.1620 |
 2022, Vol. 45
2022, Vol. 45

