直升机在发生事故迫降或坠毁时,飞行员或乘员的脊柱和骨盆会因地面传递到身体的冲击总力而受到严重的伤害,甚至威胁生命安全[1-2],抑制冲击载荷能够减少驾驶员在坠机事故中脊柱骨折和截瘫的风险,提高乘员的生存率[3]。座椅悬架是保护乘员安全的最后一道屏障,受到越来越多的关注。相比于传统的减振、隔振等应用,直升机座椅悬架面临冲击速度高、时间短的挑战。目前,最常见的座椅悬架缓冲器(耗能器)分为被动、半主动和主动形式。铝蜂窝耗能器、金属结构变形耗能器、机械式弹簧耗能器[4]等参数固定不能适应乘员质量、冲击速度或冲击能量的变化,缓冲性能有限[5]。主动缓冲着陆系统存在[6]驱动能量需求大、设计复杂等问题。基于磁流变材料的半主动耗能器通过改变输入电流(或磁场)来实现阻尼力的自适应调节,具有响应快、功耗低等优点,在减振和缓冲应用中具有广阔的发展前景及工程应用价值[7]。
对于材料和结构确定的磁流变耗能器,缓冲性能的优劣由控制算法决定,通过设计合适的控制算法找到最优的力位移曲线,在实现冲击能量吸收最大的同时避免阻尼力峰值过大对人体的伤害,实现保护人员和设备安全的目的。目前基于磁流变器件的半主动控制算法,主要针对振动或者低速冲击问题[8],而对于直升机坠毁中的高速缓冲控制问题的研究尚少。如何实现“软着陆”目标,即充分利用有效行程使承载着乘员的座椅系统安全着陆成为了控制策略设计的目标。有学者采用恒定阻尼力控制,以输出人体能承受的最大载荷耗散冲击能量,虽然可以保证人体承受的加速度低于伤害限,但不能充分利用磁流变耗能器的行程,无法有效地实现“软着陆”[9]。有学者采用“软着陆”控制策略并结合落锤的状态进行反馈控制,仿真试验验证控制策略的可行性和有效性[10],但是该方法主要应对的不是直升机这种高速冲击问题。还有学者研究了宾汉数(Bingham number, BN)控制[8, 11-14],通过在冲击初始阶段设置BN来实现软着陆的目标,但是该方法存在可控范围小,无法对高速冲击进行有效抑制的问题。为了克服使用BN控制时的不足,有学者将BN控制扩展开发了最小持续时间减速暴露控制[15],该方法虽然拓宽了缓冲抑制的速度范围,但是在低速下控制力过大,易引起人体的不适感。
模糊控制(fuzzy control,FC)是以模糊集合论、模糊语言和模糊逻辑推理为基础的一种智能控制方法。通过语言规则将专家经验知识融入到控制器设计中,可以描述任意的非线性关系,且不依赖于系统精确的数学模型、鲁棒性强,具有巨大的应用潜力[16]。为此,文中基于单自由度座椅系统模型及其运动方程,提出了鲁棒性强且不依赖数学模型的模糊控制方法,基于系统冲击响应特性及磁流变耗能器的工作原理确定了模糊控制器的输入反馈量,以“软着陆”为目标设计了控制规则。最后基于数值仿真方法以人体极限载荷为标准评估了模糊控制下缓冲效果,并与恒定总力控制和恒定屈服应力2种控制方法进行了对比。
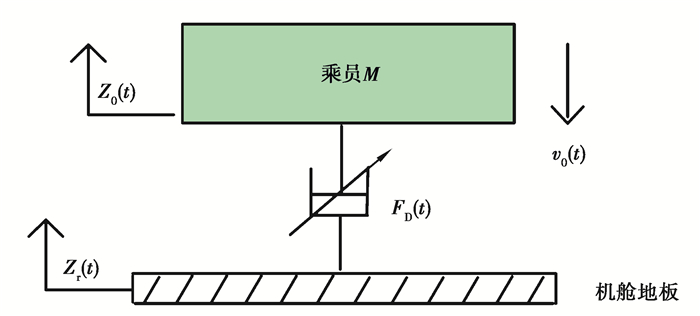
1 单自由度刚性乘员模型单自由度刚性乘员模型是一个针对固定质量乘员建立的单自由度线性模型,如图 1所示,将人体和坐垫看成一个整体,由座垫承载的有效质量为 。基于牛顿动力学定律可知人体在缓冲过程中承受的加速度大小为
| $ M{{\ddot Z}_0} = - {F_D}(t) - {M_0}g, $ | (1) |
| $ F_{D}(t)=F_{V}(t)+F_{\mathrm{MR}}(t), $ | (2) |
|
图 1 直升机座椅悬架单自由度模型 Fig. 1 Single-degree-of-freedom model of helicopter seat suspension |
式中:
| $ {F_V}(t) = c\left( {{{\dot Z}_0}(t) - {{\dot Z}_r}(t)} \right), $ | (3) |
式中:c为耗能器阻尼系数;
假设乘员以及机舱地板从坠落到落地前都以相同的速度下降,即二者之间不具有相对运动,因此数值分析的初始条件为
| $ \dot{Z}_{0}(0)=\dot{Z}_{r}(0)=-v_{0} 。$ | (4) |
考虑磁流变耗能器的可控范围,文中所用磁流变耗能器阻尼系数取800 N·s/m,其行程为40.6 cm(16英寸)[11-13],与文献[17]中的座椅参数设置相同。
2 模糊控制器的设计 2.1 控制目标为了保证直升机实现“软着陆”,本研究中设计的控制器的控制目标为:①充分利用磁流变耗能器有效行程(16英寸);②行程用完的同时系统速度降至0;③控制结束后系统加速度也降为0以避免速度波动,即控制目标满足
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot Z}_{{\rm{rel}}}}\left( {{t_f}} \right) = 0, }\\ {\left| {{Z_{0{\rm{ rel }}}}\left( {{t_f}} \right)} \right| = 16}\\ {{{\ddot Z}_0}\left( {{t_f}} \right) = 0, , } \end{array}} \right., $ | (5) |
式中,tf代表控制终止的时刻。
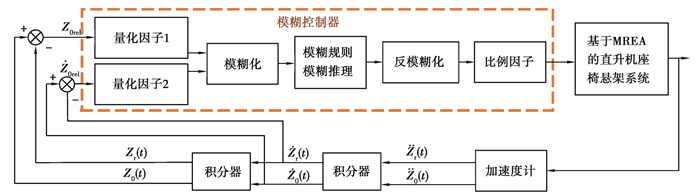
2.2 模糊控制器的设计基于磁流变耗能器直升机座椅悬架单自由度模糊控制系统框图如图 2所示。模糊控制器的第一个输入反馈量选取的是坐垫与机舱地板之间的相对位移,另外一个输入反馈量选取的是坐垫与机舱地板的相对速度,给模糊控制器实现平台输出提供反馈,经过模糊规则与模糊推理计算得到磁流变耗能器作用到座垫及人体的总力。
|
图 2 基于磁流变耗能器直升机座椅悬架单自由度模糊控制系统框图 Fig. 2 Block diagram of single-degree-of-freedom fuzzy control system for helicopter seat suspension based on MREA |
根据模糊控制器“软着陆”的控制目标及冲击特点,模糊控制器的输入反馈量分别选择为负载与地面的相对位移和相对速度,经量化因子转换到输入论域[-C, C]内,坐垫与地板的相对速度和相对位移(即磁流变耗能器行程使用量)可以通过计算得到:
| $ \begin{array}{l} {{\dot Z}_{0{\rm{rel}}}}(t) = {{\dot Z}_0}(t) - {{\dot Z}_r}(t), \\ {Z_{0{\rm{rel}}}}(t) = {Z_0}(t) - {Z_r}(t)。\end{array} $ | (6) |
量化因子的取值为
| $ k_{1}=\frac{C_{1}}{A_{1}}, k_{2}=\frac{C_{2}}{A_{2}}, $ | (7) |
式中:k1和k2分别对应负载与地面的相对位移和相对速度的量化因子;A1和A2分别为负载与地面的相对位移和相对速度的峰值;C1和C2为模糊控制器2个输入量的论域范围。
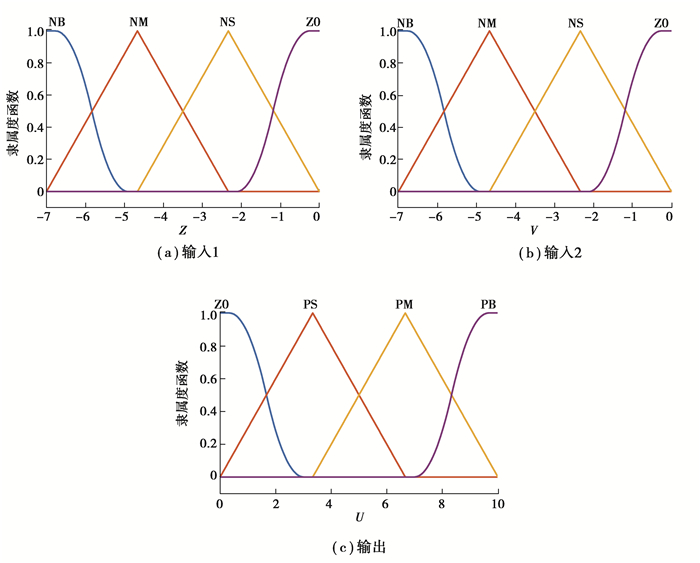
由于过多的语言变量将增加系统的复杂度和计算量,而较少的语言变量将使系统精度降低,故选取NB, NM, NS, ZO, PS, PM, PB 7个模糊语言变量对输入隶属度函数进行描述,其中NM, NS, ZO, PS, PM采用三角形隶属度函数,NB和PB采用高斯型隶属度函数。每个输入变量的论域均被隶属度函数划分为具有重叠区域的相邻间隔,既保证了控制过程中的灵敏度,又保证了控制过程中的稳定性。利用所设计的输入隶属度函数将负载与地面的相对位移和相对速度的输入量精确值转化为相应的模糊量Z和V,由于数值分析取Z轴向上为正,在冲击过程中,座板与机舱地板的相对速度和相对位移均向下,即取值为负,因此其对应的论域设置为[-7, 0], 输入隶属度函数如图 3(a)和图 3(b)所示。
|
图 3 模糊控制器隶属度函数 Fig. 3 Degree of membeship |
基于方程(1)及磁流变耗能器的工作原理,所确定的模糊控制规则如表 1所示,共包含25条模糊规则。模糊规则通常由一系列关系词连接而成,为了实现耗能最大又要避免输出的控制总力峰值太大超出人体伤害限制14.5 g[18],模糊规则设计思想是实现“平台效应”,由于控制总力中的分量粘滞阻尼力与速度成正比,在相对速度峰值处模糊控制器输出的力就应该小,可表述为:
| $ \begin{array}{l} 规则 1 :如果 Z 为 {\rm{NB}}且 V 为 NB 那么 U 为 Z0\\ 规则 2 :如果 Z 为 {\rm{NM}}且 V NM 那么 U 为 PS\\ \vdots \\ 规则 25 :如果 Z 为 {\rm{Z0}} 且 V 为 Z0B 那么 U 为 Z0 \end{array} $ |
| 表 1 模糊规则的设计 Table 1 Design of fuzzy rules |
式中,U为控制器的输出值所对应的模糊子集。文中采用Mamdani推理算法,根据输入模糊量,通过模糊规则和模糊推理得到模糊控制量。
2.2.3 反模糊化通过模糊推导所得到的控制量是模糊量,为了实现实际控制,需利用输出隶属度函数将输出值的模糊量U转化为相应的精确值u,其输出隶属度函数如图 3(c)所示,文中所采用的反模糊化方法为常用的重心法。精确值u经比例因子k3进行缩放,即为直升机座椅悬架所输出的可控库仑力FMR(t)为
| $ F_{\mathrm{MR}}(t)=u \cdot k_{3}。$ |
以上根据直升机冲击特点及磁流变耗能器的工作原理,设计了模糊控制器的结构与控制规则,为了进一步分析模糊控制器的缓冲控制效果,此外还设计了2种线性控制器——恒定总力控制和恒定屈服应力控制,并采用数值仿真分析方法进行了对比分析。
2.3 恒定总力控制器恒定总力控制器输出一个恒定的控制总力,其由两部分力组成:粘滞阻尼力和可控库仑力。根据上述的控制目标进行恒定总力控制器(total force constant controller, TFCC)设计,一定存在一个恒定总力FD(TFCC)可用尽悬架有效行程时完全吸收对应确定冲击速度下的冲击能量:
| $ E_{D}=\frac{M v_{0}{ }^{2}}{2}+M g S=F_{\mathrm{D}(\mathrm{TFCC})} S 。$ | (8) |
根据式(8)可得到对应不同速度下所需要的恒定载荷大小,据此设计一个总力恒定控制器,那么就可以计算出对应的可控库仑力为
| $ F_{\mathrm{MR}}(t)=F_{\mathrm{D}(\mathrm{TFCC})}-F_{V}(t)。$ | (9) |
恒定屈服应力控制是指在恒定电流下磁流变材料输出一个恒定屈服应力。根据这个思想设计了恒定屈服应力控制器(yield stress constant controller, YSCC)。其控制目标与TFCC的控制目标一致,该控制器对应不同的冲击速度输出一个恒定的屈服应力FMR(YSCC),再加上粘滞阻尼力即为悬架系统输出控制总力,根据能量守恒定律可得
| $ {E_D} = \int\limits_0^{tf} {{F_D}} (t){\rm{d}}{z_{{\rm{orel }}}}(t) = \int\limits_0^{tf} {\left( {{F_{{\rm{MR}}({\rm{YSCC}})}}(t) + {F_V}(t)} \right)} {\rm{d}}{z_{{\rm{orel }}}}(t) 。$ | (10) |
结合式(8)和式(10)可知对应不同下沉速率下的FMR(YSCC)大小。
3 控制仿真对比与分析为了验证所设计的控制器的缓冲效果,基于式(1)中冲击模型,选择质量为70.4 kg的第50%男性乘员[19]在6~12 m/s不同冲击速度下进行模糊控制器作用下的Matlab/Simulink控制仿真。最后分别与恒定总力控制、恒定屈服应力控制下的缓冲效果进行对比,依据标准伤害指标评估3种控制器的控制效果。
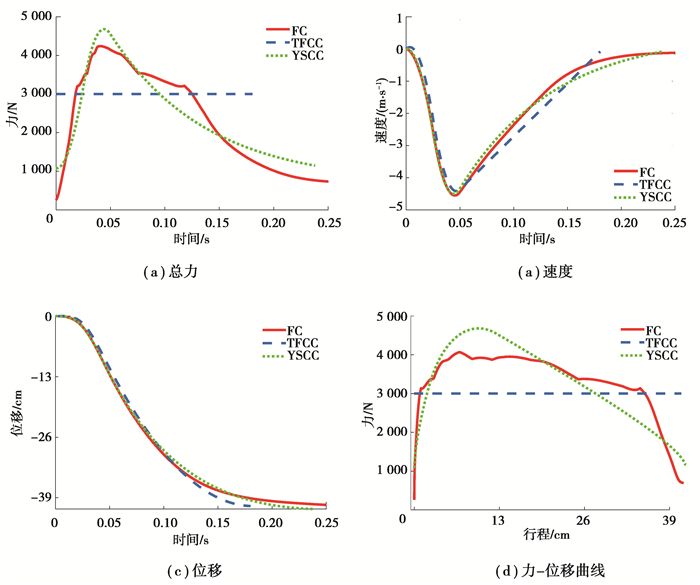
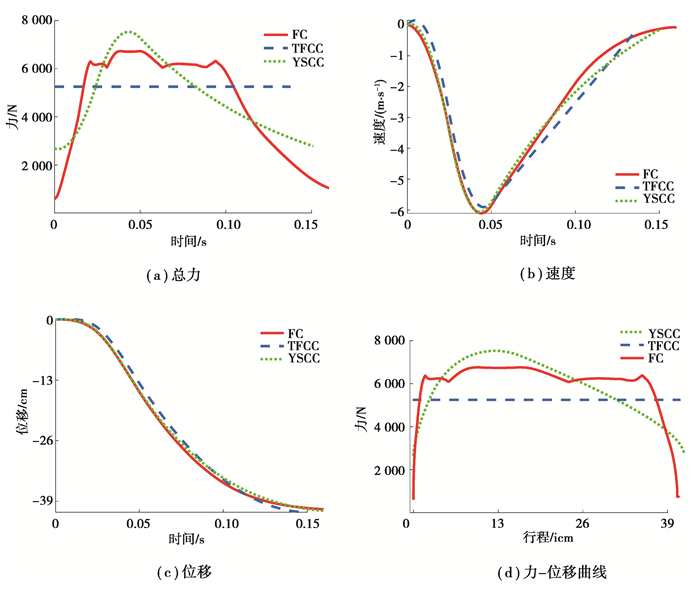
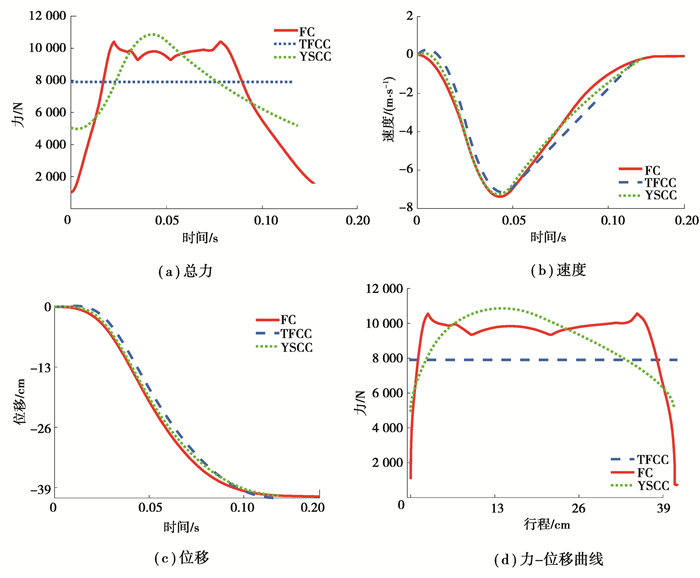
3.1 仿真结果图 4~图 6给出了6、9、12 m/s冲击速度下3种控制器对应的输出总力FD(t)响应曲线、相对速度
|
图 4 6 m/s下3种控制器的仿真结果 Fig. 4 The simulation results of three different controllers at 6 m/s |
|
图 5 9 m/s下3种控制器的仿真结果 Fig. 5 The simulation results of three different controllers at 9 m/s |
|
图 6 12 m/s下3种控制器的仿真结果 Fig. 6 The simulation results of three different controllers at 12 m/s |
随着冲击速度的增大,3种控制方法输出的控制总力峰值也增大,其人体相应加速度峰值也增大,此外在行程充分用完的同时系统速度均降为0,从控制总力位移曲线图可以看出,TFCC输出的控制力峰值最小,其次是FC,最大的是YSCC。分析不同方法对应不同速度下的控制过程可以发现:
1) TFCC控制全程输出的是恒定的总力,在不同冲击速度下坐垫的加速度响应远小于伤害限14.5g。但是在行程充分用完且系统速度降为0时,系统没有一个动态调整的过程,导致加速度在控制结束时不为0,因此有二次反弹的危险,可能对人造成不适甚至二次伤害,无法实现“软着陆”目标。
2) YSCC最大加速度值14.4g出现在12 m/s的冲击条件下,接近伤害限14.5g。但存在一个和TFCC一样的问题:在控制结束时系统加速度不为0,因此有速度发生波动,也无法实现“软着陆”目标。
3) FC拟合出的控制力位移曲线分3个阶段:上升期、平台期、下降期。上升期可以迅速地将控制力提升,平台期可较好的维持一个大小稳定的控制力,避免了出现尖峰导致身体承受加大的加速度,下降期的调整过程可以将加速度也降至0左右,避免了系统速度由于加速度波动而反弹的现象,可实现“软着陆”的控制目标。
4) 对于单自由度缓冲系统模型来说,由于传递到人体的加速度与控制总力峰值成正比,因此TFCC控制作用下传递到人体的加速度最小。但是从控制方法的可实现性来说,以上2种恒定线性控制器过于理想化,实际中难以实现,因此仅作为模糊控制器的设计参照。
3.2 对比与分析动态极限总力是根据乘员在撞击过程中可以承受的最大垂直允许总力(即耗能器的总冲程力和座椅悬架中的粘滞阻尼力)确定的。文中选择了14.5g的极限系数来评估第50%男性乘员受伤程度。换句话说,耗能器的总力峰值为不超过座垫及其承载的人体有效质量总和的14.5倍。
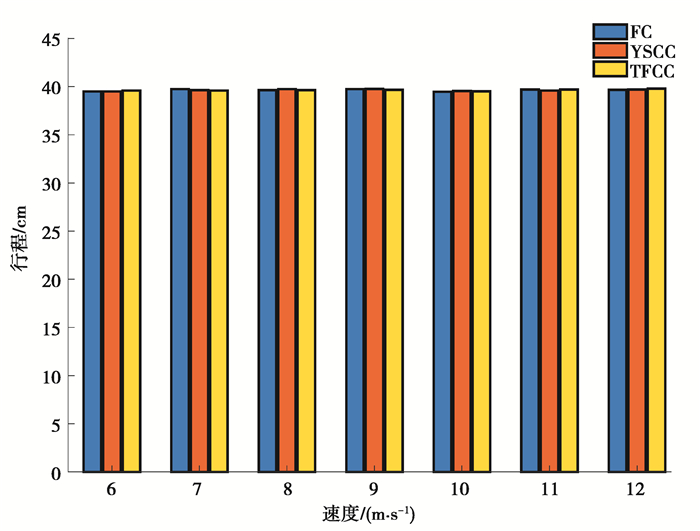
从图 7可以看出3种控制器几乎都用尽了有效冲程,在这个基础上,比较在不同速度下分别利用3种控制器后人体相应的加速度峰值,对3种控制方法进行对比评价。
|
图 7 3种控制器的位移 Fig. 7 Displacement of three different controllers |
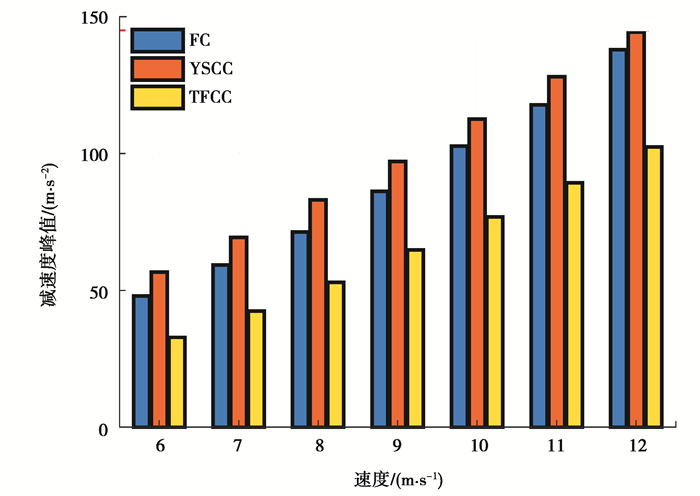
从图 8中3种控制器对应不同速度下人体的加速度响应对比可以知道,TFCC输出恒定总力大大降低了输出控制总力峰值,能将伤害降到最低,其次控制效果较好的是FC,YSCC输出的恒定屈服应力叠加了粘滞阻尼力,加速度峰值出现在相对位移的峰值处,相比另外2个控制器,其生物响应最大,但是三者在6~12 m/s的冲击速度下,均未超出14.5g。
|
图 8 6~12 m/s冲击速度下3种控制器对应的人体减速度峰值 Fig. 8 Peak deceleration of three different controllers under 6~12 m/s |
从图 9给出的对应不同速度下3种控制器在控制终止时系统加速度的大小的对比图可以看出:在行程终点处,TFCC和YSCC还保持着一个较大的力,系统加速度不为0,此外以上2种控制器均为理想控制器,实际应用中难以实现。FC拟合的力位移曲线可“达到平台效应”,且能真正实现“软着陆”,有效避免行程末端系统加速度不为0带来的反弹伤害。对比来看,FC更适用于直升机座椅悬架缓冲控制中。
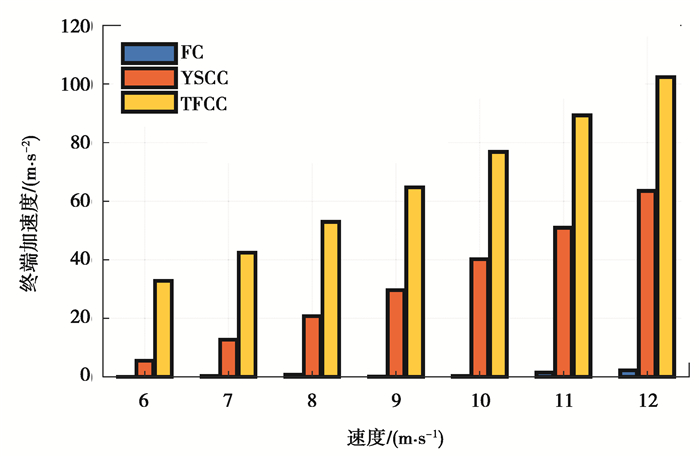
|
图 9 6~12 m/s冲击速度下3种控制器对应的系统终端加速度值 Fig. 9 Terminal acceleration of three control methods under 6~12 m/s |
针对直升机迫降或坠毁时地面对座椅的冲击问题,以“软着陆”为控制目标,分析了应用磁流变耗能器直升机单自由度座椅悬架缓冲系统的缓冲原理及运动方程,并基于分析的理想控制力位移输出曲线,提出模糊控制的设计方案,最后以人体加速度峰值为评价指标,分别与TFCC、YSCC 2种控制方法的控制效果和可实现性做了对比。得出以下结论:
1) 从控制效果上分析,尽管在冲击速度6~12 m/s的范围内3种控制器都能将人体加速度控制在伤害限以内,并且3种控制器在冲程结束时乘员速度都能减小至0,但是TFCC和YSCC在不同初始冲击速度下无法及时将系统加速度降为0, 速度仍有波动,无法同模糊控制器一样实现“软着陆”。
2) 从可实现性上比较,TFCC、YSCC以过于理想化的恒力为目标,不宜实现,实际缓冲系统中存在很多非线性因素,简易线性控制器在实际应用中效果往往不佳。
相比之下,模糊控制器可以实现“平台效应”,控制下降期可以将系统加速度降低至0,进而实现“软着陆”,因此模糊控制在不同初始冲击速度下都有更优的综合控制效果。
| [1] |
张娟, 詹月玫, 王咏梅. 2014—2016年世界直升机事故统计及分析[J]. 直升机技术, 2017(3): 68-72. Zhang J, Zhan Y M, Wang Y M. Helicopter accident statistics and analysis of the world in 2014-2016[J]. Helicopter Technique, 2017(3): 68-72. (in Chinese) DOI:10.3969/j.issn.1673-1220.2017.03.015 |
| [2] |
Harrer K L, Yniguez D, Majar M, et al. Whole body vibration exposure for mh-60s pilots[R]. Naval Medical Center San Diego CA, 2005: 303-314.
|
| [3] |
Hiemenz G J, Hu W, Wereley N W. Investigation of MR dampers for enhanced crashworthiness and vibration isolation of helicopter crew seats[C]. Annual Forum Proceedings-American Helicopter Society, INC, 2007, 63(2): 1187.
|
| [4] |
陈金宝, 聂宏, 汪岸柳, 等. 月球软着陆系统关键技术研究与发展综述[J]. 中国机械工程, 2006, 17(S2): 426-428. Chen J B, Nie H, Wang A L, et al. Development of soft landing for lunar lander[J]. China Mechanical Engineering, 2006, 17(S2): 426-428. (in Chinese) |
| [5] |
Choi Y T, Wereley N M. Biodynamic response mitigation to shock loads using magnetorheological helicopter crew seat suspensions[J]. Journal of Aircraft, 2005, 42(5): 1288-1295. DOI:10.2514/1.6839 |
| [6] |
申一霖. 小行星探测器电磁阻尼式着陆缓冲装置设计及试验研究[D]. 哈尔滨: 哈尔滨工业大学, 2020. Shen Y L. Design and experimental study of electromagnetic damping landing buffer device for asteroid probe[D]. Harbin: Harbin Institute of Technology, 2020. (in Chinese) |
| [7] |
韩晓明, 张超, 许桎嶂, 等. 基于粒子群算法的磁流变缓冲器磁路设计研究[J]. 兵器装备工程学报, 2020, 41(12): 161-165. Han X M, Zhang C, Xu Z Z, et al. Research on magnetic circuit design of magnetorheological buffer based on particle swarm optimization[J]. Journal of Ordnance Equipment Engineering, 2020, 41(12): 161-165. (in Chinese) DOI:10.11809/bqzbgcxb2020.12.030 |
| [8] |
王洁. 面向直升机座椅的磁流变缓冲器及半主动控制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2019. Wang J. Research on magnetorheological damper and semi-active control method of helicopter seat[D]. Harbin: Harbin Institute of Technology, 2019. (in Chinese) |
| [9] |
Singh H J, Wereley N M. Influence of occupant compliance on a vertically stroking helicopter crew seat suspension[J]. Journal of Aircraft, 2014, 52(4): 1286-1297. |
| [10] |
白先旭, 杨森. 磁流变半主动落锤冲击缓冲系统的"软着陆"控制试验与分析[J]. 机械工程学报, 2021, 57(1): 121-127. Bai X X, Yang S. Experimental test and analysis of "soft-landing" control for drop-induced shock systems using magnetorheological energy absorber[J]. Journal of Mechanical Engineering, 2021, 57(1): 121-127. (in Chinese) |
| [11] |
Wereley N M, Choi Y T, Singh H J. Adaptive energy absorbers for drop-induced shock mitigation[J]. Journal of Intelligent Material Systems and Structures, 2011, 22(6): 515-519. DOI:10.1177/1045389X10393767 |
| [12] |
Choi Y T, Wereley N M. Drop-induced shock mitigation using adaptive magnetorheological energy absorbers incorporating a time lag[J]. Journal of Vibration and Acoustics: Transactions of the ASME, 2015, 137(1). |
| [13] |
Singh H J, Wereley N M. Adaptive magnetorheological shock isolation mounts for drop-induced impacts[J]. Smart Materials and Structures, 2013, 22(12): 122001. DOI:10.1088/0964-1726/22/12/122001 |
| [14] |
Saleh M, Sedaghati R, Bhat R. Dynamic analysis of an SDOF helicopter model featuring skid landing gear and an MR damper by considering the rotor lift factor and a Bingham number[J]. Smart Materials and Structures, 2018, 27(6): 065013. DOI:10.1088/1361-665X/aab860 |
| [15] |
Wang M K, Chen Z B, Wereley N M. Adaptive magnetorheological energy absorber control method for drop-induced shock mitigation[J]. Journal of Intelligent Material Systems and Structures, 2021, 32(4): 449-461. DOI:10.1177/1045389X20957100 |
| [16] |
薛荣辉. 智能控制理论及应用综述[J]. 现代信息科技, 2019, 3(22): 176-178. Xue R H. Intelligent control theory and application review[J]. Modern Information Technology, 2019, 3(22): 176-178. (in Chinese) |
| [17] |
Fox R G. Helicopter crashworthiness-part one[J]. Flight Safety Foundation: Helicopter Safety, 1989, 15(6): 1-6. |
| [18] |
Desjardins S P. The evolution of energy absorption systems for crashworthy helicopter seats[J]. Journal of the American Helicopter Society, 2006, 51(2): 150-163. DOI:10.4050/JAHS.51.150 |
| [19] |
Singh H J, Choi Y T, Wereley N M. Optimal terminal trajectory control of vertically stroking crew seats using magnetorheological energy absorbers[C]//51st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference 18th 12-15 April 2010, Orlando, Florida. Reston, Virigina: AIAA, 2010.
|
 2022, Vol. 45
2022, Vol. 45


