1b. 北京化工大学高端机械装备健康监控与自愈化北京市重点实验室, 北京100029;
2. 重庆两江新区产业促进局, 重庆 401147
1b. Beijing Key Laboratory of High-end Mechanical Equipment Health Monitoring and Self-Recovery, Beijing University of Chemical Technology, Beijing 100029, P. R. China;
2. Chongqing Liangjiang New District Industry Promotion Bureau, Chongqing 401147, P. R. China
磁流变弹性体(MRE, magnetorheological elastomer)通常由非磁性聚合物基质和微米级磁性颗粒混合固化而成。固化后,铁磁颗粒被限制在基体中,因此不存在颗粒沉降和稳定性差等问题[1-2]。其力学特性可在外加磁场作用下发生显著改变,尤其是宏观的刚度和阻尼可在外加磁场控制下发生快速、连续、可逆的变化[3-5],将MRE应用于智能结构、传感机构和振动控制领域具有非常广阔的前景,近年来已成为智能材料研究的一个热点[6-10]。
作为一种智能材料,MRE具有优异的磁控变刚度力学特性,其储能模量可随外加磁场的增大而增大,表现出明显的磁流变效应。为提高MRE的磁致力学性能,研究者们在基体和填充颗粒的选择、改性等方面进行了大量研究[11-15]。研究表明,各向异性MRE比各向同性MRE具有更好的磁致性能,因此在MRE固化过程中通常会施以外加磁场进行预结构化,得到颗粒链与外加磁场同向的各向异性MRE样品。当MRE中磁性颗粒的体积分数较小时,颗粒在基体中呈链状结构排列。
有学者研究发现,MRE中颗粒链的排列会对其磁致模量产生较大影响[16-18]。从微观角度出发,基于磁偶极子理论建立了MRE的磁致剪切模量微观模型,分析了颗粒链取向角度对磁致剪切模量的影响,并预测了磁致剪切模量随取向角度的变化规律。通过对制备试样的测试表明,该微观模型的预测趋势与实验数据完全一致;根据羰基铁粉磁化规律,将微观模型参数简化,采用实测数据对简化模型参数进行识别,得到MRE磁致模量的参数模型,结果表明该参数模型能够很好的预测颗粒链取向角度和外加磁场对MRE磁致模量的影响。本研究以期为MRE的制备及磁致机理研究提供相关理论和技术支撑。
1 基于偶极子理论的磁致模量微观模型磁性颗粒是MRE具有磁控特性的根本原因。MRE内部颗粒间的相互作用力一般采用磁偶极子模型计算[19-21]。将MRE中的磁化颗粒视为大小均匀的磁偶极子,并且忽略基体以及磁化颗粒间磁场的耦合作用,通过分析磁化颗粒间相互作用机理,可得磁致模量的微观模型[22]。虽然这种简化会造成一定误差,但预测趋势却是正确的[23]。颗粒被磁化后具有与外加磁场方向相同的磁偶极矩,其大小可表示为[21]
| $ m=\frac{4}{3} \pi a_{3} \mu_{0} \mu_{1} \chi H, $ | (1) |
式中:a为颗粒半径;χ为颗粒磁化率;μ0为真空磁导率;μ1为MRE磁导率;H为颗粒所处位置的磁场。当MRE中颗粒链相对于外加磁场
| $ E_{i j}=-\frac{m_{i} m_{j}}{4 \pi \mu_{0} \mu_{1} r 3}\left[3 \cos ^{2} \theta-1\right], $ | (2) |
|
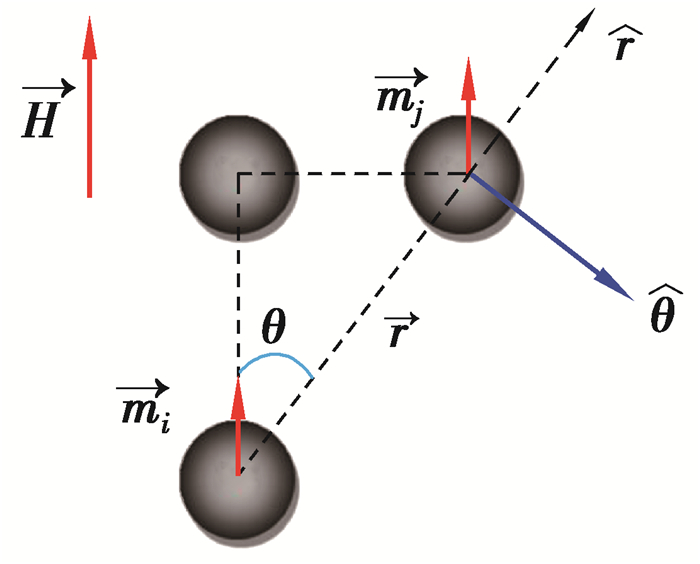
图 1 相邻磁偶极子间的位置关系 Fig. 1 Positional relationship between adjacent magnetic dipoles |
磁化颗粒之间的相互作用力
| $ \vec{F}=\frac{3 m_{i} m_{j}}{4 \pi \mu_{0} \mu_{1} r^{4}}\left[\left(1-3 \cos ^{2} \theta\right) \widehat{\boldsymbol{r}}-(2 \cos \theta \sin \theta) \hat{\boldsymbol{\theta}}\right] \circ $ | (3) |
其中:
|
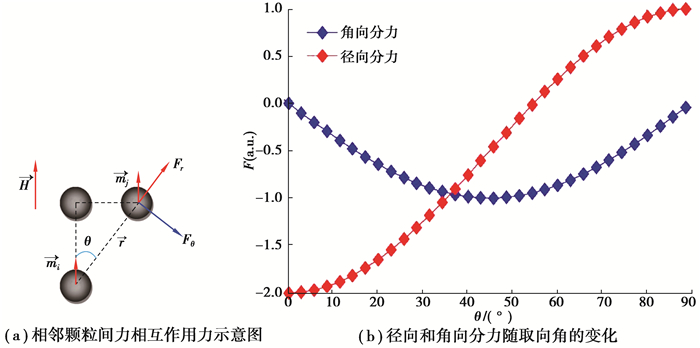
图 2 相邻颗粒间力相互作用力示意图及径向和角向分力随取向角的变化 Fig. 2 The schematic illustration of interaction forces between adjacent particles and the variation of radial and angular components with orientation angle |
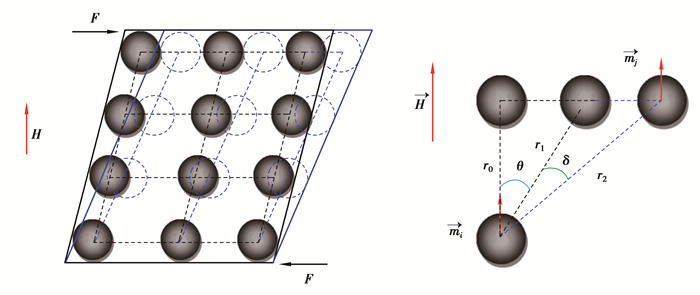
剪切受力是MRE的常见工作模式之一。MRE受剪切时产生变形,变形前后颗粒链与相邻颗粒间几何关系如图 3所示,假设变形前颗粒间沿磁场方向的距离为r0[22],变形前后颗粒间距离分别为r1和r2,颗粒链取向角为θ,应变角为δ,剪切力均匀分布在每个颗粒上。
|
图 3 剪切变形前后颗粒链及相邻磁偶极子间的几何关系 Fig. 3 Geometric relationship between particle chains and adjacent magnetic dipoles before and after shear deformation |
当MRE剪切变形时,在外加磁场作用下,内部磁化颗粒间的相互作用力
| $ F=\frac{3 C m^{2}}{2 \pi \mu_{0} \mu_{1} r^{4}}\left[5 \cos ^{2} \theta \sin \theta-\sin \theta\right], $ | (4) |
其中,
磁致剪切模量表达式为[19]
| $ \Delta G = \frac{{nF}}{{\gamma ', }} $ | (5) |
其中:n为单位截面中粒子链的数量,
| $ \Delta G=\frac{9 \varphi C r_{0}\left[5 \cos ^{2}(\theta+\delta) \sin (\theta+\delta)-\sin (\theta+\delta)\right]}{8 \pi^{2} a^{3} \mu_{0} \mu_{1} r_{2}^{4} \gamma \cos ^{2} \theta} m^{2}, $ | (6) |
从图 4中可知:
| $ K=\frac{\left[5 \cos ^{2}(\theta+\delta)-1\right] \cdot \sin (\theta+\delta) \cdot \cos ^{4}(\theta+\delta)}{\cos ^{2} \theta} 。$ | (7) |
则磁致剪切模量可表示为
| $ \Delta G=\frac{9 \varphi C K}{8 \pi^{2} a^{3} \mu_{0} \mu_{1} r_{0}^{3} \gamma} m^{2} 。$ | (8) |
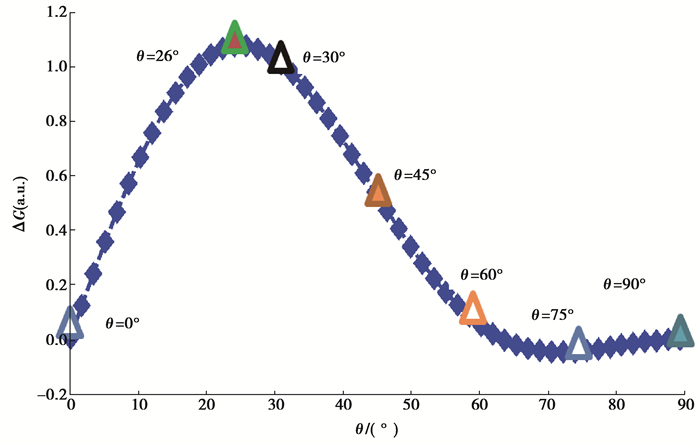
在(8)中,K与颗粒链取向角相关,在相同磁场下,取其他参数为定值,可得磁致模量随颗粒链取向角度的变化规律如图 4所示。
|
图 4 相同磁场下磁致模量随颗粒链取向角度的变化规律 Fig. 4 Variation of magneto-induced modulus modulus with particle chain orientation angle under the same magnetic field |
从图 4可以看出,磁致模量随颗粒链取向角度的增大先增大后减小,在26°附近达到最大值。当取向角大于63°时,出现负磁致模量。在几个特殊的取向角度情况下,磁致模量的绝对值表现出90° < 75° < 0° < 60° < 45° < 30°。从磁化颗粒间的相互作用来看,当MRE受外力剪切发生变形时,因为取向角度的存在,在外加磁场作用下,磁化颗粒间会在剪切方向产生一个相互作用力以抵抗变形[22]。当颗粒链与外加磁场的取向角度增大时,抵抗剪切变形的力先增大后减小,在26°附近达到最大值,直至方向发生改变。因此,磁致模量也随取向角度先增大后减小,并在较大角度表现出负磁致模量。从基体的角度看,磁化颗粒倾向于向外加磁场方向运动。由于固定在基体中的颗粒链与外加磁场方向存在取向夹角,使得这种趋势更加明显,受界面处基体的限制,颗粒产生的位移将使基体产生应力集中,MRE表现出磁致模量的变化[22]。
基于磁偶极子理论的微观磁致模型只考虑了颗粒间相互作用,未考虑基体与颗粒之间的磁场耦合对MRE磁致特性的影响,因此不能准确预测磁致模量大小。在实际应用中,为便于控制,需要准确预测不同磁场下MRE的磁致模量,因此基于参数的磁致模型更具工程应用价值[22]。通过实测值对简化微观模型中的参数进行逆向识别,可得MRE磁致模量的参数模型。将式(1)代入式(8)得
| $ \Delta G = \frac{{2\varphi CK{\mu _0}{\mu _1}}}{\gamma }{\left( {\frac{a}{{{r_0}}}} \right)^3}, {\left[ {\chi \cdot H} \right]^2} 。$ | (9) |
令
| $ \Delta G = A \cdot K \cdot {M^2}, $ | (10) |
其中A与颗粒粒径、应变、体积分数等参数相关,可视为常数;K与颗粒链取向角度相关;M为磁化强度,M=χ·H,与颗粒的磁化过程相关[22]。在羰基铁粉磁化过程中,颗粒磁化率与磁感应强度之间存在非线性特性[27],根据磁化曲线可拟合得到磁化强度与外加磁场之间的经验公式:M2=αB2+βB,代入式(10)得到磁致模量参数模型
| $ \Delta G = a{B^2} + bB , $ | (11) |
该磁致模量参数模型较为简明,仅包含a和b 2个参数,其中a=AKα,b=AKβ,都与颗粒链的取向角度有关。
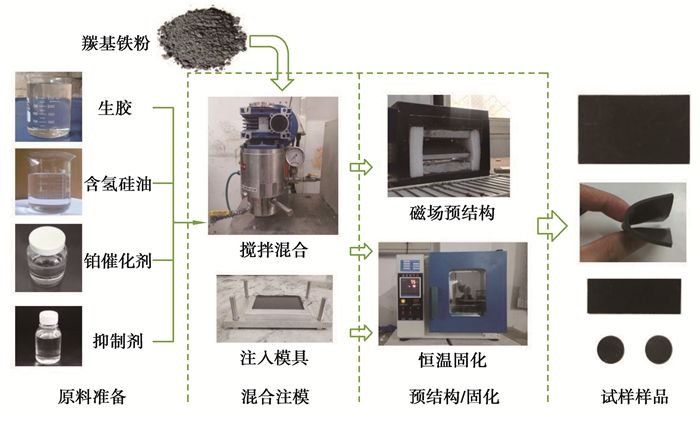
2 MRE试样制备及磁致模量测试为验证以上规律的准确性,制备了具有不同颗粒链取向角度的MRE试样并进行动态剪切力学性能测试。制备原料包括聚二甲基硅氧烷、硅油、铂催化剂和粒径分别为38 μm,75 μm,150 μm的羰基铁粉。将相同配比的羰基铁粉(质量分数33.3%)、聚二甲基硅氧烷(质量分数66.1%)以及硅油在真空状态下同铂催化剂混合搅拌均匀,将混合物倒入铝制模具中并放置在匀强磁场中,通过调整模具与磁场间的夹角,制备得到3种不同粒径,颗粒链具有6种不同取向角度的MRE试样,MRE试样的颗粒链取向角度分别为0°、30°、45°、60°、75°和90°。制备流程如图 5所示。
|
图 5 MRE试样的制备流程 Fig. 5 MRE sample preparation process |
对制备的试样进行磁场扫描测试,采用的仪器为Physica MCR301流变仪,其内置的励磁线圈可产生变化的均匀磁场。将试样裁成直径为20 mm,厚度为2 mm的圆片。测试时流变仪平行板与MRE表面接触并产生一个预压力(5 N);将流变仪设置为振荡剪切模式,测试频率为10Hz;当平行板旋转时,试样受到水平剪切,为保证MRE处于线性粘弹性区域内,设置剪切应变为0.1%[22];通过控制电流改变磁场大小,MRE内部的颗粒链取向角度为磁场方向和粒子链方向的夹角。
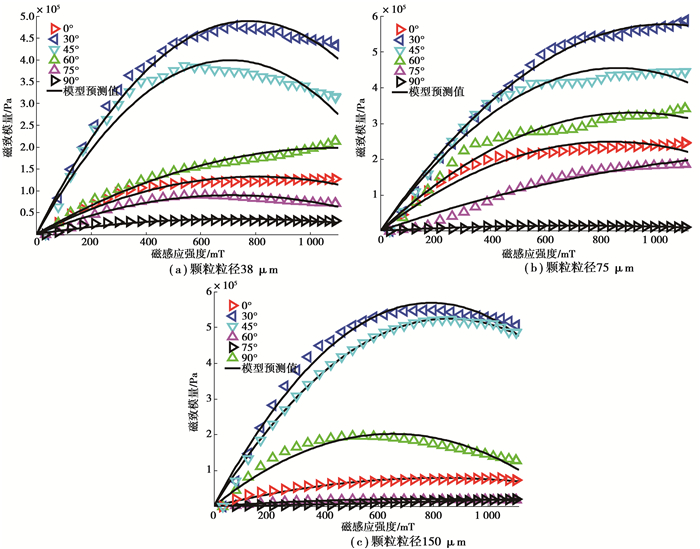
3 实验结果分析测试结果如图 6所示,测试磁场的变化范围约为0~1 100 mT,磁致剪切模量随磁场的增大呈非线性增大,这是由于颗粒磁化过程是非线性的。随外加磁场增大,MRE表现出明显的磁流变效应。3种不同粒径下MRE的磁致模量均表现出相同的规律,即90° < 75° < 0° < 60° < 45° < 30°,这与基于磁偶极子理论所推导的微观模型所表现的趋势一致,验证了该微观模型的准确性。
|
图 6 颗粒链取向角度和磁场对MRE磁致模量的影响 Fig. 6 The effect of particle chain orientation angle and magnetic field on MRE magneto-induced modulus |
根据实测的磁致剪切模量值,利用最小二乘法对式(11)中的参数进行识别,可得到不同粒径和取向角度下MRE的磁致模量参数模型中a,b的数值,如表 1所示。
| 表 1 不同粒径和取向角度下MRE磁致模量参数模型 Table 1 Parameter model of MRE magneto-induced modulus under different particle size and orientation angle |
在磁致模量参数模型中,从参数a,b的数值变化上可以看出,其绝对值都随取向角度的增大先增大后减小,并在30°时取得最大值,且在0~30°之间变化较大,这表明磁致模量对取向角度在0~30°之间的变化较为敏感,这与微观模型中的趋势符合[22]。参数模型预测值如图 6中实线所示,从图中可以看出,在不同的磁场大小下,基于参数的磁致模量模型可较为准确的预测MRE的磁致模量值,并且通过控制磁场大小可以改变取模量。为基于MRE的器件研究提供了理论参考。
4 结论基于磁偶极子理论,分析了磁化颗粒之间的相互作用,建立了虑及颗粒链取向角度的MRE磁致模量微观模型,通过分析颗粒间相互作用机理,预测了磁致模量随颗粒链取向角的变化趋势。制备了具有不同颗粒链取向角度的MRE试样,并测试了不同MRE试样的磁致模量。将所提出的磁致模量微观模型简化为含有未知参数的参数模型,并通过测试数据对模型中的参数进行识别,得到具有不同颗粒链取向角度MRE的磁致模量参数模型。主要结论如下:
1) MRE的力学性能不仅依赖于基体材料和颗粒含量,还取决于磁性颗粒在基体中的排列方式。基于磁偶极子理论建立的具有不同颗粒链取向角度的MRE的磁致剪切模量微观模型可以较好的解释和预测颗粒链取向角度对MRE磁致特性的影响。
2) MRE的磁致剪切模量与颗粒链取向角度有关。测试结果显示,在3种不同粒径(38 μm、75 μm和150 μm)下,MRE的磁致剪切模量均随颗粒链取向角度的增大先增大后减小。颗粒链取向角度为30°、45°和60°的MRE的磁致剪切模量大于传统的直链MRE的磁致剪切模型。因此,通过改变颗粒链取向角度可以提高MRE的磁致剪切模量。
3) 具有不同颗粒链取向角度MRE的磁致模量参数模型可以较准确的描述颗粒链取向角度和磁场对MRE磁致模量的影响。通过对相关参数的讨论可得,MRE的磁致模量在30°达到最大值,在0°~30°之间变化较快,与微观模型预测相符合。
| [1] |
Jolly M R, Carlson J D, Muoz B C. A model of the behaviour of magnetorheological materials[J]. Smart Materials and Structures, 1996, 5(5): 607-614. DOI:10.1088/0964-1726/5/5/009 |
| [2] |
Ginder J M, Nichols M E, Eliea L D, et al. Magnetorheological Elastomers: Properties and Applications. Part of the SPIE Conference on Smart Materials Technologies[J]. California, 1999, 3675: 131-138. |
| [3] |
Perales-Martinez I A, Palacios-Pineda L M, Lozano-Sanchez L M. Enhancement of a magnetorheological PDMS elastomers with carbonyl iron particles[J]. Polymer Testing, 2017, 57: 78-86. DOI:10.1016/j.polymertesting.2016.10.029 |
| [4] |
Shaoqi L, Yajun L, Yancheng L, et al. Investigation of dynamic properties of isotropic and anisotropic magnetorheological elastomers with a hybrid magnet shear test rig[J]. Smart Materials and Structures, 2020, 29(11): 114001. DOI:10.1088/1361-665X/ab9e09 |
| [5] |
Quan S, Li D, Xinglong G, et al. High performance magnetorheological elastomers strengthened by perpendicularly interacted flax fiber and carbonyl iron chains[J]. Smart Materials and Structures, 2020, 29(2): 025010. DOI:10.1088/1361-665X/ab5e49 |
| [6] |
Asadi Khanouki Mostafa, Sedaghati Ramin, Hemmatian Masoud. Multi-disciplinary Design Optimization of a Novel Sandwich Beam-Based Adaptive Tuned Vibration Absorber Featuring Magnetorheological Elastomer[J]. Materials, 2020, 13(10): 2261. DOI:10.3390/ma13102261 |
| [7] |
Xufeng C, Shouhu X, Jun L, et al. Magnetic-tunable sound absorber based on micro-perforated magnetorheological elastomer[J]. Smart Materials and Structures, 2020, 29(1): 015024. DOI:10.1088/1361-665X/ab57ec |
| [8] |
Armin R, Rasooli A, Sedaghati R, et al. A novel magnetorheological elastomer-based adaptive tuned vibration absorber: design, analysis and experimental characterization[J]. Smart Materials and Structures, 2020, 29(11): 115042. DOI:10.1088/1361-665X/abb575 |
| [9] |
Kim H K, Kim H S, Kim Y K. Stiffness control of magnetorheological gels for adaptive tunable vibration absorber[J]. Smart Materials and Structures, 2016, 26(1): 015016. |
| [10] |
Mi Z, Miao Y, Song Q, et al. Investigations on response time of magnetorheological elastomer under compression mode[J]. Smart Materials and Structures, 2018, 27(5): 055017. DOI:10.1088/1361-665X/aab63e |
| [11] |
Nabil H. Curing and swelling kinetics of new magnetorheological elastomer based on natural rubber/waste natural rubber gloves composites[J]. Journal of Elastomers & Plastics, 2019, 51(7-8): 583-602. |
| [12] |
Zhao D X, S S, Jun T Z, Ying Q G. Performance tests and modeling on high damping magnetorheological elastomers based on bromobutyl rubber[J]. Journal of Intelligent Material Systems and Structures, 2018, 29(6): 1025-1037. DOI:10.1177/1045389X17730909 |
| [13] |
Guanxin S, Wenju W, Guoping W, et al. Dynamic mechanical properties of FeSi alloy particles-filled magnetorheological elastomers[J]. Polymer-Plastics Technology and Materials, 2019, 58(15): 1625-1637. DOI:10.1080/25740881.2018.1563136 |
| [14] |
Bellan C, Bossis G. Field dependence of viscoelastic properties of elastomers[J]. International Journal of Modern Physics B, 2002, 16(17&18): 2447-2453. |
| [15] |
Yu M, Qi S, Fu J, et al. Understanding the reinforcing behaviors of polyaniline-modified carbonyl iron particles in magnetorheological elastomer based on polyurethane/epoxy resin IPNs matrix[J]. Composites Science and Technology, 2017(139): 36-46. |
| [16] |
Anna B, Stefan F A. Urethane Magnetorheological Elastomers-Manufacturing, Microstructure and Properties[J]. Smart Materials for Smart Devices and Structures, 2009(154): 107-112. DOI:10.4028/www.scientific.net/SSP.154.107 |
| [17] |
Boczkowska A, Awietjan SF, Pietrzko S, et al. Mechanical properties of magnetorheological elastomers under shear deformation[J]. Composites Part B: Engineering, 2011, 43(2): 636-640. |
| [18] |
Tongfei T, Masami N. Fabrication and characterisation of anisotropic magnetorheological elastomer with 45°iron particle alignment at various silicone oil concentrations[J]. Journal of Intelligent Material Systems and Structures, 2018, 29(2): 151-159. DOI:10.1177/1045389X17704071 |
| [19] |
Jolly M R, Carlson J D. The Magnetoviscoelastic Response of Elastomer Composites Consisting of Ferrous Particles Embedded in a Polymer Matrix[J]. Journal of Intelligent Material Systems and Structures, 1996, 7(6): 613-622. DOI:10.1177/1045389X9600700601 |
| [20] |
Davis L C. Model of magnetorheological elastomers[J]. Appl. Phys, 1999, 85(6): 3348-3351. DOI:10.1063/1.369682 |
| [21] |
Shen Y, Golnaraghi M F, Heppler G R.z. Experimental Research and Modeling of Magnetorheological Elastomers[J]. Journal of Intelligent Material Systems and Structures, 2004, 15(1): 27-35. DOI:10.1177/1045389X04039264 |
| [22] |
杨伟. 磁流变弹性体磁致特性研究及转子振动抑制用作动器设计[D]. 北京: 北京化工大学, 2019. YANG W. Micromechanics-based magneto-elastic constitutive modeling of particulate composites[D]. Beijing: Beijing University of Chemical Technology, 2019. |
| [23] |
Ioan B, Hyoung J C. Preparation and Electro-Thermoconductive characteristics of magneto-rheological suspensions[J]. International Journal of Modern Physics B, 2008, 22(29): 5041-5064. DOI:10.1142/S0217979208049376 |
| [24] |
Yao J, Yang W, Gao Y, et al. Magnetorheological elastomers with particle chain orientation: modelling and experiments[J]. Smart Materials and Structures, 2019, 28(9): 095008-095019. DOI:10.1088/1361-665X/ab2e21 |
| [25] |
党辉, 朱应顺, 龚兴龙, 等. 基于分布链修正的磁流变弹性体的物理模型[J]. 化学物理学报, 2005, 18(6): 971-975. Dang H, Zhu Y S, Gong X L, et al. Revised model of the magnetorhelogical elastomer based on distributed chains[J]. Chinese Journal of Chemical Physics, 2005, 18(6): 971-975. (in Chinese) DOI:10.3969/j.issn.1674-0068.2005.06.025 |
| [26] |
Antonioj. F B, Marcelo k, Mariareginaalca N S. Evaluation of Magnetorheological Suspensions Based on Carbonyl Iron Powders[J]. Journal of Intelligent Material Systems and Structures, 2002, 13(7): 471-478. DOI:10.1106/104538902030706 |
 2022, Vol. 45
2022, Vol. 45



