2. 陕西延长石油(集团)有限责任公司管道运输输气 第一分公司, 陕西 延安 716000;
3. 陕西延长石油(集团)有限责任公司管道运输第一分公司, 陕西 榆林 719000;
4. 西南石油大学 石油与天然气工程学院, 成都 610500;
5. 油气消防四川省重点实验室, 成都 611731
2. Shaanxi Yanchang Petroleum (Group) Co., Ltd. Pipeline Transport Gas First Branch, Yan'an, Shaanxi 716000, P. R. China;
3. Shaanxi Yanchang Petroleum (Group) Co., Ltd. Pipeline Transport First Branch, Yulin, Shaanxi 719000, P. R. China;
4. School of Oil & Gas Engineering, Southwest Petroleum University, Chengdu 610500, P. R. China;
5. Oil & Gas Fire Protection Key Laboratory of Sichuan Province, Chengdu 611731, P. R. China
海洋石油资源正成为各国争相开发与布局的关键领域[1-3],是全球油气资源的重点接替区之一[4-5],深水区域将成为未来海上油气开发的主战场[6-7]。海洋石油也是中国油气产量主要的增长来源,近5年来,中国重大油气田主要来自近海、深水[8],根据全国油气资源评价的结果,近海石油地质资源量为1.074×1010 t[9]。渤海油田整个盆地群在生产油田超过50个,其中探明稠油地质储量占总储量的50.4%,蕴藏着丰富的稠油资源[10]。所以,高黏原油的节能增效及采输流动安全是克服轻质原油日益贫乏、保障原油接替的重中之重,但是稠油胶质、沥青质等大分子含量高,相对直链烃含量少,具有高黏度、强吸附、高摩阻等流动特征,导致其输送具有较大挑战。目前,管输稠油流动黏附性强、能耗高、停输管线再启动困难等技术瓶颈仍然存在,尤其是停运管在海底低温工况条件下,因重质原油的高黏性,使得停输管的启动压力特别高[11];另外,稠油在开采与输送过程同时会产生油田采出水,油水两相流动过程会使稠油乳液形成,但由于稠油-水乳状液存在相反转点、油水密度差等,导致停运管线初始阶段油水状态及其演化运移复杂[12-13]。特别是稠油-水两相混输海管的停输再启动的流动保障问题[14],海洋稠油-水混输过程中不可避免的计划检修或事故停输(台风等事故需平台人员紧急撤离);虽然,管输稠油停运后不致发生相变、凝结等现象[15],但在海洋恶劣环境下,其高黏性、低流动性,导致管线启动困难,稠油-水混输给停运管线再启动压力预测与流动保障带来较大挑战[16-17]。目前,中科院许晶禹教授针对超稠油的黏弹特征、屈服应力及原油管道停运时启动应力和流动规律进行了研究[7],但适合稠油-水两相混输及其油水乳状液的启动应力模型,特别是对稠油-水两相混输停运管线再启动压力预测精准性与可靠性等还需进一步研究。因此,文中瞄准稠油-水混输再启动过程力学特性,通过分析稠油及其乳状液启动过程应力响应特性,基于正交启动实验,建立了启动应力的非线性模型,对再启动压力进行准确预测,为稠油管线停输再启动提供理论依据和实际指导。
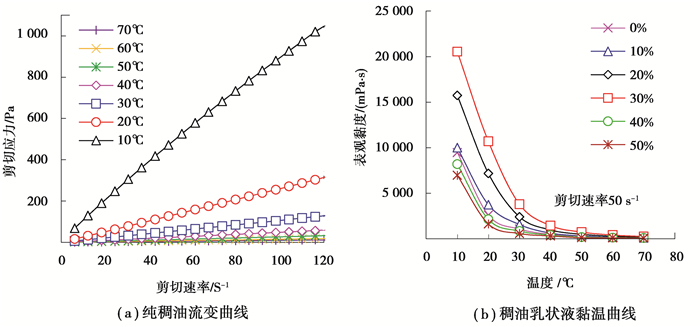
1 实验部分 1.1 实验材料选取渤海油田旅大21-2(以下简称LD 21-1)稠油及油田采出水为实验材料,其纯稠油黏度为307.20 MPa·s(50 ℃)、密度为917.5 kg/m3(20 ℃),旅大油田采出水矿化度,如表 1所示。运用Rheolab QC流变仪测量系统分析稠油及其乳状液的流变学特征,其纯稠油流变曲线、黏温曲线,如图 1所示。分析了稠油-水乳状液在不同含水率、不同温度、不同停输时间、不同启动流量等条件下再启动时力学变化规律,包括旋转启动应力与停运管道再启动压力特性。采用上述流变仪分析系统,测量油流在恒定剪切速率启动过程时,旋转启动应力随时间的变化规律,回归实验数据构建再启动应力模型,进一步计算与分析停运管线的启动压力值及其变化规律。
| 表 1 旅大油田采出水矿化度 Table 1 The salinity of produced water in Lvda Oilfield |
|
图 1 稠油及其乳状液流变特性 Fig. 1 Rheological properties of heavy oil and its emulsions |
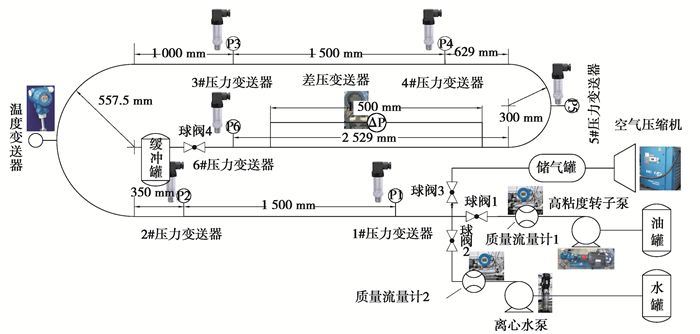
为验证停运管线再启动压力计算的精准性,研制与搭建了1套稠油乳状液环道停输再启动实验装置,测量启动压力与理论计算值进行对比,其环道的材质为304不锈钢管、管道长度为10.2 m、管道内径为25 mm,如图 2所示。
|
图 2 稠油再启动环道实验装置 Fig. 2 The heavy oil restart loop experimental device |
按照所规定的油水比例将稠油水分别通过变频油泵和水泵,把油样、水样泵送到环道管路实验装置内,而后关闭阀门4,停泵同时关闭阀门1、阀门2;等停输所给定的时间后,打开阀门1,并启动油泵,在一定的启动流量下推动停输管道内油流流动,环道沿线不同位置处安装有6个压力变送器,测量在不同条件下的压力变化[18]。
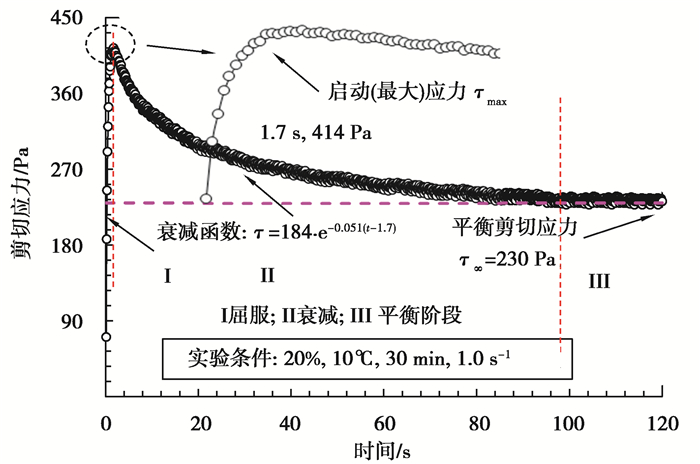
2 结果与讨论 2.1 启动应力响应特性以稠油及其油水乳状液为测试对象,分别测量在不同工况下(不同含水率、温度、静置时间、启动流量),启动初始阶段力学变化规律,剖析不同工况下,剪切应力与时间的变化关系,分析启动过程与启动应力模式。在恒定剪切速率启动条件下,不管何种类型的实验样品,在启动过程总存在着一个剪切应力上升阶段;尤其在剪切应力达到峰值前,剪切应力先随时间存在一个骤然增大阶段,再随时间缓慢增大至峰值,在启动过程中将最大剪切应力所对应的时刻认为油流将开始启动,自此剪切应力随时间由峰值开始减小,如图 3所示。分析可知,在停输管道中静置稠油乳液启动过程中与管内壁间产生的应力受到诸多因素的影响,并随时间的延长而变化,呈先迅速增大再缓慢减小至恒定值的总体趋势。为准确描述启动过程剪切应力随时间的变化关系,拟合实验数据并建立启动应力变化的模型是分析与预测停输管道再启动压力的基础。引入了含水率、启动温度、静置时间、恒定剪切速率影响因素,分析此4个因素对启动应力影响作用的定量关系,作为建立启动应力模型的一个必要及关键参数。
|
图 3 含水率20%的稠油乳状液启动过程力学响应特性 Fig. 3 The start-up mechanical response characteristics of heavy oil emulsion with 20% water content |
剖析稠油及其乳状液或稠油-水两相混合液的启动过程,研究在恒定剪切速率工况下,启动应力与时间的变化规律,可以发现油样在旋转启动过程中分为剪切应力的上升、衰减、平衡了3个应力变化阶段,通过实动过程实验数据拟合可知,满足式(1)启动过程应力变化模型[18]。
| $ \left\{\begin{array}{l} \tau_{\mathrm{s}}=\tau_{\infty}+\left(\tau_{\max }-\tau_{\infty}\right) \mathrm{e}^{-B\left(t-t_{\mathrm{s}}\right)},\left(t_{\mathrm{s}} \leqslant t<t_{\infty}\right), \\ \tau_{\mathrm{s}}=\tau_{\infty},\left(t \geqslant t_{\infty}\right) ; \end{array}\right. $ | (1) |
式中:τs为启动过程中壁面剪切应力,Pa;τmax为启动最大应力,Pa;τ∞为平衡剪切应力,Pa;B为衰减指数,其值愈大,由τmax降至τ∞愈快,单位为s-1;T为剪切时间,s;ts为启动最大应力所对应的时间,s;t∞为达到动态平衡所需要的时间,s。
分析ts为启动最大应力所对应的时间,该时间ts值的大小受油品自身性质、油流所处的条件、油流旋转启动过程测试装置惯性等影响较大,故ts不仅仅是油品自身性质的体现。为定量描述分析衰减-平衡阶段应力随剪切时间的变化过程,基于模型式(1),从ts=0开始分析,直接给停运管线一个恒定的启动流量,忽略在启动过程初始阶段的应力上升过程,启动过程应力变化模型式(1)可化为式(2)。
| $ \left\{\begin{array}{l} \tau_{\mathrm{s}}=\tau_{\infty}+\left(\tau_{\max }-\tau_{\infty}\right) \mathrm{e}^{-B t},\left(0 \leqslant t<t_{\infty}\right), \\ \tau_{\mathrm{s}} \approx \tau_{\infty},\left(\mathrm{t} \geqslant \mathrm{t}_{\infty}\right)。\end{array}\right. $ | (2) |
分析不同因素对启动应力影响的显著程度,进行4因素混合水平的正交启动实验,其影响因素及水平,如表 2所示。含水率有6种水平、温度与恒定剪切速率分别有4种水平、静置时间有2种水平,依据正交实验原理设计32组启动实验,其启动应力结果如表 3所示。在此基础上,应用SPSS软件对实验结果进行模型回归,研究各因素的影响显著程度及其与启动应力的量化关系。
| 表 2 稠油-水乳状液正交启动实验影响因素与水平 Table 2 Influencing factors and levels of heavy oil water emulsion orthogonal start up experiment |
| 表 3 四因素混合水平正交实验设计及启动应力结果 Table 3 Results of start-up stress by orthogonal test on four factors and mixed levels |
采用SPSS软件对正交启动实验结果进行方差分析,评价上述各因素对稠油乳状液或稠油-水混合液启动应力的影响作用显著程度,通过比较F值与显著性Sig.值,确定4种因素影响作用的显著程度;稠油-水油流的正交启动应力实验方差分析结果,如表 4所示。可知恒定剪切速率与启动温度对稠油乳状液启动应力的影响最为显著,关系也最为密切;静置时间对启动应力的影响也较为显著,但与启动温度和恒定剪切速率相比较次之;在0~50%范围内,含水率对启动应力也有着相当的影响,但影响较为微弱;就对其启动应力影响显著性程度而言,其总体排序有:恒定剪切速率>启动温度>静置时间>含水率。
| 表 4 四因素混合水平正交实验方差分析结果 Table 4 Results of start-up stress by orthogonal test on four factors and mixed levels |
由于启动应力的4个影响因素具有不同单位,且各因素间的水平也不在同一个数量级上,为减小拟合模型的误差,回归分析前将对各因素的水平进行归一化处理。采用最小-最大标准化的归一化处理方法。这种方法是对原始数据进行了线性变化,使其结果映射在[0-1]之间,其转化函数为
| $ \tilde{x}=\frac{x-x_{\min }}{x_{\max }-x_{\min }}, $ | (3) |
式中:
依据影响启动应力自变量和因变量的范围,应用式(3)可得各因素的转化函数。
| $ \tilde{\varphi}=\frac{\varphi-0}{0.5-0}, \widetilde{T}_{\mathrm{s}}=\frac{T_{\mathrm{s}}-4}{20-4}, \widetilde{t}_{\mathrm{st}}=\frac{t-30}{60-30}, $ |
式中:φ为含水率,无量纲;Ts为启动温度,℃;tst为静置时间,min;
| $ \tau_{\max }=a^{\prime} \cdot\left(b^{\prime}+c^{\prime} \tilde{\varphi}+d^{\prime} \tilde{\varphi}^{2}\right) \cdot \tilde{T}_{\mathrm{s}}^{\mathrm{e}^{\prime} \prime} \cdot \tilde{t}_{\mathrm{st}}^{\mathrm{f}^{\prime}} \cdot \tilde{\dot{\gamma}}^{\prime {\rm g}^{\prime}}, $ | (4) |
式中:a′为黏性模量,Pa;b′、c′、d′、e′、f′、g′为非线性启动应力预测模型的系数,单位为无量纲。
应用SPSS软件对模型及各相关系数进行非线性回归与检验,通过79次模型评估和34次导数评估后运行停止,连续残差平方和之间的相对减少量最多为SSCON=1.000E-8;相关性R2(1-残差平方和/已更正的平方和)等于0.946,R2>0.90,回归模型与正交实验数据有着较高的拟合程度;故可得到非线性回归模型系数的最优解,将模型系数代入式(4)可得稠油-水乳状液启动应力的非线性回归模型为
| $ \tau_{\max }=620.8 \cdot\left(246.5+2\ 252.1 \tilde{\varphi}-4\ 970.9 \tilde{\varphi}-^{2}\right) \cdot \tilde{T}_{\mathrm{s}}^{-1_\circ{232 ^\prime}} \cdot \tilde{t}_{\mathrm{st}}^{-1_\circ 105} \cdot \tilde{\dot{\gamma}}^{\prime 0.342} 。$ | (5) |
分析可知,随含水率的增大,稠油乳状液或混合液的启动最大应力先增大后减小,存在启动应力峰值,通过计算得到峰值φ=0.54,恰好在稠油乳状液的反相点前后;启动温度与启动最大应力呈指数减小关系,即随着启动温度增大,启动应力减小,有呈凸向温度轴的减小趋势,即温度越大,减小幅度越小;恒定剪切速率与启动应力呈正相关,随着恒定剪切速率的增大,启动应力增大;而启动应力在起始一定的静置时间内呈减小趋势,而后随静置时间基本保持不变。
启动应力τmax依据式(5)回归的非线性模型进行计算,τ∞按已经恢复流动后的稠油-水乳液的本构方程计算,故在衰减过程中应力变化为
| $ \left\{\begin{array}{l} \tau_{\mathrm{s}}=m \dot{\gamma}^{\prime n}+620.8 \cdot\left(246.5+2\ 252.1 \tilde{\varphi}-4\ 970.9 \tilde{\varphi}-^{2}\right) \cdot \tilde{T}_{\mathrm{s}}^{-1.232 ^\prime} \cdot \tilde{t}_{\mathrm{st}}^{-1.105} \cdot \tilde{\gamma}^{\prime 0.342} \cdot \mathrm{e}^{-B t}-m \dot{\gamma}^{\prime n} \cdot \mathrm{e}^{-B t} \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(0 \leqslant t<t_{\infty}\right), \\ \tau_{\mathrm{s}}=m \dot{\gamma}^{\prime n} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(t \geqslant t_{\infty}\right)。\end{array}\right. $ | (6) |
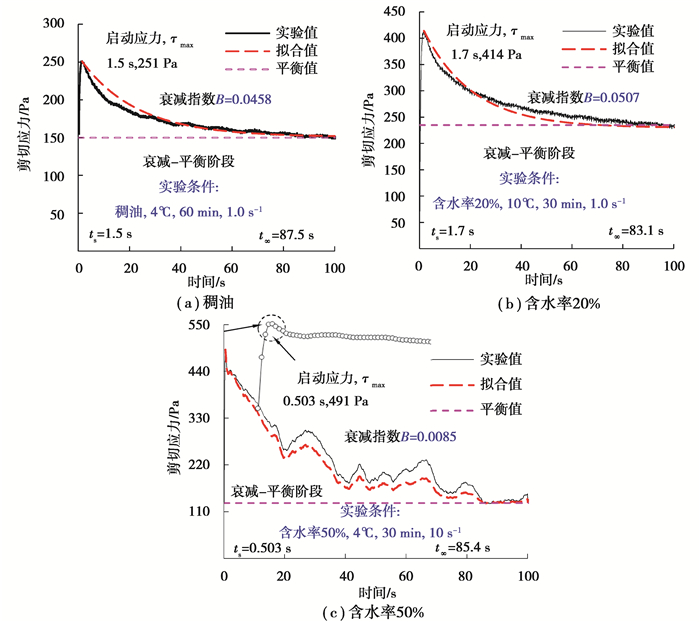
启动应力温度评价范围为4~40 ℃,通过上述启动过程应力变化模型式(6)描述其衰减过程与平衡过程。分别选取稠油-水乳状液或混合液在3种含水工况(0、20%、50%)为例进行分析,说明启动过程应力变化规律,对比实测值与拟合值的一致性情况。由图 4可见,稠油在启动温度4 ℃、静置时间60 min、恒定剪切速率1.0 s-1的启动条件下,起始时刻剪切应力随时间迅速增大,在1.5 s处达峰值251 Pa,启动最大应力;此后,剪切应力随时间慢慢降低,在87 s以后,剪切应力恒定在150 Pa,应力值随时间不再变化,如图 4(a)所示。稠油-水在剪切应力作用所形成的油包水型(W/O型)乳状液分析时可认为是单一均相体系,启动过程的衰减阶段剪切应力响应平滑,如图 4(a)与图 4(b)所示。当含水率大于反相点后,成水包油型(O/W型)乳状液,启动过程也基本遵循着这3个阶段,只是在衰减阶段有较为明显的上下波动,而非呈现出缓慢平滑的曲线,但也在某一恒定值上下变化,分析波动的原因,由于稠油-水乳状液反相之后为乳状液与游离水共存的一种油水两相混合体系,受到游离水作用在测试过程中出现小范围波动,由于处于平衡阶段剪切应力保持在恒定值130 Pa,但在该恒定值上下存在明显的、较小幅度的应力波动[19],如图 4(c)所示。图 3给出了3种工况下启动过程应力变化的拟合优度分别为2.17%、3.27%、9.06%,可见启动过程应力变化的实验测量值与理论计算值的一致性较好。
|
图 4 衰竭阶段启动应力实测值与拟合值对比 Fig. 4 The comparison of measured value and fitting value of start-up stress in failure stage |
油停输管线再启动时,需着重分析由摩阻造成的启动压力,该部分压力是因壁面应力而产生,但在启动初始阶段壁面应力将随剪切时间而变化。当给停运管施加动力后,管道起点油流受到动力挤压开始流动,压力波沿管道慢慢向管线终点传播,当施加压力为t=L/a后,压力波传播到管道终点,管线终点油流受到压力开始流动,当管线终点原油刚刚受到剪切作用开始流动时,管线起点原油在剪切作用下已流动了L/a。当压力波线传播速度保持不变时,管线中各位置处油流随至起点的距离越远,油流受到剪切作用产生流动的时间越短。
令l为某位置至管线起点的长度,则该位置油流在整条管线完全启动时已产出流动的时间为(L-l)/a,将t=(L-l)/a代入式(2),推导出管道壁面处应力值沿管线长度的变化关系式为
| $ \left\{\begin{array}{c} \tau_{\mathrm{s}}=\tau_{\infty}+\left(\tau_{\max }-\tau_{\infty}\right) \mathrm{e}^{-B\frac{t_\infty a-l}{a}} & \left(0<l \leqslant t_{\infty} a\right), \\ \tau_{\mathrm{s}}=\tau_{\infty} & \left(t_{\infty} a<l \leqslant L\right)。\end{array}\right. $ | (7) |
其中,启动时的压力波传播速度a可按下式(8)计算[20]:
| $ a=\sqrt{1 /\left[\rho\left(\frac{1}{K}+\frac{D c_{1}}{E \delta}\right)\right]}, $ | (8) |
式中:ρ为稠油及其乳状液密度,kg/m3;K为体积模量,Pa;取1.56×109 Pa;D为内径,m;c1为管道支撑情况修正因数,无量纲;取c1=1;δ为环道壁厚,m;E为管材弹性模量,Pa;取2.069×1011 Pa。
由于油流与壁面间的阻力而引起的启动压力部分,根据其轴向的受力平衡,选取半径为r的小圆柱微元体进行分析,其中长度为dl、切向应力为τs,可得:
| $ (p+\mathrm{d} p) \cdot {\rm{ \mathsf{ π} }} r^{2}-p \cdot {\rm{ \mathsf{ π} }} r^{2}=\tau_{\mathrm{s}} \cdot 2 {\rm{ \mathsf{ π} }} r \cdot \mathrm{d} l, $ | (9) |
| $ \tau_{\mathrm{s}}=\frac{r}{2} \cdot \frac{\mathrm{d} p}{\mathrm{~d} l} 。$ | (10) |
| $ \mathrm{~d} p=\frac{4 \tau_{\mathrm{s}}}{D} \mathrm{~d} l。$ | (11) |
当停运管启动过程中整条管线温度相同时,由油流在管壁黏附作用所产生的再启动压力部分ΔPl按式(12)与式(14)计算。
1) 当L/a≤t∞时,因摩阻产生的启动压力部分按式(12)计算:
| $ \begin{gathered} \Delta P_{l}=\int_{0}^{L} \frac{4 \tau_{\mathrm{s}}}{D} \mathrm{~d} l=\frac{4}{D} \int_{0}^{L}\left[\tau_{\infty}+\left(\tau_{\max }-\tau_{\infty}\right) \mathrm{e}^{-B(L-l) / a}\right] \mathrm{d} l= \\ \frac{4 \tau_{\infty} L}{D}+\frac{4 a}{D B}\left(\tau_{\max }-\tau_{\infty}\right)\left(1-\mathrm{e}^{-\frac{B L}{a}}\right) 。\end{gathered} $ | (12) |
此工况下水平管段停运时,其稠油再启动压力可按式(13)计算:
| $ \begin{gathered} \varDelta P=\frac{4 \tau_{\infty} L}{D}+\frac{4 a}{D B}\left(\tau_{\max }-\tau_{\infty}\right)\left(1-\mathrm{e}^{-\frac{B L}{a}}\right)+\frac{4 Q_{\mathrm{e}} \rho a}{{\rm{ \mathsf{ π} }} D^{2}}= \\ \frac{4 L}{D} m \dot{\gamma}^{n}+\frac{4 a}{D B}\left(\tau_{\max }-m \dot{\gamma}^{n}\right)\left(1-\mathrm{e}^{-\frac{B L}{a}}\right)+\frac{4 Q_{\mathrm{e}} \rho_{\mathrm{e}} a}{{\rm{ \mathsf{ π} }} D^{2}}, \end{gathered} $ | (13) |
式中:m为稠度系数,Pa·sn;n为流变指数,无量纲;Qe为启动流量,m3/s。
2) 当L/a>t∞时,因摩阻产生的启动压力部分,可按式(14)计算:
| $ \begin{gathered} \varDelta P_{l}=\int_{0}^{L} \frac{4 \tau_{\mathrm{s}}}{D} \mathrm{~d} l=\frac{4}{D} \int a t_{\infty}{}_{_0}\left[\tau_{\infty}+\left(\tau_{\max }-\tau_{\infty}\right) \mathrm{e}^{-B(a t _\infty-l) / a}\right] \mathrm{d} l+\frac{4}{D} \int_{a t \infty}^{L} \tau_{\infty} \mathrm{d} l= \\ \frac{4 \tau_{\infty} L}{D}+\frac{4 a}{D B}\left(\tau_{\max }-\tau_{\infty}\right)\left(1-\mathrm{e}^{-B t_{\infty}}\right) 。\end{gathered} $ | (14) |
因此,此工况下水平管段停运时,其稠油的再启动压力可按式(15)计算:
| $ \begin{gathered} \varDelta P=\frac{4 \tau_{\infty} L}{D}+\frac{4 a}{D B}\left(\tau_{\max }-\tau_{\infty}\right)\left(1-\mathrm{e}^{-B t _\infty}\right)+\frac{4 Q_{\mathrm{e}} \rho a}{{\rm{ \mathsf{ π} }} D^{2}}= \\ \frac{4 L}{D} m \dot{\gamma}^{n}+\frac{4 a}{D B}\left(\tau_{\max }-m \dot{\gamma}^{n}\right)\left(1-\mathrm{e}^{-B t_{\infty}}\right)+\frac{4 Q_{\mathrm{e}} \rho_{\mathrm{e}} a}{{\rm{ \mathsf{ π} }} D^{2}}。\end{gathered} $ | (15) |
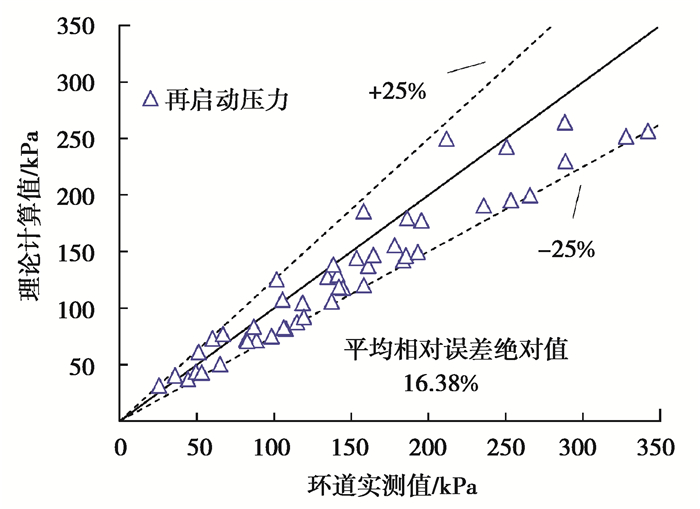
通过上述再启动压力动力学理论分析与环道实验测量,将再启动压力理论计算值与环道实测值进行了对比与误差分析,如图 5所示,相对误差在±25范围内,平均相对误差绝对值为16.38%,可见其吻合精度较好。运用所提出的“四系数七参数启动应力模型”可较好地预测稠油-水混输停运管道的再启动压力。再启动压力随启动温度提升而降低、随恒定剪切速提高而升高,因此,控制温度与启动时流量的大小,若提高Ts、减小
|
图 5 再启动压力理论计算值与环道实测值误差分析 Fig. 5 Error analysis of theoretical calculated value and measured value of restart-up pressure |
1) 稠油-水乳状液在恒定剪切速率启动过程中,整体上可分为屈服、衰减、平衡3个阶段:屈服前剪切应力迅速上升,达到应力峰值后开始缓慢减小至平衡应力,而后处于平衡阶段应力不再显著变化;
2) 基于正交启动实验,通过SPSS软件对90组正交数据进行非线性回归分析,建立了稠油-水乳状液四参量七系数启动应力预测模型;
3) 根据稠油乳状液流变学特征与启动应力特性,建立了稠油-水混合液停输管道的再启动过程动力学模型,启动压力预测值与实测值平均相对误差绝对值小于16.38%;环道再启动压力随温度升高而降低,随启动过程中启动流量的升高而升高,适当升高启动流量能减少停输管线的再启动时间,但将伴随着再启动压力的升高。
| [1] |
Tong X G, Zhang G Y, Wang Z M, et al. Distribution and potential of global oil and gas resources[J]. Petroleum Exploration and Development, 2018, 45(4): 779-789. DOI:10.1016/S1876-3804(18)30081-8 |
| [2] |
吴磊, 詹红兵. 全球海洋治理视阈下的中国海洋能源国际合作探析[J]. 太平洋学报, 2018, 26(11): 56-69. Wu L, Zhan H B. On international cooperation of China's maritime energy in the perspective of global ocean governance[J]. Pacific Journal, 2018, 26(11): 56-69. (in Chinese) |
| [3] |
Dong X H, Liu H Q, Chen Z X, et al. Enhanced oil recovery techniques for heavy oil and oilsands reservoirs after steam injection[J]. Applied Energy, 2019, 239: 1190-1211. |
| [4] |
Wang H J, Ma F, Tong X G, et al. Assessment of global unconventional oil and gas resources[J]. Petroleum Exploration and Development, 2016, 43(6): 925-940. DOI:10.1016/S1876-3804(16)30111-2 |
| [5] |
Guo K, Li H L, Yu Z X. In-situ heavy and extra-heavy oil recovery: a review[J]. Fuel, 2016, 185: 886-902. DOI:10.1016/j.fuel.2016.08.047 |
| [6] |
高德利, 朱旺喜, 李军, 等. 深水油气工程科学问题与技术瓶颈: 第147期双清论坛学术综述[J]. 中国基础科学, 2016, 18(3): 1-6. Gao D L, Zhu W X, Li J, et al. Scientific problems and technical bottlenecks in deepwater oil & gas engineering-academic review of the 147th shuangqing forum[J]. China Basic Science, 2016, 18(3): 1-6. (in Chinese) DOI:10.3969/j.issn.1009-2412.2016.03.001 |
| [7] |
Zhang J, Chen X P, Zhang D, et al. Rheological behavior and viscosity reduction of heavy crude oil and its blends from the Sui-Zhong oilfield in China[J]. Journal of Petroleum Science and Engineering, 2017, 156: 563-574. DOI:10.1016/j.petrol.2017.06.038 |
| [8] |
吕建中, 郭晓霞, 杨金华. 深水油气勘探开发技术发展现状与趋势[J]. 石油钻采工艺, 2015, 37(1): 13-18. Lv J Z, Guo X X, Yang J H. Development status and trend of deepwater oil-gas exploration and development technology[J]. Oil Drilling & Production Technology, 2015, 37(1): 13-18. (in Chinese) |
| [9] |
Song Y, Li Z, Jiang Z X, et al. Progress and development trend of unconventional oil and gas geological research[J]. Petroleum Exploration and Development, 2017, 44(4): 675-685. DOI:10.1016/S1876-3804(17)30077-0 |
| [10] |
周守为, 李清平, 朱海山, 等. 海洋能源勘探开发技术现状与展望[J]. 中国工程科学, 2016, 18(2): 19-31. Zhou S W, Li Q P, Zhu H S, et al. The Current state and future of offshore energy exploration and development technology[J]. Engineering Sciences, 2016, 18(2): 19-31. (in Chinese) DOI:10.3969/j.issn.1009-1742.2016.02.004 |
| [11] |
Moisés G V L, Alencar L S, Naccache M F, et al. The influence of thixotropy in start-up flow of yield stress fluids in a pipe[J]. Journal of Petroleum Science and Engineering, 2018, 171: 794-807. DOI:10.1016/j.petrol.2018.07.072 |
| [12] |
Jing J Q, Sun J, Tan J T, et al. Investigation on flow patterns and pressure drops of highly viscous crude oil-water flows in a horizontal pipe[J]. Experimental Thermal and Fluid Science, 2016, 72: 88-96. DOI:10.1016/j.expthermflusci.2015.10.022 |
| [13] |
王帅, 赵金柱, 王荣元, 等. 乳化/润湿耦合作用稠油流动减阻新思路[J]. 化工进展, 2021, 40(S2): 126-139. Wang S, Zhao J Z, Wang R Y, et al. New ideas of heavy oil flow drag reduction by emulsification and wetting coupling action[J]. Chemical Industry and Engineering Progress, 2021, 40(S2): 126-139. (in Chinese) |
| [14] |
Geesta C V, Guersoni V C, Bannwar A C. Experimental study of the time to restart the flow of a gelled waxy crude in rheometer and pipeline[J]. Journal of Petroleum Science and Engineering, 2019, 181: 106247: 1-10. |
| [15] |
Li H Y, Zhang J J, Xu Q G, et al. Influence of asphaltene on wax deposition: deposition inhibition and sloughing[J]. Fuel, 2020, 266: 117047. |
| [16] |
Pang S S, Pu W F, Xie J Y, et al. Investigation into the properties of water-in-heavy oil emulsion and its role in enhanced oil recovery during water flooding[J]. Journal of Petroleum Science and Engineering, 2019, 177: 798-807. |
| [17] |
Ilyin S O, Strelets L A. Basic fundamentals of petroleum rheology and their application for the investigation of crude oils of different natures[J]. Energy & Fuels, 2018, 32(1): 268-278. |
| [18] |
赵海勇, 王帅, 陈龙, 等. 稠油-水混输停运管线再启动力学响应特性研究[J]. 西安石油大学学报(自然科学版), 2021, 36(6): 117-121. Zhao H Y, Wang S, Chen L, et al. Dynamic response characteristics of heavy oil-water mixed transportation pipeline restart[J]. Journal of Xi'an Shiyou University (Natural Science Edition), 2021, 36(6): 117-121. (in Chinese) |
| [19] |
王帅, 敬加强, 宋学华, 等. 稠油乳状液屈服特性及环道启动压力预测[J]. 化工进展, 2019, 38(9): 4020-4028. Wang S, Jing J Q, Song X H, et al. Yield characteristics of heavy oil emulsion and prediction for pipeline start-up pressure[J]. Chemical Industry and Engineering Progress, 2019, 38(9): 4020-4028. (in Chinese) |
| [20] |
刘天佑, 高艳清, 曹强, 等. 原油长输管道启动压力研究[J]. 油气储运, 1997, 16(12): 7-13. Liu T Y, Gao Y Q, Cao Q, et al. A study on the restart pressure of long-distance trunkline[J]. Oil & Gas Storage and Transportation, 1997, 16(12): 7-13. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45

