2. 廊坊市北方天宇机电技术有限公司,河北 廊坊 065099
2. Langfang North Tianyu Electromechanical Technology Co., Ltd., Langfang, Hebei 065099, P. R. China
传统概念认为飞行汽车是集空中飞行与地面行驶功能于一体的陆空两栖交通工具[1]。随着城市空中交通(urban air mobility,UAM)概念的兴起,飞行汽车这一概念不断被扩大,仅具有空中飞行功能的垂直起降飞行器(vertical take off and landing,VTOL)亦被称为飞行汽车[2]。许多初创公司例如:Terrafugia、AeroMobil、PAL-V、Opener、Kitty Hawk等,及成熟的汽车和航空器制造公司例如:空客、奥迪、劳斯莱斯、阿斯顿马丁、吉利等,正不断展示其飞行汽车原型[3]。飞行汽车如火如荼发展的同时,正面临飞行汽车性能、适航认证及空中交通管理等问题。就飞行汽车性能而言,高功率密度推进与高升阻比轻质车体是飞行汽车研发面临的主要瓶颈与关键技术[1]。不断寻求高功率、轻量化、高推重比飞行汽车的同时,势必给传动系统的安全性与可靠性带来更严峻挑战。齿轮作为飞行汽车运动和动力传递的重要零部件,其工作可靠性将直接决定飞行汽车的行车安全。
齿轮传动失效将会导致飞行器发动机空停、重要零部件破坏以及重大人机安全事故等。疲劳是引发齿轮失效的主要原因之一[4-6],飞行器齿轮失效主要包括齿根弯曲疲劳破坏、齿面接触疲劳破坏等[7-8]。Cheng等[9]针对航空发动机锥齿轮齿面失效,运用失效故障树分析方法与电镜扫描、能谱分析、金相检验及硬度测量等检测表征手段,发现接触齿面疲劳失效与材料成分、金相组织、显微硬度和渗碳深度等因素有关。Manda等[10]针对直升机冷却风扇驱动齿轮疲劳断裂开展研究,发现未失效齿轮显微组织比失效齿轮更细,且该断裂主要由齿根疲劳裂纹导致。此外,众多学者针对飞行器齿轮传动可靠性分析与优化设计开展了大量研究。Chang等[11]针对飞行器起落架齿轮可靠性问题,结合基于神经网络动态仿真模型与一次二阶矩法,得到该起落架齿轮传动可靠度,并发现负载转矩与工作温度对可靠性影响较大。Sato等[12]针对新一代开式转子航空发动机行星轮系,结合计算流体动力学、有限元分析等方法开展优化设计,满足传递14 700 kW功率、效率99.5%、平均故障间隔时间5 000 h等要求。飞行汽车传动系统除结构类型设计需进一步开发外,其齿轮传动可靠性评估与优化方法也十分欠缺。飞行汽车有别于传统汽车与多数飞行器,其齿轮传动要求满足垂直起飞与巡航飞行等工况,且变速器长期处于高速运转工况下,一旦失效将会带来严重后果。笔者以某大型倾转翼飞行汽车试验偏置复合轮(offset compound gear,OCG)变速器作为研究对象,建立变速器齿轮传动可靠性分析与结构优化模型,分析各级传动与整体结构的疲劳可靠性,并获得高可靠轻量化的齿轮传动结构参数,为飞行汽车传动系统开发提供支撑。
1 疲劳可靠性分析与结构优化飞行汽车变速器齿轮传动疲劳可靠性分析与结构优化模型包括:传动结构与工况分析、疲劳可靠性分析、结构参数优化3部分,技术路线如图 1所示。

|
图 1 技术路线图 Fig. 1 Calculation flow chart |
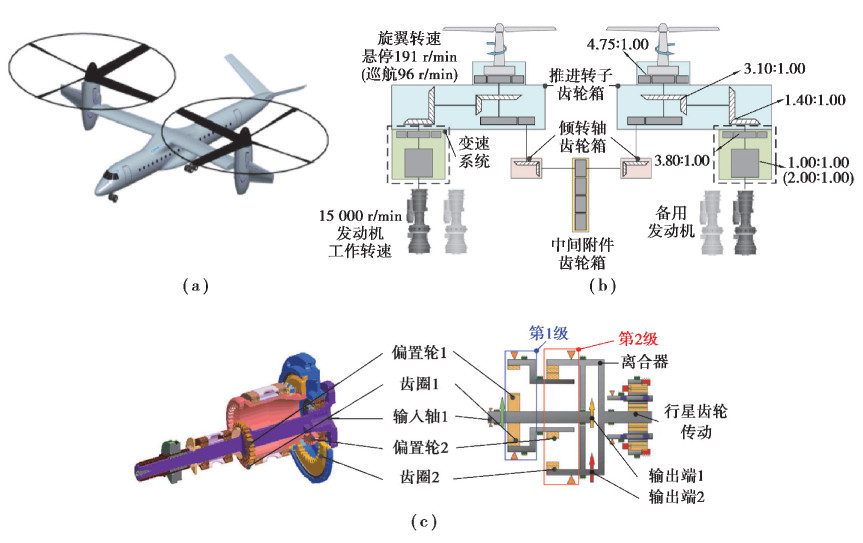
某大型倾转翼飞行汽车载客量90人,巡航速度约为550 km/h,最大航程2 220 km,飞行时由2台发动机驱动,单台发动机最大功率3 750 kW,工作转速15 000 r/min,整体结构如图 2(a)所示[13]。悬停(Hover)或巡航(Cruise)时,动力经变速系统、推进转子齿轮箱到达旋翼提供飞行升力。悬停飞行时旋翼转速约为191 r/min,系统传动比为78.34,巡航飞行时旋翼转速约为96 r/min,传动比为156.67,传动方案如图 2(b)所示。变速系统主要由OCG变速器与行星齿轮传动组成,OCG变速器主要由两级内啮合直齿轮传动与离合器组成,如图 2(c)所示。飞行模式的切换由离合器控制,当离合器闭合时发动机动力由输出端1输出,偏置轮与齿圈未啮合,变速器传动比为1。当离合器断开时(图示状态),动力经偏置轮与齿圈传递,由输出端2输出动力,此时传动比为2。由于该飞行汽车正处于测试开发阶段,参考文献[14-15]的试验工况与结构参数,以试验OCG变速器齿轮传动结构作为研究对象,为研发实物提供设计参考。试验变速器齿轮传动结构参数如表 1所示,满足功率147 kW,转速15 000 r/min的试验条件,齿轮ISO精度6级、材料为9310钢、质量约1.675 3 kg[14-16]。
|
图 2 某飞行汽车结构与传动结构简图 Fig. 2 Structure and transmission scheme of the flying car |
| 表 1 试验OCG变速器齿轮传动结构参数 Table 1 Test OCG speed changer gear transmission structure parameters |
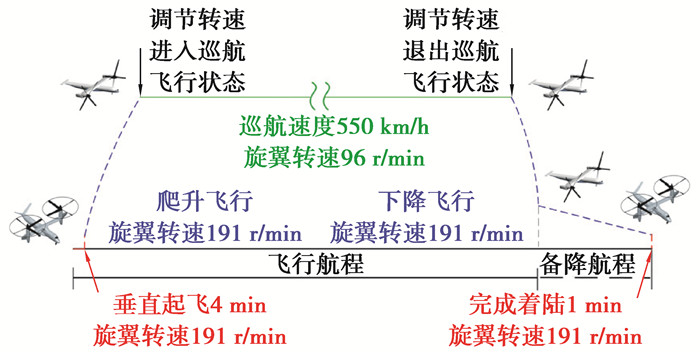
一次典型飞行中巡航飞行时间约3 h,距离约1 850 km,占比约为整个航程的90%[16],飞行任务剖面图如图 3所示。变速器齿轮主要在飞行汽车处于巡航飞行状态时工作,通过飞行任务剖面图与巡航颠簸情况可模拟典型飞行任务中试验变速器齿轮传动输入载荷谱。
|
图 3 飞行任务剖面图 Fig. 3 Mission profile of flying car |
巡航飞行时,飞行颠簸将会导致变速器齿轮传动输入转矩波动。结合文献[17],得到巡航状态下变速器齿轮传动输入转矩波动概率密度函数为
| $ T(t)=\left\{\begin{array}{l} T(t) \cdot c_{1}, P(\xi=0.97), \\ T\left(t_{\xi}\right) \cdot c_{2}, P_{1}\left(\xi_{1} \mid \xi=0.11\right), \\ T\left(t_{\xi}\right) \cdot c_{3}, P_{2}\left(\xi_{2} \mid \xi=0.77\right), \\ T\left(t_{\xi}\right) \cdot c_{4}, P_{3}\left(\xi_{3} \mid \xi=0.09\right), \\ T\left(t_{\xi}\right) \cdot c_{5}, P_{4}\left(\xi_{4} \mid \xi=0.03\right) 。\end{array}\right. $ | (1) |
式中:P(ξ=0.97)为飞行过程中未遇到颠簸的概率,过载系数为c1服从N1(1.00, 0.03)正态分布;P1(ξ1|ξ=0.11)为颠簸情况下轻颠簸概率,过载系数c2服从N2(1.00, 0.10)正态分布;P2(ξ2|ξ=0.77)为轻中颠簸概率,过载系数c3服从N3(1.00, 0.20)正态分布;P3(ξ3|ξ=0.09)为中颠簸概率,过载系数c4服从N4(1.00, 0.30)正态分布;P4(ξ4|ξ=0.03)为强颠簸概率0.03,过载系数c5服从N5(1.00, 0.40)正态分布;单位时间t为1 s,颠簸持续时间tξ服从N6(10.00, 5.00)正态分布。
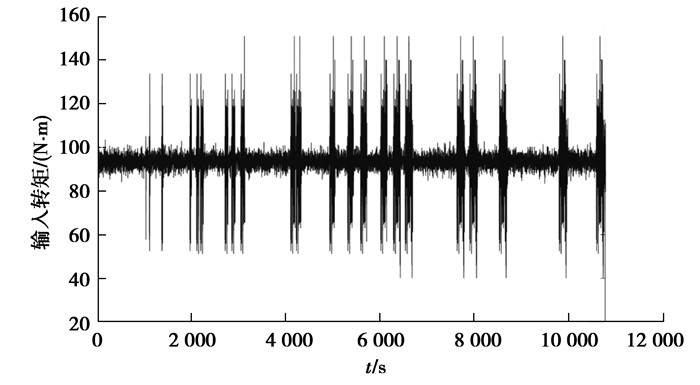
结合飞行任务剖面图与式(1)得到典型飞行任务下变速器齿轮传动输入载荷谱如图 4所示。输入转矩均值为93.39 N·m,标准差为11.34 N·m,极差为110.49 N·m。
|
图 4 典型飞行任务下模拟输入载荷谱 Fig. 4 Simulated input load spectrum during a typical mission |
根据输入工况与齿轮齿面接触、齿根弯曲疲劳强度设计方法设计计算,应力与许用应力由公式(2)~(5)表示[18],即
| $ \sigma_{\mathrm{F}}=\frac{F_{\mathrm{t}}}{b m_{\mathrm{n}}} Y_{\mathrm{F}} Y_{\mathrm{S}} Y_{\mathtt{β}} K_{\mathrm{A}} K_{\mathrm{V}} K_{\mathrm{F} \mathtt{β}} K_{\mathrm{F} \mathtt{α}}, $ | (2) |
| $ \sigma_{\mathrm{FG}}=\sigma_{\mathrm{Flim}} Y_{\mathrm{ST}} Y_{\mathrm{NT}} Y_{\mathrm{X}}, $ | (3) |
式中:σF为齿根弯曲应力,MPa;Ft为名义切向力,N;b为齿宽,mm;mn为模数,mm;YF,YS,Yβ为弯曲应力计算系数;KA,KV为工况系数;KFβ,KFα为弯曲应力载荷分配系数;σFG为弯曲极限应力,MPa;σFlim为齿轮材料试验弯曲疲劳极限,MPa;YST,YNT,YX为弯曲疲劳强度修正系数。
| $ \sigma_{\mathrm{H}}=Z_{\mathrm{H}} Z_{\mathrm{E}} Z_{\mathtt{ε}} Z_{\mathtt{β}} \sqrt{\frac{F_{\mathrm{t}}}{d_{1} b} \frac{u-1}{u} K_{\mathrm{A}} K_{\mathrm{V}} K_{\mathrm{H} \mathtt{β}} K_{\mathrm{H} \mathtt{α}}}, $ | (4) |
| $ \sigma_{\mathrm{HG}}=\sigma_{\mathrm{Hlim}} Z_{\mathrm{NT}} Z_{\mathrm{L}} Z_{\mathrm{v}} Z_{\mathrm{R}} Z_{\mathrm{W}} Z_{\mathrm{X}}, $ | (5) |
式中:σH为齿面接触应力,MPa;ZH,ZE,Zε,Zβ为接触应力计算系数;d1为小轮分度圆直径,mm;u为传动比;KHβ,KHα为接触应力载荷分配系数;σHG为接触极限应力,MPa;σHlim为齿轮材料试验接触疲劳极限,MPa;ZNT,ZL,Zv,ZR,ZW,ZX为接触疲劳强度修正系数。弯曲应力与接触应力计算参数取值如表 2所示。
| 表 2 弯曲应力与接触应力计算参数 Table 2 Values of contact and bending stress calculation parameters |
采用雨流计数法对弯曲与接触应力统计分析后得到不同应力均值下的一系列非对称应力循环载荷。将小于最大幅值载荷10%的载荷作为小载荷剔除后,采用Goodman准则对应力进行修正[19-20],即
| $ \sigma_{\mathrm{eq}}=\sigma_{\mathrm{a}} \frac{\sigma_{\mathrm{b}}}{\sigma_{\mathrm{b}}-\sigma_{\mathrm{m}}}, $ | (6) |
式中:σeq为修正后的等效应力幅值;σa为应力幅值;σm为应力均值,均为MPa;σb为材料抗拉屈服强度,取1 200 MPa。
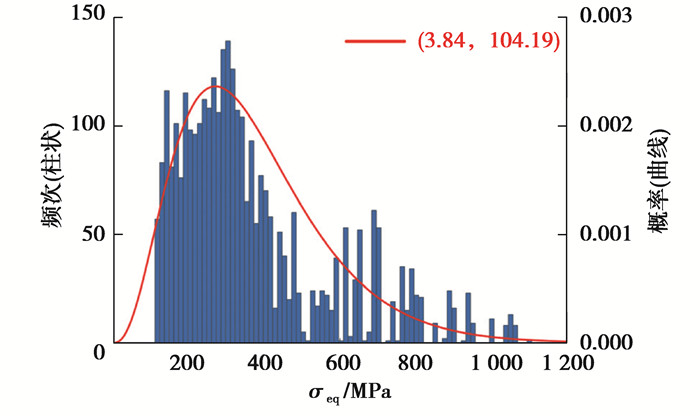
以第1级齿轮传动等效接触应力幅值拟合情况为例,均值为399.89 MPa、标准差为224.32 MPa、极差为1 126.92 MPa,近似服从伽马分布Γ(3.72, 104.19)。其等效接触应力幅值分布拟合情况如图 5所示。
|
图 5 第1级齿轮传动等效接触应力幅值分布 Fig. 5 Equivalent amplitude contact stress histogram and distribution fitting of stage I |
OCG变速器齿轮弯曲与接触应力分布均近似服从伽马分布,其分布拟合情况如表 3所示。
| 表 3 齿轮应力分布拟合情况 Table 3 Stress distribution fitting transmissions of gears |
疲劳强度退化过程可以表示为[21]
| $ r(n)=r(0)-\left[r(0)-S_{\max }\right]\left(\frac{n}{N_{\mathrm{f}}}\right)^{C_{0}}, $ | (7) |
式中:r(n)为加载n次时的剩余疲劳极限,MPa;r(0)为初始疲劳极限,MPa;Smax为齿轮等效峰值载荷,根据2倍西格玛原则确定,MPa;Nf为峰值载荷下齿轮零部件疲劳寿命;n为当前加载次数;C0为强度退化参数,这里取1。
结合应力强度干涉理论,齿轮传动的疲劳可靠度可以定义为疲劳强度大于工作应力的概率:
| $ R(t)=P\{r(t)-s(t)\}>0, $ | (8) |
式中:R(t)为t时刻疲劳可靠度;r(t)为t时刻疲劳强度;s(t)为t时刻应力大小。
t时刻的疲劳可靠度R(t)可以通过式(9)进行具体求解,即
| $ R(t)=P\left(x_{\mathrm{r}}>x_{\mathrm{s}}\right)=\int_{-\infty}^{\infty} f_{\mathrm{s}}\left(x_{\mathrm{s}}\right)\left[\int_{x_{\mathrm{s}}}^{\infty} f_{\mathrm{r}}\left(x_{\mathrm{r}}\right) \mathrm{d} x_{\mathrm{r}}\right] \mathrm{d} x_{\mathrm{s}}, $ | (9) |
式中:xr为t时刻疲劳强度;xs为t时刻应力;fs为t时刻应力密度函数;fr为t时刻疲劳强度密度函数,文中假设疲劳强度服从正态分布;其均值通过式(3)和(5)得到,方差通过变异系数获得[22]。
假设两种失效形式相互独立,且两级齿轮传动为串联系统,每一级齿轮传动疲劳可靠度与整体结构疲劳可靠度可以表示为
| $ R_{i}(t)=R_{i}^{\mathrm{F}}(t) \cdot R_{i}^{\mathrm{H}}(t), $ | (10) |
| $ R_{\mathrm{s}}(t)=\prod\limits_{i=1}^{2} R_{i}(t), $ | (11) |
式中:Ri(t)为单级齿轮传动疲劳可靠度,i=1, 2;RiF(t)为单级齿轮传动弯曲疲劳可靠度;RiH(t)为单级齿轮传动接触疲劳可靠度;Rs(t)整体结构疲劳可靠度。
1.3 结构参数优化为提高试验OCG变速器齿轮传动疲劳可靠性,选择可靠度作为目标函数,表示为:
| $ \min -f\{R(t), \boldsymbol{x}\}, $ | (12) |
由于齿轮传动宏观几何参数对可靠度有较大影响,选取齿数、模数、齿宽、压力角和变位系数作为设计变量,表示为
| $ \begin{gathered} \boldsymbol{x}=\left[z_{1}, z_{2}, z_{3}, z_{4}, m_{n 1}, m_{n 2}, b_{1}, b_{2}, b_{3}, b_{4}, \alpha_{1}, \alpha_{2}, X_{1}, X_{2}, X_{3}, X_{4}\right]= \\ {\left[x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}, x_{7}, x_{8}, x_{9}, x_{10}, x_{11}, x_{12}, x_{13}, x_{14}, x_{15}, x_{16}\right],} \end{gathered} $ | (13) |
式中:z1,z2为第1级传动齿数;z3,z4为第2级传动齿数;mn1,mn2为两级传动模数,mm;b1,b2为第1级传动齿宽,mm;b3,b4为第2级传动齿宽,mm;α1,α2为两级传动压力角, (°);X1,X2为第1级传动变位系数;X3,X4为第2级传动变位系数。
约束条件包括:基本结构约束、强度约束、质量约束。
1) 基本结构约束。
齿数应尽可能互为质数减少重复磨损[18],且限定在17~65,模数应限定在2~4 mm,齿宽限定在8~15 mm,主动轮齿宽大于从动轮齿宽2~3 mm,压力角限定在20°~25°,变位系数限定在0~0.65,且采用正变位传动减小干涉,提高强度,通过式(14)表示:
| $ \left\{\begin{array}{l} 17 \leqslant x_{1}, x_{2}, x_{3}, x_{4} \leqslant 65, \\ 2 \leqslant x_{5}, x_{6} \leqslant 4, \\ 8 \leqslant x_{7}, x_{8}, x_{9}, x_{10} \leqslant 15, \\ 2 \leqslant x_{7}-x_{8}, x_{9}-x_{10} \leqslant 3, \\ 20 \leqslant x_{11}, x_{12} \leqslant 25, \\ 0 \leqslant x_{13}, x_{14}, x_{15}, x_{16} \leqslant 0.65, \\ x_{14}-x_{13}, x_{16}-x_{15}>0。\end{array}\right. $ | (14) |
为满足巡航飞行要求,传动比应限制在1.95~2.05。同时为提高齿轮承载能力,还应满足齿宽条件要求[23]。传动比与齿宽约束通过式(15)表示:
| $ \left\{\begin{array}{l} 1.95<\frac{x_{2}}{x_{1}} \cdot \frac{x_{4}}{x_{3}}<2.05, \\ 0.6 {\rm{ \mathsf{ π} }} x_{5}-x_{7}, 0.6 {\rm{ \mathsf{ π} }} x_{6}-x_{9} \leqslant 0 。\end{array}\right. $ | (15) |
2) 强度约束。
保证设计结果正确可靠,每个设计组合(x1, x2, …, x16)的弯曲与接触安全系数应满足高可靠度要求,即弯曲安全系数大于2,接触安全系数大于1.6[18],通过式(16)表示:
| $ \left\{\begin{array}{l} \sigma_{\mathrm{F}} / \sigma_{\mathrm{FG}} \geqslant 2.0, \\ \sigma_{\mathrm{H}} / \sigma_{\mathrm{HG}} \geqslant 1.6 。\end{array}\right. $ | (16) |
3) 质量约束。
质量主要与体积相关,体积不应超过原始体积,通过式(17)表示:
| $ \frac{{\rm{ \mathsf{ π} }}\left(x_{1} x_{5}\right)^{2} x_{7}}{4}+\frac{{\rm{ \mathsf{ π} }}\left(x_{3} x_{6}\right)^{2} x_{9}}{4}+0.11 {\rm{ \mathsf{ π} }}\left[\left(x_{2} x_{5}\right)^{2} x_{8}+\left(x_{4} x_{6}\right)^{2} x_{10}\right] \leqslant V_{\mathrm{ini}}, $ | (17) |
式中Vini为原始结构参数体积,齿圈外径取1.2倍分度圆直径。
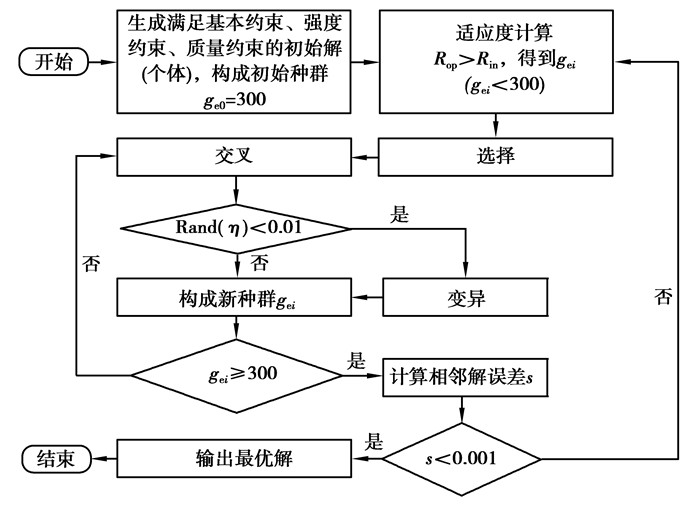
运用Matlab软件编写遗传算法(genetic algorithm,GA)获得最优结构参数解。种群中个体数量ge=300,变异率为η=0.01,收敛精度为s=0.00 1,GA求解计算流程图如6所示。
|
图 6 GA求解计算流程图 Fig. 6 Calculation flow chart of GA |
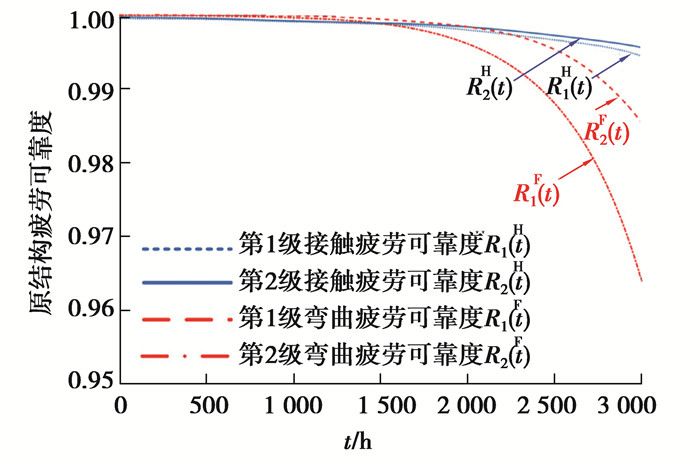
试验OCG变速器齿轮接触疲劳极限σHlim取1 500 MPa,弯曲疲劳极限σFlim取550 MPa,设计寿命3 000 h[18, 24]。通过式(9)得到试验OCG变速器各级齿轮传动疲劳可靠度如图 7所示。由疲劳强度不断退化导致齿轮传动疲劳可靠度在服役前半段(约1 500 h前),下降缓慢,后半段(约1 500 h后)下降较快。由于齿根承受弯曲应力较大,弯曲疲劳强度退化较快,导致齿轮传动弯曲疲劳可靠度下降较快。3 000 h服役时间内,第1级最低至96.39%,第2级最低至98.57%。较之弯曲疲劳可靠度,由于较小的齿面接触应力,该齿轮传动接触疲劳可靠度下降较缓,第1级最低至99.44%,第2级最低至99.58%。
|
图 7 各级齿轮传动弯曲与接触疲劳可靠度 Fig. 7 Bending and contact fatigue reliabilities of stages |
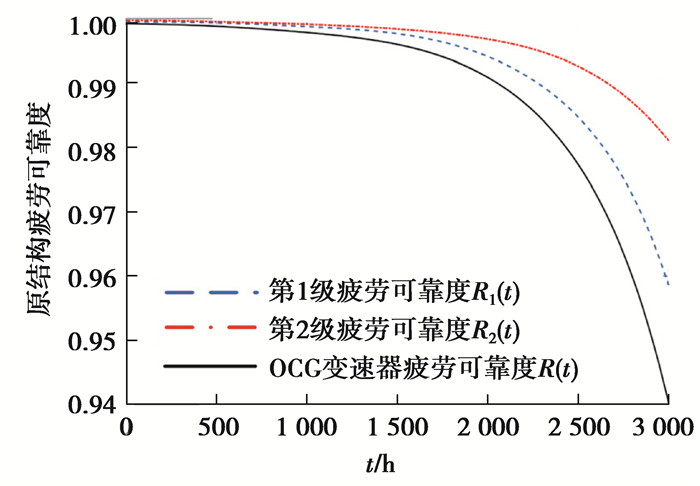
通过式(10)与(11)得到两级齿轮传动疲劳可靠度与整体结构疲劳可靠度如图 8所示。由于损伤不断累计,该试验变速器齿轮传动疲劳可靠度在服役前半段下降缓慢,后半段下降较快。3 000 h服役时间内,该变速器齿轮传动可靠度最低至94.09%。第1级齿轮传动疲劳可靠度较低,最低至95.85%,第2级最低至98.16%。受变速器齿轮传动结构参数的影响,致使两级齿轮传动承受应力差距较大,疲劳强度退化不一致。服役时间内,两级传动可靠度出现差异,且逐步加剧。说明该结构还存在可靠性优化的空间。
|
图 8 各级齿轮传动与整体疲劳可靠度 Fig. 8 Fatigue reliabilities of stages and system |
通过GA获得优化后的齿轮传动结构参数如表 4所示。原结构两级齿轮传动质量为1.675 3 kg,优化结果则为1.635 1 kg,质量约减少2.4%。
| 表 4 优化结构与原结构参数对比 Table 4 Parameters of optimized and initial structures |
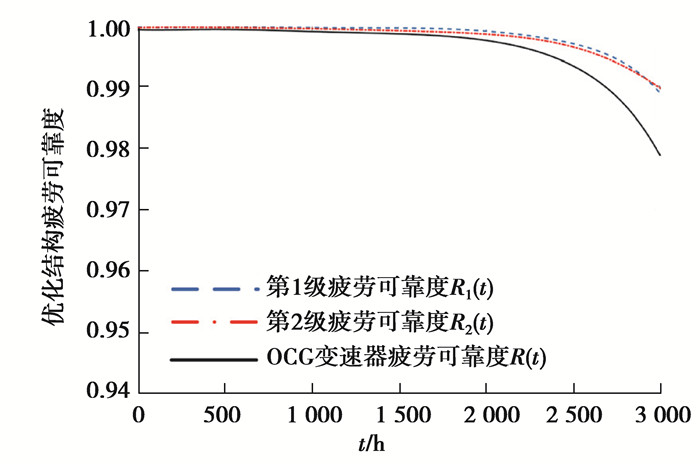
优化后的齿轮传动结构疲劳可靠度如图 9所示。在质量适当减小的条件下,优化后的齿轮传动疲劳可靠度提高3.83%。
|
图 9 优化后的齿轮传动疲劳可靠度 Fig. 9 Fatigue reliabilities of optimized structure |
优化结构适当降低第1级齿轮传动齿面和齿根应力,提高弯曲与接触疲劳安全系数,弥补较快转速带来的强度退化不匹配,从而提高可靠度,符合等强度设计原则,优化前后的结构安全系数如表 5所示。
| 表 5 原结构与优化结构安全系数对比 Table 5 Safety factors of initial and optimized structures |
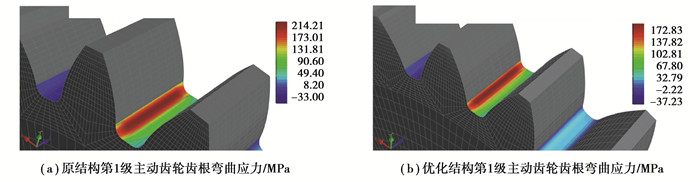
由于弯曲应力是导致该齿轮传动可靠度下降较快的原因,且第1级弯曲疲劳可靠度变化较大。运用Romax软件,对优化前后结构的齿根应力进行分析。原结构第1级主动轮齿根处最大主应力达241.21 MPa,优化结构第1级主动轮达172.83 MPa,如图 10所示。有限元分析结果与安全系数相对应,进一步说明该优化结果的合理性。
|
图 10 第1级主动轮齿根弯曲应力 Fig. 10 The bending stress of the first stage driving gear |
针对某倾转翼飞行汽车试验OCG变速器疲劳可靠性分析与结构参数优化问题,运用应力强度干涉理论与遗传算法,获得高可靠轻量化的齿轮传动结构参数,得到以下结论:
1) 该变速器齿轮传动在3 000 h服役时间内,由于损伤不断累积,前段可靠度下降缓慢,后段下降较快,可靠度最低至94.09%。第1级齿轮传动更容易发生疲劳失效且两级传动可靠度差异较大,该结构存在可靠性优化的空间。
2) 经过可靠性优化后的飞行汽车变速器齿轮传动第1级安全系数得到提高,整体的疲劳可靠度提升3.83%,质量减小2.4%,为开发国产倾转翼飞行汽车传动系统提供支撑。
| [1] |
张扬军, 钱煜平, 诸葛伟林, 等. 飞行汽车的研究发展与关键技术[J]. 汽车安全与节能学报, 2020, 11(1): 1-16. Zhang Y J, Qian Y P, Zhuge W L, et al. Progress and key technologies of flying cars[J]. Journal of Automotive Safety and Energy, 2020, 11(1): 1-16. (in Chinese) DOI:10.3969/j.issn.1674-8484.2020.01.001 |
| [2] |
Al Haddad C, Chaniotakis E, Straubinger A, et al. Factors affecting the adoption and use of urban air mobility[J]. Transportation Research Part A: Policy and Practice, 2020, 132: 696-712. DOI:10.1016/j.tra.2019.12.020 |
| [3] |
Eker U, Ahmed S S, Fountas G, et al. An exploratory investigation of public perceptions towards safety and security from the future use of flying cars in the United States[J]. Analytic Methods in Accident Research, 2019, 23: 100103. DOI:10.1016/j.amar.2019.100103 |
| [4] |
He H F, Liu H J, Zhu C C, et al. Study on the gear fatigue behavior considering the effect of residual stress based on the continuum damage approach[J]. Engineering Failure Analysis, 2019, 104: 531-544. DOI:10.1016/j.engfailanal.2019.06.027 |
| [5] |
Liu H J, Liu H L, Zhu C C, et al. A review on micropitting studies of steel gears[J]. Coatings, 2019, 9(1): 42. DOI:10.3390/coatings9010042 |
| [6] |
刘怀举, 刘鹤立, 朱才朝, 等. 轮齿齿面断裂失效研究综述[J]. 北京工业大学学报, 2018, 44(7): 961-968. Liu H J, Liu H L, Zhu C C, et al. Review on gear tooth flank fracture[J]. Journal of Beijing University of Technology, 2018, 44(7): 961-968. (in Chinese) |
| [7] |
Siddiqui N A, Deen K M, Khan M Z, et al. Investigating the failure of bevel gears in an aircraft engine[J]. Case Studies in Engineering Failure Analysis, 2013, 1(1): 24-31. DOI:10.1016/j.csefa.2012.12.001 |
| [8] |
曲震, 胡殿印, 张冰, 等. 航空发动机齿轮副动态啮合过程与齿根裂纹扩展轨迹影响因素研究[J]. 推进技术, 2019, 40(12): 2797-2805. Qu Z, Hu D Y, Zhang B, et al. Investigation on dynamic meshing process and factors influencing root crack propagation trajectory of an aero-engine gear pair[J]. Journal of Propulsion Technology, 2019, 40(12): 2797-2805. (in Chinese) |
| [9] |
Cheng L, Chen L S, Li S L, et al. Fault analysis on bevel gear teeth surface damage of aeroengine[J]. IOP Conference Series: Materials Science and Engineering, 2017, 274: 012103. DOI:10.1088/1757-899X/274/1/012103 |
| [10] |
Manda P, Rao A S, Singh S, et al. Failure analysis of cooler fan drive gear system of main gear box of helicopter[J]. Materials Today: Proceedings, 2018, 5(9): 17737-17745. DOI:10.1016/j.matpr.2018.06.097 |
| [11] |
Chang Q C, Xue C J. Reliability analysis and experimental verification of landing-gear steering mechanism considering environmental temperature[J]. Journal of Aircraft, 2017, 55(3): 1154-1164. |
| [12] |
Sato K, Goi T, Taguchi T, et al. Design, analysis, and tests of differential planetary gear system for open rotor power gearbox (final report)[C/OL]//Proceedings of ASME 2015 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, August 2-5, 2015, Boston, Massachusetts, USA. The American Society of Mechanical Engineering, 2016[2020-09-29]. https://doi.org/10.1115/DETC2015-46414.
|
| [13] |
Robuck M, Wilkerson J, Snyder C A, et al. Study and sub-system optimization of propulsion and drive systems for the large civil tiltrotor (LCTR2) rotorcraft[C/OL]//AHS 2013: Proceedings of the Future Vertical Lift Aircraft Design Conference. San Francisco, USA: American Helicopter Society, 2013[2020-09-29]. https://ntrs.nasa.gov/citations/20140005755.
|
| [14] |
Stevens M A, Lewicki D G, Handschuh R F. Concepts for multi-speed rotorcraft drive system-status of design and testing at NASA GRC[C/OL]//AHS 2015: Proceedings of the International 71th Annual Forum & Technology Display. Virginia Beach, USA: American Helicopter Society, 2015[2020-09-29]. https://ntrs.nasa.gov/citations/20150010716.
|
| [15] |
Krantz T, Handschuh R, Roberts G. Results of NASA technical challenge to demonstrate two-speed drive for vertical lift vehicle[C/OL]//AHS 2018: Proceedings of the International 74th Annual Forum & Technology Display. Phoenix, USA: American Helicopter Society, 2018[2020-09-29]. https://ntrs.nasa.gov/citations/20180003086.
|
| [16] |
Robuck M, Wilkerson J, Maciolek R, et al. The effect of rotor cruise tip speed, engine technology and engine/drive system RPM on the NASA large civil tiltrotor (LCTR2) size and performance: ARC-E-DAA-TN7289[R]. Hanover, New Hampshire, USA: NASA Center for Aerospace Information (CASI), 2012.
|
| [17] |
辜运燕. 我国西部干线飞机颠簸分布规律分析[D]. 广汉: 中国民用航空飞行学院, 2009. Gu Y Y. Airplane turbulence distribution analysis of western trunk air routes in China[D]. Guanghan: Civil Aviation Flight University of China, 2009. (in Chinese) |
| [18] |
成大先. 机械设计手册: 6版3卷[M]. 北京: 化学工业出版社, 2010. Cheng D X. Mechanical Design Manual: vol 3, 6th ed[M]. Beijing: Chemical Industry Press, 2010. (in Chinese) |
| [19] |
Jia P, Liu H J, Zhu C C, et al. Contact fatigue life prediction of a bevel gear under spectrum loading[J]. Frontiers of Mechanical Engineering, 2020, 15(1): 123-132. DOI:10.1007/s11465-019-0556-8 |
| [20] |
平安, 王德俊, 徐灏. 关于确定小载荷取舍标准的研究[J]. 农业机械学报, 1993, 24(3): 64-69. Ping A, Wang D J, Xu H. Study on determining criterion for omission of small loads[J]. Transactions of the Chinese Society of Agricultural Machinery, 1993, 24(3): 64-69. (in Chinese) |
| [21] |
Wei J, Pan Z, Lin X, et al. Copula-function-based analysis model and dynamic reliability of a gear transmission system considering failure correlations[J]. Fatigue & Fracture of Engineering Materials & Structures, 2019, 42(1): 114-128. |
| [22] |
安宗文, 辛玉. 基于重要抽样法的风电齿轮箱齿轮可靠性灵敏度分析[J]. 兰州理工大学学报, 2015, 41(3): 36-40. An Z W, Xin Y. Sensitivity analysis of reliability of gear in wind turbine gear-box based on important sampling method[J]. Journal of Lanzhou University of Technology, 2015, 41(3): 36-40. (in Chinese) DOI:10.3969/j.issn.1673-5196.2015.03.008 |
| [23] |
朱才朝, 徐向阳, 陆波, 等. 大功率船用齿轮箱传动系统模糊可靠性优化[J]. 船舶力学, 2010, 14(8): 915-921. Zhu C C, Xu X Y, Lu B, et al. Fuzzy reliability optimization for transmission system of high-power marine gearbox[J]. Journal of Ship Mechanics, 2010, 14(8): 915-921. (in Chinese) DOI:10.3969/j.issn.1007-7294.2010.08.013 |
| [24] |
殷久诚. 航空发动机主轴轴承的可靠性评估[D]. 西安: 西安工业大学, 2015. Yin J C. Reliability assessment of aero-engine spindle bearings[D]. Xi'an: Xi'an Technological University, 2015. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45


