2. 中国北方车辆研究所,北京 100072
2. China North Vehicle Research Institute, Beijing 100072, P. R. China
自齿轮副提出以来,诸多国内外学者对齿轮副的齿形设计、仿真加工和啮合特性等进行了分析,梁成成等[1]通过分析成型轮的数学模型,分别推导了成形法和展成法的轮齿齿面数学模型, 建立了齿轮精确化建模流程。李帅等[2]和陈曦等[3]则从重合度的角度对齿轮副进行参数优化, 分析了重合度对齿轮副啮合特性和系统动态啮合性能的影响规律。宋朝省等[4]则从弯曲应力的角度分析了安装误差对齿根弯曲特性的影响规律。随着齿轮副的应用越来越广泛,相关学者又提出了非圆齿轮的传动形式,以进一步扩大齿轮副的应用范围。但非圆齿轮的速比特性和轮齿加工等又不同于常规圆柱齿轮[5-7],对于非圆齿轮的节曲线设计,Bair等[8]和Li等[9]以齿轮啮合原理为基础,分别结合Jarvis步进算法和傅里叶级数等相关理论,从不同的角度建立了非圆齿轮节曲线的时变级数数学模型,能够根据给定的参数进行一定程度的通用化设计,具有一定的精度和通用性。童婷等[10]和Qiu等[11]则探讨了非圆齿轮封闭节曲线的设计方法,解决了具有内凹节曲线的非圆齿轮齿廓求解难题。李建刚等[12-14]和Li等[15]则基于齿面离散的思想,提出了一种非圆齿面离散坐标点的数值计算方法,同时对非圆齿轮轮齿根切和齿顶变尖进行了初步探索,建立了轮齿根切的理论判定方程,给出了轮齿根切的评价指标。
由于非圆齿轮的节曲线为任意曲线,因此其运动特性也与常规圆柱齿轮副不同。Penaud等[16]和Talpasanu等[17]分别基于复杂齿轮机构的机构简图和关联矩阵理论,建立了非圆齿轮及其与杆机构的组合机构的运动学分析方法。林超等[18]针对现有的间歇转动机构传动性能的缺陷,提出一种新型非圆齿轮型间歇转动机构,并从运动学角度对机构的传动性能进行了分析。杨存等[19]通过对非圆齿轮啮合传动的运动学及动态特性的分析,不仅可以解决设计上的问题, 而且还可以对其进行优化设计,消除或减少构件所产生的惯性力,减轻机械振动,降低噪声污染,提高整个机械系统的工作性能和使用寿命等,为设计研发非圆齿轮提供一种可靠有效的研究方法。
上述研究主要集中在非圆齿轮的理论设计及参数对运动特性的影响,相关应用研究较少。笔者以非圆齿轮的速比特性为基础,针对车辆中常用的带式无级变速机构的承载能力有限、传动精度不高等不足设计了全齿轮啮合形式的非圆齿轮无级调速机构,扩大了非圆齿轮和无级变速机构的应用范围。基于节曲线封闭性,采用多段线构造法,提出了非圆齿轮节曲线的反求设计方法;建立了无级调速机构分支数、非圆齿轮速比范围和转角范围间的匹配关系,并通过ADAMS仿真实验验证了非圆齿轮和无级调速机构设计的正确性。
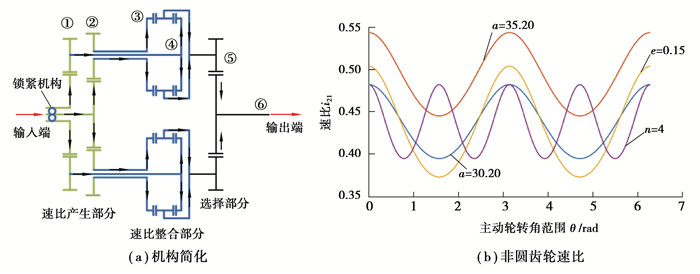
1 无级调速原理如图 1所示,在非圆齿轮无级调速机构中主要包含两部分:非圆齿轮时变速比产生部分和行星速比整合部分。在图 1(a)中,锁紧机构在改变非圆齿轮副1和2的相位角的同时还实现输入转速的分流,将输入转速分别传递到非圆齿轮副1和2;由于非圆齿轮副1和2处于不同的相位角,根据图 1(b)得到非圆齿轮的速比与相位角具有对应关系,此时图 1(a)中两非圆齿轮副输出转速不同,由此可以在速比整合部分通过差动轮系进行速度整合,最终由选择输出机构中的选择部分对整合后的速度分支进行输出,得到需要的连续调速输出。图 1(b)中,a为非圆齿轮长轴半径参数,e为非圆齿轮偏心率,n为非圆齿轮阶数,从图 1(b)中可知,非圆齿轮的速比具有随参数变化的时变性,半径参数a主要影响速比的最大最小值:具体表现为随着半径参数a的增大,速比最大值增大、最小值减小;偏心率e主要影响最大最小值间的差值,偏心率越大,最大值越大、最小值越小;阶数n主要影响非圆齿轮副速比周期数,阶数越大,速比周期越大,变化越快。由于非圆齿轮始终具有时变的速比,因此其不能直接作为无级变速机构进行使用。结合图 1(a),输入转速通过锁紧机构一分为二分别输入到非圆齿轮副①和②,对非圆齿轮副①和②设置不同的相位角即可得到具有相位差的时变输出转速;两组非圆齿轮副的输出转速分别作为速比整合部分的③和④的输入转速,通过差动轮系将两个输入转速合成为一个确定的输出转速,而不同相位角下两组非圆齿轮副①和②的输出速比也具有不同的相位差,最终通过选择齿轮副⑤进行输出选择,在输入转速不变的前提下实现输出转速的无级变速。
|
图 1 非圆齿轮无级调速机构传动原理 Fig. 1 Continuously variable transmission mechanism with non-circular gear pair |
根据图 1中所示非圆齿轮无级调速机构的结构关系可知,作为时变速比发生部分,无级调速机构中非圆齿轮副的工作段速比函数需为一次函数形式;根据高阶函数对低阶函数的包含性,非圆齿轮副对应的过渡段速比函数可以采用傅里叶级数或多项式进行构造[20], 以偏心非圆齿轮为研究对象,采用多项式构造非圆齿轮副过渡段速比函数,得到非圆齿轮副周期性速比函数如式(1)所示。
| $ {m_{21}} = \frac{{{\omega _2}}}{{{\omega _1}}} = \left\{ {\begin{array}{*{20}{l}} {{m_1}\left( {{\varphi _1}} \right) = {k_1}{\varphi _1} + {b_1}, {\varphi _1} \in [0, X], }\\ {{m_2}\left( {{\varphi _1}} \right) = \sum\limits_{i = 0}^j {\left( {{a_i}\varphi _1^i} \right)} , {\varphi _1} \in [X, T], } \end{array}} \right. $ | (1) |
式中:X为非圆齿轮工作段转角,文中设计参数X=4π/3;T=2π。
根据非圆齿轮的速比特性、节曲线的封闭性和函数的包络性,可知非圆齿轮过渡段速比函数需要通过6个边界条件和1个封闭条件进行确定,如式(2)所示。
| $ \left\{ {\begin{array}{*{20}{l}} {\int_X^T {{m_2}} \left( {{\varphi _1}} \right){\rm{d}}{\varphi _1} = \frac{{2\pi }}{{{n_2}}} - \int_0^X {{m_1}} \left( {{\varphi _1}} \right){\rm{d}}{\varphi _1}, }\\ {{m_1}(X) = {m_2}(X), {m_1}(0) = {m_2}(T), }\\ {m_1^\prime (X) = m_2^\prime (X), m_1^\prime (0) = m_2^\prime (T),}\\ {m_1^{\prime \prime }(X) = m_2^{\prime \prime }(X), m_1^{\prime \prime }(0) = m_2^{\prime \prime }(T){\rm{。}}} \end{array}} \right. $ | (2) |
最终得到非圆齿轮副周期性速比函数为
| $ {m_{21}} = \left\{ {\begin{array}{*{20}{l}} {{k_1}{\varphi _1} + {b_1}, {\varphi _1} \in \left[ {0, \frac{4}{3}\pi } \right], }\\ {\sum\limits_{i = 0}^6 {\left( {{a_i}\varphi _1^i} \right)} , {\varphi _1} \in \left[ {\frac{4}{3}\pi , 2\pi } \right]。} \end{array}} \right. $ | (3) |
由无级调速机构的应用特性可知,非圆齿轮无级调速机构需要在0°~360°范围内实现连续整周期的稳定输出速比,而根据图 1(b)和式(3)有,单对非圆齿轮副必定会出现不能满足传动和速比整合要求的过渡段。因此必须采用多组非圆齿轮组合的形式,通过输出分支的交替选择实现恒定速比变换。
|
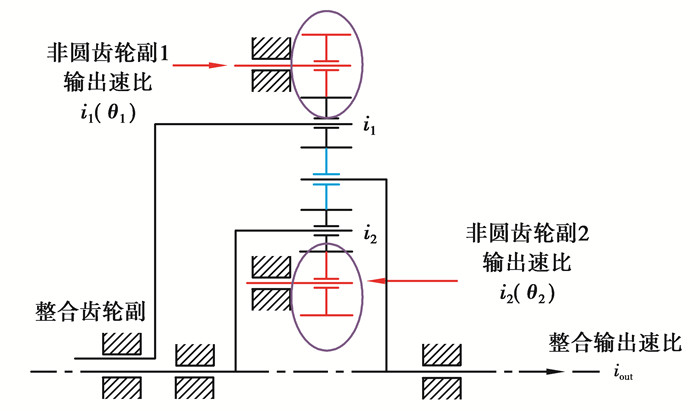
图 2 速比整合机构简化模型 Fig. 2 Simplified model of integration mechanism |
结合图 2所示差速齿轮系的速比等效简化模型,可以得到非圆齿轮无级调速机构最终输出速比与非圆齿轮副1和2的输出速比之间的关系为
| $ {i_{{\rm{out}}}} = \frac{{a \cdot {i_2} \cdot {i_2}\left( {{\theta _2}} \right) - {i_1} \cdot {i_1}\left( {{\theta _1}} \right)}}{{{i_1} \cdot {i_2} \cdot \left( {a - 1} \right)}}, $ | (4) |
式中:i1θ1和i2θ2分别是非圆齿轮副1和2的输出速比;i1和i2是整合差速齿轮副的两级速比;a是整合差速齿轮副太阳轮与外圈轮的齿数比。从式中可以看出非圆齿轮调速机构的最终输出速比函数与各级齿轮副间的速比函数有关。预设非圆齿轮的工作段函数特性如表 1所示。
| 表 1 非圆齿轮工作段参数 Table 1 Parameters of non-circular gear |
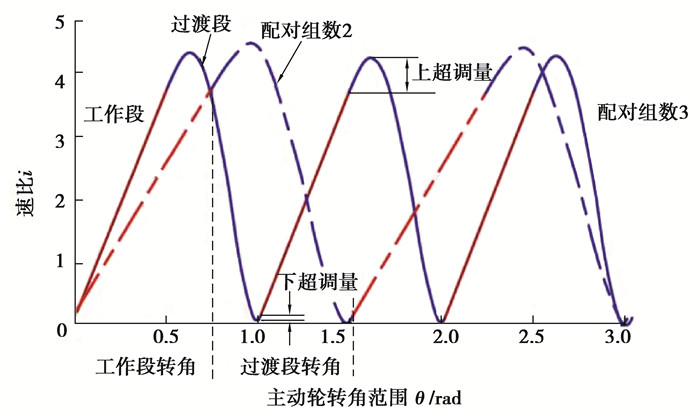
根据式(3)的整周期速比函数和表 1所示非圆齿轮副工作段基本参数可以得到不同配对分支单对非圆齿轮副的整周期速比曲线如图 3所示。
|
图 3 单对非圆齿轮副速比 Fig. 3 Transmission ratio of non-circular gear pair with different groups |
图 3显示了不同配对分支数下的非圆齿轮速比曲线。可以看到单对非圆齿轮整周期速比由两部分组成:工作段速比和过渡段速比。由于必须要满足给定工作段的速比特性,所以过渡段速比函数的上下超调量就不可避免,但其会随着配对组数和工作段速比函数进行变化。
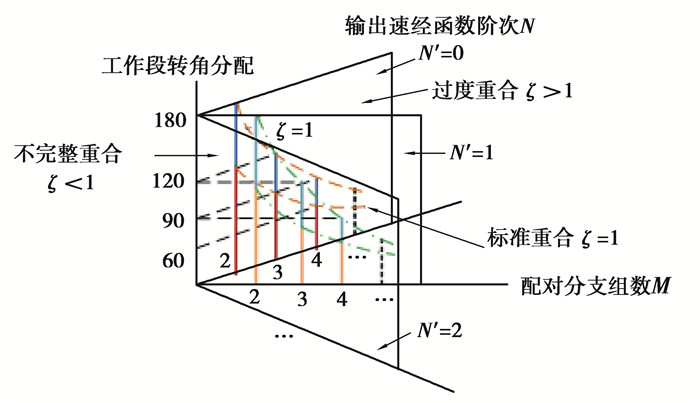
1.3 非圆齿轮参数匹配设计由于不同参数非圆齿轮具有不同的速比特性,同时对非圆齿轮的设计加工也会造成不同的影响。所以需要对非圆齿轮工作段节曲线函数可行性进行理论分析,根据非圆齿轮工作段和过渡段间的速比函数包含特性,可以得到如图 4所示的非圆齿轮配对分支数、工作段转角范围和工作段速比函数的相互关系。
|
图 4 非圆齿轮分支数、转角范围与工作速比函数的匹配关系 Fig. 4 Matching relationship between the non-circular gear groups, rotation angles and working ratio function |
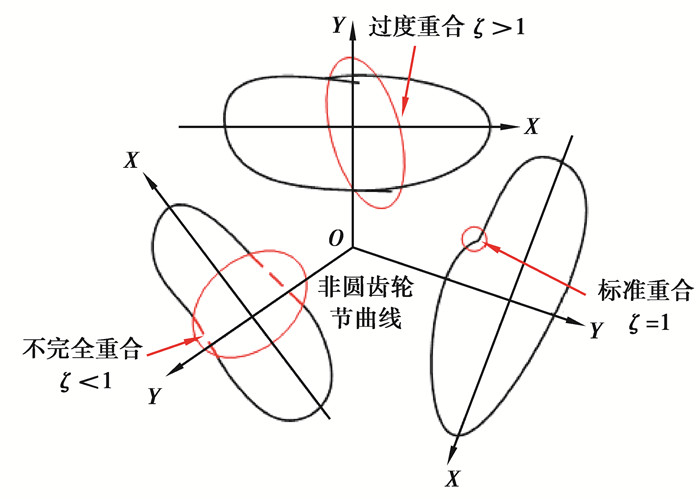
在图 4所示的有序平面上,每一平面代表同一速比函数。当所需工作速比不变时,非圆齿轮工作段转角范围的理论分布角随着配对非圆齿轮分支数的增加而减小。虚线将该平面分为3个部分:1)左下角,节曲线重合度小于1,这表示该分支数与转角范围配对情况下得到的非圆齿轮节曲线不完整,对应的整合输出速比函数有波动,如图 5所示。2)虚线上,节曲线重合度等于1,这表示此种组数与转角范围配对情况下得到的非圆齿轮节曲线刚好完整,满足设计要求;但在实际使用过程中需要瞬时切换,不然也会导致输出速比函数有波动,在此种切换模式下,齿轮副之间、轮齿之间的负载变化剧烈,容易引起寿命减少、振动冲击过大等不利情况。3)右上角,节曲线重合度大于1,这表示此种组数与转角范围配对情况下得到的非圆齿轮节曲线有重合或者输出速比函数有重合,在此种配对模式下,首选节曲线完整设计,则输出速比的重叠部分可以给予相位切换机构足够的作动时间。相较于情况1和2,情况3不仅满足了单个齿轮副的节曲线完整性,同时也满足了无级调速机构的需求,其工作转角具有一定的重合度,为相位切换提供了缓冲空间和时间,减少了快速切换带来的冲击。
|
图 5 非圆齿轮节曲线与参数关系 Fig. 5 Relationship between non-circular gear pitch curves and parameters |
表 2为图 4~5中各种情况对应的节曲线、输出时变特性的相互关系。
| 表 2 非圆齿轮节曲线与输出速比关系 Table 2 Relationship between non-circular gear pitch curve and output ratio |
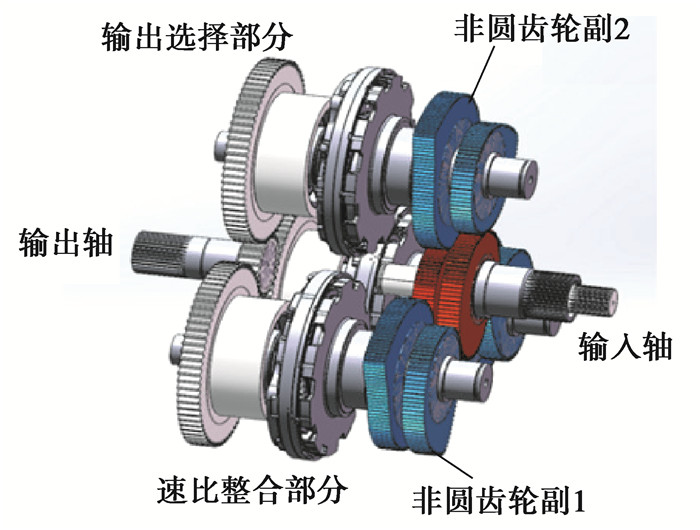
笔者主要对非圆齿轮无级调速机构主体部分输出速比规律进行仿真,仿真模型主要包含用于动力输入的输入轴,用于时变速比生产的非圆齿轮副,用于速比整合的差动轮系和作为输出选择部分的平行轴齿轮副,如图 6所示。
|
图 6 非圆齿轮无级调速机构实体模型 Fig. 6 Model of continuously variable transmission mechanism with non-circular gear pair |
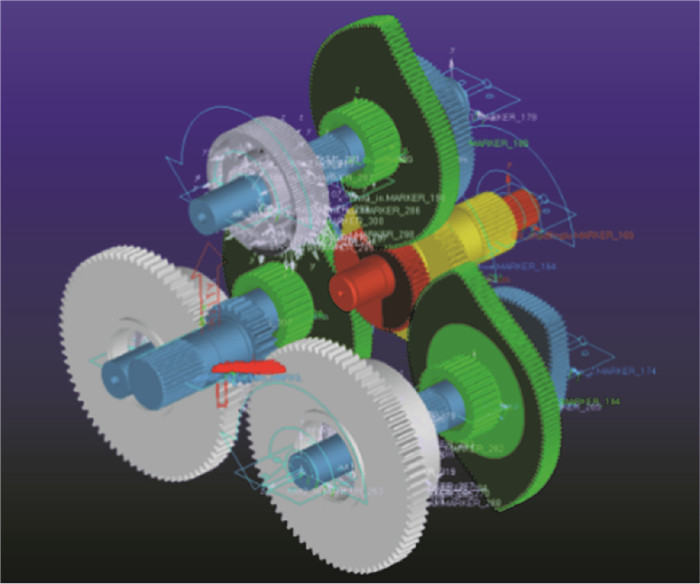
将图 6所示模型导入ADAMS(automatic dynamic analysis)中,添加相应的运动副,以输入轴为动力输入,经过非圆齿轮的速比产生和差动轮系的速比整合之后得到所需的时变函数,最后通过平行轴轮系选择对应的工作段分支进行时变输出(见图 7)。
|
图 7 运动副添加 Fig. 7 Motion joints |
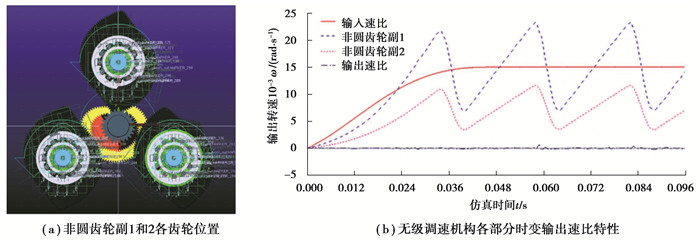
为验证非圆齿轮无级调速机构输出速比的稳定性和可变性,需要对具有不同相位差的非圆齿轮无级调速机构输出速比进行仿真,设定输入转速262 rad/s, 输出端负载扭矩200 N·mm; 仿真时间0.1 s,得到不同相位差下的无级调速机构仿真输出速比特性如图 8~10所示。
|
图 8 相位差为0°时的非圆齿轮无级调速机构输出速比特性 Fig. 8 Output characteristics of continuously variable transmission mechanism with phase difference 0° |
|
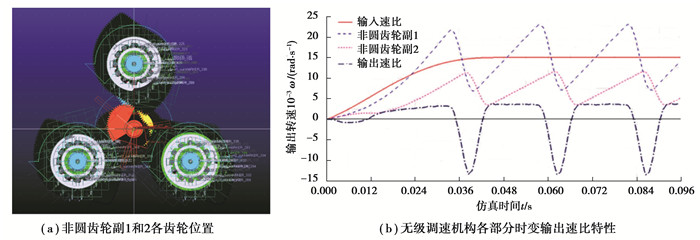
图 9 相位差为60°时的非圆齿轮无级调速机构输出速比特性 Fig. 9 Output characteristics of continuously variable transmission mechanism with phase difference 60° |
|
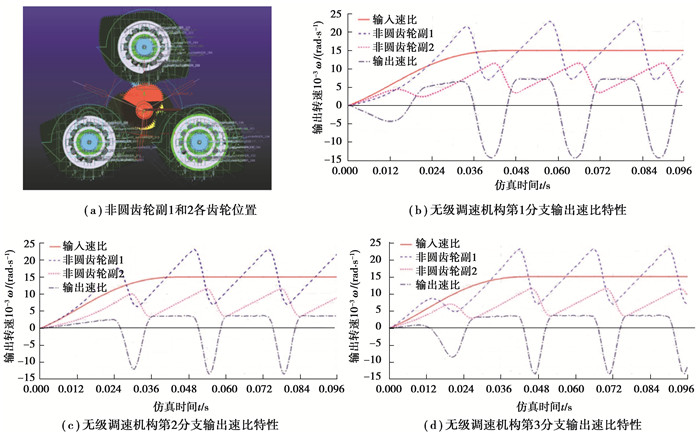
图 10 相位差为120°时的非圆齿轮无级调速机构输出速比特性 Fig. 10 Output characteristics of continuously variable transmission mechanism with phase difference 120° |
对比图 8~10所示不同相位角下的非圆齿轮无级调速机构仿真结果可知,当非圆齿轮副1和2的相位差不变时,非圆齿轮副1和2均能实现预设的一阶速比函数,同时通过速比整合部分得到工作段转角对应的稳定输出速比;进一步对比图 10(b)~(d)可知,不同非圆齿轮分支的稳定输出速比函数间具有不同的相位差,经过输出选择部分即可实现连续、稳定的时变输出。
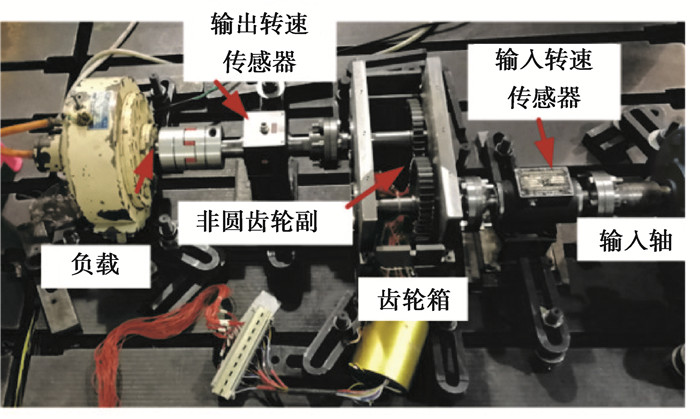
3 实验 3.1 实验台搭建为了验证非圆齿轮设计的正确性,结合式(3)对非圆齿轮的节曲线微分方程设定足够的离散精度进行近似求解,通过计算每一个离散步长下节曲线对应的弧长,得到非圆齿轮节曲线每一次积分改变的(x, y)坐标值,基于VB(visual basic语言程序设计)和Solidworks的二次开发,再通过布尔运算最终得到仿真加工的非圆齿轮,并对非圆齿轮副进行安装,搭建相应的试验台如图 11所示。
|
图 11 非圆齿轮台架实验平台 Fig. 11 Experimental platform of non-circular gear pair |
输入电机将扭矩通过梅花联轴器传递给输入轴,驱动电机和输入轴之间安装输入转速传感器,用来测定输入转速。输入轴带动主动非圆齿轮转动,通过非圆齿轮的时变速比特性产生时变转速并输出到输出转速传感器进行测量,输出转速传感器连接磁粉加载器以保证正确传动所必需的负载。驱动电机的转速、扭矩等参数通过操作控制台进行调节。
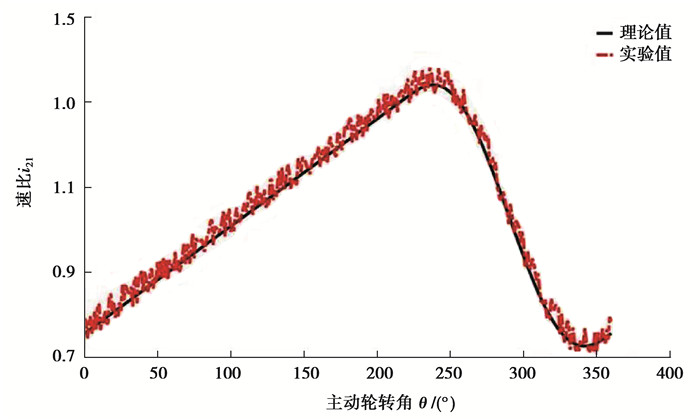
3.2 实验结果分析因为非圆齿轮是无级变速机构的理论及设计基础,所以本次试验主要验证非圆齿轮副分析和设计的正确性。给定非圆齿轮副输入转速262 rad/s, 输出端负载扭矩200 N·mm,待非圆齿轮副转动平稳之后提取输入\输出转速测量结构并结合转速与速比的关系式i21=ω1/ω2=n1/n2对输入\输出转速进行二次处理,得到速比实验结果,并与MATLAB的理论结果相比较,如图 12所示。
|
图 12 非圆齿轮速比对比 Fig. 12 Comparison of transmission ratios between theoretical and experimental values |
从图 12所示实验结果可知,该非圆齿轮副的实验传动比范围为0.8~1.2,与理论传动比基本相等;输出转速的误差最大为6.8%,考虑到非圆齿轮设计加工离散精度、安装误差和测量的灵敏度等误差,该最大误差在可接受的范围内,验证了理论分析的正确性。
4 结论笔者以非圆齿轮的时变速比特性结合工业实际,设计了具有全齿轮啮合形式的非圆齿轮无级调速机构,扩大了非圆齿轮的应用范围,改善了无级传动机构的承载能力。结合高阶函数对低阶函数的包含性,采用多段线构造法建立了非圆齿轮对给定速比特性函数的再现反求设计方法,并得到了非圆齿轮分支数、工作段速比函数和转角范围等参数对节曲线的影响规律,从理论上分析了不同参数非圆齿轮设计的可行性,确定了非圆齿轮各参数的匹配范围。采用SolidWorks结合VB建立了非圆齿轮无级调速机构的实体模型,并导入ADAMS中进行运动仿真,得到了不同相位角下不同非圆齿轮分支的时变速比特性;完成了非圆齿轮的加工与实验,并与MATLAB的理论结构进行对比,得到非圆齿轮副的时变最大误差为6.8%,验证了结构设计及分析的正确性,为非圆齿轮的实际应用提供理论基础。
| [1] |
梁成成, 宋朝省, 朱才朝, 等. 基于刀具法向基准的奥利康准双曲面齿轮精确建模与验证[J]. 重庆大学学报, 2020, 43(2): 1-11. Liang C C, Song C S, Zhu C C, et al. Accurate modeling and verification of Oerlikon hypoid gears based on tool normal benchmark[J]. Journal of Chongqing University, 2020, 43(2): 1-11. (in Chinese) |
| [2] |
李帅, 宋朝省, 朱才朝, 等. 自升式海洋平台提升齿轮箱啮合特性分析[J]. 重庆大学学报, 2019, 42(6): 13-25. Li S, Song C S, Zhu C C, et al. Mesh characteristics analysis of the promote gearbox used in jack-up offshore platforms[J]. Journal of Chongqing University, 2019, 42(6): 13-25. (in Chinese) |
| [3] |
陈曦, 宋朝省, 朱才朝, 等. 电动车高速轮边齿轮传动动态特性分析与优化[J]. 重庆大学学报, 2017, 40(10): 1-11. Chen X, Song C S, Zhu C C, et al. Analysis and optimization of the dynamic characteristics for high speed wheel reducer used in electric vehicle[J]. Journal of Chongqing University, 2017, 40(10): 1-11. (in Chinese) DOI:10.11835/j.issn.1000-582X.2017.10.001 |
| [4] |
宋朝省, 樊荣, 刘立斌. 小角度交错轴变厚齿轮齿根应力及影响因素分析[J]. 重庆大学学报, 2014, 37(1): 1-6. Song C S, Fan R, Liu L B. Analysis on tooth root stress and influencing factors of crossed beveloid gears with small shaft angle[J]. Journal of Chongqing University, 2014, 37(1): 1-6. (in Chinese) |
| [5] |
Zheng F Y, Hua L, Han X H, et al. Linkage model and manufacturing process of shaping non-circular gears[J]. Mechanism and Machine Theory, 2016, 96: 192-212. DOI:10.1016/j.mechmachtheory.2015.09.010 |
| [6] |
Zheng F Y, Hua L, Han X H, et al. Synthesis of indexing mechanisms with non-circular gears[J]. Mechanism and Machine Theory, 2016, 105: 108-128. DOI:10.1016/j.mechmachtheory.2016.06.019 |
| [7] |
林超, 张雷, 张志华. 一种新型非圆锥齿轮副的传动原理及其齿面求解[J]. 机械工程学报, 2014, 50(13): 66-72. Lin C, Zhang L, Zhang Z H. Transmission theory and tooth surface solution of a new type of non-circular bevel gears[J]. Chinese Journal of Mechanical Engineering, 2014, 50(13): 66-72. (in Chinese) |
| [8] |
Bair B W, Sung M H, Wang J S, et al. Tooth profile generation and analysis of oval gears with circular-arc teeth[J]. Mechanism and Machine Theory, 2009, 44(6): 1306-1317. DOI:10.1016/j.mechmachtheory.2008.07.003 |
| [9] |
Li B T, Hu J Q, Chen D F, et al. Numerical algorithm of non-circular gear's tooth profile based on Jarvis March[M]. Cham, Switzerland: Springer International Publishing, 2016: 689-694.
|
| [10] |
童婷, 郑方炎, 孙科, 等. 基于齿廓法线的非圆齿轮齿廓数值算法[J]. 武汉理工大学学报(交通科学与工程版), 2013, 37(3): 652-654. Tong T, Zheng F Y, Sun K, et al. Non-circular gear teeth profile numeric method based on normal tooth profile[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2013, 37(3): 652-654. (in Chinese) DOI:10.3963/j.issn.2095-3844.2013.03.048 |
| [11] |
Hua Q, Gang D. A calculation approach to complete profile of noncircular gear teeth[M]. Cham, Switzerland: Springer International Publishing, 2013: 23-33.
|
| [12] |
李建刚, 吴序堂, 毛世民, 等. 非圆齿轮齿廓数值计算的研究[J]. 西安交通大学学报, 2005, 39(1): 75-78. Li J G, Wu X T, Mao S M, et al. Numerical computation of tooth profile of noncircular gear[J]. Journal of Xi'an Jiaotong University, 2005, 39(1): 75-78. (in Chinese) DOI:10.3321/j.issn:0253-987X.2005.01.018 |
| [13] |
张瑞, 吴序堂, 聂钢, 等. 高阶变性椭圆齿轮的研究与设计[J]. 西安交通大学学报, 2005, 39(7): 726-730. Zhang R, Wu X T, Nie G, et al. Study and design on high-order deformed elliptic gears[J]. Journal of Xi'an Jiaotong University, 2005, 39(7): 726-730. (in Chinese) DOI:10.3321/j.issn:0253-987X.2005.07.017 |
| [14] |
李建刚, 吴序堂, 李泽湘. 基于插齿数值计算模型的非圆齿轮根切分析[J]. 农业机械学报, 2007, 38(6): 138-142. Li J G, Wu X T, Li Z X. Analysis of tooth undercutting in noncircular gears based on numerical computation model of shaping[J]. Transactions of the Chinese Society of Agricultural Machinery, 2007, 38(6): 138-142. (in Chinese) DOI:10.3969/j.issn.1000-1298.2007.06.034 |
| [15] |
Wu X T, Wang S Z, Wang G H, et al. Noncircular gear CAD/CAM technology[C]//Proceedings of 8th World Congress on the Theory of Machines and Mechanisms, August 26-31, 1991, Prague, Czechoslovakia: vol 8. IFToMM, 1999: 26-31.
|
| [16] |
Penaud J, Alazard D, Amiez A. Kinematic analysis of spatial geared mechanisms[J]. Journal of Mechanical Design, 2012, 134(2): 021009-021009. DOI:10.1115/1.4005596 |
| [17] |
Talpasanu I, Simionescu P A. Kinematic analysis of epicyclic bevel gear trains with matroid method[J]. Journal of Mechanical Design, 2012, 134(11): 114501. DOI:10.1115/1.4007144 |
| [18] |
林超, 夏锡光, 邢庆坤, 等. 非圆齿轮型间歇转动机构的设计与运动特性分析[J]. 中国机械工程, 2020, 31(10): 1142-1148. Lin C, Xia X G, Xing Q K, et al. Design and kinematic characteristics analysis of an intermittent rotation mechanism based on non-circular gears[J]. China Mechanical Engineering, 2020, 31(10): 1142-1148. (in Chinese) DOI:10.3969/j.issn.1004-132X.2020.10.002 |
| [19] |
杨存. 非圆齿轮运动学与动力学研究[D]. 兰州: 兰州理工大学, 2014. Yang C. Research on the kinematics and dynamics of non-circular gears[D]. Lanzhou: Lanzhou University of Technology, 2014. (in Chinese) |
| [20] |
黄忠超, 蓝兆辉. 节曲线封闭的非圆齿轮传动比函数设计[J]. 机械传动, 2011, 35(11): 30-33. Huang Z C, Lan Z H. Design of transmission ratio function of non-circular gear of closed pitch curve[J]. Journal of Mechanical Transmission, 2011, 35(11): 30-33. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45

