混凝土泵车是基建工程中的重要施工设备,目前混凝土泵车正面临大尺度、轻量化、高可靠、长寿命的巨大挑战,然而提高其大尺度与轻量化的同时又必然导致臂架低频振动加剧[1],使结构更易遭受疲劳和不稳定的问题,影响结构寿命和可靠性[2-3]。
众多学者对混凝土臂架的动力学与振动问题进行了研究。文献[4-6]采用传递矩阵法建立了泵车臂架动力学模型,求解得到了任意姿态下的固有频率,并采用虚拟样机技术研究了臂架柔体模型运动停止后的振动特性。Henikl等[7]采用基函数来近似解析梁的弹性弯曲,建立了泵车臂架振动的动力学方程,为弹性振动的主动阻尼控制策略和轨迹规划提供了数学模型。Zhong等[8]采用ADAMS虚拟样机技术,模拟了臂架由水平位姿向典型位姿转变的过程,得出了液压缸的驱动力变化曲线。Gou等[9]应用ADAMS软件,分析了臂架末端位移和加速度的频响特性。文献[10]以混凝土泵车臂架系统为研究对象进行有限元仿真分析及优化。以上研究只针对混凝土泵车臂架单一系统进行,下车(底架和混凝土泵等子系统)与臂架的动力学耦合作用未予以考虑,然而,混凝土泵车的各子系统间存在相互耦合与共同作用的关系[11-12],共同影响整机动力学效应,是一个不可分割的整体。因此,现有研究缺乏以混凝土泵车整机为研究对象的动力学建模分析。
笔者研究混凝土泵车施工作业过程中的动力学振动问题,分析整机受到的冲击激励,建立其浇筑作业时的实时动态载荷模型,提出一种符合混凝土泵车实际工作受载与动态服役行为的冲击理论与仿真模拟的方法,为混凝土泵车安全性能评估和泵车减振设计、振动控制提供有力支持。
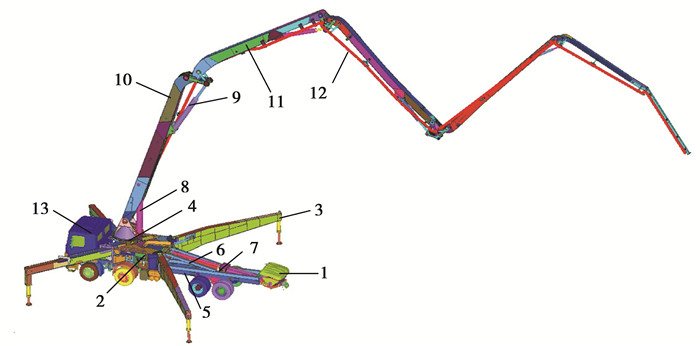
1 整机有限元建模 1.1 混凝土泵车结构简介混凝土泵车的种类可以按照臂架长度、泵送方式、分配阀类型、臂架折叠方式以及支腿形式进行划分,其基本的组成形式是相同的,常见的混凝土泵车的结构主要包括底架系统、臂架系统,泵送系统、液压系统、汽车底盘及回转机构,混凝土泵车的基本结构如图 1所示。
|
1.料斗;2.底架系统;3.支腿;4.转台;5.底盘大梁;6.副车架;7.混凝土泵;8.第1节臂架油缸;9.第2节臂架油缸;10.第1节臂架;11.第2节臂架;12.臂架输送管;13.汽车底盘 图 1 混凝土泵车主要结构图 Fig. 1 Main structure diagram of concrete pump truck |
混凝土泵车臂架与支腿箱梁采用高强度钢WELDOX960板材焊接而成,其他部位的钢材以Q345为主,2种钢材的力学性能参数见表 1。
| 表 1 材料参数 Table 1 Material parameters |
将几何模型导入HyperMesh有限元前处理软件,进行几何清理及修复、网格划分、赋予材料与属性、建立连接、施加约束与载荷等,这些步骤是复杂机械结构有限元建模的常用方法[13]。然而,对于混凝土泵车这类零部件众多的整机设备进行有限元建模时,通常采用先建立子系统有限元模型,再进行总装配的方法。本文研究对象是混凝土泵车整机,分底架系统、臂系统和汽车底盘及混凝土泵附件等三大子系统,分别对其进行有限元建模,再组装为一体建立整机有限元模型。
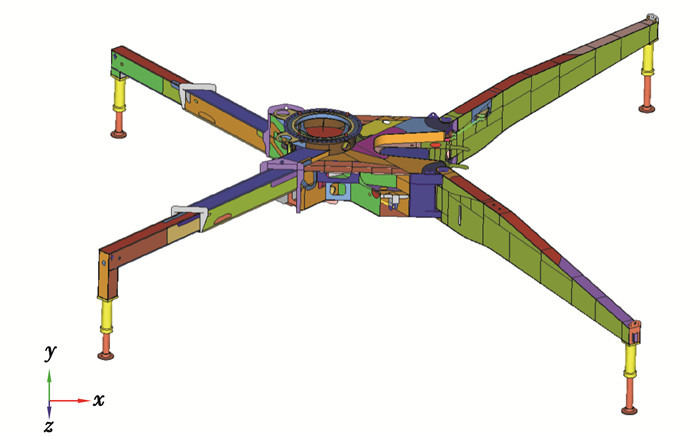
1) 底架系统。底架系统主要组成元素有钢板、销轴、轴套、油缸等部件,考虑各部件的外形尺寸和实际受力形式,采用壳、梁、杆及实体单元为主要单元类型建立了底架系统各部件的有限元模型,底架系统有限元模型如图 2所示。
|
图 2 混凝土泵车底架有限元模型总成 Fig. 2 The Finite element model of the underframe of the concrete pump truck |
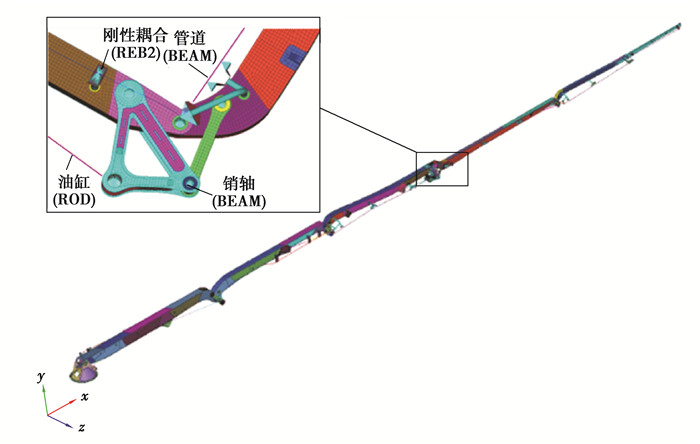
2) 臂架系统。臂架单元类型选择与底架相似,综合采用杆、梁、壳及实体单元类型对臂架各构件进行模拟,其中支撑液压缸采用杆单元建模,销轴和混凝土管采用梁单元建模,销孔壁采用梁单元模拟,销轴与孔的作用关系采用REB2刚性蛛网进行连接模拟,并释放梁单元节点处的轴向旋转自由度以保证用于模拟销轴的梁单元具有与实际相符的运动自由度,不考虑销轴与孔的配合间隙。各焊接钢板采用壳单元建模,转台底部厚板采用实体单元建模,臂架系统有限元模型如图 3所示。
|
图 3 臂架系统有限元模型 Fig. 3 The finite element model of boom system |
3) 汽车底盘及混凝土泵附件系统。混凝土泵车底架与汽车底盘通过副车架连接,混凝土泵安装在汽车底盘的副车架上,底架、混凝土泵—副车架—底盘构成泵车下车主要结构。实际结构中,底架通过其自身的耳板与副车架间的螺栓连接固定于副车架前半段,混凝土泵通过螺栓连接固定于副车架后半段。
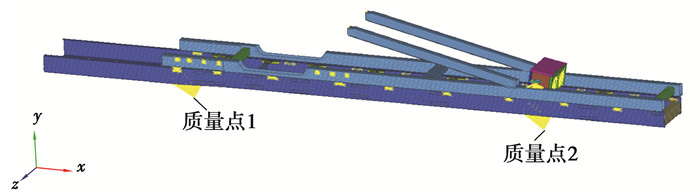
混凝土泵车作业时,混凝土泵受到的泵送反力冲击通过混凝土泵与副车架的连接结构传递到副车架上,因此,需对底盘副车架和大梁进行详细有限元建模以确保泵送反力对下车的冲击传载尽可能准确。汽车底盘视作被底架抬离地面的质量体,可采用附加于底盘大梁上的附加质量模拟该质量体以进行简化。进行有限元前处理时,应根据混凝土泵车实际的前、后轴载荷计算出底盘大梁前、后轴位置的附加质量点单元的质量大小,并通过刚性耦合将其固定在底盘前轴与后轴的相应位置,有限元模型如图 4所示。
|
图 4 大梁附加质量点单元 Fig. 4 Additional mass point element |
4) 混凝土泵车整机有限元模型。将已建立的底架系统、臂架系统、底盘及混凝土泵等三大子系统有限元模型进行组装,完成混凝土泵车整机有限元模型的建立。通过刚性耦合单元RBE2模拟底架系统与底盘及混凝土泵的螺栓固定连接,采用MPC多面约束方程耦合臂架根部转台与底架顶部圆筒顶面,以模拟臂架系统与底架系统之间的连接,以此方式实现混凝土泵车有限元模型的整机装配,整机有限元模型如图 5所示。
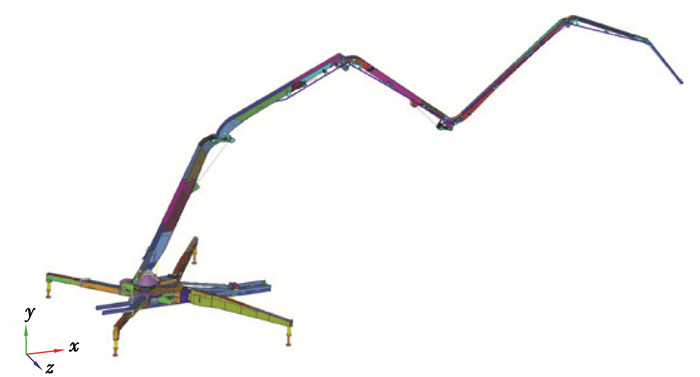
|
图 5 混凝土泵车整机有限元模型 Fig. 5 The finite element model of the concrete pump truck |
混凝土泵车浇筑作业时,泵送负载随推送过程变化,混凝土泵在推送混凝土的同时,也受到来自被推送的混凝土的反向冲击作用,该冲击载荷通过混凝土泵安装位置传递至混凝土泵车的下车;同时被推送入输送管道中的混凝土也会对输送管道产生脉动冲击。由于混凝土输送管道依附于臂架,这必然会导致悬臂梁工作原理的臂架受到来自混凝土流动而引起的摩擦冲击载荷。因此,在仿真分析中除了需要考虑泵车整机重力和混凝土重力,还必须对混凝土泵车承受的混凝土流动引起冲击激励进行分析,可以将其视为混凝土流体与混凝土泵及管道之间的相互作用荷载。
2.1 混凝土摩擦冲击模型 2.1.1 混凝土流速模型混凝土是一种典型的Binham流体,它在管道中的流动可视作柱塞流。混凝土泵浇筑作业时,双缸往复式活塞泵的2个活塞杆交替推送混凝土。文献[14]呈现了混凝土泵单个液压油缸活塞杆的工作行程变化规律,根据两连通油腔的液压油总体积不变的原理,可以得到另一个活塞杆的运动行程,如图 6所示。每个完整泵送周期内,两个混凝土缸分别完成一次推送和吸入混凝土的工作。在活塞杆每个稳定推送阶段行程位移与时间大致成正比,说明此时活塞杆做匀速运动;在推送过程中的换向阶段,活塞杆行程位移斜率逐渐变缓直至反向后又逐渐增大,说明活塞杆在换向阶段分别经历了减速阶段和加速阶段。每个周期起始和结束时刻混凝土的速度近似为0。
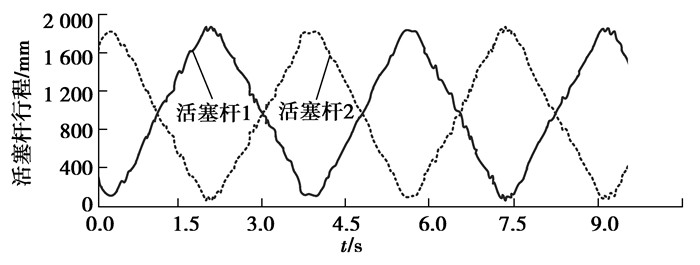
|
图 6 活塞杆工作行程图 Fig. 6 Piston rod working stroke diagram |
根据以上对混凝土泵送流速的分析,将矩形波速度曲线内每个周期的开始与结束阶段缓化过渡,用谐波表示。根据文献[15],混凝土泵分配阀换向时间与活塞杆推送混凝土的时间比为0.2~0.3,文中取为0.25。则在每个推送周期T时间内,换向时间为T/5,推送时间为4T/5,可绘制出新形式的混凝土流动速度曲线,如图 7所示。
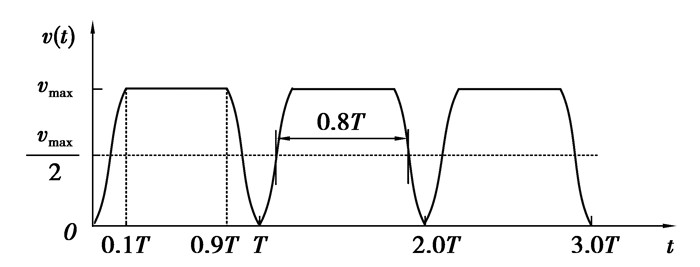
|
图 7 混凝土流动速度曲线 Fig. 7 Concrete flow velocity curve |
混凝土在管道中的实时流动速度在单个周期内的表达式为
| $ v(t)=\left\{\begin{array}{cc} \frac{v_{\max }}{2}\left\{\sin \left[\frac{10 {\rm{ \mathsf{ π} }}}{T}(t-0.05 T)\right]+1\right\} & (0.0,0.1 T) \cup(0.9 T, T), \\ v_{\max } & (0.1 T, 0.9 T) 。\end{array}\right. $ | (1) |
式中vmax为混凝土最大实时流动速度。当泵送方量为Q、输送管内半径为r时,混凝土在管道中的最大流动速度为
| $ v_{\max }=\frac{Q}{3\ 600 {\rm{ \mathsf{ π} }}\ r^{2}} 。$ | (2) |
日本学者森永繁通过对混凝土管道流进行试验研究,得到了定常流速混凝土在管道中流动的摩擦阻力f的计算关系式为[16]
| $ f=2 {\rm{ \mathsf{ π} }} r\left[K_{1}+K_{2} v_{\text {定常 }}\right] L, $ | (3) |
式中:K1为黏着系数,MPa;K2为速度系数,MPa·s/mm-1; v定常为混凝土定常流速,mm·s-1; L为直管长度,mm。系数K1和K2与混凝土坍落度SL(mm)存在如下关系:
| $ K_{1}=\left(300-S_{\mathrm{L}}\right) \times 10^{-6}, $ | (4) |
| $ K_{2}=\left(400-S_{\mathrm{L}}\right) \times 10^{-6}。$ | (5) |
混凝土不同流速对应不同的摩擦阻力,随流速增大,摩擦阻力呈线性增加,将式(3)中的混凝土定常流速v定常替换为混凝土泵送实时流速v(t),可以得到混凝土实时摩擦阻力表达式:
| $ f=2 {\rm{ \mathsf{ π} }} r\left[K_{1}+K_{2} v\right] L。$ | (6) |
文献[17]提供了混凝土泵两个活塞杆推送混凝土时的应变电压信号变化曲线,如图 8所示。在每个推送周期内,活塞杆的负载变化趋势与本文中提出的混凝土流速变化一致,证明了采用式(6)计算混凝土摩擦阻力的合理性。
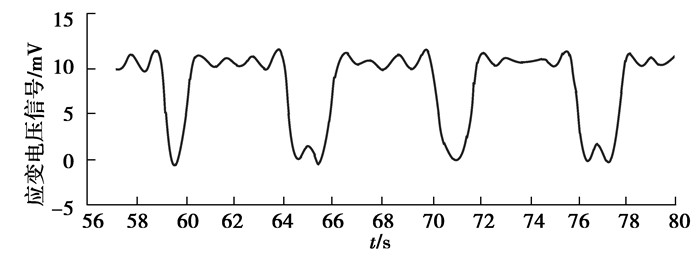
|
图 8 活塞杆应变电压信号 Fig. 8 Piston rod strain voltage signal |
混凝土泵的两个液压驱动油缸的内部结构和其工作的特点,也决定了其推送混凝土时受到反力冲击的周期性。混凝土泵通过液压驱动与控制系统对两个液压油缸的交替驱动,实现砼缸1和砼缸2的交替推送混凝土,其工作示意图如图 9所示。
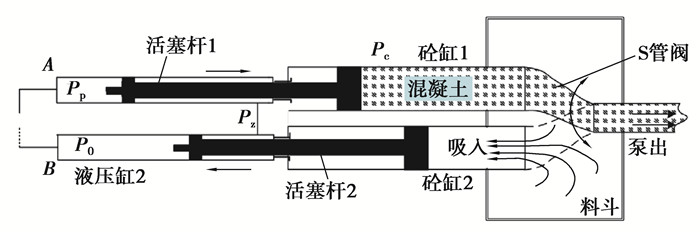
|
图 9 混凝土泵工作原理示意图 Fig. 9 Schematic diagram of concrete pump working principle |
设砼缸推送混凝土截面面积为Sc,混凝土压力为Pc,液压油缸无杆腔有效作用面积为S0,有杆腔有效作用面积为S1,供油路压力为Pp,回油路压力为P0,连通油路压力为Pz,砼缸1和砼缸2内的活塞杆在运动时受到的摩擦力分别为f1和f2。根据力平衡原理,可得:
| $ P_{\mathrm{c}} S_{\mathrm{c}}=\left(P_{\mathrm{p}}-P_{0}\right) S_{0}-f_{1}-f_{2} \text { 。} $ | (7) |
当混凝土泵空载运行,即Pc=0时:
| $ 0=\left(P_{\mathrm{p}}^{\prime}-P_{0}\right) S_{0}-f_{1}-f_{2}, $ | (8) |
联立式(7)~(8),可得混凝土对混凝土泵的作用力为:
| $ F_{\mathrm{p}}=P_{\mathrm{c}} S_{\mathrm{c}}=\left(P_{\mathrm{p}}-P_{\mathrm{p}}^{\prime}\right) S_{0}, $ | (9) |
由式(9)可知,欲求得混凝土泵送时对混凝土泵的冲击力,必须获得混凝土泵进行泵送混凝土作业时的压力Pp和空载运行时的压力P′p。Pp和P′p均可通过实验测试得到。
2.3 分析类型与边界条件混凝土泵车定姿态浇筑作业时受到多种动态冲击激励共同作用,属于受迫振动的范畴,因此在进行有限元动态分析时应选用瞬态响应分析类型。瞬态响应分析是计算受迫振动动态响应的最通用方法,其目的是计算结构在时变激励下的行为,瞬态分析获得的重要结果通常是网格节点的位移、速度和加速度,以及单元的应力[17]。文中采用MSC.NASTRAN Solver进行混凝土泵车整机有限元仿真计算,该求解器用于瞬态响应分析有直接瞬态分析法和模态瞬态分析法两种不同的数值方法:直接瞬态分析方法是对完整的耦合运动方程进行数值积分,模态瞬态分析方法是利用结构的模态形状来简化和解耦运动方程,并对各个模态响应求和以获得解。对于大型模型的长时间激励的瞬态响应分析,推荐使用模态瞬态分析方法。
设置整机有限元瞬态分析边界条件时,将4条支腿底端约束X/Y/Z 3个方向的平移自由度以模拟地面对4条支腿的支撑与固定关系。如图 10所示,在混凝土泵与副车连接处施加泵送冲击力,在臂架管道上施加混凝土摩擦冲击力。泵送油缸引起的下车体振动将通过泵送反力与副车架、底盘大梁以及被悬挂的汽车底盘的相互作用被模拟出,并且由此引起的车体振动及臂架振动影响将直接被包含在仿真结果中。
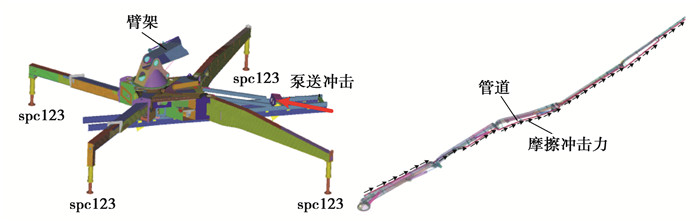
|
图 10 混凝土泵车整机有限元分析的边界条件 Fig. 10 The boundary conditions of the finite element analysis of the concrete pump truck |
在管道各节点上创建质量点单元,管道上的摩擦冲击力施加于混凝土输送管道的1D梁单元的节点上,且各个节点上的力受到梁单元划分时的长度和轴线方向的影响,这就导致手工施加的困难。为解决该问题,此处提供一种快速计算施加混凝土管道梁单元节点上的载荷的方法。首先,在HyperMesh中使用Renumber工具将管道梁单元的节点ID与自身ID按混凝土输送方向依次重新编号。然后,将管道梁单元导出的节点ID、节点全局坐标和单元ID导出至文本文件中,并使用数据处理软件,如Matlab,读取这些信息,这些信息被用于计算每个单元的方向余弦αei,同时计算每个管道梁单元所受的实时冲击力Fei。最后,使用式(10)计算每个单元在全局坐标系X/Y/Z 3个方向冲击力的分量,即
| $ \left[\begin{array}{l} F_{\mathrm{e} i x} \\ F_{\mathrm{e} i y} \\ F_{\mathrm{e} i z} \end{array}\right]=\left|\boldsymbol{F}_{\mathrm{e} i}\right| \cdot \boldsymbol{\alpha}_{\mathrm{e} i} $ | (10) |
式中i为单元ID。以单元ei为例,设该单元2节点N1ei和N2ei的全局坐标为(xN1, yN1, zN1)和(xN2, yN2, zN2),则Fei可依据式(6)计算,Fei和αei的表达式为
| $ \left|\boldsymbol{F}_{\mathrm{e} i}\right|=2 {\rm{ \mathsf{ π} }} r\left[K_{1}+K_{2} \cdot v(t)\right] * \sqrt{\left(x_{N 2}-x_{N 1}\right)^{2}+\left(y_{N 2}-y_{N 1}\right)^{2}+\left(z_{N 2}-z_{N 1}\right)^{2}}, $ | (11) |
| $ \boldsymbol{\alpha}_{\mathrm{e} i}=\left[ \begin{gathered} \frac{x_{N 2}-x_{N 1}}{\sqrt{\left(x_{N 2}-x_{N 1}\right)^{2}+\left(y_{N 2}-y_{N 1}\right)^{2}+\left(z_{N 2}-z_{N 1}\right)^{2}}}\\ \frac{y_{N 2}-y_{N 1}}{\sqrt{\left(x_{N 2}-x_{N 1}\right)^{2}+\left(y_{N 2}-y_{N 1}\right)^{2}+\left(z_{N 2}-z_{N 1}\right)^{2}}}\\ \frac{z_{N 2}-z_{N 1}}{\sqrt{\left(x_{N 2}-x_{N 1}\right)^{2}+\left(y_{N 2}-y_{N 1}\right)^{2}+\left(z_{N 2}-z_{N 1}\right)^{2}}} \end{gathered} \right]。$ | (12) |
为便于加载,每个单元的冲击力施加在该单元的第二个节点处,使用Matlab软件将这些载荷信息写出文本文件后导入至整机有限元模型中即可完成载荷施加。需要注意的是,应保证速度模型与泵送测试压力的周期起点相同,即推送速度与泵送油压关系对应。
3 实验与仿真混凝土泵车整机实验测试是为了获取整机位姿以及泵送油压等参数,为有限元动态仿真提供重要信息,也是为了获取泵车整机动态响应(位移、位移振幅、动应力等)。测量混凝土泵车施工作业的位姿参数,包括混凝土泵车支腿展开角度、转台角度以及各节布料杆臂与水平面的夹角,为有限元分析提供整机姿态参数;测试混凝土泵的供油压力动态曲线,为计算混凝土泵送冲击载荷提供参数,同时还可以获取到其推送混凝土的周期,为混凝土流动速度模型提供速度变化的时间周期;测试获得泵车施工过程中的动应力及臂架末端相对初始静止位置的垂直方向的位移量(以下简称位移量)随时间变化曲线,可以将其与仿真结果对比,检验文中提出的研究方法的正确性。实验中拟定采用恒定泵送单位在3种姿态下的混凝土泵车进行测试,将C30新拌混凝土作为泵送原料。
3.1 实验测试 3.1.1 整机位姿与泵送油压测试实验中以某型52 m 6节臂混凝土泵车为测试对象,该车自带随车智能监测平台,可以实时监测显示并记录各监测量的变化,监测平台测试项目如图 11所示。Pp是混凝土泵车的混凝土泵供油路油压,α1与α2分别是混凝土泵车左后支腿与右后支腿的展开角度,ϕ是臂架底部转台的转动角度,θi(i=1, 2,…,6)是6节杆臂的倾角。

|
图 11 随车智能监测平台测试项目示意图 Fig. 11 Onboard intelligent monitoring system |
随车智能监测平台采用不同种类的传感器对各个监测对象进行实时测量。其中,油压Pp由压力传感器测量,角度α1, α2和ϕ由角位移传感器测量,倾角θi由倾角传感器测量。通过随车智能监测平台的数据采集系统将这些传感器的电信号进行采集与处理,以获取各个传感器所测物理量,最后通过显示面板进行显示,同时将测试数据记录在数据储存卡中以供提取和使用。
3.1.2 位移与动应力测试位移与动应力测试主要是测量臂架末端位移量与臂架动应力,对这两个项目进行测试时,需搭建位移与动应力测试平台。
1) 臂架末端位移量测试。混凝土泵车臂架的振动可以看作是悬臂梁结构的受迫振动,臂架末端位移采用拉线位移传感器进行测试。将拉线位移传感器固定于臂架末端,并将拉绳一端固定于地面,使拉绳垂直于地面方向,其测得的振动是臂架末端垂直于地面方向的位移量。
2) 动应力测试。选取合作企业中工程师统计的混凝土泵车结构常发生疲劳开裂等破坏位置进行测试,测点布置示意图如图 12所示。由于梁弯曲主要是轴线方向的拉伸或压缩,应力测试实验采用单向应变片对箱梁轴向方向的正应力进行测试。
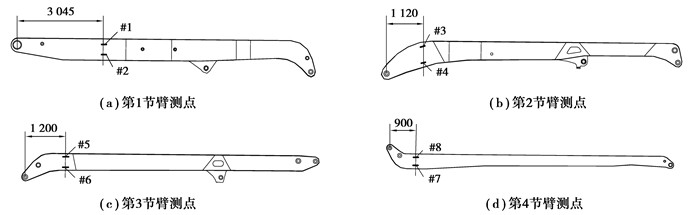
|
图 12 臂架应力测点布置示意图 Fig. 12 Positions of stress test points in booms |
各应变片沿箱梁轴线方向布置均与侧板边缘相距50mm,为保证应变片能够长期使用,采用了金属壳体进行封装。应力测试现场照片如图 13所示。

|
图 13 应力测试现场照片 Fig. 13 Stress test site |
利用电缆线进行位移量与应力测试数据的信号传输,采用NS-DAC3000单通道数据采集系统和笔记本电脑对拉线位移传感器的信号进行实时采集、示波与存储。采用一台DRA-30A多通道动静态应变仪采集8个应力测点的应变数据,并通过USB接口与计算机通讯。另外,还需一台笔记本电脑与加速度传感器配备的无线网关连接进行USB串口通信。每种测试项所使用的仪器都有该设备配套的控制软件,可以清晰直观看到各通道信号的实时变化,也可以随时控制数据采集的开始与结束,因此很容易实现各种信号的同步采集或间断采集。
实验中所采用C30新拌混凝土的坍落度约为0.18 m。通过对浇筑用料体积和浇筑时间的统计,计算出浇筑过程中泵送方量Q为85m3/h。
3.2 测试结果及对比 3.2.1 整机位姿与泵送油压测试结果由于实验场地限制,测试时,混凝土泵车的左后支腿未完全展开,右后支腿和前支腿完全伸展到极限位置。3种测试姿态下,转台转角位置略有不同,实验场地有砖墙,导致3种姿态的第1节臂都有较大角度地抬起。3种测试姿态如图 14所示,依据泵车姿态将其命名为类水平姿态、弧形姿态和M形姿态。

|
图 14 混凝土泵车浇筑作业姿态 Fig. 14 Concrete pump truck pouring operation posture |
将应变片读数值在臂架竖直姿态下做清零处理,每进行姿态调整后,应停机等待2 min左右,使臂架由于姿态调整而产生的振动消除,以便能准确测量出臂架位姿参数(包括转台转角和各节杆臂倾角),并且此时可以采集到臂架振动位移幅值衰减过程变化规律信息,通过计算得到结构阻尼比。振动衰减过程中的对数衰减率计算公式为
| $ \delta=\frac{1}{n} \ln \frac{\left|A_{i}\right|}{\left|A_{i+n}\right|}=\zeta \omega_{\mathrm{n}} \tau_{\mathrm{d}}, $ | (13) |
式中:δ为对数衰减率; n为周期数;A为振幅;ζ为阻尼比;ωn为固有频率;τd为有阻尼自由振动周期。将
| $ \zeta={\frac{\delta}{\sqrt{4 {\rm{ \mathsf{ π} }}^{2}+\delta^{2}}}}。$ | (14) |
外搭测试平台记录混凝土泵车停机过程中,臂架末端的振动幅值衰减过程如图 15所示。
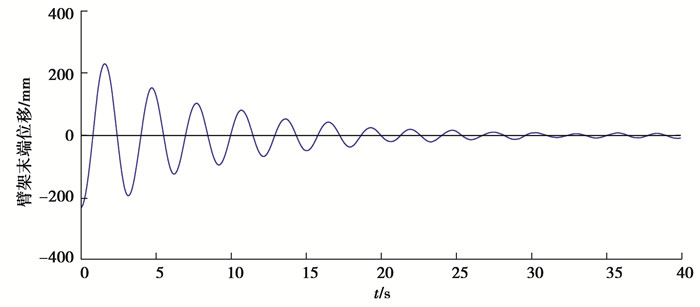
|
图 15 停机时臂架末端振位移幅值衰减曲线情况 Fig. 15 Vibration displacement amplitude of boom tip in stopping period |
臂架末端振动加速度曲线波动剧烈,难以准确取值。因此选取振动位移幅值进行计算:振动位移幅值由228 mm衰减为19 mm经历了7个周期,计算出混凝土泵车结果阻尼比为ζ=0.056,该值可以为有限元瞬态分析提供可靠的结构阻尼比。
3种姿态在浇筑作业开始前的静止状态时,混凝土泵车的下车位姿测试结果和臂架位姿测试结果如表 2所示。
| 表 2 混凝土泵车位姿角度参数 Table 2 Angles and inclination parameters of concrete pump truck |
根据随车智能监测平台记录的结果,混凝土泵空载时的供油路压力P′p为3.4 MPa,3种姿态稳定浇筑时段泵送油Pp如图 16所示。可以看出,混凝土推送周期T=3.8 s,每个周期的压力波形近似于梯形波。
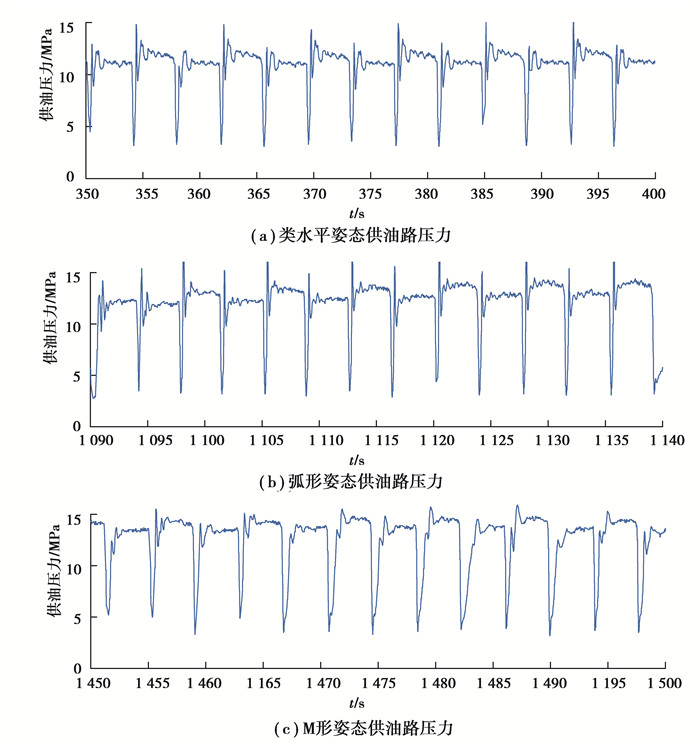
|
图 16 混凝土泵车供油路压力 Fig. 16 Oil supply pressure of concrete pump truck |
利用测试获得的混凝土泵车位姿参数及泵送油压曲线等关键信息,对整机有限元模型进行姿态调整,并完成边界条件的施加,便可以进行有限元求解计算及后处理。实验测试与有限元仿真的主要对比指标为臂架末端位移量与臂架测点应力,以下将进行这2个指标的结果对比。
1) 臂架末端位移量对比。拉线位移传感器测得的臂架末端垂直地面方向的位移量与有限元仿真分析模型的全局坐标系Y轴方向的位移结果含义一致,臂架末端位移量随时间变化曲线如图 17所示,根据曲线对比可知,有限元仿真获得的臂架末端位移量与实验测试结果在每个周期内的波动幅度与波动规律基本相同,两者间存在较小差异。
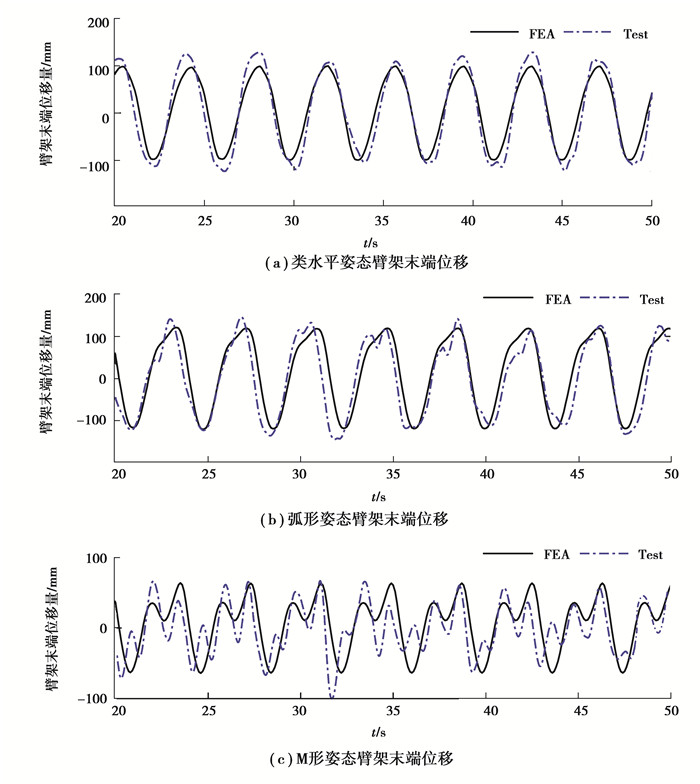
|
图 17 臂架末端位移量 Fig. 17 Vibration displacement of the boom tip |
2) 动应力对比。图 18展示了测点1在实验测试全时段的正应力曲线,可以看出:混凝土泵车浇筑时,测点动应力存在常值应力与循环应力2种组分,且循环应力组分与常值应力比值较小。为使动应力对比更清晰,可将应力结果的比较转化为常值应力和循环应力2种应力组分的比较。
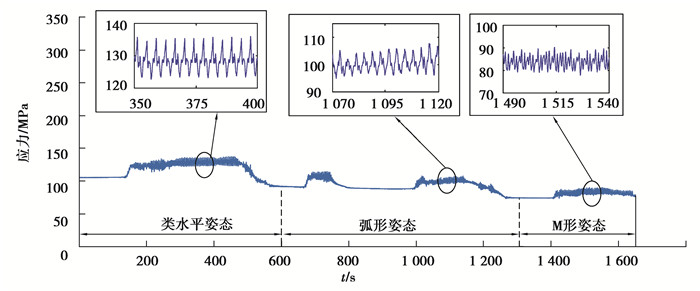
|
图 18 测点#1全时段正应力 Fig. 18 Measuring point #1 full-time normal stress |
a.常值应力组分对比。将3种姿态的仿真应力与测试应力的常值进行提取与统计,绘制的柱状对比图如图 19所示,一方面,仿真应力与实验测试应力的常值组分基本吻合;另一方面,测试应力与仿真应力差值较大的测点在3种姿态下相差的趋势相同,尤其以#1测点、#4测点和#8测点最为明显,其最大相差值接近实验测试应力的25%。
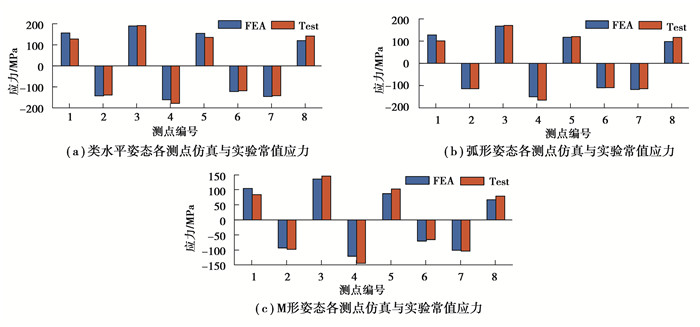
|
图 19 各测点仿真与实验常值应力对比 Fig. 19 Comparison of normal stress between simulation and experiment at each measuring point |
b.循环应力组分对比。对于混凝土泵车3种姿态浇筑时的循环波动组分的对比,将循环波动的平衡点置零进行直观比较。3种姿态下,各测点应力响应的循环应力组分曲线如图 20所示。仿真与测试得到的应力循环组分变化趋势及幅度基本相同,且仿真的循环应力组分较测试应力的循环应力组分相比,更为光滑。另外,从3种姿态的仿真与测试结果还可以看出:类水平姿态和弧形姿态的位移振幅与应力的仿真结果与M形姿态相比更接近实验测试结果。
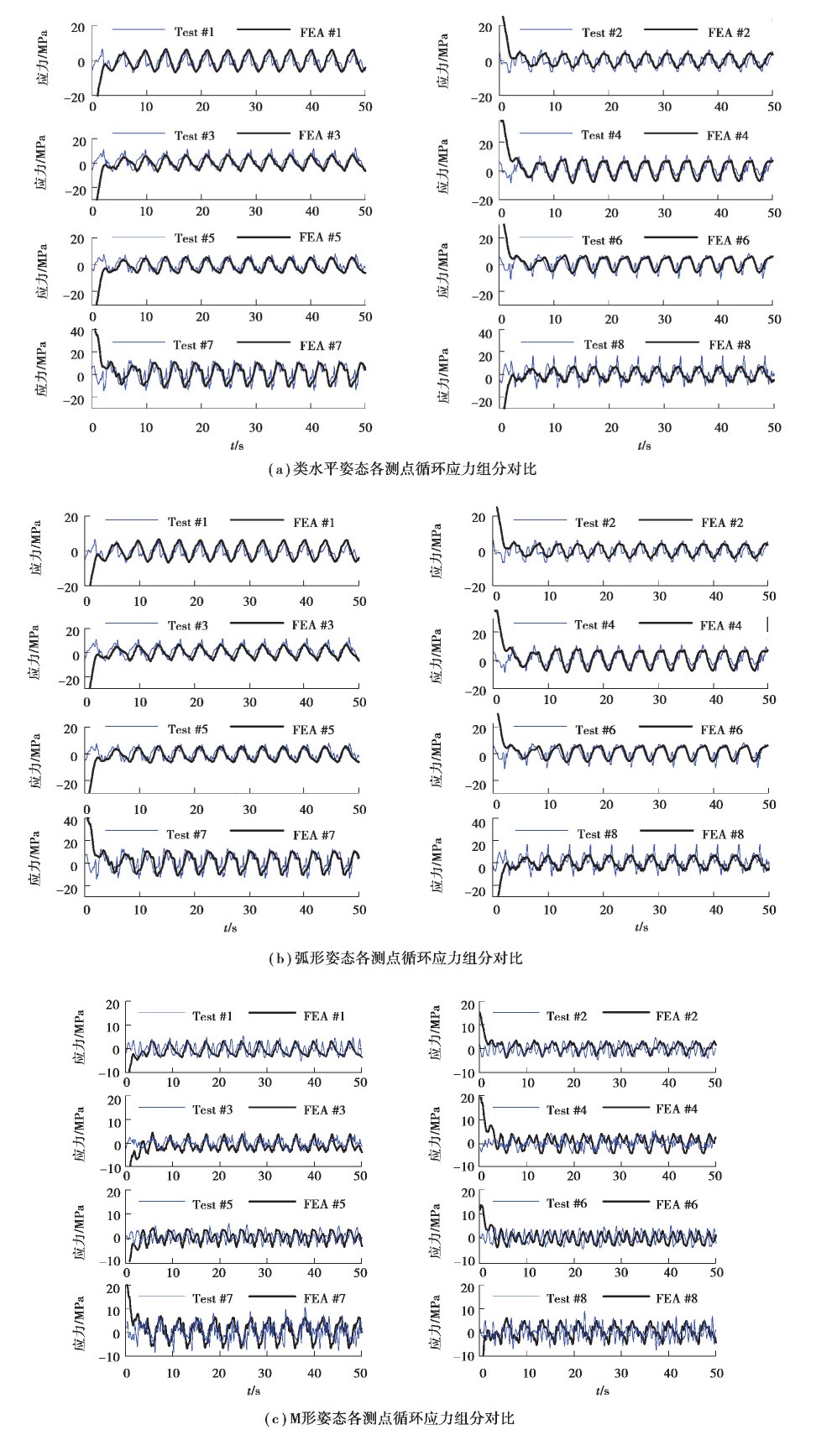
|
图 20 混凝土泵车各测点循环应力组分对比 Fig. 20 Comparison of cyclic stress at various measuring points of concrete pump truck |
分析泵车实际受载、实验测试过程等与仿真之间的差异,可以找出仿真应力与测试应力之间差异的主要原因。
有限元仿真的位移量与测试结果的误差主要来自两方面:1)仿真计算时,采用的冲击载荷每个周期完全相同,然而混凝土泵车实际受到的载荷在每个推送混凝土周期内存在波动,并且可能受到不确定的风载荷的干扰,因而每个周期的波动略有不同;2)采用拉线位移传感器测试时,由于臂架末端并不只做竖直方向的运动,因而导致测试结果与实际相比偏大,与仿真结果存在一定误差。
有限元仿真的应力结果与测试结果中的常值组分存在差异的原因有:1)测试中的臂架倾角是受重力作用下各节臂中点附近切线与水平面的夹角,与有限元模型具有一定差异。2)实际的测点位置和贴片方向与仿真应力结果提取时位置和方向具有一定差异。由于每个测点都采用单向应变片测试该点处沿杆臂箱梁轴线方向的正应力,且位于箱梁两侧,贴应变片时,其距离上下盖板的距离以及是否严格平行于箱梁轴线难以准确保证。3)由于混凝土泵车稳定浇筑状态下,各测点应力常值部分均存在一定的不确定漂移,推测可能受到一定的风载荷影响。而应力响应的循环组分存在差异的主要原因有:1)冲击载荷平稳性差异。仿真计算采用的冲击载荷连续且平滑,从测试泵送油压结果可以看出混凝土在管道内的摩擦冲击应是不平稳且有不确定性的尖刺,这是测试的循环应力组分的尖刺明显多于仿真结果的主要原因。2)测点循环应力组分每个周期的幅值范围存在差异主要由测点贴片位置和方向引起。3)混凝土泵车浇筑作业过程中,各节弯头处存在不确定性的堵塞,且堵塞度及其引起的冲击在文中所建立的冲击载荷模型中未加以考虑。
类水平姿态和弧形姿态与M形姿态相比更贴近实验测试结果的原因可能在于:在混凝土冲击载荷建模时,将混凝土在管道中的流动状态都视作柱塞流,而实际则可能在弯道处发生塞管,在负倾角管道中发生离析,这导致了与实际情况的差别。
4 结论通过文中建立的泵送冲击载荷模型,对混凝土泵车进行了整机的有限元动态仿真,并进行了3种典型姿态下的混凝土泵车施工过程中实验测试验证,得到有限元动态仿真计算得到的动态响应结果与实验测试结果两者的变化规律及变化趋势完全吻合。这可以表明:
1) 冲击载荷模型符合混凝土泵车实际工作受载情况,通过与有限元动态仿真结合,可以准确预测混凝土泵车整机作业过程中的振动情况,并且能够准确反映出混凝土泵车稳定浇筑作业过程中整体的应力变化情况。
2) 研究所使用的分析方法对于混凝土泵车浇筑时的振动响应具有针对性,并且能够为混凝土泵车结构件强度优化设计及整机疲劳提供可靠的应力载荷谱。
3) 在混凝土管道比较平直的姿态下,使用本文的方法模拟出混凝土泵车定姿态浇筑作业时的结构动力响应更加准确。相邻臂架有很大转角变化时,混凝土在弯道处发生塞管、在负倾角管道中发生离析的特性应该单独考虑,不可忽略。
| [1] |
张黎骅, 李怡, 夏小均, 等. 板梁耦合振动响应仿真分析[J]. 重庆大学学报, 2017, 40(6): 60-66. Zhang L H, Li Y, Xia X J, et al. Simulation analysis of vibration response for coupled plate-beam[J]. Journal of Chongqing University, 2017, 40(6): 60-66. (in Chinese) |
| [2] |
Resta F, Ripamonti F, Cazzulani G, et al. Independent modal control for nonlinear flexible structures: an experimental test rig[J]. Journal of Sound and Vibration, 2010, 329(8): 961-972. DOI:10.1016/j.jsv.2009.10.021 |
| [3] |
Sun X J, Ye H, Fei S M. A closed-loop detection and open-loop control strategy for booms of truck-mounted concrete pump[J]. Automation in Construction, 2013, 31: 265-273. DOI:10.1016/j.autcon.2012.12.012 |
| [4] |
Ren W, Wu Y X, Zhang Z W, et al. A numerical method of large-scale concrete displacing boom dynamic and experimental validation[J]. Advances in Mechanical Engineering, 2014, 6: 943847. DOI:10.1155/2014/943847 |
| [5] |
Zhang Z W, Wu Y X, Liu J G, et al. Research on the rigid-flexible multibody dynamics of concrete placing boom[J]. Automation in Construction, 2016, 67: 22-30. DOI:10.1016/j.autcon.2016.03.009 |
| [6] |
Ren W, Li Z W, Bi Y P, et al. Modeling and analysis of truck mounted concrete pump boom by virtual prototyping[J]. Journal of Robotics, 2017, 2017: 9182143. |
| [7] |
Henikl J, Kemmetmüller W, Bader M, et al. Modelling, simulation and identification of a mobile concrete pump[J]. Mathematical and Computer Modelling of Dynamical Systems, 2015, 21(2): 180-201. DOI:10.1080/13873954.2014.926277 |
| [8] |
Zhong Z H, Wu Y X, Ma C X. Simulation and optimization of the driving forces of hydraulic cylinders for boom of truck mounted concrete pump[C]//2011 Fourth International Conference on Intelligent Computation Technology and Automation, March 28-29, 2011, Shenzhen, China. IEEE, 2011: 915-919.
|
| [9] |
Gou Z J. The simulation of harmonic vibration response based on the rigid and flexible boom system of the ttruck-mounted concrete pump[C]//Proceedings of 2011 International Conference on Electronic & Mechanical Engineering and Information Technology, August 12-14, 2011, Harbin, China. IEEE, 2011: 2404-2407.
|
| [10] |
胡楠. 混凝土泵车臂架系统有限元分析及改进[D]. 长春: 吉林大学, 2018. Hu N. Finite element analysis and optimization of boom system for truck-mounted concrete pump[D]. Changchun: Jilin University, 2018. (in Chinese) |
| [11] |
Cazzulani G, Ghielmetti C, Giberti H, et al. Overview on the truck mounted concrete boom pump: a dynamic numerical model for active control logic definition[J]. IFAC Proceedings Volumes, 2011, 44(1): 4232-4237. DOI:10.3182/20110828-6-IT-1002.02072 |
| [12] |
Cazzulani G, Ghielmetti C, Giberti H, et al. A test rig and numerical model for investigating truck mounted concrete pumps[J]. Automation in Construction, 2011, 20(8): 1133-1142. DOI:10.1016/j.autcon.2011.04.015 |
| [13] |
林利红, 李雨龙, 李聪波, 等. 纯电动汽车驱动桥的轻量化设计[J]. 重庆大学学报, 2019, 42(4): 17-28. Lin L H, Li Y L, Li C B, et al. Lightweight design of electric rear axle of pure electric vehicle[J]. Journal of Chongqing University, 2019, 42(4): 17-28. (in Chinese) |
| [14] |
黄前春. 基于出口压力的混凝土泵排量测量方法研究[D]. 杭州: 浙江大学, 2007. Huang Q C. Research of measuring method on the pumpage of concrete pump based on discharge pressure[D]. Hangzhou: Zhejiang University, 2007. (in Chinese) |
| [15] |
易小刚, 易秀明, 王尤毅. 现代混凝土泵原理、设计与施工[M]. 北京: 机械工业出版社, 2014. Yi X G, Yi X M, Wang Y Y. Operating principles, design, and construction use of modern concrete pumps[M]. Beijing: China Machine Press, 2014. (in Chinese) |
| [16] |
Morinaga M. Pumpability of concrete and pumping pressure in pipelines[C]//Proceedings of the RILEM Seminar on Fresh Concrete: Important Properties and Their Measurement, March 22-24, 1973, Leeds, England: vol 7. Leeds: University of Leeds, 1973: 1-39.
|
| [17] |
王斌华, 吕彭民. 混凝土泵车臂架系统振动机理的研究[J]. 振动与冲击, 2011, 30(9): 259-263. Wang B H, Lü P M. Vibration mechanism of arm system of concrete pump truck[J]. Journal of Vibration and Shock, 2011, 30(9): 259-263. (in Chinese) DOI:10.3969/j.issn.1000-3835.2011.09.053 |
 2022, Vol. 45
2022, Vol. 45


