2. 南京高速齿轮制造有限公司,南京 211100
2. Nanjing High Speed Gear Manufacturing Co., Ltd., Nanjing 211100, P. R. China
长期以来,工程上评价构件和零部件疲劳强度主要依据S-N曲线,由于疲劳试验周期长,成本较高,根据传统的实验方法(成组法实验)可能存在一定的试验困难,部分学者借助仿真软件,建立有限元模型对零部件进行疲劳分析[1-3],胡建军等[4]通过威布尔分布拟合出随机疲劳载荷谱,对齿轮弯曲疲劳进行了研究,并得到了齿轮弯曲强度的S-N曲线。此外,基于小样本数据的统计与拟合方法也得到了广泛关注[5-9],由于疲劳试验中得到的循环寿命离散性较大,这就对小样本疲劳试验数据的统计以及拟合方法要求更高。
傅惠民等[10-11]根据寿命破坏和剩余强度破坏率相等原理,提出一种极小子样加速寿命试验设计和可靠性分析方法,还提出了疲劳寿命服从对数正态分布的小样本数据统计分析异方差回归的分析方法。谢里阳等[12]基于不同应力下试样疲劳寿命对应的概率分位点不一致,提出了样本信息聚集原理的小样本数据P-S-N曲线拟合方法。白恩军等[13]提出了服从威布尔分布的小样本疲劳寿命试验数据统计分析与P-S-N曲线拟合方法。刘建忠等[14]运用贝叶斯理论提出了小样本实验数据确定疲劳寿命的可靠方法。但上述方法的数学计算方式比较烦琐且精度及可靠性方面存在较大的改进空间,不能较好地满足实际工程应用需求。
笔者基于不同应力水平下试样疲劳寿命对应的概率分位点的一致性,采用数据共享与融合方法,把不同应力下的疲劳寿命分别等效到基准应力水平上,将等效寿命与基准应力水平下的循环寿命混合,根据混合后疲劳寿命与基准应力水平下疲劳寿命均值的相对误差求得各级应力水平下循环寿命的均值。同时以不同应力水平为基准,对拟合得到的S-N曲线进行了讨论。结合试验数据表明,以低应力下为基准结合改进后的方法拟合出的S-N曲线效果更好。
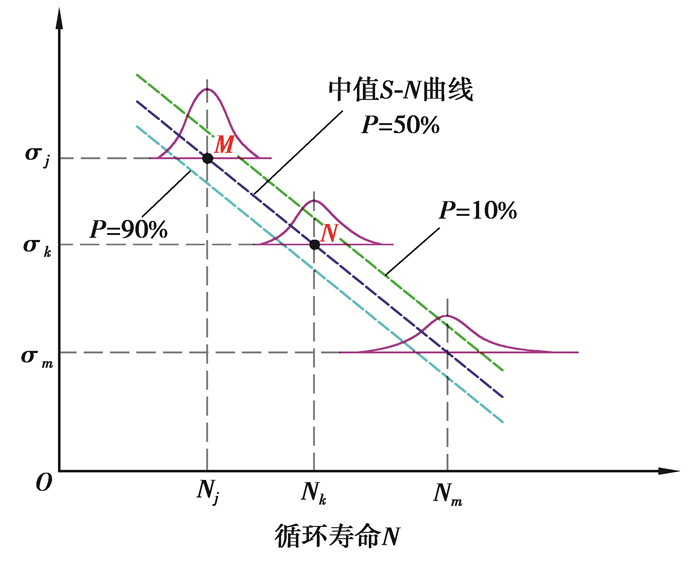
1 小样本下的信息聚集 1.1 疲劳寿命概率分位点一致性原理在工程实际中,由于材料在微观组织结构分布和力学性能方面均具有不均匀性,以及加工质量对试件的影响,即使在相同的疲劳试验条件下,各试件采集到的疲劳寿命值具有较大的分散性[15], 则应力与寿命之间不是单纯的一一对应关系,而是在不同应力水平下具有与寿命母体相同的概率分位点。根据Miner法则定义,构建的疲劳寿命与应力之间具有线性关系,可以看作如图 1所示的一组具有存活率的应力寿命曲线簇。
|
图 1 疲劳寿命概率分位点一致性原理图 Fig. 1 Schematic diagram of consistency of fatigue life probability quantile |
如图 1所示,M和N点分别为可靠度为50%时S-N曲线在应力水平σj和σk处两点,两者的存活率表达式如式(1)所示。
| $ \left.\begin{array}{l} p\left(N<N_{j}\right)=\Phi\left(\frac{n_{j, r}-\mu_{j}}{\sigma_{j}}\right), \\ p\left(N<N_{k}\right)=\Phi\left(\frac{n_{k, i}-\mu_{k}}{\sigma_{k}}\right) 。\end{array}\right\} $ | (1) |
根据寿命概率分位点一致原理,任意一条S-N曲线为同一存活率下不同应力下对应的不同循环寿命,M和N点的存活率相同,有p(N < Nj)=p(N < Nk)。因此,概率分位点一致性的表达形式如式(2)所示。
| $ \frac{n_{j, r}-\mu_{j}}{\sigma_{j}}=\frac{n_{k, i}-\mu_{k}}{\sigma_{k}}, $ | (2) |
式中:nj, r为第j级应力水平下的疲劳寿命;nk, i为第k级应力水平下的疲劳寿命;σj和σk分别为j级和k级应力水平下疲劳寿命的标准差。
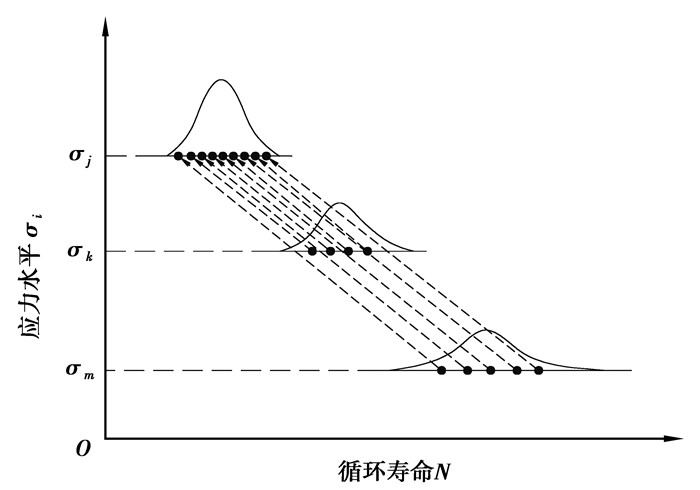
1.2 样本信息聚集原理信息聚集原理就是把各个小样本数据通过等效关系聚集成一个大样本,根据概率分位点一致性原理,把各级应力上的疲劳寿命向某一级应力进行等效,在该应力级上就可获得较多的疲劳寿命数据。根据式(1),将第k级应力水平下的疲劳寿命等效到第j级应力下,结果如式(3)所示。具体等效过程如图 2所示。
| $ n_{j, r}^{\mathrm{e}}=\left(n_{j, r}-\mu_{k}\right) \frac{\sigma_{j}}{\sigma_{k}}+\mu_{j}, $ | (3) |
|
图 2 等效寿命转换原理图 Fig. 2 Schematic diagram of equivalent life conversion |
该方法可以实现不同应力水平下疲劳寿命数据之间的相互转化,将小样本数据等效转换融合为“当量大样本”数据,形成样本聚集和信息融合效应[12]。对小样本数据进行寿命分布参数估计时,既提高了样本数据的使用效率,也提高了分布参数的估计精度。
2 基于样本信息聚集方法的改进谢里阳等[12]提出的样本信息聚集原理结合摄动搜索寻优技术,对于小子样数据而言具有较强的实用性,能够得到较为理想的疲劳P-S-N曲线,但在精度与可靠性等方面可以进一步改进。由于疲劳寿命数据的离散性较大,各级应力下疲劳寿命的均值偏差较大,而该方法中均值作为已知参数参与样本信息的聚集,难以确保疲劳S-N曲线的精确性。经典的样本信息聚集方法中,都是默认以高应力水平为基准,没有讨论以哪一级应力水平为基准拟合出的S-N曲线更精确。
传统成组法通过疲劳试验获取材料的S-N曲线,一般至少选取4级应力水平,每一级应力水平下至少进行10个数目的疲劳试样。对于小样本情况,笔者对经典样本集聚方法进行了改进,利用应力-循环寿命的线性关系,估计各个应力水平下的疲劳寿命均值。采用疲劳寿命概率分位点一致性结合信息聚集原理,进行不
同应力水平下疲劳寿命数据的等效,可将各个小样本数据等效聚集为大样本数据进行分析。把不同应力水平下的小样本疲劳试验数据向基准应力水平下进行等效,等效后可以得到大样本疲劳寿命数据,并由此拟合出高精度的S-N曲线方程。根据混合后循环寿命与基准应力水平下循环寿命均值的相对误差搜寻各级应力水平下疲劳寿命的均值。具体过程如下:
1) 选择4级应力水平进行疲劳寿命试验,选取一基准应力水平下进行大样本试验,做10个疲劳试样,记录各试样得到的疲劳寿命nj, r(r=1~10)。其他3级应力水平下进行小样本试验,各做5个(或3个)疲劳试验,并记录各个试验的疲劳寿命nk, i(i=1~5)。
2) 对选择的4级应力水平下对数疲劳寿命的标准差按式(4)进行估计,结果分别为:
| $ \hat{\sigma}_{j}=\sqrt{\frac{\sum\limits_{i=1}^{m_{j}}\left(n_{j, r}-\hat{\mu}_{j}\right)^{2}}{m_{j}-1}}, $ | (4) |
| $ \hat{\mu}_{j}=\frac{1}{m_{j}} \sum\limits_{i=1}^{m_{j}} n_{j, r}, $ | (5) |
式中mj与mk分别为第j级与第k级应力水平下的试样数。
3) 由式(6)中第sj级应力及该应力水平下的循环寿命试验数据为基准可以估计得到其他应力水平下疲劳寿命的均值,即
| $ \mu_{k}=\mu_{j}+k_{i}\left(s_{j}-s_{k}\right) 。$ | (6) |
4) 把上面计算得到的疲劳寿命均值以及标准差代入式(7),将sk级应力水平下疲劳寿命数据向sj基准应力水平下进行转换,可以得到5个等效疲劳寿命。将每一级应力水平等效后的疲劳寿命数据与基准应力水平下的疲劳寿命进行混合,分别可以得到15个疲劳寿命数据,计算出混合后的疲劳寿命均值μ′j。
| $ n_{k, i}^{\prime}=\frac{\left(n_{k, i}-\mu_{k}\right) \sigma_{j}}{\sigma_{k}}+\mu_{j}。$ | (7) |
5) 由应力与疲劳寿命之间的线性关系等式(6)可知,为了合理地进行等效,笔者通过逐步搜索的方法确定ki值。具体方法为,令初值ki=0,ki=ki+Δm,步长Δm=0.000 1,根据每一个ki值计算出混合循环寿命μ′j,当μ′j值与第sj级应力水平下的均值
| $ \left|\frac{\mu_{j}^{\prime}-\mu_{j}}{\mu_{j}}\right|<0.000\ 1。$ | (8) |
基于该改进方法,当以高应力水平为基准时,其S-N曲线的拟合方法如下:
1) 根据式(4)与式(5)分别计算出第1级应力水平下疲劳寿命均值μ1与各个应力水平下疲劳寿命的标准差
2) 由式(6)将第2,3,4级应力下的疲劳寿命等效到第1级应力水平上,以第2级应力为例,根据式(9)将第2级应力水平下的疲劳寿命等效到第1级应力水平下,得到的等效疲劳寿命为n′2, 1,n′2, 2,n′2, 3,n′2, 4,n′2, 5。同理可以得到第3,4级应力水平下等效寿命分别为n′3, i与n′4, i。
3) 将第2,3,4级应力水平等效后的疲劳寿命分别与第1级应力水平下的疲劳寿命进行混合,然后计算出混合后疲劳寿命的均值μ′k;计算混合后疲劳寿命均值μ′k与第1级应力下的疲劳寿命均值μ1的相对误差,并根据式(10)搜寻到满足要求的ki值。
因此,根据搜索可以得到3个不同应力水平下的ki值,代入式(6)可以估计得到第2,3,4级应力水平下循环寿命均值μ2,μ3,μ4;最后由最小二乘法对每级应力及该应力水平下的疲劳寿命均值进行拟合得到S-N曲线。
| $ n_{2, i}^{\prime}=\frac{\left(n_{2, i}-\mu_{2}\right) \sigma_{1}}{\sigma_{2}}+\mu_{1}, $ | (9) |
| $ \left|\frac{\mu_{k}^{\prime}-\mu_{1}}{\mu_{1}}\right|<0.000\ 1 。$ | (10) |
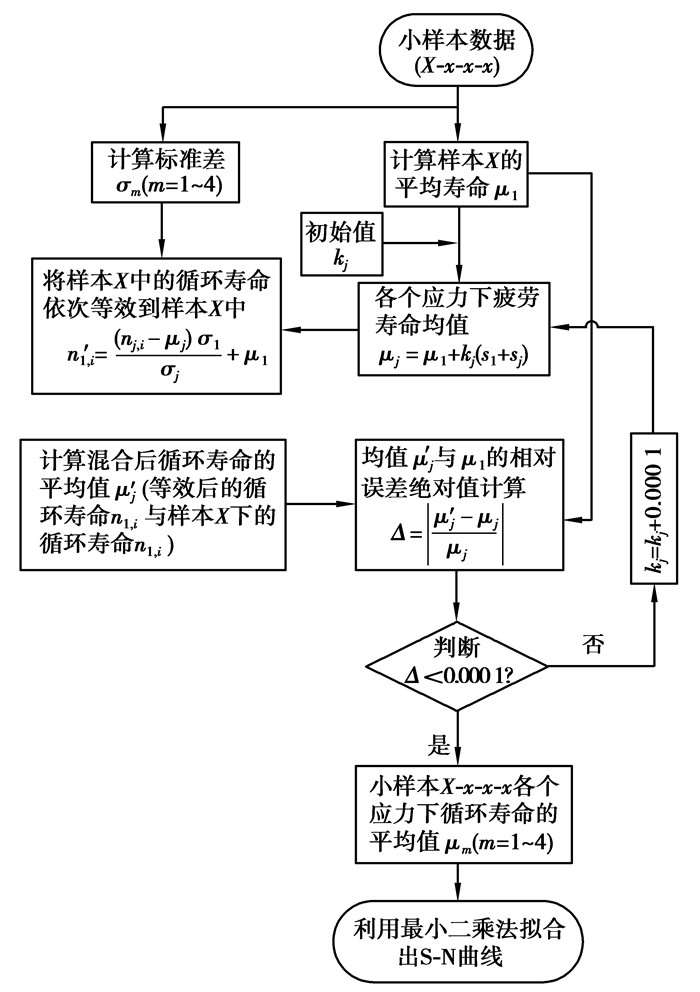
改进后样本聚集方法的具体步骤如图 3流程图所示。
|
图 3 疲劳特性曲线拟合流程图 Fig. 3 Fatigue characteristic curve fitting flowchart |
为验证改进后样本信息聚集方法的有效性和可靠性,利用文献[16]提供的齿轮弯曲疲劳寿命数据(如表 1所示)进行拟合分析,并与传统方法拟合出的结果进行对比。从表 1中的数据可以看出,同一级应力水平下的疲劳寿命离散性较大,因此,对该实验数据中应力与疲劳寿命分别取对数进行分析。
| 表 1 各级应力水平下齿轮弯曲疲劳寿命数据 Table 1 Gear bending fatigue life data under various stress levels |
为了使小样本数据拟合出的S-N曲线与完全样本下拟合效果更为接近,笔者对不同应力水平为基准拟合出的S-N曲线进行了对比。分别以高应力(第1级应力)水平、低应力(第4级应力)水平以及中间级应力(第3级应力)水平为基准,进行S-N曲线拟合对比分析,验证提出方法的可行性以及寻求小样本数据下最为合理的拟合方法。
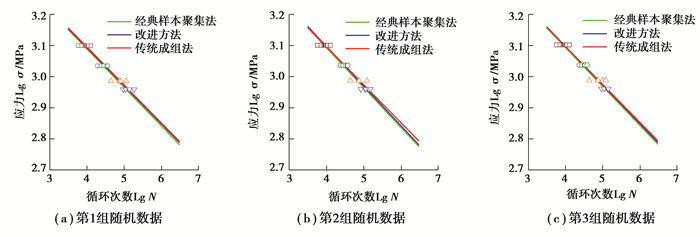
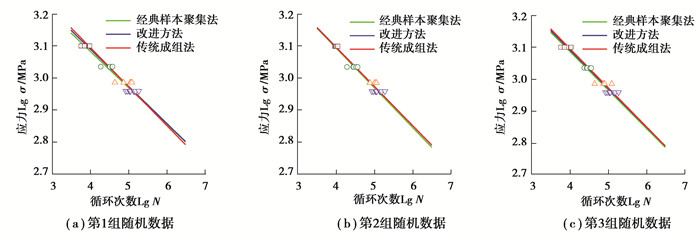
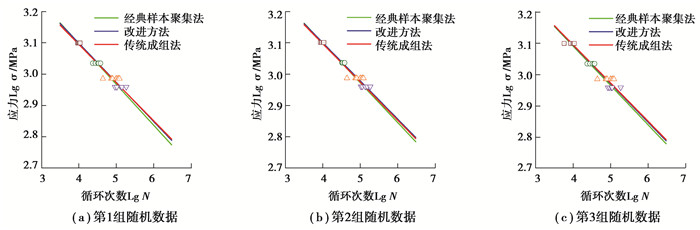
3.1 小样本数据拟合结果分析根据表 1中的齿轮弯曲疲劳寿命数据,在基准应力水平下选取完全疲劳寿命(10个数据),其他应力水平下随机选取5个疲劳寿命数据,随机选取3组数据。拟合得到的S-N曲线如图 4~6所示。
|
图 4 以第1级应力水平为基准的S-N曲线拟合 Fig. 4 S-N curve fitting based on the first-level stress level |
|
图 5 以第4级应力水平为基准的S-N曲线拟合 Fig. 5 S-N curve fitting based on the fourth-level stress level |
|
图 6 以第3级应力水平为基准的S-N曲线拟合 Fig. 6 S-N curve fitting based on the third-level stress level |
图 4为以高应力水平为基准,根据改进后的样本信息聚集方法、传统成组法以及经典样本信息聚集方法,对随机选取的3组数据分别拟合出S-N曲线。从图中可以看出,相对于经典样本聚集方法,改进后的样本信息聚集方法拟合出的S-N曲线与传统成组法更为接近。改进后的方法拟合出的曲线与传统成组法在斜率上的相对误差分别为0.410%,4.300%,2.050%,截距上的相对误差分别为0.017%,0.620%,0.620%。
图 5为以低应力水平为基准,对随机选取的3组数据分别拟合出S-N曲线。通过与传统成组法拟合结果进行对比可以看出改进后的方法拟合效果要优于经典样本聚集方法,与传统成组法拟合出的S-N曲线在斜率上的相对误差分别为0.410%,1.310%,4.840%,截距上的相对误差分别为0.078%,0.300%,0.800%。
图 6为以中间应力水平为基准,对随机选取的3组数据分别拟合出S-N曲线。通过与传统方法拟合结果进行对比可以看出改进后的方法拟合效果要优于样本聚集方法,与传统方法拟合出的S-N曲线在斜率上的相对误差分别为0.082%,0.900%,2.700%,截距上的相对误差分别为0.086%,0.089%,0.480%。
根据图 3~5中S-N曲线的拟合结果可以看出,无论以哪一级应力水平作为基准,相对于经典样本聚集方法,改进后的样本信息聚集方法拟合出的S-N曲线都更加接近传统成组法,且拟合出的S-N曲线的斜率和截距与传统方法的相对误差较小。因此,证明了笔者提出的方法对小样本疲劳数据拟合S-N曲线的可行性,并且提高了曲线的拟合精度。
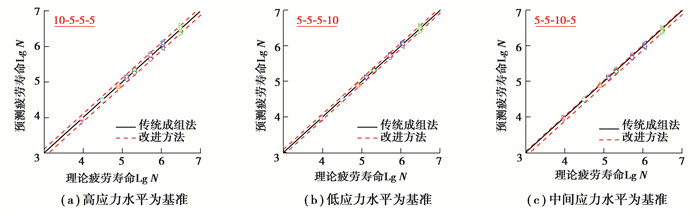
3.2 不同基准载荷下疲劳特性对比分析为了探究以哪一级应力水平作为基准能提高小样本数据拟合S-N曲线的精确性,根据改进后的样本信息聚集方法,以不同应力水平作为基准随机抽取8组数据进行S-N曲线拟合。由拟合得到的曲线,在应力599~1 316 MPa范围内从低到高随机选取8个应力值进行疲劳寿命预测,其结果作为预测疲劳寿命。由传统成组法预测出的疲劳寿命作为理论疲劳寿命,对预测出的疲劳寿命进行整理,做出了该应力区间范围内疲劳寿命分布区间,如图 7所示。
|
图 7 预测疲劳寿命分布区间 Fig. 7 Predicted fatigue life distribution interval |
根据图 7(a)可以发现,以高应力水平为基准预测得到的疲劳寿命相对于理论疲劳寿命,最大波动范围为(-0.119 7,0.106 3);从图 7(b)可以看出,以低应力水平为基准时预测出疲劳寿命相对于理论疲劳寿命,最大波动范围为(-0.076 1,0.082 8);以中间应力水平为基准时, 如图 7(c)所示,预测出的疲劳寿命相对于理论疲劳寿命的波动范围为(-0.112 5,0.031 5)。3种不同基准下, 预测得到的疲劳寿命与理论疲劳寿命误差绝对值的范围分别为: (0.000 0,0.119 7),(0.000 0,0.082 8),(0.000 0,0.112 5)。
根据上述计算结果可以发现,以高应力水平为基准预测出的疲劳寿命相对于理论疲劳寿命波动范围最大。以中间应力水平和低应力水平为基准预测得到的疲劳寿命相对于理论疲劳寿命误差最小。其中,以低应力水平为基准预测出的疲劳寿命与理论疲劳寿命误差绝对值的范围最小,且均匀分布在理论疲劳寿命线左右。以中间应力水平为基准预测出的疲劳寿命,整体上要低于理论疲劳寿命,根据该方法预测得到的疲劳寿命值偏于保守。根据构件的疲劳特性[17],当以高应力水平为基准时,由于低应力水平下的试验数据较少,在等效过程中会忽略疲劳寿命数据的离散性,使得在预测疲劳寿命时会产生较大的误差。而当以低应力水平为基准,可以考虑到其他应力水平下疲劳寿命数据向低应力水平等效时的离散性,因而可以较好地保证预测疲劳寿命的精度。因此,以低应力水平为基准对于小样本数据采用样本信息聚集原理拟合得到的S-N曲线效果更好。
在进行疲劳试验时,需要对S-N曲线的拟合精度和成本进行综合考虑,以低应力水平为基准时,应力水平过低,试件可能会产生无限寿命,导致试验过长,造成时间和资源的浪费,为提高实验效率,应选接近且不小于构件的极限疲劳强度作为最低加载载荷。
4 结论1) 笔者根据样本聚集原理对疲劳失效轨迹线进行了拓展,使其可进行定量化分析。并以此原理为基础,结合寿命概率分位点一致原理,对样本信息聚集方法进行了改进,提出了一种基于小样本数据拟合S-N曲线的方法。
2) 笔者利用齿轮弯曲疲劳寿命数据对改进后的方法进行了验证,在与传统成组法拟合得到的曲线进行了对比之后,发现改进后的方法拟合出的S-N曲线要比经典样本聚集方法效果好,拟合精度得到了提高。
3) 根据改进后的小样本拟合S-N曲线方法,对不同应力水平为基准进行了研究,发现以低应力水平为基准拟合的S-N曲线预测得到的寿命与传统成组法相比误差范围最小。所以,以低应力水平为基准结合改进后的小样本拟合方法拟合出的S-N曲线效果更好。
| [1] |
刘旭, 张开林, 刘斌, 等. 基于缺口应力法的焊接接头多轴疲劳分析[J]. 重庆大学学报, 2017, 40(4): 9-17. Liu X, Zhang K L, Liu B, et al. The multi-axle fatigue analysis of welded joints based on Notch stress method[J]. Journal of Chongqing University, 2017, 40(4): 9-17. (in Chinese) |
| [2] |
林腾蛟, 沈亮, 赵俊渝. 风电增速箱输出级齿轮副疲劳寿命有限元分析[J]. 重庆大学学报, 2012, 35(1): 1-6. Lin T J, Shen L, Zhao J Y. Fatigue life finite element analysis of output gear pair of wind turbine speed-increase gearbox[J]. Journal of Chongqing University, 2012, 35(1): 1-6. (in Chinese) |
| [3] |
林腾蛟, 钟声, 沈亮. 圆柱齿轮齿根三维裂纹扩展分析及寿命预测[J]. 重庆大学学报, 2012, 35(11): 1-7. Lin T J, Zhong S, Shen L. Three-dimensional crack propagation simulation and life prediction in tooth root of cylindrical gear[J]. Journal of Chongqing University, 2012, 35(11): 1-7. (in Chinese) DOI:10.11835/j.issn.1000-582X.2012.11.001 |
| [4] |
胡建军, 许洪斌, 高孝旺, 等. 威布尔分布随机载荷下齿轮弯曲疲劳试验分析[J]. 重庆大学学报, 2012, 35(11): 34-39. Hu J J, Xu H B, Gao X W, et al. Experimental study of gear bending fatigue strength under random load according to three-parameter Weibull distribution[J]. Journal of Chongqing University, 2012, 35(11): 34-39. (in Chinese) DOI:10.11835/j.issn.1000-582X.2012.11.006 |
| [5] |
Baptista C, Reis A, Nussbaumer A. Probabilistic S-N curves for constant and variable amplitude[J]. International Journal of Fatigue, 2017, 101: 312-327. DOI:10.1016/j.ijfatigue.2017.01.022 |
| [6] |
Leonetti D, Maljaars J, Snijder H H. Fitting fatigue test data with a novel S-N curve using frequentist and Bayesian inference[J]. International Journal of Fatigue, 2017, 105: 128-143. DOI:10.1016/j.ijfatigue.2017.08.024 |
| [7] |
Barbosa J F, Carlos Silverio Freire R Jr, Correia J A, et al. Analysis of the fatigue life estimators of the materials using small samples[J]. The Journal of Strain Analysis for Engineering Design, 2018, 53(8): 699-710. DOI:10.1177/0309324718782245 |
| [8] |
Shao Y H, Lu P, Wang B H. Analysis of fatigue characteristics of small samples[J]. Fracture and Structural Integrity, 2019, 13(48): 757-767. |
| [9] |
赵永翔, 王金诺, 高庆. 估计三种常用疲劳应力-寿命模型P-S-N曲线的统一经典极大似然法[J]. 应用力学学报, 2001, 18(1): 83-90, 160. Zhao Y X, Wang J N, Gao Q. A unified classical maximum likelihood approach for estimating P-S-N curves of three commonly used fatigue stress-life relations[J]. Chinese Journal of Applied Mechanics, 2001, 18(1): 83-90, 160. (in Chinese) DOI:10.3969/j.issn.1000-4939.2001.01.014 |
| [10] |
傅惠民, 张勇波, 王治华. 极小子样加速寿命试验设计和可靠性分析方法[J]. 机械强度, 2013, 35(1): 22-27. Fu H M, Zhang Y B, Wang Z H. Method for accelerated life test design and reliability analysis with very small sample[J]. Journal of Mechanical Strength, 2013, 35(1): 22-27. (in Chinese) |
| [11] |
傅惠民, 刘成瑞. S-N曲线和P-S-N曲线小子样测试方法[J]. 机械强度, 2006, 28(4): 552-555. Fu H M, Liu C R. Small sample test method for s-n and p-s-n curves[J]. Journal of Mechanical Strength, 2006, 28(4): 552-555. (in Chinese) DOI:10.3321/j.issn:1001-9669.2006.04.016 |
| [12] |
谢里阳, 刘建中. 样本信息聚集原理与P-S-N曲线拟合方法[J]. 机械工程学报, 2013, 49(15): 96-104. Xie L Y, Liu J Z. Principle of sample polymerization and method of P-S-N curve fitting[J]. Journal of Mechanical Engineering, 2013, 49(15): 96-104. (in Chinese) |
| [13] |
白恩军, 黄树涛, 谢里阳. 威布尔分布下小样本P-S-N曲线拟合方法[J]. 西安交通大学学报, 2019, 53(9): 96-101. Bai E J, Huang S T, Xie L Y. P-S-N curves fitting of small sample with fatigue lives obeying weibull distribution[J]. Journal of Xi'an Jiaotong University, 2019, 53(9): 96-101. (in Chinese) |
| [14] |
刘建中, 谢里阳. 疲劳寿命概率分布的模糊贝叶斯确定方法[J]. 航空学报, 1994, 15(5): 607-610. Liu J Z, Xie L Y, Xu H. Determining fatigue life reliability model with fuzzy judgment and bayes theory[J]. Acta Aeronautica et Astronautica Sinica, 1994, 15(5): 607-610. (in Chinese) |
| [15] |
彭兆春. 基于疲劳损伤累积理论的结构寿命预测与时变可靠性分析方法研究[D]. 成都: 电子科技大学, 2017. Peng Z C. Research on methods for structural life prediction and time-dependent reliability analysis using cumulative fatigue damage theories[D]. Chengdu: University of Electronic Science and Technology of China, 2017. (in Chinese) |
| [16] |
邹德志, 李凯. 齿轮材料弯曲S-N曲线测试及拟合方法[J]. 汽车工艺与材料, 2018(2): 50-54. Zou D Z, Li K. Testing and fitting method of gear material bending S-N curve[J]. Automobile Technology & Material, 2018(2): 50-54. (in Chinese) |
| [17] |
李舜酩. 机械疲劳与可靠性设计[M]. 北京: 科学出版社, 2006. Li S M. Mechanical fatigue and reliability design[M]. Beijing: Science Press, 2006. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45


