多资源受限柔性作业车间调度问题(MRC-FJSP,multi-resource constrained flexible job shop scheduling problems)是一种由经典柔性作业车间调度问题(FJSP,flexible job shop scheduling problems)扩展而来的NP-hard问题。在许多现实的生产环境中,不仅需要考虑加工机器的分配,还要考虑用于服务加工机器的各类受限附资源的分配[1]。MRC-FJSP正是为了解决这一类生产调度问题而被提出的,自2004年提出以来就备受专家学者和工程技术人员的关注。
与传统FJSP相比,MRC-FJSP增加了机器准备时间和附资源约束,是比传统FJSP更为复杂的NP-hard问题。近似方法可以在一个合理的时间范围内求得一个较优解,在MRC-FJSP的科学研究和工程实践中得到广泛的应用。在过去的十多年里,随着计算机科学与技术的发展,大量元启发式算法(如遗传算法[2-3]、果蝇算法[4]、候鸟优化算法[5]等)被用于求解MRC-FJSP,取得了不错的效果。Wu等[2]采用遗传算法(GA,genetic algorithm)求解以最小化最大完工时间为目标的MRC-FJSP;Hao等[6]采用合作分布估计算法(CEDA,cooperative estimation of distribution algorithm)求解MRC-FJSP,通过引入分治策略扩展了合作进化的框架,充分考虑了群体决策过程中相互依赖关系的影响。
随着人工智能技术的突飞猛进,近几年涌现出许多更加高级的群智能算法,这些新算法为MRC-FJSP的求解提供了新的技术思路。Wang等[7]提出采用基于知识库的多智能体进化算法(KMEA,knowledge-based multi-agent evolutionary algorithm)求解MRC-FJSP,使用混合初始化机制来平衡初始智能体群的多样性和质量,并使用知识库来存储搜索过程中获取的有用信息;Cao等[8]提出采用一种基于强化学习和代理模型的布谷鸟搜索算法(CSRS,cuckoo search algorithm with reinforcement learning and surrogate modeling)求解MRC-FJSP。但是目前大多文献只是停留在算法层面的革新,并没有深入挖掘MRC-FJSP的特征信息。
粒子群优化算法(PSO,particle swarm optimization)是Eberhart等[9]在1995年首次提出的,受自然界中鸟群觅食行为的启发,被成功应用到各种组合优化问题上[10-11]。笔者针对MRC-FJSP问题特点,对PSO算法进行改进,设计基于关键路径的邻域结构,引入基于随机网络结构的多种群策略和重新初始化策略,成功将PSO算法应用于求解MRC-FJSP,取得了较好的结果。
1 MRC-FJSP问题描述多资源柔性作业车间调度问题是传统FJSP的拓展[12],主要在FJSP的基础上增加了机器准备时间和附资源约束。MRC-FJSP包含机器分配子问题、工序排列子问题和机器配置子问题。MRC-FJSP可以被描述如下:
1) 有n个工件(J1,J2,…,Jn)要在m台机器(M1,M2,…,Mm)上加工[13];
2) 每个工件包含ni道工序,工序的顺序是预先确定的;
3) 每道工序Oij都可以从可选加工机器集Ωij中任选一台机器进行加工;
4) 工序Oij在机器Mk上的加工时间是恒定且预知的;
5) 在车间有r类附资源(R1,R2,…,Rr),每类附资源的数量是预先确定的;
6) 同一台机器在同一时刻只能加工一道工序[14];
7) 同一个附资源在同一时刻只能服务一台机器;
8) 同一工件的同一道工序在同一时刻只能被一台机器加工;
9) 每一道工序一旦开始加工就不允许中断[15];
10) 同一工件的不同工序之间有优先级约束,不同工件的不同工序之间没有优先级约束[16];
11) 所有工件在零时刻都可以被加工,所有机器和附资源在零时刻都可以被使用;
12) 考虑机器准备时间[3]。
以最小化最大完工时间为目标函数,其公式表示形式如下:
| $ \min \;{C_{\max }} = \min \left( {\max \left( {{C_i}} \right)} \right), 1 \le i \le n。$ | (1) |
式中Ci为工件i的加工完成时间。
2 基于MPSO-RDnet求解MRC-FJSP 2.1 编码与解码 2.1.1 编码由于不考虑同一类附资源的单件之间的差异性,单独编写机器配置向量会导致搜索空间过大,使算法的寻优效率降低。因此,MRC-FJSP只编写工序排列向量和机器分配向量,各加工机器的附资源配置在解码阶段动态决策。
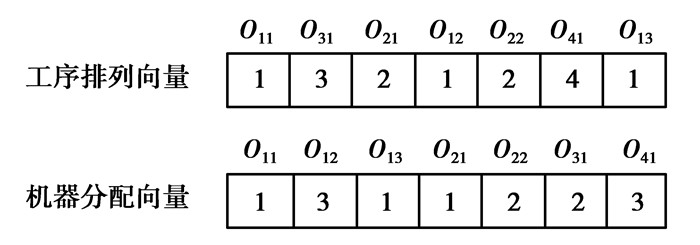
对于工序排列向量,采用FJSP研究文献中常用的基于工件编号的表示方法。使用相同的工件编号来表示同一个工件的所有工序。从左到右,第k次出现的工件编号,表示对应工件的第k道工序。以图 1为例,工序排列向量{1, 3, 2, 1, 2, 4, 1}表示的加工序列为{O11, O31, O21, O12, O22, O41, O13}。
|
图 1 粒子个体编码 Fig. 1 Encoding of individual particles |
机器分配向量采用基于机器编号的表示方法,其长度与工序排列向量相同。从左到右,依次表示1号工件第1道工序至最后一道工序的所选机器、2号工件第1道工序至最后一道工序的所选机器、…、n号工件第1道工序至最后一道工序的所选机器。以图 2为例,机器分配向量{1, 3, 1, 1, 2, 2, 3}表示的各工序与所选机器的对应关系为{(O11, 1), (O12, 3), (O13, 1), (O21, 1), (O22, 2), (O31, 2), (O41, 3)}。
2.1.2 解码解码的过程就是确定每道工序在所选机器上的开始加工时间。对于MRC-FJSP而言,如果要开始加工某一道工序,需要同时满足3个条件:
1) 工件已到达所选机器;
2) 所选机器处于空闲状态,且已完成加工前的准备工作;
3) 所选机器需要配置的所有附资源均可以立刻投入使用。
基于上述约束条件,MRC-FJSP中各工序的开始加工时间可以通过公式(2)计算得到:
| $ {s_{ij}} = \max \left( {{s_{ij - 1}} + {p_{ij - 1k'}}, {A_k} + {t_{k'k}}, {A_{hk}}} \right)。$ | (2) |
式中:sij表示工序Oij的开始加工时间;pij-1k′表示工序Oij-1在机器k′上的加工时间,sij-1+pij-1k′表示工件i的最早可用时间;Ak表示机器k的释放时间,tk′k表示机器k的准备时间,Ak+tk′k表示机器k的最早可用时间;Ahk表示机器k所需的附资源h的释放时间。
机器配置子问题采用启发式规则进行处理:在sij时刻,如果同一类附资源有多个单件可供选择的话,选择释放时间最接近sij的单件。这一选择不会推迟当前工序的开始加工时刻,但为后续工序的尽早加工留出了余地。
2.2 种群初始化种群初始化方式影响算法的收敛速度和求解质量。工序排列向量采用随机初始化方式,机器分配向量采用混合初始化方式,通过试错法设定针对机器分配向量的3种初始化策略的选择概率。其中选择随机初始化的概率为60%,选择最早完工时间(ECT,earliest completion time)优先的概率为20%,选择准备时间与加工时间之和最短(SSPT,shortest setup plus process time)优先的概率为20%。
2.3 子种群“社会认知”阶段“社会认知”阶段是子种群内部的信息交互,是子种群内较差粒子向较优粒子靠近的过程。子种群“社会认知”阶段的具体操作步骤如下。
第1步:对每个子种群中的粒子按照适应度值排序,找到每个子种群中最优的2个粒子和最差的2个粒子;
第2步:最优粒子与次劣粒子交互。交互时,工序排列向量采用改进优先工序交叉(IPOX,improved precedence operation crossover)算子,机器分配向量采用多点保留交叉(MPX,multi-point crossover)算子。从交叉得到的2个新粒子中随机选取一个,替换粒子对中的较差粒子;
第3步:次优粒子与最差粒子交互,交互和替换方法与第2步相同。
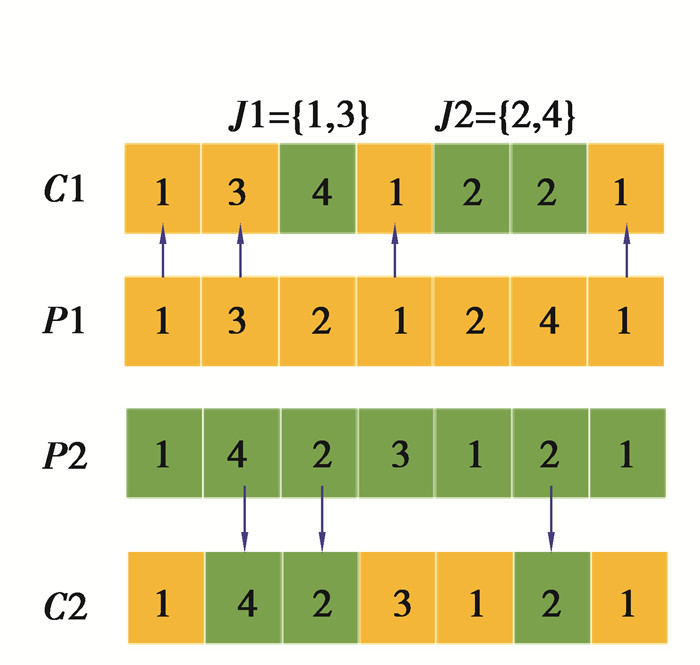
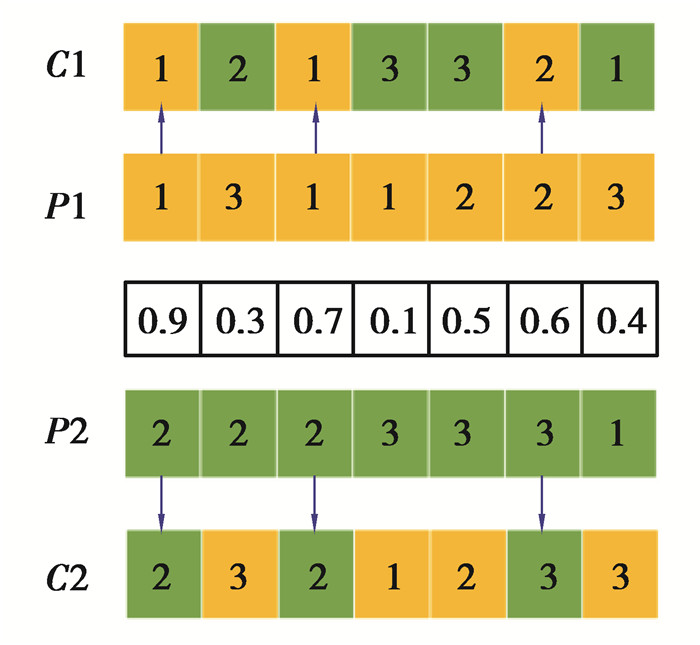
IPOX算子和MPX算子的具体执行过程如图 2和图 3。图中J1和J2表示工件集合,P1和P2表示父代1和父代2,C1和C2表示交叉得到的子代1和子代2。
|
图 2 IPOX算子操作示例 Fig. 2 Example of IPOX operator operation |
|
图 3 MPX算子操作示例 Fig. 3 Example of MPX operator operation |
“自我认知”阶段是粒子的邻域搜索过程。如果在附资源约束下进行邻域搜索,可行的移动方案会非常少,在寻找可行邻域解的过程中会消耗大量的计算资源,得不偿失。因此MRC-FJSP的邻域移动分为两步,先进行带准备时间的FJSP的邻域移动,得到一个中间解;再使用2.1.2节中所述方法完成各机器的附资源配置,得到一个可行邻域解。
定理1:当机器准备工作的完成时刻与工序的开始加工时刻相等时,机器时间利用率最大[17]。
证明:当准备工作完成后,当前机器已被某个工件锁定,不能再加工其他工件,只能等候该工件到达。如果延长这一等待时间,最大完工时间可能不会变大,但一定不会变小。当机器准备时间与工序加工时间无缝衔接时,时间利用率最高。
关键路径的变化是改变最大完工时间的关键,也是构造邻域结构的重要组成部分。关键路径的定义是从0时刻到终止时刻,顺次满足公式(3)的工序所组成的路径:
| $ {s_{{O_{ij}}}} - \left( {{s_{{\rm{KPJ}}\left[ {{O_{ij}}} \right]}} + {p_{{\rm{KPJ}}\left[ {{O_{ij}}} \right]k\left[ {{\rm{KP}}{{\rm{L}}_{\left[ {{O_{ij}}} \right]}}} \right]}}} \right) \le {t_{k'k}}。$ | (3) |
式中:KPJ[Oij]表示工序Oij所在关键路径上的紧前工序;sKPJ[Oij]+pKPJ[Oij]k[KPJ[Oij]]表示KPJ[Oij]的完工时间(开始时间+加工时间)。
以MRC-FJSP的问题特征为导向,设计出MRC-FJSP的2个邻域结构:换机器的邻域结构(N-CM,neighborhood of changing machine)和同机器的邻域结构(N-SM,neighborhood of the same machine)。
2.4.1 换机器的邻域结构基于N-CM的邻域移动可以归纳为以下步骤:
1) 从当前解的某条关键路径中随机选取一道工序,判断该工序是否有2个以上(含2个)的可选机器。若有,则进行步骤3;若没有,则重新选取工序,直至找到满足条件的工序Oij。
2) 把工序Oij从它当前机器的加工序列中删除。
3) 从工序Oij的其他可选机器中随机选择一个,把Oij插入到所选机器的加工序列中,并保证插入后的解依然为可行解。
可行插入
一个可行的插入,是要保证插入后的加工路线不存在闭合回路。
| $ {L_k}:{L_k} = \left( {{O_{xy}} \in {Q_k}\mid {s_{xy}} < {s_{ij + 1}}} \right); $ | (4) |
| $ {R_k}:{R_k} = \left( {{O_{xy}} \in {Q_k}\mid {s_{xy}} + {p_{xyk}} > {s_{ij - 1}} + {p_{ij - 1{k^\prime }}}} \right) $ | (5) |
式中:Qk表示在机器k上加工的所有工序的集合;对于集合Lk里的工序而言,不存在从Oij到Oxy的加工路径;对于集合Rk里的工序而言,不存在从Oxy到Oij的加工路径。
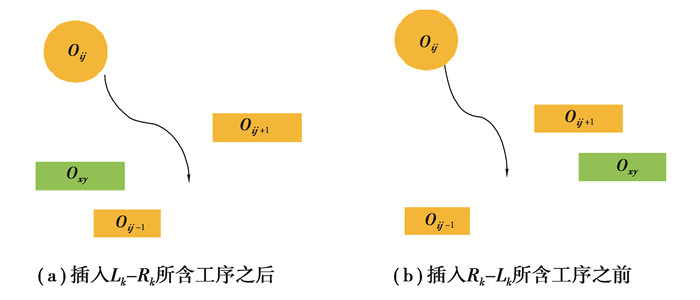
定理2:把Oij插入到Lk-Rk所含工序之后和Rk-Lk所含工序之前,都是可行插入[18]。
用Fijk表示把Oij插入机器k的加工序列中得到的可行解集。定理2的可视化示例见图 4。
|
图 4 可行插入的可视化示例图 Fig. 4 Visual examples of feasible insertion |
最优插入
在所有可行插入中,可以获得最好解的插入就是最优插入。
示例1:当Lk∩Rk≠Φ时,把Oij插入到Lk-Rk所含工序之后和Rk-Lk所含工序之前,会有一个最优插入。
示例2:当Lk∩Rk=Φ时,把Oij插入到Lk所含工序之后和Rk所含工序之前,都是最优插入。
2.4.2 同机器的邻域结构N-CM在进行邻域移动之前,必须事先确定Lk和Rk,通过二进制搜索算法获得Lk和Rk的时间复杂度为O(log |Qk|)。为了提高算法的运行速度,降低时间开销,对于不换机器的邻域移动,采用一种更加简单高效的方法。
基于N-SM的邻域移动也是在关键路径上进行的。在介绍N-SM之前,首先说明关键块的含义。关键块指的是在同一台机器上的关键工序组成的最大序列。
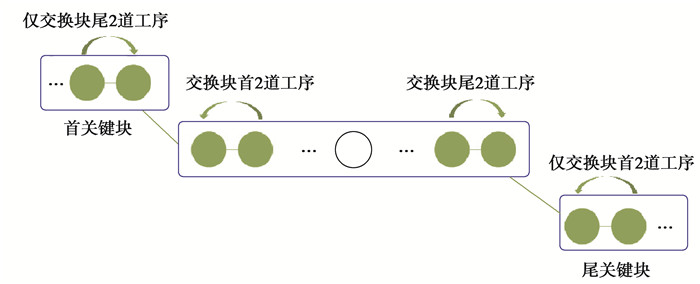
基于N-SM的邻域移动,就是交换同一关键块的块首和块尾2道工序(图 5)。但是在交换过程中,需要满足下列条件:
|
图 5 基于N-SM的邻域移动 Fig. 5 Neighborhood mobilizing based on N-SM |
1) 首关键块只交换块尾2道工序,尾关键块只交换块首2道工序;
2) 如果把工序Oij移动到工序Oi′j′之后,则必须保证Oij+1在Oi′j′之后;
3) 如果把工序Oij移动到工序Oi′j′之前,则必须保证Oij-1在Oi′j′之前;
4) 同一个工件的工序之间不得交换。
子种群“自我认知”阶段的具体操作步骤如下:
第1步:找到当前解的一条关键路径;
第2步:执行基于N-CM的邻域移动;
第3步:执行N-SM的邻域移动2次,确保2次选择的关键块分别属于不同的加工机器;
第4步:存档邻域解1,调用解码算法计算其最大完工时间Cmax;
第5步:重复第1步到第3步1次;
第6步:存档邻域解2,调用解码算法计算其Cmax;
第7步:比较邻域解1和邻域解2的Cmax,用较优的邻域解替换当前粒子。
2.5 子种群间信息交互MRC-FJSP的工件数量和机器数量都相对较多,导致解空间比较庞大,如果仅仅依靠单个种群进行迭代搜索,算法的效率比较低。多种群并行搜索机制既可以满足单次迭代搜索方向的多元化需求,也在客观上维护了种群的多样性,在复杂优化问题中被广泛应用。目前文献中常用的多种群策略是离散重组和基于网络结构通信的多种群策略。
离散重组大体操作如下:在每次迭代完成后,打破原有的子种群束缚,将所有个体重新归为一个大种群;根据适应度值高低,将种群划分为若干个层次;每个层次随机选取一定数量的个体填充入各子种群中;新组建的子种群再依据相应的规则进行下一轮迭代搜索。虽然离散重组起到了保持种群多样性的作用,但每次重组后,原有子种群个体之间建立的关系被打破,新子种群个体之间需要重新磨合,导致算法后期收敛的精度不高。
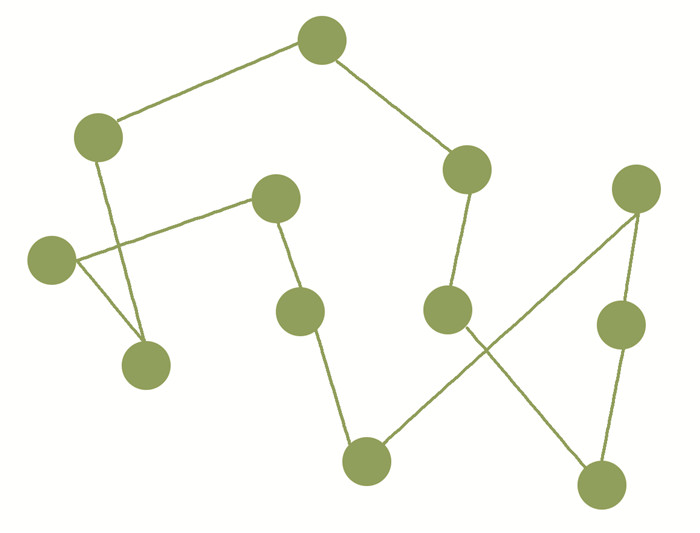
目前应用比较广泛的网络结构图有3种:无标度网络[19]、分块对角网络[19]和随机网络[20]。随机网络是指度分布满足均匀分布的网络结构,见图 6。各节点之间的连接关系通过连接概率(CP,connection probability)进行调节。当CP取值较大时,各节点的度数普遍较高;当CP取值较小时,各节点的度数普遍较低。随机网络由于连接概率的可变性,适应能力较强,能够应对许多具有不同性质的复杂问题。
|
图 6 随机网络结构图 Fig. 6 Random network structure |
本研究中采用基于随机网络结构的多种群策略,在数值实验环节会给出带有不同多种群策略的PSO算法的对比结果。
为避免算法早期精英片段在子种群之间传播过快,导致早熟收敛,特设计了自适应信息交互控制因子Pc:
| $ {P_{\rm{c}}} = {\left( {\frac{{{I_{{\rm{now}}}}}}{{{I_{\max }}}}} \right)^R}。$ | (6) |
式中:Inow表示当前迭代次数;Imax表示最大迭代次数;R为传播频率,在数值实验环节进行设置。
子种群间信息交互阶段的具体操作步骤如下。
第1步:生成一个位于区间(0, 1)内的随机数。如果该随机数小于Pc,则进行第2步到第4步;否则,本次迭代不进行子种群间信息交互;
第2步:根据连接概率CP获取用以指导子种群交互的关系矩阵A。A是一个二维矩阵,里面存储着0-1变量。当变量取值为1时,表示矩阵横纵坐标编号代表的2个子种群存在交互关系;当变量取值为0时,表示矩阵横纵坐标编号代表的2个子种群不存在交互关系;
第3步:按照关系矩阵A,2个需要交互的子种群里适应度值居中的粒子分别与另一个子种群的最优粒子进行交互,得到2个新位置。交互时,工序排列向量采用IPOX算子,机器分配向量采用MPX算子;
第4步:在2个新位置中随机选取1个替换中间粒子的当前位置。
2.6 子种群重新初始化有些时候会出现某个子种群连续多次迭代中最优解未得到更新的情况,此时子种群已陷入局部最优。为了避免浪费计算资源、提高算法的鲁棒性,对连续T次都未更新最优解的子种群执行重新初始化操作。子种群重新初始化操作是对搜索停滞的子种群中适应度值靠后的3个个体初始化。
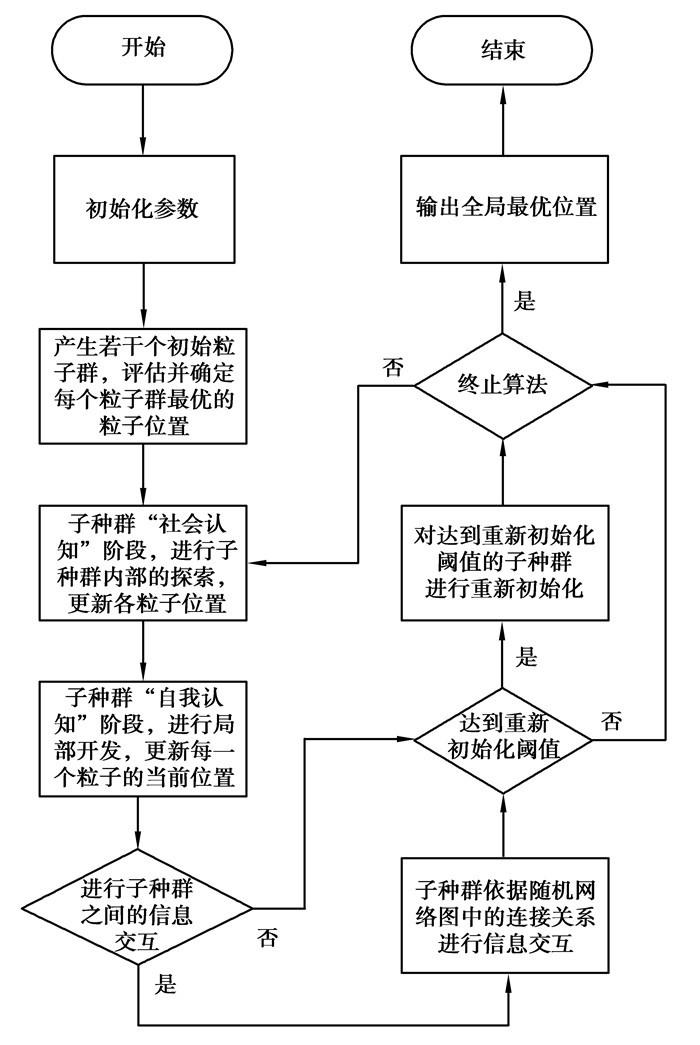
2.7 算法流程结合上文对算法各组件的论述,MPSO-RDnet的算法流程如图 7所示。
|
图 7 MPSO-RDnet算法流程图 Fig. 7 Flow chart of improved MPSO-RDnet algorithm |
目前MRC-FJSP的研究者都采用Wu等[2]在2008年提出的SFTSP算例测试自己算法的性能,该算例可以在决策分析实验室门户网站的子页:https://dalab.ie.nthu.edu.tw/newsen_content.php?id=0上找到。SFTSP算例共包含5个large-scale算例(LS1、LS2、LS3、LS4和LS5)和5个wide-range算例(WR1、WR2、WR3、WR4和WR5)。large-scale算例包含100个工件、36台机器,每台机器需要配置3类附资源,加工时间位于区间[1, 15]内, 机器准备时间位于区间[1, 5]内; wide-range算例包含60个工件、36台机器, 每台机器需要配置3类附资源, 加工时间位于区间[1, 50]内, 机器准备时间位于区间[1, 15]内。
MPSO-RDnet算法在MATLAB R2016a软件上编写,运行环境为Core 4C+6G 1.9GHz CPU及Windows10系统。
3.2 性能评价指标与参数设置 3.2.1 性能评价指标为了综合评估算法的收敛性和稳定性,提出了平均相对优胜偏差(ARSD,average relative success deviation)的概念。在介绍ARSD之前,首先给出相对优胜偏差(RSD,relative success deviation)的定义。
| $ {\rm{RSD}} = \frac{1}{{{\rm{RT}}}}\sum\limits_{{\rm{rt}} = 1}^{{\rm{RT}}} {\frac{{C_{\max }^{rt} - C_{\max }^*}}{{C_{\max }^*}}} \times 100。$ | (7) |
式中:RT为算法针对该算例的独立运行次数,Cmax*表示现存文献中给出的该算例的当前最优值,Cmaxrt为本次运行求得的该算例的最优值。
| $ {\rm{ARSD = }}\frac{{\rm{1}}}{{{\rm{BM}}}}\sum\limits_{{\rm{bm = 1}}}^{{\rm{BM}}} {{\rm{RS}}{{\rm{D}}_{{\rm{bm}}}}} 。$ | (8) |
式中:RSDbm为算法求解第bm个算例的相对优胜偏差;BM表示SFTSP的总算例数,取值为10。
ARSD越小,说明算法的综合性能越好。
3.2.2 性能评价指标为了后面算法对比的公平性,参考了文献中其他算法的参数设置,MPSO-RDnet把解的最大评估次数10 000次作为迭代终止条件,种群规模设为60。算法运行中,对子种群规模、连接概率、传播频率和子种群重新初始化阈值进行多次调整,得到使运行效果最佳的值分别为5、0.1、0.6、10。
3.3 基于随机网络结构的多种群策略的有效性验证多种群策略在维护种群多样性方面有显著的优势。为了找到最适合的多种群策略,采用实验设计法。在保证其他参数不变的前提下,PSO在不同多种群策略下针对每一个算例独立运行10次,得到的ARSD如表 1所示。
| 表 1 带有不同多种群策略的PSO求得的ARSD Table 1 ARSD obtained by PSO with multi-population strategies |
从表中可以看出,带随机网络的多种群PSO算法在求解MRC-FJSP上效果最好。这是因为随机网络结构中的连接概率可以根据问题需要进行调节,使算法的鲁棒性更高。
3.4 算法对比为了验证MPSO-RDnet在求解MRC-FJSP上的适用性和有效性,特将MPSO-RDnet算法与目前求解MRC-FJSP最先进的5个算法(nFOA[4]、KMEA[7]、SM2-MBO[5]、CCIWO[21]、WSA[22])进行比对。与这5个算法一样,MPSO-RDnet也针对每一个算例独立运行10次,得到的对比结果见表 2。从表中可以看出MPSO-RDnet得到了所有算例的上界,均值刷新了除WR4以外的原有保持记录,标准差(SD)方面也表现不错。这说明了MPSO-RDnet的鲁棒性非常高。但在运行时间(tCPU)上,MPSO-RDnet位于中等水平,这说明MPSO-RDnet的求解效率还有待提升。
| 表 2 算法对比结果表 Table 2 Algorithm comparison results |
研究了以最小化最大完工时间为目标的MRC-FJSP,提出了一种MPSO-RDnet算法,设计了基于关键路径的邻域结构。最后通过数值实验验证了基于随机网络结构的多种群策略的有效性,并与其他求解MRC-FJSP的算法进行了对比,有效地验证了MPSO-RDnet算法的优越性。
| [1] |
Gargeya V B, Deane R H. Scheduling research in multiple resource constrained job shops: a review and critique[J]. International Journal of Production Research, 1996, 34(8): 2077-2097. DOI:10.1080/00207549608905015 |
| [2] |
Wu J, Chien C. Modeling semiconductor testing job scheduling and dynamic testing machine configuration[J]. Expert Systems with Applications, 2008, 35(1/2): 485-496. |
| [3] |
Wu J Z, Hao X C, Chien C F, et al. A novel bi-vector encoding genetic algorithm for the simultaneous multiple resources scheduling problem[J]. Journal of Intelligent Manufacturing, 2012, 23(6): 2255-2270. DOI:10.1007/s10845-011-0570-0 |
| [4] |
Zheng X L, Wang L, Wang S Y. A novel fruit fly optimization algorithm for the semiconductor final testing scheduling problem[J]. Knowledge-Based Systems, 2014, 57: 95-103. DOI:10.1016/j.knosys.2013.12.011 |
| [5] |
Gao L, Pan Q K. A shuffled multi-swarm micro-migrating birds optimizer for a multi-resource-constrained flexible job shop scheduling problem[J]. Information Sciences, 2016, 372: 655-676. DOI:10.1016/j.ins.2016.08.046 |
| [6] |
Hao X C, Wu J Z, Chien C F, et al. The cooperative estimation of distribution algorithm: a novel approach for semiconductor final test scheduling problems[J]. Journal of Intelligent Manufacturing, 2014, 25(5): 867-879. DOI:10.1007/s10845-013-0746-x |
| [7] |
Wang S Y, Wang L. A knowledge-based multi-agent evolutionary algorithm for semiconductor final testing scheduling problem[J]. Knowledge-Based Systems, 2015, 84: 1-9. DOI:10.1016/j.knosys.2015.03.024 |
| [8] |
Cao Z C, Lin C R, Zhou M C, et al. Scheduling semiconductor testing facility by using cuckoo search algorithm with reinforcement learning and surrogate modeling[J]. IEEE Transactions on Automation Science and Engineering, 2019, 16(2): 825-837. DOI:10.1109/TASE.2018.2862380 |
| [9] |
Shi Y, Eberhart R. A modified particle swarm optimizer[C]//1998 IEEE International Conference on Evolutionary Computation Proceedings, IEEE World Congress on Computational Intelligence (Cat. No. 98TH8360), May 4-9, 1998, Anchorage, AK, USA. IEEE, 1998: 69-73.
|
| [10] |
郭文忠, 陈国龙, 陈振. 离散粒子群优化算法研究综述[J]. 福州大学学报(自然科学版), 2011, 39(5): 631-638. Guo W Z, Chen G L, Chen Z. Survey on discrete particle swarm optimization algorithm[J]. Journal of Fuzhou University (Natural Science Edition), 2011, 39(5): 631-638. (in Chinese) |
| [11] |
罗辞勇, 卢斌, 陈民铀, 等. 组合粒子群优化和分布估计的多目标优化算法[J]. 重庆大学学报, 2010, 33(4): 31-36. Luo C Y, Lu B, Chen M Y, et al. Hybrid multiobjective particle swarm optimization and estimation of distribution algorithm[J]. Journal of Chongqing University, 2010, 33(4): 31-36. (in Chinese) |
| [12] |
张智聪, 郑力, 张涛. 半导体测试调度研究[J]. 半导体技术, 2008, 33(1): 46-50. Zhang Z C, Zheng L, Zhang T. Investigation on semiconductor test scheduling[J]. Semiconductor Technology, 2008, 33(1): 46-50. (in Chinese) DOI:10.3969/j.issn.1003-353X.2008.01.012 |
| [13] |
王思涵, 黎阳, 李新宇. 基于鲸鱼群算法的柔性作业车间调度方法[J]. 重庆大学学报, 2020, 43(1): 1-11. Wang S H, Li Y, Li X Y. An improved whale swarm algorithm for flexible job-shop scheduling problem[J]. Journal of Chongqing University, 2020, 43(1): 1-11. (in Chinese) |
| [14] |
马庆吉. 基于改进灰狼算法的柔性作业车间调度方法研究[D]. 武汉: 华中科技大学, 2019. Ma Q J. Research on flexible job shop scheduling problem based on an improved grey wolf optimization[D]. Wuhan: Huazhong University of Science and Technology, 2019. (in Chinese) |
| [15] |
曾强, 杨育, 王小磊, 等. 应用需求时间窗的柔性作业车间调度优化模型[J]. 重庆大学学报, 2011, 34(2): 86-94. Zeng Q, Yang Y, Wang X L, et al. Optimal model and algorithm for flexible job-shop scheduling problem based on demand time window[J]. Journal of Chongqing University, 2011, 34(2): 86-94. (in Chinese) |
| [16] |
陈魁, 毕利. 改进粒子群算法在考虑运输时间下的FJSP研究[J/OL]. 系统仿真学报, 2020-07-11[2020-10-02]. https://doi.org/10.16182/j.issn1004731x.joss.19-0672. Chen K, Bi L. Research on FJSP of improved particle swarm optimization algorithm considering transportation time[J/OL]. Journal of System Simulation, 2020-07-11[2020-10-02]. https://doi.org/10.16182/j.issn1004731x.joss.19-0672. (in Chinese) |
| [17] |
徐新黎. 生产调度问题的智能优化方法研究及应用[D]. 杭州: 浙江工业大学, 2008. Xu X L. Research on intelligent production scheduling optimization methods and its applications[D]. Hangzhou: Zhejiang University of Technology, 2008. (in Chinese) |
| [18] |
Mastrolilli M, Gambardella L M. Effective neighbourhood functions for the flexible job shop problem[J]. Journal of Scheduling, 2000, 3(1): 3-20. DOI:10.1002/(SICI)1099-1425(200001/02)3:1<3::AID-JOS32>3.0.CO;2-Y |
| [19] |
Shi X Q, Long W, Li Y Y, et al. Research on the performance of multi-population genetic algorithms with different complex network structures[J]. Soft Computing, 2020, 24(17): 13441-13459. DOI:10.1007/s00500-020-04759-1 |
| [20] |
Shi X, Long W, Li Y, et al. Multi-population genetic algorithm with ER network for solving flexible job shop scheduling problems[J/OL]. PloS One, 2020, 15(5): e0233759[2020-10-02]. https://doi.org/10.1371/journal.pone.0233759.
|
| [21] |
Sang H, Duan P, Li J. An effective invasive weed optimization algorithm for scheduling semiconductor final testing problem[J]. Swarm and Evolutionary Computation, 2018, 38: 42-53. DOI:10.1016/j.swevo.2017.05.007 |
| [22] |
付坤. 基于鲸鱼群算法的柔性作业车间调度方法研究[D]. 武汉: 华中科技大学, 2019. Fu K. Research on flexible job shop scheduling methods based on whale swarm algorithm[D]. Wuhan: Huazhong University of Science and Technology, 2019. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45


