b. 重庆大学 计算机学院, 重庆 400044;
c. 重庆大学 机械工程学院, 重庆 400044
b. College of Computer Science, Chongqing University, Chongqing 400044, P. R. China;
c. College of Mechanical Engineering, Chongqing University, Chongqing 400044, P. R. China
大型圆筒广泛用于火箭、导弹、输气管、化工容器等场合。在卷制成型过程中,其轮廓形状容易发生变形而产生轮廓误差。当两节圆筒进行对焊时,由于直径和轮廓形状误差而引起的错边等问题[1-2],会导致焊接强度和安全性降低。因此制造圆筒时,需要控制圆筒不同截面(特别是管口截面)轮廓误差不超过公差规定的范围,例如对超高速导弹之类的装备,轮廓误差更需要严格控制。要控制圆筒轮廓误差,首先要解决测量问题,所以圆筒管口截面的轮廓误差测量具有重要的应用背景。目前测量轮廓误差的仪器主要是圆度仪或三坐标测量机等[3-4],此类仪器通常只适合在计量室使用,而不易在生产车间现场进行在线测量。且一般圆度仪径向尺寸测量范围有限,难以实现对大型圆筒类零件的测量[5-6]。
V形法是轮廓误差检测的常用方法,该法通过旋转被测工件,读取位移传感器在被测工件转动过程中读数的跳动量,再除以所谓“反映系数”来估计圆度误差[7-8]。“反映系数”与工件的轮廓形状(谐波次数)有关,但一般工件的轮廓形状是复杂且未知的[9],所以这种近似估计圆度误差的V形法,难以在生产实际中应用。
李进生[10]在V形法的基础上提出了轮廓定位式圆度误差的在线测量法。该方法将测量基准选在工件表面,传感器读数不受主轴回转误差的影响[11],显著提高了测量精度。但一般的轮廓定位式圆度误差在线测量法采用V形块支承,需要人工转动被测工件并进行读数,测量耗时较长且难免带来人为因素对测量结果的影响;在测量大尺寸工件时,工件的转动、分度也比较困难。针对上述问题,笔者研发了一种适合大型圆筒类零件的轮廓误差在线测量系统,为相关的自动化测量提供了一种新的解决方案。
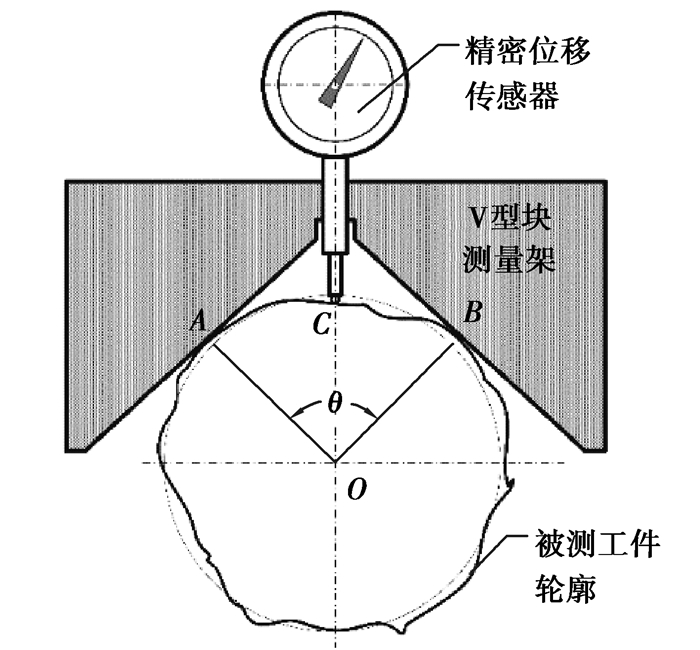
1 测量方法轮廓定位式圆度误差在线测量法的测量布局如图 1所示,V形块测量架骑在被测工件的圆柱轮廓面上,支承点分别为A、B,精密位移传感器的测头C,通过V形块测量架∠AOB的等分线,与工件轮廓面接触。
|
图 1 测量布局图 Fig. 1 Schematic diagram of the measurement system |
正式测量前,将工件的轮廓面等分为N份,作为测量时顺序编号i=1, 2, 3, …, N。测量角∠AOB记为θ,图 1中
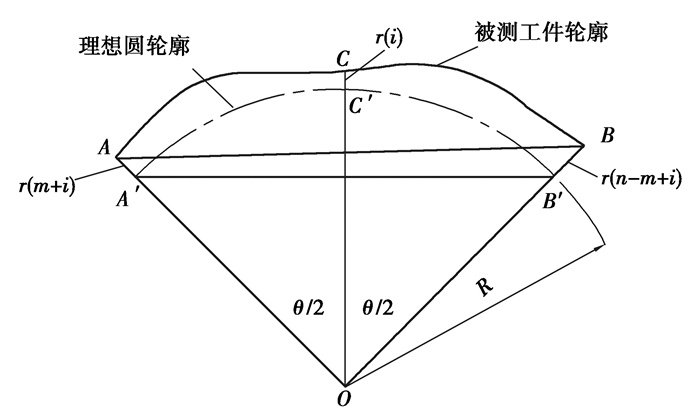
轮廓定位式圆度误差在线测量法的测量原理如图 2所示,A′、B′、C′三点分别是理想圆与OA、OB、OC的交点。在工件转动一周的过程中,位移传感器的测头C依次与第1, 2, 3, …, N个等分点接触,当工件转动到某一个转角时,与C接触的第i个等分点的待测轮廓误差值记为ri(i=1, 2, 3, …, N),此时与A, B重合的2个等分点处轮廓误差值分别为rm+i, rn-m+i。测量开始前将位移传感器在第1个等分点的读数S1设置为零,每转过一个等分角记录一次位移传感器的读数。由于A、B、C处都有误差,因此位移传感器在第i个等分点的测量值Si(i=2, 3, 4, …, N),即位移传感器读数相对于S1的变动量,应该等于三者轮廓误差的几何和。经推导轮廓误差值ri与测量值Si的函数关系式为
| $ S_{i}=r_{i}-r_{1}+K\left(r_{m+1}-r_{m+i}+r_{n-m+1}-r_{n-m+i}\right), $ | (1) |
|
图 2 测量原理图 Fig. 2 Schematic diagram of the measuring principle |
其中K=0.5cos(θ/2),将各等分点测量值Si分别代入(1)式,形成关于半径误差值ri和测量值Si的线性方程组:
| $ \left\{\begin{array}{l} S_{2}=r_{2}-r_{1}+K\left(r_{m+1}-r_{m+2}+r_{n-m+1}-r_{n-m+2}\right), \\ S_{3}=r_{3}-r_{1}+K\left(r_{m+1}-r_{m+3}+r_{n-m+1}-r_{n-m+3}\right) , \\ \vdots ~~~~~~~~~~~~~~~~~~~~~~~~~\vdots \\ S_{n}=r_{n}-r_{1}+K\left(r_{m+1}-r_{m+n}+r_{n-m+1}-r_{n-m+n}\right)。\end{array}\right. $ | (2) |
不妨将第一个测量点设置为基准点(即r1=0),即假设理想圆与实际轮廓在i=1点处相交,那么线性方程组(2)共有n-1个线性方程,同时含有n-1个未知量ri(其中i=2, 3, …, N)。求解线性方程组(2),就得到了所有等分点相对于r1的轮廓误差值,然后选取合适的方法评定工件的圆度误差。
2 轴承圈外圆轮廓形状实验为检验轮廓定位式圆度误差在线测量法在实际测量中的可行性,进行了轴承圈外圆轮廓形状检测实验。实验仪器如图 3所示,在轴承测量仪上,将被测轴承套圈1放在特制90°V形块4上。用轴承外圈相同直径的分度纸质网格将轴承轮廓表面等分。测量读数采用分度值1 μm的扭簧表 3,每转动一个等分角,记录一次扭簧表显示的位移数据,再输入到轮廓定位式圆度误差在线测量法轮廓误差值求解程序中求出各等分点的轮廓误差值,绘制被测轴承的轮廓误差曲线图。

|
21—轴承圈;2—底座;3—扭簧表;4—V形块 图 3 轴承测量仪及试件(轴承外圈) Fig. 3 Bearing measuring instrument and specimen |
实验中取测量角θ=90°,等分数N=40。从图 3的实验测量仪的布局可以得到m=(360°-90°)/2÷(360°/40)=15。对直径小于15 cm的轴承标准件进行重复多次测量并取平均值,将测量结果放大1 250倍后与威而信DTP-2000C圆度仪的测量结果进行对比。
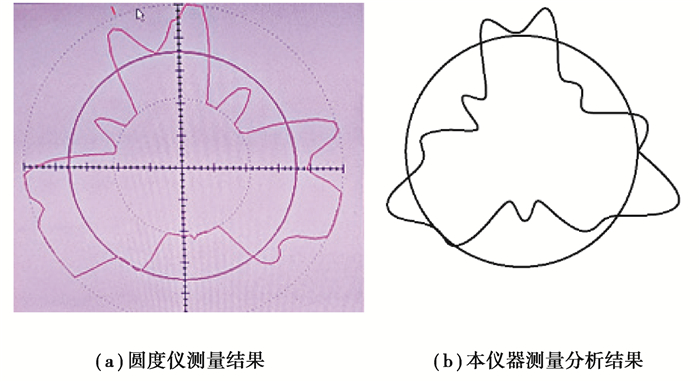
图 4(a)为威而信DTP-2000C圆度仪测量结果,图 4(b)是本实验仪器的测量和电脑分析计算结果。由于采用人工读数的方式,难免存在一定误差。由图 4测量结果对比可见,本实验仪器和圆度仪获得的两轮廓曲线形状在总体上有较好吻合度,证明本方法是可行的。
|
图 4 轴承圈轮廓实验分析结果(放大1 250倍) Fig. 4 Measured profile of bearing rail (at 1 250 times magnification) |
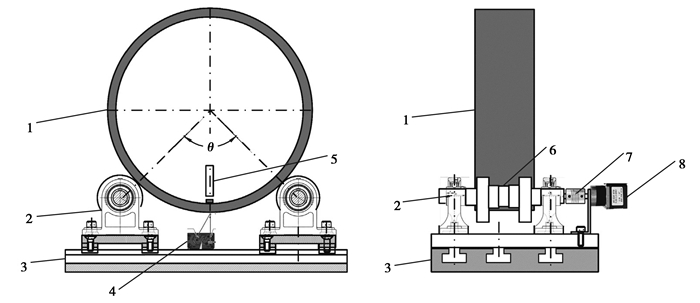
对于尺寸和重量较大的大型圆筒,采用图 1的V形块结构来布局测量装置比较困难。因而对测量系统做进一步改进(如图 5所示),特别采用了2根托辊代替V形块,托辊与大型圆筒试件接触处A、B,与圆筒中心O的夹角为测量角θ。
|
1—圆筒(外径350 mm);2—托辊支座;3—T型槽底座;4—激光位移传感器;5—霍尔传感器;6—托辊;7—联轴器;8—42步进电机 图 5 大型圆筒类零件轮廓误差在线测量系统 Fig. 5 Online measurement system for contour error of large cylindrical parts |
大型圆筒类零件轮廓误差在线测量系统采用图 5所示结构,选择一个直径为ϕ350 mm的钢管圆筒,作为示例测量对象。测量时圆筒由2根托辊支承,圆筒下方安装激光位移传感器,用于测量圆筒轮廓形状的变化,位移传感器支架安装在底座的导轨上,使传感器能够沿被测圆筒的轴线方向移动,测量不同截面的轮廓误差时,将位移传感器移动到指定截面下方。托辊一端与42步进电机的输出轴传动连接。工作时步进电机驱动2根托辊同步旋转,保证圆筒转动过程中不会出现打滑现象,从而使大型圆筒匀速转动。
安装时2根托辊的轴线应互相平行,同时托辊的径向跳动量应该严格控制在轮廓误差的百分之几以内,以减少因托辊径向跳动带来的测量误差。2套托辊支座的距离可通过滑轨调节,以满足不同直径大小圆筒的测量需求。
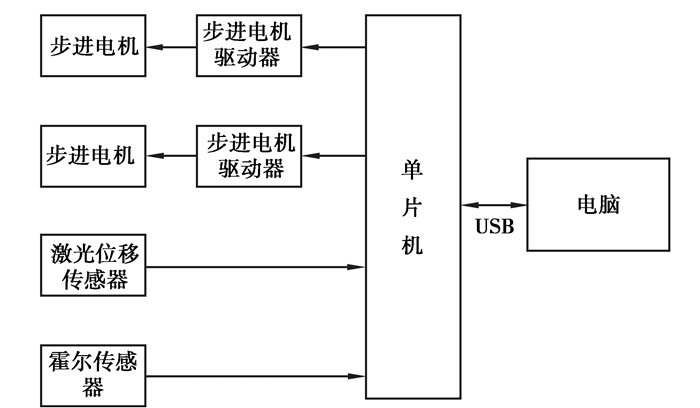
3.2 控制系统本测量系统采用的控制系统如图 6所示,由激光位移传感器、霍尔传感器、步进电机及其驱动器、单片机及电脑等组成。霍尔传感器安装在圆筒内侧,圆筒内壁设置有与之匹配的磁钢。其工作原理是:在步进电机传动大型圆筒匀速转动过程中,当霍尔传感器感应到磁钢的磁场时,霍尔传感器向单片机输出触发信号,单片机根据触发信号确定时间点,将连续2个时间点之间的间隔计为一个测量周期T。位移传感器中测得的位移信号中取N个点来表示工件的轮廓误差曲线,每1个点都有相同的时间间隔t=T/N,这样就将大型圆筒轮廓表面等分成N份[12]。测得的模拟信号经单片机进行模数转换之后发送至计算机暂存。
|
图 6 控制系统框图 Fig. 6 Block diagram of control system |
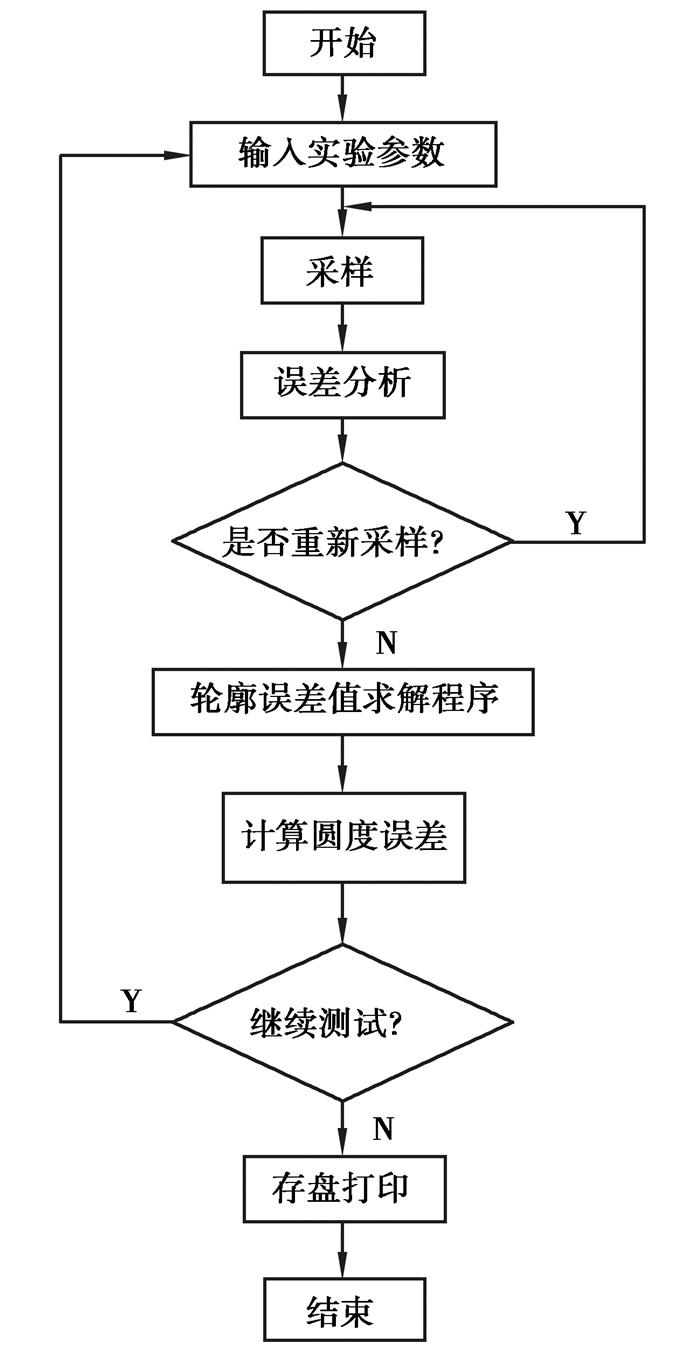
本研究中采用Visual Basic 6.0编程语言,开发了基于轮廓定位式圆度误差在线测量法的计算机软件,软件流程图如图 7所示。利用计算机软件对测量数据进行处理,求解出各等分点的轮廓误差值,分别采用最小二乘法[13]和最小区域包容法评定圆度误差。
|
图 7 软件流程图 Fig. 7 Flowchart of the software programming |
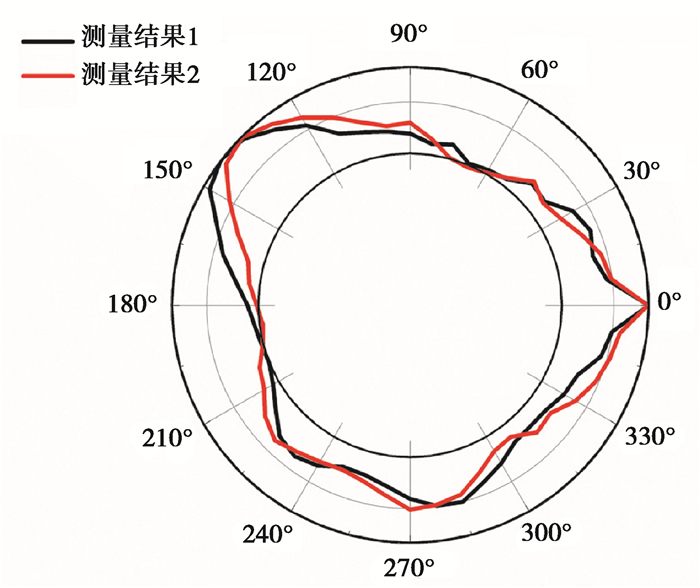
采用本测量系统对直径ϕ350 mm的圆筒进行测量。实验前根据圆筒和托辊的半径大小,调整两托辊支座的相对位置,使得测量角θ=90°。等分数N取48,则m=90°/2÷(360°/48)=6。在本研究中对圆筒同一管口截面进行3次重复测量,绘制第1次测量结果的轮廓误差曲线图,为了更直观地看出测量结果的可重复性,将第2次测量结果的轮廓误差曲线图绘于同一张图进行比较,如图 8所示。由图 8可见2条曲线的轮廓及变化趋势基本一致,各测点测量值的重复性较好。此外,为了探讨本实验中圆度在轴向方向的差别,将位移传感器沿轴向移动到3个不同截面进行重复测量并对比,结果表明本实验中测量值有较好的可重复性,也表明在所选测量范围内圆度在轴向方向的差异性较不明显。
|
图 8 测量结果(放大125倍) Fig. 8 Measurement results (at 125 times magnification) |
表 1为本测量系统对圆筒同一管口截面分别按照最小区域包容法和最小二乘法评定的3次结果,其中最小区域包容法评定圆度误差的平均值为0.653 mm,最小二乘法的平均值为0.676 mm,采用最小区域包容法可以获得较小的误差评定结果,与已有文献[14-15]结论一致。由于托辊的径向跳动量较难进行严格控制(实验前测得径向跳动量在0.05 mm左右),会造成圆度误差的结果在一定范围内波动,但总体上来说本测量系统的测量结果具有较高的可重复性。
| 表 1 圆度误差测量结果 Table 1 Measurement results of the roundness error |
介绍了轮廓定位式圆度误差在线测量法的基本原理,轴承外圆轮廓形状实验结果证明此方法是可行的。在此基础上研制了大型圆筒类零件轮廓误差在线测量系统,编写了相应的计算机软件。针对大型圆筒类零件尺寸和重量较大的特点,采用2根托辊代替V形块测量架支承的方式,通过将测量周期N等分实现圆筒轮廓表面的分度,再利用计算机软件对测量数据进行处理。此外,测量系统可以根据被测工件的大小调节托辊支座的距离,适用的圆筒直径范围为300~3 000 mm,具有自动化程度高、测量范围广和用时少等特点。圆筒测量实验证明了本测量系统对大型圆筒实现在线测量是可行的。
| [1] |
吕延茂. 薄壁筒体卧置状态圆度的测量和计算[J]. 压力容器, 2004, 21(8): 16-21. Lyu Y M. Measure and calculation for roundness of thin-walled cylindrical shell in horizontal condition[J]. Pressure Vessel Technology, 2004, 21(8): 16-21. (in Chinese) DOI:10.3969/j.issn.1001-4837.2004.08.005 |
| [2] |
申林远, 陶现宾, 孙佳欣, 等. Φ5000mm筒形舱段圆度控制技术研究[J]. 航天制造技术, 2019(4): 40-44, 47. Shen L Y, Tao X B, Sun J X, et al. Research on roundness tolerance controlling technology of large diameter cylindrical cabin[J]. Aerospace Manufacturing Technology, 2019(4): 40-44, 47. (in Chinese) DOI:10.3969/j.issn.1674-5108.2019.04.009 |
| [3] |
Rhinithaa P T, Selvakumar P, Sudhakaran N, et al. Comparative study of roundness evaluation algorithms for coordinate measurement and form data[J]. Precision Engineering, 2018, 51: 458-467. DOI:10.1016/j.precisioneng.2017.10.001 |
| [4] |
蒋峰, 邓宇锋. 一种简易的数控机床圆度误差在线测量系统[J]. 机械工程与自动化, 2015(3): 141-144. Jiang F, Deng Y F. A simple roundness error online measurement system for CNC machine tools[J]. Mechanical Engineering & Automation, 2015(3): 141-144. (in Chinese) DOI:10.3969/j.issn.1672-6413.2015.03.058 |
| [5] |
张鹏, 周广成, 单东日, 等. 重卡桥壳专用圆度圆柱度自动检测仪设计[J]. 仪表技术与传感器, 2018(6): 29-32, 57. Zhang P, Zhou G C, Shan D R, et al. Design of automated roundness and cylindricity detector for heavy truck axle housing[J]. Instrument Technique and Sensor, 2018(6): 29-32, 57. (in Chinese) DOI:10.3969/j.issn.1002-1841.2018.06.007 |
| [6] |
刘杰, 李华, 付西红. 大尺寸筒状设备圆度误差测量系统[J]. 红外与激光工程, 2016, 45(1): 264-268. Liu J, Li H, Fu X H. Measurement system of large-scale sleeve roundness error[J]. Infrared and Laser Engineering, 2016, 45(1): 264-268. (in Chinese) |
| [7] |
Yu H X, Xu M C, Zhao J. In-situ roundness measurement and correction for pin journals in oscillating grinding machines[J]. Mechanical Systems and Signal Processing, 2015, 50/51: 548-562. DOI:10.1016/j.ymssp.2014.05.009 |
| [8] |
Adamczak S, Zmarzły P, Janecki D. Theoretical and practical investigations of V-block waviness measurement of cylindrical parts[J]. Metrology and Measurement Systems, 2015, 22(2): 181-192. DOI:10.1515/mms-2015-0023 |
| [9] |
沈江, 周启武, 汪浩. 零件圆度误差测量的简易新方法[J]. 重型机械科技, 1999(3): 46-50. Shen J, Zhou Q W, Wang H. New and simple method of measuring component roundess deviation[J]. Heavy Machinery Science and Technology, 1999(3): 46-50. (in Chinese) |
| [10] |
李进生. 轮廓定位式圆度误差的在线测量法[D]. 重庆: 重庆大学, 1993. Li J S. An online profile-positioning measurement method for roundness error[D]. Chongqing: Chongqing University, 1993. (in Chinese) |
| [11] |
Janusiewicz A, Adamczak S, Makieła W, et al. Determining the theoretical method error during an on-machine roundness measurement[J]. Measurement, 2011, 44(9): 1761-1767. DOI:10.1016/j.measurement.2011.07.013 |
| [12] |
Mekid S, Vacharanukul K. In-process out-of-roundness measurement probe for turned workpieces[J]. Measurement, 2011, 44(4): 762-766. DOI:10.1016/j.measurement.2011.01.011 |
| [13] |
Nouira H, Bourdet P. Evaluation of roundness error using a new method based on a small displacement screw[J]. Measurement Science and Technology, 2014, 25(4): 044012. DOI:10.1088/0957-0233/25/4/044012 |
| [14] |
Du C L, Luo C X, Han Z T, et al. Applying particle swarm optimization algorithm to roundness error evaluation based on minimum zone circle[J]. Measurement, 2014, 52: 12-21. DOI:10.1016/j.measurement.2014.02.028 |
| [15] |
贾媛媛, 王波, 吴言功. 辊筒模具圆度误差测量及补偿方法研究[J]. 航空精密制造技术, 2018, 54(3): 7-10, 15. Jia Y Y, Wang B, Wu Y G. Roundness error measurement and compensation methods of roller mold[J]. Aviation Precision Manufacturing Technology, 2018, 54(3): 7-10, 15. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45


