2. 重庆大学 电气工程学院, 重庆 400044
2. School of Electrical Engineering, Chongqing University, Chongqing 400044, P. R. China
近年来,可再生能源包括风力发电机、光伏电源、小水电等在配电网中的渗透率不断提升,使得配电网中功率潮流双向流动,导致网络中节点电压跃升[1-3]。再者,可再生能源输出功率的随机性与间歇性、负荷的波动性都会加剧电网电压的波动,进而影响关键设备的正常运行[4-5]。为提升可再生能源的接入比例,在含分布式电源的低压配电网中,电压调节问题已成为关注焦点。
针对低压配电网电压调节问题,文献[6]提出了含有载调压变压器的配电网潮流优化模型,采用二阶锥松弛方法对问题进行求解,进而改变变压器分接头以调整系统电压,但未考虑分布式电源出力不确定性对系统的影响。文献[7-8]提出串联电容器补偿方法,通过设计网络电压偏差、电容器容抗和网络损耗最小的优化模型,求解串联电容器安装位置与容量,实现配电网电压的调节。
文献[9]针对分布式电源接入电网造成的电压越限问题,设计了基于灵敏度矩阵的方法,以调节分布式电源的出力和控制电容器的投切实现系统电压控制。基于电压功率灵敏度矩阵,文献[10]通过调节分布式电源的输出功率以调节系统的电压。肖浩等[11]分析了分布式电源对配电网电压的影响,提出了基于节点电压灵敏度矩阵的电压优化方案,采用模型预测控制理论,调节分布式电源和储能的输出功率实现了电压协调控制。文献[12-13]分析了配电网对光伏电源的消纳能力,基于电压灵敏度矩阵调节并网变流器的有功输出和无功输出,实现了光伏并网点的电压调节。文献[14]基于多agent系统思想,建立了基于电压成本和分布式电源有功消减成本的优化目标函数,通过分布式优化算法求解目标,进而调节分布式电源的有功输出和无功输出功率,确保节点电压在正常范围内。张江林等[15]提出了含有载调压变压器、电容器组和分布式储能的主动配电网电压调节方法,并设计长时间尺度电压预测方法以调节变压器接头、投切电容器组,实现节点电压的调节。考虑到短时间尺度内电压波动的问题,提出了基于电压灵敏度矩阵的分布式储能电压调节方法,通过调节分布式储能的有功、无功输出控制节点电压稳定。针对配电网中测量数据不完整的问题,柴园园等[16]设计网络简化方法,将含不完全量测的网络转换成完全量测的网络,同时将配电网分成多个区域,并设计无功调压能力评估方法和区域内电压优化控制方法,实现电压调节并降低分布式光伏电源发电损失。考虑到配电网精确建模的困难,文献[17]借用深度神经网络拟合可调节点注入功率与关键节点的电压关系,采用梯度下降法对模型进行求解,调节分布式电源的无功和有功输出,进而调节系统电压。
综上所述,含分布式电源的配电网电压控制方法总体可分为2种方法。第一种是以调节传统调压设备(如投切电容器和有载调压变压器)为手段,控制配电网电压[6-8],其优势是利用配电网现有设备,实现电压调节,但电容器和有载调压变压器不能频繁投切与调节,对含高比例可再生能源的配电网调压问题并不高效[15]。第二种方法是,根据电压灵敏度矩阵,调节分布式电源、分布式储能的有功和无功输出,实现配电网电压的控制,其优势是能够通过敏感度矩阵计算出可控节点的注入功率并实现电压调节,但节点电压敏感度矩阵计算较为复杂。
为解决以上问题,文中针对低压配电网的特性,将节点电压幅值与节点注入功率之间的关系线性化,从而避免了雅克比灵敏度矩阵的计算,并提出了基于功率里程数的电压调节模型,通过调节分布式储能电源的输出实现系统电压的调节。此外,为提升分布式储能的运行效率,设计了分布式储能荷电状态(state of charge, SoC)均衡的控制方法,实现分布式储能之间的SoC一致性控制。
1 低压配电网电压变化分析本小节主要针对分布式光伏电源接入低压配电网后对低压配电网电压造成的影响进行分析,给出电网电压变化与分布式电源功率输出的关系,进而为设计电压控制策略提供依据。
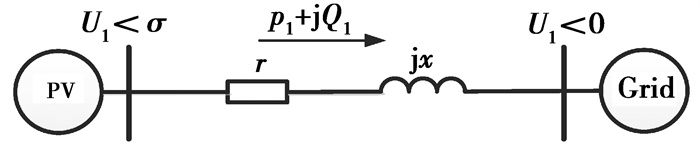
光伏电源并入配电网的工作原理[16]如图 1所示,其中光伏电源侧电压幅值为U1,电压角度为σ,电网侧电压幅值为U2,参考电压角度为0。此外,线路阻抗为Z=r+jx,线路传输功率为S1=P1+jQ1。通常,低压配电网线路中,电阻值r远大于电抗值x,因而线路呈电阻特性[16]。
|
图 1 电压型光伏电源并网原理图 Fig. 1 Schematic diagram of grid-connected PV source |
根据图 1,光伏电源输出功率与线路电压的关系为
| $ {P_1} = \frac{{{U_1}}}{{{r^2} + {x^2}}}(r({U_1} - {U_2}{\kern 1pt} {\kern 1pt} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \delta ) + x{U_2}{\kern 1pt} {\kern 1pt} {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \delta ), $ | (1) |
式中,在低压配电网中线路电阻远大于电抗,即r>>x,因而cos σ≈1,sin σ≈0,式(1)可以简化成线性模型
| $ {P_1} = \frac{{{\rm{ }}{U_1}}}{r}({U_1} - {U_2}) $ | (2) |
根据式(2)可知,光伏电源输出功率P1与电压幅值U1、U2和线路电阻r相关。对于低压电网,线路阻抗可等效为固定值,上级电网电压幅值U2近似不变,光伏输出功率与电压幅值U1相关,当光伏输出功率P1增大时,光伏发电侧电压U1增大。根据(2)得到,线路电压幅值变化量与线路传输功率的关系为
| $ \Delta V = {U_1} - {U_2} = \frac{{{P_1}\cdot r}}{{{U_1}}} \circ $ | (3) |
根据式(3)可知,电压变化量ΔV与线路传输功率P1相关。当P1过大,会引起ΔV变大,引起光伏电源侧电压幅值U1越界。
综上所述,低压配电网中,线路的电压幅值变化与线路传输的功率大小相关,并且传输的有功功率是影响电压幅值变化的主导因素。为进一步分析含分布式电源的低压配电网中节点电压与有功潮流的关系,文中引入功率里程数的概念,推导出线路电压幅值变化与有功潮流的关系。
2 基于功率里程数的配电网电压调节模型 2.1 功率里程数的定义对于给定的配电网,配电线路阻抗参数近似不变,为恒定值[16]。式(3)可以写成
| $ \Delta V = \frac{{{P_1}\cdot{L}\cdot\rho }}{{{U_1}}} = {P_1}\cdot L\cdot\frac{\rho }{{{U_1}}} = {P_1}\cdot L\cdot\beta , $ | (4) |
式中:ρ为电阻率;β=ρ/U1的大小与配电线路的材料和电压幅值U1有关。根据式(4)可知,低压配电网线路电压损失ΔV与功率流动的距离L近似成线性关系,即电压幅值损失等于幅值为P的有功潮流在参数为β的线路上流过长度为L的路程时引起的电压变化。因此在给定的线路中,功率流动的里程直接决定了线路节点的电压变化。为此,式(4)可解释为,线路电压损失与功率流过的里程数呈线性关系,其中称功率流动的距离为功率里程数。在配电网中,潮流大小固定时,潮流流动的距离越长,潮流流动的起始点与终点之间的电压幅值差越大。
此外,推导出式(4)的前提条件有:配电网中线路的参数相同,即传输线型号相同;线路中电阻参数r远大于电抗x。
2.2 基于功率里程数的电压损失计算方法通常,配电网中节点电压与线路潮流呈现复杂的非线性关系[18]。为简化节点电压的计算,文中引入一种基于功率里程数的节点电压损耗计算方法。根据式(4)可知,电压偏差ΔV与线路传输功率P、电压幅值U1和线路电阻r相关,其中U1为变化的值。为近似得到节点电压与线路潮流的线性关系,提出以下命题。
命题1:在低压辐射状配电网中,假设节点0为平衡节点,其电压幅值为U0,电压相角为0度,线路阻抗为Zi(i=1, …, N),节点注入功率为S=P+jQ,线路电压损失为ΔVi,则线路的电压损失ΔVi与线路潮流Si之间存在如下线性关系,
| $ \Delta \mathit{\boldsymbol{U}} \approx \frac{1}{{{U_0}}}{\mathit{\boldsymbol{H}}_R}P + \frac{1}{{{U_0}}}{\mathit{\boldsymbol{G}}_X}Q, $ | (5) |
| $ \Delta \mathit{\boldsymbol{U}} = {[\Delta {V_1}\Delta {V_2} \ldots {\rm{ }}\Delta {V_n}]^{\rm{T}}}, $ | (6) |
| $ {\mathit{\boldsymbol{H}}_R} = \left[ {\begin{array}{*{20}{c}} {{h_{11}}}&{{h_{12}}}& \cdots &{{h_{1N}}}\\ {{h_{21}}}&{{h_{22}}}& \cdots &{{h_{2N}}}\\ \vdots & \vdots &{}& \vdots \\ {{h_{N1}}}&{{h_{N2}}}& \cdots &{{h_{NN}}} \end{array}} \right], $ | (7) |
| $ {\mathit{\boldsymbol{G}}_X} = \left[ {\begin{array}{*{20}{c}} {{g_{_{11}}}}&{{g_{_{12}}}}& \cdots &{{g_{_{1N}}}}\\ {{g_{_{21}}}}&{{g_{_{22}}}}& \cdots &{{g_{_{2N}}}}\\ \vdots & \vdots &{}& \vdots \\ {{g_{_{N1}}}}&{{g_{_{N2}}}}& \cdots &{{g_{_{NN}}}} \end{array}} \right], $ | (8) |
式中,向量Δ U为线路电压损失,即代表节点之间的电压偏差向量。P =[pi]N×1与Q =[qi]N×1分别是节点的有功功率注入向量与无功功率注入向量。hij与gij表示节点i与节点j之间的电阻与电抗。
在低压配电网中,线路阻抗呈现电阻特性(ri>>xi),可忽略无功注入功率对系统节点电压的影响。因此,配电网电压幅值可以通过调节节点注入有功功率实现控制。需要注明的是,系统节点电压损失计算方法将节点注入功率与节点电压的关系线性化,根据式(5)得到通过调节节点注入功率来调节系统电压的线性化电压调节方法。
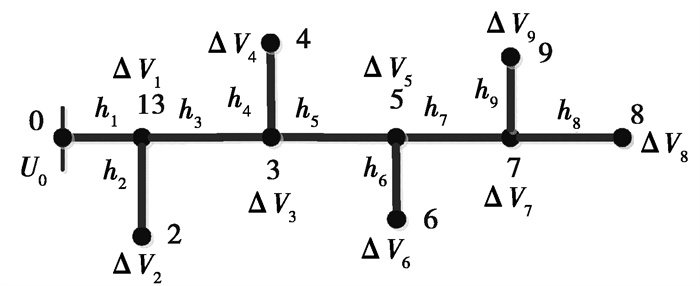
以图 2中9个节点低压配电网系统为例,对上述命题进行说明。
|
图 2 9节点低压配电网系统图 Fig. 2 Low voltage distribution network with 9 nodes |
图 2中,0号节点为平衡节点,与上级电网相连。ΔV1为节点0到节点1的支路电压损失,ΔV2为节点1到节点2的支路电压损失,依次类推。此外,H矩阵的求取分为两步。第一步:根据节点连接情况,确定支路电阻。第二步:确定支路i是否在节点0到节点j(j=0, …, N)之间的路径上,若在此路径上,则H矩阵的元素为hii,否则hij等于0。若支路2不在节点0与节点1之间的路径上,则h21=0;若支路2在节点0与节点2的路径上,则h22≠0,支路2不在节点0到节点3的路径上,则h23=0,依次类推,可以求得H矩阵的所有元素。图 2所示的H矩阵为
| $ {\mathit{\boldsymbol{H}}_9} = \left[ {\begin{array}{*{20}{c}} {{h_1}}&{{h_1}}&{{h_1}}&{{h_1}}&{{h_1}}&{{h_1}}&{{h_1}}&{{h_1}}&{{h_1}}\\ {}&{{h_2}}&{}&{}&{}&{}&{}&{}&{}\\ {}&{}&{{h_3}}&{{h_3}}&{{h_3}}&{{h_3}}&{{h_3}}&{{h_3}}&{{h_3}}\\ {}&{}&{}&{{h_4}}&{}&{}&{}&{}&{}\\ {}&{}&{}&{}&{{h_5}}&{{h_5}}&{{h_5}}&{{h_5}}&{{h_5}}\\ {}&{}&{}&{}&{}&{{h_6}}&{}&{}&{}\\ {}&{}&{}&{}&{}&{}&{{h_7}}&{{h_7}}&{{h_7}}\\ {}&{}&{}&{}&{}&{}&{}&{{h_8}}&{}\\ {}&{}&{}&{}&{}&{}&{}&{}&{{h_9}} \end{array}} \right], $ | (9) |
在给定的系统中,线路阻抗参数已知,图 2中9节点系统电压损耗与节点注入功率的关系可根据式(5)计算出。
命题1中支路电压损耗Δ V和H矩阵的定义与功率从平衡节点到其余节点流动的路径有关,此外,支路阻抗与输电线路的长度有关。上述命题给出了支路电压损耗与节点电压之间的线性关系,2.3小节建立分布式储能的配电网模型,并根据支路电压损耗与节点功率的线性关系,设计含分布式储能的低压配电网电压调节方法。
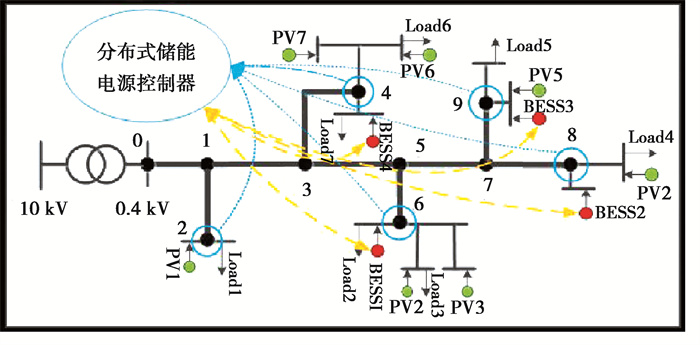
2.3 含分布式储能的配电网电压调节模型如图 3所示,低压配电网包含分布式光伏电源、分布式储能和负荷。图中绿色的节点表示分布式光伏电源,红色的节点代表分布式储能电源。模型的运行步骤分为:1)分布式储能电源控制器根据蓝色单向通信线收集部分节点的信息(注入节点的潮流信息)、根据橘黄色双向通信线采集分布式储能电源的输出信息;2)对采集的信息进行运算处理,得到分布式储能电源的输出设定值;3)通过双向通信线将储能设定值传递给分布式储能系统,用以调节储能的输出功率,进而调节系统的电压。需要注明的是,分布式光伏电源和储能电源的容量、接入位置在前期进行配电网规划时已经确定,因而为节约文章篇幅,对此不进行详细介绍。
|
图 3 含分布式光伏和分布式储能的低压配电网 Fig. 3 Low voltage distribution network with distributed PVs and distributed BESSs |
配电网中,分布式储能电源的存在使部分节点的注入功率可以被调控,通过调控节点的注入功率,可以实现系统潮流的分配,进而调节系统电压。假设配电网中含有n个节点,其中可调节点个数为m(n≥m),设计配电网电压调节目标函数如下:
目标函数为
| $ \mathop {min}\limits_{{P_{{\rm{BESS}}}}_{\rm{ - }}i \in [{P_{\min }}, {P_{{\rm{max}}}}]} f(\Delta V){\rm{ = }}\sum {_{i = 1}^m} |\Delta {V_i} = \sum {_{i = 1}^m} |{\mathit{\boldsymbol{H}}_i}\cdot\mathit{\boldsymbol{P}}(k)| =\\ \sum {_{i = 1}^m} |{\mathit{\boldsymbol{H}}_i}\cdot{\mathit{\boldsymbol{P}}_v}(k) + {\mathit{\boldsymbol{P}}_{{\rm{BESS}}}}(k) - {\mathit{\boldsymbol{P}}_L}(k){\rm{ }}){\rm{ |}}, $ | (10) |
约束条件为
| $\left\{ \begin{array}{l} {\begin{array}{*{20}{l}} {\sum {_{i \in N\mathit{\boldsymbol{PV}}}{\mathit{\boldsymbol{P}}_{V\_i}}(k) + \sum {_{i \in {N_{{\rm{BESS}}}}}{\mathit{\boldsymbol{P}}_{Bess\_i}}(k) + {\mathit{\boldsymbol{P}}_g}(k) = } \sum {_{i \in {N_{{\rm{LOAD}}}}, }{\mathit{\boldsymbol{P}}_{L\_i}}(k), {\rm{ }}} } }\\ {{V_{{\rm{min}}}} \le {V_i}(k){\rm{ }} \le {V_{{\rm{max}}}}, } \end{array}} \end{array} \right. $ | (11) |
式中:P Bess=[PBess_i]m×1是储能电源的功率输出向量;P min与Pmax分别是储能电源输出的上下限;H i为矩阵H的第i行;PV=[PV_i]m×1是分布式光伏电源输出功率,PL=[PL_i]m×1是负荷需求功率;Pg(k)是与上级电网的交互功率;Vmin与Vmax是节点电压下限值和上限值。需要注明的是,与上级电网的交互功率Pg(k)根据日前调度策略确定,另外,储能电源的SoC同样由日前调度调节。为减省文章篇幅,因此不对日前调度策略进行单独详述。
2.4 分布式储能荷电状态均衡控制策略储能的运行受到储能电源荷电状态(SoC)的限制,为提升储能电源的运行效率,通常由日前调度策略调整储能的荷电状态。在文中,光照强烈并且光伏输出大于负荷需求时对储能进行充电。在光伏输出不能满足负荷需求或者为响应调度需求时,储能进行放电。为提升分布式储能的运行效率与可调度性,设计SoC均衡控制策略。根据文献[19]可知,电池储能源的荷电状态(SoC)与储能的充/放电功率近似成积分关系,
| $ {{\rm{So}}{{\rm{C}}_i}(t) = {\rm{So}}{{\rm{C}}_i}\left( 0 \right) - a\int {_0^t} {P_{{\rm{BESS}}}}{{_ - }_i}(t){\rm{d}}t, } $ | (12) |
式中: a为与储能容量有关的常数。为实现SoC的均衡控制,设计以下命题2。
命题2:在低压配电网中,假设分布式储能采用恒功率控制模式,并且数量为m,对应的功率向量为P Bess(t)=[PBess_i(t)]m×1,荷电状态向量为S (t)=[SoCi(t)]m×1。若采用控制律
| $ \begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{P}}_{{\rm{Bess}}}}(t{\rm{ }} + 1) = \mathit{\boldsymbol{G\cdot}}{\mathit{\boldsymbol{P}}_{{\rm{Bess}}}}(t) - c\mathit{\boldsymbol{\cdot G}}'\mathit{\boldsymbol{\cdot S}}(t){\rm{ }} \circ } \end{array}} \end{array} $ | (13) |
调节储能电源的输出功率,则储能源的荷电状态与输出功率存在以下关系,
| $ \begin{array}{l} \mathop {{\rm{lim}}}\limits_{t \to \infty } {\rm{So}}{{\rm{C}}_1}(t) = {\rm{So}}{{\rm{C}}_2}(t) = \cdots = {\rm{So}}{{\rm{C}}_m}(t){\rm{ }},\\ \mathop {{\rm{lim}}}\limits_{t \to \infty } {P_{{\rm{Bess\_}}}}_1(t) = {P_{{\rm{Bess\_}}}}_2(t) = \cdots = {P_{{\rm{Bess\_}}m}}(t){\rm{ }}, \end{array} $ | (14) |
即分布式储能电源的荷电状态趋于均衡(SoC一致),输出功率趋于相等。控制律(13)中,c=2 000为常数,而控制矩阵G = G ′+ I,矩阵I为单位矩阵,此外,控制矩阵G ′为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{G}}\mathit{'}\mathit{\boldsymbol{ = }}\mathit{K}\mathit{\boldsymbol{\cdot}}{{\left[ {\begin{array}{*{20}{c}} { - \sum\limits_{i = 2}^m {{g_i}} }&{{g_2}}& \cdots &{{g_m}}\\ {{g_1}}&{ - \sum\limits_{i = 1, i \ne 2}^m {{g_i}} }& \cdots &{{g_m}}\\ \vdots & \cdots &{}& \vdots \\ {{g_1}}&{{g_2}}& \cdots &{ - \sum\limits_{i = 1}^{m - 1} {{g_i}} } \end{array}} \right]}_{m \times m}}, }\\ {k = \frac{1}{{(1 + \sum {_{i - 2}^m{g_i}} )}}, } \end{array}} \right. $ | (15) |
式中,g1=g2=…=gm=1。
下面对分布式储能SoC均衡控制律(13)进行收敛性分析。将式(12)与式(13)结合并改写成连续形式得到
| $ \left[ {\begin{array}{*{20}{l}} {{\rm{SoC(}}\mathit{t}{\rm{)}}}\\ {{\mathit{\boldsymbol{P}}_{{\rm{Bess}}}}(t)} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{0_m}}&{ - c\mathit{\boldsymbol{I}}}\\ { - c\mathit{\boldsymbol{G}}'}&{\mathit{\boldsymbol{G}}'} \end{array}} \right]\mathit{\boldsymbol{\cdot}}\left[ {\begin{array}{*{20}{l}} {{\rm{SoC(}}\mathit{t}{\rm{)}}}\\ {{\mathit{\boldsymbol{P}}_{{\rm{Bess}}}}(t)} \end{array}} \right], $ | (16) |
记,
| $ \mathit{\boldsymbol{W}} = \left[ {\begin{array}{*{20}{l}} {{0_m}}&{ - c\mathit{\boldsymbol{I}}}\\ { - c\mathit{\boldsymbol{G}}'}&{\mathit{\boldsymbol{G}}'} \end{array}} \right] \circ $ | (17) |
根据文献[19]中的定理1的证明,可以证明矩阵W存在2个零特征值并且其余特征值幅值小于0。因此根据文献[19]中定理1的结论可知式(14)成立。命题2证明完毕。
分析SoC均衡控制律可知,式(13)右边第一项起功率均衡作用,使得储能源输出的功率趋于相等;第二项代表SoC之间的偏差,使得SoC之间的偏差逐渐趋于0,即实现SoC值相等。根据式(13)可知,当SoC的偏差为0时,在等式右边第一项的作用下使得分布式储能的功率输出相等。因此,SoC均衡控制律(13)存在两个作用:实现SoC均衡控制与实现储能输出功率相等。
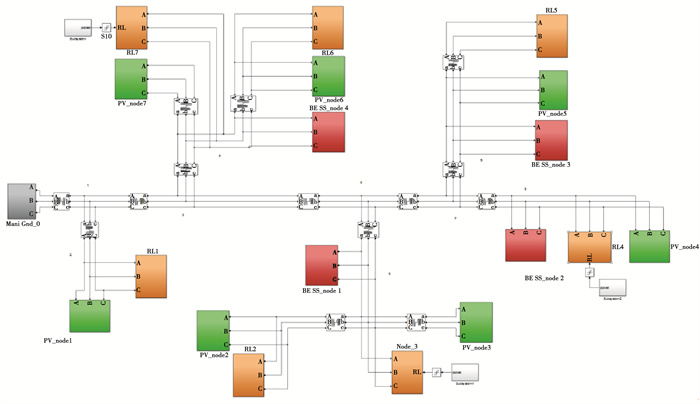
3 仿真平台设置采用Matlab/Simulink软件,建立含分布式光伏、分布式储能的低压配电网系统,该系统包含7个光伏电源、4座分布式储能电站和7组负荷,仿真模型如图 4所示。配电网中,分布式光伏和储能电源的容量见于表 1中。在低压配电网中,储能电源分别在节点6、8、9和4接入,其编号为BESS1,BESS2,BESS3和BESS4。分布式光伏PV_1~PV_7工作于最大功率跟踪(MPPT)控制模式,并且分布式光伏电源不发出无功功率。设定系统的电压幅值为380 V,线路阻抗为1.359+j0.082 Ω/km,各支路线路长度列于表 2中。
|
图 4 含分布式光伏及储能的低压配电网Simulink仿真模型 Fig. 4 The simulation model of low voltage distribution network with distributed PVs and distributed BESSs |
| 表 1 分布式光伏、储能参数设置 Table 1 Parameters of distributed PVs and BESSs |
| 表 2 线路长度参数 Table 2 Length of each branch line |
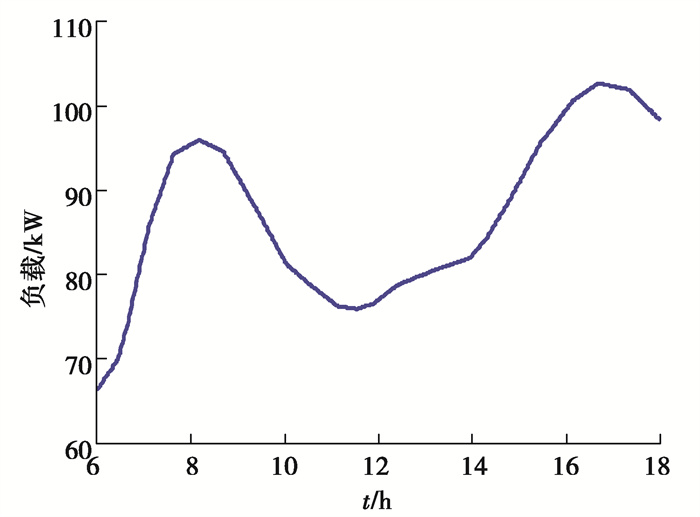
在仿真中,储能电源BESS1~BESS7工作有功无功功率控制(PQ)控制模式,其容量都为300 kW·h。分布式光伏的输出与光照有关,具有波动性。负荷变化曲线如图 5所示,可以看出,负荷高峰出现在早上7~9点和下午4~6点之间,符合居民用电习惯。
|
图 5 低压配电网中负荷变化曲线 Fig. 5 The load demand of low voltage distribution network |
为了验证所提方法的有效性,本小节设计4组仿真案例进行分析。算例1分析不含分布式光伏电源时,配电网系统电压的变化情况;算例2分析分布式光伏电源接入时,对配电网电压的影响;算例3分析分布式储能电源的对系统电压的调节作用;算例4分析通信线路故障对系统的影响。
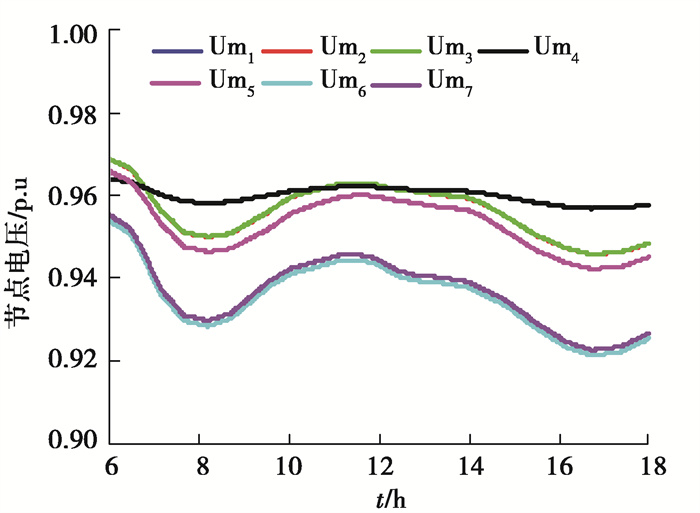
4.1 不含分布式光伏电源的配电网电压变化在本算例中,不考虑分布式光伏和储能源的接入,其网络结构图 3所示,负荷变化如图 5所示,线路阻抗参数为1.359+j0.082 Ω/km,并且电压幅值采用标幺值计算。仿真得到的结果如图 6所示。
|
图 6 不含分布式光伏的电压变化 Fig. 6 The fluctuation of node voltage without PVs |
根据图 6看出,负荷侧电压Um1~Um7分别在0.95 p.u附近波动,符合巫溪地区配电网的实际情况。此外,负荷4和6节点处的电压幅值与标准电压幅值之间差距最大。当功率从节点0处流向负荷节点4时,功率流动的距离最远,因而电压变化对于其他节点(除节点6外)电压。节点6的电压偏差最大,是因为支路阻抗和支路功率共同决定了节点电压的偏差,节点6所在支路流动的功率大于其他支路的功率,因而节点6的电压偏差最大。
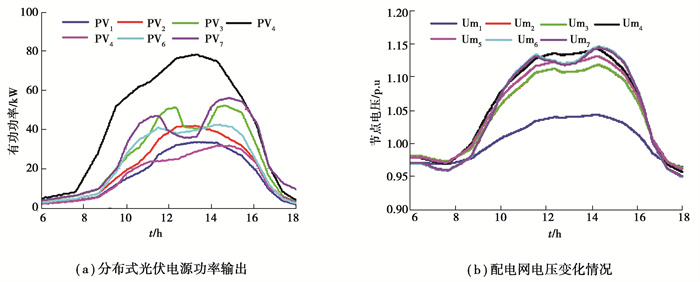
4.2 分布式光伏接入对电网电压的影响分布式光伏电源接入的配电网结构如图 3所示,分别接入节点2、4、6、8和9,容量如表 1所示。为清晰体现光伏电源对系统电压的影响,仿真算例只分析白天分布式光伏输出功率剧烈变化对系统节点电压的影响,因而设置仿真时间为早上6点~下午6点。光伏电源的输出功率如图 7(a)所示,从图中可以看出,光伏电源的功率输出波动在0~80 kW之间变化。早上8点之前,分布式光伏电源输出小于20 kW,中午12点~14点之间,光伏输出功率达到最大值,到傍晚6点,光伏电源输出小于10 kW。
|
图 7 配电网分布式光伏输出与电压波动变化 Fig. 7 The output power of PV and the voltage fluctuation in distribution network |
分布式光伏接入系统时,得到的电压波形如图 7(b)所示,从图中看出,除光伏电源PV_1节点的电压幅值小于1.05 p.u外,其余电压幅值在上午10点~下午4点时间段内都大于1.1 p.u,超出电压上限值。在上午8点之前和下午5点之后,系统电压逐渐下降至0.97 p.u附近。结合图 7(a)和图 7(b)看出,早上8点之前和下午5点之后,光伏电源的输出小,不会提升系统电压幅值。上午8点~下午5点之间,光伏电源输出功率大,导致系统电压越过上限值。需要说明的是,光伏PV_1处的节点电压在正常范围内变化,是因为PV_1节点与上级电网距离短,功率流动的距离短导致。
4.3 分布式储能对电网电压的调节分析为调节低压配电网的节点电压,在仿真算例中接入分布式储能电源,详图可见图 3中,其中红色的节点表示储能电源。储能电源的容量见于表 1中。在仿真中,考虑了储能电源的运行限制,即在储能充电和放电过程中,储能电源输出的功率不能超越上限值。
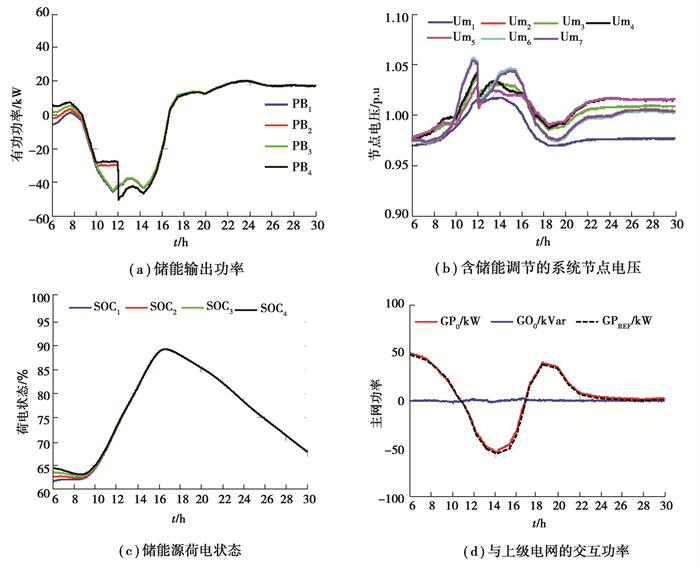
仿真中设置仿真周期为早晨6点~第二天早晨6点,得到的仿真结果如图 8所示,其中26点、28点和30点表示第二天凌晨2点、4点和早晨6点。储能电源的输出和系统电压分别如图 8(a)和图 8(b)所示。从图 8(a)中可以看出储能电源在早上8点之前输出很小的功率,随着光伏电源输出的增大,储能电源吸收的功率逐渐变大。从图 8(b)中看出,系统电压幅值在正常范围内变化,幅值皆小于1.05 p.u。由图 8(a)与图 8(c)可知,从9点~17点之间,分布式储能在吸收光伏电源发出的功率,储能的SoC在增加;17点过后,光伏电源的输出不足以为负荷提供电能,分布式储能进入发电模式,因而分布式储能的SoC逐渐降低。超过18点后,分布式光伏输出功率逐渐减小为0,因而负荷的供电需求由主网和分布式储能提供。18点过后,分布式光伏电源输出功率逐渐降为零,分布式储能输出增大,为负荷提供电能(图 8(a)所示)。系统电压在正常范围内变化(图 8(b)所示),储能电源的荷电状态逐渐降低,近似等于初始时刻(6点)的值,完成储能电源在一个周期内的充放过程。
|
图 8 分布式储能对系统电压的影响 Fig. 8 The impact of BESS to system voltage |
图 8(d)中,黑色的虚线表示配电网与主网交互功率日前调度曲线,红色的实线表示配电网与主网的交互功率。分析图 8(d)可知,配电网与上级电网的交互功率服从日前调度的情况,即实际交互功率曲线与日前调度曲线相符合。需要注明的是,含分布式储能的低压配电网日前调度策略不是文中关注的重点,因而将主网的调度功率用图 8(d)中的黑色曲线代替。分析仿真结果,文中提出的基于功率里程数的电压调节方法能够有效地调节低压配电网的节点电压。
4.4 通信线路故障对配电网系统的影响文中含分布式储能的低压配电网电压调节模型与储能SoC均衡方法依赖于高速的通信网络和高性能的中央控制器,通信线路与控制器的可靠性决定文中所提方法的性能。借助于电力线载波通信技术[20-21]的发展,通信系统的投资成本将会逐渐下降。因此,文中采用集中式通信模式,将所需要的全局信息采集到中央控制器,中央控制器根据得到的信息进行运算,得到储能系统的运行设定值。但通信线路故障势必会产生不利影响,进而仿真分析文中模型与方法对通信故障的容忍能力。
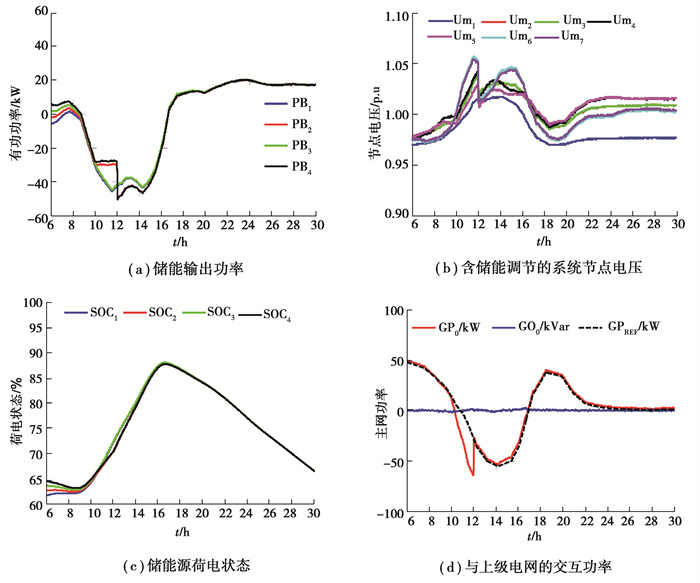
分析通信线路故障对系统的影响,仿真设置控制器与分布式储能BESS4与BESS2之间的通信线路在上午10点~中午12点之间发生故障,并假设控制器和BESS2、BESS4能够分别保存故障前一时刻的信息,得到的仿真结果如图 9所示。从图 9(a)中看出,在上午10点,控制器与储能BESS2与BESS4之间的通信线发生故障不能正常通信,BESS2和BESS4保持输出不变,直至12点故障恢复。在10点~12点之间,BESS1和BESS3按照SoC均衡控制律(8)调节其输出,而BESS2和BESS4保持其输出不变。12点过后,BESS2、BESS4与BESS1和BESS3在控制律(8)的调节下,输出功率逐渐趋于一致。同理,从图 9(c)中看出,分布式储能的SoC不能趋于一致,12点过后,在控制律(8)的作用下,SoC逐渐趋于一致,直至20点,储能SoC最终趋于一致。从图 9(b)看出,10点~12点之间,BESS2和BESS4不能有效调节,因而系统电压幅值增大,大于1.05 p.u。在故障恢复后,系统电压恢复到稳定区域。根据图 9(d)所示,主网在10点~12点为维持系统功率平衡吸收更多的功率。在故障恢复后,按照日前调度的曲线输出功率。因此,当通信线发生故障时,会影响储能电源的功率输出,进而影响系统电压。在故障恢复后,文中所提模型能够正常运行,并实现系统电压的调节和储能SoC的均衡控制。
|
图 9 通信线路故障系统的影响 Fig. 9 The impact of communication link broken on system performance |
针对低压配电网电压调节问题,文中提出了分布式储能、分布式光伏并存的配电网调压方法。首先,对分布式光伏接入电网对电网电压造成的影响进行分析,推导出节点电压与节点注入功率之间的线性关系,提出了功率里程数的定义;基于功率里程数电压损失计算模型,提出了含分布式电源、分布式储能的配电网电压调节模型。与基于节点电压灵敏度矩阵的方法不同,文中提出的模型不需要计算雅克比矩阵,降低了计算复杂程度。同时,文中提出的优化目标为线性目标,有利于提高运算速度,降低系统的响应时间。此外,考虑到分布式储能的利用效率,设计了分布式储能SoC均衡控制策略,使得SoC在运行过程中保持一致。仿真结果说明,文中提出的电压调节方法能够有效地实现低压配电网电压的调节,并实现储能电源的SoC均衡控制。值得说明的是,在通过功率里程数计算线路电压损失时,只考虑了功率流动里程的影响,忽略了节点电压之间的差异对支路电压损失计算的影响,为提升电压损失计算的精度,需要将节点电压差异考虑到下一步工作中。此外,文中的电压调节模型及储能SoC均衡方法均采用集中式控制,此方法对通信系统及中央控制器要求高。通信系统和中央控制器出现故障,会影响系统的运行性能,严重时导致系统瘫痪。因此,采用分布式的方法实现电压调节及储能SoC均衡方法将是下一步的研究内容。
| [1] |
Abbott D. Keeping the energy debate clean: how do we supply the world's energy needs?[J]. Proceedings of the IEEE, 2010, 98(1): 42-66. DOI:10.1109/JPROC.2009.2035162 |
| [2] |
李娟. 并网光伏发电系统建模及其对配电网的影响研究[D]. 济南: 山东大学, 2014. Li J. Grid-connected PV system modeling and impaction research on the distribution network[D]. Jinan: Shandong University, 2014. (in Chinese) |
| [3] |
许晓艳, 黄越辉, 刘纯, 等. 分布式光伏发电对配电网电压的影响及电压越限的解决方案[J]. 电网技术, 2010, 34(10): 140-146. Xu X Y, Huang Y H, Liu C, et al. Influence of distributed photovoltaic generation on voltage in distribution network and solution of voltage beyond limits[J]. Power System Technology, 2010, 34(10): 140-146. (in Chinese) |
| [4] |
Thomson M, Infield D G. Impact of widespread photovoltaics generation on distribution systems[J]. IET Renewable Power Generation, 2007, 1(1): 33. DOI:10.1049/iet-rpg:20060009 |
| [5] |
Mahmud N, Zahedi A. Review of control strategies for voltage regulation of the smart distribution network with high penetration of renewable distributed generation[J]. Renewable and Sustainable Energy Reviews, 2016, 64: 582-595. DOI:10.1016/j.rser.2016.06.030 |
| [6] |
刘斌, 刘锋, 梅生伟, 等. 基于二阶锥优化的含有载调压变压器主动配电网最优潮流[J]. 电力系统自动化, 2015, 39(19): 40-47. Liu B, Liu F, Mei S W, et al. Optimal power flow in active distribution networks with on-load tap changer based on second-order cone programming[J]. Automation of Electric Power Systems, 2015, 39(19): 40-47. (in Chinese) DOI:10.7500/AEPS20150104003 |
| [7] |
Cheung Victor S P, Chung Henry S H, Lo Alan W L. A modular and scalable structure using multiparallel-connected series-voltage compensators for supply voltage regulation[J]. IEEE Transactions on Power Electronics, 2016, 31(6): 4096-4110. DOI:10.1109/TPEL.2015.2469156 |
| [8] |
周鑫, 王韶, 张文龙, 等. 配电网固定串联补偿多目标优化[J]. 电力系统保护与控制, 2017, 45(24): 115-122. Zhou X, Wang S, Zhang W L, et al. Multi-objective optimization of fixed series compensation in distribution network[J]. Power System Protection and Control, 2017, 45(24): 115-122. (in Chinese) DOI:10.7667/PSPC161992 |
| [9] |
付英杰, 汪沨, 陈春, 等. 考虑分布式电源的配电网电压控制新方法[J]. 电力系统及其自动化学报, 2015, 27(6): 26-31. Fu Y J, Wang F, Chen C, et al. New method of voltage control considering distribution network containing distributed generation[J]. Proceedings of the CSU-EPSA, 2015, 27(6): 26-31. (in Chinese) DOI:10.3969/j.issn.1003-8930.2015.06.005 |
| [10] |
殷桂梁, 侯嘉怡. 一种低压微电网中的分布式电压控制算法[J]. 电力系统保护与控制, 2014, 42(20): 75-80. Yin G L, Hou J Y. A distributed voltage control algorithm in the low voltage microgrid[J]. Power System Protection and Control, 2014, 42(20): 75-80. (in Chinese) DOI:10.7667/j.issn.1674-3415.2014.20.013 |
| [11] |
肖浩, 裴玮, 邓卫, 等. 分布式电源对配电网电压的影响分析及其优化控制策略[J]. 电工技术学报, 2016, 31(S1): 203-213. Xiao H, Pei W, Deng W, et al. Analysis of the impact of distributed generation on distribution network voltage and its optimal control strategy[J]. Transactions of China Electrotechnical Society, 2016, 31(S1): 203-213. (in Chinese) |
| [12] |
徐志成, 赵波, 丁明, 等. 基于电压灵敏度的配电网光伏消纳能力随机场景模拟及逆变器控制参数优化整定[J]. 中国电机工程学报, 2016, 36(6): 1578-1587. Xu Z C, Zhao B, Ding M, et al. Photovoltaic hosting capacity evaluation of distribution networks and inverter parameters optimization based on node voltage sensitivity[J]. Proceedings of the CSEE, 2016, 36(6): 1578-1587. (in Chinese) |
| [13] |
姚宏民, 杜欣慧, 李廷钧, 等. 光伏高渗透率下配网消纳能力模拟及电压控制策略研究[J]. 电网技术, 2019, 43(2): 462-469. Yao H M, Du X H, Li T J, et al. Simulation of consumption capacity and voltage control strategy of distribution network with high penetration of photovoltaics[J]. Power System Technology, 2019, 43(2): 462-469. (in Chinese) |
| [14] |
王笑雪, 徐弢, 王成山, 等. 基于MAS的主动配电网分布式电压控制[J]. 中国电机工程学报, 2016, 36(11): 2918-2926. Wang X X, Xu T, Wang C S, et al. Distributed voltage control in active distribution networks utilizing multiple agent system[J]. Proceedings of the CSEE, 2016, 36(11): 2918-2926. (in Chinese) |
| [15] |
张江林, 庄慧敏, 刘俊勇, 等. 分布式储能系统参与调压的主动配电网两段式电压协调控制策略[J]. 电力自动化设备, 2019, 39(5): 15-21, 29. Zhang J L, Zhuang H M, Liu J Y, et al. Two-stage coordinated voltage control scheme of active distribution network with voltage support of distributed energy storage system[J]. Electric Power Automation Equipment, 2019, 39(5): 15-21, 29. (in Chinese) |
| [16] |
柴园园, 刘一欣, 王成山, 等. 含不完全量测的分布式光伏发电集群电压协调控制[J]. 中国电机工程学报, 2019, 39(8): 2202-2212. Chai Y Y, Liu Y X, Wang C S, et al. Coordinated voltage control for distributed PVs clusters with incomplete measurements[J]. Proceedings of the CSEE, 2019, 39(8): 2202-2212. (in Chinese) |
| [17] |
张宇精, 乔颖, 鲁宗相, 等. 含高比例分布式电源接入的低感知度配电网电压控制方法[J]. 电网技术, 2019, 43(5): 1528-1535. Zhang Y J, Qiao Y, Lu Z X, et al. Voltage control for partially visible distribution networks with high DG penetration[J]. Power System Technology, 2019, 43(5): 1528-1535. (in Chinese) |
| [18] |
Kashani M G, Bhattacharya S, Matamoros J, et al. Autonomous inverter voltage regulation in a low voltage distribution network[J]. IEEE Transactions on Smart Grid, 2018, 9(6): 6909-6917. DOI:10.1109/TSG.2017.2728661 |
| [19] |
Kang W F, Chen M Y, Li B, et al. Distributed reactive power control and SOC sharing method for battery energy storage system in microgrids[J]. IEEE Access, 2019, 7: 60707-60720. DOI:10.1109/ACCESS.2019.2910352 |
| [20] |
徐文涛, 李振东, 李博. 基于电力线宽带载波的双模用电信息采集系统设计[J]. 电工技术, 2019(18): 76-79. Xu W T, Li Z D, Li B. Design of dual-mode electricity information collection system based on power line broadband carrier[J]. Electric Engineering, 2019(18): 76-79. (in Chinese) DOI:10.3969/j.issn.1002-1388.2019.18.030 |
| [21] |
王新刚, 赵舫. 计及通信资源优化的电力线载波通信路由算法研究[J/OL]. 电测与仪表: 1-7[2019-10-30]. http://kns.cnki.net/kcms/detail/23.1202.TH.20191015.1518.006.html.. Wang X G, Zhao F. Research on power line carrier communication routing algorithm considering communication resource optimization[J]. Electrical Measurement & Instrumentation, 1-7[2019-10-30]. http://kns.cnki.net/kcms/detail/23.1202.TH.20191015.1518.006.html.. |
 2022, Vol. 45
2022, Vol. 45


