b. 天津大学 天津市建筑物理环境与生态技术重点实验室, 天津 300072
b. Tianjin Key Laboratory of Architectural Physics and Environmental Technology, Tianjin University, Tianjin 300072, P. R. China
可持续建筑节能效果很大程度上取决于建筑初期设计[1]。近年来,结合建筑能耗预测方法和优化算法在建筑设计初期辅助节能优化决策成为研究热点[2]。优化过程中通常会生成大量的备选方案,能否快速进行建筑能耗预测成为影响优化效率的关键因素。随着人工智能技术的不断发展,基于机器学习的能耗预测方法越来越多的应用于建筑能耗优化中。实践证明,通过机器学习预测建筑能耗大大提高了建筑节能优化设计的效率,正逐步为建筑师所接纳。在实际应用中,建筑节能优化问题多为在已知可行空间内寻找最优方案[3],但在优化过程中,个体方案多为随机生成或有引导性的随机生成[4-6],使得用于学习的训练样本集分布情况未知。现有研究中,关于样本集质量(即样本分布不均衡问题)的研究多集中于分类问题中[7-9],在关于回归问题中机器学习算法的选择及其参数设置的研究中,关于样本集质量尚无统一定义[10],多集中于样本集大小对学习效果的影响或样本个体质量对学习效果的影响,较少关注样本集样本分布情况即样本集所包含信息完整性对学习效果的影响[11-14]。但在样本分布情况未知的前提下,随意选择的算法或不合理的参数设置可能会导致算法性能不理想,从而影响建筑节能优化效果。同时,对于建筑师而言,由于机器学习原理及应用的复杂性,尚未有较统一且明确的学习方法选择及参数设置依据对其进行指导。
文中提出了基于样本量及样本覆盖性的样本集质量评价方法,通过比较几种常用的机器学习方法及参数设置在不同质量样本集情况下的学习效果,分析样本集质量与机器学习算法性能之间的关系,针对不同质量样本集提出学习方法选择及参数设置建议,为建筑师使用提供理论指导。
1 理论与方法 1.1 传统机器学习算法支持向量回归(Support Vector Regression,SVR)[15]是支持向量机的重要分支,广泛应用于非线性回归问题[16]。该算法基于核函数的小样本统计理论,其核心是VC维理论及结构风险最小化原则,可以有效避免陷入局部最优而达到全局最优, 并通过核函数将低维空间问题映射至高维空间,将其转化为线性回归关系[17]。SVR算法具有结构简单、稳定性强、泛化能力强的优点,可以有效解决模型选择与欠学习、过学习、小样本、非线性和局部最优等问题,是建筑能耗预测中常用算法[18-21]。
BP神经网络(Back-Propagation Network,BP)是一种典型的多层前向型神经网络,利用误差反向传播算法对网络进行训练,理论上通过选择适当的网络层次及神经元个数可以任意逼近非线性函数[22]。该方法具有一定的自适应与自组织能力以及非线性映射能力,在建筑能耗预测问题中显示出明显优势[16]。但性能受样本数据及神经网络拓扑结构影响较大,且随着样本量的增多训练时间会大大加长,因此,选择适当的拓扑结构对该算法尤其重要。
1.2 集成机器学习算法集成学习(Ensemble Learning)是机器学习领域重要的研究方向之一,通过多个学习算法对同一个问题进行学习,得到多个具有差异性的学习器,并通过一定组合方法对其学习结果进行组合得到最终结果,核心思想是充分利用误差较大的个体学习器所获得的局部信息来增强集成学习器的整体准确度和可靠性,而不是直接将其舍弃。集成学习具有准确度高,稳定性高,对参数设置敏感性相对较小以及学习效率高等优点,在建筑能耗预测中应用日趋广泛[23-25]。其中,应用最多且范围最广的为Bagging算法与Boosting算法。
Bagging算法通过自主采样法(Bootstrap)产生新的训练子集训练基学习器,结合策略组合各基学习器预测结果进行输出,基学习算法对训练数据越敏感,基学习器差异性越大,集成效果越好。
算法1 Bagging算法
输入:训练集D,个体学习器L,迭代次数T;
for t=1, 2, 3, …, T:
1) 对样本集进行自主采样得到训练子集Dt;
2) 使用训练子集训练得到个体学习器ht;
end
输出:
Boosting算法的基本思想是将多个预测精度较低的弱学习器提升至精度较高的强学习器。其中,最具代表性的为AdaBoost算法,核心思想是通过将自身的学习结果反馈到问题空间来进行交互,根据自身对环境的拟合程度来改变样本的采样概率[26],从而加强对精度较低个体的学习。
算法2 AdaBoost算法
输入:训练集D,个体学习器L,迭代次数T;
1) 样本权重初始化为ωi= 1/N,i = 1, 2, …, N,其中N为样本总数;
2) 通过迭代获得强学习器:
for t = 1, 2, …, T。
① 在训练集上根据权重ωi进行学习获得弱学习器ht;
② 计算当前弱学习器中每个样本的相对误差并根据误差更新权重。
相对误差:
回归误差率:
弱学习器ht的权重系数:
更新样本权重系数:
输出:
Bagging及AdaBoost算法均为使用较广泛的集成学习算法,Bagging主要通过减小方差来提高学习性能,而AdaBoost在减小方差的同时还可以减小偏差,但Bagging对方差的减小程度大于AdaBoost。且Bagging与AdaBoost相比稳定性和鲁棒性更强,但AdaBoost在降低错误率的程度上强于Bagging[27]。
2 样本集质量划分方法在使用机器学习算法时,样本集质量对绝大多数机器学习算法的学习效果影响较大,学习算法选择及其参数设置一直是机器学习研究中的热点问题,目前尚未有准确的结论可供参考,多通过参数寻优或经验验证进行设置,存在较大的主观性和局限性。在回归问题中,较少考虑样本数据分布特征,未充分利用隐含在数据集中的信息[28]。在建筑节能优化实践中,其数据集存在以下特点:1)解集空间已知,属于已知范围内的寻优问题;2)训练集为无噪声仿真数据,但训练集通过性能模拟得到,耗时较长;3)样本在解集空间中分布情况未知,可能会出现样本聚集,影响学习效果。
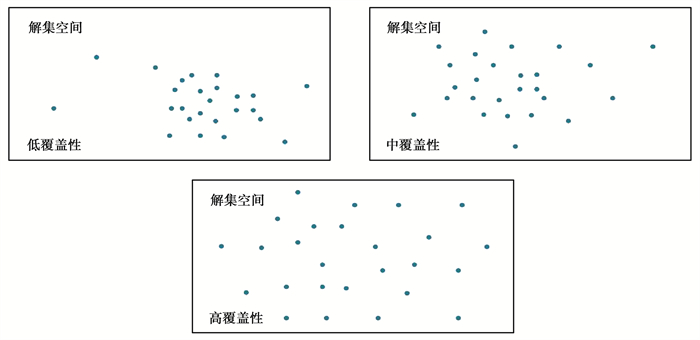
基于以上特征,文中提出一种基于样本量及样本覆盖性的样本集质量评价方法,以此为基础,测试不同样本集质量下机器学习算法的学习效果。首先,根据“3σ”准则,将样本集样本量分为小、中、大3个等级。其次,引入优化算法中解集质量评价指标——覆盖性(Coverage)评价样本在可行空间内的分布情况,如图 1所示。
|
图 1 样本集样本覆盖性示意图 Fig. 1 The coverage of sample set |
覆盖性常用于优化算法中评价解集在解集空间中分布广泛性的指标,反映了样本点在可行求解空间中的分布情况,以表现在解集空间内的搜索程度,用以衡量是否陷入局部最优。其计算方法为
| $ \mathrm{COV}=\prod\limits_{k=1}^{m} S D_{k}, $ | (1) |
其中,
| $ \begin{gathered} \mathrm{SD}_{k}=\sqrt{\frac{\sum\limits_{j=1}^{t}\left(M_{k}-h_{k j}\right)^{2}}{t}, } \\ M_{k}=\frac{\sum\limits_{j=1}^{t} h_{k j}}{t}, \end{gathered} $ |
式中,COV为覆盖性;SDk为第k个变量的标准差(k = 1, 2, …, m),m为变量个数;hkj为第j个个体第k个变量的值(j = 1, 2, …, t),t为个体数量;Mk为第k个变量的平均值。由式(1)可知,覆盖性由各样本点各变量方差乘积求得,反应样本中各变量在空间中的不均衡性,即空间覆盖程度。在样本量相同的情况下,样本的覆盖性越高,说明样本在可行空间内的分布越均匀,样本集在各变量维度上的信息完整度越高,越有利于算法进行学习。
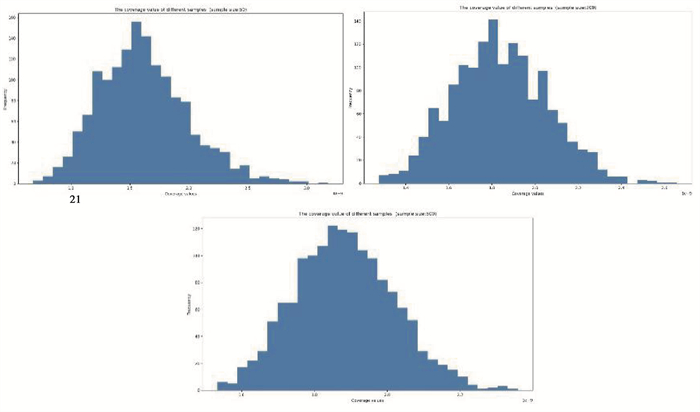
文中通过对样本量分别为50、200、500的样本集(均为随机生成)进行重复测试并计算其覆盖性。结果表明,样本集的覆盖性大致遵循正态分布,如图 2所示,故样本集覆盖性等级划分采用“3σ”准则。
|
图 2 样本量为50、200、500的样本集覆盖性分布情况 Fig. 2 Coverage Probability Histogram for sample sets in different sizes (sample size: 50, 200, 500) |
设计2组实验测试不同样本集质量对其学习算法性能的影响。首先,测试传统机器学习算法在不同质量样本集下的表现,从中选出对于每类样本集表现较好的学习方法及参数设置,将其作为第2组实验的基学习器;其次,以第一阶段的实验结果为基础,测试集成学习算法对不同质量样本集的预测效果。最后,得出较好预测效果所需样本量,以及对应的机器学习方法及其参数设置,为建筑节能优化设计提供帮助。
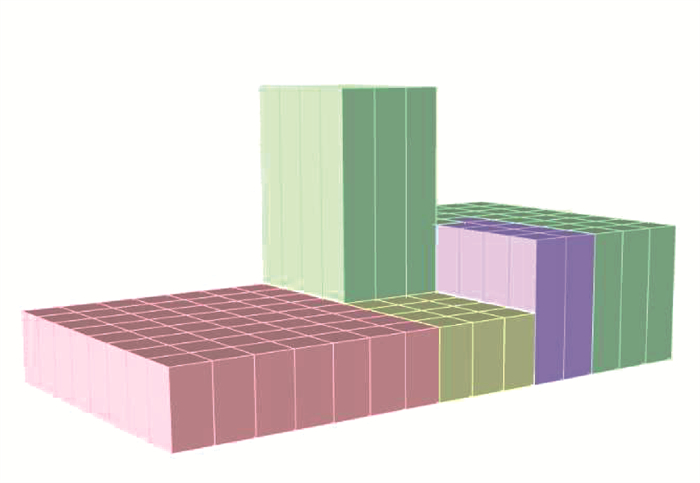
3.1 实验环境及样本集设置实验的运行环境为:Interi7 8核2.81 GHz处理器,8G RAM内存,64位Windows 10操作系统。实验样本集来自天津一虚拟办公建筑的全年平均能耗模拟数据。该建筑共包含4大功能分区,分别为办公区、多媒体会议区、餐饮区及中庭交通区。因研究重点在测试机器学习算法性能,在合理的范围内简化模型,如图 3所示。各样本集中的所有样本均为可行空间内随机生成的个体样本,其能耗通过Grasshopper中能耗模拟插件Honeybee仿真模拟得出。变量及取值范围,如表 1所示,能耗相关参数设置及运行时间设置等均依照相关办公建筑设计规范设定。
|
图 3 天津一虚拟办公建筑模型示意图 Fig. 3 The model of a virtual office building in Tianjin |
| 表 1 变量表 Table 1 Variables of case study |
基于建筑节能优化实践中数据集的特征,综合考虑实际应用中的时间成本,将样本量分为50,200,500三个等级,分别代表小、中、大样本量。针对每类样本量各生成1 500个样本集并计算其覆盖性,依据“3σ”准则将其划分为低、中、高覆盖性。具体样本集分类及其特征如表 2所示。
| 表 2 样本集分类及特征 Table 2 Classification and characteristics of sample sets |
机器学习算法通过python Scikit-Learn中的SVR、MLPRegressor、BaggingRegressor及AdaBoostRegressor工具包实现。在训练学习器之前,为消除变量量级对学习性能的影响,对样本数据进行归一化处理:
| $ x^{\prime}=\frac{x-x_{\mathrm{avg}}}{x_{\mathrm{std}}}, $ | (2) |
其中,x′为归一化后的数据,xavg, xstd分别为x的平均值和方差。
实验1:传统机器学习算法性能评价。
选取SVR算法及BP神经网络算法进行训练,各类样本集中随机选择一个作为该类样本集代表。对于每一样本集,80%的样本作为训练集,剩余20%作为测试集。对于SVR算法,主要超参数包括正则化参数C,不敏感参数ε及核函数中的参数;对于BP神经网络算法,主要超参数包括隐藏层结构,激活函数以及学习率。考虑到计算时间成本,使用与待测试样本集同维度的Scikit-Learn自带标准数据集Boston Housing进行预实验,确定较优学习效果下的各参数大致范围,并选取对学习效果影响较大的超参数作为测试参数。最终选取SVR算法中高斯核函数的系数γ及BP神经网络中神经元结构的神经元个数作为测试超参数,其余超参数设置同样依据预实验中学习效果较优的模型参数。具体算法参数设置,如表 3所示。
| 表 3 实验1算法超参数设置 Table 3 The hyperparameter setting of Experiment 1 |
实验2:集成机器学习算法性能评价。
选取实验1中综合性能较好的1组SVR及BP设定参数,作为集成学习算法的基学习器,将Bagging、AdaBoost算法作为比较算法,主要分析基学习器及集成规模对集成效果的影响。训练集及测试集划分同实验1。由于集成学习算法对于基学习器正确率的最低要求为0.5,在集成过程中剔除正确率小于0.5的基学习器。算法参数设置如表 4所示。
| 表 4 实验2算法超参数设置 Table 4 The hyperparameter setting of Experiment 2 |
算法性能评价包含拟合效果、有效率以及时间成本3方面。其中,拟合效果采用均方误差(mean squared error, MSE)及决定系数(Coefficient of determination, R2)进行评价。在实验中,R2大于0.9视为优秀的学习算法,将有效率定义为用R2大于0.9的概率,时间成本为算法运行一次的时间。
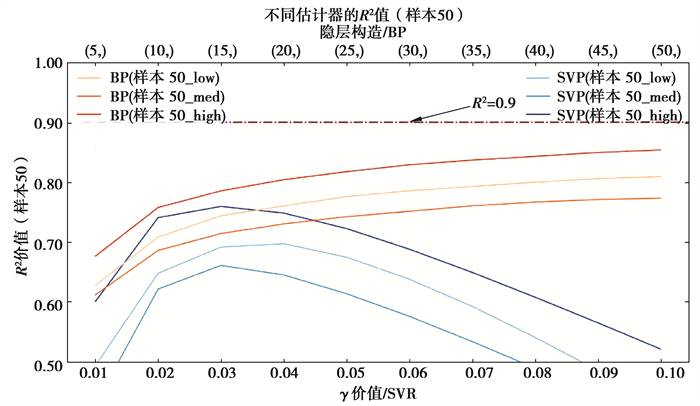
4 实验结果与分析 4.1 实验1结果与分析所有算法训练100次取平均值作为最终结果进行比较,SVR算法及BP算法对不同质量样本集的决定系数和均方误差如图 4~图 9所示,运算时间如表 5~表 6所示,有效性如表 7~表 8所示。
|
图 4 Sample50决定系数 Fig. 4 The R2 of Sample50 |
|
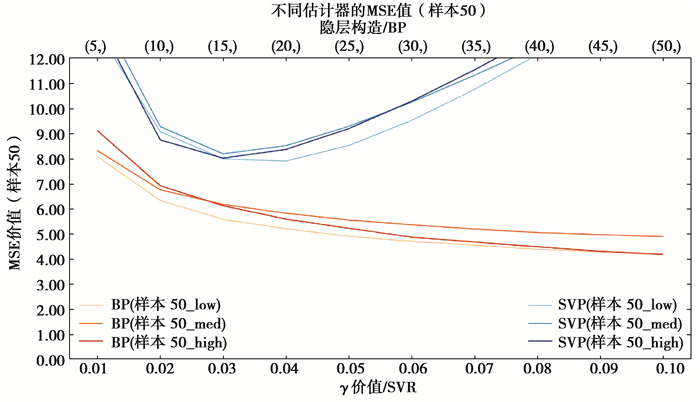
图 5 Sample50均方误差 Fig. 5 The MSE of Sample50 |
|
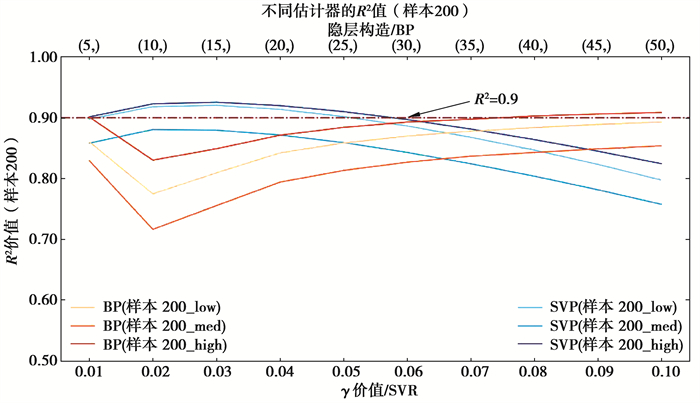
图 6 Sample200决定系数 Fig. 6 The R2 of Sample200 |
|
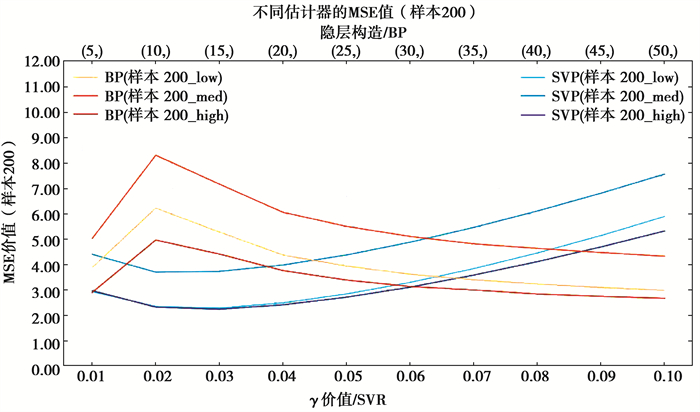
图 7 Sample200均方误差 Fig. 7 The MSE of Sample200 |
|
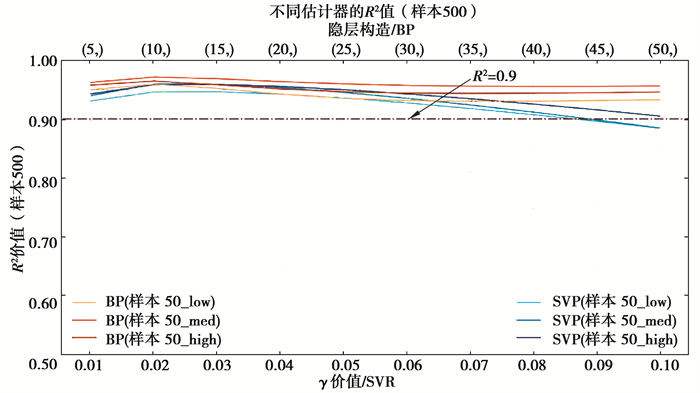
图 8 Sample500决定系数 Fig. 8 The R2 of Sample500 |
|
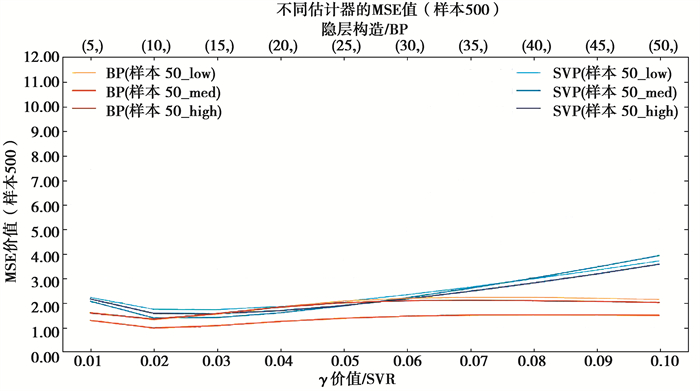
图 9 Sample500均方误差 Fig. 9 The MSE of Sample500 |
| 表 5 SVR算法计算时间 Table 5 The computation time of SVR |
| 表 6 BP算法计算时间 Table 6 The computation time of BP |
| 表 7 SVR算法有效率 Table 7 The available ratio of SVR |
| 表 8 BP算法有效率 Table 8 The available ratio of BP |
通过对实验1结果进行分析,可得到如下结论:
1) 拟合效果方面,Sample50中所有覆盖性样本集拟合效果均较差,SVR算法及BP神经网络算法均未达到R2>0.9的优秀标准,但SVR算法拟合效果普遍优于BP神经网络算法。Sample200中,拟合效果明显提升,当神经元个数小于35时,SVR算法表现优异,对于低、高覆盖性的样本集,在γ取0.03时取得最优效果并达到优秀标准,当神经元个数大于35时,BP神经网络算法的拟合效果优于SVR算法,但计算时间较长。对于中覆盖性样本集,始终未达到优秀标准。Sample500中,拟合效果极优,2种算法的r2均可达到0.9以上,BP神经网络算法甚至可达0.95;
2) 样本量越大,计算成本越高,有效率越高,准确性越强,即训练样本中包含的可行空间内的信息越丰富,学习效果越好。同时,随着样本量的增加,拟合效果对学习算法及参数设置的敏感性下降,即各算法及参数设置之间的学习差异减小;
3) 覆盖性对学习效果有一定影响,当样本量相同时,各样本集覆盖性虽然存在差异,但其学习效果的变化趋势基本相同。样本量不同时,覆盖性对学习效果的影响存异,在实验中,样本量为50,200时,其学习效果从优至劣依次为高、低、中覆盖性;当样本量为500时,SVR算法的学习效果优劣排序为高、中、低,而BP神经网络算法学习效果优劣排序则为中、高、低。由此可见,覆盖性与学习器的学习效果并不始终成正相关关系,而是与样本量及学习算法有关。印证了Zhou等[29]在“选择性集成”概念中证明的通过选择部分个体学习器来构建集成可能要优于使用所有个体学习器构建的集成;
4) 在实验中,SVR算法在不同参数设置下算法复杂度无明显差别,BP神经网络算法的复杂度随着隐藏层结构的复杂化而逐渐增加,结果表明,当隐藏层结构达到一定复杂度时,继续增加神经元个数,反而会降低学习效果,且神经元个数越多,时间成本越大,在选择算法及参数设定时,应选用适当复杂度算法,以防止出现过拟合现象;
5) 对于不同样本量样本集,计算时间虽随着样本量增加而逐渐增大,并无数量级上的差别,测试模型较为简单,随着模型复杂度的增加,样本量带来的计算时间差异会逐渐增大。在建筑优化过程中,时间成本的增加主要来自于生成样本集时所需的模拟计算时间,故当样本量增大时,整体时间成本会大大增加。
4.2 实验2结果与分析在实验1中,Sample50中所有样本集均未达到优秀水平,Sample200中覆盖性样本集未达到优秀水平,对以上样本集进行集成学习实验,以获得较好的拟合效果。基学习器综合考虑准确性、有效率及计算时间3方面,以实验1结果为参考,选取表现较好且模型复杂度适中的算法及参数设置作为基学习器。因支持向量机是一种比较稳定的学习算法,直接集成效果不佳,故基学习器均选取不同复杂度的神经网络算法。其中,Sample50因样本量较少且R2呈递增趋势,故选取4种隐藏层结构依次进行集成。具体学习器设置及集成学习参数如表 9所示。
| 表 9 集成学习参数设置 Table 9 The parameter settings of ensemble learning |
实验2算法R2如图 10~图 13所示,计算时间如表 10~表 11所示,算法有效性如表 12~表 13所示。通过对实验2结果进行分析,可得到以下结论:
|
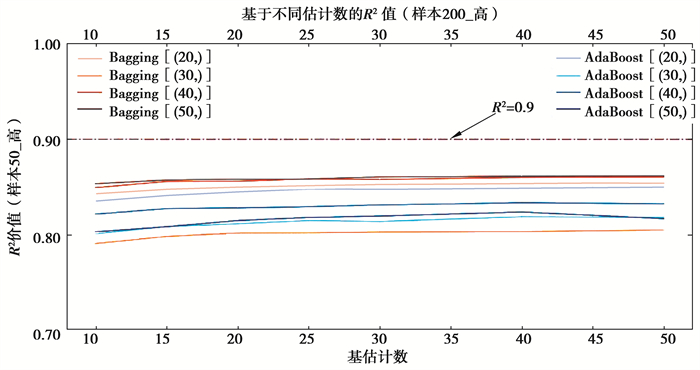
图 10 Sample50_low集成学习决定系数 Fig. 10 The R2 of Sample50_low |
|
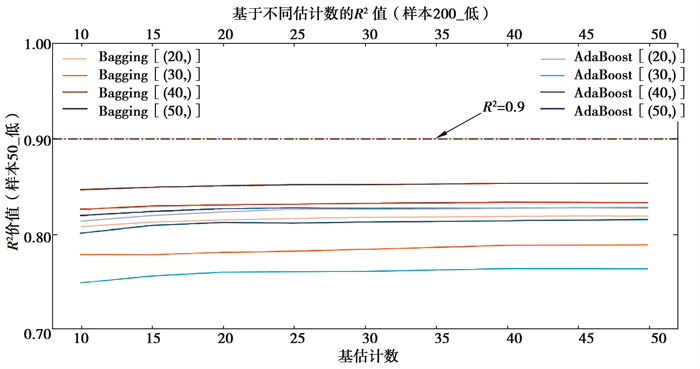
图 11 Sample50_med集成学习决定系数 Fig. 11 The R2 of Sample50_med |
|
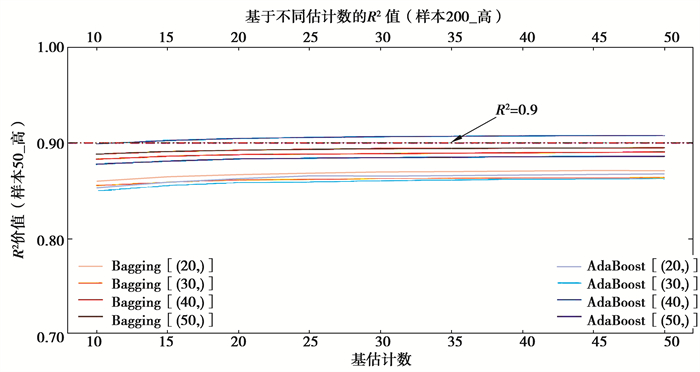
图 12 Sample50_high集成算法决定系数 Fig. 12 The R2 of Sample50_high |
|
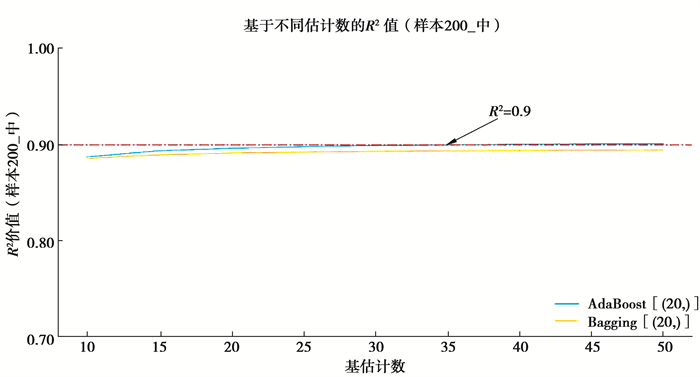
图 13 Sample200_med集成算法决定系数 Fig. 13 The R2 of Sample200_med |
| 表 10 Sample50集成算法计算时间 Table 10 The computation time of ensemble learning for Sample50 |
| 表 11 Sample200集成算法计算时间 Table 11 The computation time of ensemble learning for Sample200 |
| 表 12 Sample50集成算法结果有效率 Table 12 The available ratio of ensemble learning for Sample50 |
| 表 13 Sample200_med集成算法结果有效率 Table 13 The available ratio of ensemble learning for Sample200_med |
1) 在拟合效果方面,对于Sample50的三类样本集,由于基学习器学习效果较差,经集成之后,绝大多数集成学习器仍未达到优秀标准,仅在高覆盖性样本集中,以隐藏层结构为(40, )的BP神经网络学习器作为基学习器时,R2可达到0.9以上。但在各类覆盖性中,均有集成学习器R2可达到0.85以上,达到回归学习器可使用的基本要求。在Sample200_med样本集中,当AdaBoost算法的集成规模达到40时,R2达到0.9;
2) 在基学习器方面,基学习器的拟合效果与最终集成后的拟合效果并不完全成正相关关系。因为基学习器的复杂度过高,导致其泛化能力较弱,在集成时生成的个体学习器差异度较小,从而影响其拟合效果;
3) 在集成规模方面,当集成规模达到一定数值之后,继续增大集成规模并不会明显提升集成效果,甚至会减弱拟合效果(如图 7中AdaBoost[(50, )]);
4) 在计算时间方面,随着集成规模的扩大,时间成本逐渐增高。计算时间受样本量影响较大,当样本量增加时,时间成本明显提高。综合考虑,在设定集成规模时,应适中为宜。
综合实验结果,样本量为50时无法保证在大多数情况下达到较优学习效果,但R2可以达到0.85以上,已达到可用标准,若建筑师无充足时间且对预测精度要求较低时,可使用样本量为50的样本集。样本量为200时,全部覆盖度可以保证0.9以上的R2,耗时在可接受范围内,为较理想的样本量。样本量为500时,仅使用传统机器学习算法就可以达到极好的学习效果,R2可达0.95以上,学习用时较短,但其生成样本集时间成本巨大,若建筑师有充足的时间且对预测精度有极高要求,可采用该样本集。针对不同质量样本集的学习方法及参数设置建议及其学习效果如表 14所示。
| 表 14 不同质量样本集的学习方法选择与参数设置建议 Table 14 The suggestions on algorithm selection and parameter setting for different quality of sample sets |
文中基于样本量及样本分布特征对样本集质量进行评价与分类,针对不同质量样本集构建了建筑能耗预测模型,分析样本量与样本分布特征对机器学习算法学习性能的影响,得到以下结论:
1) 样本量及样本覆盖性对机器学习算法的学习性能有影响,其中,样本量的影响程度大于样本覆盖性。对于某一种机器学习算法,在相同样本量的情况下,不同覆盖性样本集的学习效果随参数变化的趋势相同。对于不同算法,在同样本量情况下,样本覆盖性对学习效果的影响有所不同。因此,样本覆盖性与算法的学习效果并不始终成正相关关系,而是与样本量及选择的学习算法有关。
2) 当样本量越大时,学习效果对学习算法及参数设置的敏感性越低,各算法及参数设置之间的学习效果差异减小。虽样本量越大学习效果越佳,但时间成本亦随之增加(其主要增加量来自于生成样本所需的模拟计算时间),针对本案例,当样本量为200时,无论覆盖性如何,均足以取得较优的学习效果。
3) 集成学习对拟合效果的提升较为明显,当其集成规模达到一定程度后,继续扩大集成规模,时间成本增量较大,但其拟合效果提升较小。
在实际设计应用中,需根据特定问题选择适宜的算法进行求解。文中提出了针对各类质量样本集的适用算法及其参数设置,为建筑师实际使用提供了参考。在未来研究中,将继续研究样本集质量及其余超参数与学习效果的关系,建立自适应的机器学习算法集并将其集成至优化算法中,进一步提高建筑节能优化效率。
| [1] |
中国城市科学研究会. 中国绿色建筑2017[M]. 北京: 中国建筑工业出版社, 2017. Chinese Society for Urban Studies. China green building2017[M]. Beijing: China Architecture & Building Press, 2017. (in Chinese) |
| [2] |
李紫微, 林波荣, 陈洪钟. 建筑方案能耗快速预测方法研究综述[J]. 暖通空调, 2018, 48(5): 1-8. Li Z W, Lin B R, Chen H Z. Review of rapid prediction method of building energy consumption[J]. Journal of HV&AC, 2018, 48(5): 1-8. (in Chinese) |
| [3] |
Machairas V, Tsangrassoulis A, Axarli K. Algorithms for optimization of building design: A review[J]. Renewable and Sustainable Energy Reviews, 2014, 31: 101-112. DOI:10.1016/j.rser.2013.11.036 |
| [4] |
Wang D, Tan D, Liu L. Particle swarm optimization algorithm: an overview[J]. Soft Computing, 2018, 22(2): 387-408. DOI:10.1007/s00500-016-2474-6 |
| [5] |
Yang C F, Li H J, Rezgui Y, et al. High throughput computing based distributed genetic algorithm for building energy consumption optimization[J]. Energy and Buildings, 2014, 76: 92-101. |
| [6] |
Tuhus-dubrow D, Krarti M. Genetic-algorithm based approach to optimize building envelope design for residential buildings[J]. Building and Environment, 2010, 45(7): 1574-1581. DOI:10.1016/j.buildenv.2010.01.005 |
| [7] |
Carvalho A M D, Prati r C. Improving kNN classification under unbalanced data. A New Geometric Oversampling Approach[J]. 2018, 1-6.
|
| [8] |
Sadrawi M, Sun W Z, Ma h M, et al. Ensemble genetic fuzzy neuro model applied for the emergency medical service via unbalanced data evaluation[J]. Symmetry, 2018, 10(3): 71. DOI:10.3390/sym10030071 |
| [9] |
陈圣灵, 沈思淇, 李东升. 基于样本权重更新的不平衡数据集成学习方法[J]. 计算机科学, 2018, 45(7): 31-37. Chen S L, Shen S Q, Li D S. Ensemble learning method for imbalanced data based on sample weight updating[J]. Computer Science, 2018, 45(7): 31-37. (in Chinese) |
| [10] |
蒋林, 陈涛, 屈梁生. 训练样本质量对人工神经网络性能的影响[J]. 中国机械工程, 1997(2): 123. Jiang L, Chen T, Qu L S. The effect of training sample quality on the performance of artificial neural networks[J]. China Mechanical Engineering, 1997(2): 123. (in Chinese) |
| [11] |
Tharwat A, Hassanien A E, Elnaghi B E. A BA-based algorithm for parameter optimization of Support Vector Machine[J]. Pattern Recognition Letters, 2017, 93: 13-22. DOI:10.1016/j.patrec.2016.10.007 |
| [12] |
Wu C, Tzeng G, Lin R. A Novel hybrid genetic algorithm for kernel function and parameter optimization in support vector regression[J]. Expert Systems with Applications, 2009, 36(3): 4725-4735. DOI:10.1016/j.eswa.2008.06.046 |
| [13] |
Ding S, Su C, Yu J. An optimizing BP neural network algorithm based on genetic algorithm[J]. Artificial Intelligence Review, 2011, 36(2): 153-162. DOI:10.1007/s10462-011-9208-z |
| [14] |
Ren C, An N, Wang J, et al. Optimal parameters selection for BP neural network based on particle swarm optimization: A case study of wind speed forecasting[J]. Knowledge-Based Systems, 2014, 56: 226-239. DOI:10.1016/j.knosys.2013.11.015 |
| [15] |
Vapnik V N. Support vector method for function approximation, regression estimation, and signal processing[J]. Advanced Neural Information Processing System, 1996, 9(6): 281-287. |
| [16] |
Zhao H, Magoulès F. A review on the prediction of building energy consumption[J]. Renewable and Sustainable Energy Reviews, 2012, 16(6): 3586-3592. DOI:10.1016/j.rser.2012.02.049 |
| [17] |
Gu B, Sheng V S, Wang Z, et al. Incremental learning for ν-Support vector regression[J]. Neural Networks, 2015, 67: 140-150. DOI:10.1016/j.neunet.2015.03.013 |
| [18] |
Ahmad A S, Hassan m Y, Abdullah M P, et al. A review on applications of ANN and SVM for building electrical energy consumption forecasting[J]. Renewable and Sustainable Energy Reviews, 2014, 33: 102-109. DOI:10.1016/j.rser.2014.01.069 |
| [19] |
Dong B, Cao C, Lee S E. Applying support vector machines to predict building energy consumption in tropical region[J]. Energy and Buildings, 2005, 37(5): 545-553. DOI:10.1016/j.enbuild.2004.09.009 |
| [20] |
Chou J, Bui D. Modeling heating and cooling loads by artificial intelligence for energy-efficient building design[J]. Energy and Buildings, 2014, 82: 437-446. DOI:10.1016/j.enbuild.2014.07.036 |
| [21] |
Zhong H, Wang J, Jia H, et al. Vector field-based support vector regression for building energy consumption prediction[J]. Applied Energy, 2019, 242: 403-414. DOI:10.1016/j.apenergy.2019.03.078 |
| [22] |
刘彩红. BP神经网络学习算法的研究[D]. 重庆: 重庆师范大学, 2008. Liu C H. The study of algorithm of BP neural network[D]. Chongqing: Chongqing Normal University, 2008. (in Chinese) |
| [23] |
Chen K, Jiang J, Zheng F, et al. A novel data-driven approach for residential electricity consumption prediction based on ensemble learning[J]. Energy, 2018, 150: 49-60. DOI:10.1016/j.energy.2018.02.028 |
| [24] |
Wang Z, Wang Y, Srinivasan R S. A novel ensemble learning approach to support building energy use prediction[J]. Energy and Buildings, 2018, 159: 109-122. DOI:10.1016/j.enbuild.2017.10.085 |
| [25] |
Papadopoulos S A E W W. Evaluation of tree-based ensemble learning algorithms for building energy performance estimation[J]. Journal of Building Performance Simulation, 2017, 11(3): 322-332. |
| [26] |
王永明. 集成回归问题若干关键技术研究[D]. 上海: 华东师范大学, 2015. Wang Y M. Research on some key technologies in ensemble regression problem[D]. Shanghai: East China Normal University, 2015. (in Chinese) |
| [27] |
Bauer E K R. An empirical comparison of voting classification algorithms: bagging, boosting, and variants[J]. Mach Learn, 1999, 36(1-2): 105-139. |
| [28] |
梁礼明, 冯新刚, 陈云嫩, 等. 基于样本分布特征的核函数选择方法研究[J]. 计算机仿真, 2013, 30(1): 323-328. Lang L M, Feng X G, Chen Y N, et al. , Method of selection kernel function based on distribution characteristics of samples[J]. Computer Simulation, 2013, 30(1): 323-328. (in Chinese) DOI:10.3969/j.issn.1006-9348.2013.01.075 |
| [29] |
Zhou Z H W J X T. Ensembling neural networks: Many could be better than all[J]. Artif Intell, 2002, 137(1/2): 239-263. |
 2022, Vol. 45
2022, Vol. 45


