2. 重庆大学 土木工程学院, 重庆 400045
2. School of Civil Engineering, Chongqing University, Chongqing 400045, P. R. China
施工栈桥作为跨江、跨海桥梁主体施工期间重要的临时辅助设施,其结构安全直接影响桥梁主体的正常施工和安全。实践表明,往来栈桥附近的船舶引起的波浪在一定条件下会迫使栈桥产生较大振动,影响施工安全甚至造成栈桥损伤,埋下一定安全隐患。为保证栈桥安全,亟待展开船行波下栈桥动力响应特性分析,制定具有针对性的控制措施。在船行波理论及模拟方面,王新宇等[1]基于三维势流理论,针对无限水深情况,通过Rankine源高阶面元法求解非线性船行波的波高;Abbasnia等[2]基于势能数值拖曳槽和非均匀有理B样条曲线进行全非线性和线性船舶波浪的建模[2];在船行波对船只及结构作用求解方面,主要围绕CFD数值模拟或试验展开研究[3-9],例如,石博文等[3]采用CFD方法分析了船舶在骑浪状态下的稳性损失;赵文宾等[4]借助FLOW-3D三维数值模拟软件模拟渡槽建成后的船行波、流场分布情况,对渡槽内船行波分布规律及消能设施效果展开研究;徐博等[5]基于RANS方程,模拟分析波浪对跨海桥梁高桩承台的冲击作用;李志松等[6]基于RANS方程、RNG k-ε湍流模型建立数值波浪水池,用VOF法追踪自由面的位置,并模拟内河航道中船行波的生成、传播、爬高和岸壁反射过程,对数值模型的有效性进行验证;姜辉等[8]通过实测船行波的特征参数,结合数值模拟波浪水槽仿真桥墩所受波浪力,分析了桥墩在波浪下的动力特性。上述方法具有较高的计算精度,但计算较复杂且耗时较多,特别是在水位大幅波动情况下,需根据不同工况建立不同模型,不便于工程实际应用。目前,专门针对船行波作用下施工栈桥动力响应分析的研究较少,文中以郑万高铁某特大桥施工栈桥为例,按照线性波理论简化波浪荷载,采用附加质量与附加阻尼比简化考虑流固耦合效应,在分析不同船速、船型、水深情况下,船行波对施工栈桥动力响应的影响,根据响应特性制定相应的处治措施,为保障栈桥结构安全提供技术参考。
1 工程概况郑万高铁某特大桥的施工栈桥主体部分跨径组合为6 m+3 m×9 m+6 m,其支桥跨径组合为6×6.3 m,桥面宽9.0 m。栈桥下部结构为φ1 000 mm×12 mm钢管桩,钢管桩最长为65.0 m,入岩最大深度为5 m。单排设置2根钢管桩,钢管桩横向间距6.3 m,并采用φ630 mm×10 mm钢管连成整体,桩顶设置双拼I40b作为横梁。上部结构采用贝雷梁,布于横梁上,横向间距90.0 cm、45.0 cm,梁上铺设I20b分配梁,间距352.5 mm,其上铺设10 mm厚花纹钢板作为桥面。栈桥布置如图 1所示。

|
图 1 施工栈桥主桥立面布置图(单位:m) Fig. 1 Elevation of Main Bridge of Construction Trestle (unit: m) |
为研究船行波对施工栈桥动力特性的影响,需明确船行波荷载大小,进而分析栈桥的动力响应。通过调研及施工现场的长期观察,发现该栈桥所处河流段内的船型相差不大,主要为客船和驳船,故仅针对客船和驳船两种船型作用下船行波荷载进行分析,为简化计算,采用线性波理论确定波浪荷载。
2.1 船行波波高船行波荷载的大小与船行波波高有较大关系。根据文献[10-11]的研究以及文献[14]的实际测量,在内河深水条件下,库斯科公式所得船行波参数与实际测量船行波参数有较好的吻合度,即船行波波高Hm为
| $ \left\{\begin{array}{c} H_{m}=0.55 \sqrt{\frac{20}{B^{\prime}}} \sqrt{\frac{R v}{2 g}}, \\ R=\frac{24 \rho V^{2} v}{L^{3} d} \sqrt{\frac{g}{d}}, \end{array}\right. $ | (1) |
式中:v为船舶与水的相对速度;B′为船舶离岸距离;g为重力加速度;ρ为水的密度;R为船舶兴波阻尼;V为船舶排水量;L为船舶长度;d为航道水深。
2.2 船行波波长与周期船行波的波长和周期对船行波荷载有较大影响,在确定船行波荷载之前需对波长和周期进行计算。船行波分为散波和横波,在深水条件下,影响结构动力特性的主要是散波,其扩散方向不受航速影响,在长距扩散过程中,能量衰减较少,且移动方向总是垂直于波峰线[3]。因依托栈桥工程的桩长达60 m,河流水位较深,故主要考虑散波对栈桥结构的影响。
根据OCDI经验公式[12],在水位较深情况下可得到横波的波长L0:
| $ L_{0}=T_{0} v=\frac{2 \pi}{g} v^{2}, $ | (2) |
式中: T0为横波周期。在此基础上,可得到对应散波的波长Ld和周期Td为
| $ \left\{\begin{array}{l} L_{\mathrm{d}}=L_{0} \cos ^{2} \theta, \\ T_{\mathrm{d}}=T_{0} \cos ^{2} \theta, \end{array}\right. $ | (3) |
式中: θ为凯尔文角,文献[14]建议一般情况下取19.467°。
2.3 船行波荷载根据《港口与航道水文规范》(JTS145—2015),采用Morison公式计算栈桥钢管桩波浪压力分布[13]。由于钢管桩相互之间的中心距大于4倍桩径,可忽略波浪力之间的相互干扰,无需考虑群桩效应。作用于某一高度柱体全断面上的等效波浪力分布p为
| $ p=p_{\mathrm{d}}+p_{\mathrm{I}}, $ | (4) |
其中:
| $ \left\{\begin{array}{l} p_{\mathrm{d}}=\frac{\gamma}{2 g} C_{\mathrm{D}} D_{\mathrm{Z}} u|u|, \\ p_{1}=\frac{\gamma}{g} C_{\mathrm{M}} A \frac{\partial u}{\partial t}, \\ u=\frac{\pi H}{T_{\mathrm{d}}} \frac{{ch} \frac{2 \pi z}{L_{\mathrm{d}}}}{{sh} \frac{2 \pi h}{L_{\mathrm{d}}} }\cos \omega t, \\ \frac{\partial u}{\partial t}=-\frac{2 \pi^{2} H}{T_{\mathrm{d}}^{2}} \frac{{ch} \frac{2 \pi z}{L_{\mathrm{d}}}}{{sh} \frac{2 \pi h}{L_{\mathrm{d}}}} \cos \omega t, \end{array}\right. $ | (5) |
式中: pd为波浪力速度分力;pI为波浪力惯性分力;γ为水重度;DZ为桩体直径;A为桩体断面面积;u为水质点轨道运动水平速度;H为钢管桩处船行波波高;z为计算点在水底面以上的高度;ω为波浪运动圆频率;CD为速度力系数; CM为惯性力系数。以上各系数具体取值可由《港口与航道水文规范》(JTS145—2015)确定。
2.4 客船、驳船船行波荷载计算经现场统计观测和调研,以栈桥所在河段内行驶客船、驳船最不利尺寸考虑船行波对钢管桩的荷载。客船长度L取16.3 m,满载排水量取11.60 t,最大船速取30 km/h;驳船长度L取65.0 m,满载排水量取987 t,最高船速取12 km/h。鉴于船行波作用影响时间较短,假设所有船只仅从河中央附近通行,每次只有1艘且只有1种船型通过航道。由式(1)~式(3)可得不同船型、不同船速下船行波的计算参数,如表 1、表 2所示。
| 表 1 客船在不同船速下船行波参数表 Table 1 Parameters of Ship-Induced Waves at Different Speeds |
| 表 2 驳船在不同船速下船行波参数表 Table 2 Parameters of Barge-Induced Waves at Different Speeds |
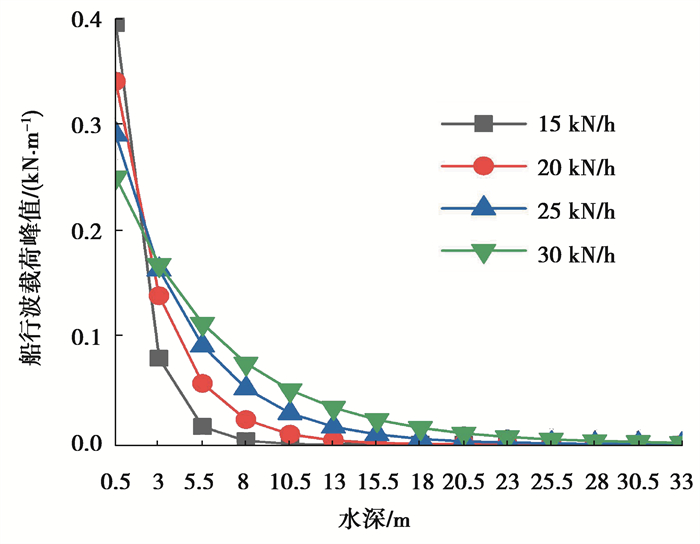
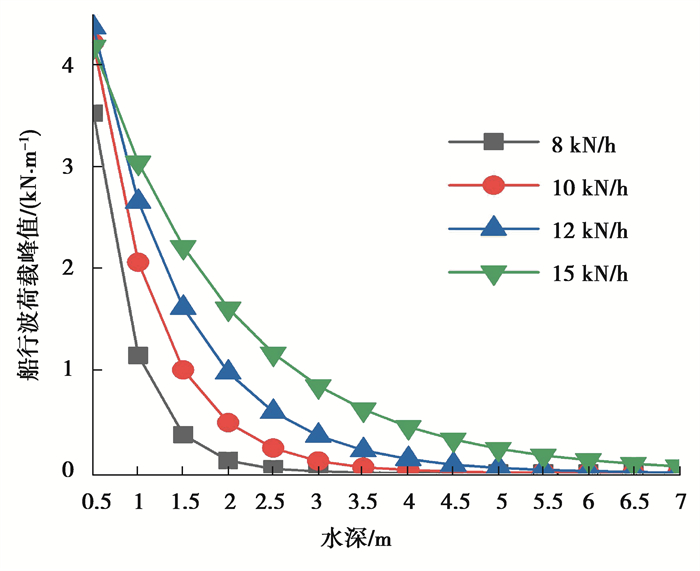
从表 1、表 2可知,船速越高,所产生的波高越大,波长越长,频率越小;驳船的排水量较大,所产生的波浪作用总体较大。采用式(4)~式(5),分别计算客船、驳船在不同行驶速度下的船行波荷载峰值如图 2、图 3所示。以30 km/h速度下客船为例,钢管桩波浪力的速度分力、惯性力分力, 如表 3所示。
|
图 2 客船在不同船速下行波荷载沿深度变化 Fig. 2 Variation of Wave Load along Depth for Ships with Different Velocities |
|
图 3 驳船在不同船速下船行波荷载沿深度变化 Fig. 3 Variation of Wave Load along Depth for Barges with Different Velocities |
| 表 3 不同水深的船行波荷载值 Table 3 Variation of Wave Load along Depth of Ship |
由图可知,船行波荷载峰值随水深增大而迅速减小;船速越小,荷载峰值变化越剧烈,其荷载峰值及辐射深度减小得越快,荷载总体趋势表现为随着船速的降低而减小。由于排水量大,驳船所产生的船行波的荷载峰值较大。
由表 3可知,船行波波浪力的惯性分力pI远大于速度分力pd,说明惯性力分力pI起主要影响作用,根据公式(5)可知,由于船行波的水质点轨道运动的水平速度u对pd的影响更大,而船行波所引起的u却较小,从而导致速度分力pd较小。
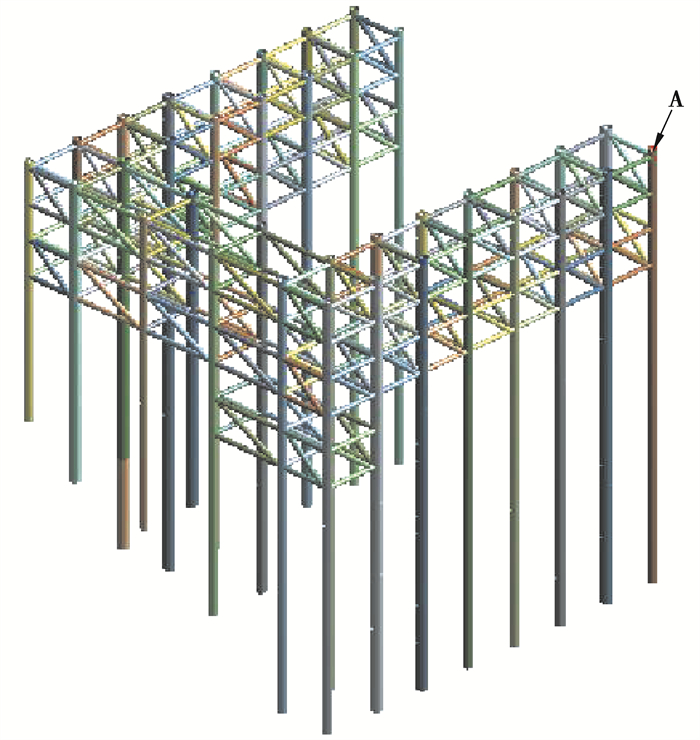
3 栈桥结构动力特性分析 3.1 有限元模型的建立船行波往往仅作用在栈桥下部的钢管桩上,故仅建立钢管桩体系的模型,栈桥上部的横梁、贝雷梁和桥面板简化为质量直接作用在钢管桩顶部。采用梁单元,根据设计图纸建立钢管桩体系有限元模型,模型划分34 239个节点,17 268个单元。因钢管桩嵌入岩层较深,且混凝土锚固桩的混凝土浇筑质量较好,将钢管桩底部近似看作固接;因上部有贝雷梁的限制作用,在钢管桩顶端限制其发生转角位移;钢管桩与横向支撑之间采用固接。建立的有限元模型如图 4所示。
|
图 4 栈桥有限元模型 Fig. 4 Finite element model of trestle |
根据附加质量原理可知,水中结构做变速运动时,受到水体质量的影响,其作用相当于在结构上附加一部分质量,如公式(6)所示:
| $ F=\left(m+m_{a}\right) a, $ | (6) |
式中:F为外力;m为结构质量;ma为附加质量;a为结构加速度。
水体对结构的作用将导致结构自振频率下降。而当前流固耦合的数值模拟较为复杂,结构频率会随着水深的变化而变化,工程在栈桥使用期间,河水的水位发生较大变动,流固耦合方法不便于在该类工程中应用。因此,将水对钢管桩的影响考虑为附加于浸水部分桩体上的分布质量。根据文献[16]的研究,对于圆筒结构,其附加质量的经验公式为
| $ m_{\mathrm{a}}=\frac{C_{a m} \rho \pi D_{\mathrm{c}}^{2} L_{\mathrm{c}}}{4}, $ | (7) |
式中:Dc为钢管桩截面外径;Lc为圆筒的长度。系数Cam为1.9,由实验数据得到[16]。
阻尼对结构动力响应的影响较大,因钢管桩入水的深度较大,需同时考虑钢管桩结构阻尼和水对钢管桩的阻尼作用。文献[17]表明,水体引起的阻尼作用可视为等效外阻尼比,与结构内阻尼比线性叠加,从而确定结构在水中的总阻尼比。在计算中,根据舒适度验算要求,栈桥结构内阻尼比取为0.015,水体引起的阻尼比根据文献[17]所给曲线,针对不同水深进行选取,对于圆筒钢管桩,水体引起的阻尼比取值宜为0.003 5~0.007 5。栈桥使用期间,河水水位将发生较大变动,需考虑不同水位深度波浪力作用下栈桥结构动力响应的变化。根据栈桥所处河道情况,主要考虑3种典型水位条件,如表 4所示,不同水位高度与栈桥高度的关系如图 1所示。为简化计算,将栈桥全桥进行节段划分,并根据第2节推导的荷载计算方法,计算每个单元的波浪荷载。假定相邻节点间的波浪荷载为线性分布,将各单元的波浪荷载分别施加在模型上,再对栈桥动力响应进行分析。结合舒适度与实际施工需求,在船行波作用下栈桥响应最大位移不应超过1 cm,最大加速度不应超过0.1 m/s2。
| 表 4 不同水位工况 Table 4 Different Water Level Conditions |
根据所建立的有限元模型及船行波荷载,采用谐响应分析,提取对应频率下栈桥的动力响应进行讨论。分析不同施工水位状态下,不同客船行驶速度产生船行波对栈桥的动力响应,结果表明,栈桥最大位移和最大加速度均发生在桩长最大且靠近河道的钢管柱顶端,如图 4中A点所示。该点的动力响应结果如表 5所示。
| 表 5 客船船行波作用下施工栈桥动力响应 Table 5 Dynamic Response of Construction Trestle under Ship-Induced Waves |
由表 5可知,栈桥顺桥向最大位移与最大加速均出现在船行速度为20 km/h时,对应的船行波频率为0.316 Hz,与结构第一自振频率0.327 Hz较接近,易发生共振现象,故栈桥结构将产生较大的位移或加速度;当船速加快后,船行波频率将远离结构自振频率,结构的动力响应也相应减小。为此,需对船行速度进行限制,避免栈桥结构出现共振。因船速高于15 km/h时,栈桥结构的最大位移超过了1 cm的限值,仅针对船行速度为15 km/h时,不同水位条件下栈桥结构的动力响应进行分析,其结果如表 6所示。
| 表 6 不同水位下船行波作用栈桥动力响应 Table 6 Dynamic Response of Trestle under Ship-Induced Waves at Different Water Levels |
由表可知在最低水位时,结构自振频率为0.383 Hz,波浪力频率为0.421 Hz,两者的频率较接近,此时的响应大于其他水位条件下的动力响应。在最高水位时,结构频率降低,与波浪力频率相差更远,此时,荷载作用位置上移以及受力面积增大,但结构响应增加程度却不大。因此,不同船速导致船行波频率改变对栈桥产生的作用远大于不同水位高度产生的作用。
通过上述分析可得,为保证栈桥结构在主桥施工期间的安全,综合考虑对位移与加速度的限制,应限制客船等小型船只的船行速度在15 km/h以下。
3.3 驳船动力响应分析分析常规施工水位条件下,不同驳船行驶速度产生的船行波对栈桥动力响应的影响。与客船规律相同,驳船行驶下最大位移和加速度发生在图 4中的A点处,其位移和加速度如表 7所示。
| 表 7 驳船船行波作用下施工栈桥动力响应 Table 7 Dynamic Response of Construction Trestle under Barge-Induced Waves |
由表可知,当船速增加时,栈桥结构最大位移和最大加速度均增加,且增加速度较快。因此,对此类大型船只船行速度的控制应更加严格。由图 2、图 3可知,相对于客船,驳船所产生的船行波荷载较大,因此在船速较低的时候也有较大响应。船速在15 km/h以下时,船行波所能影响水位深度较浅,并且船速降低时,对应荷载峰值将大幅减小,影响深度也将进一步减小,在降低船速的时候栈桥的响应迅速减小。结合表 7结果,为保证施工安全,驳船的航行速度应限制在10 km/h以下。
4 参数影响分析 4.1 附加质量的影响为验证文中所采用的附件质量简化方法的准确性,针对文献[16]中的圆柱桩模型试验条件建立考虑附加质量的模型,进行结构频率分析,并与文献[17]所给FSI边界流固耦合模型的计算结果及文献[16]实验所得数据进行对比,如表 8所示。
| 表 8 不同方案结构频率对比 Table 8 Frequency Comparison of Different Schemes |
由表 8计算结果可知,水深越小,附加质量简化方法和流固耦合计算方法所得结果与试验结果越接近。在所有水深条件下,附加质量简化算方法计算结果与试验结果较为接近,误差在10%以内,与精细化的数值耦合计算方法结果的误差小于3.5%,基本满足工程应用精度的实际要求。
采用附加质量法计算不同水位条件下栈桥自振频率如表 9所示。
| 表 9 不同工况下结构的自振频率 Table 9 Natural Frequency of Structures under Different Working Conditions |
由表 9可知,水位高度对结构自振频率影响较大,随着水位的上升,结构自振频率下降;最高水位与不考虑水体影响情况下自振频率将降低47.2%,必须重视水位高度对结构频率的影响。
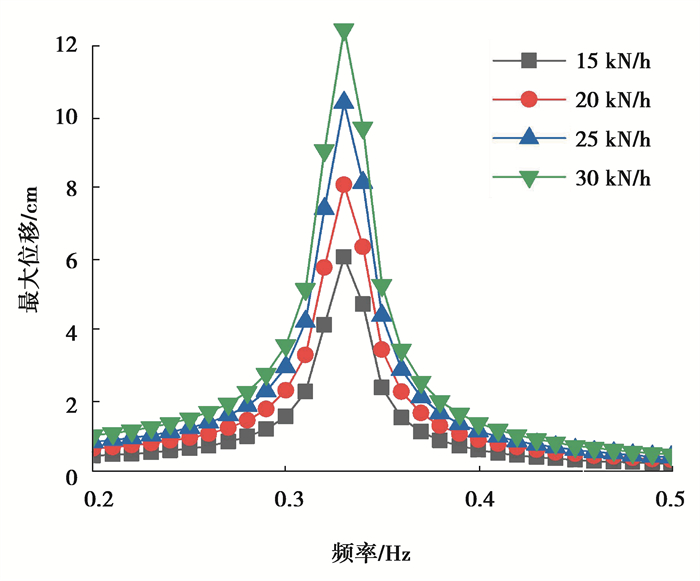
4.2 船行波频率的影响因客船这类中小型船产生波浪力的频率可能与结构自振频率相近,此时结构的动力响应将急剧增加,通过谐响应分析,得到不同频率下栈桥结构最大位移响应如图 5所示。
|
图 5 不同波浪频率下栈桥最大位移 Fig. 5 Maximum Displacement of Trestle under Different Wave Frequencies |
由图 5可知,当波浪力频率接近结构自振频率时,结构的位移响应急剧增大;而波浪力频率远离结构自振频率时,位移响应均较小。根据结构动力学原理,取栈桥基频的±15%为共振区,当波浪力频率在共振区以外时,由于客船船行波荷载值较小,由船只造成的结构位移响应的变化不大。若船只速度限制在15km/h以内,可保证栈桥结构不发生共振,从而预防栈桥发生过大变形。
4.3 阻尼比取值的影响以客船船速为15 km/h为例,分析考虑和不考虑水体附加阻尼时,船行波对结构动力响应的影响,结果如表 10和表 11所示。
| 表 10 水体附加阻尼引起最大位移 Table 10 Maximum Displacement Response Induced by Water Damping |
| 表 11 水体附加阻尼引起最大加速度 Table 11 Maximum Acceleration Response Induced by Water Damping |
由表 10和表 11可知,在水位较高时,水体附加阻尼对结构速度与加速度均有抑制作用,但其影响不大,在施工水位以下时无明显作用;在最高水位时,考虑与不考虑水体附加阻尼时位移和加速度的偏差均在4%以下。因此,针对船行波对结构的动力响应计算,不考虑水体引起附加阻尼对结构动力响应分析的影响不大,偏于安全。
5 结论文中针对郑万高铁某特大桥施工过程中的深水栈桥进行动力分析,基于线性波理论确定波浪荷载,通过采用附加质量与附加阻尼比简化考虑流固耦合作用,并分析不同水位、船速以及船只种类下钢管桩结构的动力响应,得到如下结论:
1) 水位对钢管桩结构体系自振频率的影响较大,水位上涨最大会使结构基频下降47.2%,此性质将左右结构动力响应和控制措施的制定;同时,水位上涨将增大结构总阻尼比,但对船行波作用下结构位移响应的影响在4%以内,从简化计算角度考虑,可忽略水体附加阻尼比的影响。
2) 对客船等中小型船只,船行速度变化范围较大,所产生的船行波频率范围涵盖了钢管桩结构基频,可能发生共振响应。为使船行波频率低于结构自振频率15%,当船只通过栈桥附近时,船速应限制在15 km/h以下。
3) 对驳船等大型船舶,钢管桩结构响应主要受船行波荷载大小控制,应限制船速降低对船行波荷载及影响深度。为使钢管桩位移响应小于1 cm,应控制大型船舶的船行速度在10 km/h以下。
| [1] |
王新宇, 朱仁传, 陈曦, 等. 高阶面元法求解非线性船行波问题[J]. 哈尔滨工程大学学报, 2018, 39(2): 229-235. Wang X Y, Zhu R C, Chen X, et al. A solution of ship waves with nonlinear free surface by high order panel method[J]. Journal of Harbin Engineering University, 2018, 39(2): 229-235. (in Chinese) |
| [2] |
Abbasnia A, Soares C G. Fully nonlinear and linear ship waves modelling using the potential numerical towing tank and NURBS[J]. Engineering Analysis With Boundary Elements, 2019, 103: 137-144. DOI:10.1016/j.enganabound.2019.03.009 |
| [3] |
石博文, 刘正江, 杨波. CFD方法的船舶骑浪稳性研究[J]. 哈尔滨工程大学学报, 2017, 38(7): 1035-1040. Shi B W, Liu Z J, Yang B. Study on the surf-riding stability of a vessel based on CFD[J]. Journal of Harbin Engineering University, 2017, 38(7): 1035-1040. (in Chinese) |
| [4] |
赵文宾, 管煜琼. 澜沧江某渡槽内船行波分布规律研究及消能设施效果研究[J]. 珠江水运, 2019(7): 110-111. Zhao W B, Guan Y Q. Study on the distribution law of ship traveling wave in an aqueduct of lancang river and the effect of energy dissipation facilities[J]. Pearl River Water Transport, 2019(7): 110-111. (in Chinese) |
| [5] |
徐博, 魏凯. 基于RANS的跨海桥梁高桩承台波浪作用数值模拟[J]. 铁道标准设计, 2019, 63(12): 79-84. Xu B, Wei K. Numerical simulation of wave forces on elevated pile cap of sea-crossing brid ges based on RANS[J]. Railway Standard Design, 2019, 63(12): 79-84. (in Chinese) |
| [6] |
李志松, 吴卫, 陈虹, 等. 内河航道中船行波在岸坡爬高的数值模拟[J]. 水动力学研究与进展(A辑), 2016, 31(5): 556-566. Li Z S, Wu W, Chen H, et al. Numerical simulation of run-up of ship waves on slope bank in channel[J]. Chinese Journal of Hydrodynamics, 2016, 31(5): 556-566. (in Chinese) |
| [7] |
陈虹, 吴少霖. 上海内河船行波研究[J]. 水运工程, 2017(11): 124-128. Chen H, Wu S L. Study on ship wave in the inland waterway of Shanghai[J]. Port & Waterway Engineering, 2017(11): 124-128. (in Chinese) |
| [8] |
姜辉, 马长飞, 王波. 刚构-连续梁组合桥悬臂施工阶段船行波动力响应分析[J]. 世界桥梁, 2017, 45(4): 61-65. Jiang H, Ma C F, Wang B. Analysis of ship moving undulation force during cantilever construction of combined rigid-frame and continuous beam bridge[J]. World Bridges, 2017, 45(4): 61-65. (in Chinese) |
| [9] |
陈星, 徐雪松. 船行波对系泊船的影响因素[J]. 水运工程, 2018(2): 25-28. Chen X, Xu X S. Influence factors of ship-generated waves on moored ships[J]. Port & Waterway Engineering, 2018(2): 25-28. (in Chinese) |
| [10] |
王亥索. 船行波对大型船舶与游艇组成的复式航道船舶间富裕宽度的影响[D]. 2011. Wang H S. Influence of ship traveling wave on the margin width between ships in the compound channel composed of large ships and yachts[D]. 2011. (in Chinese) |
| [11] |
高凯. 船舶兴波对船舶影响研究及其在受限水域中的应用[D]. 大连: 大连海事大学, 2004. Gao K. The research of vessel generated waves and it's application in restricted waters[D]. Dalian: Dalian Maritime University, 2004. (in Chinese) |
| [12] |
汪舟红, 韩国松. 船行波对系泊船的影响分析[J]. 水运工程, 2015(9): 28-34. Wang Z H, Han G S. Effect of ship wave on moored ship[J]. Port & Waterway Engineering, 2015(9): 28-34. (in Chinese) |
| [13] |
JTS 145—2015, 《港口与航道水文规范》[S]. 中华人民共和国交通运输部. 港口与航道水文规范: JTS 145—2015[S]. 北京: 人民交通出版社, 2016. JTS 145—2015, code for hydrology of ports and waterways[S]. Ministry of transport of the people's Republic of China Hydrological code for port and waterway: JTS 145—2015[S]. Beijing: People's Communications Press, 2016. (in Chinese) |
| [14] |
刘政伟, 夏齐勇. 船行波激励下深水桥墩的动力响应分析[J]. 桥梁建设, 2018, 48(3): 85-89. Liu Z W, Xia Q Y. Dynamic response analysis of bridge pier in deep water under excitation of ship-induced waves[J]. Bridge Construction, 2018, 48(3): 85-89. (in Chinese) |
| [15] |
张敏. 桥墩与河水流固耦合振动分析[D]. 大连: 大连交通大学, 2006. Zhang M. Vibration analysis of solid-fluid interaction for the pier-river water[D]. Dalian: Dalian Jiaotong University, 2006. (in Chinese) |
| [16] |
于肖宇, 张继革, 顾卫国, 等. 薄壁圆筒结构附加质量的实验研究[J]. 水动力学研究与进展A辑, 2010, 25(5): 655-659. Yu X Y, Zhang J G, Gu W G, et al. Experimental study of added mass of the thin-walled cylinder structure[J]. Chinese Journal of Hydrodynamics, 2010, 25(5): 655-659. (in Chinese) |
| [17] |
王元战, 王朝阳. 考虑流固耦合影响的水中桩基结构振动特性分析[J]. 水道港口, 2013, 34(1): 73-79. Wang Y Z, Wang Z Y. Vibration characteristics analysis for underwater pile foundation structure considering fluid-structure interation[J]. Journal of Waterway and Harbor, 2013, 34(1): 73-79. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45


