1b. 重庆医科大学 医学数据研究院, 重庆 400016;
2. 重庆科技学院 智能技术与工程学院, 重庆 401331
1b. Medical Data Science Academy, Chongqing Medical University, Chongqing 400016, P. R. China;
2. College of Intelligent Technology and Engineering, Chongqing University of Science and Technology, Chongqing 401331, P. R. China
高分辨率磁共振图像(MRI, magnetic resonance images)可以为医生提供更加丰富的病理信息,提高诊断可信度,在医疗诊断中极其重要。然而在MRI成像过程中,获取高分辨率的图像需要更长的扫描时间和更高的信噪比,但病人难以长时间保持静止不动。为了缩短扫描时间,通常采用方法是加大扫描层厚,但是这将会导致3D-MRI图像的分辨率降低,最终限制后期对图像的处理、分析和疾病的诊断。
超分辨率(SR, super resolution)重建是一种利用单幅或多幅低分辨率图像重建出高分辨率图像的技术。近年来,随着深度学习技术的发展,基于学习的SR重建算法取得了较好的效果。基于深度卷积神经网络(DCNN, deep convolutional neural network)的SR重建算法能够自动从数据中提取特征,可以构建更为抽象的特征表示,因此取代了手工提取特征和创建算法的传统机器学习方法以及其它浅层学习算法。Pham[1]和Srinivasan[2]等人将卷积神经网络(CNN, convolutional neural network)用于SR重建3D-MRI图像,取得了较理想的重建结果。为不断提高3D-MRI图像SR重建精度,研究者们提出了多种不同的网络结构。如Pham[1]等提出了3D残差卷积神经网络,对脑部3D-MRI图像进行多尺度SR重建;Chen[3]等人使用3D稠密网络(DenseNet)在K空间对3D-MRI图像进行SR重建,该算法可以实现特征复用,减少模型参数。然而,上述基于CNN的SR重建算法以提高峰值信噪比(PSNR, peak signal to noise ratio)为训练目标,但PSNR度量无法模拟人类的视觉机制,会导致SR结果过于平滑、细节模糊,具有重建精度低、感知质量差等缺点。近年来,生成对抗网络(GAN, generative adversarial network)的出现在一定程度上解决了上述问题,进一步提高图像SR重建结果的视觉感知质量。相比较于一般的CNN模型,GAN采用判别网络隐式地作为优化目标,能够在概率密度无法计算时逼近目标函数,生成与原始高分辨率图像几乎无法区分的、更加符合人眼视觉的真实图像,有着更强的生成能力和学习能力。随后,研究者们将GAN网络引入到了3D-MRI图像的SR重建研究中[4-5]。Chen[6]等人证明利用GAN网络SR重建3D-MRI图像可以获得更丰富的纹理细节信息。但目前利用GAN网络对3D-MRI图像进行SR重建的相关研究较少,其主要原因是MRI图像为3D数据,会导致GAN网络模型的参数量急剧增大,网络模型训练时间较长,对内存的需求也急剧增加。
将增强型超分辨率生成对抗网络(ESRGAN, enhanced super-resolution generative adversarial networks)[7]模型引入到3D-MRI图像的SR重建中,并采用视觉损失函数作为目标优化函数,从而使SR重建结果更符合人类视觉机制。此外,为了降低模型的复杂度,减少参数,加快模型训练的速度,利用3D-MRI图像的跨层面自相似性,将3D-MRI图像SR重建任务降维。
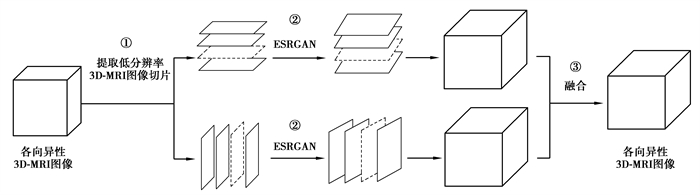
1 研究算法研究主要采用ESRGAN网络对3D-MRI图像进行SR重建,并利用3D-MRI图像的跨层面自相似性,将SR重建任务降维。算法的主要步骤如下图 1所示:
|
图 1 算法框架 Fig. 1 The algorithm framework of this paper |
① 提取低分辨率3D-MRI图像切片:分别沿层面选择方向提取各向异性3D-MRI图像的低分辨率二维切片图像,该过程可提取出2种尺寸的低分辨率图像。
② SR重建:将两组低分辨率二维切片分别输入ESRGAN网络,重建高分辨图像,以复原图像的细节信息,ESRGAN网络的具体结构将进行详细介绍。
③ 融合图像:分别将SR重建后的高分辨率图像按照切片的原索引位置还原,以产生3D-MRI图像,然后将产生的2幅三维图像融合,最终产生1幅各向同性高分辨率3D-MRI图像。
1.1 ESRGAN网络结构ESRGAN网络包含1个生成网络、1个鉴别网络。在不断提高判断能力的鉴别网络的持续反馈下,不断改善生成网络的生成参数,直到生成网络生成的结果能够通过鉴别网络的判断。
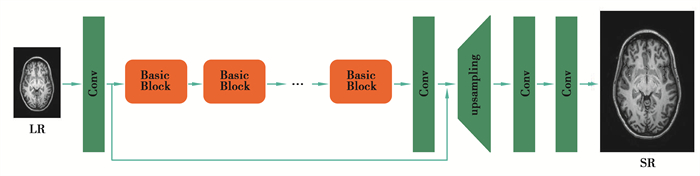
1.1.1 ESRGAN生成网络ESRGAN的生成网络部分仍然采用了SRResNet[8](如图 2所示)的基本网络架构,其中大部分计算是在LR特征空间中完成的。在LR特征空间进行计算,处理的数据量会较小,因此对计算量和显存消耗也较少,可以提高SR重建的速度。原始的SRResNet网络架构中包含16个基本残差块,每个残差块中包含2个3×3的卷积层,卷积层后接批量归一化层(BN, batch normalization)和参数化ReLU[9]作为激活函数,2个尺度为2的子像素卷积层(sub-pixel convolution layers)[10]用来增大特征图尺寸。使用的ESRGAN对其“Basic Block”进行了修改并取得了更好的性能。ESRGAN网络相较于SRGAN网络的主要改进有以下几个方面:
|
图 2 SRResNet结构(ESRGAN的生成网络) Fig. 2 The structure of Generative Network of ESRGAN |
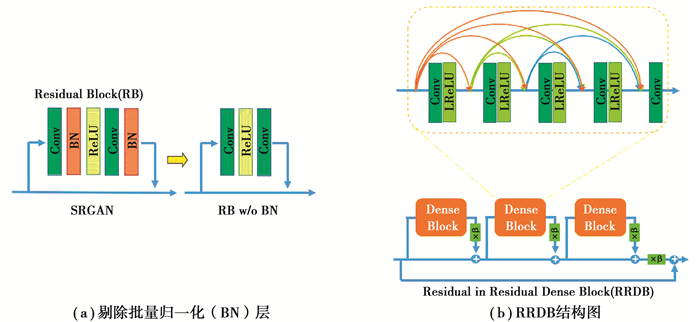
1) 剔除了生成网络中所有的BN层,如图 3(a)所示。研究发现,在不同的面向PSNR的任务中(包括SR和去模糊任务),去除BN层可以提高性能并降低计算复杂度。当训练数据集和测试数据集的统计差异很大时,BN层容易引入伪影,限制了模型的泛化能力,降低了模型的稳定性。因此,为了提高模型的稳定性和泛化能力,ESRGAN网络剔除了BN层,同时也可以降低计算复杂度和对内存的需求。
|
图 3 ESRGAN网络改进 Fig. 3 The improvement of Generative network of ESRGAN |
2) 使用RRDB(residual in residual dense block)替代了生成网络中的基本残差块[7]。RRDB比SRGAN中基本残差块的网络结构更深、更复杂。一般来说,增加网络结构的层数和连接数量可以有效地提高网络性能[11-13]。具体地,RRDB结合了多层残差网络和稠密连接,网络结构如图 3(b)所示。所提出的RRDB在残差结构中包含残差结构,即在不同层次使用残差结构。同时,RRDB引入稠密连接块,进一步提高了网络的性能。
1.1.2 ESRGAN鉴别网络ESRGAN采用相对鉴别网络[11-13]。SRGAN中的标准鉴别网络预测一个输入图像是真实和自然图像的概率;与SRGAN中的标准鉴别网络不同,相对鉴别网络试图预测真实图像xr相对比伪图像xf更真实的概率。在SRGAN中,标准鉴别网络被表示为
| $ D(x)=\sigma(C(x)), $ | (1) |
其中,σ是sigmoid函数,C(x)是非变换鉴别网络输出。因此,相对鉴别网络的公式为
| $ D_{R a}\left(x_{r}, x_{f}\right)=\sigma\left(C\left(x_{r}\right)-E_{x_{f}}\left[C\left(x_{f}\right)\right]\right), $ | (2) |
其中,Exf[C(xf)]代表小批量中所有假数据取平均值。由此,相对鉴别网络损失函数定义为
| $ L_{D}^{R a}=-E_{x_{r}}\left[\log \left(D_{R a}\left(x_{r}, x_{f}\right)\right)\right]-E_{x_{f}}\left[\log \left(1-D_{R a}\left(x_{f}, x_{r}\right)\right)\right], $ | (3) |
相应的生成网络的对抗损失函数定义为
| $ L_{D}^{R a}=-E_{x_{r}}\left[\log \left(1-D_{R a}\left(x_{r}, x_{f}\right)\right)\right]-E_{x_{f}}\left[\log \left(D_{R a}\left(x_{f}, x_{r}\right)\right)\right] 。$ | (4) |
因此,采用ESRGAN网络中的生成网络在对抗训练过程中能够同时利用生成数据和真实数据的梯度进行学习;而SRGAN网络中只有生成数据的梯度在对抗训练的过程中发挥作用。
1.2 基于视觉机制的损失函数基于更接近感知相似性的思想[14-16],Johnson[17]等人提出了感知损失Lpercep,并在SRGAN中进行了扩展。感知损失一般是定义在预先训练的深层网络的激活层上,由于特征通过激活层后会变得非常稀疏,而稀疏特征不利于模型的监督学习,会导致模型性能较差。因此,Wang[7]等人在ESRGAN模型中提出了一种更有效的感知损失计算方法,即利用激活层之前的特征计算感知损失,可以使重建后的图像有更锐利的边缘和丰富的纹理,提高图像的高频信息质量;同时使重建图像的亮度更接近真实图像。为进一步提高3D-MRI重建结果的视觉质量,使用基于视觉机制的损失函数,包含3个主要部分:感知损失、对抗损失和内容损失。损失函数的计算公式如下
| $ L_{\rm{G}}=L_{\text {percep }}+\lambda L_{G}^{R a}+\eta L_{1}, $ | (5) |
其中:L1是评估重建图像和真实图像之间的1范式距离内容损失;λ和η是平衡不同损失项的系数。
1.3 ESRGAN网络模型的训练由于3D-MRI图像是多参数、原生三维成像,图像自身具有丰富的先验信息,不同扫描层面的图像具有跨层面自相似性,根据上述3D-MRI图像的特性,构建了各向异性3D-MRI图像SR重建数据集。3D-MRI图像的跨层面自相似性指的是:在同一幅3D-MRI图像的不同层面的二维切片图像中,存在许多相同或不同尺度的相似性组织结构[18]。因此,针对原始高分辨率3D-MRI图像O,利用均值下采样,模拟生成3幅低分辨率各向异性3D-MRI图像,即横轴低分辨率3D-MRI图像A,冠状低分辨率3D-MRI图像C,矢状低分辨率3D-MRI图像S。再根据上述图像生成如下训练集合,即高、低分辨率图像对:图像O的冠状面与图像A的冠状面,图像O的矢状面与图像A的矢状面;图像O的横轴面与图像C的横轴面,图像O的矢状面与图像C的矢状面;图像O的横轴面与图像S的横轴面,图像O的冠状面与图像S的冠状面。该思路通过降维的方式扩大了训练集合的尺寸,如一幅高分辨率3D-MRI图像(图像尺寸170×256×256)可提取1 364幅2D-MRI层面作为训练集合。根据3D-MRI图像的跨层面自相似性,可以有效地扩大训练集规模,对于充分发挥DCNN的性能具有重要作用。使用不同层面方向的3D-MRI切片同时训练网络,可以使一个网络同时SR重建不同层面方向的3D-MRI图像切片,而不用分别针对不同层面选择方向训练不同的SR重建网络。此外,该方法还能利用3D-MRI图像中的三维特征信息,提升二维DCNN的SR重建性能。
2 实验结果及分析为了验证算法的有效性,分别与非局部均值法(NLM, Non-Local means)[19]、基于稀疏编码的SR重建算法(SC, sparse coding)[20]、基于DCNN的代表性方法SRCNN[21]和VDSR[22]算法、基于残差学习卷积神经网络的各向异性3D-MRI图像SR重建算法(RLSR, residual learning based super-resolution reconstruction algorithm)[23]做了对比分析。
2.1 实验设置与参数选择通过Python编程语言处理3D-MRI图像。主要硬件环境为搭载Intel Xeon CPU E5-2620 v4处理器、32 GB内存以及一块NVIDIA GTX2080Ti(11GB显存)显卡的图形工作站,模型训练和测试基于pytorch深度学习框架。模型训练中批样本数量为4,训练图像切块大小为128×128,初始学习率为0.000 1,且每迭代5 000次学习率减半,总迭代次数为400 000。学习率的初始值和衰减规律是根据实验经验设定,如此设定能使模型较快的稳定收敛。
2.2 数据集笔者采用公开的临床真实数据集Kirby 21数据集[24]中10幅(KKI33-KKI42)T1加权像3D-MRI图像生成训练集合,图像的分辨率为1×1×1.2 mm3,图像大小为170×256×256。研究使用含有胶质瘤的BraTS数据集[25]以及Brainweb[26]数据集对训练好的网络模型进行测试。其中,BraTS采用2015年公布的T1加权像和T2加权像进行测试,图像的分辨率为1×1×1 mm3,图像大小为240×240×155,该数据集为临床真实数据集;采用Brainweb数据集中的T1加权像进行测试,图像的分辨率为1×1×1 mm3,图像大小为181×217×181,该数据集为模拟数据集。
2.3 评价指标自Dong[21]等人提出SRCNN的开创性以来,DCNN方法迎来了蓬勃发展。各种网络结构的设计和训练策略不断地提高了SR的性能,特别是基于PSNR值优化训练的策略[13-22]。然而,这些面向PSNR的方法往往在没有足够高频细节的情况下输出过于平滑的结果,使得重建图像产生不必要的伪影,因为PSNR度量基本上不符合人类观察者的主观评估[23-27]。当重建图像达到一定质量以上时,PSNR值的提高并不能伴随视觉效果的提高。因此,PSNR评价与人类的主观评估不成正相关性。
近年来,图像SR领域出现了新的图像质量评价指标——感知指数(PI, perceptual index)[27]。研究发现相较于PSNR,PI能够更加符合人类视觉感知特征。PSNR值越大,就代表失真越少。然而,Blau[28]等人研究发现失真和感知质量是相互矛盾的。感知质量的判断依据是2个非参考性指标Ma’s score[29]和NIQE[29],即感知指数
| $ \mathrm{PI}=\frac{1}{2}((10- Ma )+\mathrm{NIQE})。$ | (6) |
因此采用PSNR、SSIM[30-31]、RMSE等常规评价指标评价重建结果,同时采用感知质数PI评价重建结果的感知质量。其中PSNR和SSIM的值越高,表明重建结果越好;RMSE和PI的值越低表明重建精度越高。
2.4 实验结果与讨论 2.4.1 定量分析1) 模拟数据集T1加权像重建结果
为了验证算法的SR重建效果,测试了ESRGAN算法在BrainWeb模拟数据集T1加权像的SR重建结果。通过预处理(均值下采样)BrainWeb数据集中T1加权像得到的各向异性低分辨率3D-MRI图像的分辨率为1 mm×1 mm×2 mm,由不同算法SR重建得到的3D-MRI图像的分辨率分别为1 mm×1 mm×1 mm,图像SR重建结果如表 1所示,最好的结果加粗显示。
| 表 1 不同方法重建BrainWeb T1w MRI图像的结果评估 Table 1 The results evaluation of different methods to reconstruct BrainWeb T1w MRI images |
从表 1中可以看出,算法SR重建BrainWeb数据集的T1加权3D-MRI图像时得到的PNSR/SSIM/RMSE/PI分别为41.8565dB/0.9946/2.1028/4.1683,它的PNSR值比NLM算法低1.624 9 dB,RMSE值比NLM算法高0.3587,PI的值则低0.3263。上述结果表明,算法虽在PSNR和RMSE指标上略差于传统基于重建的3D-MRI图像SR重建算法,但在PI上优于传统基于重建的3D-MRI图像SR重建算法。同样,对比基于浅层学习的SR重建算法(SP)以及其他的基于深度学习的SR重建算法(SRCNN、VDSR、RSLR),算法虽PSNR、SSIM以及RMSE值略差,但在PI上取得了最优。结果证明,重建图像的PI与PSNR、SSIM和RMSE等指标并不构成正向比例,而算法在保证图像质量的同时,更加注重图像高频细节的复原,更倾向于生成视觉感知效果更优的SR图像。
综上所述,算法在对BrainWeb数据集T1加权像的重建中,虽不能取得最佳的PSNR、SSIM以及RMSE值,但可以得到最佳的PI,使生成图像的视觉感知效果最好。
2) 临床数据集T1加权像重建结果
为进一步验证算法的SR重建效果,用了含有胶质瘤的BraTS数据集进行测试。通过预处理(均值下采样)BraTS数据集中T1加权像得到的各向异性的低分辨率3D-MRI图像的分辨率为1 mm×1 mm×2 mm,由不同算法SR重建得到的3D-MRI图像的分辨率分别为1 mm×1 mm×1 mm,SR重建结果如表 2所示,最好的结果加粗显示。
| 表 2 不同方法重建BraTS T1w MRI图像的结果评估 Table 2 The results evaluation of different methods to reconstruct BraTS T1w MRI images |
从表 2可以看出,算法SR重建BraTS数据集的T1加权3D-MRI图像时得到的PNSR/SSIM/RMSE/PI分别为45.320 1dB/0.995 6/5.397 4/5.419 3,它的PNSR值比NLM算法高0.753 1 dB,而RMSE和PI的值则分别低0.488 9和1.138 8。上述结果表明,研究算法在PSNR、RMSE和PI 3个指标上均优于传统基于重建的3D-MRI图像SR重建算法。与基于浅层学习的SR重建算法SP相比,算法的PSNR值提高了0.303 3 dB,而RMSE和PI的值则分别降低0.1922和0.4918,研究算法优于基于浅层学习的SP算法。在基于DCNN的3D-MRI图像SR重建算法中,算法在BraTS数据集的T1加权像上取得了最优的PI值。与SRCNN算法比较,PSNR提高了0.9424dB,而RMSE/PI降低了0.618 5/0.062 5,说明研究算法在PSNR、RMSE和PI 3个指标上均优于SRCNN算法。与VDSR和RLSR算法比较,PSNR分别降低了0.31 dB和0.289 4 dB,RMSE分别增加了0.189 2和0.176 8,PI分别降低了1.077 6和0.913 8,结果表明研究算法虽在PSNR和RMSE指标上略差于VDSR和RLSR,但在PI指标上仍然优于VDSR和RLSR重建算法。虽然算法在BraTS数据集T1加权像上的重建结果SSIM值较低,但与其他算法相差不大。
综上所述,研究算法在BraST数据集T1加权像的重建结果取得了最优的PI值;传统的基于DCNN的重建方法(RLSR,SRCNN,VDSR)普遍比基于重建的方法(NLM)和基于浅层学习的算法(SP)性能更好。在基于深度学习的重建方法中,RLSR和VDSR方法的PSNR表现优异,但PI相对SRCNN方法较差。而方法则取得了PI上的最优。在以上所有方法SR重建结果中,研究方法的SSIM虽然略低于其他方法,但差值较小,无明显差异;方法的PSNR和RMSE虽然不是最优,但这正是所要表达的观点之一:在PSNR和RMSE达到一定高度时,图像质量不再伴随PSNR和RMSE的提高而提高,而是随着PI的降低而提高。
因此,研究算法在提高SR重建结果的感知质量上有较大优势。为进一步论证该结论,采用Kirby 21数据集中的非训练集样本的T1加权像(KKI01-KKI10)进行重建,并计算了研究算法重建结果的PI值,实验结果如表 3所示。其中PI最大值为3.961 2、最小值为3.197 0、均值为3.582 9、方差为0.052 9。可以看出研究算法重建图像的PI值较低且稳定,再次证明了研究算法能够取得较好的感知质量。
| 表 3 重建T1加权像(KKI01-KKI10)的PI值 Table 3 The PI value of the results of reconstructing the T1 weighted image (KKI01-KKI10) |
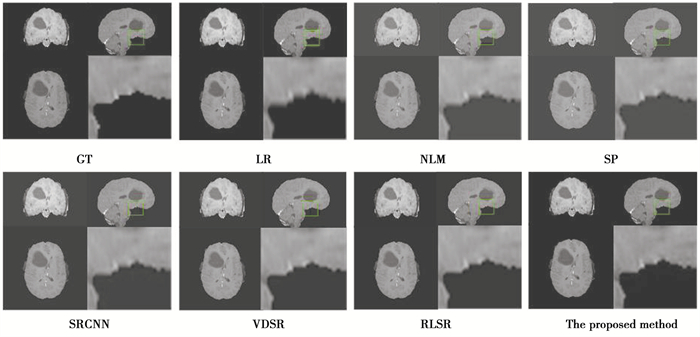
为了进一步验证算法的优越性和能否恢复有病理3D-MRI图像的细节信息,展示了BraTS数据集T1加权像重建结果,即将分辨率从1 mm×1 mm×2 mm重建为1 mm×1 mm×1 mm。
实验重建结果如图 4所示,分别展示了不同SR方法重建结果中3个不同层面方向的图像与局部细节放大图。可以看出,低分辨率(LR)MRI图像比较模糊,放大区域的图像高频信息不清晰,且存在明显的块效应。与LR相比,NLM算法和SP算法SR重建得到的图像边缘清晰度有一定提升。基于DCNN算法的重建结果相较于基于重建的算法,取得了较优的重建结果。在所有对比方法中,算法SR重建的3D-MRI图像整体质量最好,高频信息比较丰富,且放大区域的脑组织结构的边缘比较清晰,更加接近真实图像的边缘。研究算法能够更好的恢复3D-MRI图像的细节信息,尤其是高频细节。
|
图 4 不同方法以1×1×2为比例系数对BraTS T1w图像重建的结果 Fig. 4 The results of BraTS T1w image reconstructed by different methods with scale factor 1×1×2 |
为了验证方法对不同模态3D-MRI图像重建效果,实验采用Kirby 21数据集中的T1加权像为训练数据集,训练重建尺度为1×1×2的网络模型,对BraTS数据集T2加权像进行重建,同样取得了令人满意的结果,重建结果如表 4所示,部分定性结果展示如图 5所示。
| 表 4 不同方法重建BraTS T2w MRI图像的结果评估 Table 4 The results evaluation of different methods to reconstruct BraTS T2w MRI images |
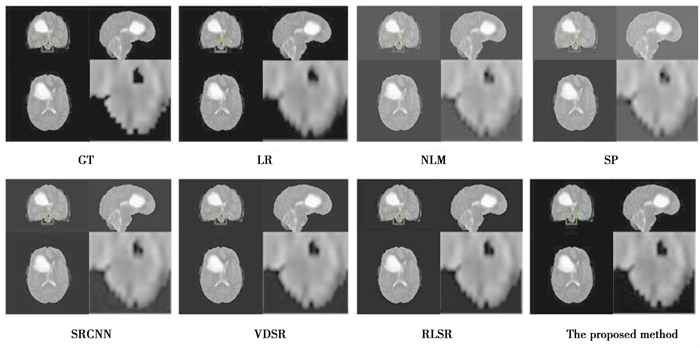
|
图 5 不同方法以1×1×2为比例系数对BraTS T2w图像重建的结果 Fig. 5 The results of BraTS T2w image reconstructed by different methods with scale factor 1×1×2 |
从表 4中可以看出,算法SR重建BraTS数据集的T2加权3D-MRI图像时得到的PNSR/SSIM/RMSE/PI分别为43.816 4 dB/0.996 2/4.936 1/5.391 7,它的PNSR值比NLM算法高1.422 9 dB,RMSE值比NLM算法低0.8786,PI的值比NLM算法低0.942 8,上述结果表明,算法在PSNR、RMSE和PI 3个指标上均优于传统基于重建的3D-MRI图像SR重建算法。同样的,对比基于浅层学习的SR重建算法(SP),研究算法在PSNR、RMSE以及PI 3个指标上均优于基于浅层学习的SR重建算法(SP);与基于DCNN的VDSR和RLSR方法相比,研究算法在PSNR、RMSE以及PI 3个指标上均取得最优,尤其PI指标差异显著。上述结果证明,算法在PSNR、RMSE以及PI 3个指标上均优于NLM、SP、VDSR和RLSR 4种方法,虽然SSIM指标略差,但差值较小。最后,与SRCNN方法相比较,虽然算法的PI(且仅有PI)略差于SRCNN,但是差值不大,无明显差距。
综上所述,在对BraTS数据集的T2加权像的重建中,算法在至少3个指标上优于其他方法,且剩余指标差值较小,无显著差异。因此,算法总体上取得最优重建效果。
从图 5中所展示的局部放大图可以看出,与其他的SR重建算法相比,算法的重建结果中高频细节更加接近原始真实图像,而其他方法重建结果的图像边缘过于平滑,与原始真实图像差距明显。
同样的,为了进一步论证算法的多模态SR重建效果,采用Kirby 21数据集中的T2加权像(KKI01-KKI10)进行重建,并计算了算法重建结果的PI值,实验结果如表 5所示。其中PI最大值为4.368 7、最小值为3.963 6、均值为4.116 2、方差为0.017。可以看出算法重建图像的PI值较低且稳定,再次证明了算法在多模态SR重建也能够取得较好的感知质量。
| 表 5 重建T2加权像(KKI01-KKI10)的PI值 Table 5 The PI value of the results of reconstructing the T2 weighted image (KKI01-KKI10) |
根据上述实验结果可以得出结论:虽然训练集仅含有T1加权图像,但算法却可以SR重建T1加权图像和T2加权图像,因此具有多模态3D-MRI超分辨率重建效果。
3 结语研究提出使用ESRGAN网络SR重建3D-MRI图像,并利用3D-MRI图像的跨层面自相似性,将重建任务降维到2D,减少了参数量,降低了对内存的需求,同时加快了模型训练速度。通过与传统方法实验对比证明,方法在视觉质量方面取得了最好的效果,能够生成感知质量更好、更加符合人类观察者视觉感知的高分辨率3D-MRI图像,并且算法可以重建多模态的3D-MRI图像。因此,方法可用于临床3D-MRI图像的SR重建,提高疾病诊断的精度。
| [1] |
Pham C H, Tor-Díez C, Meunier H, et al. Multiscale brain MRI super-resolution using deep 3D convolutional networks[J]. Computerized Medical Imaging and Graphics, 2019, 77: 101647. DOI:10.1016/j.compmedimag.2019.101647 |
| [2] |
Srinivasan K, Ankur A, Sharma A. Super-resolution of magnetic resonance images using deep convolutional neural networks[C]//2017 IEEE International Conference on Consumer Electronics-Taiwan. June 12-14, 2017, [S. L. ]: IEEE, 2017: 41-42.
|
| [3] |
Chen Y H, Xie Y B, Zhou Z W, et al. Brain MRI super resolution using 3D deep densely connected neural networks[C]//2018 IEEE 15th International Symposium on Biomedical Imaging. April 4-7, 2018, Washington, DC, USA. IEEE, 2018: 739-742.
|
| [4] |
Chen Y H, Shi F, Christodoulou A G, et al. Efficient and accurate MRI super-resolution using a generative adversarial network and 3D multi-level densely connected network[C]//Medical Image Computing and Computer Assisted Intervention-MICCAI 2018. Granada, Spain: Springer, 2018: 91-99.
|
| [5] |
Sánchez I, Vilaplana V. Brain MRI super-resolution using 3D generative adversarial networks[J]. arXiv preprint arXiv: 1812.11440, 2018.
|
| [6] |
Chen Y, Christodoulou A G, Zhou Z, et al. Mri super-resolution with gan and 3d multi-level densenet: Smaller, faster, and better[J]. arXiv preprint arXiv: 2003.01217, 2020.
|
| [7] |
Wang X T, Yu K, Wu S, et al. Esrgan: Enhanced super-resolution generative adversarial networks[C]//Proceedings of the European conference on computer vision (ECCV) workshops. Munich German: IEEE, 2019: 63-79.
|
| [8] |
Ledig C, Theis L, Huszár F, et al. Photo-realistic single image super-resolution using a generative adversarial network[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition. July 21-26, 2017. Honolulu, HI, USA: IEEE, 2017: 105-114.
|
| [9] |
He K M, Zhang X Y, Ren S Q, et al. Delving deep into rectifiers: surpassing human-level performance on ImageNet classification[C]//2015 IEEE International Conference on Computer Vision. December 7-13, 2015. Santiago, Chile: IEEE, 2015: 1026-1034.
|
| [10] |
Shi W Z, Caballero J, Huszár F, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition. June 27-30, 2016. Las Vegas, NV, USA: IEEE, 2016: 1874-1883.
|
| [11] |
Lim B, Son S, Kim H, et al. Enhanced deep residual networks for single image super-resolution[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops. July 21-26, 2017. Honolulu, HI, USA: IEEE, 2017: 1132-1140.
|
| [12] |
Zhang Y L, Tian Y P, Kong Y, et al. Residual dense network for image super-resolution[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. June 18-23, 2018. Salt Lake City, UT, USA: IEEE, 2018: 2472-2481.
|
| [13] |
Zhang Y L, Li K P, Li K, et al. Image super-resolution using very deep residual channel attention networks[M]. Cham: Springer International Publishing, 2018: 294-310.
|
| [14] |
Jolicoeur-Martineau A. The relativistic discriminator: a key element missing from standard GAN[J]. arXiv preprint arXiv: 1807.00734, 2018.
|
| [15] |
Gatys L A, Ecker A S, Bethge M. Texture synthesis using convolutional neural networks[EB/OL]. 2015: arXiv: 1505.07376[cs. CV]. https://arxiv.org/abs/1505.07376.
|
| [16] |
Bruna J, Sprechmann P, LeCun Y. Super-resolution with deep convolutional sufficient statistics[EB/OL]. 2015: arXiv: 1511.05666[cs. CV]. https://arxiv.org/abs/1511.05666.
|
| [17] |
Johnson J, Alahi A, Li F F. Perceptual losses for real-time style transfer and super-resolution[EB/OL]. 2016: arXiv: 1603.08155[cs. CV]. https://arxiv.org/abs/1603.08155.
|
| [18] |
Plenge E, Poot D H J, Niessen W J, et al. Super-resolution reconstruction using cross-scale self-similarity in multi-slice MRI[J]. Medical Image Computing and Computer-Assisted Intervention: MICCAI International Conference on Medical Image Computing and Computer-Assisted Intervention, 2013, 16(Pt 3): 123-130. |
| [19] |
Manjón J V, Coupé P, Buades A, et al. Non-local MRI upsampling[J]. Medical Image Analysis, 2010, 14(6): 784-792. DOI:10.1016/j.media.2010.05.010 |
| [20] |
Jia Y Y, He Z S, Gholipour A, et al. Single anisotropic 3-D MR image upsampling via overcomplete dictionary trained from in-plane high resolution slices[J]. IEEE Journal of Biomedical and Health Informatics, 2016, 20(6): 1552-1561. DOI:10.1109/JBHI.2015.2470682 |
| [21] |
Dong C, Loy C C, He K, et al. Learning a deep convolutional network for image super-resolution[C]//European Conference on Computer Vision. Zürich, Switzerland: Springer, 2014: 184-199.
|
| [22] |
Kim J, Lee J K, Lee K M. Accurate image super-resolution using very deep convolutional networks[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition. June 27-30, 2016. Las Vegas, NV, USA: IEEE, 2016: 1646-1654.
|
| [23] |
Du J L, He Z S, Wang L L, et al. Super-resolution reconstruction of single anisotropic 3D MR images using residual convolutional neural network[J]. Neurocomputing, 2020, 392: 209-220. DOI:10.1016/j.neucom.2018.10.102 |
| [24] |
Landman B A, Huang A J, Gifford A, et al. Multi-parametric neuroimaging reproducibility: a 3-T resource study[J]. NeuroImage, 2011, 54(4): 2854-2866. DOI:10.1016/j.neuroimage.2010.11.047 |
| [25] |
Menze B H, Jakab A, Bauer S, et al. The multimodal brain tumor image segmentation benchmark (BRATS)[J]. IEEE Transactions on Medical Imaging, 2015, 34(10): 1993-2024. DOI:10.1109/TMI.2014.2377694 |
| [26] |
Cocosco C A, Kollokian V, Kwan R K S, et al. Brainweb: Online interface to a 3D MRI simulated brain database[J]. NeuroImage, 1997, 5(4): 24. |
| [27] |
Blau Y, Mechrez R, Timofte R, et al. The 2018 PIRM challenge on perceptual image super-resolution[C]//European Conference on Computer Vision. Munich, Germany: Springer, 2018: 334-355.
|
| [28] |
Blau Y, Michaeli T. The perception-distortion tradeoff[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. June 18-23, 2018. Salt Lake City, UT, USA: IEEE, 2018: 6228-6237.
|
| [29] |
Ma C, Yang C Y, Yang X K, et al. Learning a no-reference quality metric for single-image super-resolution[J]. Computer Vision and Image Understanding, 2017, 158: 1-16. DOI:10.1016/j.cviu.2016.12.009 |
| [30] |
Mittal A, Soundararajan R, Bovik A C. Making a "completely blind" image quality analyzer[J]. IEEE Signal Processing Letters, 2013, 20(3): 209-212. DOI:10.1109/LSP.2012.2227726 |
| [31] |
Wang Z, Bovik A C, Sheikh H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transactions on Image Processing: a Publication of the IEEE Signal Processing Society, 2004, 13(4): 600-612. DOI:10.1109/TIP.2003.819861 |
 2022, Vol. 45
2022, Vol. 45


