分类问题是数据挖掘中的难点。绝大多数分类算法只是在平衡数据集分类效果显著,而在不均衡数据集上分类效果欠佳。但现实生活中的分类问题往往是类别不均衡的,例如银行欺诈的检测、垃圾邮件的检测、车辆识别、疾病诊断等。不均衡数据分类问题已经成为机器学习、数据挖掘等领域的重要研究方向之一[1-2]。在实际的生活中,不均衡分类问题大多数是多分类问题,因此更具有研究意义。而多数类的不均衡分类问题与二分类的分类问题相比,多数类对于分类模型要求更高,获取少数类的代价也更大,类间数据的分布也更多样化,也更难被分类。针对不均衡数据分类的研究主要集中在数据层面与算法层面的改进研究。数据层面的改进主要集中在对数据集的改进,增加少数类数据或减少多数类数据,使得原本的数据集相对均衡,主要的改进方法是过采样与欠采样。早期,Chawla等[3-4],提出了一种SMOTEBoost(synthetic minority over-sampling technique and boost)的方法,将SMOTE采样算法与集成算法Boost相结合,加强了对小类样本的关注度;武森等[5]将聚类算法运用到采样中,先利用聚类欠采样方法将数据集均衡化,然后利用AdaBoost算法对新生成的数据集进行分类操作;2013年,Krawczyk等[6]使用PUSBE(pruned under-sampling balanced ensemble)方法,该方法有效运用了特征选择技术;2014年,Krawczyk等[7]又提出了CS-MCS(cost-sensitive multiple classifier systems)集成方法,运用随机欠采样结合遗传算法相结合的方式。在低维数据集上效果明显,但是高维数据集上效果欠佳。文献[8]指出采样方法虽然可以提升小类样本的识别率,但是容易引入噪声,丢失有用信息,分类器对小类样本过分的关注也易使得算法陷入局部最优。对此,TAO等[9]提出了一种新的过采样技术,该技术使用实值否定选择(RNS)过程来生成人工少数类数据,而无需实际的少数类数据。生成的少数类数据(如果有的话)会与实际的少数类数据一起使用,并与多数类数据相结合,作为二分类学习方法的输入,并且在实验中证明了其有效性。
从算法的角度来看,改变概率密度,单类学习分类,集成学习,代价敏感学习,核方法等五种主要方法来解决数据分类不平衡问题[10]。国际机器学习界的权威Dietterich已经将集成学习列为机器学习4大研究之首[11]。TAO等[12]提出了一种新的基于自适应权重的支持向量机成本敏感集成方法,用于不平衡数据分类,还创新性的提出了一种自适应的顺序错误分类权重确定方法。该方法可以基于在提升过程中先前获得的分类器,在每次迭代时自适应地考虑少数实例对SVM分类器的不同贡献,这可以使其产生不同的分类器,从而提高泛化性能。随后,Tao等[13]又提出了一种新的基于亲和度和类别概率的模糊支持向量机技术(ACFSVM)。多数类样本的亲和力是根据支持向量描述域(SVDD)模型计算的,该模型仅由给定的多数类训练样本在内核空间中进行训练,类似于FSVM学习所使用的模型。针对噪声样本的处理,Tao等[13]采用核k最临近法来确定与以前相同的核空间中多数类别样本的类别概率。具有较低分类概率的样本更有可能是噪音,并且通过将相似度和分类概率结合起来构成的低隶属度, 减少了噪声样本的影响。张苗燕等[14]结合细菌觅食算法的思想,提出了一种新的算法AdAdaboost,并对加权系数进行了改进,全局优化最佳弱分类器,改善了AdaBoost算法误检率的同时得到了较好的检测性能;Guo等[15]将AdaBoost.M1算法与特征选择结合起来,提出了一种新的集成方法BAK(BPSO-AdaBoost-KNN),使用KNN作为基分类器,但KNN的缺点是不能直接处理带权数据,需要借助re-samplingd的方法转化数据集后使用,而且AdaBoost.M1针对于基分类器的要求过于严苛,错误率不能超过50%。对此,将胡旺[16]等提出的SPSO(simple particle swarm optimization)算法进行改进,并与Zhu等[17]提出的SAMME.R版本的AdaBoost算法相结合,提出了WSPSO-SAMME.R-DT算法,用以解决不平衡多分类问题。与AdaBoost.M1算法所不同的,SAMME.R使用决策树作为基分类器,避免在训练样本上花费时间,降低对基分类器的要求。为了降低基分类器的相关性,引入了随机化的方法。使用AUCarea作为性能度量指标,并将其作为适应度值,优化特征选择。提升了小类样本的识别率。
1 算法介绍 1.1 SAMME.R AdaBoost算法AdaBoost算法是一个迭代过程,弱分类器的生成是串行的。在AdaBoost的训练过程中,分类器的重心将转移到那些更难分类的样本上,即多次错误分类的样本。随后的训练也会偏重于这些样本,这是通过在算法运行期间为训练样本分配权重来实现的。样本权重最初都是一致的,后续过程中每轮都会对样本权重进行更新,最终得到一组弱分类器,将所有弱分类器加权组合成一个强分类器。
AdaBoost算法适用于二分类问题,AdaBoost.M1可用于解决多分类问题。但是AdaBoost.M1的前提条件是基分类器的错误率小于50%,这一要求过于严格,易导致训练失败。针对以上不足,笔者选择Zhu等[17]提出的SAMME.R版本的AdaBoost算法,降低了对基分类器过于严苛的要求,仅比随机猜测略好即可。同时,使用分类器的类别估计概率值来对样本权重进行更新。
在该算法中,获得加权类概率估计的公式为:
| $ p(t)_{k}(x)={\rm{Pro}}b_{w}(h=k \mid x), k=1, \cdots, K, $ | (1) |
其中:t为迭代次数,k为类标签,Prob函数是返回区域中的数值落在指定区间内的对应概率。获得加权类概率估计后,利用拉格朗日定理对称约束优化得到h(t)k(x)
| $ h(t)_{k}(x)=(K-1)\left(\log p(t)_{k}(x)-\frac{1}{k} \sum\limits_{k^{\prime}=1}^{K} \log p(t)_{k^{\prime}}(x)\right), $ | (2) |
更新样本权重wi:
| $ w_{i}=w_{i} \cdot \exp \left(-\frac{K-1}{K} \boldsymbol{y} T_{i} \log p(t)\left(x_{i}\right)\right), i=1, \cdots, m, $ | (3) |
其中: y=(y1, …,ym)T
| $ y_{k}=\left\{\begin{array}{cc} 1, & \text { if } \quad \boldsymbol{y}=k \\ -\frac{1}{K-1}, & \text { if } \quad \boldsymbol{y} \neq k \end{array}\right. $ |
对于不平衡二分类问题来说,经常使用ROC曲线来度量分类中的不平衡性,ROC是接受者操作特性曲线(receiver operating characteristic),利用ROC曲线下的面积(area under the curve)作为算法的评价标准,理想中分类器的AUC为1.0,随机猜测的分类器AUC为0.5。
AUC评价标准无法直接应用与多分类问题,需要对其进行拓展。最常用的2种扩展方法分为[18]:1)一对一方法;2)一对多方法。为了更加清晰的对比这2种方法,令Y={y1, y2, …,yk},Y表示的是数据的类标签的集合。在一对一的方法中,计算所有类的两两组合(yi, yj)(i≠j) 的AUC值。一对多的方法中,先定义成二分类问题,令yi∈Y,属于yi的样本定义为正类,剩余的样本为负类,然后计算定义后的AUC值。由此将会得到一组AUC值{r1, r2,…,rn},最后取平均值,记作avgAUC,作为性能度量值使用。以上2种方法都可简单的实现,但是无法做到可视化。因为当多个AUC都变化时,avgAUC的值可能没有任何变化。例如,当ri变为ri+σ,rj变为rj-σ,(i,j)∈{1, 2,…,n}), 最终其avgAUC的值没有改变,也无法进行分类模型调整的评价。
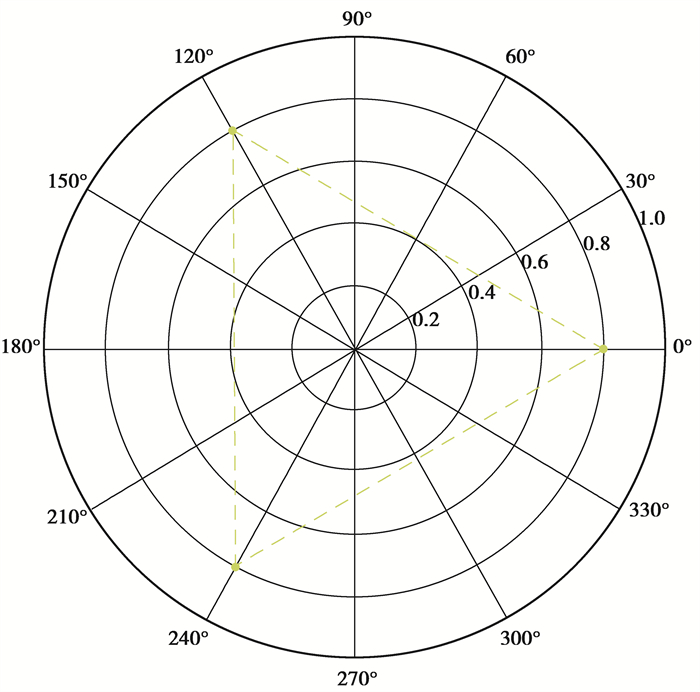
采用Hand DJ[19]提出的一种具有可视化优点的度量指标方法AUCarea。AUCarea会将所有的AUC的值在极坐标上绘制出来。如图 1所示,黄色虚线三角形代表的就一个是三分类的AUCarea极坐标图示,黄色虚线所覆盖的面积就是最终度量值。AUCarea的计算公式如下
|
图 1 三分类的AUCarea极坐标图示 Fig. 1 Three-category AUCare polar plot |
| $ \text { AUCarea }=\frac{1}{2} \sin \left(\frac{2 {\rm{ \mathsf{ π} }}}{n}\right)\left(\left(\sum\limits_{i=1}^{n-1} r_{i} \times r_{j}\right)+\left(r_{n} \times r_{1}\right)\right), $ | (4) |
其中:n为AUC的总数; r为每对类组合(yi, yj)(i≠j)的AUC的值。
当所有AUC的值为1时,就达到了理想中的最优状态,即AUCarea的最大值,如公式(5)所示
| $ \text { AUCarea_max }=\left(\frac{n}{2}\right) \sin \left(\frac{2 {\rm{ \mathsf{ π} }}}{n}\right), $ | (5) |
计算归一化的为公式(6)
| $ \text { AUCarea_nor }=\frac{\text { AUCarea }}{\text { AUCarea_max }}=\frac{\left(\sum\limits_{i=1}^{n-1} r_{i} \times r_{i+1}\right)+\left(r_{n}+r_{1}\right)}{n}, $ | (6) |
使用归一化公式(6)所得值记为AUCarea,AUCarea除了可视化的优点之外,也对单个差的AUC较为敏感。
2 基于WSPSO特征选择方法虽然AdaBoost算法可通过增加小样本的权重来增强对小样本的关注,但它仍然使用正确率作为优化目标,并且容易引起过拟合。因此,将特征选择方法与SAMME.R AdaBoost算法结合。SAMME.R算法中加入特征选择是基于以下考虑:去除不相干特征,减少时间与空间的浪费,加强对特征和特征值之间的联系,从而更好的进行分类[20]。特征选择算法主要有三类:嵌入式(embedded)、过滤式(filter)和封装式(wrapper)。嵌入式算法的思路是学习器自身自动进行选择,虽然效果较好,但是对于参数的设置需要较高的知识背景;过滤式算法的思路是先对各特征的相关性或发散性进行评估排序,根据设置的阈值来选择。但是对特征之间的相关性难以评估,会造成部分有用信息的遗失;封装式算法的思路是利用学习算法来评估特征的优劣,相对于嵌入式算法与过滤式算法,虽然需要巨大的搜索空间,执行时间稍长,但不需要过多的背景知识,可直接面向算法优化,并且特征间的组合效应也得到了充分的挖掘。综上,选择封装式算法来进行特征选择。
粒子群优化(PSO, particle swarm optimization)[21]算法,具有易实现、结构简单、没有复杂变异交叉操作的优点,可运用于特征选择优化问题在。文献[16]在证明PSO进化过程与粒子速度无关后提出了简化版粒子群优化(SPSO, simple particle swarm optimization)算法,去掉了速度选项,SPSO的进化公式为
| $ x t+1_{i d}=\omega x t_{i d}+c_{1} r_{1}\left(p_{i d}-x t_{i d}\right)+c_{2} r_{2}\left(p_{g d}-x t_{i d}\right), $ | (7) |
其中:xt+1id表示的是第t代第i个粒子的第d维分量;ω是惯性权重因子;c1和c2是学习因子常数;r1和r2是随机数,服从U(0, 1);pid表示第i个粒子个体极值的第d维,而pgd表示全局最优解的第d维分量。
在粒子群算法中,惯性权重是重要的参数之一。其主要功能是平衡整个粒子群的全局搜索能力和局部搜索能力,从而显著的提高算法的整体收敛速度。而在标准SPSO算法中,ω是固定的数值,无法改变。当惯性权重较小时,如果最优解在初始搜索空间中,则粒子群算法可以快速找到全局最优解,反之则无法正确找到。而惯性权值较大时,粒子群算法更像是全局搜索算法,总会探索新的区域。这意味着需要更多的迭代来寻找全局最优,并且更有可能在找不到最优解同时算法的时间复杂度也会增加。因此,ω应该在算法的初期设置为较大值,在算法的后期设置为较小值。这样设置的优点在于:初始阶段的全局寻优能力会得到增强,有利于避免局部最优;而在算法的后期,可增强算法在局部的搜索能力,同时提高算法收敛速度。因此,借鉴文献[22]运用的一种线性递减动态获取惯性权重ω的方法,即
| $ \omega=\frac{\left(\omega_{\text {ini }}-\omega_{\text {end }}\right)(T-t)}{T}+\omega_{\text {end }}, $ | (8) |
其中的参数取值为:ωini=0.9;ωend=0.4时效果较好。t =当前迭代次数,T=最大迭代次数。
特性选择可看成0~1组合优化问题,Kennedy[23]等最早提出了二进制粒子群优化(BPSO, binary particle swarm optimization)算法将PSO算法扩展到了离散二进制空间,针对PSO在特征选择应用很多都是建立在BPSO的基础上的,但其缺点是离散的PSO丧失了一些连续PSO的特性。在此情况下,选择在特征选择过程中,将特征选择问题转换为一个向量,由(0, 1)来表示。F=(fti1, fti2, …, ftid),ftid等于1时,该维特征被选中,等于0时,则未被选中。设定一个阈值δ来判断是否被选中,如公式(9)所示
| $ \boldsymbol{f t}_{i d}=\left\{\begin{array}{lc} 1, & x t_{i d} \geqslant \delta , \\ 0, & \text { other }, \end{array}\right. $ | (9) |
δ是随机数,取值范围U(0.2, 0.8)。根据公式(9)粒子的位置向量在连续空间域与离散问题域中完成特征向量转换。
在标准的PSO算法中,假设初始种群中存在先验近似最优粒子,则可确定整体的搜索方向,这将大幅度地缩短WSPSO的进化时间。所以,需要对数据预处理,得到特征的重要性。Brieman[24]提出了一种确定特征重要性的方法,其主要思想是:每次选择特征时,随机替换特征的值,并记录预测精度的变化,预测的准确性越高说明该特征的重要性越高。这里所提的特征重要性也就是对预测结果贡献的百分比。因此可以得到占比最高的粒子,加入初始的种群。
2.1 WSPSO-SAMME.R-DT算法给出基于封装式特征选择的WSPSO-SAMME.R-DT算法的具体步骤。其中DT代表基分类器决策树。为了增加集成学习中基分类器间的多样性,将随机选择决策树中的最佳分割点。
算法2:WSPSO-SAMME.R-DT算法
输入: 训练集{(xi, yi)|i=1, 2, …, n},最大迭代次数T,种群大小m。
1) 初始化种群。依据特征重要性,选择重要性最高的一个粒子作为初始粒子,剩余的m-1个粒子以随机的方式生成。这m个粒子的各维分量都是U(0, 1)的随机数,将所有粒子进行组合,完成初始种群的构建;
2) 判断是否满足条件t≤T and pg的适应度小于1。若成立继续下一步,不成立跳出循环;
3) 对于粒子i=1,2,…,m;
4) 根据公式(9)将粒子xi转化为特征向量,基于特征向量从训练集中选取训练子集。然后根据算法SAMME.R,训练出一个强分类器H;
5) 根据强分类器H得到的预测结果,计算每对类别组合的AUC,然后按照公式(6)计算AUCarea,作为xi粒子的适应度值;
6) 根据得到的AUCarea的值来更新个体最优pi和全局最优pg;
7) 根据公式(7)、(8)更新粒子位置;
8) 根据公式(9)将pg转化为特征向量;
输出:最优特征子集、强分类器H。
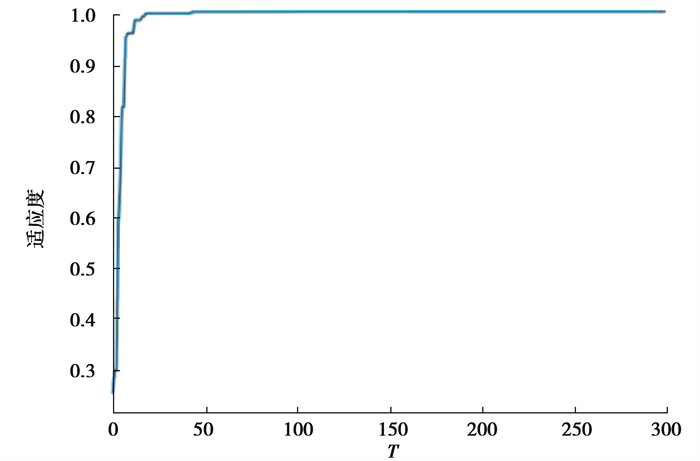
3 实验仿真与分析实验机器配置为:Window7,内存6 GB,CPU2.50 GHz,算法基于Python3.6.2实现。实验所用的10组数据集来自KEEL官网与UCI数据集,数据都源于实际中的应用领域,表 1给出具体信息。不均衡比IR(imbalance ratio)是最大多数类别的样本数与最小少数类别的样本数之比。学习因子c1 =c2 =2,经实验显示,种群粒子数m=100时效果最佳,初始设置迭代次数T为300次,图 2给出了每代最优个体适应度值的曲线,随着迭代次数增加,可以看出迭代次数T=50时个体适应度值已趋于稳定,所以最终选择的迭代次数为T=50。
| 表 1 数据集信息 Table 1 Dataset information |
|
图 2 最优个体适应度值的曲线 Fig. 2 Curve of optimal individual fitness value |
实验结果利用AUCarea以及另一个被广泛应用的不平衡分类指标GM(G-Mean)[25]对算法进行评价。GM定义如下
| $ \mathrm{GM}=\sqrt{\frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FP}}} \times \sqrt{\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}}, $ | (10) |
其中TP, FP, FN, TN分别表示:小类正确分类的数量,预测为小类但是真实为大类,预测为大类但是真实为小类,大类正确分类的数量。
文献[6][7][15]各自提出了PUSBE、CS-MCS、BAK算法,与提出的WSPSO-SAMME.R-DT进行对比。采取一对一方法将PUSBE和CS-MCS扩充到多分类问题上,结果见表 2、3。
| 表 2 4种算法的AUCarea值对比 Table 2 Comparison of AUCarea values of four algorithms |
| 表 3 四种算法的GM值对比 Table 3 Comparison of GM values of four algorithms |
根据表 2与表 3可以得到如下结论:提出的算法WSPSO-SAMME.R-DT总体性能略优于要其他3种算法,尤其是在New_thyroid、Wine与Zoo数据集上,AUCarea与GM的值都达到了100%。除了Contraceptive数据集外,在其他数据集上,WSPSO-SAMME.R-DT也略好于其他3种算法。其中CS-MCS在AUCarea上的平均值为0.832,比PUSBE的平均值低了2.1%;比BAK的平均值低了5.6%;比提出的WSPSO-SAMME.R-DT的平均值低了10.3%。而在GM值上CS-MCS的平均值为0.875,比PUSBE的平均值低了2.8%;比BAK的平均值低了2.4%;比提出的WSPSO-SAMME.R-DT的平均值低了5.3%。由此可看出算法总体性能相对较差,这是因为CS-MCS算法并没有跟其他3种算法一样采用特征选择技术,这也证明了特征选择可有效的应用于不均衡多分类的问题。
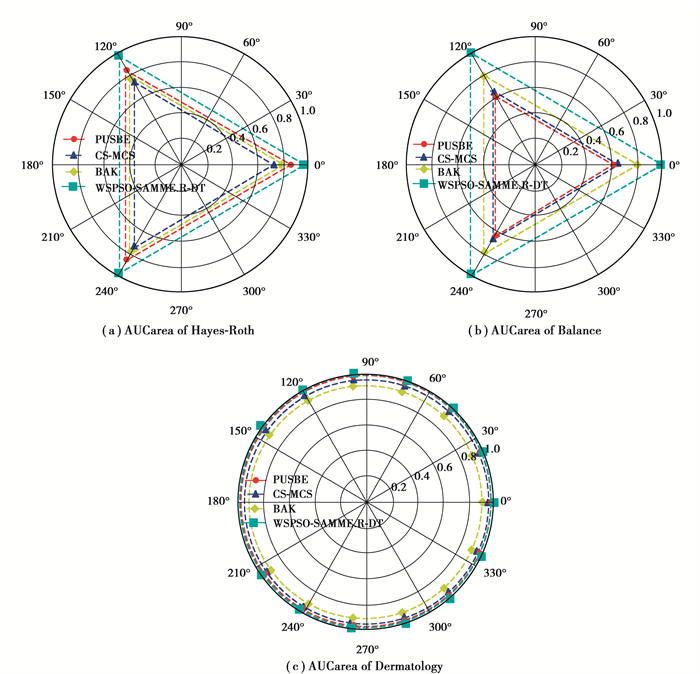
为了更直观的对比4种算法的分类效果,图 3给出了4种算法AUCarea值的部分polar图。根据图 3所示,图中红色虚线代表PUSBE;蓝色虚线代表CS-MCS;黄色虚线代表BAK;青色虚线代表WSPSO-SAMME.R-DT。他们所围成的面积就是其对应的AUCarea的值。从图中可以看出WSPSO-SAMME.R-DT在Hayes-Roth与Balance数据集中面积最大,意味着在这两种数据集下,WSPSO-SAMME.R-DT优于其他3种算法,在Dermatology算法中排名第二,但是与该数据集下的最优算法PUSBE所产生的面积相差不多。
|
图 3 4种算法的AUCarea极坐标图示比较 Fig. 3 Comparison of AUCarea polar coordinates of four algorithms |
结合特征选择与集成学习方法提出了WSPSO-SAMME.R-DT算法,在10组不均衡数据集上对本算法进行实验测试,实验结果验证了该算法的有效性。WSPSO-SAMME.R-DT使用了WSPSO算法并且以AUCarea作为适应度值,来优化特征选择。其中,AUCarea具可视化的优点,并且对较差的AUC值更加敏感。笔者并没有采用采样技术对初始数据集进行数据层面的改进,避免了丢失重要信息、引入噪声等情况。WSPSO-SAMME.R-DT可直接应用于多分类算法且并不需要进行拓展。
| [1] |
Napierala K, Stefanowski J. Types of minority class examples and their influence on learning classifiers from imbalanced data[J]. Journal of Intelligent Information Systems, 2016, 46(3): 563-597. DOI:10.1007/s10844-015-0368-1 |
| [2] |
Glauner P, Boechat A, Dolberg L, et al. Large-scale detection of non-technical losses in imbalanced data sets[C]//2016 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference. September 6-9, 2016, Minneapolis, MN, USA. IEEE, 2016: 1-5.
|
| [3] |
Chawla N V, Lazarevic A, Hall L O, et al. SMOTEBoost: Improving prediction of the minority class in boosting[C]//European conference on principles of data mining and knowledge discovery. Berlin, Heidelberg: Springer, 2003: 107-119.
|
| [4] |
Chawla N V, Bowyer K W, Hall L O, et al. SMOTE: synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2002, 16: 321-357. DOI:10.1613/jair.953 |
| [5] |
武森, 刘露, 卢丹. 基于聚类欠采样的集成不均衡数据分类算法[J]. 工程科学学报, 2017, 39(8): 1244-1253. Wu S, Liu L, Lu D. Imbalanced data ensemble classification based on cluster-based under-sampling algorithm[J]. Chinese Journal of Engineering, 2017, 39(8): 1244-1253. (in Chinese) |
| [6] |
Krawczyk B, Schaefer G. An improved ensemble approach for imbalanced classification problems[C]//2013 IEEE 8th International Symposium on Applied Computational Intelligence and Informatics. May 23-25, 2013. Timisoara, Romania: IEEE, 2013: 423-426.
|
| [7] |
Krawczyk B, Woz'niak M, Herrera F. Weighted one-class classification for different types of minority class examples in imbalanced data[C]//2014 IEEE Symposium on Computational Intelligence and Data Mining. December 9-12, 2014. Orlando, FL, USA: IEEE, 2014: 337-344.
|
| [8] |
王莉莉, 付忠良, 陶攀, 等. 基于主动学习不平衡多分类AdaBoost算法的心脏病分类[J]. 计算机应用, 2017, 37(7): 1994-1998. Wang L L, Fu Z L, Tao P, et al. Heart disease classification based on active imbalance multi-class Ada Boost algorithm[J]. Journal of Computer Applications, 2017, 37(7): 1994-1998. (in Chinese) |
| [9] |
Tao X M, Li Q, Guo W J, et al. Self-adaptive cost weights-based support vector machine cost-sensitive ensemble for imbalanced data classification[J]. Information Sciences, 2019, 487: 31-56. DOI:10.1016/j.ins.2019.02.062 |
| [10] |
陶新民, 郝思媛, 张冬雪, 等. 不均衡数据分类算法的综述[J]. 重庆邮电大学学报(自然科学版), 2013, 25(1): 101-110, 121. Tao X M, Hao S Y, Zhang D X, et al. Overview of classification algorithms for unbalanced data[J]. Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition), 2013, 25(1): 101-110, 121. (in Chinese) |
| [11] |
Dietterich T G. Ensemble methods in machine learning[C]//International workshop on multiple classifier systems. Berlin, Heidelberg: Springer, 2000: 1-15.
|
| [12] |
Tao X M, Li Q, Ren C, et al. Real-value negative selection over-sampling for imbalanced data set learning[J]. Expert Systems With Applications, 2019, 129: 118-134. DOI:10.1016/j.eswa.2019.04.011 |
| [13] |
Tao X M, Li Q, Ren C, et al. Affinity and class probability-based fuzzy support vector machine for imbalanced data sets[J]. Neural Networks, 2020, 122: 289-307. DOI:10.1016/j.neunet.2019.10.016 |
| [14] |
张苗燕, 王登飞, 魏宗寿. 一种改进的AdaBoost快速训练算法[J]. 西北工业大学学报, 2017, 35(6): 1119-1124. Zhang M Y, Wang D F, Wei Z S. An improved Ada boost training algorithm[J]. Journal of Northwestern Polytechnical University, 2017, 35(6): 1119-1124. (in Chinese) DOI:10.3969/j.issn.1000-2758.2017.06.028 |
| [15] |
Guo H X, Li Y J, Li Y N, et al. BPSO-Adaboost-KNN ensemble learning algorithm for multi-class imbalanced data classification[J]. Engineering Applications of Artificial Intelligence, 2016, 49: 176-193. DOI:10.1016/j.engappai.2015.09.011 |
| [16] |
胡旺, 李志蜀. 一种更简化而高效的粒子群优化算法[J]. 软件学报, 2007, 18(4): 861-868. Hu W, Li Z S. A simpler and more effective particle swarm optimization algorithm[J]. Journal of Software, 2007, 18(4): 861-868. (in Chinese) |
| [17] |
Hastie T, Rosset S, Zhu J, et al. Multi-class AdaBoost[J]. Statistics and Its Interface, 2009, 2(3): 349-360. DOI:10.4310/SII.2009.v2.n3.a8 |
| [18] |
Nakas C T, Yiannoutsos C T. Ordered multiple-class ROC analysis with continuous measurements[J]. Statistics in Medicine, 2004, 23(22): 3437-3449. DOI:10.1002/sim.1917 |
| [19] |
Hand D J, Till R J. A simple generalisation of the area under the ROC curve for multiple class classification problems[J]. Machine Learning, 2001, 45(2): 171-186. DOI:10.1023/A:1010920819831 |
| [20] |
Qu Y, Fang Y, Yan F Q. Feature selection algorithm based on association rules[J]. Journal of Physics: Conference Series, 2019, 1168: 052012. DOI:10.1088/1742-6596/1168/5/052012 |
| [21] |
Bratton D, Kennedy J. Defining a standard for particle swarm optimization[C]//2007 IEEE Swarm Intelligence Symposium. April 1-5, 2007. Honolulu, HI, USA: IEEE, 2007: 120-127.
|
| [22] |
行鸿彦, 郭敏, 张兰, 等. 基于改进SPSO-BP神经网络的温度传感器湿度补偿[J]. 传感技术学报, 2018, 31(3): 380-385. Xing H Y, Guo M, Zhang L, et al. The humidity compensation for temperature sensor based on improved SPSO-BP neural network[J]. Chinese Journal of Sensors and Actuators, 2018, 31(3): 380-385. (in Chinese) DOI:10.3969/j.issn.1004-1699.2018.03.011 |
| [23] |
Kennedy J, Eberhart R C. A discrete binary version of the particle swarm algorithm[C]//1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation. October 12-15, 1997. Orlando, FL, USA: IEEE, 1997: 4104-4108.
|
| [24] |
Breiman L. Bagging predictors[J]. Machine Learning, 1996, 24(2): 123-140. |
| [25] |
Galar M, Fernández A, Barrenechea E, et al. EUSBoost: Enhancing ensembles for highly imbalanced data-sets by evolutionary undersampling[J]. Pattern Recognition, 2013, 46(12): 3460-3471. DOI:10.1016/j.patcog.2013.05.006 |
 2022, Vol. 45
2022, Vol. 45

