海量档案文本数据急剧增长,也伴随着文本数据描述的多样化[1]。例如,一则新闻消息可以通过不同的语言进行表达和传播;一个文本可以利用不同的特征描述(Word2Vec、TF-IDF等)进行分析。这样的数据称为多模态数据,不同领域或不同描述形式可以代表一种模态。通常,不同模态之间可以为语义相同的数据对象相互补充信息,结合多个模态的数据信息对一个物体进行描述相比于单模态可以更加全面地了解该物体的特征并且精准对该物体进行辨别。另外,随着档案文本不断增长,给档案管理带来了一定困难,有效对档案数据进行聚类、划分,能够按主题对档案文本进行分类管理,便于后期查阅、处理。
近年来多模态文本数据聚类或分类算法的研究备受关注[2]。例如,Amini等[3]将不同语言的文档看作是原始文档的不同模态,成功设计了多视图多数投票和多视图共分类[4]等方法对文档进行学习;Bickel等[5]研究了众多多模态数据形式下的聚类方法,例如k-means、k-medoids和EM(expectation-maximization)等。挖掘不同模态结合过程中潜在的数据信息是研究者们共同的目标,由此可见,研究多模态数据融合的有效方法已成为文本大数据分析中的重要方向。文中针对海量档案文本数据的多模态特点,研究有效的增量多模态文本聚类方法。
非负矩阵分解[6](NMF, nonnegative matrix factorization)是一种经典的矩阵分解技术,它可以将每个观测对象解释为非负基向量的线性组合相加后得到的结果[7],这恰好符合了人们在大脑和心理上所习惯的“局部构成整体”的思想[8-9]。近几年内,NMF已经被广泛运用于数据聚类中,它与许多先进的无监督聚类算法相比,其性能极具竞争力[10]。例如,Xu等[11]将NMF应用于文本聚类,取得了较好的结果;Brunet等[12]在生物数据聚类方面也获得了类似的成功。这些基于NMF的单模态聚类算法都取得了不错的成果。如果将NMF技术应用于多模态档案文本数据将取得令人期待的结果。NMF本身具有属性降维的功能,可以很好地解决多模态档案文本大数据存在的维数灾难问题。然而,基于NMF的多模态文本数据聚类方法也将面临以下问题:多模态文本数据存在异构性,如何充分结合多个模态的数据信息是首要的挑战;当多模态的文本数据出现爆炸式增长的时候,传统的学习方法需要损耗大量的空间和时间成本。
针对以上问题,文中将研究基于NMF的增量多模态文本聚类方法。与传统的非负矩阵分解方法使用得到的系数矩阵进行数据分析不同,文中提出的方法将直接用融合后的共享特征矩阵进行聚类分析,检测融合数据的效果。该方法是基于语义的,在考虑每种模态的实际意义的情况下求得所有模态的共享特征,并且在多模态数据语义融合的基础上引入图规则化的思想,保证各模态数据与共享特征的几何结构相似性,力求能够获得更好的特征学习与聚类分析效果。然而,当大规模档案文本数据遇到实时性的需求时,传统的多模态数据融合算法无法满足在短时间对大量数据进行处理的任务,因此实现2种增量自适应文本数据特征学习方案,并求解对应的增量优化规则,可以节约数据处理的时间成本,同时学习的增量方法在一定程度上也更加节省数据占据的存储空间。2个实际文本数据集上的实验结果表明:文中提出方法优于现有的一些增量和非增量学习方法,能够对多模态文本数据进行有效划分。
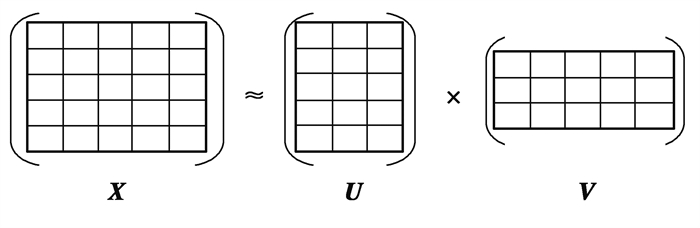
1 相关技术 1.1 非负矩阵分解给定一个M×N大小的非负矩阵X(矩阵中的元素均为负),每个列向量代表一个数据实例,数据实例大小为N,每个行向量代表一种特征属性,共有M维特征属性。这个矩阵被近似分解为一个M×d的基矩阵U和一个N×d的编码矩阵V,其原理如图 1所示[6]。
|
图 1 非负矩阵分解原理原理 Fig. 1 The principle of non-negative matrix factorization |
通常,设定d的数值远远小于N,假设d为数据聚类的类数。非负矩阵分解可以形式化表示为
| $ \boldsymbol{X} \approx \boldsymbol{U} \boldsymbol{V}^{\mathrm{T}}(\boldsymbol{U} \geqslant 0, \boldsymbol{V} \geqslant 0)。$ | (1) |
为了求得矩阵X的近似表示,可以将目标函数最小化:
| $ \min \left\|\boldsymbol{X}-\boldsymbol{U} \boldsymbol{V}^{\mathrm{T}}\right\|_{F}^{2} \text {, s.t. } \boldsymbol{U} \geqslant 0, \boldsymbol{V} \geqslant 0 \text {, } $ | (2) |
式中,||·||F表示Frobenius范数,矩阵X的Frobenius范数定义为矩阵X各项元素的绝对值平方的总和的平方根。观察式(2)可以发现,目标函数仅仅对于变量U或V是凸函数,即其局部最小值为全局最小值,但是函数同时在2个变量上并不是凸的。因此,找到函数的全局最小值是十分困难的,人们往往寻找它的局部最小值。Lee等[6]研究出以下迭代规则对目标函数进行更新,该乘法更新规则保证了函数收敛的速度,并且易于实现:
| $ U_{i k} \leftarrow U_{i k} \frac{\boldsymbol{X} \boldsymbol{V}}{\boldsymbol{U} \boldsymbol{V}^{\mathrm{T}} \boldsymbol{V}}, $ | (3) |
| $ V_{k j} \leftarrow V_{k j} \frac{\boldsymbol{X}^{\mathrm{T}} \boldsymbol{U}}{\boldsymbol{V} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{U}}。$ | (4) |
按照式(3)和式(4)依次对U、V进行交替迭代直到函数收敛,求得最后的U、V矩阵。
非负矩阵分解将一个原始矩阵分解成一个基矩阵和一个编码矩阵相乘的形式,要求得到的基矩阵和编码矩阵非负,因此原矩阵中的某一行数据可以看作编码矩阵中所有列向量的加权和,具体的系数对应编码矩阵中列向量的元素。该分解过程可以理解为一种特征提取的行为,编码矩阵则为原始矩阵的潜在特征表示。
1.2 多模态非负矩阵分解给定一个具有nv个模态的数据集
| $ \min \sum\limits_{v=1}^{n_{v}}\left\|\boldsymbol{X}^{(v)}-\boldsymbol{U}^{(v)} \boldsymbol{V}^{\mathrm{T}}\right\|_{F}^{2}, \text { s.t. } \boldsymbol{V} \geqslant 0, \boldsymbol{U}^{(v)} \geqslant 0, v=1, 2, 3, \cdots, n_{v} 。$ | (5) |
通过共享矩阵V的耦合,联合迭代更新各变量,得到优化后的多模态共享特征。
2 增量多模态文本聚类方法文中提出的增量多模态算法考虑每个模态的语义信息,使用NMF抽取出多模态数据的共享特征子空间。为提升其学习特征的有效性,算法还嵌入图拉普拉斯正则化项,保证高维数据在降维过程中尽量维持其原始的数据结构,进一步提升共享特征学习的准确性。最后,为每个模态设立模态权值,通过权值的自适应更新,合理控制每个模态对于特征子空间的贡献。在实际应用中,数据往往是分批到来的,这导致了非增量算法时间开销巨大。因此,在上述基础算法的基础上,进行算法的2种增量改进来大幅度减少时间消耗。第一种增量改进算法基于数据相对独立这一假设[13]:当新数据到来时,它仅通过计算新数据的特征子空间从而减少时间开销。第二种增量改进算法结合了缓冲区的思想[14],为数据开创时间缓冲区,通过缓冲区来减少时间开销。
2.1 基于图规则化的多模态NMF拉普拉斯特征映射是一种基于图的降维方法,它可以使图中原本相近的2个点在降维后依然尽量地靠近。因此,拉普拉斯矩阵使数据中具有相似性的实例在降维后的空间内依旧保持高度相似,以达到后续更好的特征学习效果[15]。
根据数据间的欧氏距离,采用p-最近邻算法构造出一个邻接矩阵W,Wij表示数据实例i和数据实例j的相似度,要求在降维后的子空间内原本靠近的数据仍旧相近,即在共享特征子空间V中,原始空间相近的行向量vi与行向量vj(Wij较大)的距离要尽可能的小。故得到目标函数:
| $ \begin{gathered} \min \frac{1}{2} \sum\limits_{i, j}\left\|\boldsymbol{v}_{i}^{\mathrm{T}}-\boldsymbol{v}_{j}^{\mathrm{T}}\right\|^{2} \boldsymbol{W}_{i j}=\sum\limits_{i, j} \boldsymbol{v}_{i} \boldsymbol{v}_{i}^{\mathrm{T}} \boldsymbol{D}_{i i}-\sum\limits_{i, j} \boldsymbol{v}_{j} \boldsymbol{v}_{i}^{\mathrm{T}} \boldsymbol{W}_{i j}= \\ \boldsymbol{T}_{r}\left(\boldsymbol{V} \boldsymbol{D} \boldsymbol{V}^{\mathrm{T}}\right)-\boldsymbol{T}_{r}\left(\boldsymbol{V} \boldsymbol{W} \boldsymbol{V}^{\mathrm{T}}\right)=\boldsymbol{T}_{r}\left(\boldsymbol{V} \boldsymbol{L} \boldsymbol{V}^{\mathrm{T}}\right), \end{gathered} $ | (6) |
式中:L是图的拉普拉斯矩阵,L=D-W;W是邻接矩阵;D是度矩阵,它是一个对角矩阵,其每一行的对角元素是W矩阵中对应每一行或列之和。
根据上述方法计算得到每一个模态数据的拉普拉斯矩阵L(v)后,便可得到基于图规则化的多模态NMF的目标函数:
| $ \begin{aligned} &\min \sum\limits_{v=1}^{n_{v}}\left(\left\|\boldsymbol{X}^{(v)}-\boldsymbol{U}^{(v)} \boldsymbol{V}^{\mathrm{T}}\right\|_{F}^{2}+\lambda \boldsymbol{T}_{r}\left(\boldsymbol{V} \boldsymbol{L}^{(v)} \boldsymbol{V}^{\mathrm{T}}\right)\right), \\ &\text { s.t. } \quad \boldsymbol{V} \geqslant 0, \boldsymbol{U}^{(v)} \geqslant 0, v=1, 2, 3, \cdots, n_{v} 。\end{aligned} $ | (7) |
式中,λ为图正则化项的控制参数。
2.2 增量自适应图规则化多模态NMF基于2.1节的图规则化的多模态NMF,文中提出增量自适应图非负矩阵分解模型(IAGNMF, incremental adaptive graph regularized multi-modal NMF)。模型中假设新数据与原有数据是相对独立的,因此对于新到来的数据,在保持原有数据共享特征子空间不变的基础上为新数据开辟新的特征子空间。对于图的增量计算则是对每个模态新数据在全局数据集合空间上的分布特点进行拟合,保证新数据对应特征子空间分布与各个模态所有数据分布相似。最后为每个模态设立一个模态权值,通过权值自适应更新来控制各模态对于新数据特征子空间学习的贡献,具体细节如下:
给定已完成特征学习的多模态数据,包括其数据集
当新数据Xnew={Xl(v)}v=1nv
| $ \begin{aligned} &\sum\limits_{v=1}^{n_{v}}\left\|\left[\boldsymbol{X}_{k}^{(v)}, \boldsymbol{X}_{l}^{(v)}\right]-\boldsymbol{U}_{k+l}^{(v)}\left[\boldsymbol{V}_{k}, \boldsymbol{V}_{l}\right]\right\|_{F}^{2}, \\ &\text { s.t. } \quad \boldsymbol{U}_{k+l}^{(v)}, \boldsymbol{V}_{l} \geqslant 0, v=1, 2, 3, \cdots, V。\end{aligned} $ | (8) |
然后在式(8)的基础上,加入图拉普拉斯正则化项,来保证特征空间分布与数据分布相似。图的顶点对应数据空间中的每个数据,计算文本数据的余弦距离来构造p-最近邻图。通过沿用以前数据的近邻图Wk(v),仅计算与新数据相关部分的图结构来实现图的增量构建。当新数据到来时,新的图结构矩阵计算如下:
| $ \boldsymbol{W}_{k+l{i j}}^{(v)}=\left\{\begin{array}{cc} \boldsymbol{W}_{k i j}^{(v)} & 1 \leqslant i, j \leqslant k, \\ \frac{\boldsymbol{x}_{i}^{(v)} T \boldsymbol{x}_{j}^{(v)}}{\left|\boldsymbol{x}_{i}^{(v)}\right|\left|\boldsymbol{x}_{j}^{(v)}\right|} \quad & \boldsymbol{x}_{i}^{(v)} \in \boldsymbol{N}_{p}\left(\boldsymbol{x}_{j}^{(v)}\right)\left\|\boldsymbol{x}_{j}^{(v)} \in \boldsymbol{N}_{p}\left(\boldsymbol{x}_{i}^{(v)}\right), j>k\right\| i>k, \\ 0 & \text { 否则, } \end{array}\right. $ | (9) |
式中,W(v)k+lij为图结构矩阵Wk+l(v)的第i行第j列的数值。xi(v),xj(v)表示的是数据矩阵X(v)的第i,j个实例的数据。Np(xi(v))表示xi(v)的p个最近邻居实例的集合。Lk+l(v)=Dk+l(v)-Wk+l(v),Lk+l(v)是第v个模态在数据空间上的拉普拉斯矩阵,Dk+l(v)是对角矩阵,上边的每一个元素为对应Wk+l(v)上每一行或者列的加和,Tr(·)表示矩阵的迹,上标T表示矩阵的转置。在式(8)基础上,加入图拉普拉斯正则化项后得到:
| $ \begin{gathered} \sum\limits_{v=1}^{n_{v}}\left\|\left[\boldsymbol{X}_{k}^{(v)}, \boldsymbol{X}_{l}^{(v)}\right]-\boldsymbol{U}_{k+l}^{(v)}\left[\boldsymbol{V}_{k}, \boldsymbol{V}_{l}\right]\right\|_{F}^{2}+\lambda \boldsymbol{T}_{r}\left(\left[\boldsymbol{V}_{k}, \boldsymbol{V}_{l}\right] \boldsymbol{L}_{k+l}^{(v)}\left[\boldsymbol{V}_{k}, \boldsymbol{V}_{l}\right]^{\mathrm{T}}\right), \\ \text { s.t. } \quad \boldsymbol{U}_{k+l}^{(v)}, \boldsymbol{V}_{l} \geqslant 0, v=1, 2, 3, \cdots, V_{。} \end{gathered} $ | (10) |
最后,在式(10)的基础上为模态添加自适应权重因子(α(v))γ,其中,α(v)为第v个模态的权重因子,γ为控制权重分散程度的参数。自动更新自身模态权重,约束不同模态对特征子空间的影响。这样得到了目标函数:
| $ \begin{gathered} \min \sum\limits_{v=1}^{n_{v}}\left(\alpha^{(v)}\right) \gamma\left\|\left[\boldsymbol{X}_{k}^{(v)}, \boldsymbol{X}_{l}^{(v)}\right]-\boldsymbol{U}_{k+l}^{(v)}\left[\boldsymbol{V}_{k}, \boldsymbol{V}_{l}\right]\right\|_{F}^{2}+\lambda \boldsymbol{T}_{r}\left(\left[\boldsymbol{V}_{k}, \boldsymbol{V}_{l}\right] \boldsymbol{L}_{k+l}^{(v)}\left[\boldsymbol{V}_{k}, \boldsymbol{V}_{l}\right]^{\mathrm{T}}\right), \\ \text { s.t. } \boldsymbol{U}_{k+l}^{(v)}, \boldsymbol{V}_{l} \geqslant 0, v=1, 2, 3, \cdots, V。\end{gathered} $ | (11) |
观察式(11),当变量Uk+l(v),(α(v))γ,Vl耦合在一起时式(11)是非凸,寻找全局最优解十分困难。因此,在更新某一变量时固定无关变量这一策略来寻求式(11)的局部最优解,具体步骤如下:
1) 给定α(v),Vl,更新Uk+l(v)。
因为Uk+l(v)之间是相互独立的,式(11)可以简化成:
| $ \min \left(\alpha^{(v)}\right) \gamma\left\|\left[\boldsymbol{X}_{k}^{(v)}, \boldsymbol{X}_{l}^{(v)}\right]-\boldsymbol{U}_{k+l}^{(v)}\left[\boldsymbol{V}_{k}, \boldsymbol{V}_{l}\right]\right\|_{F}^{2} 。$ | (12) |
令Xk+l(v)=[Xk(v), Xl(v)], Vk+l=[Vk, Vl], 利用拉格朗日优化函数对式(12)进行优化表示得到:
| $ L\left(\boldsymbol{U}_{k+l}^{(v)}\right)=\left(\alpha^{(v)}\right) \gamma \boldsymbol{T}_{r}\left(-2 \boldsymbol{X}_{k+l}^{(v)}\left(\boldsymbol{U}_{k+l}^{(v)} \boldsymbol{V}_{k+l}\right)^{\mathrm{T}}+\boldsymbol{U}_{k+l}^{(v)} \boldsymbol{V}_{k+l}\left(\boldsymbol{U}_{k+l}^{(v)} \boldsymbol{V}_{k+l}\right)^{\mathrm{T}}\right)+\boldsymbol{T}_{r}\left({\mathit{\pmb{\varphi}}}^{(v)} \boldsymbol{U}_{k+l}^{(v)}\right), $ | (13) |
其中,φ(v)为限定条件Uk+l(v)≥0的拉格朗日乘子,用式(13)对Uk+l(v)求偏导得到:
| $ \frac{\partial L\left(\boldsymbol{U}_{k+l}^{(v)}\right)}{\partial \boldsymbol{U}_{k+l}^{(v)}}=\left(\alpha^{(v)}\right) \gamma\left(-2 \boldsymbol{X}_{k+l}^{(v)} \boldsymbol{V}_{k+l} T+2 \boldsymbol{U}_{k+l}^{(v)} \boldsymbol{V}_{k+l} \boldsymbol{V}_{k+l}{ }^{\mathrm{T}}\right)+{\mathit{\pmb{\varphi}}}^{(v)} 。$ | (14) |
通过KKT(Karush-Kuhn-Tucher)条件(φ(v))ij(Uk+l(v))ij=0,得到Uk+l(v)的更新规则为:
| $ \left(\boldsymbol{U}_{k+l}^{(v)}\right)_{i j} \leftarrow \frac{\left(\boldsymbol{X}_{k+l}^{(v)} \boldsymbol{V}_{k+l} T\right)_{i j}}{\left(\boldsymbol{U}_{k+l}^{(v+l} \boldsymbol{V}_{k+l} \boldsymbol{V}_{k+l} T\right)_{i j}}\left(\boldsymbol{U}_{k+l}^{(v)}\right)_{i j }。$ | (15) |
2) 给定α(v),Uk+l(v),更新Vl。
记Lk+l(v)为
| $ \boldsymbol{L}_{k+l}^{(v)}=\left[\begin{array}{cc} \boldsymbol{L}_{k}^{(v)} & \boldsymbol{L}_{k \sim l}^{(v)} \\ \left(\boldsymbol{L}_{k \sim l}^{(v)}\right)^{\mathrm{T}} & \boldsymbol{L}_{l \sim l}^{(v)} \end{array}\right], $ | (16) |
因为Vl与Vk,Xk(v)无关,式(11)可以简化成:
| $ \min \sum\limits_{v=1}^{n_{v}}\left(\alpha^{(v)}\right) \gamma\left\|\boldsymbol{X}_{l}^{(v)}-\boldsymbol{U}_{k+l}^{(v)} \boldsymbol{V}_{l}\right\|_{F}^{2}+2 \lambda \boldsymbol{T}_{r}\left(\boldsymbol{V}_{l}^{\mathrm{T}} \boldsymbol{V}_{k} \boldsymbol{L}_{k \sim l}^{(v)}\right)+\lambda \boldsymbol{T}_{r}\left(\boldsymbol{V}_{l}^{\mathrm{T}} \boldsymbol{V}_{l} \boldsymbol{L}_{l \sim l}^{(v)}\right)。$ | (17) |
利用拉格朗日优化函数对式(17)进行优化表示得到:
| $ \begin{aligned} L\left(\boldsymbol{V}_{l}\right)=& \sum\limits_{v=1}^{n_{v}}\left(\alpha^{(v)}\right) \gamma \boldsymbol{T}_{r}\left(-2 \boldsymbol{X}_{k+l}^{(v)}\left(\boldsymbol{U}_{k+l}^{(v)} \boldsymbol{V}_{k+l}\right)^{\mathrm{T}}+\boldsymbol{U}_{k+l}^{(v)} \boldsymbol{V}_{k+l}\left(\boldsymbol{U}_{k+l}^{(v)} \boldsymbol{V}_{k+l}\right)^{\mathrm{T}}\right)+\\ & 2 \lambda \boldsymbol{T}_{r}\left(\boldsymbol{V}_{l}^{\mathrm{T}} \boldsymbol{V}_{k} \boldsymbol{L}_{k \sim l}^{(v)}\right)+\lambda \boldsymbol{T}_{r}\left(\boldsymbol{V}_{l}^{\mathrm{T}} \boldsymbol{V}_{l} \boldsymbol{L}_{l \sim l}^{(v)}\right)+\boldsymbol{T}_{r}\left({\mathit{\pmb{\phi}}} \boldsymbol{V}_{l}\right), \end{aligned} $ | (18) |
其中:Ø为限定条件Vl≥0的拉格朗日乘子,用式(18)对Vl求偏导得到:
| $ \frac{\partial L\left(\boldsymbol{V}_{l}\right)}{\partial \boldsymbol{V}_{l}}=\sum\limits_{v=1}^{n_{v}}\left(\alpha^{(v)}\right) \gamma\left(-2 \boldsymbol{U}_{k+l}^{(v) }{ }^{\mathrm{T}} \boldsymbol{X}_{k+l}^{(v)}+2 \boldsymbol{U}_{k+l}^{(v)}{ }^{\mathrm{T}} \boldsymbol{U}_{k+l}^{(v)} \boldsymbol{V}_{k+l}\right)+2 \lambda \boldsymbol{V}_{k} \boldsymbol{L}_{k \sim l}^{(v)}+2 \lambda \boldsymbol{V}_{l} \boldsymbol{L}_{l \sim l}^{(v)}+\varnothing。$ | (19) |
通过KKT(Karush-Kuhn-Tucher)条件(Ø)ij(Vl)ij=0,得到Vl的更新规则为:
| $ \left(\boldsymbol{V}_{l}\right)_{i j} \leftarrow \frac{\left(\boldsymbol{U}_{k+l}^{(v)} T \boldsymbol{X}_{k+l}^{(v)}+2 \lambda \boldsymbol{V}_{k} \boldsymbol{W}_{k \sim l}^{(v)}+2 \lambda \boldsymbol{V}_{l} \boldsymbol{W}_{l \sim l}^{(v)}\right)_{i j}}{\left(\boldsymbol{U}_{k+l}^{(v)} T \boldsymbol{U}_{k+l}^{(v)} \boldsymbol{V}_{k+l}+2 \lambda \boldsymbol{V}_{k} \boldsymbol{D}_{k \sim l}^{(v)}+2 \lambda \boldsymbol{V}_{l} \boldsymbol{D}_{l \sim l}^{(v)}\right)_{i j}}\left(\boldsymbol{V}_{l}\right)_{i j}。$ | (20) |
3) 给定Vl, Uk+l(v),更新α(v)。
令F(v)=||[Xk(v), Xl(v)]-Uk+l(v)[Vk, Vl]||F2, 那么式(11)可以简化成:
| $ \begin{gathered} \min \sum\limits_{v=1}^{n_{v}}\left(\alpha^{(v)}\right) \gamma \boldsymbol{F}^{(v)}, \\ \text { s.t. } \sum\limits_{v=1}^{V} \alpha^{(v)}=1, \alpha^{(v)} \geqslant 0 。\end{gathered} $ | (21) |
利用拉格朗日优化公式对式(21)进行优化表示得到
| $ \sum\limits_{v=1}^{n_{v}}\left(\alpha^{(v)}\right) \gamma \boldsymbol{F}^{(v)}-\mu\left(\sum\limits_{v=1}^{V} \alpha^{(v)}-1\right)。$ | (22) |
利用式(22)对α(v)求导,使导数为0,得到:
| $ \alpha^{(v)}=\left(\frac{\mu}{\gamma \boldsymbol{F}^{(v)}}\right) \frac{1}{\gamma-1} 。$ | (23) |
将式(23)代入α(v)的限制条件
| $ \alpha^{(v)}=\frac{\left(\gamma \boldsymbol{F}^{(v)}\right) \frac{1}{1-\gamma}}{\sum\limits_{v=1}^{V}\left(\gamma \boldsymbol{F}^{(v)}\right) \frac{1}{1-\gamma}} 。$ | (24) |
这样,通过式(15),式(20),式(24)迭代更新变量Uk+l(v),Vl,α(v)使得目标函数(11)收敛,即可获得新数据的低维特征Vl。
2.3 在线自适应图规则化多模态NMF与IAGNMF不同,在线自适应图非负矩阵分解(OAGNMF, online adaptive graph regularized multi-modal NMF)假设新数据总是与它到达时间相近的数据关联性更强,而与到达时间较远的数据关联更弱。因此,模型中设立一个固定大小的缓冲区,总是存放s个最近到来的数据,将其他较早到来的数据丢弃。运用缓存区的数据进行特征子空间学习。
定义X[s, t](v)=[xt-s+1(v), …, xt(v)] ∈
因此,在构造图正则化项时,仅需要计算缓冲区实例的p-最近邻图即可。顶点对应缓存区的实例,同样采用余弦距离来衡量文本实例的相似度:
| $ \boldsymbol{W}_{s i j}^{(v)}=\left\{\begin{array}{cc} \frac{\boldsymbol{x}_{i}^{(v)} T \boldsymbol{x}_{j}^{(v)}}{\left|\boldsymbol{x}_{i}^{(v)}\right|\left|\boldsymbol{x}_{j}^{(v)}\right|} & \boldsymbol{x}_{i}^{(v)} \in \boldsymbol{N}_{p}\left(\boldsymbol{x}_{j}^{(v)}\right)|| \boldsymbol{x}_{j}^{(v)} \in \boldsymbol{N}_{p}\left(\boldsymbol{x}_{i}^{(v)}\right), \\ 0 & \text { 否则。} \end{array}\right. $ | (25) |
得到图的拉普拉斯矩阵Ls(v)=Ds(v)-Ws(v), Ds(v)是对角矩阵,里边的每一个元素为对应Ws(v)上每一行或者列之和。添加模态自适应权重因子,得到目标函数:
| $ \begin{gathered} \min \sum\limits_{v=1}^{n_{v}}\left(\alpha^{(v)}\right) \gamma\left\|\boldsymbol{X}_{[s, t+1]}^{(v)}-\boldsymbol{U}_{t+1}^{(v)} \boldsymbol{V}_{s}\right\|_{F}^{2}+\lambda \boldsymbol{T}_{r}\left(\boldsymbol{V}_{s} \boldsymbol{L}_{s}^{(v)} \boldsymbol{V}_{s}^{\mathrm{T}}\right), \\ \text { s.t. } \boldsymbol{U}_{t+1}^{(v)}, \boldsymbol{V}_{s} \geqslant 0, v=1, 2, 3, \cdots n_{v} 。\end{gathered} $ | (26) |
式中:Ut+1(v)∈
类似的,目标函数(26)是非凸的,采取同样的策略寻找局部最优解:
1) 给定α(v),Vl,更新Ut+1(v)。
对目标函数(26)进行拉格朗日优化表示后对Ut+1(v)求导得到:
| $ \frac{\partial L\left(\boldsymbol{U}_{t+1}^{(v)}\right)}{\partial \boldsymbol{U}_{t+1}^{(v)}}=\left(\alpha^{(v)}\right) \gamma\left(-2 \boldsymbol{X}_{[s, t+1]}^{(v)} \boldsymbol{V}_{s}^{\mathrm{T}}+2 \boldsymbol{U}_{t+1}^{(v)} \boldsymbol{V}_{s} \boldsymbol{V}_{s}^{\mathrm{T}}\right)+{\mathit{\pmb{\varphi}}}^{(v)}, $ | (27) |
式中,φ(v)为限定条件Uk+l(v)≥0的拉格朗日乘子,通过KKT条件(φ(v))ij(Ut+1(v))ij=0,得到Uk+l(v)的更新规则为:
| $ \left(\boldsymbol{U}_{t+1}^{(v)}\right)_{i j} \leftarrow \frac{\left(\boldsymbol{X}_{[s, t+1]}^{(v)} \boldsymbol{V}_{s}^{T}\right)_{i j}}{\left(\boldsymbol{U}_{t+1}^{(v)} \boldsymbol{V}_{s} \boldsymbol{V}_{s}^{\mathrm{T}}\right)_{i j}}\left(\boldsymbol{U}_{t+1}^{(v)}\right)_{i j }。$ | (28) |
2) 给定α(v),Ut+1(v),更新Vs。
同理,对目标函数(26)进行拉格朗日优化表示后对Vs求导,通过KKT条件使导数为0得到Vl的更新规则:
| $ \left(\boldsymbol{V}_{s}\right)_{i j} \leftarrow \frac{\left(\boldsymbol{U}_{t+1}^{(v)} T \boldsymbol{X}_{[s, t+1]}^{(v)}+2 \lambda \boldsymbol{V}_{s} \boldsymbol{W}_{s}^{(v)}\right)_{i j}}{\left(\boldsymbol{U}_{t+1}^{(v)} T \boldsymbol{U}_{t+1}^{(v)} \boldsymbol{V}_{s}+2 \lambda \boldsymbol{V}_{k} \boldsymbol{D}_{s}^{(v)}\right)_{i j}}\left(\boldsymbol{V}_{s}\right)_{i j} 。$ | (29) |
3) 给定Vs, Ut+1(v),更新α(v)。
与IAGNMF算法中α(v)更新相同,令F(v)=||X[s, t+1](v)-Ut+1(v)Vs||F2,可以得到α(v)的更新规则为:
| $ \alpha^{(v)}=\frac{\left(\gamma \boldsymbol{F}^{(v)}\right) \frac{1}{1-\gamma}}{\sum\limits_{v=1}^{n_{v}}\left(\gamma \boldsymbol{F}^{(v)}\right) \frac{1}{1-\gamma}} 。$ | (30) |
通过式(28)~(30)迭代更新变量Ut+1(v),Vs,α(v)使得目标函数(26)收敛,得到了共享特征子空间矩阵Vs。Vs=[v1, v2, …, vs-l+1, …, vs],令Vl=[vs-l+1, …, vs-1, vs],计算得到新实例对应的低维特征Vl。
2.4 复杂度分析为运行IAGNMF,在增量迭代的过程中需要储存多模态数据Xk(v), Xl(v),投影矩阵Uk+l(v),共享子空间特征矩阵Vk, Vl,图结构矩阵Wk+l(v),对角矩阵Dk+l(v)、图的拉普拉斯矩阵Lk+l(v), 控制参数γ,λ和α(v)。在每一次增量过程中,主要时间开销分为两部分:一部分为图结构矩阵Wk+l(v)的计算,时间复杂度为O(Mvl(k+l))。另一部分为矩阵Uk+l(v),Vl,控制参数α(v)的迭代更新。
设多模态数据平均模态维度为M,算法IAGNMF的空间复杂度为O(V(Mk+Ml+MMc+3(k+l)2+1)+Mc(k+l)+2)(V(Mk+Ml+MMc+3(k+l)2+1)+Mc(k+l)+2)≈O((k+l)2)。假设迭代更新平均收敛次数是tt,多模态数据平均模态维度为M,算法IAGNMF一次增量过程的时间复杂度为O(Vt(2MMc(k+l)+Ml(k+l))+VMvl(k+l))≈O(k)O(Vt(2MMc(k+l)+Ml(k+l))+VMvl(k+l))O(Vt(2MMc(k+l)+Ml(k+l))+VMvl(k+l))。
与IAGNMF算法类似,为运行OAGNMF,在增量迭代的过程中需要储存多模态数据X[s, t+1](v),投影矩阵Ut+1(v),共享子空间特征矩阵Vs,图结构矩阵Ws(v),对角矩阵Ds(v)、图的拉普拉斯矩阵Ls(v), 控制参数γ,λ和α(v)。算法OAGNMF在每一次增量过程中,主要时间开销分为两部分:一部分为图结构矩阵Ws(v)的计算,时间复杂度为O(Mvs2);另一部分为矩阵Ut+1(v),Vs,控制参数α(v)的迭代更新。
设多模态数据平均模态维度为M,算法OAGNMF的空间复杂度为O(V(Ms+MMc+3s2+1)+Mcs+2)≈O(1)O(V(Ms+MMc+3s2+1)+Mcs+2)O(V(Ms+MMc+3s2+1)+Mcs+2)。假设迭代更新平均收敛次数是tt,多模态数据平均模态维度为M,那么算法OAGNMF一次增量过程的时间复杂度为O(Vt(2MMcs+Ms2)+VMvs2)≈O(1)O(Vt(2MMcs+Ms2)+VMvs2)O(Vt(2MMcs+Ms2)+VMvs2)。
3 实验分析为验证文中提出算法的有效性,设计了一系列算法对比实验,并在多模态文本数据集LegalText和Webkb上验证算法IAGNMF和OAGNMF和现有的一些相关算法:ConcatNMF(concatenation NMF)[6],INMF (incremental NMF)[13],MultiINMF (multi-view Incremental NMF) [10]和MultiGNMF(multi-view graph NMF) [15]的性能。一是比较共享特征学习效果,将算法提取出来的低维特征进行k-means聚类分析,分析聚类的准确度(ACC, accuracy)和纯度(PUR, purity)。二是比较运行算法的时间开销。
3.1 数据集 3.1.1 数据集LegalTextLegalText数据集是具有7个大类6 300个法律案例的文本数据,分别是渎职,妨害社会管理秩序,破坏社会主义市场经济秩序,侵犯财产,侵犯公民人身权利、民主权利,贪污受贿,危害公共安全。通过预处理得到150维word2vec特征和500维tfidf特征2个模态。
3.1.2 数据集WebkbWebkb数据集[16]源自于康奈尔大学计算机科学系的网页文本内容,该数据集包含属于4个类别的8 282个数据样例,共有2 500维网页中的文本特征属性和1 380维网页中超链接的锚文本特征属性2种模态信息。
3.2 算法比较文中基于NMF提出2种增量多模态聚类算法,实验中,将提出的2种算法与现有的一些基于NMF的增量和非增量方法进行比较,验证提出算法的性能。具体比较算法包括:①ConcatNMF:将多模态数据的所有模态属性进行直接拼接后进行非负矩阵分解[6];②INMF [13]:为单模态增量非负矩阵分解方法,实验中对数据集中多有模态数据进行单模态增量学习,并采用最好模态结果;③MultiINMF:为多模态非负矩阵分解MultiNMF的增量算法[10],其增量实现与INMF相同;④MultiGNMF为基于图规则化的多模态数据融合算法,其实现拓展了图正则化NMF[15]到多模态数据。
3.3 实验设置实验当中,比较算法ConcatNMF、INMF、MultiINMF和MultiGNMF的参数选择与其原始文献中相同。文中提出的IAGNMF图正则化参数λ=15,权重分散程度参数γ=1.3;OAGNMF图正则化参数λ=15,权重分散程度参数γ=1.3,缓冲区大小设置为40%数据集大小。每次实验非重复地取1/10数据集的实例作为新到来的实例运行算法学习其低维共享特征,运行10次之后完成对整个数据集的特征学习。对于增量算法,每次学习新实例的低维共享特征后,记录学习时间,与已经完成特征学习的实例的低维共享特征一起进行聚类分析验证学习效果;对于非增量算法,新实例和已完成特征学习的实例一起进行特征学习,记录学习时间,将学习到的所有实例的低维共享特征进行聚类分析验证学习效果。对于每次模型运行,都能得到其时间开销,聚类精度和纯度。每个实验重复运行15次,并取其均值输出比较结果。
实验环境为Windows10操作系统,Matlab R2018a软件平台,硬件环境为IntelⓇCoreTM i5-7300HQ CPU @ 2.50GHz处理器,8G内存。
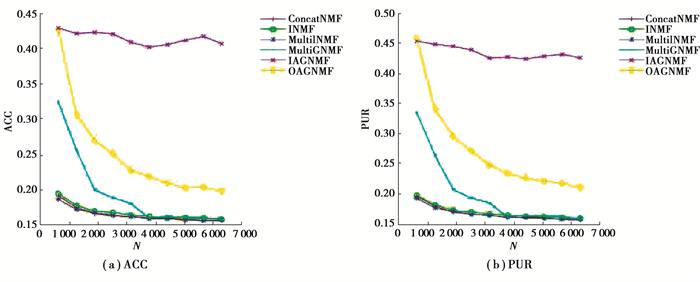
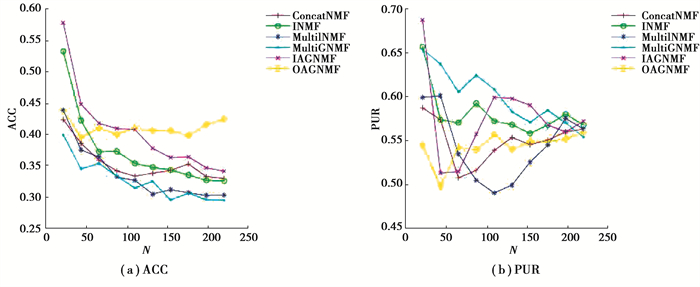
3.4 结果分析LegalText和Webkb 2个文本数据集上的各算法聚类有效性比较结果如图 2和图 3所示。
|
图 2 LegalText数据集上的聚类结果比较 Fig. 2 Comparison of clustering results on LegalText dataset |
|
图 3 Webkb数据集上的聚类结果比较 Fig. 3 Comparison of clustering results on Webkb dataset |
从图 2和图 3可以看出,相比于ConcatNMF、INMF、MultiINMF和MultiGNMF,文中提出的2种增量多模态文本聚类方法具有一定的优势。例如,在LegalText数据集上IAGNMF在ACC和PUR 2种聚类指标上一直优于所有比较算法,这是因为IAGNMF实现了增量的图规则化机制保证了融合空间特征与原始数据具有一致的几何相似结构,此外IAGNMF实现了模态权重的自适应调整,保证了各模态的有效信息。同样OAGNMF和MultiGNMF也是用了图规则化项,也得到了较好的结果。OAGNMF采用数据缓存机制,假设一段时间内数据具有相似性,而在实际的数据集LegalText中这个假设很难保证,但在标准数据集Webkb中便能得到较好的效果(如图 4)。MultiGNMF实现没有考虑各模态的权重,所以相比于文中提出的算法其性能略有下降。
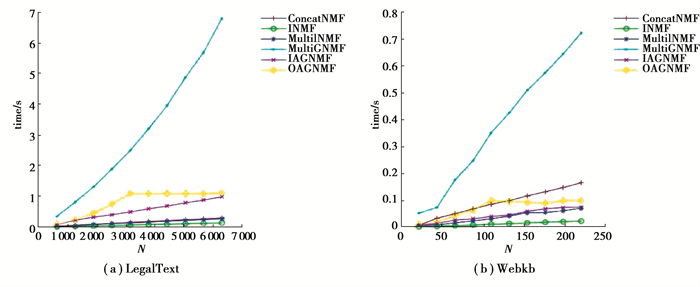
|
图 4 2个数据集上的时间开销比较 Fig. 4 Comparison of time consumption on two datasets |
图 4给出了几种比较算法的时间性能。从图中可以看出,基于图规则化的MultiGNMF比ConcatNMF、INMF和MultiINMF需要消耗更多的时间。IAGNMF和OAGNMF同样使用图规则化提升算法的性能,但其增量实现能够有效减少算法的时间开销。
综上,相比于比较算法文中提出的2种算法在聚类性能和时间消耗上均具有一定的优势,适合海量多模态文本数据的增量融合学习与聚类分析。当数据集中数据样本随采集时间有一定的前后依赖时,采用数据缓存机制的OAGNMF算法能够得到较好的性能;而当数据间没有时间依赖时,采用增量图相似结构度量的IAGNMF算法具有更加的聚类性能。
4 结束语文中提出2种增量多模态文本聚类算法,基于NMF构建多模态文本数据特征学习基本模型,利用局部相似图规则化保证学习特征空间的结合结构与原始数据空间的一致性,提升多模态融合特征学习的准确性。设计了2种增量多模态数据特征学习机制,并对各模态权重进行自适应调整,实现海量多模态文本数据的快速、有效融合学习。通过2个实际文本数据集上的实验结果表明,文中提出的2种算法具有一定的优越性。
| [1] |
Zhao J, Xie X J, Xu X, et al. Multi-view learning overview: recent progress and new challenges[J]. Information Fusion, 2017, 38: 43-54. DOI:10.1016/j.inffus.2017.02.007 |
| [2] |
Zhao L, Chen Z K, Wang Z J. Unsupervised multiview nonnegative correlated feature learning for data clustering[J]. IEEE Signal Processing Letters, 2018, 25(1): 60-64. DOI:10.1109/LSP.2017.2769086 |
| [3] |
Amini M R, Usunier N, Goutte C. Learning from multiple partially observed views-an application to multilingual text categorization[J]. Advances in Neural Information Processing Systems, 2009, 28-36. |
| [4] |
Amini M R, Goutte C. A co-classification approach to learning from multilingual corpora[J]. Machine Learning, 2010, 79(1/2): 105-121. |
| [5] |
Blum A, Mitchell T. Combining labeled and unlabeled data with co-training[C]//Proceedings of the Eleventh Annual Conference on Computational Learning Theory. New York, USA: ACM Press, 1998: 92-100.
|
| [6] |
Lee D D, Seung H S. Algorithms for non-negative matrix factorization[C]//Advances in Neural Information Processing Systems, 2001: 556-562.
|
| [7] |
李乐, 章毓晋. 非负矩阵分解算法综述[J]. 电子学报, 2008, 36(4): 737-743. Li L, Zhang Y J. A survey on algorithms of non-negative matrix factorization[J]. Acta Electronica Sinica, 2008, 36(4): 737-743. (in Chinese) DOI:10.3321/j.issn:0372-2112.2008.04.023 |
| [8] |
Zhao L, Chen Z, Yang Y, et al. Incomplete multi-view clustering via deep semantic mapping[J]. Neurocomputing, 2018, 275: 1053-1062. DOI:10.1016/j.neucom.2017.07.016 |
| [9] |
Li Z, Tang J, He X. Robust structured nonnegative matrix factorization for image representation[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017, 29(5): 1947-1960. |
| [10] |
Zheng H, Liang Z X, Tian F, et al. NMF-based comprehensive latent factor learning with multiview Data[C]//2019 IEEE International Conference on Image Processing (ICIP). IEEE, 2019: 489-493.
|
| [11] |
Xu W, Liu X, Gong Y. Document clustering based on non-negative matrix factorization[C]//Proceedings of the 26th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval. Toronto, Canada, 2003: 267-273.
|
| [12] |
Brunet J P, Tamayo P, Golub T R, et al. Metagenes and molecular pattern discovery using matrix factorization[J]. Proceedings of the National Academy of Sciences of the United States of America, 2004, 101(12): 4164-4169. DOI:10.1073/pnas.0308531101 |
| [13] |
Bucak S S, Gunsel B. Incremental subspace learning via non-negative matrix factorization[J]. Pattern Recognition, 2009, 42(5): 788-797. DOI:10.1016/j.patcog.2008.09.002 |
| [14] |
Shao W X, He L F, Lu C T, et al. Online unsupervised multi-view feature selection[C]//2016 IEEE 16th International Conference on Data Mining (ICDM). IEEE, 2016: 1203-1208.
|
| [15] |
Cai D, He X F, Han J W, et al. Graph regularized nonnegative matrix factorization for data representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(8): 1548-1560. DOI:10.1109/TPAMI.2010.231 |
| [16] |
Qiu X, Chen Z, Zhao L, et al. Unsupervised multi-view non-negative for law data feature learning with dual graph-regularization in smart Internet of Things[J]. Future Generation Computer Systems, 2019, 100: 523-530. DOI:10.1016/j.future.2019.05.055 |
 2022, Vol. 45
2022, Vol. 45

