b. 重庆大学 机械与运载工程学院, 重庆 400044
b. College of Mechanical and Vehicle Engineering, Chongqing University, Chongqing 400044, P. R. China
石油危机和环境污染促使了纯电动汽车的快速发展。动力锂电池包作为纯电动汽车的重要组成部分,其性能直接影响纯电动汽车的续航里程和安全表现。动力锂电池包的最佳工作温度区间为20~45 ℃,最佳温差低于5 ℃[1],若超过此温度范围,动力锂电池包的使用性能、寿命及安全性将会降低[2]。因此,为保证动力锂电池包处于合理的温度范围,采取散热措施至关重要。
目前,众多学者主要采用空气冷却、液体冷却、相变材料和热管等方式对电池包进行散热。在空气冷却方面,Yu等[3]设计了一种集成气流的热管理方案,基于该方案建立了电池温度场理论模型,进行了电池温度分布仿真与实验验证。相比空气冷却,液体冷却具有更好的冷却效果[4]。Rao等[5]提出了一种基于液体冷却的可变接触面热管理系统,通过模拟仿真得出可变接触面对电池内部温度分布均匀性的影响规律。在相变材料和热管冷却方面,部分学者也开展了相关研究。例如,Azizi等[6]将相变材料和铝丝网板构成的复合材料用于LiFePO4电池组的热管理系统,仿真发现使用该材料能够显著降低电池组的温度;Zhao等[7]针对圆柱形动力电池设计了一套热管和相变材料耦合的热管理方案,并进行实验验证了该方案的有效性。
以上文献对电池包常规的热管理方式进行了研究。近年来,随着换电模式的发展[8],半导体制冷片逐渐应用到可更换动力锂电池包的热管理中。相比于传统的热管理方式,半导体制冷片具有体积小、质量轻、制冷效率快、制冷量可通过电流精确控制的优点[9-10],但目前鲜有文献探究半导体制冷量对电池包温度性能的影响。
同时,也有部分学者通过优化电池包内单体电池的排布间距,使其具有较好的散热性能。例如,Zhao等[11]建立了圆柱形锂离子动力电池组的空冷数值模型,探究了不同电池间距对电池温度场的影响,并获得了最优的单体电池间距;Chen等[12]基于流动阻力网络模型和传热模型,对单体电池间距进行了优化设计;Yang等[13]对圆柱单体电池的对齐排列方式和交错排列方式进行了研究,建立了电池模组温度场模型,并进行电池模组温度分布仿真。以上文献通过优化单体电池排布间距使电池包温度表现性能(最高温度、最大温差)最佳,但忽略了排布间距对电池包能量密度的影响。相邻单体电池的排布间距将会影响电池包间距体积的大小,在保证电池包温度表现性能最佳的基础上,减小间距体积能够有效提升电池包的能量密度,对电池包的优化设计具有重要的意义。
综上所述,笔者以重庆某公司研发的半导体制冷动力锂电池包为研究对象,考虑半导体制冷量和单体电池排布间距对电池包温度表现性能和能量密度的影响,结合半导体热分析模型,采用拉丁超立方实验设计和代理模型方法,建立以间距体积和最大温差为目标的多目标优化模型。基于该模型,采用MOGA求解出单体电池排布距离和半导体制冷量,以此为基础加工出电池包实物,并进行了相关的实验研究和验证。
1 基于半导体制冷方案的散热优化框架 1.1 问题描述换电模式下的电池包需要经常拆换,采用常规的散热方式会破坏其密封性,降低电池包的能量密度且难以实现对温度的精确控制。因此,笔者采用半导体制冷片对动力锂电池包进行散热,散热方案如图 1所示。该方案采用导热硅胶将半导体制冷片的冷端与单体电池的极耳贴合,热端与电池包箱体内壁贴合,使电池产生的热量由冷端吸收传递到热端,最终传递到电池箱体外壁。为保证半导体制冷片的散热效率,在箱体外壁设置水冷板,保证半导体热端的热量能够及时地散发出去。
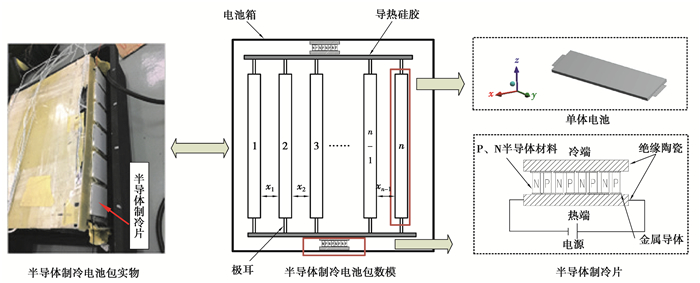
|
图 1 半导体散热方案 Fig. 1 Heat dissipation scheme of semiconductor |
传统电池包设计中,排布间距x1,x2,…,xn设定为等值,导致中间单体电池温度远高于边缘电池,从而影响了整个电池包的温度表现性能[14]。因此,笔者基于半导体散热方案,提出一种单体电池非等间距排列方式,相邻电池间距设置为xi,同时对半导体制冷量进行优化,使电池包表现性能最佳。
1.2 基于半导体制冷方案的散热优化框架以采用半导体制冷方案的动力锂电池包为研究对象,提出一种面向动力锂电池包性能最佳的多目标优化方法,优化框架如图 2所示。
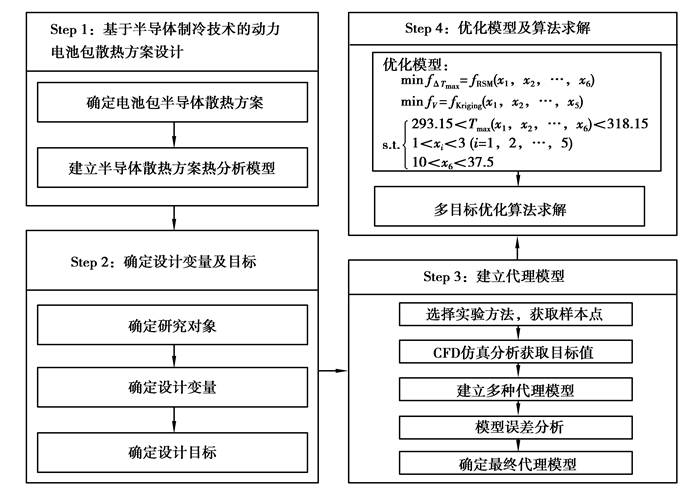
|
图 2 动力锂电池包散热优化框架 Fig. 2 Heat dissipation optimization framework of power lithium battery pack |
优化步骤如下:
1) 基于半导体制冷的动力锂电池包散热方案设计。结合换电模式的特点,确定动力锂电池包半导体散热方案,并建立相应的热分析模型。
2) 确定设计变量及目标。根据半导体散热方案,选取电池模组为研究对象,将半导体制冷量、电池模组内单体电池排列间距作为设计变量,将电池模组最高温度、最大温差及间距体积作为设计目标。
3) 建立代理模型。采用拉丁超立方试验获取设计变量样本点,通过计算流体动力学(computational fluid dynamics, CFD)仿真软件获取相应的响应值,并采用RBF, RSM, Kriging代理模型拟合出设计目标的近似模型,采用误差评价方法选取拟合精度最高的代理模型。
4) 优化模型及算法求解。建立多目标优化模型并采用MOGA求解出的最优的排布间距和半导体制冷量。
2 基于半导体制冷方案的热分析模型 2.1 电池热模型建立电池热模型揭示了电池的产热、传热和散热规律,能够真实反映电池在工作过程中温度场的变化。基于直角坐标系建立单体电池三维传热模型为
| $ \rho c \frac{\partial T}{\partial t}=\lambda_{x} \frac{\partial^{2} T}{\partial x^{2}}+\lambda_{y} \frac{\partial^{2} T}{\partial y^{2}}+\lambda_{z} \frac{\partial^{2} T}{\partial z^{2}}+q, $ | (1) |
式中:ρ为电池密度;c为电池比热容;T为电池工作温度;t为时间;λx, λy, λz为电池在x, y, z方向的热导率;q为电池单位体积生热速率。
求解传热模型需要获取电池的热物性参数ρ, c, λ,生热速率q和边界条件。
2.1.1 电池热物性参数电池的热物性参数是研究单体电池内部传热及温升的关键,精确的热物性参数是保证电池热仿真结果准确性的基础。热物性参数主要包括电池密度ρ、比热容c及热导率λx, λy, λz, 具体参数如表 1所示。
| 表 1 单体电池热物性参数 Table 1 Thermal properties of single battery |
单体电池在放电过程中,主要产热部分为单体电池内核,在计算单体电池内核生热速率时,采用美国加州大学伯克利分校Bernardi提出的理论计算模型[15]。
| $ q_{\mathrm{c}}=\frac{1}{V}\left(I^{2} R+I T \frac{\partial U}{\partial T}\right), $ | (2) |
式中:qc为单体电池内核的生热速率;V为单体电池体积;I为放电电流;R为单体电池内阻(取1 mΩ);T为环境温度;
电池的散热方式主要为空气自然对流换热和半导体制冷片与电池的热传导换热,可表示为
| $ \begin{cases}-\lambda_{x} \frac{\partial T}{\partial x}=h\left(T-T_{\infty}\right) & x=0, l_{x}, \\ -\lambda_{y} \frac{\partial T}{\partial y}=h\left(T-T_{\infty}\right) & y=0, l_{y}, \\ -\lambda_{z} \frac{\partial T}{\partial z}=h\left(T-T_{\infty}\right) & z=0, l_{z}, \end{cases} $ | (3) |
| $ q_{\mathrm{r}}=-\lambda_{\mathrm{r}} \frac{\partial T}{\partial r} $ | (4) |
式中:h为电池与外界换热系数;T∞为环境温度;qr为热流密度;λr为热导率;
半导体制冷片的数值模型主要包括制冷片的传热模型和制冷量。半导体制冷片可通过等效热阻建立传热模型。单个PN结的热导率如公式(5)所示[17]。
| $ \lambda_{\mathrm{np}}=\frac{\lambda_{\mathrm{n}} S_{\mathrm{n}}}{d_{\mathrm{n}}}+\frac{\lambda_{\mathrm{p}} S_{\mathrm{p}}}{d_{\mathrm{p}}} 。$ | (5) |
基于公式(5)可得整个半导体制冷片的传热模型:
| $ \lambda_{\mathrm{s}}=\frac{\sum\limits_{i=1}^{j} d_{i}}{\sum\limits_{i=1}^{j} \frac{d_{i}}{\lambda_{i}}}=\frac{2 d_{\mathrm{t}}+2 m d_{\mathrm{cu}}+m d_{\mathrm{np}}}{\frac{2 d_{\mathrm{t}}}{\lambda_{\mathrm{t}}}+\frac{2 m d_{\mathrm{cu}}}{\lambda_{\mathrm{cu}}}+2 m d_{\mathrm{np}} /\left(\frac{\lambda_{\mathrm{n}} S_{\mathrm{n}}}{d_{\mathrm{n}}}+\frac{\lambda_{\mathrm{p}} S_{\mathrm{p}}}{d_{\mathrm{p}}}\right)}, $ | (6) |
式中:λs为半导体制冷片的热导率;dt, dcu, dnp分别为陶瓷片、铜片及PN结的厚度;λt, λcu, λp, λn分别为陶瓷片、铜片及P, N结的热导率;Sp, Sn分别为P, N结的面积;m为PN结的数量。
半导体制冷量的大小与电流及本身材料性质相关,对动力锂电池包散热性能的好坏起着重要作用。忽略半导体内阻焦耳热的影响,制冷量如公式(7)所示。
| $ Q=\sum\limits_{i=1}^{j}\left[m\left(\alpha_{\mathrm{p}}-\alpha_{\mathrm{n}}\right) T_{\mathrm{c}} I-\lambda_{\mathrm{srs}}\left(T_{\mathrm{h}}-T_{\mathrm{c}}\right)\right], $ | (7) |
式中:αp, αn为P和N型电偶温差电系数;Tc为冷端温度,Th为热端温度;I为电流大小。
3 基于半导体制冷方案的动力锂电池包散热优化模型 3.1 设计目标及变量的选取 3.1.1 研究对象如图 3所示,动力锂电池包共有6个模组,每个模组由16块单体电池组成,模组两端极耳处贴有半导体制冷片。由于模组间具有隔热棉,使不同模组的温度场互不影响,因此笔者选取单个电池模组进行研究。
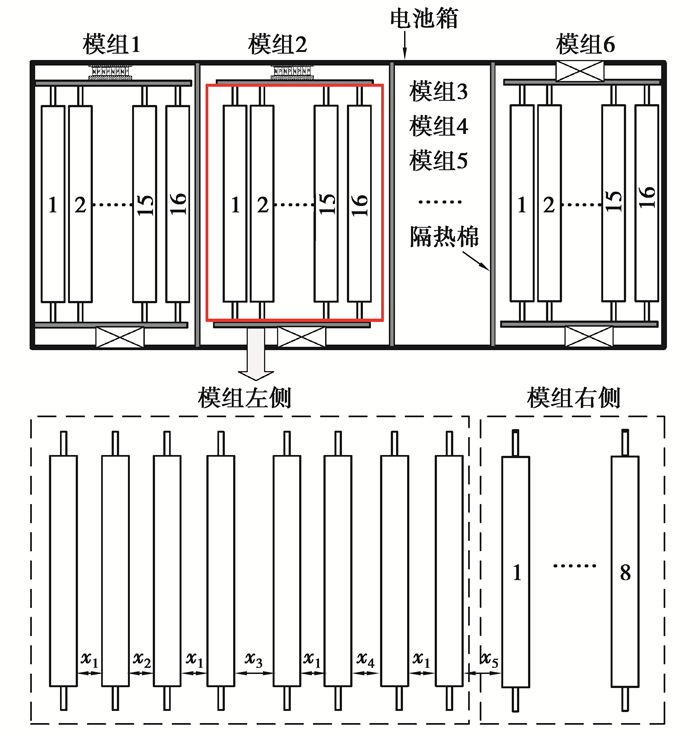
|
图 3 基于半导体制冷技术的电池包设计方案 Fig. 3 Battery pack design scheme based on semiconductor refrigeration technology |
电池模组的表现性能由温度表现性能和间距体积来衡量。温度表现性能主要包括模组最高温度Tmax和单体电池间最大温差ΔTmax,将它们控制在合理的范围内能够有效避免电池出现热失控现象。在保证电池模组温度具有良好表现性能的前提下,较小的间距体积能够显著提高电池包的能量密度,有助于提升电动汽车续航里程。因此将最高温度Tmax、最大温差ΔTmax及间距体积V作为设计目标。
3.1.3 设计变量单体电池排布间距直接影响上述设计目标,因此选取排布间距作为设计变量。考虑模组内单体电池左右对称,选取任一侧的8个单体电池为研究对象,同时为减少设计变量,以2个单体电池为一组,最终得到5个设计变量:x1, x2, x3, x4, x5。电池模组的温度表现同样受半导体制冷量的影响,因此,将半导体制冷量x6也作为设计变量。
3.2 代理模型的建立动力锂电池包优化设计问题是一个多变量非线性且无显式函数关系的工程问题,很难建立相应的数学模型。采用拉丁超立方试验设计和RBF, RSM, Kriging等代理模型建立电池包设计目标的近似模型,并选取最优的近似模型来建立优化模型。
采用拉丁超立方试验设计方法获取80个设计变量样本点。图 4给出了6个设计变量样本点的分布,图中各个变量的样本点均匀分布在设计空间中,具有很好的空间填充性和均衡性,保证了试验因素和优化目标间函数模型的精确性。
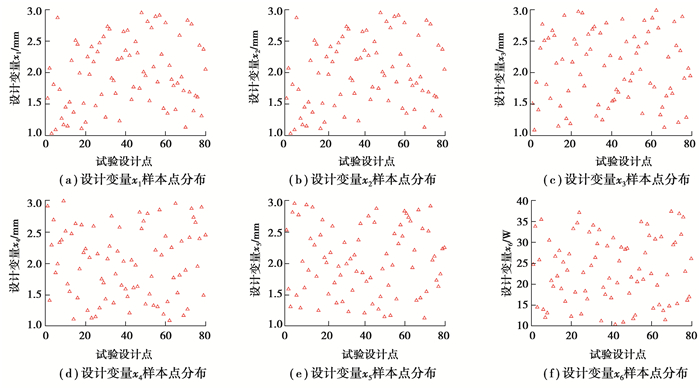
|
图 4 设计变量样本分布点 Fig. 4 Design variable sample distribution points |
RBF无须指定目标函数表达式或导数信息,能够采用较少的样本点构造相对精确的代理模型;RSM对于一些非线性程度不高的函数具有很好的拟合效果;Kriging模型在一定区域内对目标函数值进行无偏、最优估计,对于低于10个变量的复杂非线性的函数具有很好的拟合效果。RBF, RSM, Kriging等模型的基本形式如下:
| $ f_{\mathrm{RBF}}(x)=\sum\limits_{i=1}^{j}\left[\alpha_{i} \varphi_{i}(x)\right]+\alpha_{j+1}=\sum\limits_{i=1}^{j}\left[\alpha_{i}\left\|x-x_{i}\right\| c\right]+\alpha_{j+1}, $ | (8) |
| $ f_{\mathrm{RSM}}(x)=\beta_{0}+\sum\limits_{i} \beta_{i} x_{i}+\sum\limits_{i<j} \sum\limits_{i} \beta_{i j} x_{i} x_{j}+\sum \beta_{i i} x_{i}{ }^{2}+\varepsilon $ | (9) |
| $ f_{\text {Kriging }}(x)=f^{\mathrm{T}}(x) \beta+Z(x), $ | (10) |
式中:αi为线性叠加权系数,n为样本点个数,φi(x)为径向函数,c为形状参数;xi表示参与拟合的尺寸变量,β0,βi,βij,βii表示回归方程的系数,ε表示回归值与试验数据的误差;β为回归系数,fT(x)为回归模型,用来模拟全局近似,Z(x)为随机分布误差,用来模拟局部偏差近似。
笔者采用中位数绝对偏差(median absolute deviation, MAD)、最大绝对误差(maximum absolute error, MAE)、均方根误差(root mean square error, RMSE)3个评价指标对代理模型进行精度评估,评价值越小,代理模型越精确,表达式为:
| $ f_{\mathrm{MAD}}(f, \hat{f})=\operatorname{med}\left|f_{i}-\hat{f}_{i}\right|, $ | (11) |
| $ f_{\mathrm{MAE}}(f, \hat{f})=\max \left|f_{i}-\hat{f}_{i}\right|, $ | (12) |
| $ f_{\mathrm{RMSE}}(f, \hat{f})=\sqrt{\frac{1}{N} \sum\limits_{i=1}^{N}\left(f_{i}-\hat{f}_{i}\right)^{2}}, $ | (13) |
式中:fi为样本目标值,
将样本点带入CFD仿真软件Fluent18.1中得到对应的设计目标响应值。部分样本数据点如表 2所示,根据实际情况,确定6个设计变量的取值范围为:1 mm≤x1,x2,x3,x4,x5≤3 mm, 10 W≤x6≤37.5 W。
| 表 2 部分样本点数据及目标值 Table 2 Part of the sample point data and target value |
将80个样本点分为两部分,前70个作为训练集,来建立设计目标的3种代理模型,剩余的10个样本点作为测试集来检验代理模型的精度。图 5为不同设计指标对应的3个代理模型的测试结果,由图知ΔTmax采用RSM模型精度最高,Tmax,V采用Kriging模型具有更高的精度,因此选取RSM模型来构建最大温差ΔTmax的代理模型,选取Kriging模型来建立最高温度Tmax和间距体积V的代理模型。
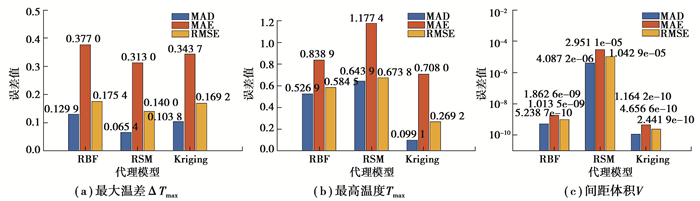
|
图 5 3种代理模型测试结果 Fig. 5 Three surrogate model test results |
通过RSM和Kriging方法拟合出电池模组设计目标代理模型,其中Tmax与ΔTmax具有协同关系,无法得到Pareto解集,而较小的V会导致电池模组ΔTmax变大。因此将最大温差ΔTmax与间距体积V作为优化目标,以最高温度Tmax、电池排布距离和半导体制冷量为约束条件,其中Tmax的取值范围为293.15~318.15 K (20~45 ℃),建立的电池模组多目标优化模型如下:
| $ \begin{aligned} \min \left\{f_{\Delta T_{\max }}=\right.&\left.f_{\mathrm{RSM}}\left(x_{1}, x_{2}, \cdots, x_{6}\right), f_{V}=f_{\text {Kriging }}\left(x_{1}, x_{2}, \cdots, x_{5}\right)\right\}, \\ \text { s.t. } \quad &\left\{\begin{array}{l} 293.15<T_{\max }\left(x_{1}, x_{2}, \cdots, x_{6}\right)<318.15, \\ 1<x_{i}<3(i=1, 2, \cdots, 5), \\ 10<x_{6}<37.5。\end{array}\right. \end{aligned} $ | (14) |
MOGA因简单易用、鲁棒性好,在优化过程中能够产生大量非劣解,有助于获取优化目标的最优解集。因此采用MOGA对动力锂电池优化模型进行求解,其流程如图 6所示。
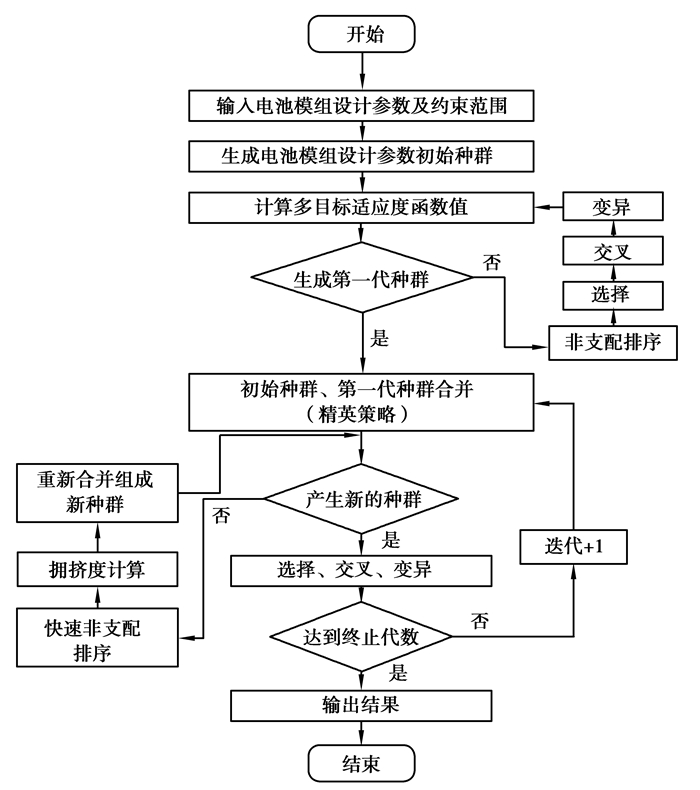
|
图 6 多目标遗传算法优化流程图 Fig. 6 Multi-objective genetic algorithm optimization flowchart |
设置种群个体总数为100,交叉概率为0.8,变异概率为0.2,最优个体系数为0.4,迭代500次,得到的40组Pareto解集如图 7所示。从图中可以看出,当间距体积处于较小水平时,电池模组最大温差处于较高水平,说明间距体积的减小是以牺牲最大温差为代价;当电池模组最大温差处于较低水平时,间距体积处于较高水平,降低了电池模组的能量密度。为提升电动汽车续航里程,选取Pareto解集P1为理想设计点。P1点对应方案的最大温差在设计范围之内且间距体积最小,电池包的能量密度更高。
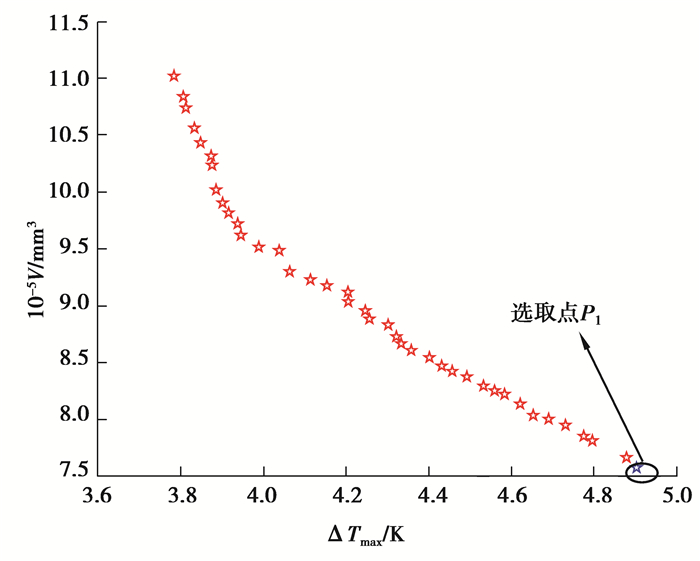
|
图 7 优化目标Pareto解集 Fig. 7 Optimization target Pareto solution set |
P1点对应的设计变量及目标值如表 3所示。
| 表 3 设计变量及目标值 Table 3 Design variables and target values |
根据P1点对应的设计变量值加工出动力电池包实物,搭建实验测试平台如图 8所示,主要包括3个部分:电池包热测试部分、充放电部分(星云动力锂电池充放电测试系统)、温度采集部分(温度采集仪、T型热电偶)。实验测试对象为电池包内的单个模组,将测温点布置在单个模组左侧的8块单体电池上,且位于每个单体电池的中间位置。温度采集仪共有20个温度采集通道,搭载T型热电偶,最高测试温度达到350 ℃,精度±0.75%。采用直流电源设备对水冷板流量和半导体制冷量进行调节控制,使其符合实验的设计需求。

|
图 8 半导体制冷方案实验测试平台 Fig. 8 Semiconductor refrigeration program experimental test platform |
实验具体过程为:电池包以0.5 C倍率恒流充电至荷电状态(state of charge, SOC)值为1.0,在室温下静置1 h,然后在常温下以0.8 C倍率放电8 000 s,通过温度采集仪获取各测点温度变化值。
将放电结束后采集的温度数据与优化后单体电池温度仿真结果进行对比,如表 4所示,从表中发现,实验和仿真数据最大误差为2.75%,说明建立的散热优化模型与仿真结果具有较高的可靠性。
| 表 4 仿真结果与实验结果对比 Table 4 Comparison of simulation results and experimental results |
图 9为放电8 000 s,电池模组初始方案和优化方案的温度分布云图。为方便对比优化前后电池模组的温度分布,将云图的图例上下限设置为相同,由图知,优化后的电池模组温度分布更加均匀。电池模组中间单体电池温度低于边缘单体电池温度,主要原因是半导体制冷片贴在电池模组中间位置,能够更快地吸收中间单体电池产生的热量,说明了半导体制冷片具有良好的制冷效果。
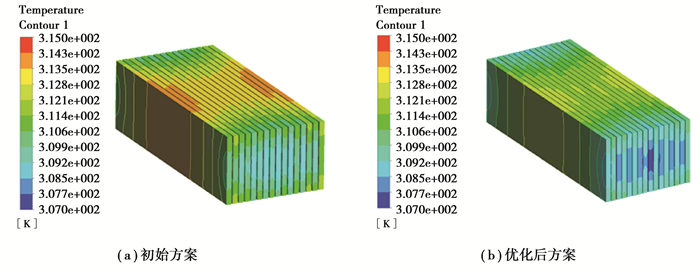
|
图 9 电池模组温度场分布云图 Fig. 9 Cloud map of battery module temperature field distribution |
图 10为电池模组左侧8块单体电池的初始方案和优化后方案温度上升曲线对比,可以明显发现优化后的单体电池温度低于优化前,且能够更快达到稳定状态。同时,优化后的单体电池的温升曲线几乎一致,证明了该方案能够有效保障模组中单体电池温度的均匀性。
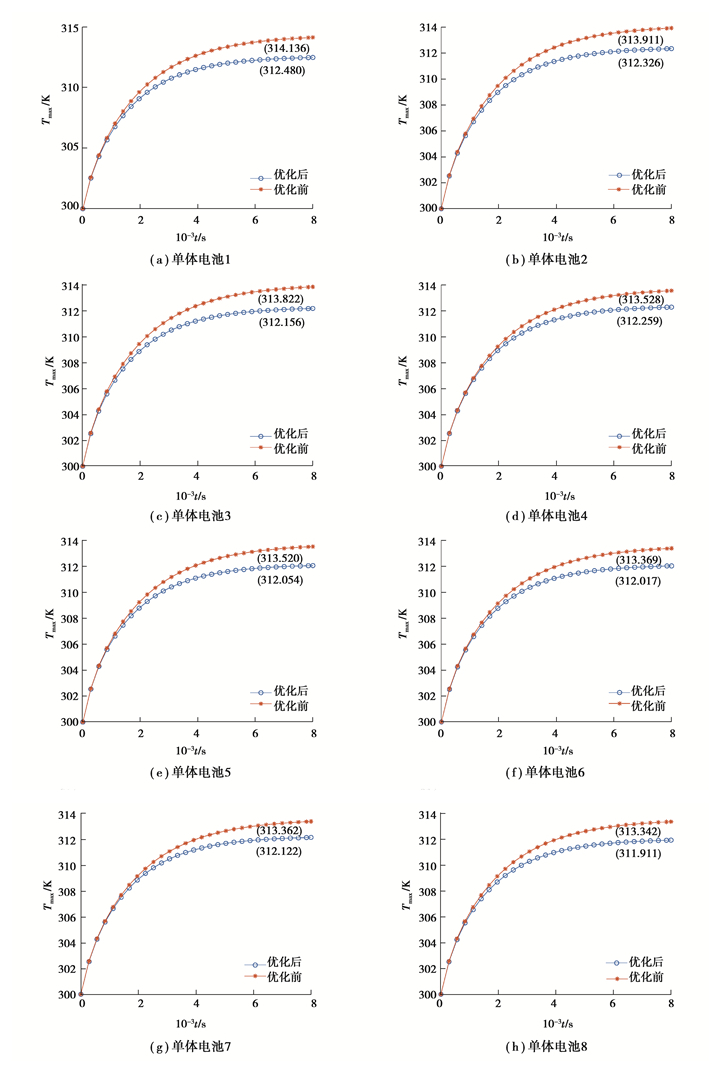
|
图 10 电池模组中单体电池温度上升曲线 Fig. 10 Temperature rise curve of single cell in battery module |
表 5为电池模组优化前后指标参数的对比。由表 5知,优化后的电池模组的表现性能得到了很大的提升。设计变量x1, x2, x3, x4, x5由初始值2.000 0 mm分别降到1.400 0, 1.280 9,1.213 1,1.316 4,1.451 1 mm,间距表现性能提升了30%,35.96%,39.35%,34.18%,27.45%。而x6出现了一定的上升,主要是因为在单体电池间距都变小的情况下,为保证电池模组的温度处于合理的范围内,需要增加半导体制冷量来增强电池模组的散热效果。最高温度Tmax、最大温差ΔTmax由314.14 K和5.50 K分别降到312.48,4.75 K,温度性能分别提升了0.53%,13.64%。间距体积V由1 121 400 mm3降到757 792 mm3,体积性能提升了32.42%。
| 表 5 优化前后设计参数值 Table 5 Design parameter values before and after optimization |
1) 针对换电模式下的动力锂电池包,综合考虑电池包使用场景对密封性、散热性的需求,提出一种使用半导体制冷片的散热方案,并基于该方案建立相应的热分析模型。
2) 采用拉丁超立方设计和代理模型方法建立电池模组设计指标近似模型,以最大温差和间距体积为优化目标,最高温度为约束条件建立多目标优化模型,采用MOGA对电池模组排布间距和半导体制冷量进行多目标寻优设计;根据优化结果加工出电池包实物,并搭建实验平台进行验证,结果表明,优化后的方案能够有效提升电池包的温度表现性能和能量密度。
3) 在电池实际生产中,电池材料属性及加工制造过程中的不确定性会导致每个单体电池的产热率不同。因此,后续的研究工作将考虑该不确定性因素对电池包温度均匀性的影响,并以此为基础进一步对动力锂电池包进行散热优化设计。
| [1] |
Qian X, Xuan D, Zhao X, et al. Heat dissipation optimization of lithium-ion battery pack based on neural networks[J]. Applied Thermal Engineering, 2019, 162: 114289. DOI:10.1016/j.applthermaleng.2019.114289 |
| [2] |
Yang T, Yang N, Zhang X, et al. Investigation of the thermal performance of axial-flow air cooling for the lithium-ion battery pack[J]. International Journal of Thermal Sciences, 2016, 108: 132-144. DOI:10.1016/j.ijthermalsci.2016.05.009 |
| [3] |
Yu K, Yang X, Cheng Y, et al. Thermal analysis and two-directional air flow thermal management for lithium-ion battery pack[J]. Journal of Power Sources, 2014, 270: 193-200. DOI:10.1016/j.jpowsour.2014.07.086 |
| [4] |
Yang X H, Tan S C, Liu J. Thermal management of Li-ion battery with liquid metal[J]. Energy Conversion and Management, 2016, 117: 577-585. DOI:10.1016/j.enconman.2016.03.054 |
| [5] |
Rao Z, Qian Z, Kuang Y, et al. Thermal performance of liquid cooling based thermal management system for cylindrical lithium-ion battery module with variable contact surface[J]. Applied Thermal Engineering, 2017, 123: 1514-1522. DOI:10.1016/j.applthermaleng.2017.06.059 |
| [6] |
Azizi Y, Sadrameli S M. Thermal management of a LiFePO4 battery pack at high temperature environment using a composite of phase change materials and aluminum wire mesh plates[J]. Energy Conversion and Management, 2016, 128: 294-302. DOI:10.1016/j.enconman.2016.09.081 |
| [7] |
Zhao J, Lv P, Rao Z. Experimental study on the thermal management performance of phase change material coupled with heat pipe for cylindrical power battery pack[J]. Experimental Thermal and Fluid Science, 2017, 82: 182-188. DOI:10.1016/j.expthermflusci.2016.11.017 |
| [8] |
张晓波, 张保会, 董梁. 微电网中电动汽车充电模式与换电模式的运行优化[J]. 电力系统自动化, 2016, 40(9): 56-63. Zhang X B, Zhang B H, Dong L. Operation optimization of electric vehicle charging mode and power exchange mode in microgrid[J]. Automation of Electric Power Systems, 2016, 40(9): 56-63. (in Chinese) |
| [9] |
Siddique A R M, Mahmud S, Van H B. A comprehensive review on a passive (phase change materials) and an active (thermoelectric cooler) battery thermal management system and their limitations[J]. Journal of Power Sources, 2018, 401: 224-237. DOI:10.1016/j.jpowsour.2018.08.094 |
| [10] |
Lyu Y, Siddigque A R M, Majid S H, et al. Electric vehicle battery thermal management system with thermoelectric cooling[J]. Energy Reports, 2019, 5: 822-827. DOI:10.1016/j.egyr.2019.06.016 |
| [11] |
Zhao J, Rao Z, Huo Y, et al. Thermal management of cylindrical power battery module for extending the life of new energy electric vehicles[J]. Applied Thermal Engineering, 2015, 85: 33-43. DOI:10.1016/j.applthermaleng.2015.04.012 |
| [12] |
Chen K, Wang S, Song M, et al. Configuration optimization of battery pack in parallel air-cooled battery thermal management system using an optimization strategy[J]. Applied Thermal Engineering, 2017, 123: 177-186. DOI:10.1016/j.applthermaleng.2017.05.060 |
| [13] |
Yang N, Zhang X, Li G, et al. Assessment of the forced air-cooling performance for cylindrical lithium-ion battery packs: A comparative analysis between aligned and staggered cell arrangements[J]. Applied Thermal Engineering, 2015, 80: 55-65. DOI:10.1016/j.applthermaleng.2015.01.049 |
| [14] |
Li W, Xiao M, Peng X B, et al. A surrogate thermal modeling and parametric optimization of battery pack with air cooling for EVs[J]. Applied Thermal Engineering, 2018, 147: 90-100. |
| [15] |
秦大同, 马兆强, 胡明辉, 等. 混合动力车用镍氢电池组散热系统CFD仿真分析与实验验证[J]. 重庆大学学报, 2013, 36(8): 1-8. Qin D T, Ma Z Q, Hu M H, et al. CFD simulation analysis and experimental verification on heat dissipation system of Ni-MH battery packs in HEV[J]. Journal of Chongqing University, 2013, 36(8): 1-8. (in Chinese) |
| [16] |
李军求, 吴朴恩, 张承宁. 电动汽车动力电池热管理技术的研究与实现[J]. 汽车工程, 2016, 38(1): 22-27. Li J Q, Wu P E, Zhang C N. Study and implementation of thermal management technology for the power batteries of electric vehicles[J]. Automotive Engineering, 2016, 38(1): 22-27. (in Chinese) |
| [17] |
Cai Y, Wang Y, Liu D, et al. Thermoelectric cooling technology applied in the field of electronic devices: Updated review on the parametric investigations and model developments[J]. Applied Thermal Engineering, 2019, 148: 238-255. DOI:10.1016/j.applthermaleng.2018.11.014 |
 2022, Vol. 45
2022, Vol. 45


