电池管理系统作为保障电动车辆动力电池性能与安全的重要部件,直接影响电动汽车的驾乘体验与安全[1]。由传感器所完成的数据采集是实现电池管理系统功能的基础,但由于汽车较为复杂恶劣的运行工况,电池传感器故障时有发生,因此,针对电动车辆锂离子电池传感器的故障诊断具有较为重要的意义[2]。
近年来,关于故障诊断的研究日益深入[3-5],而针对电动车辆锂离子电池传感器故障诊断的研究成果却相对较少。主要的成果有:Lombardi等[6]基于基尔霍夫定律测试了传感器测量值之间的电气关系产生残差,根据电池组结构与对应传感器的残差集实现电流、电压、温度传感器故障的诊断与分离;Liu等[7]提出了1种应用结构分析理论来实现电流、电压、温度传感器故障的诊断与分离。上述2种方法均可以实现对3种传感器故障的诊断与分离,但同时会受到未知扰动和故障初始条件的影响。为此,通过构建观测器以实现残差生成的方法更多地被应用于传感器的故障诊断,Xu等[8]将电流传感器信号作为偏置信号,并将其作为系统的输入,使用比例积分观测器实现电流传感器故障的诊断,该方法精确度较高且较为简单,但也存在由于观测器参数设置不当致使诊断系统不稳定的缺陷;Dey等[9]采用滑膜观测器实现了电流、电压、温度传感器故障的诊断与分离,该方法对模型的不确定性较为敏感;He等[10]和Liu等[11]采用自适应扩展卡尔曼滤波观测器实现了串联电池组电流传感器与电压传感器的故障诊断与分离;Liu等[12]采用结构分析理论与EKF观测器相结合的方法,实现了电流、电压和温度传感器的故障诊断与分离,这2种方法都存在系统复杂度大、计算成本较高的问题。
为了保证较好的诊断效果,笔者选择基于观测器的诊断方法,同时,选取EKF观测器以实现残差生成,提出构建双观测器以实现故障分离,此方案实现了单体电池电流、电压、表面温度传感器故障的全面诊断与分离,同时兼顾系统的复杂度,保证了其实车应用价值。
1 锂离子电池电热耦合动态模型基于观测器的方法最重要的是要建立一个精度足够的数学模型,这里建立电热耦合动态模型,包括了等效电路模型(图 1)与热模型(图 2)。
|
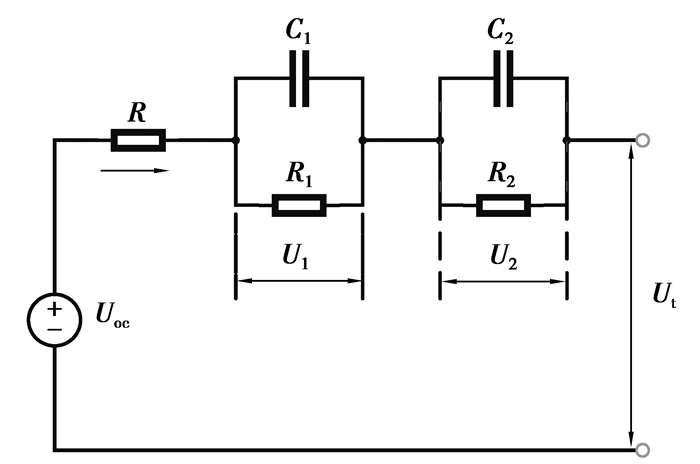
图 1 二阶RC等效电路模型 Fig. 1 Second order equivalent circuit model |
|
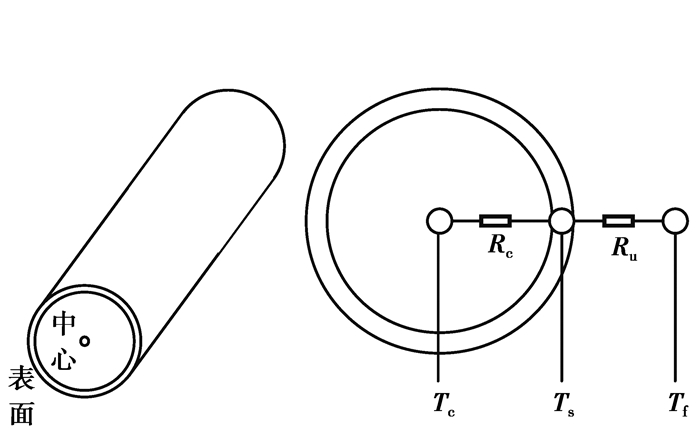
图 2 双状态集中参数热模型 Fig. 2 Two-state thermal model |
二阶RC等效电路模型[13]精确度高,复杂度适中,该模型包括1个开路电压源,1个欧姆内阻R,2个并联RC网络。模型可用如下数学表达式表示[14]
| $ \frac{\mathrm{d} U_{1}}{\mathrm{~d} t}=-\frac{U_{1}}{R_{1} C_{1}}+\frac{I}{C_{1}}, $ | (1) |
| $ \frac{\mathrm{d} U_{2}}{\mathrm{~d} t}=-\frac{U_{2}}{R_{2} C_{2}}+\frac{I}{C_{2}}, $ | (2) |
| $ U_{\mathrm{t}}=U_{\mathrm{oc}}-U_{1}-U_{2}-I \cdot R, $ | (3) |
式中:I为电流,规定放电为正,充电为负;U1为电容C1两端的电压;U2为电容C2两端的电压;模型参数R,R1,C1,R2,C2受到电池SOC、温度以及电流的方向的影响;电池的开路电压OCV,此处写为Uoc,是SOC的非线性函数;这里用Ssoc表示锂离子电池的SOC,可由下式计算得到
| $ \frac{\mathrm{d} S_{\mathrm{soc}}}{\mathrm{d} t}=-\frac{\eta I}{C_{\mathrm{bat}}}, $ | (4) |
式中Cbat表示电池可用容量。
1.2 锂离子电池热模型这里使用的电池为圆柱形A123 26650磷酸铁锂电池,此处建立双状态集中参数热模型[15],可推出式(5)~(7)。
| $ \frac{\mathrm{d} T_{\mathrm{c}}}{\mathrm{d} t}=\frac{T_{\mathrm{s}}-T_{\mathrm{c}}}{R_{\mathrm{c}} C_{\mathrm{c}}}+\frac{Q}{C_{\mathrm{c}}}, $ | (5) |
| $ \frac{\mathrm{d} T_{\mathrm{s}}}{\mathrm{d} t}=\frac{T_{\mathrm{f}}-T_{\mathrm{s}}}{R_{\mathrm{u}} C_{\mathrm{s}}}-\frac{T_{\mathrm{s}}-T_{\mathrm{c}}}{R_{\mathrm{c}} C_{\mathrm{s}}}, $ | (6) |
| $ Q=I\left(U_{\mathrm{oc}}-U_{\mathrm{t}}\right), $ | (7) |
式中:Ts,Tc分别为电池的表面温度和中心温度;Rc,Cc,Ru,Cs分别为热传导内阻、电池中心容量、对流内阻、电池表面热容量;Q为产热量,默认电池表面的冷却对流速率恒定,环境温度Tf近似恒定[16]。
1.3 电热耦合动态模型离散时间内非线性时变系统的状态方程与测量方程为
| $ \begin{aligned} &\mathit{\boldsymbol{x}}_{k+1}=f\left(\mathit{\boldsymbol{x}}_{k}, \mathit{\boldsymbol{u}}_{k}\right)+\mathit{\boldsymbol{w}}_{k} ,\\ &\mathit{\boldsymbol{y}}_{k}=g\left(\mathit{\boldsymbol{x}}_{k}, \mathit{\boldsymbol{u}}_{k}\right)+\mathit{\boldsymbol{v}}_{k}, \end{aligned} $ | (8) |
式中:xk表示系统状态变量;yk表示系统测量输出量;u为系统输入量;wk为系统状态噪声;vk为测量噪声,二者都是独立的、均值为零的高斯噪声;f为非线性系统状态方程;g为测量方程。这里设状态变量为xk=[U1(k)U2(k)Ssoc(k)Tc(k)Ts(k)]T;输入量为I(k);输出量为yk=[Ut(k)Ts(k)]T,由此便可建立状态方程以及测量方程形式的离散电热耦合动态模型为
| $ f\left(\mathit{\boldsymbol{x}}_{k}, \mathit{\boldsymbol{u}}_{k}\right)=\left\{\begin{array}{l} \exp \left(-\Delta t /\left(R_{1} C_{1}\right)\right) \cdot U_{1}(k)+R_{1} \cdot\left(1-\exp \left(\Delta t /\left(R_{1} C_{1}\right)\right)\right) \cdot I(k), \\ \exp \left(-\Delta t /\left(R_{2} C_{2}\right)\right) \cdot U_{2}(k)+R_{2} \cdot\left(1-\exp \left(-\Delta t /\left(R_{2} C_{2}\right)\right)\right) \cdot I(k), \\ S_{\mathrm{soc}}(k)-\frac{\eta \Delta t I(k)}{C_{\mathrm{bat}}}, \\ \left(1-\frac{\Delta t}{R_{\mathrm{c}} C_{\mathrm{c}}}\right) T_{\mathrm{c}}(k)+\frac{\Delta t}{R_{\mathrm{c}} C_{\mathrm{c}}} T_{\mathrm{s}}(k)+\frac{U_{1}(k)+U_{2}(k)+R \cdot I(k)}{C_{\mathrm{c}}} \Delta t, \\ \frac{\Delta t}{R_{\mathrm{u}} C_{\mathrm{s}}} T_{\mathrm{f}}+T_{\mathrm{s}}(k)\left(1-\frac{\Delta t}{R_{\mathrm{u}} C_{\mathrm{s}}}-\frac{\Delta t}{R_{\mathrm{c}} C_{\mathrm{s}}}\right)+\frac{\Delta t}{R_{\mathrm{c}} C_{\mathrm{s}}} T_{\mathrm{c}}(k), \end{array}\right. $ | (9) |
| $ g\left(\mathit{\boldsymbol{x}}_{k}, \mathit{\boldsymbol{u}}_{k}\right)=\left\{\begin{array}{l} \text { spline }\left(S_{\mathrm{soc}}(k)\right)-U_{1}(k)-U_{2}(k)-R \cdot I(k), \\ T_{\mathrm{s}}(k), \end{array}\right. $ | (10) |
式中:Δt为采样间隔;k为采样时刻。
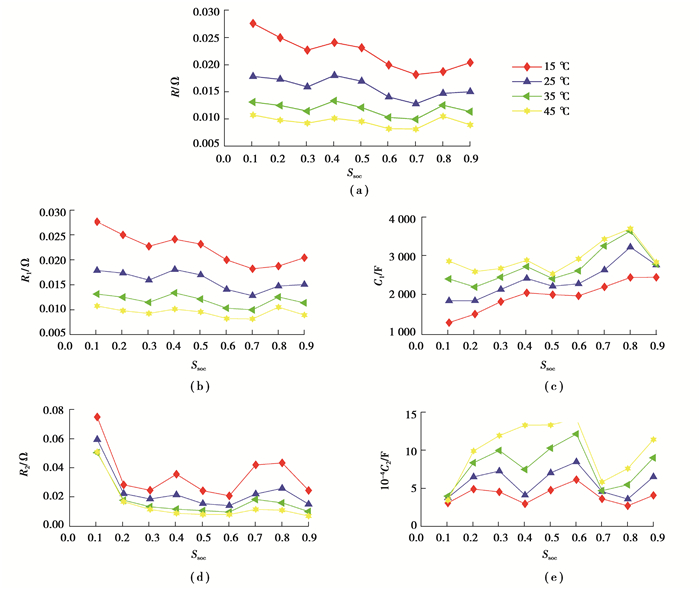
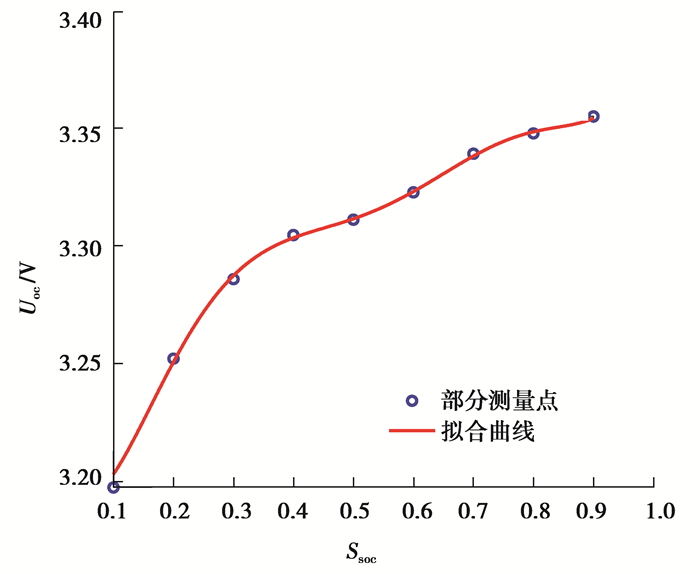
1.4 模型参数确定A123 26650电池型号与文献[13]一致,文中所确定的模型参数满足本论文的要求,在这里加以使用,表 1为热模型参数,图 3为等效电路模型的参数,图 4为此电池OCV与SOC的关系。
| 表 1 热模型参数 Table 1 Two-state thermal model parameters |
|
图 3 等效电路模型参数值 Fig. 3 Parameters of equivalent circuit model |
|
图 4 被测电池OCV与SOC的关系 Fig. 4 The relationship between OCV and SOC |
基于EKF观测器的故障诊断方法, 其核心是在建立数学模型后,构建状态观测器从而生成状态估计量,与测量值对比生成残差,当传感器发生故障时,残差信号也会出现异常变化,通过对残差进行评价分析,便可以实现故障诊断[17]。
2.1 基于EKF观测器的诊断算法设计卡尔曼滤波算法(Kalman filter, KF)是一种基于最小均方误差的递推估计算法,该算法利用现时刻的观测值与上一时刻的估计值,递推更新出现时刻的状态量的估计值,扩展卡尔曼滤波算法(EKF)是为将算法应用于非线性系统而对标准卡尔曼滤波算法进行改进的结果,其具体计算过程如下[18]。
对于离散化后表达式如式(9)的非线性系统,系统状态噪声协方差Qk与测量噪声协方差Rk分别可用下式表示,
| $ \mathit{\boldsymbol{Q}}_{k}=E\left(\mathit{\boldsymbol{\omega}}_{k} {\mathit{\boldsymbol{\omega}}_{k}}^{\mathrm{T}}\right), \quad \mathit{\boldsymbol{R}}_{k}=E\left(\mathit{\boldsymbol{v}}_{k} {\mathit{\boldsymbol{v}}_{k}}^{\mathrm{T}}\right), $ | (11) |
定义
具体迭代公式:
| $ \begin{aligned} &\hat{\mathit{\boldsymbol{x}}}_{k}^{-}=\mathit{\boldsymbol{A}}_{k-1} \hat{\mathit{\boldsymbol{x}}}_{k-1}^{+}+\mathit{\boldsymbol{B}}_{k-1} \mathit{\boldsymbol{u}}_{k-1}, \\ &\mathit{\boldsymbol{P}}_{k}^{-}=\mathit{\boldsymbol{A}}_{k-1} \mathit{\boldsymbol{P}}_{k-1}^{+} \mathit{\boldsymbol{A}}_{k-1}^{\mathrm{T}}+\mathit{\boldsymbol{Q}}_{k-1}, \\ &\mathit{\boldsymbol{G}}_{k}=\mathit{\boldsymbol{P}}_{k}^{-} \mathit{\boldsymbol{C}}_{k}\left(\mathit{\boldsymbol{C}}_{k} \mathit{\boldsymbol{P}}_{k}^{-} \mathit{\boldsymbol{C}}_{k}^{\mathrm{T}}+\mathit{\boldsymbol{R}}_{k}\right)^{-1}, \\ &\hat{\mathit{\boldsymbol{x}}}_{k}^{+}=\widehat{\mathit{\boldsymbol{x}}}_{k}^{-}+\mathit{\boldsymbol{G}}_{k}\left(\mathit{\boldsymbol{y}}_{k}-g\left(\hat{\mathit{\boldsymbol{x}}}_{k}^{-}, \mathit{\boldsymbol{u}}_{k}\right)\right), \\ &\mathit{\boldsymbol{P}}_{k}^{+}=\left(I-\mathit{\boldsymbol{G}}_{k} \mathit{\boldsymbol{C}}_{k}\right) \mathit{\boldsymbol{P}}_{k}^{-}, \end{aligned} $ | (12) |
残差由EKF观测器所生成的状态估计值与传感器测量得到的测量值作差得到,表达式为
| $ \mathit{\boldsymbol{r}}(t)=\mathit{\boldsymbol{y}}(t)-\hat{\mathit{\boldsymbol{y}}}(t)。$ | (13) |
在了解残差的生成之后,还需要对残差进行评价,以便于检测到残差的异变响应,这里采用的是CUSUM测试方法[19]。假设H0和H1分别表示无故障与有故障情况,无故障情况下,残差为满足高斯分布的随机变量,其平均值为μ0,方差为σ02;故障情况下,残差为满足平均值为μ1,方差为σ12的高斯分布。至此,可以通过检测均值或者方差的变化实现故障诊断,残差对数似然比定义为
| $ s(r)=\log _{\rm e} \frac{p_{1}(r)}{p_{0}(r)}, $ | (14) |
式中:r为残差;s(·)为残差对数似然比;p1为假设H1的概率密度函数;p0为假设H0的概率密度函数,当残差的均值或方差发生变化的时候,式(14)可化为
| $ s(r(k))=\log _{\mathrm{e}} \frac{p_{1} r(k)}{p_{0} r(k)}=\log _{\mathrm{e}} \frac{\sigma_{0}}{\sigma_{1}}-\frac{z-\mu_{1}^{2}}{2 \sigma_{1}^{2}}+\frac{z-\mu_{0}^{2}}{2 \sigma_{0}^{2}} 。$ | (15) |
至此,残差最大似然比的累计和为
| $ S_{k}= \begin{cases}S_{k-1}+s(r(k)) & \text { if } S_{k-1}+s(r(k))>0, \\ 0 & \text { if } S_{k-1}+s(r(k))<0,\end{cases} $ | (16) |
式中:用Sk来表示对数似然比累积和,当故障发生时它将会不断增大,故障检测逻辑为
| $ d= \begin{cases}1 & \text { if } S_{k}>J \Rightarrow H_{1}, \\ 0 & \text { if } S_{k}<J \Rightarrow H_{0},\end{cases} $ | (17) |
式中J表示故障报警阈值,可由大量实验确定。
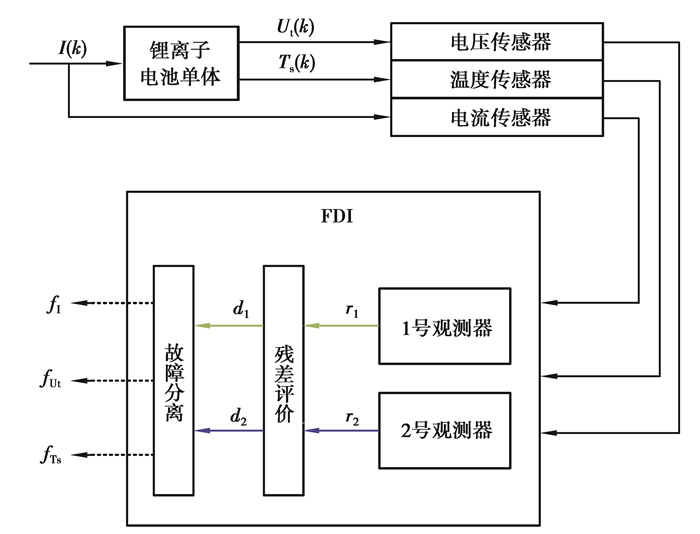
2.3 故障诊断与分离策略由于多个传感器同时故障的情况发生概率较低,因此只考虑单个传感器故障,同时也不考虑电池本身或其他部件发生故障。为了实现锂离子电池单体电流传感器、电压传感器、表面温度传感器故障的诊断与分离,提出了基于EKF观测器的诊断与分离策略,其核心思想为:构建2个EKF观测器,1号观测器将电流传感器信号与电压传感器信号作为输入,生成残差,对电流、电压传感器故障做出响应,2号观测器将电流传感器与表面温度传感器作为输入,生成残差r2,对电流、表面温度传感器故障做出响应,如图 5所示。残差生成后,使用CUSUM测试方法对残差进行评价,根据式(18),当故障发生时,残差评价将输出d=1。至此,可以根据残差评价结果判断是否有传感器故障发生,但并不能判断是哪一个传感器存在故障。表 2列出了不同传感器故障下的残差评价结果,其中,fI为电流传感器发生故障,fUt为电压传感器故障,fTs为表面温度传感器故障。不同传感器故障所对应的残差组合响应情况不同,可据此判断是哪一个传感器发生了故障,由此实现传感器的故障分离。
|
图 5 基于观测器的锂离子电池传感器故障诊断与分离策略 Fig. 5 Observer-based sensors fault diagnosis and isolation strategy for lithium-ion battery |
| 表 2 不同传感器故障下残差评价结果 Table 2 Residual evaluation results under different sensor faults |
笔者将基于DST(dynamic stress test)测试对上文所提出的传感器故障诊断与分离策略进行仿真验证分析。这里假设传感器测量信号可由模型输入输出数据加上高斯白噪声获得,因此,电流传感器测量信号由DST测试数据加上高斯白噪声获得,电压传感器测量信号与表面温度传感器测量信号由模型输出值加上高斯白噪声获得。设环境温度为25 ℃,算法相关参数与状态量初始值设置如下:
状态量初始值定义为
| $ \mathit{\boldsymbol{x}}_{0}=\left[\begin{array}{lllll} U_{1} & U_{2} & S_{\mathrm{soc}} & T_{\mathrm{c}} & T_{\mathrm{s}} \end{array}\right]^{\mathrm{T}}=\left[\begin{array}{lllll} 0 & 0 & 0.95 & 25 & 25 \end{array}\right]^{\mathrm{T}}。$ | (18) |
EKF算法初始状态估计的误差协方差矩阵P0设为
| $ \mathit{\boldsymbol{P}}_{0}=\left[\begin{array}{lllll} 0.01 & 0.00 & 0.00 & 0.00 & 0.00 \\ 0.00 & 0.01 & 0.00 & 0.00 & 0.00 \\ 0.00 & 0.00 & 0.01 & 0.00 & 0.00 \\ 0.00 & 0.00 & 0.00 & 0.01 & 0.00 \\ 0.00 & 0.00 & 0.00 & 0.00 & 0.01 \end{array}\right] 。$ | (19) |
状态噪声协方差矩阵与测量噪声协方差矩阵分别设定为
| $ \mathit{\boldsymbol{Q}}_{0}=\left[\begin{array}{lllll} 0.030 & 0.000 & 0.000 & 0.000 & 0.000 \\ 0.000 & 0.010 & 0.000 & 0.000 & 0.000 \\ 0.000 & 0.000 & 0.005 & 0.000 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.030 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.050 \end{array}\right], \quad \mathit{\boldsymbol{R}}_{0}=1。$ | (20) |
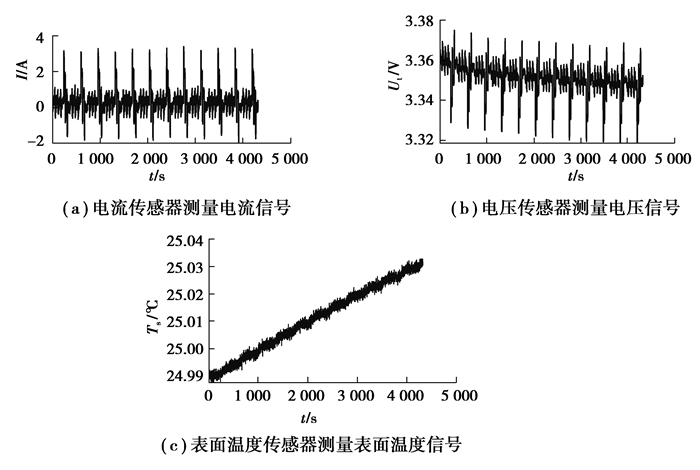
A123 26650电池在无任何传感器故障的情况下运行DST测试工况时的电流传感器、电压传感器、表面温度传感器的测量信号如图 6所示。
|
图 6 无传感器故障时的测量信号 Fig. 6 Signals without any sensor fault |
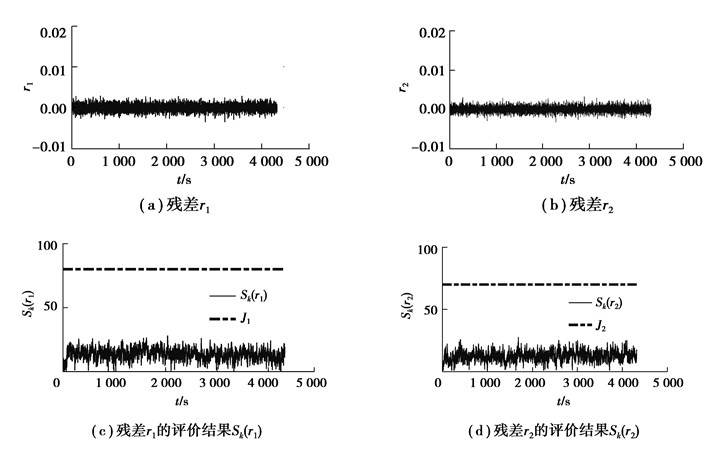
图 7为该型号锂离子电池传感器无故障情况下2个观测器生成的残差信号r1和r2,并给出了相应残差的评价结果。据图 7(a)和(b)可以发现,即使在完全无传感器故障的情况下,残差也不会完全为零,这是由于系统模型以及传感器测量均存在一定的噪声。由图 7(c)和(d)可知,将2个观测器的报警阈值J1和J2设为80和70,阈值设置比Sk的峰值要大一些,是为了避免Sk的波动造成故障的误报。
|
图 7 无传感器故障时残差信号以及CUSUM测试结果 Fig. 7 Residuals and CUSUM test results in sensor fault-free case |
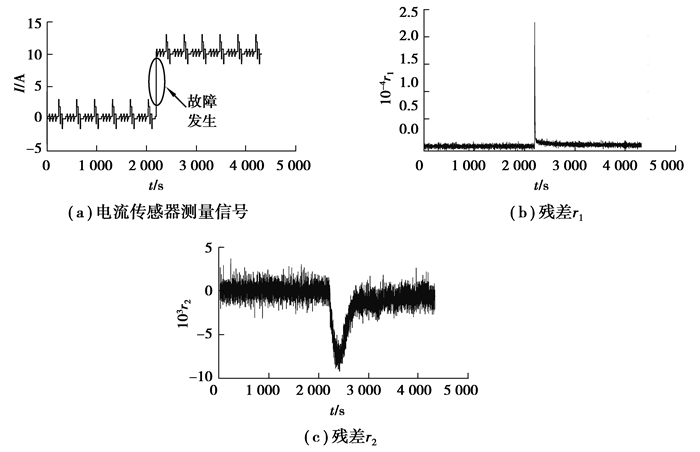
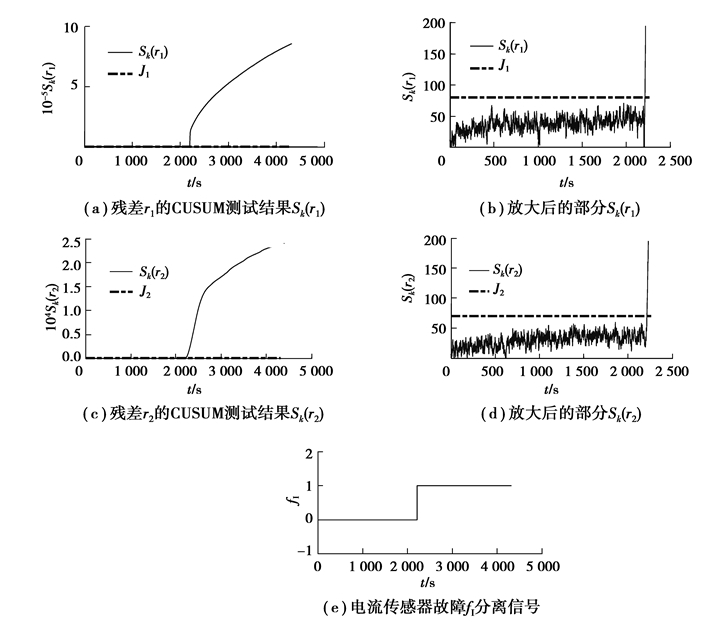
图 8(a)为锂离子电池在DST测试工况下电流传感器在2 200 s时发生+10 A的偏移故障时的电流传感器电流测量信号,(b)和(c)分别为2个观测器生成的2个残差r1和r2。当故障发生时,由于2个观测器均以电流传感器测量值为输入,所以2个残差均发生了一定的变化,但变化微小,不易捕捉。图 9为利用CUSUM测试方法对残差进行评价后的结果,从图 9(a)(b)可以发现,Sk(r1)在故障发生后的2 216 s时刻到达阈值J1,触发故障报警,图 9(c)(d)显示,Sk(r2)在2 200 s处到达并在随后越过阈值J2引发故障报警,可以依据表 2确定电流传感器发生故障,图 9(e)为锂离子电池电流传感器故障fI的分离结果。该故障最终被分离时的时间为2 216 s,此时距故障发生时刻的间隔时长为16 s,存在16 s的故障诊断延时。
|
图 8 电流传感器故障时(+10 A)的信号 Fig. 8 Signals in the current sensor fault case (+10 A) |
|
图 9 电流传感器故障诊断结果 Fig. 9 Diagnostic results for the current sensor fault |
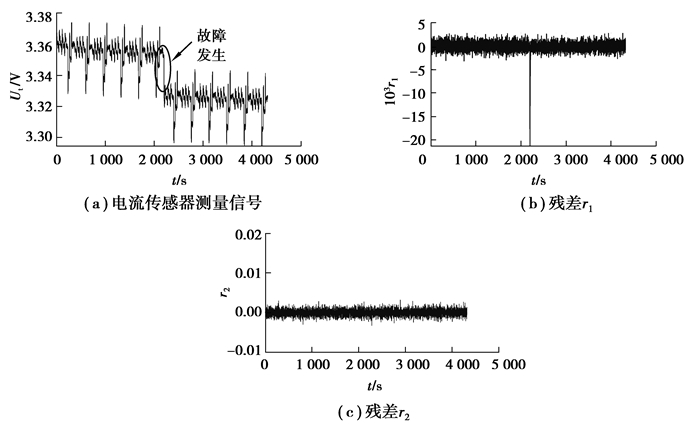
图 10(a)为电压传感器在2 200 s时发生了-0.8%的故障时电压传感器测量的电压信号,(b)和(c)分别为2个观测器生成的2个残差r1和r2。由图可知,残差r1在故障发生时发生了异常变化,而残差r2没有发生明显异常。图 11为CUSUM测试结果,图 11(a)(b)显示Sk(r1)在2 264 s处到达阈值J1,触发故障警报,而由图 11(c)可知Sk(r2)始终没有突破阈值,说明残差r2无响应,因此可据表 2确定电压传感器发生故障,存在64 s的诊断延时。图 11(d)为电压传感器故障fUt分离结果。
|
图 10 电压传感器故障时(-0.8% V)的信号 Fig. 10 Signals in the voltage sensor fault case(-0.8% V) |

|
图 11 电压传感器故障诊断结果 Fig. 11 Diagnostic results for the voltage sensor fault |
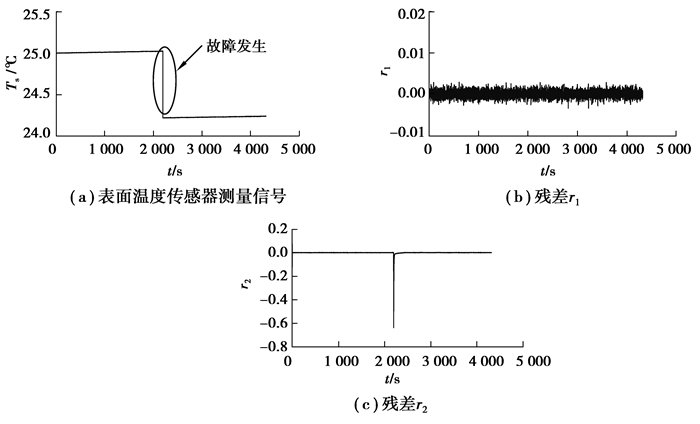
图 12(a)为表面温度传感器在2 200 s发生了-0.8 ℃的故障时表面温度传感器测量的表面温度信号,(b)和(c)分别为2个观测器生成的2个残差r1和r2。图 13为CUSUM测试结果,由图可知只有Sk(r2)在2 234 s达到阈值J2,说明只有残差r2有响应,因此可据表 2确定表面温度传感器发生了故障,诊断延时34 s,图 13(d)为表面温度传感器故障fTs分离结果。
|
图 12 表面温度传感器故障时(-0.8 ℃)的信号 Fig. 12 Signals in the surface temperature sensor fault case (-0.8 ℃) |

|
图 13 表面温度传感器故障诊断结果 Fig. 13 Diagnostic results for the surface temperature sensor fault |
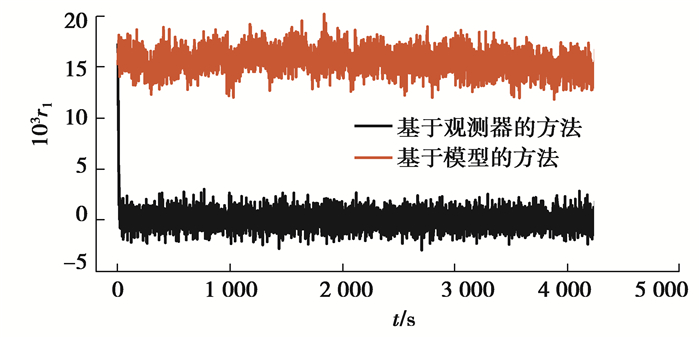
传统的基于模型的故障诊断方法,是通过直接对比模型输出值与传感器测量值来生成残差,与该方法相比,基于观测器的方法可以提高故障诊断的鲁棒性。图 14为无传感器故障情况下,存在故障初始误差时(这里设初始SOC存在误差),基于模型的方法与基于观测器的方法所生成的残差r1的对比图。由图 14可知,当存在初始SOC误差时,2种方法所产生的残差在初始时刻均出现了响应,但是,基于观测器的方法可以在极短的时间内将状态估计值收敛至测量值附近,使得残差回到0附近,而基于模型则无法实现收敛,初始误差会始终存在,残差会保持在非0附近振荡,从而导致故障的误诊,因此,基于观测器的故障诊断方法可以有效地减少由于故障初始条件不确定引起的故障误诊,改善了故障诊断的鲁棒性。
|
图 14 基于模型的方法与基于观测器的方法所生成的残差r1的对比图 Fig. 14 Comparison of residuals r1 generated by model-based and observer-based methods |
电动车辆锂离子电池传感器对于电池管理系统以及整车的性能与安全有着重要的意义,为了实现对锂离子电池单体电流传感器、电压传感器和表面温度传感器的故障诊断与分离,提出了一种基于EKF观测器的电池传感器故障诊断方法。该方法通过结合电热耦合动态模型构建EKF观测器,获得状态量的估计值,与传感器测量值对比生成残差。故障的发生将导致残差的异变,但是较为微小难以捕捉,这里使用CUSUM测试方法对残差进行评价,由残差异变导致的残差评价结果迅速增大并突破阈值可以指示故障的发生。通过与传统的基于模型的故障诊断方法的诊断结果对比,说明了基于观测器的诊断方法具有改善故障诊断鲁棒性的优势。
为了实现电流、电压以及表面温度传感器的故障分离,构建2个EKF观测器,根据残差组合的不同响应情况便可以判断是哪一个传感器发生故障。
为了验证所提出的诊断与分离策略的有效性,分别在无任何传感器故障、电流传感器故障、电压传感器故障、表面温度传感器故障4种情况下,利用该诊断与分离策略进行测试,最终较好地检测并分离了各个故障情况,表明该故障诊断策略具有较好的有效性。
| [1] |
Hu X S, Zou C F, Zhang C P, et al. Technological developments in batteries: a survey of principal roles, types, and management needs[J]. IEEE Power and Energy Magazine, 2017, 15(5): 20-31. DOI:10.1109/MPE.2017.2708812 |
| [2] |
王震坡, 孙逢春. 电动车辆动力电池系统及应用技术[M]. 北京: 机械工业出版社, 2012. Wang Z P, Sun F C. Electric vehicle power battery system and application technology[M]. Beijing: China Machine Press, 2012. (in Chinese) |
| [3] |
张友鹏, 朱涛伟, 赵斌. 基于模糊定性趋势分析的JTC综合故障诊断方法[J]. 重庆大学学报, 2019, 42(3): 65-75. Zhang Y P, Zhu T W, Zhao B. Comprehensive fault diagnosis method for jointless track circuit based on fuzzy qualitative trend analysis[J]. Journal of Chongqing University, 2019, 42(3): 65-75. (in Chinese) |
| [4] |
李嫄源, 袁梅, 王瑶, 等. SVM与PSO相结合的电机轴承故障诊断[J]. 重庆大学学报, 2018, 41(1): 99-107. Li Y Y, Yuan M, Wang Y, et al. Fault diagnosis of motor bearings based on SVM and PSO[J]. Journal of Chongqing University, 2018, 41(1): 99-107. (in Chinese) |
| [5] |
柯炎, 樊波, 谢一静, 等. 基于小波包分析和Elman神经网络的军用电源智能故障诊断[J]. 重庆大学学报, 2019, 42(9): 67-73. Ke Y, Fan B, Xie Y J, et al. Fault diagnosis of military power based on wavelet packet analysis and Elman neural network[J]. Journal of Chongqing University, 2019, 42(9): 67-73. (in Chinese) |
| [6] |
Lombardi W, Zarudniev M, Lesecq S, et al. Sensors fault diagnosis for a BMS[C]//2014 European Control Conference (ECC). June 24-27, 2014, Strasbourg, France. IEEE, 2014: 952-957.
|
| [7] |
Liu Z T, He H W, Ahmed Q, et al. Structural analysis based fault detection and isolation applied for a lithium-ion battery pack[J]. IFAC-PapersOnLine, 2015, 48(21): 1465-1470. DOI:10.1016/j.ifacol.2015.09.731 |
| [8] |
Xu J, Wang J, Li S Y, et al. A method to simultaneously detect the current sensor fault and estimate the state of energy for batteries in electric vehicles[J]. Sensors (Basel, Switzerland), 2016, 16(8): E1328. DOI:10.3390/s16081328 |
| [9] |
Dey S, Mohon S, Pisu P, et al. Sensor fault detection, isolation, and estimation in lithium-ion batteries[J]. IEEE Transactions on Control Systems Technology, 2016, 24(6): 2141-2149. DOI:10.1109/TCST.2016.2538200 |
| [10] |
He H W, Liu Z T, Hua Y. Adaptive extended Kalman filter based fault detection and isolation for a lithium-ion battery pack[J]. Energy Procedia, 2015, 75: 1950-1955. DOI:10.1016/j.egypro.2015.07.230 |
| [11] |
Liu Z T, He H W. Sensor fault detection and isolation for a lithium-ion battery pack in electric vehicles using adaptive extended Kalman filter[J]. Applied Energy, 2017, 185: 2033-2044. DOI:10.1016/j.apenergy.2015.10.168 |
| [12] |
Liu Z T, Ahmed Q, Zhang J Y, et al. Structural analysis based sensors fault detection and isolation of cylindrical lithium-ion batteries in automotive applications[J]. Control Engineering Practice, 2016, 52: 46-58. DOI:10.1016/j.conengprac.2016.03.015 |
| [13] |
胡晓松, 唐小林. 电动车辆锂离子动力电池建模方法综述[J]. 机械工程学报, 2017, 53(16): 20-31. Hu X S, Tang X L. Review of modeling techniques for lithium-ion traction batteries in electric vehicles[J]. Journal of Mechanical Engineering, 2017, 53(16): 20-31. (in Chinese) |
| [14] |
刘真通. 基于模型的纯电动车辆动力系统故障诊断研究[D]. 北京: 北京理工大学, 2016. Liu Z T. Model-based fault diagnosis of electrified driven powertrains in pure electric vehicles[D]. Beijing: Beijing Institute of Technology, 2016. (in Chinese) |
| [15] |
宋丽, 魏学哲, 戴海峰, 等. 锂离子电池单体热模型研究动态[J]. 汽车工程, 2013, 35(3): 285-291. Song L, Wei X Z, Dai H F, et al. A review on the research of thermal models for lithium ion battery cell[J]. Automotive Engineering, 2013, 35(3): 285-291. (in Chinese) DOI:10.3969/j.issn.1000-680X.2013.03.017 |
| [16] |
Lin X F, Perez H E, Mohan S, et al. A lumped-parameter electro-thermal model for cylindrical batteries[J]. Journal of Power Sources, 2014, 257: 1-11. DOI:10.1016/j.jpowsour.2014.01.097 |
| [17] |
Sidhu A, Izadian A, Anwar S. Adaptive nonlinear model-based fault diagnosis of Li-ion batteries[J]. IEEE Transactions on Industrial Electronics, 2015, 62(2): 1002-1011. DOI:10.1109/TIE.2014.2336599 |
| [18] |
Chen C, Xiong R, Yang R X, et al. State-of-charge estimation of lithium-ion battery using an improved neural network model and extended Kalman filter[J]. Journal of Cleaner Production, 2019, 234: 1153-1164. DOI:10.1016/j.jclepro.2019.06.273 |
| [19] |
Liu Z T, He H W. Model-based sensor fault diagnosis of a lithium-ion battery in electric vehicles[J]. Energies, 2015, 8(7): 6509-6527. DOI:10.3390/en8076509 |
 2022, Vol. 45
2022, Vol. 45

