在企业的实际管理中,生产计划的制订是企业实现生产资源合理分配的重要步骤,生产调度是保证完成生产计划的重要环节,车间调度问题是企业生产过程必须考虑的重要问题。随着市场需求不断变化,为了提高自身的竞争力,企业必须能够快速适应市场的变化,提高自身的柔性制造能力,因此产生了柔性制造系统[1]。基于此背景的柔性作业车间调度问题被提出,成为了研究热点[2]。而在柔性作业车间调度过程中,常常受到不确定事件的干扰,比如设备故障、紧急订单插入等,需要经常性地调整原调度计划,造成调度不稳定。所以笔者将结合以上内容研究柔性作业车间动态调度问题(dynamic flexible job shop scheduling problem,DFJSP)。
目前,国内外关于DFJSP问题的报道主要通过制定策略或依据经验规则来处理或者利用启发式算法来求解动态调度问题。王春等[3]通过滚动窗口机制将动态调度问题转化为多个连续静态调度问题来求解;吴正佳等[4]针对机器故障问题制订完全重调度和插入重调度的响应策略来解决DFJSP;宋李俊等[5]考虑生产设备出现故障情况,利用滚动时域优化策略来求解DFJSP。张国辉等[6]以时间和偏差度为指标,结合车间工人的经验制订了多阶段人机协同调度策略。顾泽平等[7]提出了结合离散仿真和层次分析法的混合遗传算法来求解加工时间不确定、到达时间不确定、排队规则出错三类不确定事件下的多目标DFJSP模型,得到鲁棒性较好的较优解;龙田等[8]针对7个目标设计了一种免疫调度算法,能根据车间情况选择对应规则求解调度问题;张祥等[9]利用动态交互层机制,结合PSGA(pole search genetic algorithm)算法,提高了动态调度处理紧急订单的能力;陈超等[10]利用结合遗传算法和模拟退火算法的混合算法,求解以平均流经时间和能耗为目标的DFJSP优化模型;Zhou等[11]建立了与时间指标有关的多目标DFJSP模型,并基于多目标遗传规划提出了4种超启发式算法。此外,一些学者研究了如何提升调度模型对环境的适应性。王玉芳等[12]提出一种结合聚类动态搜索的Q-learning强化学习算法,根据环境动态选择调度策略;Shen等[13]利用自启发式框架以加强对环境的适应性,并用结合进化算法的动态响应策略来求解DFJSP。
以上研究存在一些值得改进的地方:1)针对一种或几种动态事件干扰下的车间调度研究较多,需要提高在多种动态事件干扰下的处理能力,提高调度模型对动态环境的适应性。2)在多个动态事件干扰下,如何根据环境的变化动态地评价调度行为,即建立更有效的环境行为评价模型。3)在求解目标上,多以时间、成本、机器负荷等效益指标为评价指标,而综合考虑时间、能耗等指标的较少,对动态调度的稳定性评价也较少。因此,笔者将同时考虑平均延期惩罚、能耗、偏差度3项指标,构建多目标柔性作业车间动态调度优化模型,在多种动态事件的干扰下,通过深度Q学习神经网络算法DQN(deep Q-learning network)建立环境-行为评价神经网络模型,作为遗传算法的适应度函数,并利用结合混沌搜索方法的量子遗传算法QGA(quantum genetic algorithm)求解优化模型。
1 柔性作业车间动态调度优化模型 1.1 问题描述现有待加工工件集J={J1, J2, …, JN}和加工设备集A={A1, A2, …, AM},每个工件Ji包含Oi道工序,根据柔性作业调度的要求,每道工序可有一台或多台设备供选择。根据工件的工艺路径和各自工序的可选加工设备集合,将各道工序分配给满足加工条件的设备。同时,在满足工艺约束和符合设备加工条件的前提下,对各个加工设备上分配到的工序集进行排序。
对DFJSP问题,需要考虑动态不确定因素的影响,比如机器故障或阻塞、不合格工件重返工、订单变化等随机性事件。同时,为了提高动态调度的稳定性,提高模型的预见性和整体性,还需要进行周期性重调度。基于上述问题,考虑机器故障、到达时间不确定、紧急订单插入3种不确定事件对调度模型的影响,在周期性重调度的环境下,合理地进行设备分配和工序作业分配,使延期惩罚、能耗、偏差度3项指标达到最优。
基于以下假设构建模型:
假设1 同一工件的工序之间有顺序要求,不同工件之间没有顺序要求;
假设2 在开始加工时,所有加工设备资源均可使用,所有工件均可被加工;
假设3 一道工序只能选择一台设备,一台设备在任一时刻只能加工一道工序;
假设4 加工设备在加工过程中不会故障,不考虑工序加工中断的情况;
假设5 系统内所有设施缓冲区无限,忽略运输时间、准备时间等;
假设6 工件的加工路线不变,所有工件的优先级一致。
本模型中使用的参数和指标如下:
N表示工件总数;
i表示工件索引号,i∈{1, 2, …, N};
Oi表示工件i的最大工序数;
j为工序索引号,j∈{1, 2, …, Oi};
M表示可用加工设备数;
m表示加工设备索引号,m∈{1, 2, …, M};
u表示一台设备上工序的加工顺序索引号;
Qm表示加工设备m上安排生产的工序总数;
Ti, jm表示工件i的工序j在生产设备m上所花费的生产时间;
Di表示工件i的交货期;
Gm(u)表示在生产设备m上按顺序开始加工工序u的起始时间;
Bi, j表示工件i的工序j的开始加工时间;
Cmax表示整个调度过程的最大完工时间;
Ci, j表示工件i的工序j的完工结束时间;
xi, jm表示工件i的工序j是否选择在设备m上加工,是为1,否为0;
δi, jm(u)表示工件i的工序j在加工设备m上的加工顺序索引号是否为u,是则为1,否则为0;
Ec表示加工总能耗;
Ec(i, j, m)表示工件i的工序j在设备m上的所产生的能耗;
Ek表示空载总能耗;
Xa为衡量机器在调度开始后发生故障时刻的随机变量;
Xr为衡量机器维修时间的随机变量;
Xg为衡量工件到达时间的随机变量;
Xe为衡量紧急订单到来时刻的随机变量。
1.2 优化目标为保证模型的有效性,以最小化平均延期惩罚FEDP、最小化能耗Ep为优化目标。同时,为了兼顾动态调度过程中对稳定性的要求,需要评定动态调度中调度计划调整的程度,即相对于原始调度计划的偏离程度,故以最小化偏差度FDV作为第3个优化目标,并以此建立优化模型:
| min(FEDP,Ep,FDV)。 | (1) |
基于均衡生产理念,将调度目标确定为最小化平均延期惩罚FEDP:
| FEDP=minN∑i=1FiEP⋅max{Ci−Di,0}N; | (2) |
| Di=Tai+fiOj∑j=1Tij; | (3) |
| Ci=Oj∑j=1Ci,j; | (4) |
| Ci,j=Bi,j+M∑m=1xmi,j×Tmi,j,j∈{1,2,⋯,Oi}。 | (5) |
式中: FEPi为工件i的延期惩罚系数;fi为交货因子;Tij为工件i的工序j的实际加工时间;Tai为工件i原材料的到达时间;工件i的工序j的完工时间Ci, j由开始时间和该道工序花费的生产时间构成。
1.2.2 能耗柔性作业车间的能耗主要体现为生产能耗和辅助环节能耗。生产能耗主要是指与加工环节直接相关的能源消耗,包括加工能耗、换刀能耗、换夹具能耗、机床空载等待能耗等。辅助环节能耗主要是在辅助生产的过程中产生的能源消耗,比如切削液的能耗、工件运输能耗等。由于部分能耗对调度结果的影响不大,且实际测量复杂,故根据问题的描述简化对能耗的定义,只考虑因加工顺序不同和分配方式的差异而变化较大的能耗,包括加工能耗和设备空载能耗。
加工能耗包括整个调度流程中所产生的切削能耗、空切能耗、换刀能耗和装夹能耗等。所以,实际生产中的加工能耗为:
| Ec=N∑i=1Oi∑j=1M∑m=1xmi,j×Ec(i,j,m)。 | (6) |
用对所有设备的上下道工序之间的时间间隔的累积表示设备的等待能耗:
| Ek=M∑m=1Qm−1∑u=1[Gm(u+1)−Gm(u)−N∑i=1Oi∑j=1δmi,j(u)×Tmi,j]。 | (7) |
故总能耗为:
| Ep=Ec+Ek。 | (8) |
偏差度是衡量在重调度时刻,旧调度计划中待加工工序的开始时间与新调度计划中待加工工序的开始时间的差值。
| FDV=Ns∑n=1N∑i=1Nd∑j=1(|S′n,i,j−Sn,i,j|)N∑i=1Di。 | (9) |
式中:Ns表示整个调度过程中的调度调整次数,Nd表示在重调度时刻的待加工工序的总工序数,S′n, i, j和Sn, i, j分别表示第n次重调度前后工件i的工序j的计划开始时间。
1.3 约束条件| Bi,j+1Ci,j,j∈{1,2,⋯,Oi−1}; | (10) |
| m∈{1,2,⋯,M},u∈{1,2,⋯,Qm−1},M∑m=1xmi,j=1; | (11) |
| Gm(u+1)⩾ | (12) |
| \sum\limits_{j=1}^{O i} \delta_{i, j}^{m}=Q_{m}; | (13) |
| \sum\limits_{j=1}^{O_{i}} C_{i, j} \leqslant D(i), | (14) |
| B_{i, j} \geqslant 0, \quad G_{m}(u) \geqslant 0 ; | (15) |
| x_{i, j}^{m} \in\{0,1\}, \quad \delta_{i, j}^{m}(u) \in\{0,1\} ; | (16) |
| X_{\mathrm{a}} \sim G\left(\alpha_{\mathrm{a}}, \beta_{\mathrm{a}}\right), \quad X_{\mathrm{r}} \sim G\left(\alpha_{\mathrm{r}}, \beta_{\mathrm{r}}\right), \quad X_{\mathrm{g}} \sim G\left(\alpha_{\mathrm{g}}, \beta_{\mathrm{g}}\right), \quad X_{\mathrm{e}} \sim G\left(\alpha_{\mathrm{e}}, \beta_{\mathrm{e}}\right)。 | (17) |
式中:αa和βa为发生故障时刻的伽马分布的参数,G(αa, βa)为发生故障时刻的伽马分布;αr和βr为机器维修时间的伽马分布的参数,G(αr, βr)为机器维修时间的伽马分布;αg和βg为工件到达时间的伽马分布的参数,G(αg, βg)为工件到达时间的伽马分布;αe和βe为紧急订单到来时刻的伽马分布的参数,G(αe, βe)为紧急订单到来时刻的伽马分布。
式(10)表示同一工件内的工序满足工艺路线约束;式(11)表示一道工序只能选择一台设备加工;式(12)表示加工设备约束,一台设备在任一时刻只能加工一道工序;式(13)表示设备m上加工的工序总数约束;式(14)为工件的交货期约束;式(15)表示对决策变量在数值上的约束;式(16)表示在调度时刻正在机器上加工的工序将不受影响,继续完成原来的加工;式(17)表示动态事件的随机变量均服从伽马分布。
1.4 动态调度响应策略采用基于DQN和QGA的动态调度响应策略。该策略结合了动态事件重调度和周期性重调度,是一种完全反应式调度策略,在动态事件和周期性重调度的触发下,基于当前系统的状态,动态地根据基于DQN和QGA的调度算法进行重调度,制定新的调度计划,以适应车间制造环境的动态变化。
为了准确地描述当前系统状态,将工序分为以下5类:已完工工序、正在加工工序、已调度但待加工工序、不可调度工序、待调度工序。已完工工序是指在重调度时刻已经完成加工的工序,正在加工工序指在重调度时刻正在加工的工序,已调度但待加工工序指上一个调度周期内已经分配但等待加工的工序,不可调度工序指上一个调度周期和本调度周期内,按照工艺流程下一步不可进行加工的工序,待调度工序指上一调度周期内不可调度但当前调度周期内可调度的工序。重调度需要解决的是在当前重调度周期内需要汇总可调用工序,包括已调度但待加工工序和待调度工序,并对其进行调度和安排加工。
在重调度时刻对系统的状态进行描述,选择耦合性低、对目标影响大的属性,主要有与时间有关的属性和与能耗有关的属性。与时间有关的属性包括工序加工时间TP、工件剩余工序数NR、各工件剩余加工时间TR、工序到达时间TA、设备的可用时间Tm、交货期D、工件的权重ω。与能耗有关的属性包括工序的加工能耗EP、工件的剩余加工能耗ER。
2 基于QGA和DQN的动态调度算法 2.1 量子遗传算法量子遗传算法是一种将具有概率性的量子计算与GA算法融合在一起的算法[14]。该算法在一般的编码过程中添加了对基因的量子矢量表达,一位基因可由两位量子比特表示,并利用量子旋转门对量子比特的相位旋转实现染色体进化,与一般的遗传算法相比有更好的收敛和多样性。
种群个体的染色体采用基于量子比特形式的编码解码方式,即传统算法中表达信息的一位基因用两位基因来表达,该段信息数据处于“0”态和“1”态的叠加态中,根据概率具体选择处于某种量子态中的基因。这赋予QGA算法更好的多样性特征。量子比特在物理意义上表示同时处在两个量子态的叠加态,如式(18)所示:
| |\varphi\rangle=\alpha|0\rangle \beta|1\rangle。 | (18) |
式中:0〉和1〉分别对应量子计算中的“0”态和“1”态;(α, β)表示处于“0”态和“1”态的概率幅,也就是以多大的概率取到0或1。该参数满足如下条件:
| |\alpha|^{2}+|\beta|^{2}=1。 | (19) |
量子遗传算法的收敛通过量子旋转门更新来实现,一个量子比特b经过量子门的相位调整后,会逐渐向某一状态倾斜,最终收敛于局部最优解。量子旋转门的表达式如下:
| \mathit{\boldsymbol{U}}\left(\theta_{b}\right)=\left[\begin{array}{cc} \cos \left(\theta_{b}\right) & -\sin \left(\theta_{b}\right) \\ \sin \left(\theta_{b}\right) & \cos \left(\theta_{b}\right) \end{array}\right] 。 | (20) |
量子比特的相位上的调整如下:
| \left[\begin{array}{c} \alpha_{b}^{\prime} \\ \beta_{b}^{\prime} \end{array}\right]=\mathit{\boldsymbol{U}}\left(\theta_{b}\right)\left[\begin{array}{l} \alpha_{b} \\ \beta_{b} \end{array}\right]=\left[\begin{array}{cc} \cos \left(\theta_{b}\right) & -\sin \left(\theta_{b}\right) \\ \sin \left(\theta_{b}\right) & \cos \left(\theta_{b}\right) \end{array}\right]\left[\begin{array}{l} \alpha_{b} \\ \beta_{b} \end{array}\right] 。 | (21) |
式中:θb是旋转角,由θ=fs(α, β)Δθ得到,Δθ表示旋转角的大小;fs(α, β)表示旋转角的方向,可由表 1查得;(αb, βb)T和(α′b, β′b)T分别表示染色体的量子比特b通过量子旋转门调整前后的概率幅。
| 表 1 旋转角调整策略 Table 1 Helix angle adjustment strategy |
量子旋转门的原理是通过比较当前个体和最优个体的适应度,选择合适的旋转角大小和方向使相应的基因向适应度更高的方向演化,从而收敛于局部最优解。
2.2 深度Q学习神经网络算法深度Q学习神经网络算法是一种结合强化学习和神经网络的算法。该算法定义了一种智能体,该智能体能够对复杂的环境做出响应,依据策略执行动作,并得到在该环境下的反馈,利用该反馈进行不断学习,训练能够对动态环境做出最优响应的神经网络模型,从而提升对环境的适应能力。
该算法主要包括以下3个要素:环境的状态S、智能体的动作A、环境对智能体的奖励R。本研究的环境状态包括时间和能耗有关的属性,时刻t的环境状态St描述为:
| S_{t}=\left\{T_{\mathrm{p}}, N_{\mathrm{R}}, T_{\mathrm{R}}, T_{\mathrm{A}}, T_{\mathrm{m}}, D, \omega, E_{\mathrm{P}}, E_{\mathrm{R}}\right\} 。 | (22) |
当智能体执行动作后,状态由St变化到St+1,设定状态变化的一步为最早的一个或一批工件加工完成,此时会进入下一个状态。
在t时刻,动态调度系统所执行的动作At是下一步加工的工序集,动作At是由动作选择策略产生的。该策略根据对环境的观察,根据概率ε选择获得价值最大的动作。
奖励函数R的选取要考虑整个调度系统的优化目标,同时确保强化学习模型能够向着奖励最大化的方向拟合,本研究中对各个调度目标采取加权方式求和,并将求解目标的最小化转化为强化学习中的奖励最大化,奖励函数如下:
| R_{t}= \begin{cases}\frac{\eta}{\alpha_{1} F_{\mathrm{EDP}}+\alpha_{2} E_{\mathrm{P}}+\alpha_{3} F_{\mathrm{DV}}}, & \text { 调度结束并按期完成; } \\ 0, & \text { 调度末结束; } \\ -1, & \text { 调度结束但延期完成。}\end{cases} | (23) |
式中:η表示缩放因子,用以控制对奖励值的调整;α1、α2、α3分别表示对平均延期惩罚、能耗、偏差率的权值。
在动态调度系统中,评价动态调度动作的优劣程度可用动作价值函数Q(S, A)来描述,该价值函数是一个神经网络模型,即DQN算法要求出的模型。该神经网络的训练数据在强化学习过程中产生,将一段周期内的学习数据输入神经网络模型中,进行训练得到神经网络模型。训练该神经网络的成本函数如下:
| L_{e}\left(\theta_{g}\right)=E_{s, a \sim \rho(\cdot)}\left[\left(y_{e}-Q\left(s, a ; \theta_{g}\right)\right)^{2}\right], e=1,2, \cdots, N_{\mathrm{A}}, g=1,2, \cdots, M_{\mathrm{N} }。 | (24) |
式中:s表示当前的环境状态; a表示采取的具体行动; e表示算法的迭代序号; g表示神经网络的参数序号; NA表示算法的迭代次数; MN表示神经网络的参数个数; ye是当前环境下采取行动得到的现实值,即训练数据的输出值; θg表示神经网络模型的第g号参数; Q(s, a; θg)是根据当前评估神经网络求出的估计值;Es, a~ρ(·)表示神经网络估计值和现实值的误差累积。
DQN算法关键的一步是对ye求解,ye是根据现实神经网络求出的现实值,现实神经网络是上一个迭代周期内的评估神经网络。在算法中采用两个神经网络的目的是减少算法的不稳定性。ye的求解公式如下:
| y_{e}=r_{e}+\gamma \max _{a^{\prime}} Q\left(s^{\prime}, a^{\prime} ; \theta_{e-1}\right) 。 | (25) |
式中:γ表示奖励衰减因子,在0~1之间取值;s′和a′表示执行动作a后智能体进入的下一个状态和可选动作; Q(s′, a′; θe-1)是现实神经网络,该算法基于贪婪策略,通过遍历下一个状态的可选动作集,选择其中使现实值最大化的动作;re表示奖励值。
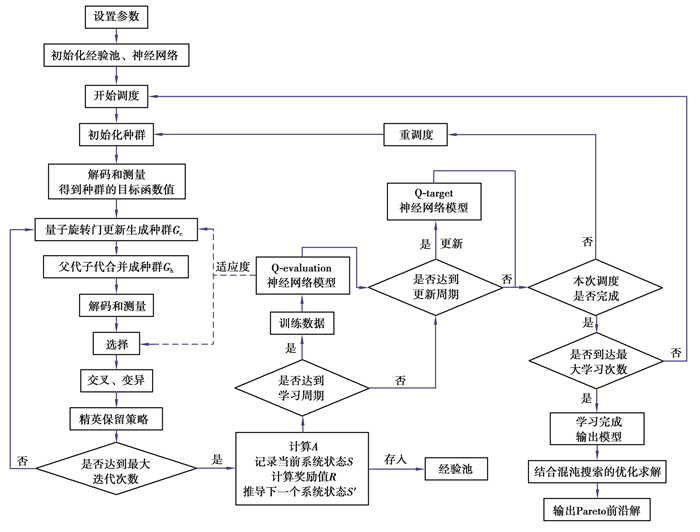
2.3 基于QGA和DQN的调度算法整体框架本研究中改进了一般的QGA算法,利用DQN算法学习出的Q价值神经网络模型作为调度模型的适应度函数,提高了算法对动态环境的学习性和适应性,融合了动态调整旋转角策略,增强了其收敛能力,并结合混沌搜索方法均匀遍历解空间。算法流程见图 1, 算法具体步骤如下。
|
图 1 基于DQN和QGA的调度算法流程 Fig. 1 Scheduling algorithm flow based on DQN and QGA |
步骤1 设定个体总数popsize、单个个体的基因总数w、变异概率Pv、交叉概率Pc、种群进化代数MaxGen、重调度周期TL、动态事件的概率参数、最大学习调度次数MaxL、学习周期GapL、更新周期GapUp等参数。
步骤2 初始化用来训练神经网络的经验池,初始化Q评估神经网络模型(Q-evaluation)和Q现实神经网络模型(Q-target),初始化学习调度次数TLS为1,学习步数step为1。
步骤3 在初始调度时刻,对已到达工件进行调度,记录当前初始系统状态S0。
步骤4 按照均匀规则初始化种群G0,生成popsize条概率幅一致的染色体。
步骤5 对染色体解码,得到下一步加工的工序集,记录当前系统状态S,通过Q-evaluation价值函数得到适应度,并以此来更新量子旋转门,生成子代种群Gc。
步骤6 将父代Gp与子代Gc种群合并成种群Gh,并对其解码,通过Q-evaluation价值函数测量出种群的适应度。
步骤7 按照适应度大小挑选出下一代种群。
步骤8 对挑选出的种群以设定的概率执行交叉操作,并根据一定规则取部分个体变异,生成种群Gb。
步骤9 采取精英保留策略,选择Gh中适应度高的个体与种群Gb合并,生成下一代种群G。
步骤10 返回步骤4循环,直到达到最大种群进化次数。
步骤11 解码种群中适应度最高的染色体,得到下一步的加工工序集A,记录当前系统状态S,计算出奖励值R,并由执行动作推导出下一个系统状态S′,将{A, S, R, S′ }记录到经验池中,并更新step。
步骤12 通过step判断是否达到一个Q-target更新周期,达到即用Q-evaluation神经网络更新Q-target神经网络,未达到则继续下一步。
步骤13 通过step判断是否达到一个学习周期,如果达到即开始进行Q-evaluation神经网络训练,随机抽取经验池中的一批数据作为网络模型的输入数据,对应的输出数据根据公式计算得出,以此来训练Q-evaluation神经网络,未达到则继续下一步。
步骤14 判断一次调度是否完成,未完成则返回步骤4,完成则更新学习调度次数TLS。
步骤15 判断学习调度次数TLS是否达到最大学习调度次数MaxL,未达到则返回步骤3,达到则表明强化学习过程结束,适应度函数模型学习完成。
步骤16 根据适应度函数模型求解最优解,执行步骤4~9。
步骤17 对种群进行混沌搜索,如果找到一个非支配解,则将该非支配解对应的个体代替种群中前端序值低的个体。
步骤18 返回步骤16循环,直到达到最大迭代次数,此时求出最优解。
2.4 算法具体设计 2.4.1 初始化种群的初始化影响最终求解的质量和收敛速度。种群的初始化涉及工件加工顺序和设备选择两方面。为了保证种群多样性同时兼顾初始种群的质量,将种群中所有个体的量子比特都设定为
由柔性作业车间动态调度的问题特性可知其编码由两部分组成,分别是工序排序向量(operation sequence vector,OV)和加工设备选择向量(machine assignment vector,MV)。
量子编码是QGA算法中十分关键的步骤,也是相对较复杂的步骤。在本研究中,根据不同的部分,制定不同的编码策略,实现多层编码。对于工序排序向量,根据工件中的最大工序数k,每一道工序分配长度为LP=[log2k]+1的量子比特位;对于加工设备向量,根据所有工序的最大可选择设备数M,为每道需选择设备的工序分配长度为LA=([log2M]+2)×M的量子比特位。最后染色体的总位数w为:
| w=L_{\mathrm{P}} \times H+L_{\mathrm{A}} \times H, | (26) |
式中H为所有工件的工序总数。
接下来需要对二进制染色体进行解码。由于量子比特是通过概率幅对解的一种线性叠加态,首先将二进制染色体转换为十进制染色体,再根据各自的解码策略,将十进制染色体转换为最终解。针对种群某一个体的染色体的解码方案如下。
1) 对于w位的初始解Q,根据概率幅将双行的初始解转换为单行的二进制代码Q。设Q(t)为第t位的量子比特,系统产生一个0到1的随机数r,若|αt|2>r2,则令B(t)=1,否则令其为0。由此得到w位的二进制解B =(b1, b2, …, bt, …, bw);
| \mathit{\boldsymbol{Q}}=\left[\begin{array}{llllll} \alpha_{1} & \alpha_{2} & \cdots & \alpha_{t} & \cdots & \alpha_{w} \\ \beta_{1} & \beta_{2} & \cdots & \beta_{t} & \cdots & \beta_{w} \end{array}\right] 。 | (27) |
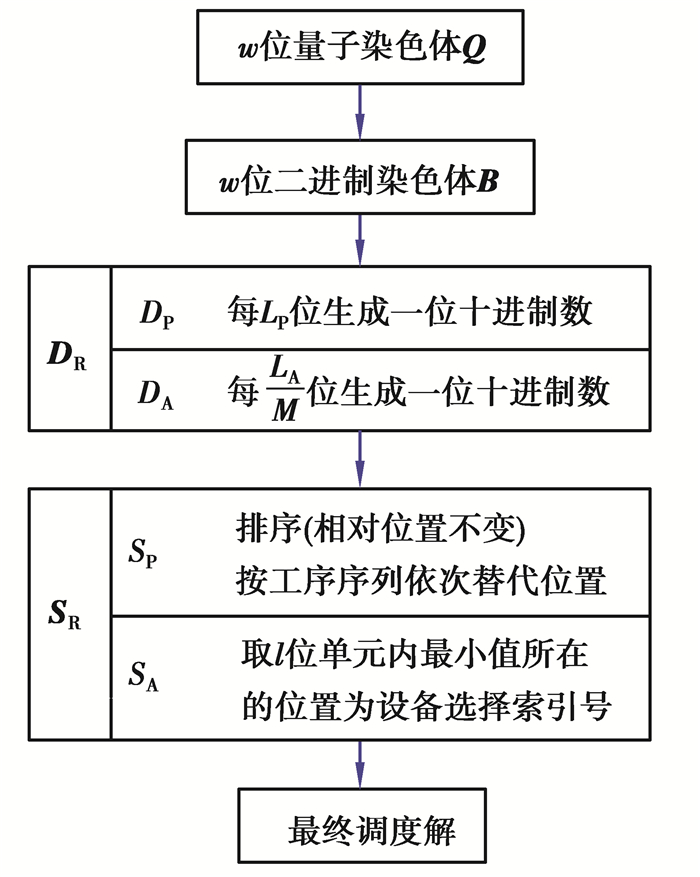
2) 根据上面的编码策略,按照OV和MV分别进行十进制解码。对于OV,将每LP位的二进制串解码成十进制串,由此得到长度为H的十进制串DP;对于MV,将每LA/M位的二进制串转换为十进制串,由此得到长度为M×H的十进制串DA。最终得到的十进制染色体DR如下:
| \mathit{\boldsymbol{D}}_{\mathrm{R}}=\left[D_{\mathrm{P}} \mid D_{\mathrm{A}}\right] 。 | (28) |
3) 对于十进制染色体DR,同样按照两部分分别处理。
对于OV,将DP中的数按从小到大标记序号,标记序号最小的数所在的位置被替换为第一个加工的工件索引号,标记序号次小的数所在的位置被替换为第二个工件索引号,依此类推。如果在DP中出现相等的数字,则位置序号较小的数代表工序号较小的工件。由此得到所有工序的加工顺序序列SP。SP中第n次出现的数i将表示工件i的第n道工序。
对于MV,每M位为一个单元,在一个单元内有M位十进制数,根据能够加工该单元对应的工序的最大设备数h,取前h位中的最小数,该最小数所在的位置序号即为加工该道工序所对应的设备选择索引号,如果最小数有相同的,则对大小相同的位置随机选择一个作为设备选择序号。由此得到设备选择序列SA。
最终得到工序调度染色体SR如下:
| \mathit{\boldsymbol{S}}_{\mathrm{R}}=\left[S_{\mathrm{P}} \mid S_{\mathrm{A}}\right] 。 | (29) |
4) 根据MV将OV中的每道工序分配到对应设备中,完成调度,得到最终调度解。
解码流程如图 2所示。
|
图 2 解码流程图 Fig. 2 Decoding flowchart |
量子旋转角大小的选择对量子遗传算法的性能影响很大。如果旋转角幅值太小,可能导致收敛速度比较慢,如果旋转角太大,则可能导致在最优解附近徘徊,无法收敛。一般情况下,量子旋转角的大小是固定的,无法对进化情况做出自适应调整,导致收敛速度较慢或无法收敛。
本研究中提出一种动态调整旋转角策略。当种群中个体的适应度与种群中最优个体的适应度的差距较大时,可适当调大旋转角的幅值,以达到快速收敛的目的;反之则可适当减小旋转角的幅值,对个体进行微调,防止在最优解周围来回震荡以致无法收敛。旋转角幅值的调整函数如下:
| \Delta \theta=\frac{f_{\max }-f_{\mathrm{c}}}{f_{\max }}\left(\theta_{\max }-\theta_{\min }\right) 。 | (30) |
式中:Δθ表示旋转角幅值,θmax和θmin限定了旋转角的极值,fmax和fmin表示种群的个体适应度极值,fc表示个体的适应度。该策略关联了旋转角与个体适应度,可动态自适应调整旋转角度,从而提升整体的收敛速率。
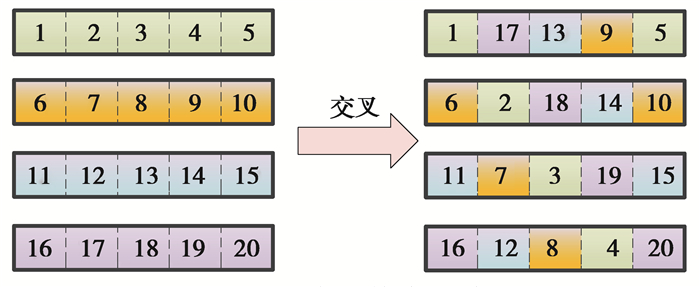
2.4.4 交叉操作在本研究中使用了一种关联所有染色体的交叉技术,即全干扰交叉方式。这种方法的特点是所有染色体均受影响。例如假设人口为4,基因数为5,其中每个数字代表染色体上的一个量子位(图 3)。交叉操作完成后,染色体的每一位都将重新排列并斜向连接以形成新的种群。该交叉操作可以最大化地利用整个种群的染色体信息,提高种群的多样性,并有效地减少早熟现象的发生。
|
图 3 全干扰交叉演示 Fig. 3 Demonstration of full interference crossover |
与经典遗传算法相比较,量子遗传算法同样位数的量子比特包含了更丰富的信息,种群多样性更好,但仅靠量子态带来的多样性对搜索全局最优解仍然不够,还是可能出现过早地收敛于局部解的问题,因此需要加入量子变异来提升算法的性能。变异操作可以有效地减少早熟现象的发生,提高算法的寻优能力。
在QGA算法中通常使用量子非门来进行变异操作,量子非门的表示形式如下:
| \mathit{\boldsymbol{X}}=\left[\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right]。 | (31) |
对某位量子比特进行量子非门转换,可得到:
| \left[\begin{array}{c} \alpha_{b}^{\prime} \\ \beta_{b}^{\prime} \end{array}\right]=\left[\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right]\left[\begin{array}{l} \alpha_{b} \\ \beta_{b} \end{array}\right]=\left[\begin{array}{l} \beta_{b} \\ \alpha_{b} \end{array}\right]。 | (32) |
该操作交换了量子比特|0和|1〉的概率幅,从而互换了测量计算时的概率,以达到变异的目的。
2.4.6 混沌搜索为了避免种群早熟,本研究中引入混沌搜索算法,可对解空间比较均匀地遍历。混沌变量的迭代采用基于Tent映射的混沌搜索方法[15]。Tent映射函数有良好的物理性能,可以得到比较均匀的解集,能提高对解空间的搜索能力,但容易产生不动点情况,在算法中需要避开它。混沌变量的迭代步骤如下:
1) 初始化迭代次数e=1。
2) 取某一染色体Qe,对该染色体的第一行进行迭代,迭代公式如下:
| x_{b}^{e+1}= \begin{cases}2 x_{b}^{e} & 0 \leqslant x_{b}^{e} \leqslant 0.5 ; \\ 2\left(1-x_{b}^{e}\right) & 0.5 \leqslant x_{b}^{e} \leqslant 1 。\end{cases} | (33) |
式中xbe表示第1行的第b位基因。根据量子比特的性质,生成双行的染色体Qe+1。令e=e+1,并判断是否达到设定条件,若未达到则进入步骤3),否则直接结束。
3) 判断得到的染色体第1行的基因是否满足xbe={0, 0.25, 0.50, 0.75}或者xbe=xbe-z,z ={1, 2, 3, 4}。若满足则说明此时混沌搜索陷入不动点,跳转到步骤4);否则返回步骤2)继续迭代。
4) 按照如下公式对xbe进行更新,并返回步骤2)。
| x_{b}^{e}=x_{b}^{e} \operatorname{rand}(0,1) 。 | (34) |
在此基础上将当前代种群引入混沌变量进行混沌搜索,在最大迭代次数内,若迭代得到的解不受当前所有种群支配,则结束迭代并记录当前非劣解; 若始终没有得到非劣解,则迭代至最大迭代次数后停止迭代。
3 算例验证 3.1 测试数据通过测试案例来验证算法解决多目标DFJSP的可行性。当前并没有标准测试算例来测试柔性作业车间调度问题,本研究中参考Brandimarte[16]柔性作业车间调度问题标准算例,生成一系列的测试算例。为简化问题,设每个工件的工序数一致。测试算例的参数如表 2所示。
| 表 2 测试算例参数 Table 2 Test case parameters |
具体生成步骤以算例MK01为例:工件总数目为6,单个工件的工序数为4,某道工序的可选加工设备以一定概率随机选取,在[1, 9]之间随机生成不同机器上工序的生产时间,并且是整数;在加工设备上加工不同工序所用的能耗在[2, 8]之间随机选取,且为实数;各个工件的交货期设为50乘以工件设备数之比。
3.2 评价指标采用迭代距离Ds指标[17]来评价算法的收敛性能:Ds表示的是当前算法的非劣解集I相对于真实Pareto解集I*的距离。该距离越小,表明当前算法的非劣解集越接近真实Pareto解,算法求优性能就越好。
| D_{\mathrm{s}}=\frac{1}{N_{I^{*}}} \sum_{y \in I^{*}} \min \left\{\sigma_{x y} \mid x \in I\right\}。 | (35) |
式中:NI*表示该非劣解集的元素个数;σxy表示解I与I*中元素y在归一化空间内的距离。真实Pareto解集可由所有算法算得的非劣解集构成的集合中的非劣解近似表示。
采用ΔMetric指标[18]来衡量非劣解集的多样性。通过非劣解集中相邻解的欧式距离与平均距离的差值累加来反映解空间分布的均匀性。其数学表达式如下:
| \mathit{\Delta}=\frac{d_{\mathrm{L}}+d_{\mathrm{R}}+\sum\limits_{\gamma=1}^{V-1}\left|d_{\gamma}-\bar{d}\right|}{d_{\mathrm{L}}+d_{\mathrm{R}}+(N-1) \bar{d}}。 | (36) |
式中:V为非劣解的数目;dL和dR分别表示真实Pareto解集的两个极值解和非劣解集对应的两个边界解的距离;dγ表示依次排列的两个非劣解的距离,d表示均值。当Δ值越大,说明算法的多样性越差,反之则算法的多样性好。
3.3 实验结果本次实验首先需要验证通过DQN强化学习得到的Q适应度函数的有效性,将其与其他评估适应度的方法对比。常用的求解多目标解适应度的方法有两种,一种是将多目标通过加权方式转换为单目标来进行评价,另一种是构造基于非支配排序等级的实值函数来评价多目标解。在本次实验以MK04作为算例,设定种群迭代次数为80,种群个体数为40,单位延期惩罚系数为0.4,且当前只考虑设备发生故障的情况,为了统一计量各个评价方法的优劣,设定设备在时刻8出现故障,并在时刻20维修好。在量子遗传算法的基础上,分别调用这3种方法,各自重复运行10次,选择调度结果中较优解(平均延期惩罚最小优先),运行结果如图 4~6和表 3所示。
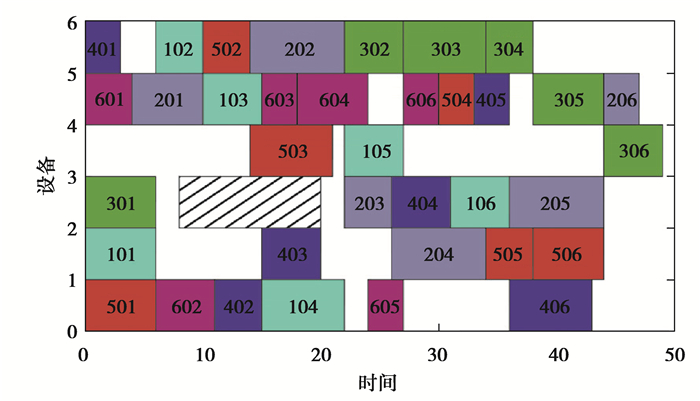
|
图 4 采用Q适应度函数的重调度甘特图 Fig. 4 Rescheduling Gantt chart using Q fitness function |
|
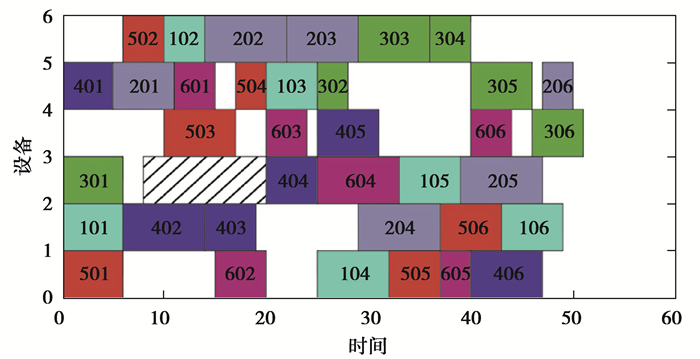
图 5 采用加权适应度函数的重调度甘特图 Fig. 5 Rescheduling Gantt chart using weighted fitness function |
|
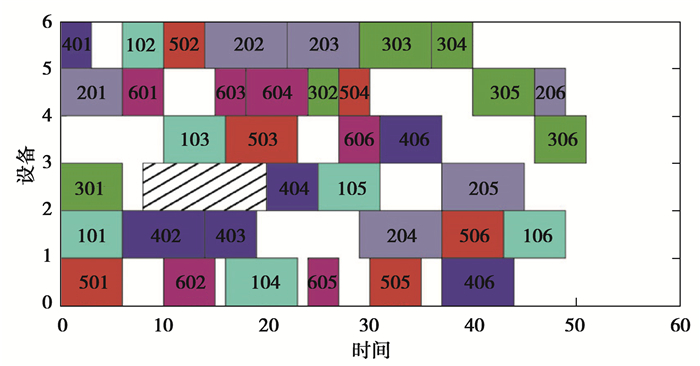
图 6 采用基于非支配排序等级的适应度函数的重调度甘特图 Fig. 6 Rescheduling Gantt chart using fitness function based on non-dominated ranking |
| 表 3 采用各种适应度函数的实验结果 Table 3 Experimental results using various fitness functions |
表 3列出所有Pareto解中的各项目标的最小值及Pareto解个数,在所求解的各项目标上,采用Q适应度函数的算法算出的最小值均明显优于其他两种方法算出的结果,表明Q适应度函数对解空间的寻优能力更强,能够更好地评估染色体的适应度。而且Q适应度函数对动态事件有很好的响应,能够根据当前环境做出整体的最优选择,如图 4~6是采用各种适应度函数得到的最小平均延期惩罚解对应的重调度结果,当机器故障修复后,采用Q适应度函数的算法并不急于在机器3上安排工件4加工,而是选择等待工件2的加工,而其他两种算法都急于在机器3上安排工件4加工,不能达到整体最优。
在DFJSP问题上,为验证算法的有效性,将本文的深度强化学习-量子遗传算法(DQN-QGA)与求解DFJSP的常用算法非支配遗传排序算法(non-dominated sorting genetic algorithm,NSGA)进行比较,同时为了验证该算法在环境适应性上的提升,与一般非支配量子遗传算法(non-dominated sorting quantum genetic algorithm,NSQGA)进行比较,并在各个测试案例中进行测试验证。为保证一致性,对各个算法设定同样的参数,包括种群进化代数为100,种群个体总数为80,动态事件均服从伽马分布,根据文献[8]中对动态事件的仿真策略,α取0.2,β取0.4。同时对各个算例重复运行20次,取20次运算结果的Pareto前沿解作为算法的运算结果。实验结果见表 4。
| 表 4 各类算法关于指标Ds和Δ的计算结果 Table 4 The calculation results of various algorithms on the indicators Ds and Δ |
在收敛性指标上,DQN-QGA算法明显优于其他算法。在16个算例中,DQN-QGA的Ds指标均比NSQGA和NSGA小,表明其求出的非劣解接近实际Pareto解,与常规算法相比,极大地提高了算法收敛性。在多样性指标上,DQN-QGA算法在超过2/3的算例中,Δ指标比其他算法小,由于编码解码复杂和智能算法自身的随机性,在剩下的算例中,DQN-QGA的Δ指标比其他算法大。总体说来,与传统的遗传算法和量子遗传算法相比,DQN-QGA算法在收敛性和多样性上有明显的优势。
4 结束语研究了柔性作业车间动态调度问题及其求解。首先建立了考虑了平均延期惩罚、能耗、偏差度的DFJSP优化模型,采用动态重调度和周期性重调度相结合的动态调度响应策略;然后利用DQN算法学习环境-行为评价神经网络模型作为优化模型的适应度函数,基于该适应度函数,通过改进的量子遗传算法对优化模型求解,该算法设计了多层编码解码方案,对量子交叉和变异操作进行了适当改进,并引入了混沌变量,对种群进行基于Tent映射的混沌搜索以提升对解空间的均匀遍历能力,避免早熟现象。最后通过测试算例,验证了环境-行为评价神经网络模型的有效性,能够根据当前环境做出较优的选择,提高了优化算法的鲁棒性和自适应性。提出的基于Q学习神经网络的改进QGA算法,通过不断地学习,可以适应新环境下的动态事件干扰,具有很强的鲁棒性,相较于传统的遗传算法,该算法在收敛性、多样性、稳定性上有了较大的提升,可以作为求解DFJSP问题的一个途径。
| [1] |
吴秀丽, 张志强, 杜彦华, 等. 改进细菌觅食算法求解柔性作业车间调度问题[J]. 计算机集成制造系统, 2015, 21(5): 1262-1270. Wu X L, Zhang Z Q, Du Y H, et al. Improved bacteria foraging optimization algorithm for flexible job shop scheduling problem[J]. Computer Integrated Manufacturing Systems, 2015, 21(5): 1262-1270. (in Chinese) |
| [2] |
Wu X L, Sun Y J. A green scheduling algorithm for flexible job shop with energy-saving measures[J]. Journal of Cleaner Production, 2018, 172: 3249-3264. DOI:10.1016/j.jclepro.2017.10.342 |
| [3] |
王春, 张明, 纪志成, 等. 基于遗传算法的多目标动态柔性作业车间调度[J]. 系统仿真学报, 2017, 29(8): 1647-1657. Wang C, Zhang M, Ji Z C, et al. Genetic algorithm for solving multi-objective dynamic flexible job shop scheduling[J]. Journal of System Simulation, 2017, 29(8): 1647-1657. (in Chinese) |
| [4] |
吴正佳, 何海洋, 黄灿超, 等. 带机器故障的柔性作业车间动态调度[J]. 机械设计与研究, 2015, 31(3): 94-98. Wu Z J, He H Y, Huang C C, et al. Flexible job shop dynamic scheduling problem research with machine fault[J]. Machine Design & Research, 2015, 31(3): 94-98. (in Chinese) |
| [5] |
宋李俊, 赵虎. 基于滚动时域优化策略的柔性作业车间动态调度研究[J]. 现代制造工程, 2015(2): 30-35, 42. Song L J, Zhao H. Dynamic flexible job shop scheduling research based on rolling time domain optimization strategy[J]. Modern Manufacturing Engineering, 2015(2): 30-35, 42. (in Chinese) DOI:10.3969/j.issn.1671-3133.2015.02.007 |
| [6] |
张国辉, 王永成, 张海军. 多阶段人机协同求解动态柔性作业车间调度问题[J]. 控制与决策, 2016, 31(1): 169-172. Zhang G H, Wang Y C, Zhang H J. Multi-stage man-machine cooperated scheduling method for dynamic flexible job shop scheduling problem[J]. Control and Decision, 2016, 31(1): 169-172. (in Chinese) |
| [7] |
顾泽平, 杨建军, 周勇. 不确定因素扰动下多目标柔性作业车间鲁棒调度方法[J]. 计算机集成制造系统, 2017, 23(1): 66-74. Gu Z P, Yang J J, Zhou Y. Multi-objective flexible job-shop robust scheduling optimization under disturbance of uncertainties[J]. Computer Integrated Manufacturing Systems, 2017, 23(1): 66-74. (in Chinese) |
| [8] |
龙田, 王俊佳. 基于调度规则和免疫算法的作业车间多目标调度[J]. 信息与控制, 2016, 45(3): 278-286. Long T, Wang J J. Multi-target job-shop scheduling based on dispatching rules and immune algorithm[J]. Information and Control, 2016, 45(3): 278-286. (in Chinese) |
| [9] |
张祥, 王艳, 纪志成. 基于动态交互层的柔性作业车间动态调度问题研究[J]. 系统仿真学报, 2020, 32(11): 2129-2137. Zhang X, Wang Y, Ji Z C. Research on dynamic flexible job shop scheduling problem based on dynamic interaction layer[J]. Journal of System Simulation, 2020, 32(11): 2129-2137. (in Chinese) |
| [10] |
陈超, 王艳, 严大虎, 等. 面向能耗的柔性作业车间动态调度研究[J]. 系统仿真学报, 2017, 29(9): 2168-2174, 2181. Chen C, Wang Y, Yan D H, et al. Research on dynamic flexible job shop scheduling problem for energy consumption[J]. Journal of System Simulation, 2017, 29(9): 2168-2174, 2181. (in Chinese) |
| [11] |
Zhou Y, Yang J J, Huang Z. Automatic design of scheduling policies for dynamic flexible job shop scheduling via surrogate-assisted cooperative co-evolution genetic programming[J]. International Journal of Production Research, 2020, 58(9): 2561-2580. DOI:10.1080/00207543.2019.1620362 |
| [12] |
王玉芳, 严洪森. 基于改进Q学习的知识化制造自适应动态调度策略[J]. 控制与决策, 2015, 30(11): 1930-1936. Wang Y F, Yan H S. Adaptive dynamic scheduling strategy in knowledgeable manufacturing based on improved Q-learning[J]. Control and Decision, 2015, 30(11): 1930-1936. (in Chinese) |
| [13] |
Shen X N, Yao X. Mathematical modeling and multi-objective evolutionary algorithms applied to dynamic flexible job shop scheduling problems[J]. Information Sciences, 2015, 298: 198-224. DOI:10.1016/j.ins.2014.11.036 |
| [14] |
Han K H, Kim J H. Genetic quantum algorithm and its application to combinatorial optimization problem[C]//Proceedings of the 2000 Congress on Evolutionary Computation, CEC00 (Cat. No. 00TH8512), July 16-19, 2000, La Jolla, CA, USA. IEEE, 2000: 1354-1360.
|
| [15] |
聂瑞, 章卫国, 李广文, 等. 基于Tent映射的自适应混沌混合多目标遗传算法[J]. 北京航空航天大学学报, 2012, 38(8): 1010-1016. Nie R, Zhang W G, Li G W, et al. Adaptive chaos hybrid multi-objective genetic algorithm based on the Tent map[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(8): 1010-1016. (in Chinese) |
| [16] |
Brandimarte P. Routing and scheduling in a flexible job shop by tabu search[J]. Annals of Operations Research, 1993, 41(3): 157-183. DOI:10.1007/BF02023073 |
| [17] |
Schutze O, Esquivel X, Lara A, et al. Using the averaged Hausdorff distance as a performance measure in evolutionary multi-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2012, 16(4): 504-522. DOI:10.1109/TEVC.2011.2161872 |
| [18] |
Deb K, Pratap A, Agarwal S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017 |
 2022, Vol. 45
2022, Vol. 45



