近年来增材制造技术的快速发展使复杂点阵结构的加工制造成为可能,基于三周期极小曲面(triply periodic minimal surface, TPMS)的点阵结构因具有轻质高强度、连通性好、拓扑结构可控等优点[1-2],在结构轻量化设计、生物植入物中得到广泛应用[3-4],受到国内外专家学者的关注[5-6]。
围绕TPMS点阵结构建模设计的研究主要分为空间单元映射和布尔运算两类方法。空间单元映射是通过对实体进行六面体网格划分,将标准的TPMS单元用形函数分别映射到实体中的每个六面体单元,从而构建出异构点阵结构模型[7-8]。张壮雅等[9-10]通过形函数变换以及模板法对点阵结构进行局部加密,设计出孔隙可控的TPMS点阵结构。空间单元映射法构建的TPMS点阵结构一定程度上可以拟合不规则实体的轮廓,在力学性能和模拟天然组织的多孔结构上也有较为优异的表现,但由于六面体单元尺寸及制造工艺的限制,存在轮廓拟合精度不高、无法保证加工质量、拓扑结构不易调整等问题。
布尔运算法通过将隐函数表示的TPMS单元点阵结构与复杂轮廓实体进行布尔运算来解决空间单元映射法存在的问题[11-12]。Yoo[13]提出了一种基于距离场和TPMS的布尔运算算法,可以获得具有复杂微观结构和较高质量的点阵结构。刘飞[14]系统地研究了包括密度梯度、单元尺寸梯度、异构结构梯度的TPMS点阵单元建模。Aremu等[15]提出了一种基于体素的点阵结构建模制造方法,构造点阵结构蒙皮来解决点阵结构在实体边界处悬空的问题,改善力学性能。虽然通过手动调整TPMS的隐函数参数,可以控制TPMS点阵结构的拓扑,但无法根据模型的受力情况自动、灵活地调整。许多学者通过将TPMS与拓扑优化相结合,从而建模具有应力自适应性的TPMS点阵结构。Cheng等[16]根据拓扑优化后的应力分布来填充梯度的杆状点阵结构,提高了结构拓扑优化后的力学性能。Kim等[17]通过多尺度的拓扑优化,将微观点阵结构嵌入到实体拓扑优化后得到的空白区域内,从而提高结构的刚度和结构的能量吸收率。Li等[18]使用一种拓扑设计方法,通过将TPMS与基于密度的拓扑优化相结合,开发了基于TPMS的功能梯度点阵结构。但布尔运算法建模的点阵结构存在大量的三角面片错误,甚至会导致运算失败。而传统的基于距离场的复杂轮廓点阵结构设计,虽然可以解决上述问题,但是存在计算量大,运算时间过长的问题。
为解决TPMS点阵结构建模中遇到的速度慢、过程繁琐、易出错的问题,基于体素距离场和TPMS提出了一种简便、高效的复杂轮廓TPMS点阵结构建模方法。通过移动立方体法实现TPMS单元三角面片模型的建模;对空间域中点与几何模型的拓扑位置关系进行判定,将空间中的点体素化;通过计算体素的邻域体素数量,获取位于模型边界的点集;求解点集相对于几何模型轮廓的距离场,并与TPMS曲面的距离场进行布尔运算,从而构建具有复杂轮廓的TPMS点阵结构。
1 基于TPMS的单元建模 1.1 TPMS点阵结构的数学表达TPMS是一种基于数学表达的隐式曲面,是一类在3个独立的方向上呈现周期性变化的极小曲面。因此将TPMS用于点阵结构建模,并可通过修改数学表达式中的常数来调整点阵结构的特征变化。TPMS的点坐标可通过如下的Enneper-Welerstrass参数化方程精确表达。
| $ \left\{\begin{array}{l} x=\operatorname{Re}\left(\mathrm{e}^{\mathrm{i} \theta} \int_{\omega 0}^{\omega}\left(1-\tau^{2}\right) R(\tau) \mathrm{d} \tau\right), \\ y=\operatorname{Re}\left(\mathrm{e}^{\mathrm{i} \theta} \int_{\omega 0}^{\omega}\left(1+\tau^{2}\right) R(\tau) \mathrm{d} \tau\right), \\ z=\operatorname{Re}\left(\mathrm{e}^{\mathrm{i} \theta} \int_{\omega 0}^{\omega} 2 \tau R(\tau) \mathrm{d} \tau\right)。\end{array}\right. $ | (1) |
式中:τ表示一个复变量;ω为一个称为Bonnet的角度;Re是笛卡尔坐标中任意一点轮廓积分的实部;i为虚数,满足i2=-1;R(τ)为随不同曲面而变化的函数,R(τ)是Weierstrass函数,对于不同类型的周期曲面R(τ)的表达式不同,比如primitive、gyroid、diamond周期曲面
| $ \phi (r) = \sum\limits_{k = 1}^K {{A_k}} \cos \left[ {\frac{{2{\rm{ \mathsf{ π} }}r}}{{{\lambda _k}}} + {P_k}} \right] = C 。$ | (2) |
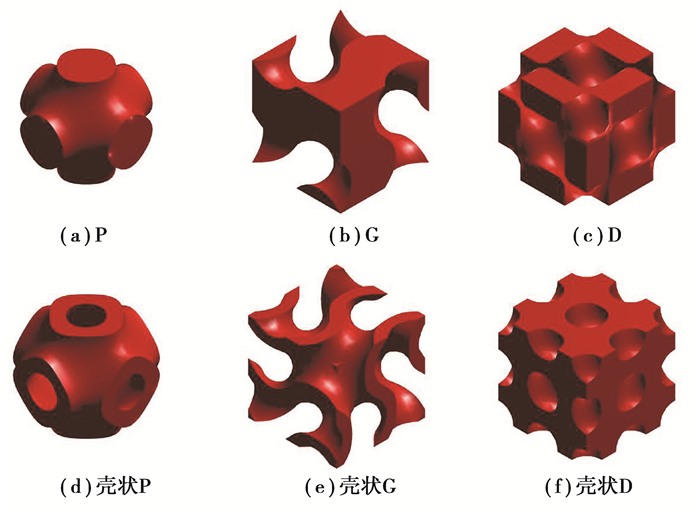
式中:Ak为函数的振幅;λk为三角函数的周期;Pk为函数的相对移动量;函数变量C(也称为距离常数)控制曲面的偏移量;K为三角函数个数;r为自变量。近似的TPMS是用隐式函数来表述的,并且在曲面上各点均有恒定的值,具有这种性质的曲面也被称为等值面。表 1列出了6种典型的TPMS函数,其中前3种可以通过封闭曲面来生成杆状TPMS点阵结构;后3种通过将曲面的C值分别朝两个方向偏移,并封闭两个曲面的中间区域来生成壳状TPMS点阵结构。
| 表 1 TPMS的隐函数表达式 Table 1 Implicit function expression of TPMS |
表中X=2πx/T,Y=2πy/T,Z=2πz/T,通过改变周期T的值,可以改变点阵结构的单胞大小。通过改变距离常数C,调整曲面的偏移可以改变点阵结构单胞的体积分数。
1.2 距离场距离场是几何模型的一种高效数字化表示方式,其定义为空间域中的点集与几何模型的距离的标量场,每个点的标量的绝对值表示该点与几何模型的最小距离,标量的正负表示该点是否在模型的内部。如图 1所示,负值表示该点在模型内部,正值表示该点在模型外部。对于TPMS而言,空间中某点P0(x0, y0, z0)到曲面的距离为
| $ \phi ({P_0}) = \sum\limits_{k = 1}^K {{A_k}} \cos \left[ {\frac{{2{\rm{ \mathsf{ π} }}{P_0}}}{{{\lambda _k}}} + {P_k}} \right] 。$ | (3) |

|
图 1 距离场概念示意图 Fig. 1 Schematic diagram of the concept of distance field |
TPMS单元的建模是通过移动立方体(marching cubes,MC)法,首先将建模空间划分为若干个小的立方体区域,通过求解TPMS曲面,获取每个立方体与曲面的关系,并通过插值的方法来获取与TPMS曲面近似的等值面,具体的建立过程如下。
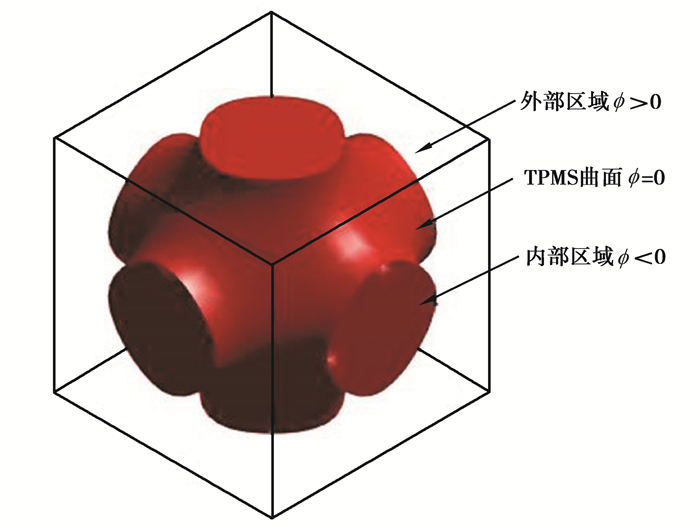
1) 在建模空间中,TPMS曲面ϕ=0会将空间分隔成两个独立的子空间ϕ < 0和ϕ>0,分别为内部区域和外部区域,如图 2所示。
|
图 2 TPMS单元表征空间 Fig. 2 Element representation space of TPMS |
2) 将建模空间体素化为若干个立方体,立方体的长宽高尺寸即为TPMS曲面在三个维度上的采样精度。将立方体的八个顶点分别代入TPMS的隐函数方程式(2)中求解,若大于0,则将该点的状态置1;若小于0,则将该点的状态置0,从而得到立方体的8位二进制状态值cubeIndex,总共有256个状态。
3) 若cubeIndex=0或cubeIndex=255,则表示该立方体不与TPMS曲面相交,其余的254个状态值表示该立方体与TPMS等值面相交。同理,若立方体上的某一条棱边上的两个点P(xi, yi, zi)、P(xj, yj, zj)的状态值不同(其对应的函数值分别用ϕi, ϕj表示),表示该边与等值面相交,有交点P(x0, y0, z0),根据线性插值理论可得:
| $ \left\{\begin{array}{l} x_{0}=x_{i}+k_{1}\left(x_{j}-x_{i}\right), \\ y_{0}=y_{i}+k_{1}\left(y_{j}-y_{i}\right), \\ x_{0}=z_{i}+k_{1}\left(z_{j}-z_{i}\right), \\ k_{1}=\frac{\phi_{i}}{\phi_{i}-\phi_{j}} 。\end{array}\right. $ | (4) |
4) 根据cubeIndex查找边索引表及三角剖分索引表,得到每个立方体的边状态edgeStatus和三角剖分状态triaStatus,通过edgeStatus及线性插值理论,求得交点的坐标值,并根据三角剖分状态triaStatus连接各个交点,组成与等值面近似拟合的三角面片。
5) 连接所有立方体求解出的三角面片,便获得TPMS的拟合曲面。
|
图 3 TPMS单元 Fig. 3 TPMS Elements |
复杂轮廓点阵结构的建模是通过对给定空间域中的距离场进行布尔运算,如式(5)所示:
| $ \phi_{\text {modelLattice }}=\phi_{\text {model }} \cap \phi_{\text {TPMS }}=\max \left(\phi_{\text {model }}, \phi_{\text {TPMS }}\right), $ | (5) |
式中:ϕmodel、ϕmodelLattice和ϕTPMS分别表示空间域中几何模型和TPMS曲面的距离场。因此,首先需要分别计算给定几何模型包围盒(将模型包含在内的三维长方体区域)中TPMS曲面的距离场以及几何模型的距离场,而距离场的计算量取决于采样精度,例如在10 mm × 10 mm × 10 mm的空间域中,采样精度取为0.1[19],则需要计算的点的数量为1.0×106。如上所述,由于已知TPMS曲面的隐函数方程,计算TPMS曲面的距离场速度较快。而在增材制造的前处理中,几何模型通常是由STL格式文件定义,几何特征由三角面片拟合而成,因此对几何模型的距离场求解实质上是计算空间采样点到三角面片集ΣΔs的最短距离,计算量随采样精度提高成几何倍数增大。而将几何模型填充成点阵结构,实际上是求相交后的距离场的0值等值面,而几何模型的距离场只在轮廓上存在0值。因此提出了一种几何模型边界体素提取算法,在不降低建模的点阵结构质量的情况下,大大减少需要计算距离场的采样点数量。
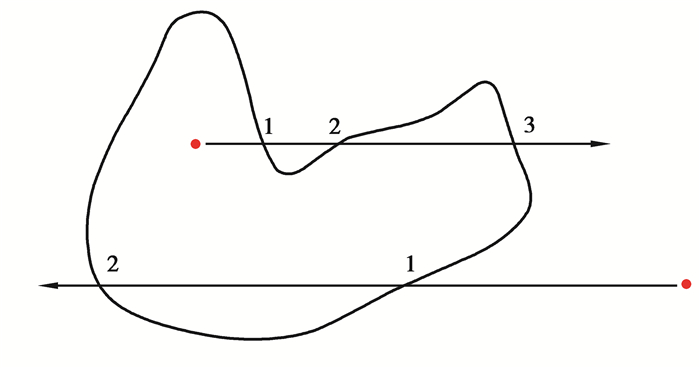
2.1 复杂轮廓点阵结构的边界点提取为了提取位于复杂轮廓点阵结构的边界的采样点,首先需要将点体素化,即将点的状态置为0或1,本研究中将位于模型内部的点状态置为激活态1,位于模型外部的点置为未激活态0。采用射线法[20]判断点与三角面片组成的模型的拓扑位置关系的算法已经比较成熟,即从查询点朝任意方向发出一条射线,如果点在模型内部,则与模型的交点个数为奇数,否则为偶数,如图 4所示。
|
图 4 拓扑关系算法原理图 Fig. 4 Schematic diagram of topological relation algorithm |
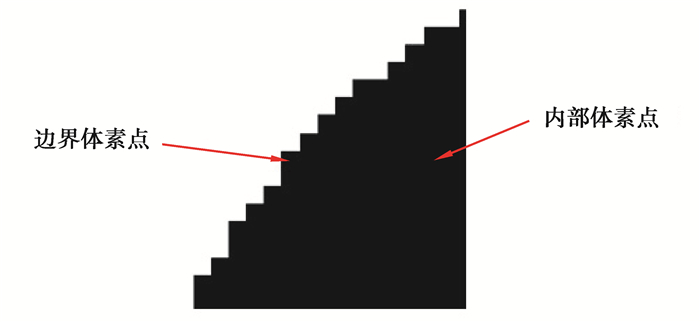
在将空间中的点体素化后,提取体素化模型边界上的体素,将其称为边界体素。边界体素可以根据该体素周围处于激活态的体素数量来判断。在二维空间中,处于内部的体素,周围共有8个体素是处于激活状态,而边界的体素周围处于激活态的体素少于8个,如图 5示;而在三维空间中,一个体素点的周围共有26个体素(面相邻6个,边相邻12个,点相邻8个)。由于上述体素点均在模型轮廓内部,因此将其定义为内部边界体素。若位于模型内部空间域中的体素点状态用矩阵Iijk表示,边界上的体素点用矩阵BIijk表示,则有如下计算公式。
| $ \boldsymbol{B}_{\mathrm{I} i j k}= \begin{cases}1, & \text { 如果 }\left(\boldsymbol{I}_{i j k}=1\right) \wedge\left(f\left(\boldsymbol{I}_{i j k}\right) <8\right) ; \\ 0, & \text { 否则 } 。\end{cases} $ | (6) |
|
图 5 内外体素点示意图 Fig. 5 Schematic diagram of internal and external voxel points |
式中:i, j, k分别表示矩阵中的行、列、页索引,f(Iijk)表示体素点Iijk周围的被激活的体素点的数量。
由MC算法的原理可知求解曲面的拟合三角面片需要让空间中的立方体与轮廓相交,再进行插值运算。因此,除了获取内部的边界体素点,还需要获取外部的体素点。通过对体素点矩阵Iijk进行膨胀,即把模型体素周围的26个体素点激活,使激活的点可以覆盖模型的轮廓,并再次取其边界体素,得到的体素点定义为外部边界体素点,用矩阵BOijk表示。最后,对得到的内部边界体素点矩阵BIijk和外部边界体素点矩阵BOijk做合并的布尔运算,即可得到边界体素点矩阵Bijk,数学模型如式(7)所示。
| $ \left\{\begin{array}{l} \boldsymbol{B}_{i j k}=\max \left(\boldsymbol{B}_{\mathrm{I} i j k}, \boldsymbol{B}_{\mathrm{O} i j k}\right) ; \\ \boldsymbol{B}_{\mathrm{I} i j k}=f_{\mathrm{bw}}\left(\boldsymbol{I}_{i j k}\right) ; \\ \boldsymbol{B}_{\mathrm{O}ijk}=f_{\mathrm{bw}}\left(f_{\mathrm{dil}}\left(\boldsymbol{I}_{i j k}\right)\right) 。\end{array}\right. $ | (7) |
式中:fbw表示提取体素模型边界体素点的算法函数;fdil表示对体素模型进行膨胀处理的算法函数。图 6所示为二维空间中一个正六边形区域的边界体素点提取过程。

|
图 6 正六边形边界体素点提取过程 Fig. 6 Extraction process of voxel points on the boundary of a regular hexagon |
假定复杂轮廓的几何模型由一组三角面片ΣΔs(例如STL、OBJ文件格式)组成,则无符号距离场的定义为空间域中的采样点P与ΣΔs的最短欧式距离dist(P),Pt表示其对应的三角面片,如式(8)所示:
| $ {\rm{dist}}\left( P \right) = \mathop {\min }\limits_{{P_{\rm{t}}} \in \sum {{\varDelta _{\rm{s}}}} } \left\| {{P_{\rm{t}}} - P} \right\|。$ | (8) |
为了区分点与几何封闭模型的拓扑关系,模型的距离场一般使用符号距离场(signed distance function, SDF)。SDF返回空间域中采样点到模型轮廓的最小距离,符号表示点P与模型的拓扑关系,则空间采样点到模型轮廓的SDF公式如下。
| $ \left\{\begin{array}{l} \operatorname{dist}(P)=\operatorname{sign}(P) \min\limits_{P \mathrm{t} \in \sum \varDelta_{\mathrm{s}}}\left\|P_{\mathrm{t}}-P\right\| ; \\ \operatorname{sign}(P)=\left\{\begin{array}{l} -1, \text { if } P \in M, \\ 1, \text { if } P \notin M 。\end{array}\right. \end{array}\right. $ | (9) |
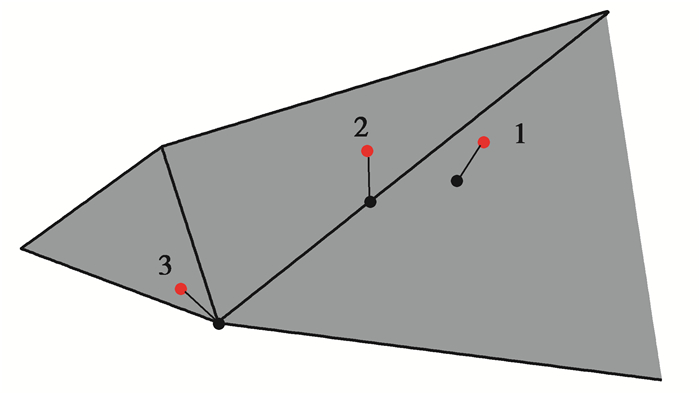
式中M表示模型内部。计算采样点到ΣΔs的最短距离采用正交投影算法[21],算法基本原理是将点到三角形的距离分为如图 7所示的3种情况:
|
图 7 计算点到空间三角形的最小距离的3种情况 Fig. 7 Three cases for the calculation of minimum distance from a point to a triangle |
1) 当点P正交投影于三角形Δ内部的时候,距离dist(P)为点到三角形所在平面的最短距离。
2) 当点P正交投影于三角形Δ的3条边上时,距离dist(P)为点到边的最短距离。
3) 当点P正交投影于三角形Δ的3个顶点上时,距离dist(P)即为点与点的距离。
根据2.2节中计算的边界体素点状态矩阵Bijk从空间点集中取出边界体素点坐标,并计算距离场。由于模型内部是由TPMS填充,可将模型内部的点的距离标量设置为小于TPMS距离场最小值的任意值;为使模型外部的点的距离场不影响到0等值面插值运算,只需将模型外部的点距离场值置为大于TPMS的距离场的最大值即可。复杂轮廓TPMS点阵结构的距离场数学模型如式(10)所示。
| $ \left\{\begin{array}{l} \operatorname{dist}(P)=\operatorname{sign}(P) \min\limits_{P_{\mathrm{t}} \in \sum \varDelta_{\mathrm{s}}}\left\|P_{\mathrm{t}}-P\right\|, \quad P \in \boldsymbol{C}_{P}\left(\operatorname{find}\left(\boldsymbol{B}_{i j k}=1\right)\right) ; \\ \operatorname{dist}(P)=\min \left(\phi_{\mathrm{TPMS}}\right)-1, \quad P \in \boldsymbol{C}_{P}\left(\operatorname{find}\left(\boldsymbol{I}_{\mathrm{n} i j k}=1\right)\right) ; \\ \operatorname{dist}(P)=\max \left(\boldsymbol{\phi}_{\mathrm{TPMS}}\right)+1, \quad P \in \boldsymbol{C}_{P}\left(\operatorname{find}\left(\boldsymbol{I}_{\mathrm{O} i j k}=1\right)\right) ; \\ \boldsymbol{I}_{\mathrm{n} i j k}=\boldsymbol{I}_{i j k} \oplus \boldsymbol{B}_{\mathrm{i} i j k}, \boldsymbol{I}_{\mathrm{Oijk}}=\neg\left(\boldsymbol{I}_{i j k} \cup \boldsymbol{B}_{\mathrm{O} i j k}\right)。\end{array}\right. $ | (10) |
式中:Inijk表示模型内部的体素,IOijk表示模型外部的体素,CP表示包含点坐标的矩阵。在获得TPMS曲面及几何模型在包围盒空间中的距离场后,通过式(5)进行布尔运算,便能获得具有几何模型轮廓的TPMS点阵结构的距离场。
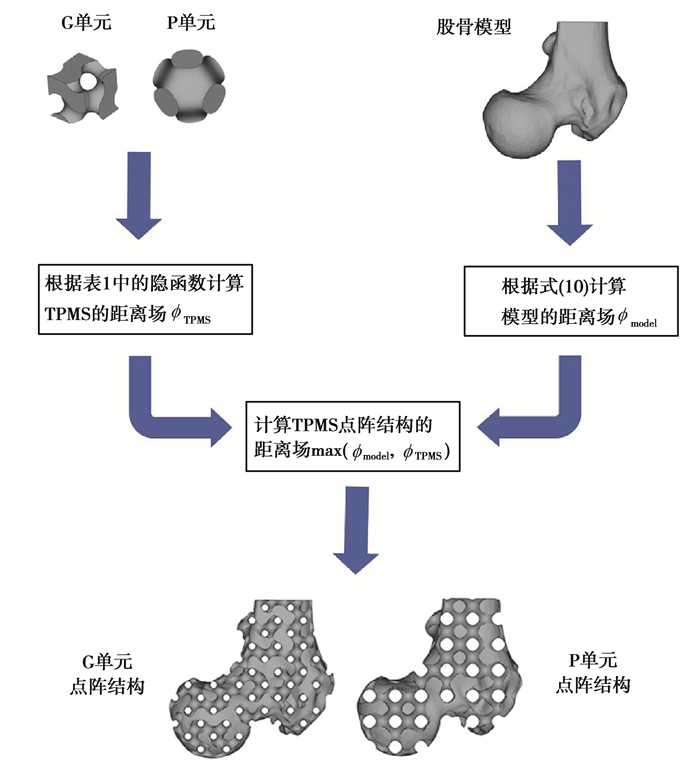
3 复杂轮廓点阵结构建模为了验证提出的建模方法的鲁棒性和有效性,对一组具有任意形状和拓扑结构的几何模型进行点阵结构填充。图 8所示为构建具有股骨轮廓的TPMS点阵结构的流程示意图。点阵结构建模算法使用Matlab编写,运行的电脑环境为I5-8500,3 GHz CPU,运行内存16 GB,程序只要读入模型的STL文件,便能自动运算并输出TPMS点阵结构的STL文件。如图 8~9所示,根据本文中提出的算法设计的程序成功生成了具有薄壁圆筒轮廓和股骨轮廓的P和G单元点阵结构。测试结果见表 2,可见本文中提出的方法与原始的求解全局采样点的距离场方法相比较,可有效减少需要求解距离场的点的数量。在建模具有股骨轮廓的点阵结构时,原算法中的距离场计算时间为本算法的41倍;在建模具有薄壁圆筒轮廓的点阵结构时,原算法中的距离场计算时间为本算法的31倍。距离场计算时间大幅缩短是因为需要计算距离场的采样点数量大幅减少。设模型的包围盒长宽高分别为L、W、H,模型的表面积为S,采样精度为a,则时间缩短倍数可由式(11)估算:
| $ F \geqslant \frac{(L / a+1) \times(W / a+1) \times(H / a+1)}{S / a^{2}} \geqslant \frac{a \times(L+a) \times(W+a) \times(H+a)}{S} 。$ | (11) |
|
图 8 股骨轮廓的点阵结构建模示意图 Fig. 8 Schematic diagram of modeling lattice structure of femoral contour |
|
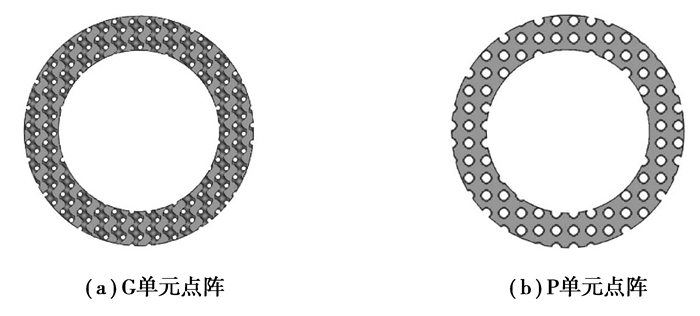
图 9 薄壁圆筒轮廓的点阵结构 Fig. 9 Lattice structure of thin-walled cylinder |
| 表 2 建模参数对比 Table 2 Comparison of modeling parameters |
从图 8~9可见构建的点阵结构模型具有平滑的几何轮廓,证明了本文中提出的建模方法具有良好的轮廓适应性,能够在构建TPMS点阵结构的同时保留原始几何模型的轮廓特征,能够稳定地对具有复杂轮廓的TPMS点阵结构建模。
4 结论提出了一种高效的复杂轮廓点阵结构建模方法,采用隐函数表达的TPMS作为点阵结构单元,通过构建TPMS曲面的空间距离场,再使用移动立方体法来重建TPMS曲面的拟合等值面,为设计具有复杂轮廓的点阵结构提供了基础。同时提出了一种基于体素的几何模型距离场计算方法,通过将空间采样点体素化,并提取边界体素,膨胀体素矩阵,再次提取边界体素,实现了几何模型轮廓边界点的快速提取,显著提高了点阵结构建模过程中的几何模型距离场的计算速度。最后通过对TPMS曲面的距离场及几何模型的距离场进行布尔运算,并拟合等值面,构建出了具有复杂几何轮廓的点阵结构。该方法可进一步扩展到各种功能性复杂轮廓TPMS点阵结构的建模,比如功能梯度TPMS点阵结构、应力自适应TPMS点阵结构等,为拓宽TPMS单元类型点阵结构的应用提供了一种稳定、高效的建模方法。
| [1] |
Nakajima H. Fabrication, properties and application of porous metals with directional pores[J]. Progress in Materials Science, 2007, 52(7): 1091-1173. DOI:10.1016/j.pmatsci.2006.09.001 |
| [2] |
Evans A G, Hutchinson J W, Fleck N A, et al. The topological design of multifunctional cellular metals[J]. Progress in Materials Science, 2001, 46(3/4): 309-327. |
| [3] |
肖然. 个性化多孔下颌骨假体的轻量化设计与激光选区熔化成型研究[D]. 广州: 华南理工大学, 2018. Xiao R. Study on the lightweight design and manufacturing of customized porous mandibular prothesis based on selective laser melting[D]. Guangzhou: South China University of Technology, 2018. (in Chinese) |
| [4] |
朱继宏, 周涵, 王创, 等. 面向增材制造的拓扑优化技术发展现状与未来[J]. 航空制造技术, 2020, 63(10): 24-38. Zhu J H, Zhou H, Wang C, et al. Status and future of topology optimization for additive manufacturing[J]. Aeronautical Manufacturing Technology, 2020, 63(10): 24-38. (in Chinese) |
| [5] |
Helou M, Kara S. Design, analysis and manufacturing of lattice structures: an overview[J]. International Journal of Computer Integrated Manufacturing, 2018, 31(3): 243-261. DOI:10.1080/0951192X.2017.1407456 |
| [6] |
Feng J W, Fu J Z, Shang C, et al. Porous scaffold design by solid T-splines and triply periodic minimal surfaces[J]. Computer Methods in Applied Mechanics and Engineering, 2018, 336: 333-352. DOI:10.1016/j.cma.2018.03.007 |
| [7] |
Cai S Y, Xi J T, Chua C K. A novel bone scaffold design approach based on shape function and all-hexahedral mesh refinement[M]//Liebschner M. Computer-aided tissue engineering: methods in molecular biology (methods and protocols). Volume 868. Totowa, New Jersey: Humana Press, 2012: 45-55.
|
| [8] |
Ma S H, Song K L, Lan J, et al. Biological and mechanical property analysis for designed heterogeneous porous scaffolds based on the refined TPMS[J]. Journal of the Mechanical Behavior of Biomedical Materials, 2020, 107: 103727. DOI:10.1016/j.jmbbm.2020.103727 |
| [9] |
张壮雅, 赵珂, 李跃松, 等. 基于体素和三周期极小曲面的骨支架多孔结构设计[J]. 计算机集成制造系统, 2020, 26(3): 697-706. Zhang Z Y, Zhao K, Li Y S, et al. Porous structure design method of bone scaffold based on voxel and triple cycle minimal surfaces[J]. Computer Integrated Manufacturing Systems, 2020, 26(3): 697-706. (in Chinese) |
| [10] |
张壮雅, 赵珂, 杨晓峰, 等. 基于三周期极小曲面和等参单元法的骨支架建模方法研究[J]. 机械设计与制造, 2017(11): 234-237, 241. Zhang Z Y, Zhao K, Yang X F, et al. Reseachon bone scaffold modeling method basedon triply periodic minimaland isoperimetric element method[J]. Machinery Design & Manufacture, 2017(11): 234-237, 241. (in Chinese) |
| [11] |
Zhao M, Zhang D Z, Liu F, et al. Mechanical and energy absorption characteristics of additively manufactured functionally graded sheet lattice structures with minimal surfaces[J]. International Journal of Mechanical Sciences, 2020, 167: 105262. DOI:10.1016/j.ijmecsci.2019.105262 |
| [12] |
Zhou H L, Zhao M, Ma Z B, et al. Sheet and network based functionally graded lattice structures manufactured by selective laser melting: Design, mechanical properties, and simulation[J]. International Journal of Mechanical Sciences, 2020, 175: 105480. DOI:10.1016/j.ijmecsci.2020.105480 |
| [13] |
Yoo D J. Porous scaffold design using the distance field and triply periodic minimal surface models[J]. Biomaterials, 2011, 32(31): 7741-7754. DOI:10.1016/j.biomaterials.2011.07.019 |
| [14] |
刘飞. 选择性激光熔化成形的功能梯度多孔结构性能研究[D]. 重庆: 重庆大学, 2019. Liu F. Performance study of functionally graded porous structure fabricated by selective laser melting[D]. Chongqing: Chongqing University, 2019. (in Chinese) |
| [15] |
Aremu A O, Brennan-Craddock J P J, Panesar A, et al. A voxel-based method of constructing and skinning conformal and functionally graded lattice structures suitable for additive manufacturing[J]. Additive Manufacturing, 2017, 13: 1-13. DOI:10.1016/j.addma.2016.10.006 |
| [16] |
Cheng L, Bai J X, To A C. Functionally graded lattice structure topology optimization for the design of additive manufactured components with stress constraints[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 344: 334-359. DOI:10.1016/j.cma.2018.10.010 |
| [17] |
Kim J E, Park K. Multiscale topology optimization combining density-based optimization and lattice enhancement for additive manufacturing[J/OL]. International Journal of Precision Engineering and Manufacturing-Green Technology, 2020[2021-02-01]. https://link.springer.com/article/10.1007/s40684-020-00289-1#change-history.
|
| [18] |
Li D W, Dai N, Tang Y L, et al. Design and optimization of graded cellular structures with triply periodic level surface-based topological shapes[J]. Journal of Mechanical Design, 2019, 141(7): 071402. DOI:10.1115/1.4042617 |
| [19] |
冯紫鑫. 基于三周期极小曲面的模型轻量化方法[D]. 辽宁大连: 大连理工大学, 2017. Feng Z X. The lightweight of models using three-periodic minimal surfaces[D]. Dalian, Liaoning: Dalian University of Technology, 2017. (in Chinese) |
| [20] |
翟艳, 徐卫亚, 张强. 点与多边形或多面体的拓扑关系判断[J]. 计算机工程与设计, 2015, 36(4): 972-976. Zhai Y, Xu W Y, Zhang Q. Judgment of topological relation between point and polygon or polyhedron[J]. Computer Engineering and Design, 2015, 36(4): 972-976. (in Chinese) |
| [21] |
Frisch D. Point2trimesh()-distance between point and triangulated surface[EB/OL]. [2021-01-05]. https://www.mathworks.com/matlabcentral/fileexchange/52882-point2trimesh-distance-between-point-and-triangulated-surface.
|
 2022, Vol. 45
2022, Vol. 45


