2. 重庆长安汽车股份有限公司, 重庆 400023
2. Chongqing Chang'an Automobile Company Limited, Chongqing 400023, P. R. China
随着越来越多新技术应用到现代发动机[1-3],如VVT(variable valve timing)、EGR(exhaust gas recirculation)、VGT (variable geometry turbocharger)等,进气歧管内的流动变得更为复杂,给缸内新鲜充量的估计带来巨大的挑战。2016年颁布的国Ⅵ排放法规引入实际行驶排放(real driving emission,RDE)试验,对汽车瞬态排放提出了更高的要求[4-5]。缸内进气量作为发动机燃油喷射量和空燃比控制的基础,其准确估算非常重要,通过将空燃比控制在化学计量空燃比附近,使三元催化器转换效率达到最高,有效减少污染物排放[6-7]。
为此,国内外学者提出很多缸内进气量计算方法。基于进气歧管绝对压力(manifold absolutely pressure, MAP)传感器的速度密度法[8]具有较好的动态性能,但需要进气歧管压力、温度以及容积效率在不同运转工况下的查表值,尤其在VVT发动机中,需要标定多维脉谱图,标定工作量巨大且没有可移植性。空气质量流量(mass air flow, MAF)传感器稳态下测量的节气门处质量流量等同于气缸内的空气质量流量,但由于瞬态工况歧管压力动态变化大,MAF测量值无法准确反映缸内进气量。基于MAP和MAF传感器测量值设计观测器的方法可以很好弥补MAF传感器瞬态工况的不足,进而准确估算瞬态进气量[9-10]。另外,Leroy等[11]对VVT发动机的研究中提出的进气量计算模型包含的3个脉谱图均为发动机转速和负荷的非平滑函数,需要对每个转速和负荷进行回归,因此标定工作量大。
近年来,缸压分析逐渐被应用于缸内充量估算[12-13],其中一种被称为ΔP方法[14],通过测量缸压曲线,选择压缩行程上任意两点的压力及估算缸内温度来计算缸内进气量,由于需要较为准确的残余废气分数,无法应用到配备EGR和VVT技术的发动机。除此之外,部分学者[15-16]根据换气过程热力学关系建立预测算法并逐循环迭代,可以较为准确地计算发动机瞬态进气量,但算法复杂,计算时间过长,且使用成本过高,因此无法实现面向控制的缸内充量计算。
为了实现简单精确地计算缸内进气量,笔者提出一种基于物理方法的缸内充量模型,引入GT-POWER热力学模型辅助标定,完成对充量模型中进气道传热因子、驻留废气关键参数和气门实际流通面积的标定。由于小排量增压发动机逐渐成为众多车企青睐的搭载机型,本研究中对1.5T增压汽油机展开研究,建立的充量模型仅使用普通商用传感器即可实现不同运行工况下发动机稳态进气量的计算,可移植性强,且满足稳态进气量误差在5%以内。
1 充量模型 1.1 模型概述根据气体状态方程,进气门关闭时刻,进入气缸内的新鲜充气量为
| $ m_{\mathrm{air}}=\frac{p_{\mathrm{air}} V_{\mathrm{IVC}}}{R_{\mathrm{g}} T_{\mathrm{air}}} 。$ | (1) |
式中:Rg为气体常数;pair为缸内新鲜充气压力;Tair为缸内新鲜充气温度;VIVC为进气门关闭时刻气缸容积。
为便于数据分析,将残余废气质量、新鲜充气质量均与标况下的空气质量对比,进行量纲归一化处理。将发动机缸内新鲜充量与标况下的空气质量m0的比值定义为充气效率Rc,即:
| $ {R_{\rm{c}}} = \frac{{{m_{{\rm{air}}}}}}{{{m_0}}} = \frac{{{p_{{\rm{air}}}}}}{{{p_0}}}\frac{{{V_{{\rm{IVC}}}}}}{{{V_{\rm{d}}}}}\frac{{{T_0}}}{{{T_{{\rm{air}}}}}}。$ | (2) |
式中:p0为标况下的空气压力,p0=101.3 kPa;T0为标况下的空气温度,T0=273 K; Vd为发动机的工作容积。
进气门关闭时,缸内气体成分包括新鲜空气和残余废气。本研究中假设进气门关闭前新鲜气体进入缸内与缸内废气不发生混合,维持自身状态[17],忽略进气过程中的流动损失,进气门关闭时刻缸内新鲜气体压力近似用进气歧管压力pim与缸内残余废气压力pr之差表示:
| $ {p_{{\rm{air}}}} = {p_{{\rm{im}}}} - {p_{\rm{r}}}。$ | (3) |
因此,发动机充气效率Rc与进气歧管压力pim的关系可以表示为具有一定斜率K和截距pr的线性函数,其表达式如式(4)。随着运行工况变化,充气效率与进气歧管压力的拟合曲线相应变化,该拟合曲线斜率和截距主要受转速、负荷、进排气正时[18]等影响。
| $ \left\{\begin{array}{l} R_{\mathrm{c}}=K\left(p_{\mathrm{im}}-p_{\mathrm{r}}\right), \\ K=\frac{V_{\mathrm{IVC}}}{V_{\mathrm{d}}} \frac{T_{0}}{T_{\text {air }}} \frac{1}{p_{0}} 。\end{array}\right. $ | (4) |
根据式(2),残余废气相对分数Rrg表示为:
| $ R_{\mathrm{rg}}=\frac{m_{\mathrm{rg}}}{m_{0}}=\frac{p_{\mathrm{r}}}{p_{0}} \frac{V_{\mathrm{IVC}}}{V_{\mathrm{d}}} \frac{T_{0}}{T_{\mathrm{r}}}, $ | (5) |
式中:Tr为进气门关闭时缸内废气温度;mrg为残余废气质量。
将充气效率与进气歧管压力曲线斜率K代入式(5),残余废气分数为:
| $ R_{\mathrm{rg}}=\frac{K T_{\mathrm{air}}}{T_{\mathrm{r}}} p_{\mathrm{r} }。$ | (6) |
因此本研究中考虑通过计算进气门关闭时刻缸内废气温度、缸内新鲜充气温度和残余废气分数来估算缸内残余废气压力pr。
| $ p_{\mathrm{r}}=\frac{R_{\mathrm{rg}} T_{\mathrm{r}}}{K T_{\text {air }}}。$ | (7) |
由于进气门开启初期上升缓慢,为了在进气开始时进气门能有足够大的开度以减小进气阻力,进气门通常开启在上止点前,此时发动机仍在进行排气过程。则进气门开启时刻缸内已燃废气温度接近于排气温度。在进气门开启到关闭期间,假设缸内残余废气经过绝热膨胀过程,进气门关闭时缸内残余废气膨胀后的温度如式(8)。
| $ T_{\mathrm{r}}=T_{\mathrm{exh}}\left(\frac{p_{\mathrm{im}}}{p_{\mathrm{exh}}}\right)^{\frac{\gamma-1}{\gamma}}, $ | (8) |
式中:Texh为排气温度,pexh为排气压力,γ为绝热指数。
1.3 缸内新鲜充气温度计算新鲜空气由进气歧管进入缸内过程中,不可避免地受到进气歧管壁面、进气道壁面、气门处高温部件的加热,与废气混合前的缸内新鲜充气温度Tair如式(9)。
| $ T_{\text {air }}=\left(T_{\text {wat }}-T_{\text {out }}\right)\left(1-\mathrm{e}^{-\frac{1200}{N}}\right)+T_{\text {out }}, $ | (9) |
式中:Twat为气道壁面温度,通常以冷却水温表示;Tout为进气道出口气流温度;N为发动机转速。
定义ΔTp为进气歧管入口与进气道出口气流温度差Tout-Tim,受不同运行工况下的传热影响,根据牛顿冷却公式,在进气歧管入口与进气道出口的传热速率
| $ \dot{Q}=\dot{m} c_{\mathrm{v}} \Delta T_{\mathrm{p}}=h A\left(T_{\text {wall }}-T_{\mathrm{im}}\right) 。$ | (10) |
则ΔTp由下式计算:
| $ \Delta T_{\mathrm{p}}=\frac{h A\left(T_{\text {wall }}-T_{\mathrm{im}}\right)}{c_{\mathrm{v}} \dot{m}} 。$ | (11) |
式中:h为换热系数;
为反映不同运行工况下的进气歧管和进气道内的传热影响,引入待定参数进气道传热因子α1,将式(11)定义为:
| $ \Delta T_{\mathrm{p}}=\alpha_{1}\left(T_{\text {wat }}-T_{\mathrm{im}}\right) 。$ | (12) |
因此,进气道出口温度简化为:
| $ T_{\text {out }}=T_{\text {im }}+\alpha_{1}\left(T_{\text {wat }}-T_{\text {im }}\right) 。$ | (13) |
结合式(4)和(7)~(9),得出缸内充量模型:
| $ \left\{\begin{array}{l} R_{\mathrm{c}}=\frac{V_{\mathrm{IVC}}}{V_{\mathrm{d}}} \frac{T_{0}}{T_{\mathrm{air}}} \frac{\left(p_{\mathrm{im}}-p_{\mathrm{r}}\right)}{p_{0}}, \\ p_{\mathrm{r}}=\frac{R_{\mathrm{rg}} T_{\mathrm{r}}}{K T_{\text {air }}}, \\ T_{\mathrm{r}}=T_{\mathrm{exh}}\left(\frac{p_{\mathrm{im}}}{p_{\mathrm{exh}}}\right)^{\frac{\gamma-1}{\gamma}}, \\ T_{\text {air }}=\left(T_{\text {wat }}-T_{\text {out }}\right)\left(1-\mathrm{e}^{-\frac{1200}{N}}\right)+T_{\text {out }} 。\end{array}\right. $ | (14) |
在发动机运行过程中,进气门通常提前开启于上止点前。为充分利用排气管内气体流动惯性,排气门推迟关闭,实现过后排气,这一阶段进、排气门同时开启,由于进排气歧管两端的压力差,发动机将发生扫气或者回流。根据Fox等[19]的研究,将缸内残余废气分为进气门开启时刻上一循环的缸内驻留废气及气门重叠期间回流废气或者扫气废气组成,如式(15)。
| $ m_{\mathrm{rg}}=\left\{\begin{array}{l} m_{\text {trap }}+m_{\mathrm{bk}}, p_{\mathrm{im}}<p_{\mathrm{exh}}, \\ m_{\text {trap }}+m_{\mathrm{scv}}, p_{\mathrm{im}} \geqslant p_{\mathrm{exh}} 。\end{array}\right. $ | (15) |
式中:mtrap为驻留废气质量,mbk为回流废气质量,mscv为扫气废气质量。
在进气门开启时刻,根据气体状态方程缸内驻留废气量由此时缸内气体温度和压力可得:
| $ m_{\text {trap }}=m_{\text {IVO }}=\frac{p_{\text {IVO }} V_{\text {IVO }}}{R_{\mathrm{g}} T_{\text {IVO }}}, $ | (16) |
式中:pIVO、VIVO和mIVO分别为进气门开启时刻缸内压力、气缸容积和缸内质量。
为方便将模型应用于发动机控制系统中,则不考虑将缸压传感器引入系统,而缸内瞬时温度无法通过传感器直接测量。为准确计算缸内驻留废气量,用待定系数α2及排气压力和温度等表示驻留废气分数Ftrap是准确计算残余废气量的一种可行方法,即:
| $ F_{\text {trap }}=\frac{m_{\text {trap }}}{m_{0}}=\alpha_{2} \frac{p_{\text {exh }} V_{\text {IVO }}}{R_{\mathrm{g}} T_{\text {exh }}} \frac{1}{m_{0}}=\alpha_{2} \frac{p_{\text {exh }}}{p_{0}} \frac{V_{\text {IVO }}}{V_{\mathrm{d}}} \frac{T_{0}}{T_{\text {exh }}} 。$ | (17) |
气门重叠期间,缸内气体流动的复杂性增加,进排气门处的气流运动适宜用孔口处的一维流动方程描述[20]。根据喉口上下游压力、上游温度和有效流通面积,流经气门处的回流或者扫气质量流量G定义如下:
| $ \left\{ \begin{array}{l} G = {C_{\rm{D}}}{A_{\rm{R}}}\varPsi \left( {{p_{\rm{u}}}\left( t \right),{p_{\rm{d}}}\left( t \right),{T_{\rm{u}}}\left( t \right)} \right);\\ \varPsi \left( {{p_{\rm{u}}}\left( t \right),{p_{\rm{d}}}\left( t \right),{T_{\rm{u}}}\left( t \right)} \right) = \left\{ \begin{array}{l} \frac{{{p_{\rm{u}}}\left( t \right)}}{{\sqrt {{R_{\rm{g}}}{T_{\rm{u}}}\left( t \right)} }}{\left( {\frac{{{p_{\rm{d}}}\left( t \right)}}{{{p_{\rm{u}}}\left( t \right)}}} \right)^{\frac{1}{\gamma }}}{\left\{ {\frac{{2\gamma }}{{\gamma - 1}}\left[ {1 - {{\left( {\frac{{{p_{\rm{d}}}\left( t \right)}}{{{p_{\rm{u}}}\left( t \right)}}} \right)}^{\left( {\gamma - 1} \right)/\gamma }}} \right]} \right\}^{1/2}},\;\;\;\;\;\;\frac{{{p_{\rm{d}}}\left( t \right)}}{{{p_{\rm{u}}}\left( t \right)}} > {\left[ {\frac{2}{{\gamma + 1}}} \right]^{\frac{\gamma }{{\gamma - 1}}}};\\ \frac{{{p_{\rm{u}}}\left( t \right)}}{{\sqrt {{R_{\rm{g}}}{T_{\rm{u}}}\left( t \right)} }}{\gamma ^{\frac{1}{2}}}{\left( {\frac{2}{{\gamma + 1}}} \right)^{\frac{{\gamma + 1}}{{2\left( {\gamma - 1} \right)}}}},\;\;\;\;\;\;\;\;\frac{{{p_{\rm{d}}}\left( t \right)}}{{{p_{\rm{u}}}\left( t \right)}} \le {\left[ {\frac{2}{{\gamma + 1}}} \right]^{\frac{\gamma }{{\gamma - 1}}}}。\end{array} \right. \end{array} \right. $ | (18) |
式中:CD为流量系数,AR为气门处参考流通面积,pu和pd分别为上下游压力,Tu为上游温度。
在四缸汽油机的换气过程中,进气压力波动相对较小,由此引起的各缸进气不均匀性也相对较小。基于平均值发动机模型扩展,对进气量计算影响不大的情况下可以忽略进气压力波动和各缸进气不均匀性。由于进、排气压力循环平均值与换气过程中的瞬时压力较为接近,为了简化计算,取进排气压力、温度的循环平均值作为换气过程瞬时值[12]。因此,式(18)又表示为:
| $ G = {C_{\rm{D}}}{A_{\rm{R}}}\varPsi \left( {\overline {{p_{\rm{u}}}} ,\overline {{p_{\rm{d}}}} ,{{\bar T}_{\rm{u}}}} \right)。$ | (19) |
在换气过程中,当排气压力大于进气压力时,流入排气管的已燃废气会经过排气门回流到气缸和进气道内;当进气压力大于排气压力时,则会发生进气气流带走缸内的已燃废气的扫气现象。规定由排气门向进气门的回流过程为正向,由进气歧管到排气歧管的扫气过程为负向。因此,式(20)设定回流废气质量为正值,扫气质量流量为负值。
| $ \varPsi \left( {\overline {{p_{\rm{u}}}} ,\overline {{p_{\rm{d}}}} ,{{\bar T}_{\rm{u}}}} \right) = \left\{ {\begin{array}{*{20}{c}} {\varPsi \left( {\overline {{p_{{\rm{im}}}}} ,\overline {{p_{{\rm{exh }}}}} ,{{\bar T}_{\rm{e}}}} \right),\quad {p_{{\rm{im}}}} < {p_{{\rm{exh }}}};}\\ { - \varPsi \left( {\overline {{p_{{\rm{im}}}}} ,\overline {{p_{{\rm{exh }}}}} ,{{\bar T}_{\rm{i}}}} \right),\quad {p_{{\rm{im}}}} \ge {p_{{\rm{exh }}}}}。\end{array}} \right. $ | (20) |
令
| $ G = {C_{\rm{D}}}{A_{\rm{R}}}\varphi \left( {\overline {{p_{{\rm{im}}}}} ,\overline {{p_{{\rm{exh }}}}} ,{{\bar T}_{{\rm{im}}}},{{\bar T}_{{\rm{exh}}}}} \right)。$ | (21) |
流过进排气门处的质量流量G与最大质量流量Gmax之比为:
| $ G/{G_{\max }} = \left\{ \begin{array}{l} 1,\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{{\bar p}_{\rm{d}}}}}{{{{\bar p}_{\rm{u}}}}} \le {\left( {\frac{2}{{\gamma + 1}}} \right)^{\frac{\gamma }{{\gamma - 1}}}};\\ {\left( {\frac{{{{\bar p}_{\rm{d}}}}}{{{{\bar p}_{\rm{u}}}}}} \right)^{\frac{1}{\gamma }}}\sqrt {\frac{2}{{\gamma - 1}}{{\left( {\frac{{\gamma + 1}}{2}} \right)}^{\frac{{\gamma + 1}}{{\gamma - 1}}}}\left[ {1 - {{\left( {\frac{{{{\bar p}_{\rm{d}}}}}{{{{\bar p}_{\rm{u}}}}}} \right)}^{(\gamma - 1)/\gamma }}} \right]} ,\;\;\;\;\;\;\frac{{{{\bar p}_{\rm{d}}}}}{{{{\bar p}_{\rm{u}}}}} > {\left( {\frac{2}{{\gamma + 1}}} \right)^{\frac{\gamma }{{\gamma - 1}}}}。\end{array} \right. $ | (22) |
在IVO到EVC阶段对式(21)积分,得发动机气缸内的回流质量mbk为:
| $ {m_{{\rm{bk}}}} = \int\limits_{{\rm{IVO}}}^{{\rm{EVC}}} {G{\rm{d}}t} \frac{{\sqrt \gamma }}{{6N}}{\left( {\frac{2}{{\gamma + 1}}} \right)^{\frac{{\gamma + 1}}{{2(\gamma - 1)}}}}\frac{G}{{{G_{\max }}}}\frac{{{p_{{\rm{exh}}}}}}{{\sqrt {{R_{\rm{g}}}{T_{{\rm{exh}}}}} }}\int\limits_{{\rm{IVO}}}^{} {{A_{{\rm{eff}}}}{\rm{d}}\theta } 。$ | (23) |
式中:Aeff为气门处有效流通面积;t为时间变量;θ为曲轴转角。
mscv扫气质量为:
| $ m_{\mathrm{scv}}=\int\limits_{\mathrm{IVO}}^{\mathrm{EVC}} G \mathrm{~d} t=-\frac{\sqrt{\gamma}}{6 N}\left(\frac{2}{\gamma+1}\right)^{\frac{\gamma+1}{2(\gamma-1)}} \frac{G}{G_{\max }} \frac{p_{\mathrm{im}}}{\sqrt{R_{\mathrm{g}} T_{\mathrm{im}}}} \int\limits_{\mathrm{IVO}}^{\mathrm{EVC}} A_{\mathrm{eff}} \mathrm{d} \theta 。$ | (24) |
在发动机运行过程中,无法直接对气门处实际流通面积进行测量,因此测量发动机进排气温度、压力等参数,通过标定方法得到换气过程中的气门处实际流通面积,使用待标定系数α3表示气门实际流通面积。
| $ \alpha_{3}=\int\limits_{\text {IVO }}^{\text {EVC }} C_{\mathrm{D}} A_{\mathrm{R}} \mathrm{d} \theta=\int\limits_{\mathrm{IVO}}^{\mathrm{EVC}} A_{\mathrm{eff}} \mathrm{d} \theta 。$ | (25) |
根据式(5)和(15),残余废气分数为:
| $ R_{\mathrm{rg}}= \begin{cases}\frac{m_{\text {trap }}+m_{\mathrm{bk}}}{m_{0}}=F_{\mathrm{trap}}+F_{\mathrm{bk}}, & p_{\mathrm{im}} < p_{\mathrm{exh}} ; \\ \frac{m_{\text {trap }}+m_{\mathrm{scv}}}{m_{\mathrm{o}}}=F_{\mathrm{trap}}+F_{\mathrm{scv}}, & p_{\mathrm{im}} \geqslant p_{\mathrm{exh} 。}\end{cases} $ | (26) |
式中:Ftrap为驻留废气分数,Fbk为气门重叠期间回流废气相对分数,Fscv为气门重叠期间扫气废气相对分数。
将式(15)和(23)~(26)联立,得到残余废气分数如下:
| $ {R_{{\rm{rg}}}} = \left\{ {\begin{array}{*{20}{l}} {{\alpha _2}\frac{{{p_{{\rm{exh}}}}}}{{{p_0}}}\frac{{{V_{{\rm{IVO}}}}}}{{{V_{\rm{d}}}}}\frac{{{T_0}}}{{{T_{{\rm{exh}}}}}} + {\alpha _3}\frac{{\sqrt \gamma }}{{6N}}{{\left( {\frac{2}{{\gamma + 1}}} \right)}^{\frac{{\gamma + 1}}{{2(\gamma - 1)}}}}\frac{G}{{{G_{{\rm{max}}}}}}\frac{{{p_{{\rm{exh}}}}}}{{\sqrt {{R_{\rm{g}}}{T_{{\rm{exh}}}}} }}\frac{{{n_{{\rm{cyl}}}}}}{{{m_0}}},\quad {p_{{\rm{im}}}} < {p_{{\rm{exh}}}};}\\ {{\alpha _2}\frac{{{p_{{\rm{exh}}}}}}{{{p_0}}}\frac{{{V_{{\rm{IVO}}}}}}{{{V_{\rm{d}}}}}\frac{{{T_0}}}{{{T_{{\rm{exh}}}}}} - {\alpha _3}\frac{{\sqrt \gamma }}{{6N}}{{\left( {\frac{2}{{\gamma + 1}}} \right)}^{\frac{{\gamma + 1}}{{2(\gamma - 1)}}}}\frac{G}{{{G_{{\rm{max}}}}}}\frac{{{p_{{\rm{im}}}}}}{{\sqrt {{R_{\rm{g}}}{T_{{\rm{im}}}}} }}\frac{{{n_{{\rm{cyl}}}}}}{{{m_0}}},\quad {p_{{\rm{im}}}} \ge {p_{{\rm{exh}}}}}。\end{array}} \right. $ | (27) |
式中ncyl为气缸数。
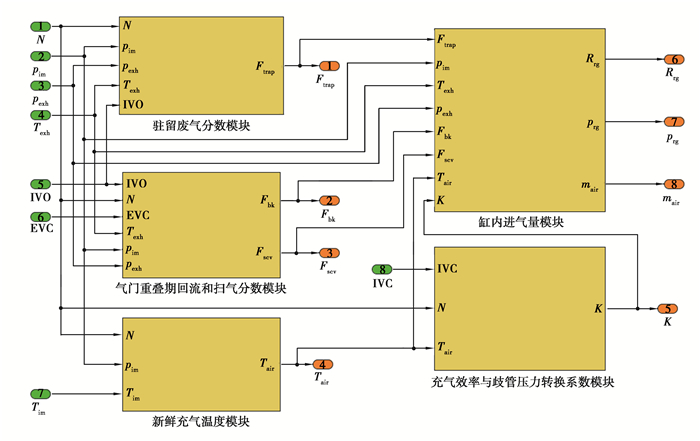
2 模型构建及标定基于Simulink软件构建完整的缸内充量模型如图 1所示,其中包括驻留废气分数计算模块、回流废气分数计算模块、缸内新鲜充气温度模块、缸内进气量模块、充气效率与歧管压力转换系数模块,以及待标定脉谱图进气道传热因子α1、驻留废气关键参数α2、气门重叠期间实际流通面积α3。在完成对模型的标定后,在发动机结构参数已知的情况下,根据不同运行工况下的进排气门正时、进排气压力和温度便可以准确计算缸内进气量。
|
图 1 充量模型框图 Fig. 1 Air charge estimation block diagram |
为进一步研究发动机缸内充量模型,选取了带有进排气双独立VVT的1.5 L直喷增压汽油发动机进行台架试验,其技术参数如表 1。试验过程中,发动机充分暖机,水温控制在(360±3) K,测量进排气压力、温度等参数,油耗量由油耗仪测量,空燃比由空燃比分析仪测量,根据油耗量和空燃比计算得到相应的进气量试验值。
| 表 1 发动机技术参数 Table 1 Engine technical parameters |
根据发动机结构参数、增压器特性数据、机械损失测试数据、气道稳流测试数据等测试参数,基于一维仿真软件GT-POWER建立发动机热力学仿真模型,具体包括空滤器、增压器、中冷器、气缸、进排气系统、三元催化器等部件。
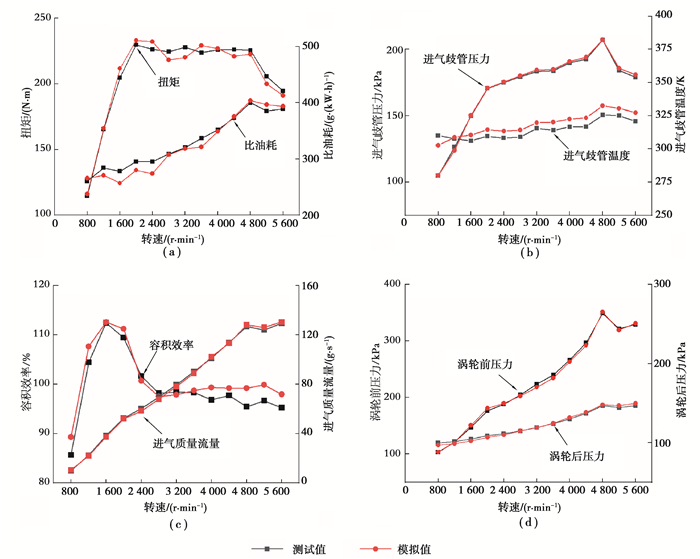
为保证建立的模型准确可靠,并反映发动机的实际运行工况,在外特性工况下对发动机仿真模型进行校准,如图 2所示。由图可知,扭矩、油耗、进气歧管温度、压力及进气质量流量等试验值和仿真值在外特性工况下基本一致。
|
图 2 台架测试值与模型值在外特性工况下对比 Fig. 2 Calibration simulation model under external characteristic |
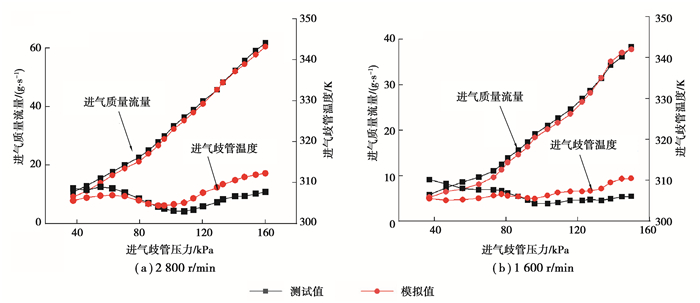
在全负荷下对模型验证后,将已经验证的全负荷模型扩展到部分负荷并进行验证。根据发动机台架测试实验数据,以及进排气VVT、燃烧特征参数、中冷器脉谱图、喷油器参数等建立不同转速下部分负荷发动机模型,在转速2 800 r/min和1 600 r/min下的部分负荷校准如图 3所示,仿真模型与实验数据误差值均在5%以内,因此认为该仿真模型可反映发动机的真实运转工况。为将建立的充量模型扩展到多工况下进行标定,引入该仿真模型作为辅助标定工具。
|
图 3 台架测试值与模型值在部分负荷工况对比 Fig. 3 Calibration simulation model under part load condition |
仿真模型运行在1 200~5 200 r/min,由低负荷逐渐到全负荷,涉及不同进排气门正时,标定采集数据如表 2所示。进、排气门正时选择压缩上止点为参考点,进气门正时维持在曲轴转角350 ℃A,排气门正时曲轴转角为350~420 ℃A,间隔为10 ℃A。仿真模型覆盖发动机绝大多数运行工况,满足发动机实际运行过程中进气量的估算。
| 表 2 标定数据 Table 2 GT-POWER Calibration data |
仿真运行过程中,采集不同运行工况下的稳态数据,包括进气歧管的压力和温度、排气歧管的压力和温度、进排气门正时、进气道的温度和残余废气分数。对于低转速工况点,大负荷进气歧管压力无法达到180 kPa时,取其能达到的最大歧管压力。
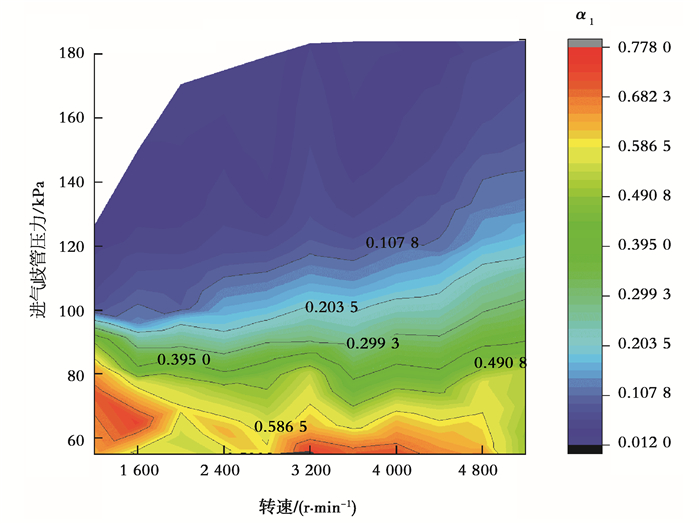
用仿真模型采集的进气道出口温度及进气歧管温度,根据式(13)对不同转速、不同负荷下的进气道传热因子α1进行标定,标定脉谱如图 4所示。在低负荷下,传热因子α1相对较大,表明在低负荷下,进气道气流温度较高;负荷增大时,传热因子快速减小,负荷变化不大时,随转速增加,传热因子α1增大相对较少。
|
图 4 进气道传热因子 Fig. 4 Heat transfer factor of intake port |
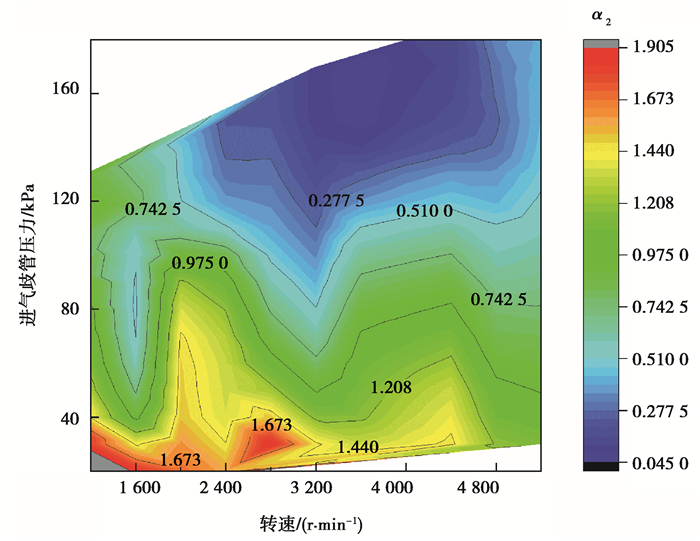
用仿真模型采集不同运行工况下的残余废气分数,根据式(27),使用MATLAB多项式拟合工具,确定发动机在进气门开启时的驻留废气分数,以及不同重叠角下的回流分数或者扫气分数,完成对驻留废气关键参数α2、气门实际流通面积α3的标定,标定脉谱如图 5和6所示。在怠速工况下,驻留残余废气量较大;发动机转速增大时,驻留废气量逐渐减少。原因是小负荷时,由于节气门开度小,导致缸内驻留废气量增大;在大负荷及全负荷工况,节气门开度不断增加,进气量逐渐增加,缸内驻留废气量减少。在低转速工况下缸内驻留废气量较大,随着转速增大,驻留废气量同步减少。高转速的驻留废气量较低转速明显减少,符合不同运行工况下缸内残余废气量变化规律。
|
图 5 驻留废气关键参数 Fig. 5 Key parameters of trapped gas |
|
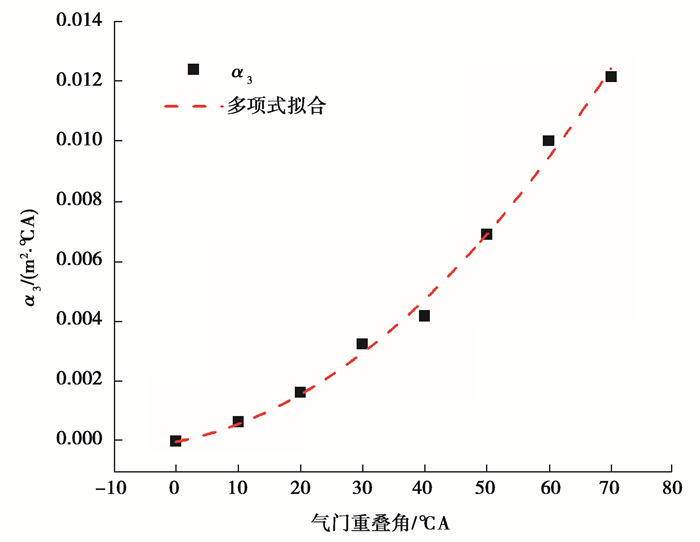
图 6 气门流通面积 Fig. 6 Valve flow area |
VVT发动机在不同转速下运行,通过改变进排气门开闭的时间,进而改变进排气门重叠角。由于进排气上下游的压力差引起发动机的回流现象或者扫气现象,因此有必要对不同重叠角下的气门流通面积进行评估。如图 6所示,将标定的气门流通面积与气门重叠角进行多项式拟合,得到气门流通面积与气门重叠角呈抛物线规律。该图直观表明气门重叠角增大时,气门流通面积大幅增大,尤其是在大气门重叠角期间,由于增压发动机进气压力高,扫气效应显著减少缸内已燃废气,进一步提高进气量。
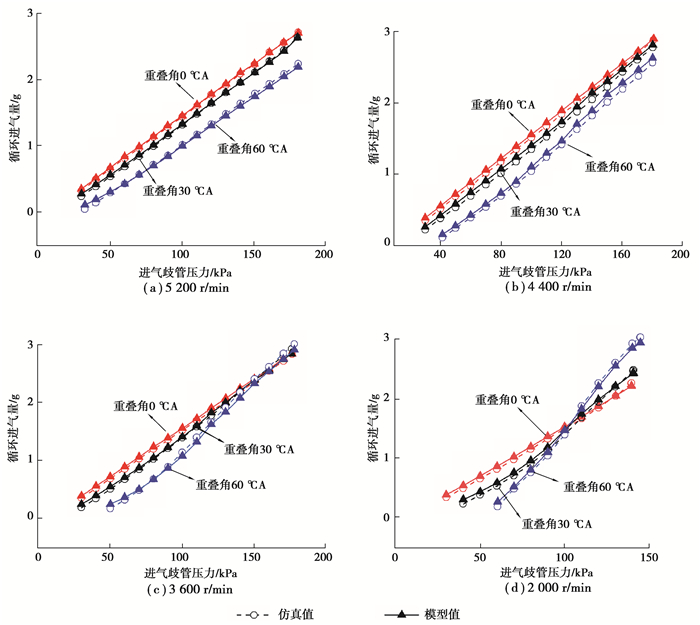
3 充量模型验证 3.1 仿真实验验证对建立的缸内充量控制模型在不同进排气门正时及不同负荷下仿真验证,结果如图 7所示。充量模型计算的进气量与仿真采集的进气量在5 200 r/min下变化规律基本一致,并在给定误差范围内;在4 400, 3 600, 2 000 r/min大多数工况下,充量模型计算的进气量与仿真进气量规律符合,并满足5%误差要求;怠速工况及大负荷工况下的少部分点的进气量与实验值误差在5%~10%,原因是怠速时节气门开度小,残余废气会引起一定的误差;在大负荷工况下的扫气现象使残余废气和新鲜充气由于气流惯性直接流入排气管,因而使误差增大。
|
图 7 仿真进气量与模型计算进气量对比 Fig. 7 Comparison of fresh intake charge (simulation and model calculation) |
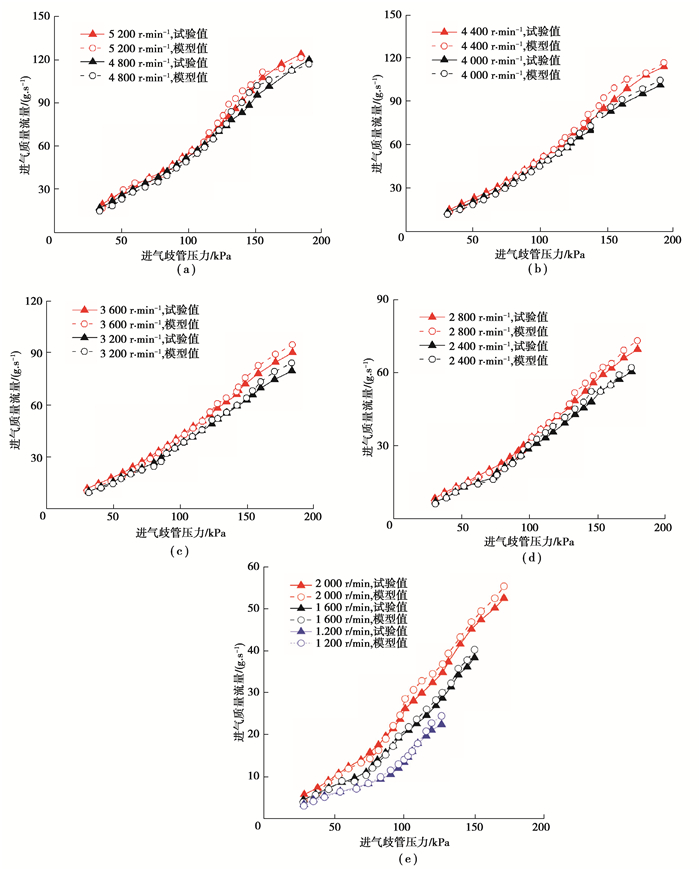
为保证建立的充量模型准确可靠,基于台架全特性试验从高转速到低转速对模型进一步验证。1 200~5 200 r/min下的验证对比结果如图 8所示,台架试验测得的进气质量流量与进气充量模型计算的进气质量流量有很好的一致性,除怠速工况及大负荷工况下的个别点外,试验测得的进气质量流量与充量模型计算的进气质量流量的偏差均在5%以内,台架试验过程进排气正时在各转速、负荷下均以最佳VVT相位运行,故图 8中进气质量流量与歧管压力为近似线性关系。鉴于上述验证分析,所建立的缸内充量模型可以很好地反映发动机换气过程中的气体流动特性,满足工程要求。
|
图 8 台架实测进气质量流量与模型计算进气质量流量对比 Fig. 8 Comparison of intake mass flow rate (bench and model calculation) |
缸内充量模型是汽车发动机系统控制的重要部分。根据发动机换气过程热力学关系,利用Simulink软件构建了面向控制的缸内充量模型,模型包含进气道传热因子α1、驻留废气关键参数α2和气门重叠期间实际流通面积α3。引入GT-POWER仿真模型扩展到多工况下对充量模型中的α1、α2和α3进行标定,并用台架试验进一步验证了模型的正确性,得出如下结论。
1) 仿真模型辅助标定的传热因子α1反映了低负荷下较高的进气道出口温度。标定的驻留废气关键参数α2表明怠速工况驻留废气量较大,随着负荷增大,驻留废气量逐渐减少;中、高转速时,缸内驻留废气量较少。标定的气门实际流通面积α3表明气门实际流通面积与不同重叠角近似呈抛物线关系。
2) 建立的缸内充量模型覆盖了绝大多数发动机工况点,将仿真模型和台架试验分别与缸内充量控制模型结果进行验证对比,结合低转速、中转速和高转速对比结果,不同负荷下缸内充量模型与台架试验及仿真模型的稳态进气量误差基本满足在5%以内的要求。
3) 缸内充量模型反映发动机实际运行工况,仅使用普通商用传感器,简单易实现,减少大量标定工作,是进气模型控制策略的一种可行方法。本研究主要在稳态下对充量模型标定及验证,可以进一步应用于瞬态工况。
| [1] |
Wang Z, Zhu Q L, Prucka R. A review of spark-ignition engine air charge estimation methods[J/OL]. SAE Technical Papers, 2016: 2016-01-0620[2021-02-05]. https://www.sae.org/publications/technical-papers/content/2016-01-0620/.
|
| [2] |
Li Q Y, Liu J P, Fu J Q, et al. Comparative study on the pumping losses between continuous variable valve lift (CVVL) engine and variable valve timing (VVT) engine[J]. Applied Thermal Engineering, 2018, 137: 710-720. DOI:10.1016/j.applthermaleng.2018.04.017 |
| [3] |
Piqueras P, De la Morena J, Sanchis E J, et al. Impact of exhaust gas recirculation on gaseous emissions of turbocharged spark-ignition engines[J]. Applied Sciences, 2020, 10(21): 7634. DOI:10.3390/app10217634 |
| [4] |
Wang Y C, Hao C X, Ge Y S, et al. Fuel consumption and emission performance from light-duty conventional/hybrid-electric vehicles over different cycles and real driving tests[J]. Fuel, 2020, 278: 118340. DOI:10.1016/j.fuel.2020.118340 |
| [5] |
Khameneian A, Wang X, Dice P, et al. Model-based dynamic in-cylinder air charge, residual gas and temperature estimation for a GDI spark ignition engine using cylinder, intake and exhaust pressures[C/OL]//ASME 2020 Dynamic Systems and Control Conference, October 5-7, 2020, Virtual, Online. Volume 2: Intelligent Transportation/Vehicles; Manufacturing; Mechatronics; Engine/After-Treatment Systems; Soft Actuators/Manipulators; Modeling/Validation; Motion/Vibration Control Applications; Multi-Agent/Networked Systems; Path Planning/Motion Control; Renewable/Smart Energy Systems; Security/Privacy of Cyber-Physical Systems; Sensors/Actuators; Tracking Control Systems; Unmanned Ground/Aerial Vehicles; Vehicle Dynamics, Estimation, Control; Vibration/Control Systems; Vibrations. The American Society of Mechanical Engineers, 2020: DSCC2020-3280[2021-02-05]. https://asmedigitalcollection.asme.org/DSCC/proceedings/DSCC2020/84287/V002T26A002/1096544.
|
| [6] |
Kakaee A H, Mashadi B, Ghajar M. A novel volumetric efficiency model for spark ignition engines equipped with variable valve timing and variable valve lift Part 1: model development[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2017, 231(2): 175-191. DOI:10.1177/0954407016650545 |
| [7] |
Luján J M, Climent H, García-Cuevas L M, et al. Volumetric efficiency modelling of internal combustion engines based on a novel adaptive learning algorithm of artificial neural networks[J]. Applied Thermal Engineering, 2017, 123: 625-634. DOI:10.1016/j.applthermaleng.2017.05.087 |
| [8] |
Guardiola C, Pla B, Bares P, et al. Cylinder charge composition observation based on in-cylinder pressure measurement[J]. Measurement, 2019, 131: 559-568. DOI:10.1016/j.measurement.2018.08.024 |
| [9] |
Wang Z, Zhu Q L, Prucka R, et al. Observer-based cylinder air charge estimation for spark-ignition engines[J]. Journal of Engineering for Gas Turbines and Power, 2017, 139(10): 1-7. |
| [10] |
Meng L, Luo J, Yang X, et al. Intake air mass observer design based on extended Kalman filter for air-fuel ratio control on SI engine[J]. Energies, 2019, 12(18): 3444. DOI:10.3390/en12183444 |
| [11] |
Leroy T, Chauvin J. Control-oriented aspirated masses model for variable-valve-actuation engines[J]. Control Engineering Practice, 2013, 21(12): 1744-1755. DOI:10.1016/j.conengprac.2013.08.012 |
| [12] |
Eriksson L, Thomasson A. Cylinder state estimation from measured cylinder pressure traces -a survey[J]. IFAC-PapersOnLine, 2017, 50(1): 11029-11039. DOI:10.1016/j.ifacol.2017.08.2483 |
| [13] |
Wang X, Khameneian A, Dice P, et al. Model-based combustion duration and ignition timing prediction for combustion phasing control of a spark-ignition engine using in-cylinder pressure sensors[C]//Proceedings of ASME 2019 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, August 18-21, 2019, Anaheim, California, USA. The American Society of Mechanical Engineers, 2019: DETC2019-97703.
|
| [14] |
Desantes J M, Galindo J, Guardiola C, et al. Air mass flow estimation in turbocharged diesel engines from in-cylinder pressure measurement[J]. Experimental Thermal and Fluid Science, 2010, 34(1): 37-47. DOI:10.1016/j.expthermflusci.2009.08.009 |
| [15] |
Thomasson A, Nikkar S, Höckerdal E. Cylinder pressure based cylinder charge estimation in diesel engines with dual independent variable valve timing[J/OL]. SAE Technical Papers, 2018: 2018-01-0862[2021-02-05]. https://www.sae.org/publications/technical-papers/content/2018-01-0862/.
|
| [16] |
Yazdani A, Naber J, Shahbakhti M, et al. Air charge and residual gas fraction estimation for a spark-ignition engine using in-cylinder pressure[J/OL]. SAE Technical Papers, 2017: 2017-01-0527[2021-02-05]. https://www.sae.org/publications/technical-papers/content/2017-01-0527/.
|
| [17] |
任亚丹, 王龙, 李涛, 等. 涡轮增压天然气发动机电控系统进气模型研究[J]. 西安交通大学学报, 2018, 52(12): 93-98. Ren Y D, Wang L, Li T, et al. Intake charge model of electronically controlled turbocharged natural gas engine[J]. Journal of Xi'an Jiaotong University, 2018, 52(12): 93-98. (in Chinese) |
| [18] |
Magner S, Jankovic M, Cooper S. Methods to reduce air-charge characterization data for high degree of freedom engines[J/OL]. SAE Technical Papers, 2004: 2004-1-0903[2021-02-05]. https://www.sae.org/publications/technical-papers/content/2004-01-0903/.
|
| [19] |
Fox J W, Cheng W K, Heywood J B. A model for predicting residual gas fraction in spark-ignition engines[J]. SAE Transactions, 1993, 102: 1538-1544. |
| [20] |
Heywood J B. Internal combustion engine fundamentals[M]. New York: McGraw-Hill, 1998.
|
 2022, Vol. 45
2022, Vol. 45

