2. 深圳供电局有限公司,广东 深圳 440310;
3. 国家电网公司西南分部,成都 610041;
4. 重庆电力交易中心有限公司, 重庆 400013
2. Shenzhen Power Supply Bureau Co., Ltd., Shenzhen 440310, Guangdong, P. R. China;
3. Southwest Subsection of State Grid, Chengdu 610041, P. R. China;
4. Chongqing Electric Power Trading Center Co., Ltd., Chongqing 400013, P. R. China
电力用户的窃电行为将会给电网公司造成巨大经济损失[1],传统的物理窃电方式正发展为以数字存储和网络通信技术为手段的新型窃电方式,通过攻击智能电表注入虚假用电数据实施窃电[2],因此对新型窃电方式检测方法的研究具有重要工程价值。
针对虚假用电数据注入的窃电方式,现有检测方法一般遵循“特征设计检测判别”的范式[3]。然而多数方法的研究侧重检测判别阶段,重点研究检测判别算法的选择或改进,提出了多种窃电检测模型,包括基于分类的支持向量机[4]、随机森林[5]、极限学习机[6],基于聚类的最优路径森林[7]、密度聚类[8],以及基于回归的自回归模型[9]等。而针对检测特征设计的研究较少,已有研究主要通过特征提取算法对用电曲线进行抽象凝练;文献[10]首先通过小波分解提取负荷曲线的时域和频域特征,然后通过多个分类器的分类结果交叉验证检测窃电用户;文献[11]首先通过主成分分析算法提取用户用电曲线中的用电特征,然后通过密度聚类算法对异常用电曲线进行检测;文献[3]以堆叠去相关自编码器提取周负荷曲线的用电特征,然后用定制惩罚项的支持向量机检测窃电用户。可见,现有窃电检测方法更多依赖通用特征提取算法对用电数据数值特征的提取能力,缺乏对正常用电或窃电情景的分析,导致特征设计过程与检测对象的物理背景耦合度低,使得所提取特征可解释性差,难以依据其物理意义调整改进,同时一些较为明显的窃电数据特征没能纳入检测特征,使得检测特征的针对性不强。
据此,文中提出了一种基于多层次非负稀疏编码和支持向量机的窃电检测方法。该方法以用户月度用电曲线为检测对象,首先,将月度用电曲线切分为周、日两个层次并基于非负稀疏编码算法提取多层次用电曲线用电模式特征;然后,基于正常用户和窃电用户用电情景对比分析,手工提取周、日两层次用电曲线的数值统计特征;最后,以用电模式特征和数值统计特征的融合检测特征为输入,通过SVM算法对用电曲线进行窃电检测。该方法主要创新点在于:1)周、日两层次用电特征提取呼应用电行为具有周周期性和日周期性的实际,用电特征刻画更精细;2)综合用电模式特征和数值统计特征构建曲线的融合检测特征,可解释性好、针对性强。
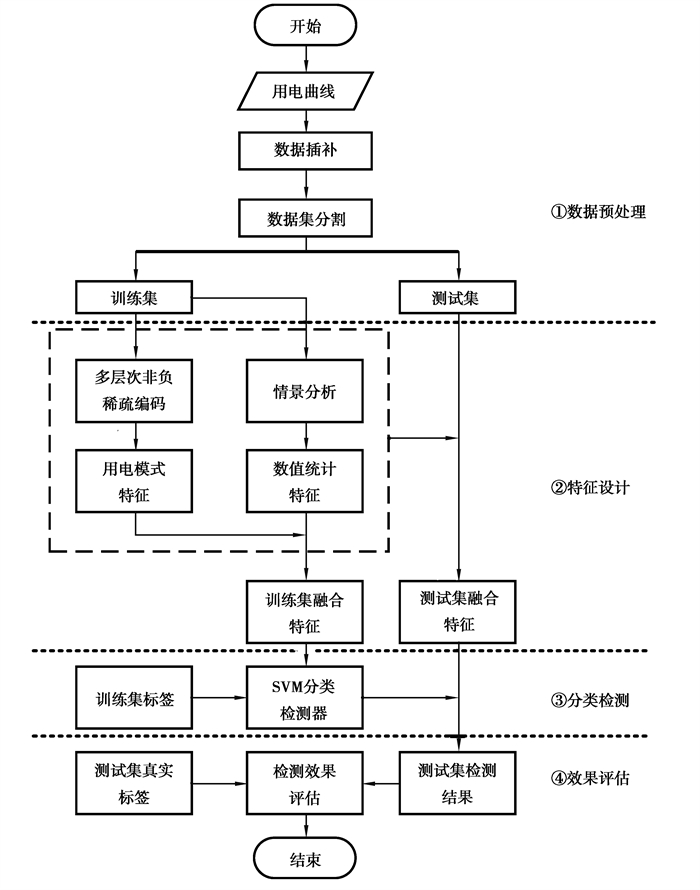
1 基于多层次非负稀疏编码和SVM的窃电检测方法整体设计电力用户窃电检测的难点在于现实中台区电网接线复杂,网络拓扑参数信息未知,难以通过潮流等精确物理约束检测窃电用户;此外,用户的用电负荷低、随机性高,简单的统计分析也难以捕捉用户的用电规律,检测准确率低。得益于智能电表在终端用户数据采集中的应用,海量高分辨率的用户用电数据为数据驱动的窃电检测方法提供了条件,用户窃电检测的研究逐渐转向数据驱动方法,形成了一种“特征设计检测判别”的范式,设计待检测用电曲线样本的检测特征,并采取各种机器学习检测算法对样本进行检测。参考现有数据驱动窃电检测方法的通用范式,文中提出一种基于多层次非负稀疏编码和SVM的窃电检测方法,其整体框架设计如图 1所示。
|
图 1 基于多层次非负稀疏编码和SVM的窃电检测方法整体框架 Fig. 1 Framework of electricity theft detection method based on multi-level non-negative sparse coding and SVM |
由图 1可见,该整体框架分为4个阶段。
阶段1:数据预处理阶段。该阶段对用电曲线的缺失数据进行插补,并将数据集分割为训练集和测试集;
阶段2:特征设计阶段。基于多层次非负稀疏编码提取月度用电曲线的周、日多层次用电模式特征,以及正常用电和窃电情景分析提取用电曲线的数值统计特征,综合用电模式特征和数值统计特征形成曲线的融合检测特征;
阶段3:分类检测阶段。利用阶段2中训练集的融合检测特征及其对应标签训练SVM分类器,将测试集的融合检测特征输入SVM分类器,得到测试集用电曲线的分类检测结果;
阶段4:效果评估阶段。将测试集分类检测结果与真实标签对比,通过精确率、召回率、F1值等指标评价窃电样本的检测效果。
上述4个阶段中,数据预处理阶段主要借鉴现有文献采取线性插值法对缺失数据进行填充,文中重点研究特征设计阶段、分类检测阶段和效果评估阶段等3个阶段。
2 基于多层次非负稀疏编码和情景分析的月度曲线检测特征设计用电曲线的特征主要分为形状和数量特征2类,若要充分提取用电曲线的用电特征,需同时对用电曲线的形状特征和数量特征进行刻画。采取多层次非负稀疏编码算法将月度用电曲线切分为周层次曲线和日层次曲线,并对其分别进行非负稀疏编码,获取用电曲线的周周期和日周期用电模式,借此提取用电曲线的形状特征;而后基于正常用电和窃电情景的对比分析,手动提取用电曲线的数值统计特征,作为曲线的数量特征。
2.1 基于多层次非负稀疏编码的月度曲线用电模式特征构建 2.1.1 非负稀疏编码原理及算法稀疏编码是一种信息压缩算法,广泛应用于数据压缩领域,其原理是寻找一组过完备基向量对样本变量进行线性组合表示。基向量组由于过完备性将是非正交且冗余的,用少于样本变量维度数目的基向量即可实现对样本的线性表示,基向量的线性组合系数具备稀疏性,非负稀疏编码则在稀疏编码的基础上对基向量元素和线性组合系数增加了非负性约束。
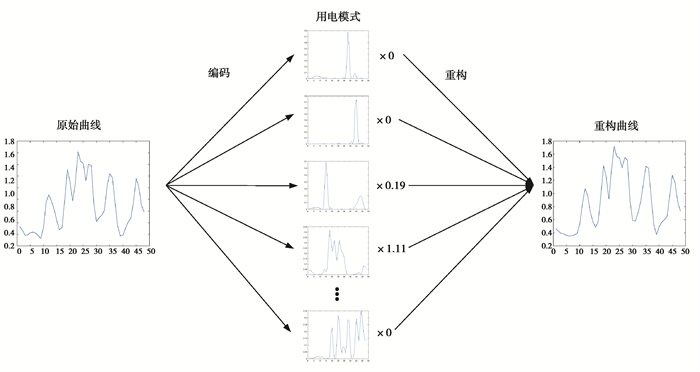
电力用户的用电曲线可以看作是若干种用电模式下用电曲线的加权线性组合,这与非负稀疏编码的思想非常契合,因此可以将非负稀疏编码引入用电曲线的用电模式特征提取过程。非负稀疏编码中的每个基向量代表一种用电模式,而每个基向量对应的稀疏编码值则代表该种用电模式的线性组合系数,通过非负稀疏编码过程可将原始用电曲线解构为少数几种用电模式的线性叠加,即可实现用电曲线的用电模式特征提取。用电曲线的非负稀疏编码解构与重构如图 2所示。
|
图 2 用电曲线的非负稀疏编码解构与重构 Fig. 2 Deconstruction and reconstruction of electricity consumption curve by non-negative sparse coding |
样本矩阵X的非负稀疏编码求解模型为
| $ \begin{aligned} &\min _{D, C}\|\boldsymbol{X}-\boldsymbol{D C}\|_{F}^{2}+\lambda \sum\limits_{m=1}^{M}\left\|c_{m}\right\|_{0} \text {, }\\ &\text { s.t. }\left\|c_{m}\right\|_{0} \leqslant L, 1 \leqslant m \leqslant M ; d_{n k} \geqslant 0, 1 \leqslant n \leqslant N, 1 \leqslant k \leqslant K ; c_{k m} \geqslant 0, 1 \leqslant m \leqslant M, 1 \leqslant k \leqslant K \text { 。} \end{aligned} $ | (1) |
式中:X是N×M维样本矩阵,含有M个N维样本变量;D为过完备基向量组,包含K个N维基向量,且K>N以保证基向量的过完备性。通常称D为编码字典,D中的基向量为字典原子;C为样本的稀疏编码矩阵,是样本变量解构为字典原子线性组合时的权重系数,为一稀疏矩阵;‖ ‖F(F-范数)表示矩阵元素平方和的平方根;‖ ‖0(0范数)表示向量非零元素个数;λ为稀疏度约束惩罚系数。
由于模型中字典D和稀疏编码C都是变量,难以同时优化,故通常将优化模型分解为稀疏编码和字典更新两阶段,采取分阶段交替优化迭代的策略求解。文献[12-13]提出了一种适用于非负稀疏编码的字典学习算法,该算法采取基追踪(BP,basis pursuit)算法求解样本的稀疏编码阶段,而采取迭代奇异值分解(K-SVD, K-singular value decomposition)算法更新编码字典。
稀疏编码阶段,固定字典D为常量,将目标函数中稀疏度约束的0范数转化成1范数。同时基于稀疏编码的非负性,可将目标函数式(1)转化为
| $ \begin{gathered} \min _{C}\|\boldsymbol{X}-\boldsymbol{D C}\|{ }_{F}^{2}++\lambda \sum\limits_{m=1}^{M} \sum\limits_{k=1}^{K} c_{k m} \text {, }\\ \text { s.t. } c_{k m} \geqslant 0, 1 \leqslant m \leqslant M, 1 \leqslant k \leqslant K \text { 。} \end{gathered} $ | (2) |
根据文献[13]的推导,可得到稀疏编码矩阵C的迭代求解为
| $ \boldsymbol{C}(t+1)=\boldsymbol{C}(t) . *\left(\boldsymbol{D}^{\mathrm{T}} \boldsymbol{X}\right) \cdot /\left(\boldsymbol{D}^{\mathrm{T}} \boldsymbol{D}\;\boldsymbol{C}(t)+\lambda \boldsymbol{I}\right) \text {, } $ | (3) |
式中,稀疏编码矩阵的初值C(0)初始化为零矩阵。为确保稀疏编码向量c有指定数值的稀疏度约束L,需将样本变量x用其对应编码向量c中编码最大的L个字典原子进行线性表示。
| $ \mathop {\min }\limits_{c_m^L} \left\|x_{m}-\boldsymbol{D}_{m}{ }^{L} c_{m}^{L}\right\|{ }_{F}^{2} \text { 。} $ | (4) |
字典更新阶段,固定稀疏编码C为常量,目标函数转化为
| $ \mathop {\min }\limits_D\|\boldsymbol{X}-\boldsymbol{D C}\|{ }_{F}^{2}=\left\|\boldsymbol{X}-\left(\boldsymbol{D} \boldsymbol{C}-\boldsymbol{d}_{k} \boldsymbol{c}^{k}\right)-\boldsymbol{d}_{k} \boldsymbol{c}^{k}\right\|{ }_{F}^{2} \triangleq\left\|\boldsymbol{E}_{k}-\boldsymbol{d}_{k} \boldsymbol{c}^{k}\right\|_{F}^{2} \text {, } $ | (5) |
式中,
遍历更新所有字典原子dk及其对应编码行向量ck,使重构误差逐步降低,同时实现对字典原子的更新
| $ \mathop {\min }\limits_{{d_k},c_{\rm{R}}^k}\left\|\boldsymbol{E}_{k}^{\mathrm{R}}-\boldsymbol{d}_{k} \boldsymbol{c}_{\mathrm{R}}^{k}\right\|_F^2 \text {, } $ | (6) |
式中,
| $ \boldsymbol{E}_{k}^{\mathrm{R}}=\boldsymbol{U} \Delta \boldsymbol{V}^{\mathrm{T}}, \boldsymbol{d}_{k}^{(0)}=\boldsymbol{u}_{1}, \boldsymbol{c}_{\mathrm{R}}^{k}(0)=\sigma_{1} \boldsymbol{v}_{1}^{\mathrm{T}} \text {, } $ | (7) |
同时,为保证字典原子和编码的非负性,通过下述迭代处理将dk和ck中的负值截断为零:
| $ \begin{gathered} \boldsymbol{d}(t+1)_{k}=\frac{\boldsymbol{E}_{k}^{\mathrm{R}}\left(\boldsymbol{c}_{\mathrm{R}}^{k}(t)\right)^{\mathrm{T}}}{\boldsymbol{c}_{\mathrm{R}}^{k}(t)\left(\boldsymbol{c}_{\mathrm{R}}^{k}(t)\right)^{\mathrm{T}}} \text {, 取 } \boldsymbol{d}(t+1)_{k}(n)=\left\{\begin{array}{l} 0, \boldsymbol{d}(t+1)_{k}(n)<0 \\ \boldsymbol{d}(t+1)_{k}(n), \text { 其他 } \end{array}, 1 \leqslant n \leqslant N \right. ,\\ \boldsymbol{c}_{\mathrm{R}}^{k}(t+1)=\frac{\boldsymbol{d}(t+1)_{k}^{\mathrm{T}} \boldsymbol{E}_{k}^{R}}{\boldsymbol{d}(t+1)_{k}^{\mathrm{T}} \boldsymbol{d}(t+1)_{k}}, \text { 取 } \boldsymbol{c}_{\mathrm{R}}^{k}(t+1)(j)=\left\{\begin{array}{l} 0, \boldsymbol{c}_{\mathrm{R}}^{k}(t+1)(j)<0 \\ \boldsymbol{c}_{\mathrm{R}}^{k}(t+1)(j), \text { 其他 } \end{array}, 1 \leqslant j \leqslant J 。\right. \end{gathered} $ | (8) |
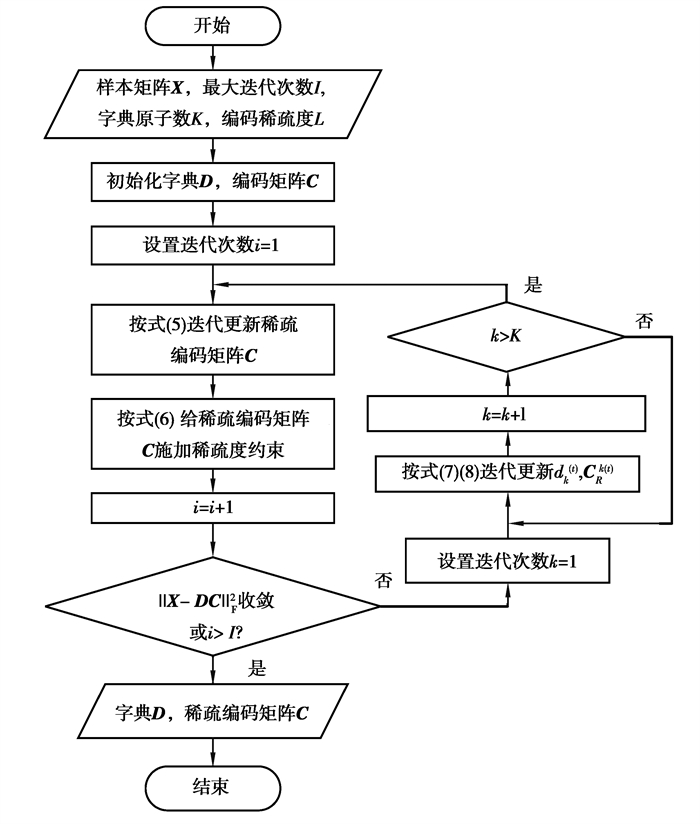
非负稀疏编码算法的流程如图 3所示。
|
图 3 非负稀疏编码算法流程图 Fig. 3 Flow chart of non-negative sparse coding algorithm |
考虑到用户月度负荷曲线在时序上具有周周期性和日周期性,用户用电曲线是否具有稳定且普遍的周周期性和日周期性是判断用户是否窃电的重要依据,因此可以将月度负荷曲线切分为周、日两个层次的曲线子序列,分别通过上述非负稀疏编码算法提取其用电模式特征,以考察其周周期性和日周期性。
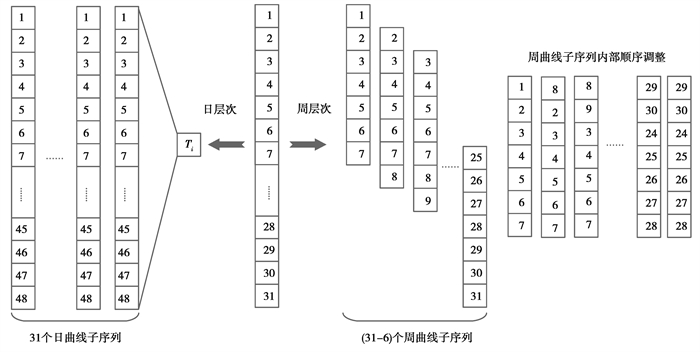
设月度用电曲线跨度为T天,则将月度曲线按日切分,可得到T个日层次曲线子序列。另用长度为7天的滑窗对月度曲线进行切分,步长为1 d,可获得(T-6)个周层次曲线子序列。同时考虑到一周内各天(尤其是工作日与周末)之间用电特性的区别,将每个周曲线子序列内部各天都按照同一顺序排列,一条时长31 d、数据采集分辨率30 min一次的月度用电曲线的周、日两层次切分过程如图 4所示。
|
图 4 月度曲线样本的周日两层次切分 Fig. 4 Weekly-daily two-level segmentation of monthly curve samples |
含有M个用户、采集时长跨度T天且数据采集日分辨率为t点/天的月度用电曲线样本集XN×M(其中N=Tt)做上述两层次切分,可得到周层次、日层次曲线子序列样本集分别为
通过上述多层次非负稀疏编码过程已获取了表征月度曲线周、日两层次用电模式特征的稀疏编码,然而由于字典原子的冗余性,稀疏编码特征具有高维度、高稀疏性的特点,价值密度低,不适合直接作为用电曲线的模式特征。同时,由于正常样本远多于窃电样本且正常用电模式相对窃电用电模式更少、更集中,非负稀疏编码对正常用电曲线和窃电曲线的重构误差存在结构性差别,也应作为用电模式特征的辅助特征。据此,在多层次非负稀疏编码的基础上对月度用电曲线的用电模式特征进行进一步构建,新构建的用电模式特征分两个部分:一是基于周、日两层次用电曲线的稀疏编码构建的用电模式正常度特征;二是周、日两层次用电曲线的非负稀疏编码重构相对平均误差。
用电模式正常度特征的构建过程如下:首先,忽略用电曲线的数量特征而仅考虑其形状特征,将样本曲线的稀疏编码转化成各编码系数的占编码系数总和比例的分数形式,用以表征原始曲线中各用电模式的占比为
| $ \begin{aligned} &\tilde{c}_{k_{\mathrm{w}}, m_{\mathrm{w}}}^{\mathrm{w}}=c_{k_{\mathrm{w}}, m_{\mathrm{w}}}^{\mathrm{w}} / \sum\limits_{k_{\mathrm{w}}=1}^{K_{\mathrm{w}}} c_{k_{\mathrm{w}}, m_{\mathrm{w}}}^{\mathrm{w}}, k_{\mathrm{w}}=1, 2, \cdots, K_{\mathrm{w}} ; m_{\mathrm{w}}=1, 2, \cdots, M_{\mathrm{w}}, \\ &\tilde{c}_{k_{\mathrm{d}}, m_{\mathrm{d}}}^{\mathrm{d}}=c_{k_{\mathrm{d}}, m_{\mathrm{d}}}^{\mathrm{d}} / \sum\limits_{k_{\mathrm{d}}=1}^{K_{\mathrm{d}}} c_{k \mathrm{~d}, m_{\mathrm{d}}}^{\mathrm{w}}, k_{\mathrm{d}}=1, 2, \cdots, K_{\mathrm{d}} ; m_{\mathrm{d}}=1, 2, \cdots, M_{\mathrm{d}}\text { 。} \end{aligned} $ | (9) |
然后,根据各用电模式在全体样本中占比的总和确定各用电模式的正常度为:
| $ \begin{split} &s_{k_{\mathrm{w}}}^{\mathrm{w}}=\sum\limits_{m_{\mathrm{w}}=1}^{M_{\mathrm{w}}} \tilde{c}_{k_{\mathrm{w}}, m_{\mathrm{w}}}^{\mathrm{w}}, k_{\mathrm{w}}=1, 2, \cdots, K_{\mathrm{w}}, \\ &s_{k_{\mathrm{d}}}^{\mathrm{d}}=\sum\limits_{m_{\mathrm{d}}=1}^{M_{\mathrm{d}}} \tilde{c}_{k_{\mathrm{d}}, m_{\mathrm{d}}}^{\mathrm{d}}, k_{\mathrm{d}}=1, 2, \cdots, K_{\mathrm{d}}\text { 。} \end{split} $ | (10) |
最后,将样本曲线中各用电模式的正常度加权求和即可得该样本的用电模式正常度为:
| $ \begin{aligned} & s_{m_{\mathrm{w}}}^{\mathrm{w}}=\sum\limits_{k_{\mathrm{w}}=1}^{K_{\mathrm{w}}} s_{k_{\mathrm{w}}}^{\mathrm{w}} \tilde{c}_{k_{\mathrm{w}}, m_{\mathrm{w}}}^{\mathrm{w}}, m_{\mathrm{w}}=1, 2, \cdots, M_{\mathrm{w}}, \\ & s_{m_{\mathrm{d}}}^{\mathrm{d}}=\sum\limits_{k_{\mathrm{d}}=1}^{K_{\mathrm{d}}} s_{k_{\mathrm{d}}}^{d} \tilde{c}_{k_{\mathrm{d}}, m_{\mathrm{d}}}^{\mathrm{d}}, m_{\mathrm{d}}=1, 2, \cdots, M_{\mathrm{d}}\text { 。} \end{aligned} $ | (11) |
对于每个用户,将其周、日两层次用电曲线子序列样本的用电模式正常度整合,即可得到该用户用电模式正常度特征为
| $ \boldsymbol{S}_{m}=\left[S_{(T-6) \times(m-1)+1}^{\mathrm{w}}, S_{(T-6) \times(m-1)+2}^{\mathrm{w}}, \cdots, S_{(T-6) \times m}^{\mathrm{w}}, S_{T \times(m-1)+1}^{\mathrm{d}}, S_{T \times(m-1)+2}^{\mathrm{d}}, \cdots, S_{T \times m}^{\mathrm{d}}\right] \text { 。} $ | (12) |
样本曲线的非负稀疏编码重构平均相对误差定义为重构曲线与原始曲线之间的相对误差,具体定义为:
| $ \begin{aligned} e_{m_{\mathrm{w}}}^{\mathrm{w}} &=\frac{1}{N_{\mathrm{w}_n}} \sum\limits_{n_{\mathrm{w}=1}}^{N_{\mathrm{w}}}\left|x_{n_{\mathrm{w}}, m_{\mathrm{w}}}^{\mathrm{w}}-\hat x_{n_{\mathrm{w}}, m_{\mathrm{w}}}^{\mathrm{w}}\right| / x_{n_{\mathrm{W}}, m_{\mathrm{w}}}^{\mathrm{w}} \\ e_{m_{\mathrm{d}}}^{\mathrm{d}} &=\frac{1}{N_{\mathrm{d}}} \sum\limits_{n_{\mathrm{d}}=1}^{N_{\mathrm{d}}}\left|x_{n_{\mathrm{d}}, m_{\mathrm{d}}}^{\mathrm{d}}-\hat x_{n_{\mathrm{d}}, m_{\mathrm{d}}}^{d}\right| / x_{n_{\mathrm{d}}, m_{\mathrm{d}}}^{\mathrm{d}}\text {, } \end{aligned} $ | (13) |
式中,
| $ \boldsymbol{e}_{m}=\left[e_{(T-6) \times(m-1)+1}^{\mathrm{w}}, e_{(T-6) \times(m-1)+2}^{\mathrm{w}}, \cdots, e_{(T-6) \times m}^{\mathrm{w}}, e_{T \times(m-1)+1}^{\mathrm{d}}, e_{T \times(m-1)+2}^{\mathrm{d}}, \cdots, e_{T \times m}^{\mathrm{d}}\right] \text { 。} $ | (14) |
现实中窃电用户与正常用户电量数值存在一些系统性差异,通过捕捉这些差异构建用电曲线的数值统计特征,可提高窃电检测效率。一般而言,窃电行为在时间上有持续性且在数量上有较大幅度,窃电用户平均负荷水平相较正常用户将有一定幅度的差距;同时窃电用户电量通常会出现长时间为0或者某一较低数值的情况,且数值波动小。鉴于窃电行为的上述特征,可将电量平均值、方差和非重复数值个数等系统性差异变量作为月度用电曲线的数值统计特征,依旧分周、日两个层次,为:
| $ \begin{aligned} &\bar{x}_{m_{\mathrm{w}}}^{\mathrm{w}}=\frac{1}{N_{\mathrm{w}}} \sum\limits_{n_{\mathrm{w}}=1}^{N_{\mathrm{w}}} x_{n_{\mathrm{w}}, m_{\mathrm{w}}}^{\mathrm{w}}, \bar{x}_{m_{\mathrm{d}}}^{\mathrm{d}}=\frac{1}{N_{\mathrm{d}}} \sum\limits_{n_{\mathrm{d}}=1}^{N_{\mathrm{d}}} x_{n_{\mathrm{d}}, m_{\mathrm{d}}}^{\mathrm{d}} \text {, }\\ &v_{m_{\mathrm{w}}}^{\mathrm{w}}=\frac{1}{N_{\mathrm{w}}} \sum\limits_{n_{\mathrm{w}}=1}^{N_{\mathrm{w}}}\left(x_{n_{\mathrm{w}}, m_{\mathrm{w}}}^{\mathrm{w}}-\bar{x}_{m_{\mathrm{w}}}^{\mathrm{w}}\right)^{2}, v_{m_{\mathrm{d}}}^{\mathrm{d}}=\frac{1}{N_{\mathrm{d}}} \sum\limits_{n_{\mathrm{d}}=1}^{N_{\mathrm{d}}}\left(x_{n_{\mathrm{d}}, m_{\mathrm{d}}}^{\mathrm{d}}-\bar{x}_{m_{\mathrm{d}}}^{\mathrm{d}}\right)^{2}, \\ &u_{m_{\mathrm{w}}}^{\mathrm{w}}=\text { unique }\left(x_{m_{\mathrm{w}}}^{\mathrm{w}}\right), u_{m_{\mathrm{d}}}^{\mathrm{d}}=\text { unique }\left(x_{m_{\mathrm{d}}}^{\mathrm{d}}\right), \end{aligned} $ | (15) |
式中,unique(x)表示向量x中非重复数值的个数。整合上述周、日两层次用电曲线的数值统计特征可得用户月度用电曲线的数值统计特征为:
| $ \begin{gathered} \overline{\boldsymbol{x}}_{m}=\left[\bar{x}_{(T-6) \times(m-1)+1}^{\mathrm{w}}, \bar{x}_{(T-6) \times(m-1)+2}^{\mathrm{w}}, \cdots, \bar{x}_{(T-6) \times m}^{\mathrm{w}}, \bar{x}_{T \times(m-1)+1}^{\mathrm{d}}, \bar{x}_{T \times(m-1)+2}^{\mathrm{d}}, \cdots, \bar{x}_{T \times m}^{\mathrm{d}}\right], \\ \boldsymbol{v}_{m}=\left[v_{(T-6) \times(m-1)+1}^{\mathrm{d}}, v_{(T-6) \times(m-1)+2}^{\mathrm{w}}, \cdots, v_{(T-6) \times m}^{\mathrm{w}}, v_{T \times(m-1)+1}^{\mathrm{w}}, v_{T \times(m-1)+2}^{\mathrm{d}}, \cdots, v_{T \times m}^{\mathrm{d}}\right], \\ \boldsymbol{u}_{m}=\left[u_{(T-6) \times(m-1)+1}^{\mathrm{d}}, u_{(T-6) \times(m-1)+2}^{\mathrm{w}}, \cdots, u_{(T-6) \times m}^{\mathrm{w}}, u_{T \times(m-1)+1}^{\mathrm{d}}, u_{T \times(m-1)+2}^{\mathrm{d}}, \cdots, u_{T \times m}^{\mathrm{d}}\right]\text { 。} \end{gathered} $ | (16) |
上述多层次非负稀疏编码算法在周、日两个层次上构建了月度用电曲线的用电模式特征和数值统计特征,综合二者设计用户的融合检测特征为
| $ \boldsymbol{f}_{m}=\left[\boldsymbol{s}_{m}, \boldsymbol{e}_{m}, \overline{\boldsymbol{x}}_{m}, \boldsymbol{v}_{m}, \boldsymbol{u}_{m}\right], m=1, 2, \cdots, M\text { 。} $ | (17) |
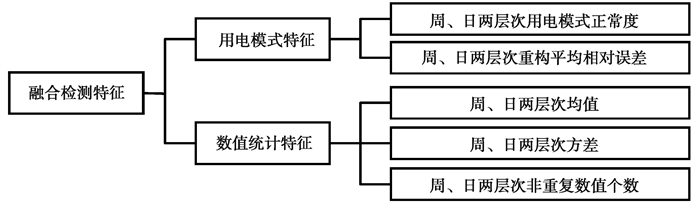
上述融合检测特征的组成结构如图 5所示。
|
图 5 融合检测特征的组成结构 Fig. 5 Composition structure of fusion detection features |
由图 5可知,融合检测特征兼顾了周、日两个层次下月度用电曲线形状和数量两方面特征,即用电模式特征和数值统计特征。其中,用电模式特征包括用电曲线的用电模式正常度和重构平均相对误差;数值统计特征包括用电曲线的均值、方差以及非重复数值个数。
3 基于SVM的窃电样本检测及检测效果评估SVM是一种有监督分类算法,其基本原理是寻找一个最优超平面将特征空间中的样本点一分为二,并使得不同标签的两类样本点离超平面的间隔最大。对于线性不可分问题,通过核技巧将输入样本映射到高维空间,使得低维特征空间中线性不可分的样本在高维空间中线性可分。SVM由于其在高维特征分类问题上良好求解性[14],多次被用于窃电检测,故文中选用高斯核函数非线性SVM算法进行窃电样本的检测判别。通过带标签的训练集对高斯核函数非线性SVM分类器进行训练求解,以测试集测试分类器的检测效果,高斯核函数非线性SVM分类器的求解流程[15]如下:
1) 将训练集样本的融合检测特征fi及其标签yi∈{-1,1}(i=1, 2, …, N,y=1表示窃电)作为输入,线性SVM的模型为:
| $ \begin{aligned} &\min _{\omega, b, \xi} \frac{1}{2}\|\boldsymbol{\omega}\|^{2}+C \sum\limits_{i=1}^{N} \xi_{i}, \\ &\text { s.t. } y_{i}\left(\omega \cdot f_{i}+b\right) \geqslant 1-\xi_{i}, i=1, 2, \cdots N, \\ &\xi_{i} \geqslant 0, i=1, 2, \cdots N \text { 。} \end{aligned} $ | (18) |
式中:ω为特征权重向量;ξi为函数间隔松弛变量;C为松弛变量的惩罚超参数。
2) 将线性SVM转化为其对偶问题,同时引入高斯核函数可得到高斯核函数非线性SVM模型,为:
| $ \begin{aligned} &\min _{\alpha} \frac{1}{2} \sum\limits_{i=1}^{N} \sum\limits_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j} K\left(f_{i} \cdot f_{j}\right)-\sum\limits_{i=1}^{N} \alpha_{i}, \\ &\text { s.t. } \sum\limits_{i=1}^{N} \alpha_{i} y_{i}=0, 0 \leqslant \alpha_{i} \leqslant C, i=1, 2, \cdots N\text { 。} \end{aligned} $ | (19) |
式中α=(α1, α2, …, αN)T为拉格朗日乘子向量;K(·)表示高斯核函数,为:
| $ K(x, z)=\exp \left(-\frac{\|x-z\|^{2}}{2 \sigma^{2}}\right)=\exp \left(-\gamma\|x-z\|^{2}\right)\text { 。} $ | (20) |
式中,γ为核函数待定超参数。
3) 求解式(19)得最优解α*,然后计算
| $ b^{*}=y_{j}-\sum\limits_{i=1}^{N} \alpha_{i}^{*} y_{i} K\left(\boldsymbol{f}_{i}, \boldsymbol{f}_{j}\right)\text { 。} $ | (21) |
4) 构造决策函数,预测样本的分类结果为
| $ f(\boldsymbol{f})=\operatorname{sign}\left(\sum\limits_{i=1}^{N} \alpha_{i}^{*} y_{i} K\left(\boldsymbol{f}, \boldsymbol{f}_{i}\right)+b^{*}\right)\text { 。} $ | (22) |
窃电样本检测效果评价指标选择基于混淆矩阵的精确率P、召回率R、F1值,具体表达式为式(23)。其中,精确率是指被判定为异常的样本中实际为异常的比例;回率是指实际异常样本被检测出来的比例,而F1值则是精确率与召回率的调和平均值,只有精确率与召回率都较高才能取得较高的F1值。
| $ P=\frac{T_{\mathrm{P}}}{T_{\mathrm{P}}+F_{\mathrm{P}}}, R=\frac{T_{\mathrm{P}}}{T_{\mathrm{P}}+F_{\mathrm{N}}}, F_{1}=\frac{2 P R}{P+R}, $ | (23) |
式中:TP表示真阳性(窃电)样本数;FP表示假阳性样本数;FN表示假阴性样本数。
4 算例分析 4.1 基础数据以爱尔兰智能电表数据集[16]为基础构造本算例基础数据。该数据集包括了6 000多户低压台区用户近18个月的用电量数据,时间分辨率为30 min。以数据集中3 000个用户某月用电数据构造算例样本,随机选取20%的样本模拟窃电样本,按文献[17-19]中的数据篡改方式对选中窃电样本作表 1所示6种处理,通过分层抽样方法将样本集按7∶3的比例随机分为训练集和测试集。
| 表 1 窃电数据篡改方式及对应数学表达式 Table 1 Data tampering methods for electricity theft and corresponding mathematical expressions |
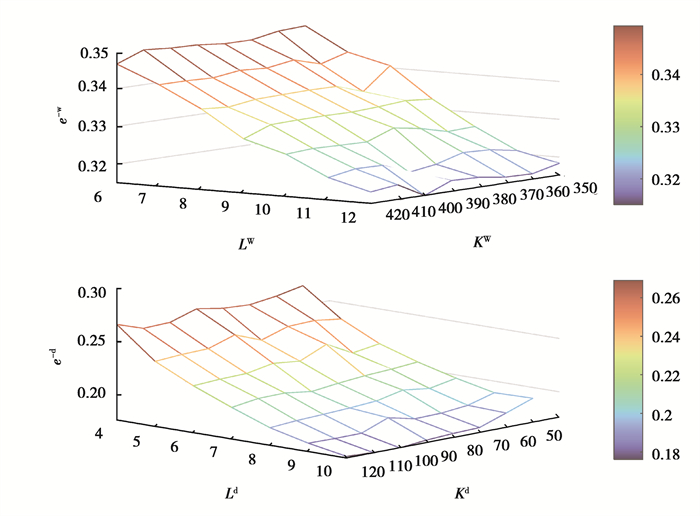
非负稀疏编码能够有效提取用电曲线用电模式特征的关键在于编码字典和编码稀疏能够良好地重构原始用电曲线,因此需要考察非负稀疏编码对原始用电曲线的重构效果。非负稀疏编码算法中字典原子数目K和编码稀疏度L 2个参数对用电曲线的重构平均相对误差平均值
|
图 6 参数K和L对非负稀疏编码重构平均相对误差的影响 Fig. 6 The influence of parameters K and L on the average relative error of non-negative sparse coding reconstruction |
由图 6可知,增大字典原子数目K和稀疏度L都可以降低周、日层次用电曲线非负稀疏编码重构的平均相对误差,且相对而言增加编码稀疏度L对于提升曲线重构精度的效果更加明显。平衡重构效果与计算负担,选取周层次非负稀疏编码参数Kw为400,Lw为12、日层次参数Kd为80,Ld为10,在上述参数设置下,周、日两个层次下典型正常、窃电曲线的直观重构效果如图 7所示。
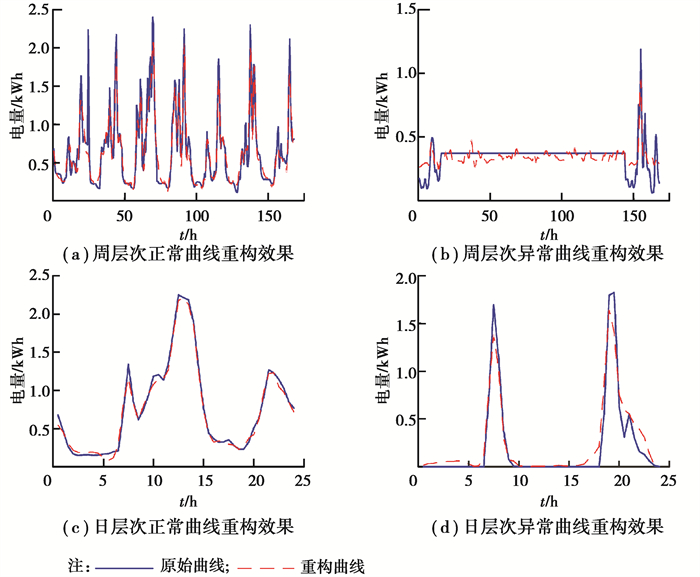
|
图 7 周、日层次典型正常、窃电曲线的重构效果 Fig. 7 Reconstruction effect of typical normal and abnormal curve at weekly and daily levels |
周、日两个层次下正常、窃电曲线样本重构平均相对误差的平均值、中位数、最大值、最小值如表 2所示。
| 表 2 周、日层次正常、窃电曲线的重构误差 Table 2 Reconstruction error of normal and abnormal curve at weekly and daily levels |
由表 2可知,周、日两个层次下正常曲线和窃电曲线样本重构平均相对误差的平均值、中位数都处于较低水平,说明非负稀疏编码算法能够实现对用电曲线的良好重构,因此基于非负稀疏编码提取用电曲线的用电模式特征是合理的。
4.3 基于多层次非负稀疏编码和SVM的窃电检测方法的有效性验证文中所提基于多层次非负稀疏编码和SVM的窃电检测方法核心在于改善窃电检测特征的设计方式,进而提高窃电检测的准确率,因此只需验证在同一检测判别算法下采取文中特征设计方式能够取得相较其他方式更高的检测准确率,即可验证文中方法有效性,据此设计5种特征方式如下:
1) 直接以原始变量为特征,不做额外特征设计处理;
2) 基于主成分分析(principal component analysis, PCA)构建检测特征;
3) 基于独立成分分析(independent component analysis, ICA)构建检测特征;
4) 基于日曲线单一层次非负稀疏编码和窃电情景分析构建检测特征;
5) 基于周、日曲线多层次非负稀疏编码和窃电情景分析构建检测特征。
为叙述方便,将上述5种特征设计方式分别简记为ORIGIN、PCA、ICA、DSC和WDSC。以高斯核函数非线性SVM为检测判别算法,各种特征设计方式下窃电样本的检测效果以及对应SVM超参数的取值如表 3所示。
| 表 3 各种特征设计方式下样本的检测效果 Table 3 Detection results of the samples under various feature processing methods |
由表 3可见,ORIGIN取得了最低的F1值,说明额外的特征设计可以在一定程度上排除随机性等因素对样本曲线的干扰,聚焦于用户的主要用电特征,提高检测判别方法的精确率与召回率。
对比WDSC、DSC和ICA、PCA特征设计方式下的检测结果,WDSC和DSC取得了相较ICA和PCA更高的F1值,表明文中所提基于非负稀疏编码和情景分析的特征设计方法相比ICA、PCA特征设计方法更有效。这是由于WDSC、DSC将月度曲线的用电特征分为形状特征和数量特征分别构建,分别赋予各分量特征以物理意义,保证了特征的可解释性和针对性,易于修正改进;而ICA、PCA等通用特征提取算法没有依据窃电检测问题数据特征对方法作适应性调整,故对高度随机的用户用电曲线样本适应性差。
对比WDSC和DSC特征设计方式下的检测结果,两种特征提取方式在检测精确率上效果接近,但周、日多层次稀疏编码算法在召回率上明显高于日曲线单一层次稀疏编码算法,说明周、日两个层次的用电特征的确存在,多层次的特征提取能更加充分地刻画用户的用电特征。
综上,文中所提基于多层次非负稀疏编码和SVM窃电检测方法通过改善窃电检测特征的设计方法,能够有效提高窃电样本的检测精确率和召回率。
5 结论虚假数据注入的新型窃电方式下,现有窃电检测方法准确率不高。文中提出了一种基于多层次非负稀疏编码和SVM的窃电检测方法,主要研究结论如下:
1) 相较于直接以原始用电曲线为特征,对原始用电曲线进行额外特征设计处理有助于排除随机性等因素对曲线用电特征的干扰,聚焦用户主要特征,进而可提高窃电样本检测的准确率。
2) 正常曲线和窃电曲线的非负稀疏编码重构平均相对误差平均值、中位数都处于较低水平,说明非负稀疏编码算法能够实现对用电曲线的良好重构,基于非负稀疏编码提取用电曲线的用电模式特征是合理的。
3) 基于多层次非负稀疏编码和情景分析的用电曲线融合特征设计方法能够有效提取用电曲线的用电特征,相较其他通用特征提取方法,文中方法在窃电检测的精确率和召回率上具有明显优势。
4) 多层次非负稀疏编码由于同时考虑了月度用电曲线的日周期性和周周期性,相较单一层次非负稀疏编码特征提取方法更能全面刻画用户用电特征,能取得更高的窃电样本检出率。
| [1] |
陈启鑫, 郑可迪, 康重庆, 等. 异常用电的检测方法: 评述与展望[J]. 电力系统自动化, 2018, 42(17): 189-199. Chen Q X, Zheng K D, Kang C Q, et al. Detection methods of abnormal electricity consumption behaviors: review and prospect[J]. Automation of Electric Power Systems, 2018, 42(17): 189-199. (in Chinese) DOI:10.7500/AEPS20171128013 |
| [2] |
Mclaughlin S, Podkuiko D, Mcdaniel P. Energy theft in the advanced metering infrastructure[J]. Lecture Notes in Computer Science, 2009, 6027: 176-187. |
| [3] |
胡天宇, 郭庆来, 孙宏斌. 基于堆叠去相关自编码器和支持向量机的窃电检测[J]. 电力系统自动化, 2019, 43(1): 119-125. Hu T Y, Guo Q L, Sun H B. Nontechnical loss detection based on stacked uncorrelating autoencoder and support vector machine[J]. Automation of Electric Power Systems, 2019, 43(1): 119-125. (in Chinese) |
| [4] |
Nagi J, Yap K S, Tiong S K, et al. Nontechnical loss detection for metered customers in power utility using support vector machines[J]. IEEE Transactions on Power Delivery, 2010, 25(2): 1162-1171. DOI:10.1109/TPWRD.2009.2030890 |
| [5] |
许刚, 谈元鹏, 戴腾辉. 稀疏随机森林下的用电侧异常行为模式检测[J]. 电网技术, 2017, 41(6): 1964-1973. Xu G, Tan Y P, Dai T H. Sparse random forest based abnormal behavior pattern detection of electric power user side[J]. Power System Technology, 2017, 41(6): 1964-1973. (in Chinese) |
| [6] |
Nizar A H, Dong Z Y, Wang Y. Power utility nontechnical loss analysis with extreme learning machine method[J]. IEEE Transactions on Power Systems, 2008, 23(3): 946-955. DOI:10.1109/TPWRS.2008.926431 |
| [7] |
Passos L A J, Oba Ramos C C, Rodrigues D, et al. Unsupervised non-technical losses identification through optimum-path forest[J]. Electric Power Systems Research, 2016, 140: 413-423. DOI:10.1016/j.epsr.2016.05.036 |
| [8] |
田力, 向敏. 基于密度聚类技术的电力系统用电量异常分析算法[J]. 电力系统自动化, 2017, 41(5): 64-70. Tian L, Xiang M. Abnormal power consumption analysis based on density-based spatial clustering of applications with noise in power systems[J]. Automation of Electric Power Systems, 2017, 41(5): 64-70. (in Chinese) |
| [9] |
Liu X, Nielsen P. Regression-based online anomaly detection for smart grid data[EB/OL]. (2016-06-18)[2020-10-01]. https://arxiv.org/pdf/1606.05781.pdf.
|
| [10] |
Jiang R, Tagaris H, Lachsz A, et al. Wavelet based feature extraction and multiple classifiers for electricity fraud detection[C]//IEEE/PES Transmission and Distribution Conference and Exhibition. October 6-10, 2002, Yokohama, Japan. IEEE, 2002: 2251-2256.
|
| [11] |
Badrinath Krishna V, Weaver G A, Sanders W H. PCA-based method for detecting integrity attacks on advanced metering infrastructure[M]. Quantitative Evaluation of Systems, 2015: 70-85.
|
| [12] |
Aharon M, Elad M, Bruckstein A M. K-SVD and its non-negative variant for dictionary design[C]//Optics and Photonics 2005. Proc SPIE 5914, Wavelets XI, San Diego, California, USA. 2005, 5914: 591411.
|
| [13] |
Hoyer P O. Non-negative sparse coding[C]//Proceedings of the 12th IEEE Workshop on Neural Networks for Signal Processing. September 6-6, 2002, Martigny, Switzerland. IEEE, 2002: 557-565.
|
| [14] |
王见, 陈义, 邓帅. 基于改进SVM分类器的动作识别方法[J]. 重庆大学学报, 2016, 39(1): 12-17. Wang J, Chen Y, Deng S. A gesture-recognition algorithm based on improved SVM[J]. Journal of Chongqing University, 2016, 39(1): 12-17. (in Chinese) |
| [15] |
李航. 统计学习方法[M]. 2版. 北京: 清华大学出版社, 2019. Li H. Statistical learning methods[M]. 2rd. Beijing: Tsinghua University Press, 2019. (in Chinese) |
| [16] |
Irish Social Science Data Archive. CER smart metering project-electricity customer behaviour trial [EB/OL]. (2012-12-30) [2021-03-05]. https://www.ucd.ie/issda/data/commissionforenergyregulationcer/.
|
| [17] |
McLaughlin S, Holbert B, Fawaz A, et al. A multi-sensor energy theft detection framework for advanced metering infrastructures[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(7): 1319-1330. |
| [18] |
Han W L, Xiao Y. Combating TNTL: non-technical loss fraud targeting time-based pricing in smart grid[C]//Cloud Computing and Security, 2016: 48-57.
|
| [19] |
Zanetti M, Jamhour E, Pellenz M, et al. A tunable fraud detection system for advanced metering infrastructure using short-lived patterns[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 830-840. |
 2022, Vol. 45
2022, Vol. 45


