2. 重庆大学 输配电装备及系统安全与新技术国家重点实验室,重庆 400044;
3. 国网湖南省电力有限公司,长沙 410029
2. State Key Laboratory of Power Transmission Equipment & System Security and New Technology, Chongqing University, Chongqing 400044, P. R. China;
3. State Grid Hunan Electric Power Co., Ltd., Changsha 410029, P. R. China
近年来,在应对能源危机和气候变化的背景下,以光伏、风电为代表的新能源机组的装机容量逐年增加[1-2]。截至2019年底,中国新能源发电装机容量达到4.1亿kW,占全国总装机容量的20.6%[3]。而高比例新能源的渗透无疑降低了电力系统的惯量,给电网的调频带来了严峻的挑战。
自动发电控制(AGC, automatic generation control)是一个维持电力系统频率稳定,确保电网安全可靠运行的重要研究领域[4-5]。在传统AGC控制中,电网通过感知系统频率偏差ΔF和联络线功率偏差ΔPT确定区域的总调节功率ΔPG,并且按照某种功率分配机制确定各AGC机组的调节功率[6]。而诸如以按装机容量比例或者按预设的分担系数进行功率分配的比例分配法以其简便高速的优点成为目前电网AGC功率分配的主流方法。为了进一步考虑AGC功率分配的经济性和安全性,基于优化模型的功率分配方法也被广泛提出。文献[7-9]>提出了一种以系统总调频费用最小为目标,充分考虑功率平衡、机组爬坡约束、出力上下限、线路功率系统频率偏差以及控制性能标准(CPS, control performance standard)指标约束的AGC功率分配模型。文献[10]引入新能源出力预测误差随机变量,基于随机规划理论来建立CPS标准下AGC机组动态优化调度的机会约束模型。文献[11]研究了光储联合系统参与系统频率响应辅助服务,并且分析了光储联合系统的经济性。文献[12]建立了风电参与能量—调频联合市场的优化决策模型,考虑了调频性能指标与偏差惩罚等机制,并求解了风电的最优投标策略。文献[13]为实现风水火多种类型资源在不同时间尺度上的配合,以发电、调峰、调频总成本最小为目标函数,兼顾系统、风电、梯级水电和火电的多种运行约束,构建了多能源协调优化调度模型。但是,上述文献提出的方法都是针对传统能源或者新能源的,并没有考虑在高比例新能源渗透下的常规AGC机组和新能源AGC机组的协调优化问题。随着火电机组的逐步退出和新能源机组的逐步增加,新能源势必参与AGC控制,因此,未来电网AGC控制必将是涉及风光水火多类型电源的协调优化控制问题。
针对上述问题,文中提出风光水火的多目标AGC协调控制模型。首先,基于某地区电网长期AGC统计数据,计算风光水火不同类型AGC机组的调频收益、调频速度以及调频精度;然后,参照华中电网2020年“两个细则”的相关要求,充分考虑对电网调频经济性和调频质量的要求以及不同类型的AGC机组的出力和网架潮流的耦合关系,建立风光水火多目标优化模型;最后,结合中国华中地区的电网网架结构,采用多目标粒子群进行模型求解,得到不同机组的AGC功率分配方案,验证文中提出方法的有效性和适用性。
1 基于“两个细则”的调频指标计算为确保发电机组向华中电网提供的电能质量,国家能源局华中监管局正式印发了《华中区域并网发电厂辅助服务管理实施细则》和《华中区域发电厂并网运行管理实施细则》[14-15]。“两个细则”对AGC机组参与调频辅助服务提出了严格的要求与考核的标准。因此,文中结合华中某地区电网的AGC长期统计数据,参照2020年华中电网“两个细则”对各项调频指标的计算方法,计算了该地区不同类型的AGC机组的平均调节速度和调节精度。之后,再计算AGC机组的调节速率指标k1和调节精度指标k2。最后,在k1和k2的基础上,计算各个AGC机组的单位补偿收益。
调节速度是机组响应上层调度指令的速率,表示AGC机组在调节期间,有功出力对时间的变化率,其单位为MW/min,其计算公式为
| $ V_{t}=\frac{P_{1}-P_{0}}{t_{1}-t_{0}}, $ | (1) |
式中:P0和P1分别是机组的调节初值和目标;t0和t1分别是机组开始调节时刻和达到调节目标的时刻。
调节精度是指机组进入稳定运行阶段之后,机组调节功率和目标指令的偏差。而这种偏差将不可避免地带来频率波动,影响电网调频质量,考虑到实际采样取值得到的AGC指令值和机组出力值都是离散的,调节偏差百分比的计算公式为
| $ e=\frac{\sum\limits_{i=1}^{N}\left|P_{1}-P_{i}\right|}{N}, $ | (2) |
式中:Pi表示机组功率的采样值;N表示采样点个数。
在计算出机组的调节速度和调节精度之后,根据2020年修订的华中电网“两个细则”的所给出的性能系数的计算公式,就可以进一步计算AGC机组的性能指标系数k1和k2[14-15]为
| $ \left\{\begin{array}{l} k_{1}=\frac{\Delta P \times T_{0} \times\left(P_{z}-P\right)}{\left|\Delta P_{z}\right| \times \Delta T \times\left|P_{z}-P\right|}, \\ T_{0}=T_{1}+\frac{\left|\Delta P_{z}\right| \times 60}{V_{t}}, \end{array}\right. $ | (3) |
| $ k_{2}=\left\{\begin{array}{cc} 0.01 / e & e>0.01 ,\\ 1 & e \leqslant 0.01。\end{array}\right. $ | (4) |
式中:P为调节过程实际出力,MW;ΔPz为调节过程最终指令初始出力,MW;ΔP为实际调节过程中的调节幅度,MW;ΔT为实际调节过程的调节时间,s;Pz为调节过程中任意一点的指令,P为该点对应的实际出力。T1为调节补偿时间,其中对于火电亚临界机组取0~30 s,超临界机组取0~20 s,水电取0~5 s。V0为机组调节速度,e为调节精度。
AGC按照单元(单机、全厂或多个发电厂组成的计划单元)参与所在控制区频率或者联络线偏差控制调节(ACE, area control error),对其贡献量进行补偿。定义其单位补偿收益为
| $ c=6 \times \beta \times k_{1} \times k_{2}, $ | (5) |
式中:k1为AGC的响应速度;k2为AGC的调节精度;β为指标系数,水电β=1,火电β=1.4。
2 风光水火多目标AGC功率分配模型在电网频率控制中,当确定系统的总调节功率之后,需要基于一定方法将总调节功率分配给各个AGC机组,并且给予其调频补偿。为了协调常规机组与新能源机组的出力,使得在调频补偿成本和网损成本最小化的同时,保证电网的调频质量要求。文中建立了综合考虑电网调频成本、网损成本、调频速度,以及调频精度的多目标有功优化模型。在给定约束下,通过对模型的多目标并行求解,确定风光水火各个场站的有功出力。
2.1 目标函数为了使各个AGC场站向电网提供高质量的调频服务,同时也进一步降低电网的调频成本和网损成本,文中以电网侧的调频和网损成本、电网的调频速度和调频精度作为有功优化模型的目标函数,为:
| $ \left\{ \begin{array}{l} \min {F_1} = \sum\limits_{i = 1}^{{N_w}} {{c_{w,i}}} {P_{w,i}} + \sum\limits_{i = 1}^{{N_P}} {{c_{P,i}}} {P_{P,i}} + \sum\limits_{i = 1}^{{N_H}} {{c_{H,i}}} {P_{H,i}} + \sum\limits_{i = 1}^{{N_T}} {{c_{T,i}}} {P_{T,i}} + \pi {P_{{\rm{loss}}}},\\ \max {F_2} = \frac{{\sum\limits_{i = 1}^{{N_w}} {{v_{w,i}}} {P_{w,i}} + \sum\limits_{i = 1}^{{N_P}} {{v_{P,i}}} {P_{P,i}} + \sum\limits_{i = 1}^{{N_H}} {{v_{H,i}}} {P_{H,i}} + \sum\limits_{i = 1}^{{N_T}} {{v_{T,i}}} {P_{T,i}}}}{{\sum\limits_{i = 1}^{{N_w}} {{P_{w,i}}} + \sum\limits_{i = 1}^{{N_P}} {{P_{P,i}}} + \sum\limits_{i = 1}^{{N_H}} {{P_{H,i}}} + \sum\limits_{i = 1}^{{N_T}} {{P_{T,i}}} }},\\ \min {F_3} = \frac{{\sum\limits_{i = 1}^{{N_w}} {{q_{w,i}}} {P_{w,i}} + \sum\limits_{i = 1}^{{N_P}} {{q_{P,i}}} {P_{P,i}} + \sum\limits_{i = 1}^{{N_H}} {{c_{H,i}}} {P_{H,i}} + \sum\limits_{i = 1}^{{N_T}} {{q_{T,i}}} {P_{T,i}}}}{{\sum\limits_{i = 1}^{{N_w}} {{P_{w,i}}} + \sum\limits_{i = 1}^{{N_P}} {{P_{P,i}}} + \sum\limits_{i = 1}^{{N_H}} {{P_{H,i}}} + \sum\limits_{i = 1}^{{N_T}} {{P_{T,i}}} }}。\end{array} \right. $ | (6) |
式中:cw, i、cP, i、cH, i、cT, i分别为相应第i台风、光、水、火机组辅助服务单位补偿费用;vw, i、vP, i、vH, i、vT, i分别为相应第i台风、光、水、火机组的平均调节速度;qw, i、qP, i、qH, i、qT, i分别为相应第i台风、光、水、火机组的平均调频精度;Pw, i、PP, i、PH, i、PT, i分别为相应第i台风、光、水、火机组参与二次调频的出力;π为电价;Ploss为网损。其中,目标F1为电网的调频成本和网损成本之和;目标F2为电网的平均调频速度;目标F3为电网的平均调频精度。
2.2 约束条件为了使电网可以实现安全、可靠、经济的运行,同时保证机组功率可以及时送出,避免电网出现功率阻塞以及功率不平衡导致的失负荷问题,设置以下约束条件如下所示。
1) 系统功率平衡约束。
| $ P_{W}+P_{P}+P_{H}+P_{T}-P_{D}-K \Delta f=0, $ | (7) |
式中:PD为预测负荷;KΔf为一次调频量;K为控制区单位调节功率(含机组和负荷的单位调节功率);Δf为系统频率相对初始频率的偏差。
2) 调频功率约束。
| $ P_{\mathrm{ACE}}=\sum\limits_{i=1}^{N_{w}} P_{w, i}+\sum\limits_{i=1}^{N_{P}} P_{P, i}+\sum\limits_{i=1}^{N_{H}} P_{H, i}+\sum\limits_{i=1}^{N_{T}} P_{T, i}, $ | (8) |
式中,PACE是通过计算区域控制偏差ACE所求到的系统总调节功率。
3) 机组出力约束。
| $ \left\{\begin{array}{l} \underline{P}_{w, i} \leqslant P_{w, i} \leqslant \bar{P}_{w, i} \text {,}\\ \underline{P}_{P, i} \leqslant P_{P, i} \leqslant \bar{P}_{P, i} \text {,}\\ \underline{P}_{H, i} \leqslant P_{H, i} \leqslant \bar{P}_{H, i} \text {,}\\ \underline{P}_{T, i} \leqslant P_{T, i} \leqslant \bar{P}_{T, i} \text {,} \end{array}\right. $ | (9) |
式中:
4) 线路传输功率限制约束。
| $ \left\{\begin{array}{l} -1 \leqslant \rho_{l} \leqslant 1 \text {,}\\ \rho_{1}=\frac{P_{l}}{P_{l}^{\max }}\text {,} \end{array}\right. $ | (10) |
式中:ρl为线路的负载率;Pl为线路功率;Plmax为第l条支路的最大线路传输功率,为了充分考虑网架的送出能力,避免网络发生功率阻塞,线路功率应该始终满足如上约束条件。
2.3 直流潮流为了实现模型的快速求解,考虑到文中研究对象是高压配电网,因此文中基于直流潮流求解线路功率和网损。
在直流潮流中,假设统的节点数为n,PQ节点数为m,m+1及其后的节点均为PV节点,第n个节点是平衡节点。已知其节点注入的有功功率的交流潮流方程为
| $ P_{i}=U_{i} \sum\limits_{j=1}^{n} U_{j}\left(G_{i j} \cos \delta_{i j}+B_{i j} \sin \delta_{i j}\right), (i=1, 2, \cdots, n-1) 。$ | (11) |
根据电力系统运行特点,当节点电压在额定电压附近时,sinδij=sin(δi-δj)≈δi-δj,cosδij≈1,同时考虑在超高压网络中, 线路电阻比电抗小得多, 电阻可以忽略,因此潮流方程可以被简化为
| $ P_{i n j}=B_{i j}\left(\delta_{i}-\delta_{j}\right), (i=1, 2, \cdots, n-1), $ | (12) |
式中,B为系统的电抗矩阵,支路两端相角差很小,将式(12)写成矩阵形式,可以得到相角的计算公式[16]为
| $ \boldsymbol{\theta}=\boldsymbol{B}^{-1} P_{i n j}\text { 。} $ | (13) |
在得到系统的相角矩阵θ之后,可以求得线路的有功功率和系统网损[17]为
| $ \left\{\begin{array}{l} P_{i j}=\frac{\theta_{i}-\theta_{j}}{x_{i j}},\\ P_{\text {loss }}=\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{H} \boldsymbol{\theta},\end{array}\right. $ | (14) |
式中,H是Ploss关于θ的海森矩阵,为:
| $ \left\{\begin{array}{l} P_{i j}=\frac{\theta_{i}-\theta_{j}}{x_{i j}} ,\\ P_{\mathrm{loss}}=\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{H} \boldsymbol{\theta},\end{array}\right. $ | (15) |
| $ \left\{\begin{array}{l} H_{i j}=-g_{i j} k_{i j}, i \neq j,\\ H_{i i}=\sum\limits_{i=1}^{n} \sum\limits_{n} g_{i j} k_{i j}, i=j 。\end{array}\right. $ | (16) |
式中:gij为支路电导;kij为折算到i侧的非标准变压器变比值。
2.4 模型求解文中采用多目标粒子群算法(multi objective particle swarm optimization algorithm, MOPSO)对模型进行求解,粒子群算法是一种模拟鸟类捕食的群体智能算法[18],MOPSO在优化求解过程中,每个粒子的位置代表问题的可行解, 粒子的速度决定了粒子移动的方向和距离,粒子的适应函数值可以带入模型求解得到。
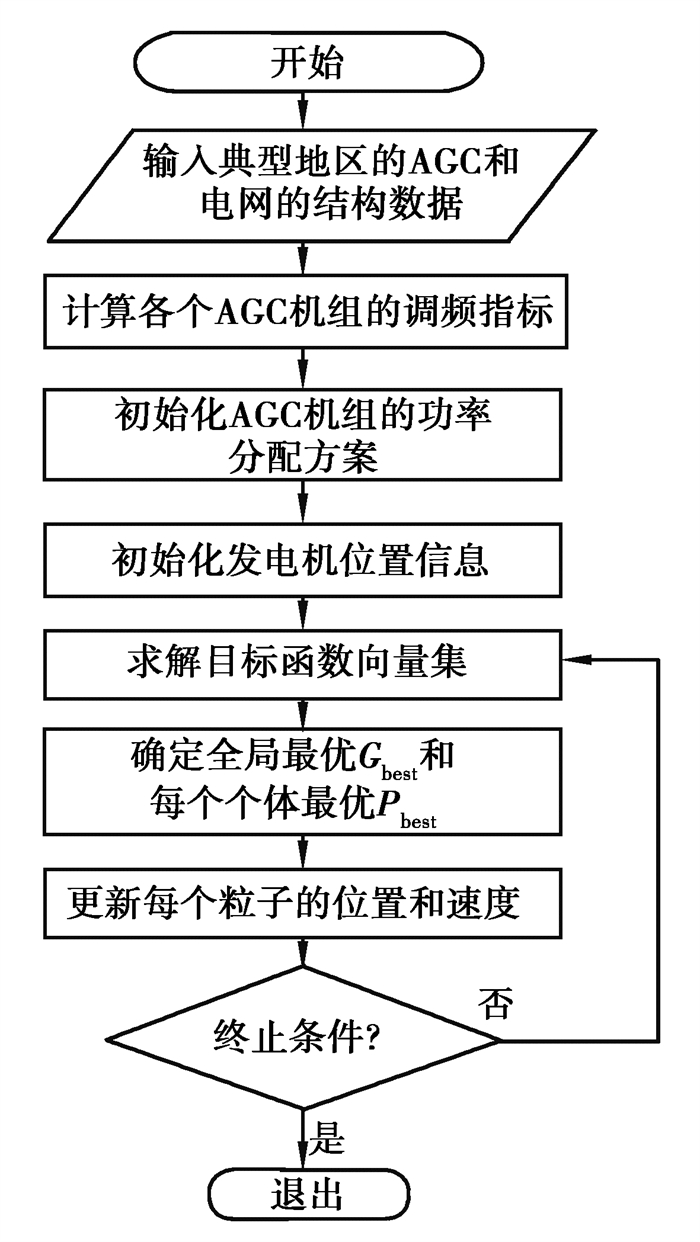
在多目标优化求解中,当以多个目标为搜索指标时,往往会出现其解集互不支配的现象。在此种情况下,很难对互不支配的解集做出评定,因此将这些互不支配的解集称为非劣解[19-20],并且将这些非劣解归到一个集合,称为外部档案集,将其作为多目标粒子群全局最优的来源。文中采用多目标粒子群模型求解流程如图 1所示,优化求解的步骤[21]为:
|
图 1 模型求解的流程图 Fig. 1 Flow chart of model solving |
Step1. 输入典型地区AGC和网架结构数据;
Step2. 计算每个机组的调频性能指标,包括单位调频收益、平均调频精度和调节速度;
Step3. 设定系统和算法参数,初始化每个粒子的速度、位置、个体最优和全局最优;
Step4. 将每个粒子代表的决策方案带入模型计算系统的经济成本、调频速度和调频精度,得到其目标函数向量集;
Step5. 添加非劣解到外部档案,并且进行维护更新,再采用自适应网格法从外部档案集中选择Gbest作为本次的全局最优解,通过每个粒子前后两次目标向量的帕累托支配关系,选择支配解作为粒子新的个体最优Pbest;
Step6. 更新粒子新的速度和位置,得到新的决策方案;
Step7. 判断是否达到最大迭代次数,若迭代次数达到终止条件,则停止搜索输出结果,否则转向Step4。
3 算例分析 3.1 数据和系统为了验证文中所提方法的有效性,根据中国中部某内陆地区2020年涵盖500 kV、220 kV、110 kV三级电压的电源结构和网架结构等信息,仿真分析新能源AGC和常规AGC的协调优化策略。2020年该区域有3座火电厂和1座水电厂通过500 kV线路为该地区供电,5个光伏和2个风电场通过220 kV或者110 kV线路并网。同时文中采集整理了该地区的风光水火机组的单位调频成本、平均调频速度、平均调频精度如表 1所示。
| 表 1 各场站的数据 Table 1 Data from different stations |
由表 1可知,在风光水火中,水电机组单位调频成本最低,调节速度较快;火电机组调频成本较高,调频精度较高;新能源机组调频成本介于水电和火电之间,调频速度和调频精度一般。因此,如何权衡系统调频性能指标,综合考虑调频成本、调频速度和调频精度,协调各种不同类型机组的调频特性,科学合理地确定各个场站的调节功率是文中研究重点。
3.2 比例分配法和优化法的对比分析在现行的AGC控制中,当通过频率和联络线偏差计算出ACE,再通过ACE按照计算出电网功率缺额之后,经常采取按照各场站总装机容量比例分配区域有功调节功率。为了验证模型的有效性,文中设置以下2个算例进行了对比分析。
Case1: 当电网的总调节功率为300 MW时,各个场站按照装机容量比例进行功率分配;
Case2: 当电网的总调节功率为300 MW时,按照文中提出的模型进行功率分配。
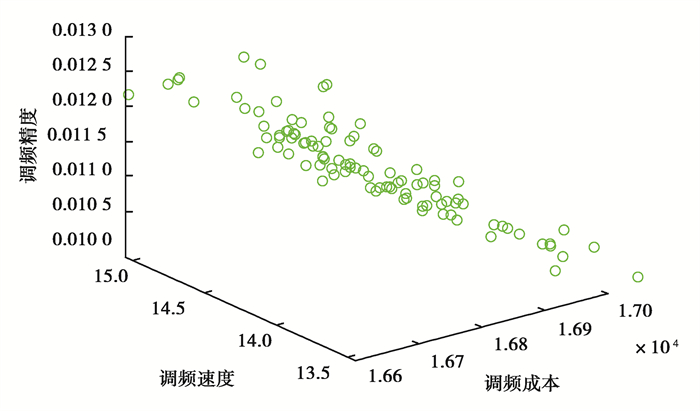
基于岳阳地区的网架模型、机组负荷数据和仿真运行场景,采用配置为corei5-9400系列CPU、2.90 GHz主频、16 GB内存、Win10 64bit操作系统的计算机,基于Matlab R2019a软件编程,采用多目标粒子群算法对模型进行求解,得到帕累托最优解集如图 2所示。
|
图 2 帕累托最优解集 Fig. 2 Pareto optimal solution set |
在得到帕累托最优解集之后,采取权值系数法,从最优解集中选取和确定模型的最优解,由此可以得到本模型求解出的AGC总调节功率分配方案为图 3所示。
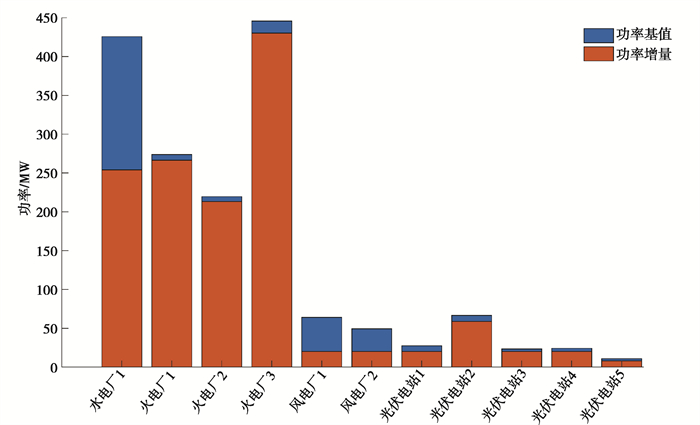
|
图 3 功率分配方案 Fig. 3 Power allocation scheme |
在图 3中,功率基值为系统稳定运行,没有调频需求时的各个机组的出力,功率增量为电网感知到系统频率偏差的存在,计算出系统总调节功率之后,按照文中提出的方法进行功率分配所计算出的功率增量。
从图 3可知,水电的单位调频成本较低,且调节速度较快,调频质量较好,因此水电在功率分配时水电占了很大比例。水电的出力上限是500 MW,模型中计算的结果水电还存在很大的出力空间,这是为了防止网络传输功率阻塞,将其余的调频量分别由火电和新能源承担,通过协调水电、火电和新能源的控制策略,在保证调频经济性和质量的同时,兼顾了网架功率外送能力和线路的传输能力。
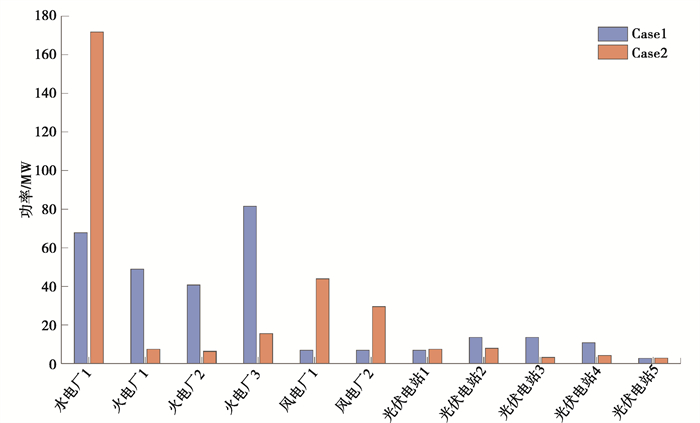
按照装机容量所占比例进行功率分配的结果为图 4所示,同时给出2种不同方案的指标对比结果如表 2所示,其中,表 2还给出了Case2相对于Case1的各项指标的增量百分比Inc。
|
图 4 Case1和Case2功率分配方案对比 Fig. 4 Comparison of Power allocation scheme between Case1 and Case2 |
| 表 2 Case1和Case2调频结果对比 Table 2 Comparison of results of regulating frequency between Case1 and Case2 |
由表 2可知,通过文中的风光水火多目标协调优化模型进行AGC功率分配,使调频成本和网损成本分别下降9.56%和13.87%。调频成本下降的主要原因是通过模型间接引入市场竞争的机制,电网选择了大量价格实惠的水电以及新能源以应对功率缺额,并通过合理调节各个机组的出力比例,降低了网损成本,使电网侧运行更加经济。另外,水电调频占比的提升,也进一步提升了系统的平均调频速度,使得电网的调频速度由13.70 MW/min提升到17.83 MW/min。但是,为了降低成本和提升调频速度,火电出力比例降低,使得系统的调频精度也有所下降。另外,也可以看出,Case1的线路最大负载率为1.044 7,超出线路最大传输功率的限制,而Case2却在可控范围内,并且网架平均负载率也比Case1低6.6%。二者的区别是因为文中提出的模型充分考虑了电网的实际网架结构和功率送出能力,通过合理协调新能源和火电机组出力,为所在区域电网提供功率支撑,分担高负载率线路的功率传输压力,保证线路传输功率都在允许范围内,而传统的比例分配法脱离实际网架结构,根本无法兼顾线路传输能力,容易导致发生网络功率阻塞。
3.3 不同调节方案下的结果对比为了验证文中提出模型的适用性,文中设置2个算例对机组功率分配方案进行更深入地分析。
Case3: 当电网计算出总调节功率为300 MW时,按照文中提出的模型进行功率分配,上调各机组出力;
Case4: 当电网计算出总调节功率为-300 MW时,按照文中提出的模型进行功率分配,下调各机组出力。
按照上述的方法进行计算,得到不同调节方案下机组的调节功率分配方案如图 5和表 3所示。
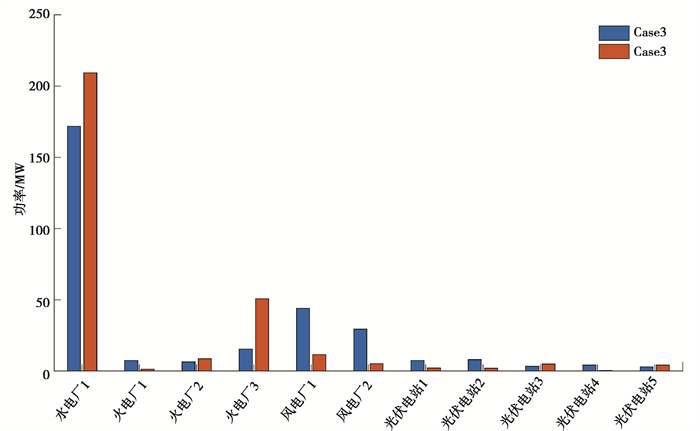
|
图 5 Case3和Case4功率方案对比 Fig. 5 Comparison of Power allocation scheme between Case3 and Case4 |
| 表 3 Case3和Case4调频结果对比 Table 3 Comparison of results of regulating frequency between Case3 and Case4 |
由表 3可知,当总调节功率相同,调节方向不一样时,其调频成本和调频精度的变化不大,但是由于改变了各个机组的功率分配比例,引起了网损成本和调频速度的显著变化。在下调时,通过合理地配置机组的出力,使系统的网损成本下降了21.20%,调频速度上升了14.60%。同时,其线路最大负载率也在允许范围内,由于各个机组出力减少,使线路的平均负载率降低了36.23%。因此,文中提出的方法具有一定的适用性,不仅适用于功率上调时,也适用于功率下调时,在降低电网运行成本的同时,还保证了系统的调频质量,始终都有较为优质的调频资源投入电网,保证了电网的安全可靠健康运行。
4 结束语针对现有采用比例分配方法进行功率分配的不足,文中以调频和网损成本最优、调频速度最快、调频精度最高为目标,建立了风光水火多目标协调优化模型,充分考虑到了电网的功率平衡、线路传输功率等约束。同时,结合华中某地区电网进行了算例分析,验证了文中方法的优越性和有效性,并且得出结论如下:
1) 对比传统的方法,文中提出的模型可以在保证调频质量的同时极大降低电网的调频和网损成本。
2) 基于优化模型的调频方法,可以充分考虑网架结构和机组出力特性,避免网络出现功率阻塞,保证电网安全健康运行。
3) 在含风光水火的AGC协调优化中,火电机组调频精度高,水电机组调频速度快,新能源分布独立接入,为所在区域电网提供功率支撑,减轻高负载线路功率传输压力,避免网络功率阻塞。
| [1] |
汪宁渤, 马明, 强同波, 等. 高比例新能源电力系统的发展机遇、挑战及对策[J]. 中国电力, 2018, 51(1): 29-35, 50. Wang N B, Ma M, Qiang T B, et al. High-penetration new energy power system development: challenges, opportunities and countermeasures[J]. Electric Power, 2018, 51(1): 29-35, 50. (in Chinese) |
| [2] |
程耀华, 张宁, 王佳明, 等. 面向高比例可再生能源并网的输电网规划方案综合评价[J]. 电力系统自动化, 2019, 43(3): 33-42, 57. Cheng Y H, Zhang N, Wang J M, et al. Comprehensive evaluation of transmission network planning for integration of high-penetration renewable energy[J]. Automation of Electric Power Systems, 2019, 43(3): 33-42, 57. (in Chinese) |
| [3] |
中国电力企业联合会. 中国电力行业年度发展报告2020[R]. 北京: 中国电力企业联合会, 2020. China Federation of Electric Power Enterprises. Annual development report of China electric power industry 2020[R]. Beijing: China Electric Power Enterprise Federation, 2020. |
| [4] |
Ibraheem N, Kumar P, Kothari D P. Recent philosophies of automatic generation control strategies in power systems[J]. IEEE Transactions on Power Systems, 2005, 20(1): 346-357. DOI:10.1109/TPWRS.2004.840438 |
| [5] |
Jaleeli N, VanSlyck L S, Ewart D N, et al. Understanding automatic generation control[J]. IEEE Transactions on Power Systems, 1992, 7(3): 1106-1122. DOI:10.1109/59.207324 |
| [6] |
颜伟, 赵瑞锋, 赵霞, 等. 自动发电控制中控制策略的研究发展综述[J]. 电力系统保护与控制, 2013, 41(8): 149-155. Yan W, Zhao R F, Zhao X, et al. Review on control strategies in automatic generation control[J]. Power System Protection and Control, 2013, 41(8): 149-155. (in Chinese) |
| [7] |
颜伟, 王聪, 毛艳丽, 等. 基于OPF的互联电网AGC优化模型[J]. 电力系统保护与控制, 2015, 43(23): 35-40. Yan W, Wang C, Mao Y L, et al. AGC optimal model based on OPF technology for interconnected power grid[J]. Power System Protection and Control, 2015, 43(23): 35-40. (in Chinese) DOI:10.7667/j.issn.1674-3415.2015.23.006 |
| [8] |
Yan W, Zhao R, Zhao X, et al. Dynamic optimization model of AGC strategy under CPS for interconnected power system[J]. International Review of Electrical Engineering, 2012, 7(5): 5733-5743. |
| [9] |
Zhao R F, Yan W, Zhang J G, et al. Dynamic coordination optimization model of regional and provincial AGC unit control for ultra-high voltage line interconnected power system[C]//2018 International Conference on Power System Technology (POWERCON). November 6-8, 2018, Guangzhou, China. IEEE, 2018: 3497-3506.
|
| [10] |
赵霞, 张荣荣, 赵瑞锋, 等. CPS标准下AGC机组动态优化调度的改进模型[J]. 电工技术学报, 2016, 31(5): 99-106. Zhao X, Zhang R R, Zhao R F, et al. An extended dynamic optimization model for AGC generators dispatch under CPS[J]. Transactions of China Electrotechnical Society, 2016, 31(5): 99-106. (in Chinese) DOI:10.3969/j.issn.1000-6753.2016.05.013 |
| [11] |
金楚, 周博, 艾小猛, 等. 考虑光储联合系统参与频率响应的储能容量优化配置方法[J]. 全球能源互联网, 2018, 1(3): 361-368. Jin C, Zhou B, Ai X M, et al. Optimal configuration of energy storage capacity with PV-storage system participating in frequency regulation service[J]. Journal of Global Energy Interconnection, 2018, 1(3): 361-368. (in Chinese) |
| [12] |
崔达, 史沛然, 陈启鑫, 等. 风电参与能量—调频联合市场的优化策略[J]. 电力系统自动化, 2016, 40(13): 5-12. Cui D, Shi P R, Chen Q X, et al. Optimal strategy for wind power bidding in energy and frequency regulation markets[J]. Automation of Electric Power Systems, 2016, 40(13): 5-12. (in Chinese) DOI:10.7500/AEPS20151112004 |
| [13] |
葛晓琳, 金言, 夏澍, 等. 面向调峰调频需求的风水火电协调优化调度[J]. 电网技术, 2019, 43(11): 3917-3926. Ge X L, Jin Y, Xia S, et al. A coordinated optimization scheduling of wind-hydro-thermal power system based on requirement of peak load and frequency regulation[J]. Power System Technology, 2019, 43(11): 3917-3926. (in Chinese) |
| [14] |
国家能源局华中监管局. 华中区域发电厂并网运行管理实施细则[R]. 武汉: 国家能源局华中监管局, 2020. Central China Regulatory Bureau of State Energy Administration. Implementation rules for grid connected operation management of power plants in Central China [R]. Wuhan: Central China Regulatory Bureau of State Energy Administration, 2020. (in Chinese) |
| [15] |
国家能源局华中监管局. 华中区域并网发电厂辅助服务管理实施细则[R]. 武汉: 国家能源局华中监管局, 2020. Central China Regulatory Bureau of State Energy Administration. Implementation rules for auxiliary service management of grid connected power plants in Central China [R]. Wuhan: Central China Regulatory Bureau of State Energy Administration, 2020. (in Chinese) |
| [16] |
刘连光, 张晓晴, 蒋智化, 等. 直流配电网潮流算法与电压分布研究[J]. 科学技术与工程, 2015, 15(32): 42-48. Liu L G, Zhang X Q, Jiang Z H, et al. Research on power flow calculation and voltage profile in DC distribution network[J]. Science Technology and Engineering, 2015, 15(32): 42-48. (in Chinese) DOI:10.3969/j.issn.1671-1815.2015.32.008 |
| [17] |
刘焕志, 李扬, 柏瑞, 等. 区域电力市场中实用网损计算及分摊的研究[J]. 电网技术, 2003, 27(3): 63-67, 77. Liu H Z, Li Y, Bai R, et al. Practical calculation and allocation of transmission losses in regional electricity market[J]. Power System Technology, 2003, 27(3): 63-67, 77. (in Chinese) DOI:10.3321/j.issn:1000-3673.2003.03.016 |
| [18] |
Ganjehkaviri A, Mohd Jaafar M N. Multi-objective particle swarm optimization of flat plate solar collector using constructal theory[J]. Energy, 2020, 194: 116846. DOI:10.1016/j.energy.2019.116846 |
| [19] |
Sierra M R, Coello Coello C A. Improving PSO-based multi-objective optimization using crowding, mutation and ∈-dominance[M]//Lecture Notes in Computer Science. Berlin, Heidelberg: Springer Berlin Heidelberg, 2005.
|
| [20] |
Li X D. Better spread and convergence: particle swarm multiobjective optimization using the maximin fitness function[C]//6th Annual Genetic and Evolutionary Computation Conference (GECCO 2004). Springer Berlin Heidelberg, 2004.
|
| [21] |
Lin Q Z, Li J Q, Du Z H, et al. A novel multi-objective particle swarm optimization with multiple search strategies[J]. European Journal of Operational Research, 2015, 247(3): 732-744. DOI:10.1016/j.ejor.2015.06.071 |
 2022, Vol. 45
2022, Vol. 45

