b. 天津大学 建筑工程学院,天津 300072
b. School of Civil Engineering, Tianjin University, Tianjin 300072, P. R. China
为了缓解城市交通拥堵,地铁隧道的建设已经成为城市化的重要组成部分,而基坑开挖对临近地铁隧道产生的影响也成为工程中不可忽视的问题[1]。在基坑开挖过程中,周围土体应力状态发生改变,相邻隧道会因为卸载效应而受损[2]。因此,为了保证地铁隧道的安全和正常使用,对隧道位移进行可靠准确的评估至关重要。已有的研究表明,隧道变形受地质条件、施工条件、开挖深度、隧道相对位置、隧道衬砌刚度、支护结构位移等因素的影响[3-7]。现有研究主要是通过数值模拟和模型试验对临近基坑开挖引起隧道变形的机理进行分析。王卫东等[8]利用数值模型对实际施工工况进行模拟,动态分析了施工过程中开挖卸荷对地铁隧道的影响。陈仁朋等[9]进行了一系列离心试验,研究了干砂地层中基坑开挖对旁侧隧道影响及隔断墙保护作用。Chen等[10]基于有限元法(FEM),认为隧道的弯矩和位移与临近基坑开挖的卸荷效果和周围土体的位移有关,提出了相应的保护措施。实际工程中,将隧道的最大侧向变形作为评价隧道安全性和适用性的标准。由于涉及多元变量问题,无法建立精确的预测模型,通常采用回归方法进行统计分析[11]。Zheng等[12]采用传统多项式回归(PR)模型的经验方法评价隧道位移。然而,PR模型在计算上是不切实际的,其准确性高度依赖模型假设[13],且PR模型的建立和优化过程比较复杂,有必要建立一个更加简单的模型来高效预测结果。
人工神经网络(ANN)是回归方法和统计方法的一种替代方法,其中,最常用的算法是BP算法,它是一种误差逆传播型学习算法。反向传播神经网络(BPNN)模型由多层神经元组成,按照相应的规律有序连接,具有很强的非线性映射能力[14]。高浪等[15]综述了ANN在各种岩土工程问题中的应用,说明其独特的优点。例如,BPNN模型可以用来预测基坑开挖过程中挡土墙的最大位移、边坡稳定性、单桩竖向极限承载力以及由隧道开挖引起的地面沉降等,在岩土工程中具有广阔的应用前景[15-18]。
文中研究的目的是运用BPNN技术预测隧道响应以及评价输入变量的敏感性。采用考虑小应变刚度效应的土体硬化模型进行有限元分析,通过数值模拟得到了一系列关于隧道变形的数据,并利用生成的数据库和收集的17个工程案例对BPNN模型进行准确性验证。
1 有限单元模型隧道变形受多种因素影响,在预测模型中考虑所有影响因素会使模型的建立复杂化。Zheng等[12]指出基坑宽度、土体条件、挡土墙刚度、施工工艺等因素与支护结构最大水平位移δRmax直接相关,可以将这些因素考虑在对支护结构的变形影响中,用支护结构最大水平位移δRmax间接反映这些因素对隧道变形的影响,从而简化分析过程。因此,文中仅考虑开挖深度He、隧道中心的埋深Ht、隧道中心至支护结构的水平距离Lt、支护结构的最大水平位移δRmax这4种因素对隧道变形的影响。表 1显示了数值模拟分析中使用的变量,共考虑了360个案例,通过调整支撑的刚度来控制支护结构的最大水平位移。需要注意的是,将上述4个因素转换成3个无量纲输入参数用于生成BPNN模型,即:相对埋深x1(Ht/He),隧道与支护结构之间的相对水平距离x2(Lt/He),支护结构的最大位移x3(δRmax)。
| 表 1 参数列表 Table 1 Parameters of hypothetical cases |
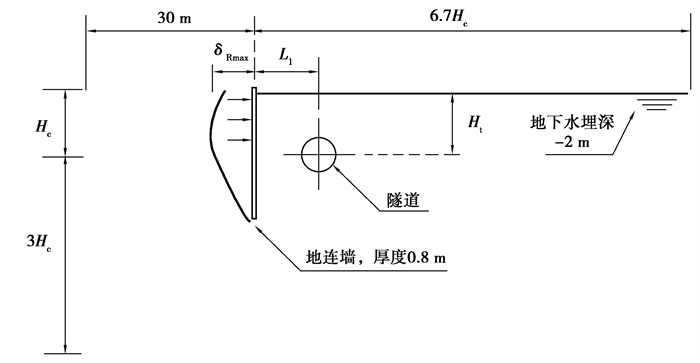
采用有限元软件Plaxis 3D进行数值模拟,建立一个理想化的数值模型来生成一系列数据,其结构和网格如图 1所示。土体采用考虑小应变情况下,应力应变关系的模型(小应变土体硬化模型),且土体与支护结构之间的相互作用采用界面单元进行模拟,该界面单元具有9个高斯点,每个节点有3个自由度,支持节点对之间的相对位移,界面强度参数取相邻土体的0.65倍。模型的边界条件为:模型顶面为自由面,无约束;模型底面每个方向均约束;模型4个侧面均只约束法向,其余方向自由无约束。Zheng等[12]已对模型验证过程进行详细介绍,由于篇幅限制,文中不再赘述。
|
图 1 数值模型 Fig. 1 Numerical model |
设隧道外径为6.2 m,管片厚度为0.35 m,隧道衬砌的杨氏模量为34.5 GPa,泊松比为0.2,土层为典型的粉质黏土,与前人研究所采用的黏土相似[12, 19]。与基坑开挖相邻的隧道衬砌在水平和垂直方向上均发生变形,但水平变形比垂直变形更加显著,研究主要关注的是隧道的水平响应。支护结构深度与开挖深度的比值为2.0,基坑宽度为60 m,由于模型的对称性,只建立了整个模型的1/2,故水平长度取30 m,为了避免边界效应,将基坑外部模型的深度和宽度分别设置为开挖深度的3倍和6.7倍[19]。每种工况中的有限元网格由约5 000个元素和8 000个节点组成。
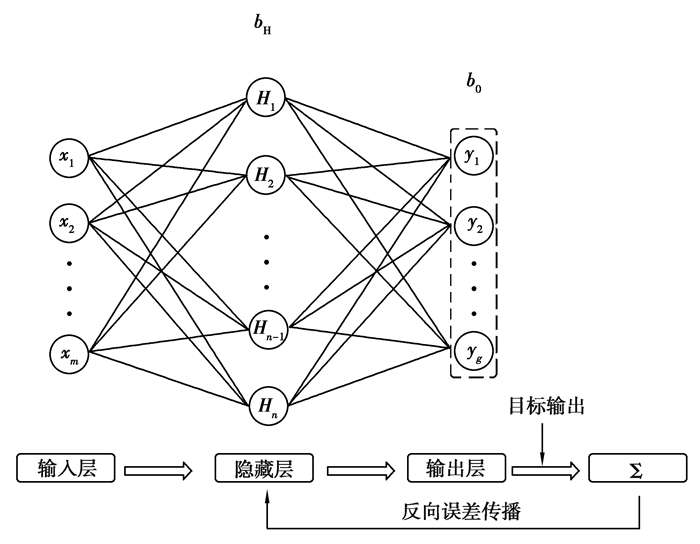
2 BPNN的原理BPNN是一个自适应非线性动态系统,由许多简单的基本成分所组成,即神经元。BPNN最大的优点是能够解决传统数学建模不能解决的复杂问题。图 2为BPNN的三层结构。其中,第一层为输入层,第二层为隐藏层,最后一层为输出层。层与层之间采用全互连方式,同一层之间不存在相互连接,隐藏层数目由待解决问题决定,可以有一个或多个[14]。BPNN包含2个过程:正向传播和反向繁衍。在正向传播阶段,数据从输入层经过隐含层处理传播到输出层。中间层神经元的值从前一层神经元扩散出来,数据加权后,通过一定的函数运算得到新的值,将中间层传播到下一层。在误差反向传播阶段,如果输出层不能得到期望的目标值,那么目标值与预测值之间的误差从输出层反向传播,不断修正权值和偏差值,目的是使目标值与预测值之间残差的平方和最小化[21],如式(1)所示:
|
图 2 BPNN的结构 Fig. 2 Architecture of the BPNN |
| $ E = \sum\limits_{l = 1}^{{N_{\rm{s}}}} {\sum\limits_{k = 1}^{{N_0}} {{{\left( {{{\hat y}_{lk}}\left( {{x_l}} \right) - {y_{lk}}} \right)}^2}} } ,$ | (1) |
式中:Ns为样本的数量;N0为输出的数量;
输入变量和输出变量之间的关系可以表示为[12]:
| $ y=f_{2}\left\{b_{0}+\sum\limits_{k=1}^{n}\left[W_{k} f_{1}\left(b_{H K}+\sum\limits_{i=1}^{m} W_{i k} P_{i}\right)\right]\right\},$ | (2) |
式中:b0为输出层的偏差;Wk为输出层的权重;bHK为隐藏层的偏差;Wik为隐藏层的权重;Pi为第i个输入变量;f(·)为激励函数,通常使用S型函数,如log-sigmoid函数,可表示为
| $ f(v)=\frac{1}{1+e^{-v}} 。$ | (3) |
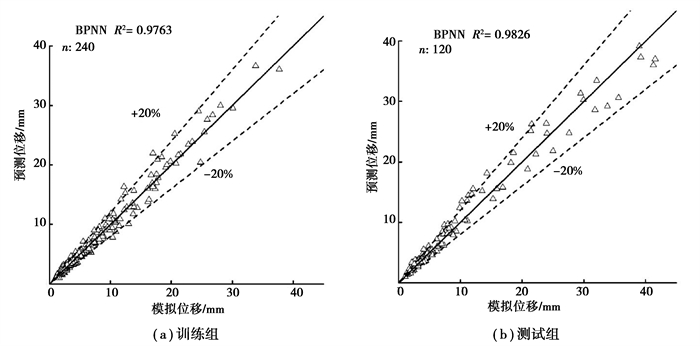
在已生成的数据库中,随机选择2/3的数据(240个实例)作为训练组,选择另外1/3(120个实例)作为测试组[13]。通过训练组正向传播与反向繁衍得到多维非线性复杂关系式,训练好的网络已经具备了计算隧道衬砌变形的能力,为了验证训练效果,在此关系式的基础上利用测试组进一步检测BPNN模型的准确性。图 3为有限元软件模拟位移与BPNN模型预测位移间的相互关系,显示了BPNN模型的预测性能,采用相关系数(R2)来定量的评估BPNN模型的准确性。可以看出,模拟值与预测值的相关曲线为过原点且与两坐标轴呈45°的直线,训练组和测试组中BPNN模型的R2分别为0.976 3和0.982 6,说明模拟值与预测值之间具有较好的一致性,BPNN模型可以准确预测隧道衬砌的变形。
|
图 3 BPNN模型的预测性能 Fig. 3 Performances of the BPNN model |
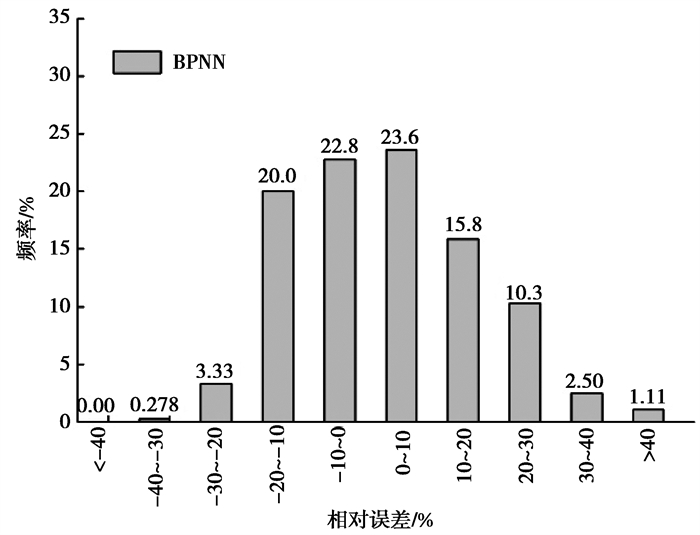
另一个重要的评价指标为相对误差,即隧道最大侧向变形的预测值和目标值之差与目标值的比值。图 4为BPNN模型的相对误差直方图,可以看出,BPNN模型的预测误差都在-30% ~ +30%,只有个别数据的相对误差大于40%,且超过80%的数据在-20% ~ +20%的相对误差范围,由工程经验可知,这一误差可以接受,满足精度要求,说明BPNN具有较好的预测能力。进一步分析可知,相对误差的大小与隧道最大侧向变形值有关,变形值越小的数据相对误差越大,说明BPNN对于预测位移量较小的工况难以确保精确性,位移量较大时预测结果精度高。
|
图 4 BPNN模型的相对误差直方图 Fig. 4 Histogram of the relative errors for the BPNN model |
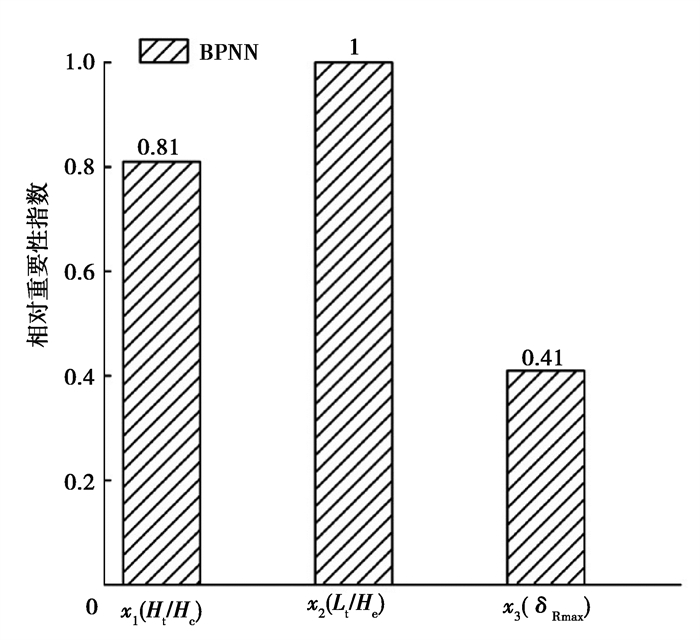
BPNN模型还可以通过计算各输入变量的偏导数来评估各输入变量对输出变量的相对贡献程度,根据计算结果分析各因素的相对重要性。图 5为各变量的重要性指数,体现了各变量对输出结果的影响程度。输入变量x1(Ht/He)和x2(Lt/He)的相对重要性指数分别为0.81和1.0,说明隧道相对埋深和隧道与支护结构相对水平距离对输出变量δTmax有显著的影响。在实际工程中,隧道水平变形比相对基坑位置更为敏感,在基坑设计阶段,尤其需要关注隧道与基坑的相对水平距离,当两者水平距离较小时,需要进一步优化基坑支护方案,降低基坑在开挖过程中对隧道变形的影响。
|
图 5 重要性指数 Fig. 5 Importance index of each variabl |
Zheng等[12]分析了由临近基坑开挖引起隧道位移的14个案例。文中收集了另外3个案例作为扩展数据库,用于验证所提出的BPNN模型,如表 2所示。
| 表 2 与既有隧道相邻的基坑开挖案例的扩展数据库 Table 2 An extended database of excavation cases adjacent to existing tunnels |
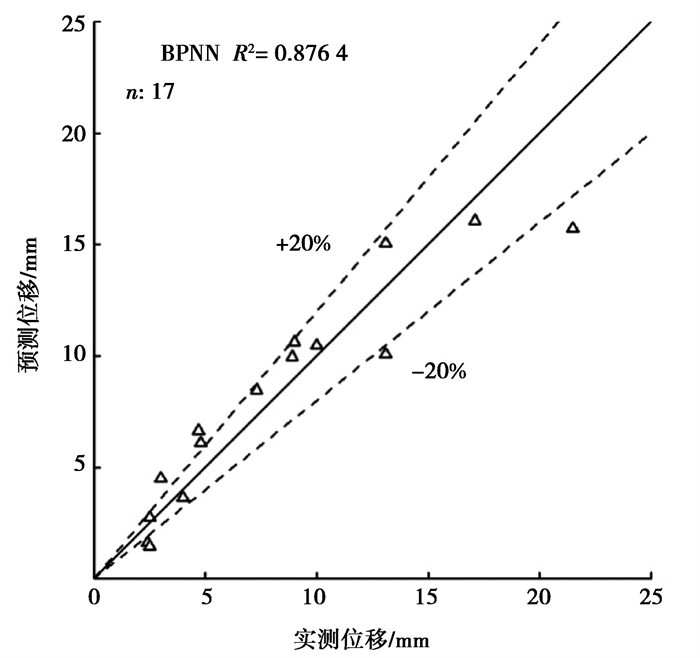
图 6为BPNN模型预测变形值与实测变形值的对比图,二者之间趋于线性相关关系。可以看出,案例中BPNN模型的相关系数R2值为0.8764,超过70%的数据在-20% ~ +20%的相对误差范围,只有个别数据相对误差较大。说明预测值与实测值比较吻合,具有较高的可信度,证明了BPNN模型能够有效预测隧道变形。文中所选取的17个工程案例主要来源于天津、上海、台北等沿海城市,这些地区的土质以软黏土为主,文中所用预测模型对于软黏土地区的工程适用性较好。
|
图 6 BPNN模型对17个案例的预测能力 Fig. 6 Performances of the BPNN model for 17 case histories |
采用有限元数值模拟,分析基坑开挖对临近地铁隧道变形的影响,在此基础上得到完备的数据库来训练检测BPNN模型,根据此模型进一步评估不同输入变量的相对重要性。通过对17个实际工程案例实测数据与BPNN模型预测结果进行对比,进一步验证BPNN模型的准确性。得到以下结论:
1) 通过数值模拟计算获得的数据库进行训练得到预测隧道变形的BPNN模型,通过监测数据验证具有较高的准确性,超过80%的BPNN模型预测结果在±20%的相对误差范围。
2) 通过BPNN模型对输入参数重要性分析发现,隧道相对埋深(Ht/He)和隧道与支护结构的相对水平距离(Lt/He)对隧道的最大水平位移δTmax有显著影响。在工程设计中应合理安排隧道的相对位置,达到最优的变形控制作用。
3) BPNN模型具有很强的构建复杂非线性输入输出关系的能力。BPNN模型预测结果与实测数据具有很好的一致性,证明BPNN模型能够有效预测临近基坑开挖引起的隧道变形,可以为实际工程提供一种简单直接的预测方法。
| [1] |
郑刚, 朱合华, 刘新荣, 等. 基坑工程与地下工程安全及环境影响控制[J]. 土木工程学报, 2016, 49(6): 1-24. Zheng G, Zhu H H, Liu X R, et al. Control of safety of deep excavations and underground engineering and its impact on surrounding environment[J]. China Civil Engineering Journal, 2016, 49(6): 1-24. (in Chinese) |
| [2] |
丁智, 张霄, 金杰克, 等. 基坑全过程开挖及邻近地铁隧道变形实测分析[J]. 岩土力学, 2019, 40(S1): 415-423. Ding Z, Zhang X, Jin J K, et al. Measurement analysis on whole excavation of foundation pit and deformation of adjacent metro tunnel[J]. Rock and Soil Mechanics, 2019, 40(S1): 415-423. (in Chinese) |
| [3] |
Do N A, Dias D, Oreste P, et al. 2D numerical investigations of twin tunnel interaction[J]. Geomechanics and Engineering, 2014, 6(3): 263-275. DOI:10.12989/gae.2014.6.3.263 |
| [4] |
章润红, 刘汉龙, 仉文岗. 深基坑支护开挖对临近地铁隧道结构的影响分析研究[J]. 防灾减灾工程学报, 2018, 38(5): 857-866. Zhang R H, Liu H L, Zhang W G. Numerical investigation on tunnel responses induced by adjacent deep braced pit excavations[J]. Journal of Disaster Prevention and Mitigation Engineering, 2018, 38(5): 857-866. (in Chinese) |
| [5] |
Ng C W W, Sun H S, Lei G H, et al. Ability of three different soil constitutive models to predict a tunnel's response to basement excavation[J]. Canadian Geotechnical Journal, 2015, 52(11): 1685-1698. DOI:10.1139/cgj-2014-0361 |
| [6] |
Ng C W W, Shi J W, Mašín D, et al. Influence of sand density and retaining wall stiffness on three-dimensional responses of tunnel to basement excavation[J]. Canadian Geotechnical Journal, 2015, 52(11): 1811-1829. DOI:10.1139/cgj-2014-0150 |
| [7] |
Nawel B, Salah M. Numerical modeling of two parallel tunnels interaction using three-dimensional finite elements method[J]. Geomechanics and Engineering, 2015, 9(6): 775-791. DOI:10.12989/gae.2015.9.6.775 |
| [8] |
王卫东, 吴江斌, 翁其平. 基坑开挖卸载对地铁区间隧道影响的数值模拟[J]. 岩土力学, 2004, 25(S2): 251-255. Wang W D, Wu J B, Weng Q P. Numerical modeling of affection of foundation pit excavation on metro tunnel[J]. Rock and Soil Mechanics, 2004, 25(S2): 251-255. (in Chinese) |
| [9] |
陈仁朋, Ashraf A, 孟凡衍. 基坑开挖对旁侧隧道影响及隔断墙作用离心模型试验研究[J]. 岩土工程学报, 2018, 40(S2): 6-11. Chen R P, Ashraf A, Meng F Y. Three-dimensional centrifuge modeling of influence of nearby excavations on existing tunnels and effects of cut-off walls[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(S2): 6-11. (in Chinese) |
| [10] |
Chen R P, Meng F Y, Li Z C, et al. Investigation of response of metro tunnels due to adjacent large excavation and protective measures in soft soils[J]. Tunnelling and Underground Space Technology, 2016, 58: 224-235. DOI:10.1016/j.tust.2016.06.002 |
| [11] |
仉文岗, 洪利, 黎泳钦. 基于多元自适应回归样条的高维岩土工程问题分析[J]. 河海大学学报(自然科学版), 2019, 47(4): 359-365. Zhang W G, Hong L, Li Y Q. Analysis of multi-dimensional geotechnical engineering problems based on multivariate adaptive regression splines[J]. Journal of Hohai University (Natural Sciences), 2019, 47(4): 359-365. (in Chinese) |
| [12] |
Zheng G, Yang X Y, Zhou H Z, et al. A simplified prediction method for evaluating tunnel displacement induced by laterally adjacent excavations[J]. Computers and Geotechnics, 2018, 95: 119-128. DOI:10.1016/j.compgeo.2017.10.006 |
| [13] |
Zhang W G, Goh A T C. Multivariate adaptive regression splines and neural network models for prediction of pile drivability[J]. Geoscience Frontiers, 2016, 7(1): 45-52. DOI:10.1016/j.gsf.2014.10.003 |
| [14] |
李友坤. BP神经网络的研究分析及改进应用[D]. 淮南: 安徽理工大学, 2012. Li Y K. Analysis and improvement applications of bp neural network[D]. Huainan: Anhui University of Science & Technology, 2012. (in Chinese) |
| [15] |
高浪, 谢康和. 人工神经网络在岩土工程中的应用[J]. 土木工程学报, 2002, 35(4): 77-81. Gao L, Xie K H. Application of artificial neural networks to geotechnical engineering[J]. China Civil Engineering Journal, 2002, 35(4): 77-81. (in Chinese) DOI:10.3321/j.issn:1000-131X.2002.04.014 |
| [16] |
Abdalla J A, Attom M F, Hawileh R. Prediction of minimum factor of safety against slope failure in clayey soils using artificial neural network[J]. Environmental Earth Sciences, 2015, 73(9): 5463-5477. DOI:10.1007/s12665-014-3800-x |
| [17] |
Ornek M. Estimation of ultimate loads of eccentric-inclined loaded strip footings rested on sandy soils[J]. Neural Computing and Applications, 2014, 25(1): 39-54. DOI:10.1007/s00521-013-1444-5 |
| [18] |
Alias R, Kasa A, Taha M R. Artificial neural networks approach for predicting the stability of cantilever RC retaining walls[J]. International Journal of Applied Engineering Research, 2015, 10(10): 26005-26014. |
| [19] |
左殿军, 史林, 李铭铭, 等. 深基坑开挖对邻近地铁隧道影响数值计算分析[J]. 岩土工程学报, 2014, 36(S2): 391-395. Zuo D J, Shi L, Li M M, et al. Numerical analysis of influence of deep excavations on adjacent subway tunnels[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(S2): 391-395. (in Chinese) |
| [20] |
Shi J W, Liu G B, Huang P, et al. Interaction between a large-scale triangular excavation and adjacent structures in Shanghai soft clay[J]. Tunnelling and Underground Space Technology, 2015, 50: 282-295. DOI:10.1016/j.tust.2015.07.013 |
| [21] |
Das S K. Artificial neural networks in geotechnical engineering[M]//Metaheuristics in Water, Geotechnical and Transport Engineering. Amsterdam: Elsevier, 2013: 231-270.
|
| [22] |
Chang C T, Sun C W, Duann S W, et al. Response of a taipei rapid transit system (TRTS) tunnel to adjacent excavation[J]. Tunnelling and Underground Space Technology, 2001, 16(3): 151-158. |
| [23] |
Hu Z F, Yue Z Q, Zhou J, et al. Design and construction of a deep excavation in soft soils adjacent to the Shanghai Metro tunnels[J]. Canadian Geotechnical Journal, 2003, 40(5): 933-948. DOI:10.1139/t03-041 |
| [24] |
张治国, 张谢东, 王卫东. 临近基坑施工对地铁隧道影响的数值模拟分析[J]. 武汉理工大学学报, 2007, 29(11): 93-97. Zhang Z G, Zhang X D, Wang W D. Numerical modeling analysis on deformation effect of metro tunnels due to adjacent excavation of foundation pit[J]. Journal of Wuhan University of Technology, 2007, 29(11): 93-97. (in Chinese) |
| [25] |
Liu G B, Huang P, Shi J W, et al. Performance of a deep excavation and its effect on adjacent tunnels in Shanghai soft clay[J]. Journal of Performance of Constructed Facilities, 2016, 30(6): 04016041. |
 2022, Vol. 45
2022, Vol. 45

