1b. 武汉理工大学 汽车零部件技术湖北省协同创新中心, 武汉 430070;
2a. 卡尔斯鲁厄理工大学 亥姆霍兹研究所, 89081 乌尔姆, 德国;
2b. 卡尔斯鲁厄理工大学 物理化学学院, 76131卡尔斯鲁厄, 德国
1b. Hubei Collaborative Innovation Center for Automotive Components Technology, Wuhan University of Technology, Wuhan 430070, P. R. China;
2a. Helmholtz Institute, Karlsruhe Institute of Technology, 89081 Ulm, Germany;
2b. Institute of physical Chemistry, Karlsruhe Institute of Technology, 76131 Karlsruhe, Germany
近些年来,基于磷酸掺杂的聚苯并咪唑(polybenzimidazole,PBI)膜的高温质子交换膜燃料电池(high-temperature proton-exchange membrane fuel cell,HT-PEMFC)成了传统质子交换膜燃料电池的有效替代品。借助PBI膜,HT-PEMFC可以在远高于水沸点的温度下工作,通常在140℃至200℃之间[1-2]。工作温度提高可以改善阳极和阴极反应动力学,并抵消CO在阳极催化剂表面上的吸附,使HT-PEMFC具有明显更高的抗CO毒化能力和更灵活的燃料选择[3-6]。此外,由于高温下水以气相形式存在[7-9],不需要进行反应物加湿以及设计流场来除去液态水, 可以简化水的管理和流道的设计,利于节约系统成本。但是仍然存在一些挑战阻碍了HT-PEMFC的广泛部署,例如不希望的副反应和碳载体腐蚀等。
大多数的研究模型都未直接考虑电极中的磷酸分布。Chevalier等[10]通过孔网格模型(pore network model,PNM)来研究微孔层(microporous layer,MPL)在气体扩散电极(gas diffusion electrode,GDE)中对磷酸再分布的作用,发现MPL的存在促进了磷酸在催化层(catalyst layer,CL)中的再分布,并抑制了磷酸向流道浸出。Bevilacqua等[11]通过对GDE进行磷酸注射实验和PNM建模发现MPL的存在增加了CL内部的毛细管压力,导致CL孔隙中的饱和度较高;减少裂缝的存在能抑制磷酸从碳纤维基底侵入,避免不希望的磷酸浸出。上述研究使用的PNM虽然考虑了微观层面磷酸在CL中的分布,但是侧重于较大的孔隙空间,简化了真实材料的几何形状。Salomov等[12-14]使用BGK-格子Boltzmann方法(lattice Boltzmann method,LBM)评估HT-PEMFC中GDE的传输特性。他们工作的主要重点是多孔介质模型的重构和对流体渗透率的研究。虽然他们的模型真实反映了CL在微观层面的几何形貌,验证了LBM在高温燃料电池领域的可行性,但是却没有深入地对磷酸流动行为进行研究,缺乏对磷酸再分布和浸出的孔尺度了解。所以这里仍然缺乏对磷酸在微观孔隙中流动行为的研究。
笔者首先采用多重弛豫时间(multiple relaxation time,MRT)LBM研究真实CL几何形貌中的两相流,研究了磷酸侵入CL的过程以及不同分布形式对电化学反应表面积(electrochemical active surface area,ECSA)的影响,然后采用孔尺度模型(pore scale model,PSM),对不同磷酸分布下阴极CL的有效气体传输性质进行了研究。
1 方法 1.1 几何重构和模型描述所研究的气体扩散电极是通过将催化剂墨水直接多层喷涂到具有微孔层的气体扩散层(德国Freudenberg的H2315 C2)上来制备的。采用商用的碳基催化剂粉末(20% Pt/C, Heraus)和质量分数60%的聚四氟乙烯(polytetrafluoroethylene, PTFE)悬浮液来制备催化剂墨水,异丙醇和水按照1 ∶1的比例混合作为溶剂,最后得到的催化剂墨水悬浮液中,Pt和PTFE在非液体物质的总质量中占比分别为18%和10%。为了制备均匀的悬浮液,用磁力搅拌器来充分混合墨水。然后在基材温度为80 ℃下,将墨水多次喷涂到微孔层上。喷雾头与基材之间的距离约为20 cm,平均液滴尺寸在0.5 nm以下,并且每层约在1 min后干燥。所制得GDE的Pt负载为1 mg/cm2,最终的厚度约为200 μm。采用聚焦离子束扫描电子显微镜(focused ion beam-scanning electron microscopy, FIB-SEM)对GDE样品进行成像。原始FIB-SEM灰度图像被处理并转换为8位图像,并在0~255的范围内分配像素值。因此,通过分割像素值可以区分孔、碳载体、PTFE和铂催化剂的空间分布。根据Otsu算法[15]确定用于区分图像相位的灰度值范围,即碳载体为70至100,PTFE为155,铂为255,孔隙为0,如图 1(a)所示。本研究中的模拟着重于磷酸的流动行为,而不考虑电化学反应的效果。因此,重构的CL几何在计算域中仅具有2个固相(碳载体和Pt)。用于LBM计算的几何模型如图 1(b)所示,该模型在所有方向上具有5 nm的体积边缘长度和1 μm的总长。
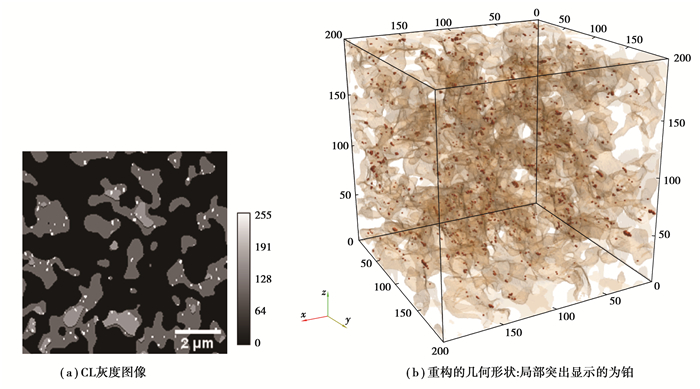
|
图 1 处理后的图像和重构CL微观结构。 Fig. 1 Post-processed image and reconstructed CL microstructure |
计算域分为200×200×200立方晶格。根据文献中的实验结果,纯磷酸在碳载体上的接触角约为100°,并且在混合其他电解质的情况下,接触角会逐渐减小[16]。因此,在模拟中使用的磷酸和碳之间接触角为100°。
1.2 多弛豫时间格子玻尔兹曼方法LBM是一种介观方法,近年来受到研究人员的极大关注[2]。它源自格子气自动机(lattice gas automata,LGA),已被广泛用于模拟两相流[17]。与LGA模型不同,LBM跟追踪粒子的分布,而LGA模型主要追踪特定粒子的运动。LBM已被用于模拟多孔介质中的两相流,与其他方法(例如,有限体积方法)相比,它更容易在复杂几何中实现边界条件。
本文的LBM体系中采用了扩散界面理论模型,该模型可用于具有高密度比和各种黏度的多相流的建模[9, 18]。模型中引入了一个典型的一维阶参数φ来表示2个流体相的密度差,其中φ =1表示液相,φ=-1气相。多相和多组分系统可以使用以下自由能函数F来描述热力学行为:
| $ F=\int \varPsi {\mathrm{d}} V+\int \frac{k}{2}|\Delta \varphi|^{2} {\mathrm{~d}} V+\int {\mathrm{d}} S \varPsi_{\mathrm{s} }。$ | (1) |
式中:V是控制体积;S是润湿壁面的表面积;k为控制表面张力大小的常数,它不利于组分的较大梯度;φ为序参数;Ψs为表面能;Ψ为体积自由能[19]:
| $ \varPsi=A\left(\varphi^{2}-1\right)^{2}。$ | (2) |
式中A为与温度和黏度相关的常数。参数κ和A确定界面张力
方程(1)中的第二项是解释表面张力的梯度项,它会体现序参数中的任何变化。该项捕获2个流体相或组分之间界面的自由能。方程(1)中的最后一项描述了流体与周围固体之间的相互作用。
由于表面能的影响,在固液边界处的特定润湿相互作用导致在平面壁上的静态接触角θ。在方程(3)中给出了润湿势能γ与平衡接触角θ之间的关系[21]。
| $ \gamma=2 {\rm{sign}}\left(\frac{\pi}{2}-\theta\right) \sqrt{\cos \frac{\beta}{3}\left(1-\cos \frac{\beta}{3}\right)} \sqrt{2 A \kappa}, $ | (3) |
式中β=arccos(sin2θ)。两相流体的动态行为受Navier-Stokes方程和Cahn-Hilliard方程控制[19, 22]。
| $ \frac{\partial \rho {\boldsymbol{u}}}{\partial t}+\nabla \cdot \rho {\boldsymbol{u}} {\boldsymbol{u}}=-\nabla \cdot {\boldsymbol{P}}+\eta \nabla^{2} {\boldsymbol{u}}+{\boldsymbol{F}}_{\mathrm{b}}; $ | (4) |
| $ \frac{\partial \varphi}{\partial t}+\nabla \cdot(\varphi {\boldsymbol{u}})=\nabla \cdot(M \nabla \mu)。$ | (5) |
式中:u是流体速度,P是压力张量的梯度,Fb是外力,M是迁移率参数,μ是化学势,t为时间,ρ为密度;η为动力黏度。
为了提高模拟的稳定性和准确性,本研究中选用了MRT算法。所用松弛参数遵循MRT模型的相关分析以减小黏度依赖性速度场[23]。方程(4)和方程(5)可以用以下2个方程式来求解:
| $ {\boldsymbol{f}}_{i}\left({\boldsymbol{r}}+{\boldsymbol{e}}_{i} \delta t, t+\delta t\right)={\boldsymbol{f}}_{i}({\boldsymbol{r}}, t)-{\boldsymbol{Q}}^{-1} {\boldsymbol{\varLambda}}_{f}\left({\boldsymbol{m}}_{f}({\boldsymbol{r}}, t)-{\boldsymbol{m}}_{f}^{\mathrm{eq}}({\boldsymbol{r}}, t)\right)+\delta t\left(1-\frac{1}{2} {\boldsymbol{Q}}^{-1} {\boldsymbol{\varLambda}}_{f} {\boldsymbol{Q}}\right) {\boldsymbol{G}}_{i}({\boldsymbol{r}}, t); $ | (6) |
| $ {\boldsymbol{ g}}_{i}\left({\boldsymbol{ r}}+{\boldsymbol{ e}}_{i} \delta t, t+\delta t\right)={\boldsymbol{ g}}_{i}({\boldsymbol{r }}, t)-{\boldsymbol{ Q}}^{-1} {\boldsymbol{\varLambda}}_{\boldsymbol{ g}}\left({\boldsymbol{ m}}_{\boldsymbol{ g}}({\boldsymbol{r}}, t)-{\boldsymbol{ m}}_{{\boldsymbol{ g}}}^{\mathrm{eq}}({\boldsymbol{r}}, t)\right) 。$ | (7) |
式中:i = 1,2,…,N,表示模型的N个方向。fi和gi分别是在格子位置r和时间t处的速度分布函数和序参数分布函数的向量;ei为离散速度;δt为离散时间;对于D3Q19模型,Q是19×19矩阵,该矩阵分别将分布函数f和g从集群空间线性变换到速度矩空间mf和mg;Λf(α= f, g)为对角松弛矩阵;mfeq和mgeq为平衡分布函数。Gi为体积力:
| $ {\boldsymbol{G}}_{i}=\omega_{i} \frac{\left({\boldsymbol{e}}_{i}-{\boldsymbol{u}}\right)}{c_{\mathrm{s}}^{2}} \cdot\left({\boldsymbol{F}}_{\mathrm{b}}+\mu \nabla \varphi\right), $ | (8) |
式中:ωi为离散速度的权重系数;cs为声速。
局部密度ρi和序参数φi计算如下:
| $ \rho_{i}=\sum\limits_{i} {\boldsymbol{ f}}_{i}; $ | (9) |
| $ \varphi_{i}=\sum\limits_{i} {\boldsymbol{ g}}_{i}。$ | (10) |
为了模拟流体的浸入,在垂直于流动方向的下边界(入口边界)处设置了固定厚度的液相层(200×10×200个立方格子单位),并具有较高的压力值。而在出口边界处设置了一个较低的压力值,该压力梯度允许水层中的液相浸入计算域并在其中继续迁移。周期性边界条件用于速度场的所有区域。对于序参数,将入口边界面设定为1(液相),以保证足量的液相能流入计算域,而将其他4个垂直于流动方向的侧面设为周期性边界条件。由丰田实验室开发并与MRT-LBM结合的代码经调试后用于模拟这项工作[24]。
1.3 孔尺度模型本研究中采用了PSM来研究磷酸分布对电极传输性能的影响。PSM解决了重构模型中气体扩散与带电物质(离子和电子)传导的耦合传输[25]。与MRT-LBM不同,PSM模型获得了单相流的稳态解。为了计算CL中的有效气体扩散率,采用了同时考虑了Fickian扩散和Knudsen扩散的Stefan-Maxwell公式:
| $ \nabla y_{{\mathrm{O}}_{2}}=\frac{R_{{\mathrm{u}}} T}{p}\left(\frac{y_{{\mathrm{O}}_{2}} \varGamma_{{\mathrm{H}}_{2} {\mathrm{O}}}-y_{{\mathrm{H}}_{2} {\mathrm{O}}} \varGamma_{{\mathrm{O}}_{2}}}{D_{{\mathrm{O}}_{2}-{\mathrm{H}}_{2} {\mathrm{O}}}}+\frac{y_{{\mathrm{O}}_{2}} \varGamma_{{\mathrm{N}}_{2}}-y_{{\mathrm{N}}_{2}} \varGamma_{{\mathrm{O}}_{2}}}{D_{{\mathrm{O}}_{2}-{\mathrm{N}}_{2}}}-\frac{\varGamma_{{\mathrm{O}}_{2}}}{D_{{\mathrm{O}}_{2}, {\mathrm{Kn}}}}\right), $ | (11) |
| $ \nabla y_{{\mathrm{H}}_{2} {\mathrm{O}}}=\frac{R_{{\mathrm{u}}} T}{p}\left(\frac{y_{{\mathrm{H}}_2 {\mathrm{O}}} \varGamma_{{\mathrm{N}}_{2}}-y_{{\mathrm{N}} 2} \varGamma_{{\mathrm{H}}_2 {\mathrm{O}}}}{D_{{\mathrm{H}}_{2} {\mathrm{O}}-{\mathrm{N}}_{2}}}+\frac{y_{{\mathrm{H}}_2 {\mathrm{O}}} \varGamma_{{\mathrm{O}}_{2}}-y_{{\mathrm{O}}_{2}} \varGamma_{{\mathrm{H}}_2 {\mathrm{O}}}}{D_{{\mathrm{H}}_{2} {\mathrm{O}}-{\mathrm{O}}_{2}}}-\frac{\varGamma_{{\mathrm{H}}_2 {\mathrm{O}}}}{D_{{\mathrm{H}}_{2} {\mathrm{O}}, {\mathrm{Kn}}}}\right), $ | (12) |
| $ \nabla y_{{\mathrm{N}}_{2}}=\frac{R_{{\mathrm{u}}} T}{p}\left(\frac{y_{{\mathrm{N}}_{2}} \varGamma_{{\mathrm{O}}_{2}}-y_{{\mathrm{O}}_{2}} \varGamma_{{\mathrm{N}}_{2}}}{D_{{\mathrm{O}}_{2}-{\mathrm{N}}_{2}}}+\frac{y_{{\mathrm{N}}_{2}} \varGamma_{{\mathrm{H}}_{2} {\mathrm{O}}}-y_{{\mathrm{H}}_{2} {\mathrm{O}}} \varGamma_{{\mathrm{N}}_{2}}}{D_{{\mathrm{H}}_{2} {\mathrm{O}}-{\mathrm{N}}_{2}}}-\frac{\varGamma_{{\mathrm{N}}_{2}}}{D_{{\mathrm{N}}_{2}, {\mathrm{~K}}_{{\mathrm{n}}}}}\right) 。$ | (13) |
式中:yn是物质n的摩尔分数;Γn是物质n的流速;Ru是通用气体常数;Dn1-n2是物质n1和n2的二元扩散系数;Dn, Kn是它们的克努森扩散系数;T为温度;p为压力。
2 分析与讨论作为HT-PEMFC的电解质,阴极CL中的磷酸分布对于电池性能至关重要。从CL中浸出的磷酸会明显降低电池性能。因此,对磷酸的流动行为和分布的研究可为优化设计HT-PEMFC和减轻电池衰退提供见解和指导。以下工作旨在研究磷酸在催化层中的分布形式对电极性能的影响。首先讨论了基准案例下的LBM模拟结果,然后通过改变外界条件获得燃料电池工作过程中可能出现的理想磷酸分布形式,比较不同形式下的ECSA。最后基于LBM计算得到磷酸分布数据,采用PSM模拟计算相应条件下的电极传输性质。
2.1 磷酸侵入催化层的过程磷酸通常是在装配过程中被压入催化层中,采用具有均匀分布接触角(q=100°)的重构CL模型来研究磷酸的侵入过程。沿流动方向的压力梯度设置为δp=5。磷酸从计算域的一侧进入,入口边界处的水层模拟了PBI膜的电解质池。图 2显示了磷酸侵入重构的CL后其饱和度SP达到不同程度时在CL中运动过程的三维可视化图片,为清楚起见未显示出CL结构。由于多孔材料的疏水性,磷酸表现出毛细管指状渗透行为且呈多条通路并行的状态。图 3展示了垂直于流动方向的横截面上磷酸的含量随相对位置变化的关系。需要注意的是图中几何模型入口处(y=10)为相对位置0,出口处(y=210)表示相对位置1。可以观察到沿压力梯度方向磷酸基本上是均匀稳定地侵入到催化层中。这表明催化层被流体彻底润湿,而不是液体在某些多孔材料中通过建立一条细小通路突然穿透,例如,PEMFC的纤维状气体扩散层。在相对位置x=0.25处标记了一条灰色虚线,在此位置横截面上的各相分布显示在图 4中。磷酸倾向于优先侵入大的孔隙,然后逐步润湿周围环境。
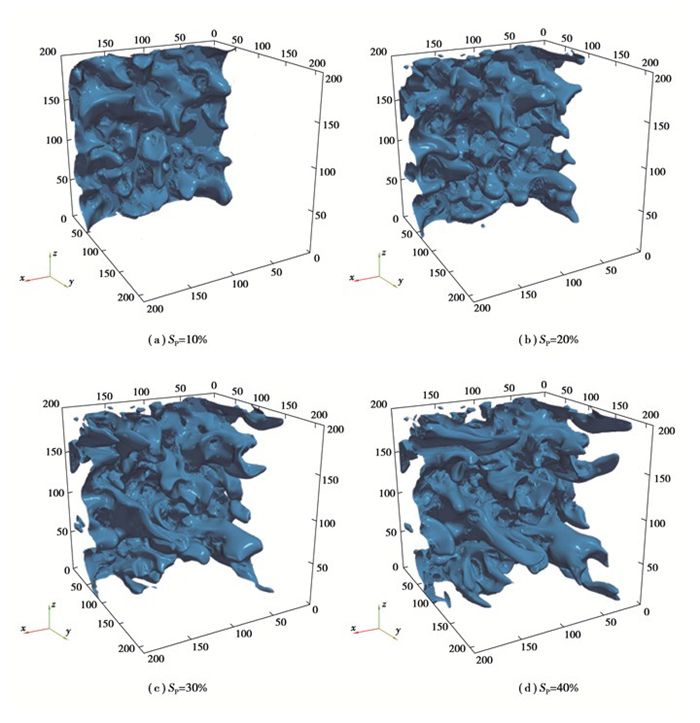
|
图 2 磷酸饱和度SP达到不同数值时的气液传输过程 Fig. 2 Gas-liquid transmission process with a different phosphoric acid saturation SP |
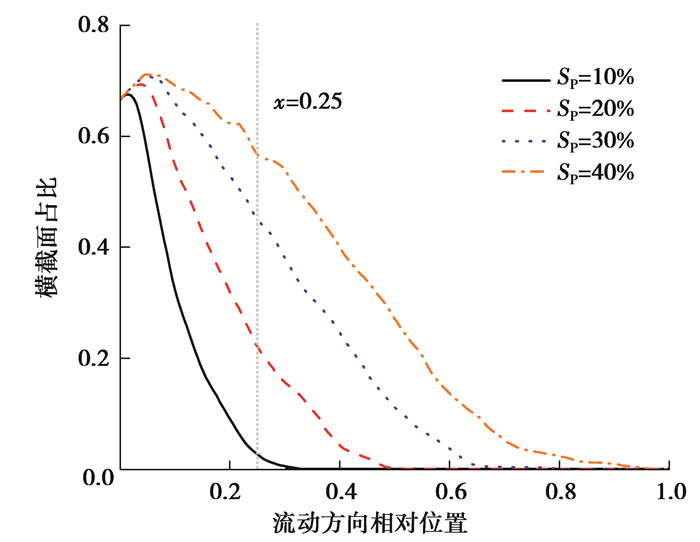
|
图 3 不同磷酸饱和度下,沿流动方向(y轴)横截面上液相占比随位置变化曲线 Fig. 3 Various liquid phase proportions in the xz cross-section along the flow direction (y axis) under different phosphoric acid contents |
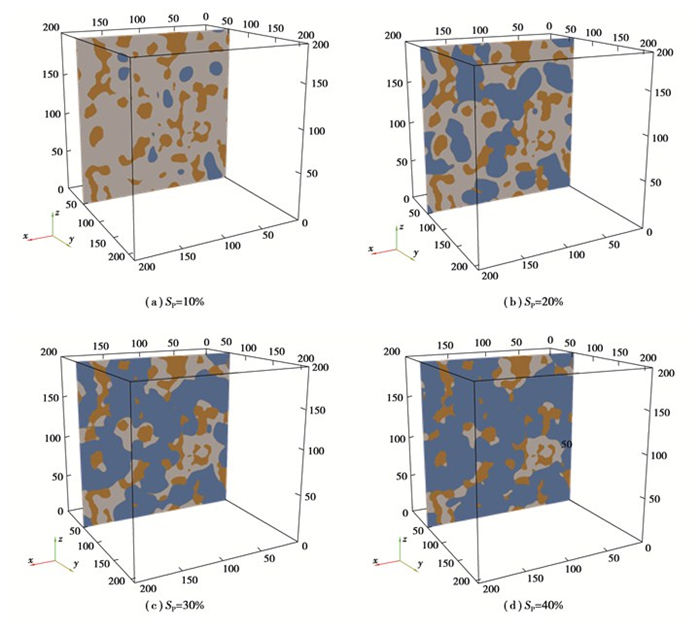
|
图 4 y=50处横截面上各相分布图 Fig. 4 Distribution of each phase in the cross-section at y=50 |
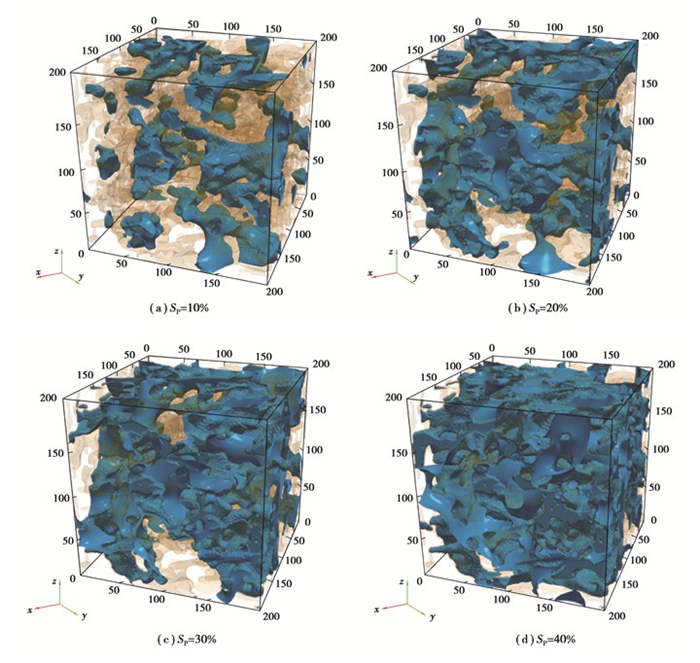
在上一节案例的基础上,在4种选定的磷酸饱和度条件下,停止向CL中压入磷酸。将流动方向的序参数函数设置为周期性边界条件,使定量的磷酸能在计算域中有足够的迁移再分布时间,以便达到平衡态,并尽可能实现均匀分布。最终获得的磷酸分布形式如图 5所示。磷酸饱和度为10%时,较难形成连续的磷酸网络,即有效的质子传导通路。而在磷酸饱和度为40%时,磷酸几乎润湿了所有的壁面,并且形成了密集的质子传输网络,但也因此极易堵塞气体传输网络。
|
图 5 不同磷酸含量下的准均匀分布形式 Fig. 5 Quasi-uniform distribution under different phosphoric acid contents |
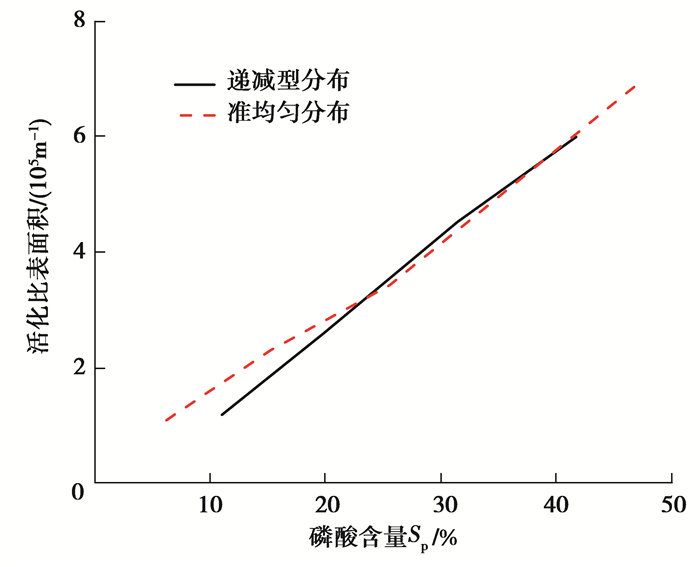
图 6中比较了不同磷酸分布形式下活化比表面积随磷酸含量的变化。此处的活化比表面积是通过处理LBM计算得到的各相分布数据得到的,它被定义为被磷酸覆盖的铂粒子的表面积和碳载铂体积之比。催化层中的磷酸含量用其饱和度表示。从图 6中的低磷酸含量区域(SP < 25%)可以观察到准均匀分布拥有较高的活化比表面积。这是因为在磷酸不足的情况下,均匀型分布使磷酸具有更大的面积伸展,可以更多地与催化剂粒子接触。而当磷酸含量足够时,2种分布形式具有相似的活化比较面积,这得益于催化剂粒子在催化层中的均匀分布(图 1(b))。因此,对于HE-PEMFC,在不流失的情况下,磷酸在CL中的分布形式对ECSA的影响不大,但磷酸流失会导致ECSA显著降低。
|
图 6 不同磷酸含量下活化比表面积的比较 Fig. 6 Comparison of electrochemical active surface area under different phosphoric acid contents |
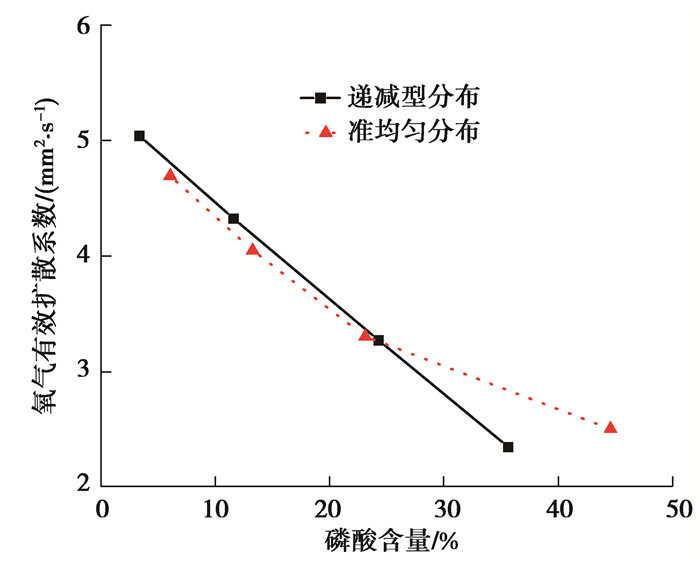
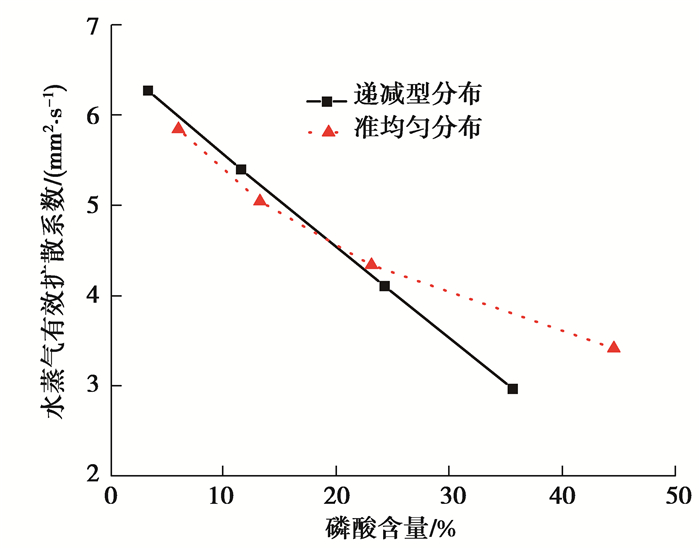
磷酸在高温下(>140 ℃)会发生脱水缩聚反应,形成焦磷酸或者多磷酸。尽管水主要以蒸汽的形式存在于催化层中,但是磷酸分子中的磷原子会与水分子中的氧原子形成一系列势能键,使磷酸具有一定的锁水能力,并使磷酸在高温下仍以液态形式存在。磷酸在催化层中的再分布不仅决定电极的质子传导能力,还影响气体物质在电极中的传输性质。图 7和图 8分别比较了在递减型和准均匀型2种分布形式下氧气和水蒸气的有效扩散系数随磷酸含量变化。在磷酸含量较低的时候(SP < 20%),递减型磷酸分布的氧气和水蒸气有效扩散系数略高于准均匀型;而在高磷酸含量区域(SP>25%),准均匀型磷酸分布的有效扩散系数更高,并且差距随磷酸含量增加逐渐变大。递减型磷酸分布的有效扩散系数随磷酸含量升高稳定减小,而准均匀型分布的有效扩散系数下降速率在饱和度较低区域比较稳定,在高饱和度区域随磷酸含量增加,下降趋势逐渐变缓。这是由于指数递减型分布的气体扩散系数受入口区域的影响较大,而磷酸含量增大导致入口段气体通路的堵塞现象更明显。均匀型分布由于其分散性,相较于递减型分布,在磷酸含量较高时(SP>25%)能保证磷酸具有更多的可润湿孔隙,局部截面出现堵塞的可能性降低。因此,让磷酸在CL中更均匀地分布能够有效改善气体物质的有效扩散系数,从而优化电极性能。
|
图 7 不同磷酸分布形式下氧气有效扩散系数比较 Fig. 7 Comparison of effective oxygen diffusion coefficient under different distribution types |
|
图 8 不同磷酸分布形式下水蒸气有效扩散系数比较 Fig. 8 Comparison of effective diffusion coefficient of water vapor under different distribution types |
使用FIB-SEM扫描得到的CL图片重构得到了能真实反映CL几何形貌的三维模型,用于研究磷酸在CL中的迁移与再分布对电极性能的影响。利用LBM模拟获得磷酸在CL中2种不同的分布形式:递减型分布和准均匀型分布。通过对比发现准均匀型分布在CL中磷酸含量较低时(SP < 25%)的ECSA略高于递减型分布,但整体上2种分布类型的ECSA差别不大。随着CL中磷酸含量增加,准均匀型分布的氧气和水蒸气的有效扩散系数逐渐优于递减型分布。综上所述,提高磷酸在催化层中分布的均匀性,可改善低磷酸含量时催化层中ECSA,并有效提升较高磷酸含量时催化层的气体物质有效扩散系数,获得更好的电极性能。
| [1] |
Lee D, Lee D G. Carbon composite bipolar plate for high-temperature proton exchange membrane fuel cells (HT-PEMFCs)[J]. Journal of Power Sources, 2016, 327: 119-126. DOI:10.1016/j.jpowsour.2016.07.045 |
| [2] |
Kim M, Lim J W, Lee D G. Surface modification of carbon fiber phenolic bipolar plate for the HT-PEMFC with nano-carbon black and carbon felts[J]. Composite Structures, 2015, 119: 630-637. DOI:10.1016/j.compstruct.2014.09.010 |
| [3] |
Oh K, Ju H. Temperature dependence of CO poisoning in high-temperature proton exchange membrane fuel cells with phosphoric acid-doped polybenzimidazole membranes[J]. International Journal of Hydrogen Energy, 2015, 40(24): 7743-7753. DOI:10.1016/j.ijhydene.2015.01.107 |
| [4] |
Wagner N, Gülzow E. Change of electrochemical impedance spectra (EIS) with time during CO-poisoning of the Pt-anode in a membrane fuel cell[J]. Journal of Power Sources, 2004, 127(1/2): 341-347. |
| [5] |
Krishnan P, Park J S, Kim C S. Performance of a poly(2, 5-benzimidazole) membrane based high temperature PEM fuel cell in the presence of carbon monoxide[J]. Journal of Power Sources, 2006, 159(2): 817-823. DOI:10.1016/j.jpowsour.2005.11.071 |
| [6] |
Wagner N, Schulze M. Change of electrochemical impedance spectra during CO poisoning of the Pt and Pt-Ru anodes in a membrane fuel cell (PEFC)[J]. Electrochimica Acta, 2003, 48(25/26): 3899-3907. |
| [7] |
Chandan A, Hattenberger M, El-Kharouf A, et al. High temperature (HT) polymer electrolyte membrane fuel cells (PEMFC)-a review[J]. Journal of Power Sources, 2013, 231: 264-278. DOI:10.1016/j.jpowsour.2012.11.126 |
| [8] |
Zhang C Z, Zhou W J, Zhang L, et al. An experimental study on anode water management in high temperature PEM fuel cell[J]. International Journal of Hydrogen Energy, 2015, 40(13): 4666-4672. DOI:10.1016/j.ijhydene.2015.02.037 |
| [9] |
Jannelli E, Minutillo M, Perna A. Analyzing microcogeneration systems based on LT-PEMFC and HT-PEMFC by energy balances[J]. Applied Energy, 2013, 108: 82-91. DOI:10.1016/j.apenergy.2013.02.067 |
| [10] |
Chevalier S, Fazeli M, Mack F, et al. Role of the microporous layer in the redistribution of phosphoric acid in high temperature PEM fuel cell gas diffusion electrodes[J]. Electrochimica Acta, 2016, 212: 187-194. DOI:10.1016/j.electacta.2016.06.121 |
| [11] |
Bevilacqua N, George M G, Bazylak A, et al. Phosphoric acid distribution patterns in high temperature PEM fuel cells[J]. ECS Transactions, 2017, 80(8): 409-417. DOI:10.1149/08008.0409ecst |
| [12] |
Salomov U R, Chiavazzo E, Asinari P. Pore-scale modeling of fluid flow through gas diffusion and catalyst layers for high temperature proton exchange membrane (HT-PEM) fuel cells[J]. Computers & Mathematics with Applications, 2014, 67(2): 393-411. |
| [13] |
Salomov U R, Chiavazzo E, Asinari P. Gas-dynamic and electro-chemical optimization of catalyst layers in high temperature polymeric electrolyte membrane fuel cells[J]. International Journal of Hydrogen Energy, 2015, 40(15): 5425-5431. DOI:10.1016/j.ijhydene.2015.01.059 |
| [14] |
Salomov U R, Chiavazzo E, Fasano M, et al. Pore- and macro-scale simulations of high temperature proton exchange fuel cells - HTPEMFC - and possible strategies for enhancing durability[J]. International Journal of Hydrogen Energy, 2017, 42(43): 26730-26743. DOI:10.1016/j.ijhydene.2017.09.011 |
| [15] |
Silva R A, Hashimoto T, Thompson G E, et al. Characterization of MEA degradation for an open air cathode PEM fuel cell[J]. International Journal of Hydrogen Energy, 2012, 37(8): 7299-7308. DOI:10.1016/j.ijhydene.2011.12.110 |
| [16] |
Mack F, Galbiati S, Gogel V, et al. Evaluation of electrolyte additives for high-temperature polymer electrolyte fuel cells[J]. ChemElectroChem, 2016, 3(5): 770-773. DOI:10.1002/celc.201500561 |
| [17] |
Molaeimanesh G R, Googarchin H S, Moqaddam A Q. Lattice Boltzmann simulation of proton exchange membrane fuel cells - a review on opportunities and challenges[J]. International Journal of Hydrogen Energy, 2016, 41(47): 22221-22245. DOI:10.1016/j.ijhydene.2016.09.211 |
| [18] |
McCracken M E, Abraham J. Multiple-relaxation-time lattice-Boltzmann model for multiphase flow[J]. Physical Review E, 2005, 71: 036701. DOI:10.1103/PhysRevE.71.036701 |
| [19] |
Kendon V M, Cates M E, Pagonabarraga I, et al. Inertial effects in three-dimensional spinodal decomposition of a symmetric binary fluid mixture: a lattice Boltzmann study[J]. Journal of Fluid Mechanics, 2001, 440: 147-203. DOI:10.1017/S0022112001004682 |
| [20] |
Zheng H W, Shu C, Chew Y T. Lattice Boltzmann interface capturing method for incompressible flows[J]. Physical Review E, 2005, 72: 056705. DOI:10.1103/PhysRevE.72.056705 |
| [21] |
Mohamad A A. Lattice boltzmann method[M]. London: Springer London, 2011.
|
| [22] |
Jacqmin D. Calculation of two-phase navier-stokes flows using phase-field modeling[J]. Journal of Computational Physics, 1999, 155(1): 96-127. DOI:10.1006/jcph.1999.6332 |
| [23] |
d'Humières D, Ginzburg I, Krafczyk M, et al. Multiple-relaxation-time lattice Boltzmann models in three dimensions[J]. Philosophical Transactions Series A, Mathematical, Physical, and Engineering Sciences, 2002, 360(1792): 437-451. DOI:10.1098/rsta.2001.0955 |
| [24] |
Niu X D, Munekata T, Hyodo S A, et al. An investigation of water-gas transport processes in the gas-diffusion-layer of a PEM fuel cell by a multiphase multiple-relaxation-time lattice Boltzmann model[J]. Journal of Power Sources, 2007, 172(2): 542-552. DOI:10.1016/j.jpowsour.2007.05.081 |
| [25] |
Lange K J, Sui P C, Djilali N. Determination of effective transport properties in a PEMFC catalyst layer using different reconstruction algorithms[J]. Journal of Power Sources, 2012, 208: 354-365. DOI:10.1016/j.jpowsour.2011.11.001 |
 2022, Vol. 45
2022, Vol. 45


