2. 重庆大学 汽车工程学院, 重庆 400044
2. School of Automotive Engineering, Chongqing University, Chongqing 400044, P. R. China
无人驾驶拖拉机在农业生产中的运用越来越广泛,已成为农业智能化生产中的关键设备[1-5]。农田中障碍物类型复杂,如机井、泵房、电线杆、树木、人和动物等[6-7],当无人驾驶拖拉机在工作中前方存在障碍物时,如果拖拉机没有实时自主规划避障路径的功能,那么障碍物会阻碍无人驾驶拖拉机的正常工作,因此避障路径规划技术是无人驾驶拖拉机的必备技术。
当无人驾驶拖拉机作业遇到障碍物时,需要规划出一条无碰撞风险的避障路径。目前已经有一些学者对无人驾驶拖拉机的避障路径规划算法进行了研究,韩冰等[8]提出用五次多项式函数对拖拉机的行驶路径进行设计,该方法具有计算时间短、路径光滑等优点,但拖拉机并不能回到原始作业路线,并且没有考虑路径的起止点如何确定。霍迎辉等[9]提出一种用最短切线法来规划避障路径,该方法具有生成路径简单快捷、路径长度短等优点,但路径存在折角。刘向锋[10]提出一种改进最短切线法,但该方法规划的路径存在曲率不连续,不易跟踪控制。奚小波等[11]提出一种用Bezier曲线优化避障路径的方法,但该方法存在曲率变化过快、优化调整复杂等缺点。郭成洋等[12]提出一种基于改进人工势场法的农机避障方法,该方法虽然能让农机绕过障碍物,但是路径过长,导致作业区域覆盖率减小。A*算法[13]、神经网络算法[14]、模糊逻辑算法[15]等避障路径规划算法生成路径不够简单快捷,且生成的路径过长,目前很少用于无人驾驶拖拉机的避障路径规划。
田间障碍物有活动障碍物和固定障碍物,文中只对存在固定障碍物的情况进行研究。首先对障碍物进行简化处理,避免路径冗余,然后采用改进最短切线法求路径上的相关坐标点,保证避障路径的安全且长度短,最后基于求得的坐标点用两段五次多项式函数求解路径,使路径光滑且曲率连续,满足拖拉机的动力学约束。基于常州东风无人驾驶拖拉机建立车辆模型,通过Simulink与CarSim联合仿真平台对无人驾驶拖拉机的避障路径规划及跟踪控制进行联合仿真,与改进最短切线法进行对比分析,证明该路径规划算法规划的路径跟踪控制精度更高,更能满足拖拉机的动力学约束,更易于跟踪控制。
1 作业环境分析农业机械在田间作业时,其作业路径为全区域覆盖路径,需要满足转弯数最少、作业消耗最少、总作业路径最短和有效作业路径比最大,所以无人驾驶拖拉机的全局作业路径多数情况下是平行的直线,在极少情况下不是直线[16-17]。文中主要研究无人驾驶拖拉机在按照原有直线路径作业时前方有固定障碍物的情况下,实时规划出一条避障路径的方法。
在研究无人驾驶拖拉机避障路径规划时不考虑活动障碍物,只考虑固定障碍物,如机房、泵房、电线杆、树木等,同时固定障碍物已通过无人机或者其他定位设施进行了标定。目前大多学者对田间的障碍物都假设为规则的圆形,这一假设太过于理想,面对尺寸过长的障碍物,会存在路径冗余[18-20]。为了解决避障路径冗余,同时保证无人驾驶拖拉机在机械结构约束和几何约束下具有可行性和实时性,对田间障碍物的外形和尺寸进行简化处理,其简化步骤如下:
1) 为了保证无人驾驶拖拉机能够安全地绕过障碍物,需要让拖拉机与障碍物之间保持一定的安全距离。以后轴中心表示拖拉机的位置,设拖拉机和农业机具最宽处的尺寸为l,障碍物几何中心到边缘的最大距离为rb,为保证拖拉机行驶安全,拖拉机与障碍物之间最少保持0.5 m的距离,则拖拉机到障碍物几何中心的最小安全距离为rb+l/2=0.5,设这个距离为障碍物安全距离Rb。
2) 针对尺寸小的障碍物,如电线杆、树木等,其安全距离Rb小于或等于无人驾驶拖拉机的最小转弯半径rmin,统一简化为圆形障碍物。
3) 针对尺寸较大的障碍物,如机房、电塔等,其安全距离大于拖拉机的最小转弯半径,统一简化为矩形障碍物,且矩形障碍物的4条边垂直或者平行于原作业路径。面对矩形障碍物,需要保证横向上与障碍物的安全距离,设障碍物的最小横向安全距离为Db。
圆形障碍物与矩形障碍物为何以rmin为划分标准,将在下文进行分析说明。
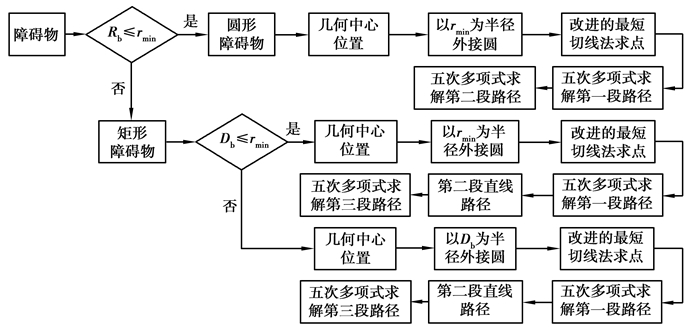
2 避障路径规划无人驾驶拖拉机的避障路径需要解决两个关键问题,第一个是避障路径的曲率要连续,同时避障路径起点和终点的曲率为零,满足拖拉机的动力学约束,使其更易于跟踪控制;第二个是在安全性和实时性好的前提下,避障路径长度尽可能短,减小避障代价和保证作业区域覆盖率高。针对这两个问题,用改进最短切线法求解避障路径的相关坐标点,可使最终得到的路径长度短;将得到的相关坐标点作为分段路径的起止点,用五次多项式函数求解路径,由于五次多项式函数的一阶导数和二阶导数都是连续的,所以五次多项式函数路径光滑且曲率连续,满足拖拉机的动力学约束,易于跟踪控制。避障路径规划算法如图 1所示。
|
图 1 避障路径规划算法 Fig. 1 Obstacle avoidance path planning algorithm |
根据障碍物的形状、尺寸和位置的不同,可分为以下3种情况进行分析。
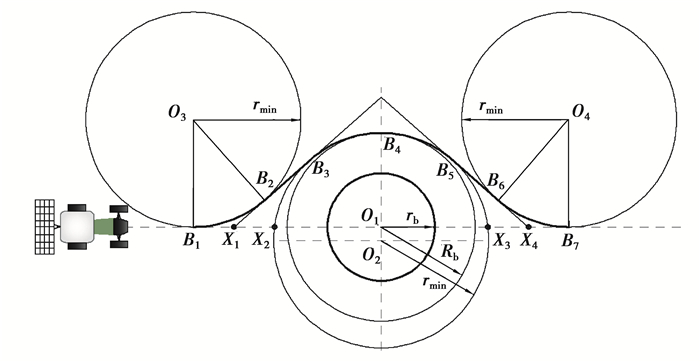
1) 障碍物为圆形障碍物,其障碍物安全距离Rb小于或等于拖拉机的最小转弯半径rmin,障碍物中心位于原路径上或右边。利用改进最短切线法求点B1,B4,B7的坐标,原理如图 2所示,步骤如下:
|
图 2 改进最短切线法规划路径原理 Fig. 2 Principle of path planning by the improved shortest tangent method |
a.以障碍物中心O1为圆心,以Rb为半径作圆,该圆与垂直于原路径的极轴交于点B4,此时Rb小于拖拉机的最小转弯半径rmin;
b.以点B4为公切点,以rmin为半径,外接作圆,圆心为O2,与原路径交于点X2和X3;
c.以圆弧X2B4的中点B3为切点作切线,与原路径交于点X1,同时以圆弧B4X3的中点B5为切点作切线,与原路径交于点X4;
d.以直线B1X1和直线X1B3为切线,以rmin为半径作圆,切点为B1和B2,同时以直线B5X4和直线X4B7为切线,以rmin为半径作圆,切点为B6和B7;
e.弧线B1B2、线段B2B3、弧线B3B5、线段B5B6和圆弧B6B7共同组成改进最短切线法规划的避障路径,点B1, B4, B7为所求的坐标点。
由图 2可知,当障碍物几何中心位于原路径上或右侧时,避障路径在原路径左侧;当障碍物几何中心位于原路径左侧时,其路径规划原理一样,避障路径将在原路径右侧。
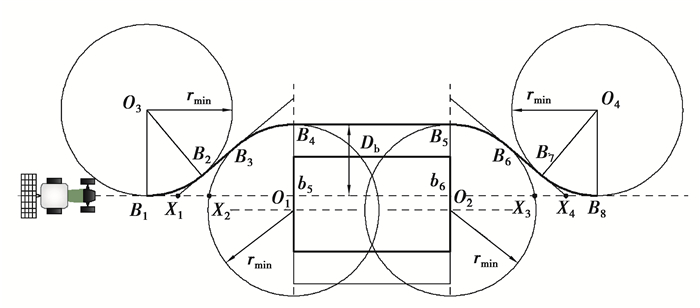
2) 障碍物为矩形障碍物,几何中心位于原路径上或右边,此时设障碍物的最小横向安全距离为Db,Db的值为障碍物左边缘到原路径的距离加上l/2+0.5,且Db小于或等于rmin。利用改进最短切线法求点B1, B4, B5, B8的坐标,原理如图 3所示。该原理的步骤与第一种情况相似,主要区别为圆心O1和O2在障碍物边上,线段B4B5平行于矩形障碍物边缘,以rmin为半径,分别过点B4, B5做圆,与原路径交于点X2, X3,剩下的步骤与第一种情况相同。
|
图 3 改进最短切线法规划路径原理 Fig. 3 Principle of path planning by the improved shortest tangent method |
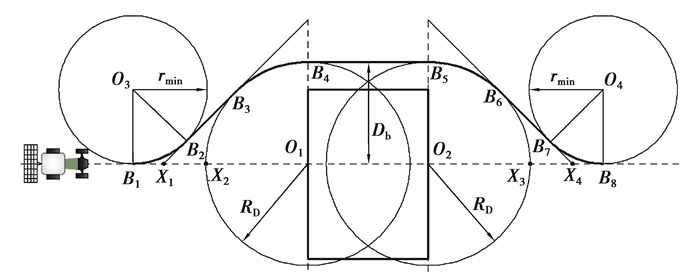
3) 障碍物为矩形障碍物,几何中心位于原路径上或右边,此时设障碍物的最小横向安全距离为Db,Db的值为障碍物左边缘到原路径的距离加上l/2+0.5,且Db大于rmin。利用改进最短切线法求点B1, B4, B5, B8的坐标,原理如图 4所示。该原理的步骤与第二种情况相似,主要区别为圆心O1, O2在原路径与障碍物的交点上,以横向安全距离为半径,用RD表示,过点B4, B5作圆,与原路径交于点X2, X3,剩下的步骤与第二种情况相同。
|
图 4 改进最短切线法规划路径原理 Fig. 4 Principle of path planning by the improved shortest tangent method |
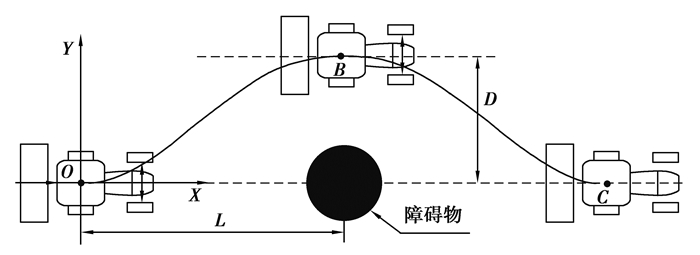
无人驾驶拖拉机避障路径示意图如图 5所示,以避障起始点O为坐标原点,原路径前进方向为x轴,垂直于原路径的方向为y轴,建立坐标系,以后轴中心的位置表示拖拉机的位置。如果是圆形障碍物,避障路径由OB和BC两段曲线组成,如果是矩形障碍物,避障路径还包括一段直线。OB和BC都是五次多项式函数路径,点O、点B和点C为五次多项式函数路径的起止点,其坐标由改进最短切线法求得,D为避障路径到障碍物几何中心的最大横向距离,L为避障起点到障碍物几何中心的纵向距离。
|
图 5 无人驾驶拖拉机避障路径示意图 Fig. 5 Schematic diagram of the obstacle avoidance path of an unmanned tractor |
设五次多项式的函数表达式为
| $y(x) = {a_0}{x^5} + {a_1}{x^4} + {a_2}{x^3} + {a_3}{x^2} + {a_4}x + {a_5}{\rm{。}}$ | (1) |
在避障起点O(0, 0)时,拖拉机应满足横向位移为零,航向角为零,横向加速为零,所以对应的路径函数应满足约束方程
| $y(0) = 0, \dot y(0) = 0, \ddot y(0) = 0{\rm{。}}$ | (2) |
由式(1)和式(2)求解可得到
| $\left\{ {\begin{array}{*{20}{l}} {{a_3} = 0, }\\ {{a_4} = 0, }\\ {{a_5} = 0{\rm{。}}} \end{array}} \right.$ | (3) |
当拖拉机到达点B时,纵向位移为L,其状态应满足横向位移为D,航向角为零,横向加速为零,所以对应的路径函数应满足约束方程
| $y(L) = D, \dot y(L) = 0, \ddot y(L) = 0{\rm{。}}$ | (4) |
由式(1)和式(4)可得表达式
| $\left\{ {\begin{array}{*{20}{c}} {{a_0}{L^5} + {a_1}{L^4} + {a_2}{L^3} + {a_3}{L^2} + {a_4}L + {a_5} = D, }\\ {5{a_0}{L^4} + 4{a_1}{L^3} + 3{a_2}{L^2} + 2{a_3}L + {a_4} = 0, }\\ {20{a_0}{L^3} + 12{a_1}{L^2} + 6{a_2}L + 2{a_3} = 0{\rm{。}}} \end{array}} \right.$ | (5) |
由式(3)和式(5)求解可以得到路径OB段的五次多项式路径函数
| $y(x) = D\left[ {6{{\left( {\frac{x}{L}} \right)}^5} - 15{{\left( {\frac{x}{L}} \right)}^4} + 10{{\left( {\frac{x}{L}} \right)}^3}} \right]{\rm{。}}$ | (6) |
当拖拉机到达避障路径终点C时,纵向位移为2L,其状态应满足横向位移为零,航向角为零,横向加速为零,所以对应的路径函数应满足约束方程
| $y(2L) = D, \dot y(2L) = 0, \ddot y(2L) = 0{\rm{。}}$ | (7) |
由式(1)和式(7)可得表达式
| $\left\{ {\begin{array}{*{20}{c}} {32{a_0}{L^5} + 16{a_1}{L^4} + 8{a_2}{L^3} + 4{a_3}{L^2} + 2{a_4}L + {a_5} = 0,}\\ {80{a_0}{L^4} + 32{a_1}{L^3} + 12{a_2}{L^2} + 4{a_3}L + {a_4} = 0,}\\ {160{a_0}{L^3} + 48{a_1}{L^2} + 12{a_2}L + 2{a_3} = 0{\rm{。}}} \end{array}} \right.$ | (8) |
由式(5)和式(8)求解可以得到路径BC段的五次多项式路径函数
| $y(x) = D - D\left[ {6{{\left( {\frac{{x - L}}{L}} \right)}^5} - 15{{\left( {\frac{{x - L}}{L}} \right)}^4} + 10{{\left( {\frac{{x - L}}{L}} \right)}^3}} \right]{\rm{。}}$ | (9) |
设曲线的曲率为K,则曲线曲率表达式为
| $K = \frac{{|\ddot y|}}{{{{\left( {1 + {{\dot y}^2}} \right)}^{\frac{3}{2}}}}}{\rm{。}}$ | (10) |
在五次多项式避障路径起止点上的二阶导数都为零,所以曲率也为零,满足避障路径连续且曲率没突变的要求。东风无人驾驶拖拉机宽度为2.1 m,某款农业播种机宽度为2.6 m,根据障碍物形状和尺寸的不同,在MATLAB软件中对避障路径规划算法进行仿真分析,规划的路径有以下几种:
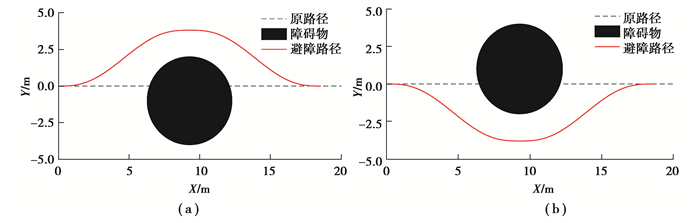
1) 障碍物为圆形障碍物,障碍物半径为3.0 m,当几何中心位于原路径上或右侧时,避障路径如图 6(a)所示,当几何中心位于原路径左侧时,避障路径如图 6(b)所示。
|
图 6 避障路径 Fig. 6 Obstacle avoidance path |
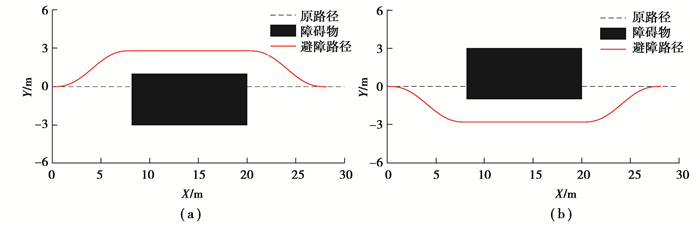
2) 障碍物为矩形障碍物,其纵向长度较大,当几何中心位于原路径上或右侧时,避障路径如图 7(a)所示,当几何中心位于原路径左侧时,避障路径如图 7(b)所示。
|
图 7 避障路径 Fig. 7 Obstacle avoidance path |
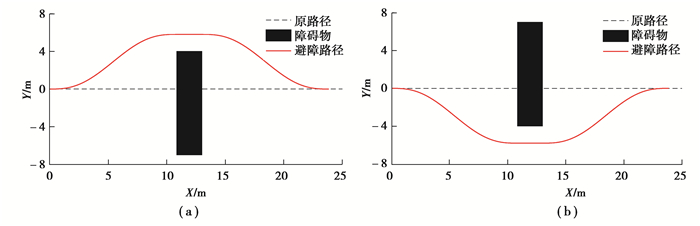
3) 障碍物为矩形障碍物,其横向长度较大,当几何中心位于原路径上或右侧时,避障路径如图 8(a)所示,当几何中心位于原路径左侧时,避障路径如图 8(b)所示。
|
图 8 避障路径 Fig. 8 Obstacle avoidance path |
由避障路径规划仿真结果可知,无人驾驶拖拉机的避障路径光滑且曲率连续,但除此之外,为了提高和保证避障路径的安全性,避障路径还要满足另外两个约束条件。第一个约束条件是避障路径的最小曲率半径大于或等于最小转弯半径rmin,用R表示曲率半径,Rmin表示最小曲率半径,即
| $R = \frac{{{{\left( {1 + {{\dot y}^2}} \right)}^{\frac{3}{2}}}}}{{|\ddot y|}}\geqslant {r_{\min }}{\rm{。}}$ | (11) |
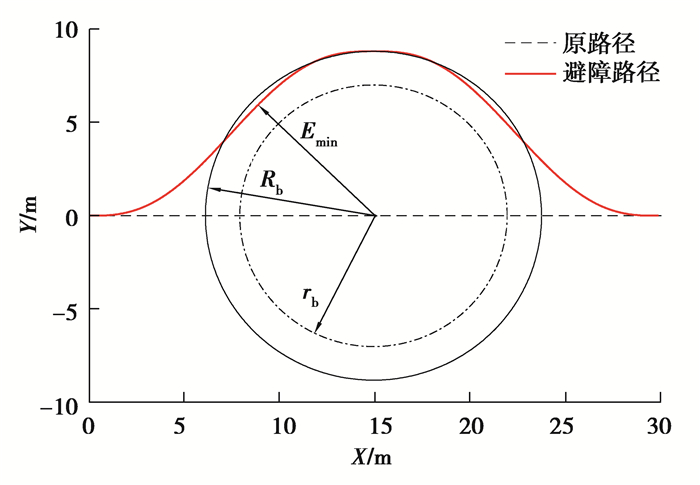
第二个约束条件是拖拉机与障碍物的最小距离大于或等于障碍物的安全距离,用Emin表示拖拉机与障碍物的最小距离,即Emin≥Rb或Emin≥Db。(12)
| ${E_{\min }}\geqslant{R_{\rm{b}}}{\rm{或 }}{E_{\min }}\geqslant{D_{\rm{b}}}{\rm{。}}$ | (12) |
对五次多项式函数曲线路径进行分析发现,当圆形障碍物几何中心位于原路径上,障碍物安全距离Rb接近和等于rmin时,Rmin略小于rmin,Emin略小于Rb,但它们的差值极小,可以忽略不计,这种情况下没有发生碰撞的风险。随着障碍物的安全距离Rb越来越大,如果障碍物还是简化为圆形障碍物,拖拉机与障碍物的最小距离将明显小于障碍物的安全距离,有发生碰撞的风险,如图 9所示。为了防止无人驾驶拖拉机与障碍物发生碰撞,把障碍物的安全距离大于拖拉机最小转弯半径的障碍物简化为矩形障碍物,此时Emin等于障碍物横向安全距离Db。仿真结果表明,基于改进最短切线法和五次多项式函数规划的避障路径长度短、光滑且曲率连续,具有很高的安全性,同时该方法生成路径简单快捷,具有很好的实时性。在保证安全作业为第一的情况下,该避障路径规划算法适用于无人驾驶拖拉机直线作业时的实时避障路径规划。
|
图 9 避障路径 Fig. 9 Obstacle avoidance path |
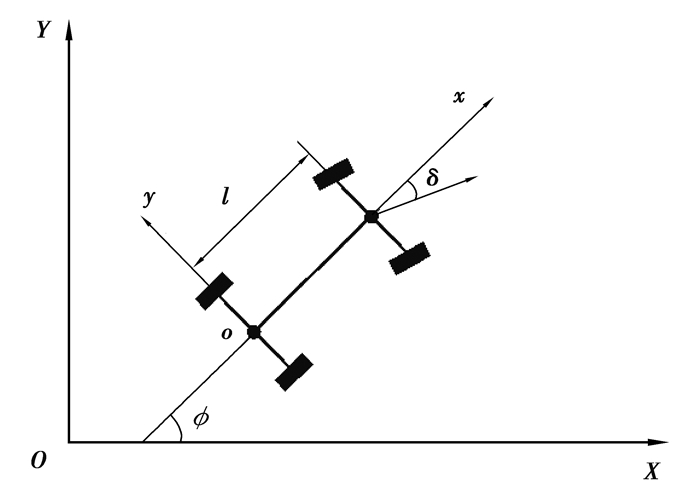
使用模型预测控制器作为无人驾驶拖拉机的路径跟踪控制器来验证路径的可跟踪性。无人驾驶拖拉机工作速度低,基于运动学模型设计的路径跟踪控制器具有可靠的控制性能和实时性,且对硬件设备要求低,适合无人驾驶拖拉机低成本、高可靠性的要求[21-23]。拖拉机运动学模型如图 10所示。
|
图 10 拖拉机运动学模型 Fig. 10 Tractor kinematics model |
根据文献[23]介绍的方法,以XOY建立地面坐标系,坐标系xoy表示车辆自身坐标系,建立车辆运动学方程
| $\left[ {\begin{array}{*{20}{l}} {\dot x}\\ {\dot y}\\ {\dot \phi } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \phi }\\ {\sin \phi }\\ {(\tan \delta )/l} \end{array}} \right]v{\rm{。}}$ | (13) |
对车辆运动学方程进行处理,得到线性化的车辆误差模型为
| $\mathop {\mathit{\boldsymbol{\widetilde X}}}\limits^\mathit{\boldsymbol{.}} = \left[ {\begin{array}{*{20}{c}} {\dot x - {{\dot x}_{\rm{r}}}}\\ {\dot y - {{\dot y}_{\rm{r}}}}\\ {\dot \phi - {{\dot \phi }_{\rm{r}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&0&{ - {v_{\rm{r}}}\sin {\phi _{\rm{r}}}}\\ 0&0&{{v_{\rm{r}}}\cos {\phi _{\rm{r}}}}\\ 0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {x - {x_{\rm{r}}}}\\ {y - {y_{\rm{r}}}}\\ {\phi - {\phi _{\rm{r}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\cos {\phi _{\rm{r}}}}&0\\ {\sin \varphi {\phi _{\rm{r}}}}&0\\ {\left( {\tan {\delta _{\rm{r}}}} \right)/l}&{{v_{\rm{r}}}/\left( {l{{\cos }^2}{\phi _{\rm{r}}}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {v - {v_{\rm{r}}}}\\ {\phi - {\phi _{\rm{r}}}} \end{array}} \right]{\rm{。}}$ | (14) |
为了使运动学模型满足在模型预测控制器中应用的要求,需要对式(14)进行离散化处理
| $\mathit{\boldsymbol{\widetilde X}}(k + 1) = {\mathit{\boldsymbol{A}}_{k, t}}\mathit{\boldsymbol{\widetilde X}}(k) + {\mathit{\boldsymbol{A}}_{k, t}}\mathit{\boldsymbol{\widetilde u}}(k){\rm{。}}$ | (15) |
系统的控制过程实际是一个优化求解过程,需要确定一个合适的优化目标,才能得到合适的控制量,采用的目标函数[24-25]为
| $\mathit{\boldsymbol{J}}(k) = \sum\limits_{i = 1}^{{N_{\rm{p}}}} {\left\| {\mathit{\boldsymbol{\eta }}(k + i\mid t) - {\mathit{\boldsymbol{\eta }}_{{\rm{ref}}}}(k + i\mid t)} \right\|_Q^2} + \sum\limits_{i = 1}^{{N_{\rm{c}}} - 1} {\left\| {\Delta \mathit{\boldsymbol{U}}(k + i\mid t)} \right\|_R^2} + \rho {\varepsilon ^2}{\rm{。}}$ | (16) |
无人驾驶拖拉机在行驶过程中会受到其自身机械结构约束、系统设定约束等,在路径跟踪控制过程中需要满足控制量极限约束和控制增量约束,表达式为
| $\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_{\min }}(t + k) \leqslant \mathit{\boldsymbol{u}}(t + k) \leqslant {\mathit{\boldsymbol{u}}_{\max }}(t + k), }\\ {\Delta {\mathit{\boldsymbol{u}}_{\min }}(t + k) \leqslant \Delta \mathit{\boldsymbol{u}}(t + k) \leqslant \Delta {\mathit{\boldsymbol{u}}_{\max }}(t + k){\rm{。}}} \end{array}} \right.$ | (17) |
考虑约束条件后,将目标函数转化为标准二次型形式,模型预测控制器的求解过程转化为求解以下优化问题
| $\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{J}}}(\xi (t), {\mathit{\boldsymbol{u}}}(t - 1), \Delta {\mathit{\boldsymbol{u}}}(t)) = {{\left[ {\Delta {\mathit{\boldsymbol{u}}}{{(t)}^{\rm{T}}}, \varepsilon } \right]}^{\rm{T}}}{{\mathit{\boldsymbol{H}}}_t}\left[ {\Delta {\mathit{\boldsymbol{u}}}{{(t)}^{\rm{T}}}, \varepsilon } \right] + {{\mathit{\boldsymbol{G}}}_t}\left[ {\Delta {\mathit{\boldsymbol{u}}}{{(t)}^{\rm{T}}}, \varepsilon } \right], }\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}\Delta {{\mathit{\boldsymbol{U}}}_{\min }} \leqslant \Delta {{\mathit{\boldsymbol{U}}}_t} \leqslant \Delta {{\mathit{\boldsymbol{U}}}_{\max }}, }\\ {{{\mathit{\boldsymbol{U}}}_{\min }} \leqslant {\mathit{\boldsymbol{A}}}\Delta {{\mathit{\boldsymbol{U}}}_t} + {{\mathit{\boldsymbol{U}}}_t} \leqslant {{\mathit{\boldsymbol{U}}}_{\max }}{\rm{。}}} \end{array}} \right.$ | (18) |
对式(18)求解后得到控制时域内的控制增量序列
| $\Delta \mathit{\boldsymbol{U}}_t^* = {\left[ {\Delta \mathit{\boldsymbol{u}}_t^*, \Delta \mathit{\boldsymbol{u}}_{t + 1}^*, \cdots , \Delta \mathit{\boldsymbol{u}}_{t + {N_{\rm{c}}} - 1}^*} \right]^{\rm{T}}}{\rm{。}}$ | (19) |
将该控制增量序列中的第一个元素作为当前时刻系统的输入增量,即
| $\mathit{\boldsymbol{u}}(t) = \mathit{\boldsymbol{u}}(t - 1) + \Delta \mathit{\boldsymbol{u}}_t^*{\rm{。}}$ | (20) |
在下一时刻,重复上述步骤,以此循环实现对无人驾驶拖拉机的路径跟踪。
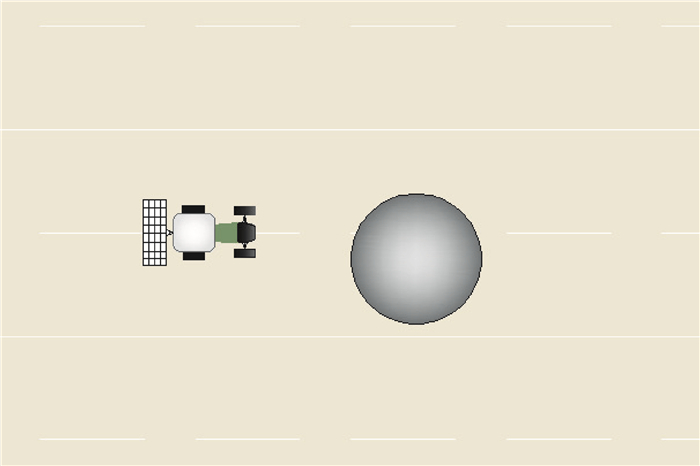
3.2 联合仿真分析搭建Simulink与CarSim联合仿真平台对无人驾驶拖拉机的避障路径规划及跟踪控制进行联合仿真。拖拉机工作速度一般比较低,根据不同作业类型速度也有所不同,常州东风无人驾驶拖拉机耕地时的工作速度为4~8 km/h,基于该型无人驾驶拖拉机在CarSim仿真平台中建立拖拉机模型。农业机具的宽度一般比拖拉机的宽度大,仿真时选用的某款农业播种机的宽度为2.6 m。仿真中,拖拉机避障速度设置为8 km/h,障碍物半径为3.0 m,障碍物几何中心位于原路径右侧1.0 m处,场景如图 11和12所示。模型预测控制器的基本参数设置为:预测时域NP=60,控制时域Nc=30,控制周期T=0.01 s,仿真时间设置为9.00 s,仿真结果如图 13和14所示。
|
图 11 简化场景 Fig. 11 The Simplified scene |

|
图 12 CarSim仿真场景 Fig. 12 CarSim simulation scene |
|
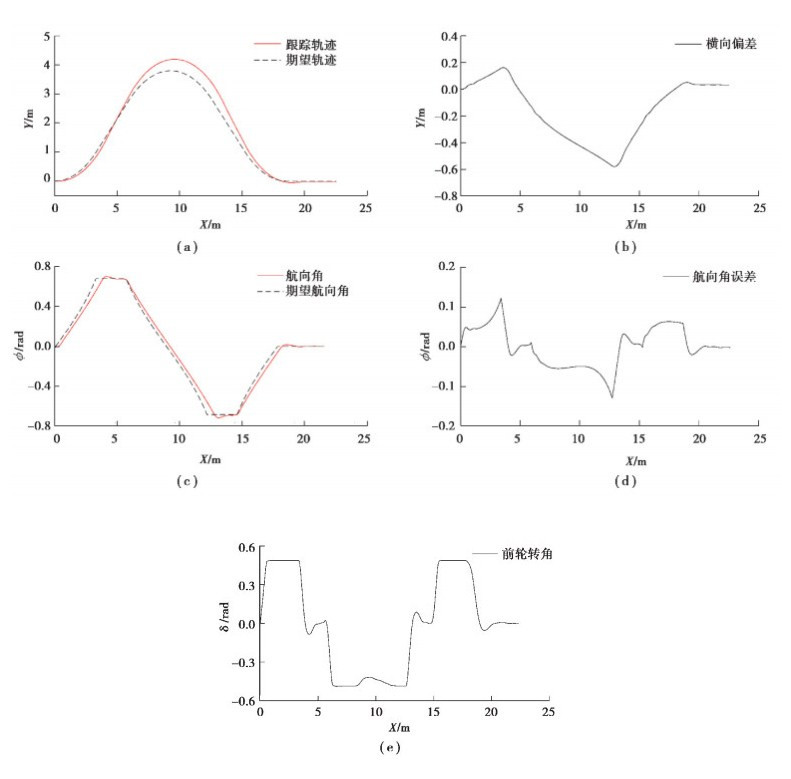
图 13 基于改进最短切线法的实时避障仿真结果 Fig. 13 Real-time obstacle avoidance simulation results based on the improved shortest tangent method |
|
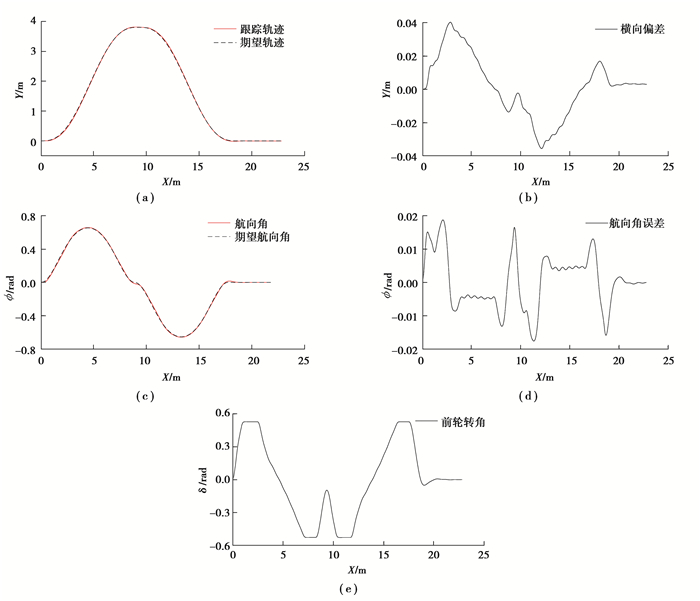
图 14 基于实时避障路径规划算法的实时避障仿真结果 Fig. 14 Real-time obstacle avoidance simulation results based on real-time obstacle avoidance path planning algorithm |
分别用改进最短切线法和文中实时避障路径规划算法与相同的跟踪控制算法结合进行避障仿真,图 13为基于改进最短切线法的实时避障仿真结果,图 14为基于该路径规划算法的实时避障仿真结果。对比分析可以看出,基于实时避障路径规划算法的避障跟踪轨迹与期望轨迹基本重合,轨迹横向偏差更小,偏差在4.1 cm以内,同时航向角偏差也更小,偏差控制在0.02 rad以内,跟踪控制精度更高,说明该路径规划算法规划的路径更易于跟踪控制,适用于无人驾驶拖拉机作业时的实时避障路径规划。
无人驾驶拖拉机实时避障路径规划算法的理论设计和仿真分析已经完成,在后续的工作中将进行实车测试,其准备工作正在有条不紊地进行中,以进一步验证实时避障路径规划算法的有效性。
4 结论1) 对固定障碍物进行简化处理,把障碍物简化为圆形障碍物和矩形障碍物,简化方法简单有效,减少了路径的冗余,提高了作业区域的覆盖率。
2) 基于改进最短切线法和五次多项式函数规划的避障路径长度短、光滑且曲率连续,具有很高的安全性,不管是针对圆形障碍物还是矩形障碍物,该路径规划算法简单快捷,具有很高的实时性。
3) 联合仿真结果表明,与改进最短切线法相比,基于实时避障路径规划算法的避障跟踪轨迹与期望轨迹基本重合,轨迹横向偏差更小,航向角偏差也更小,跟踪控制精度更高,更易于跟踪控制,适用于无人驾驶拖拉机作业时的实时避障路径规划。
| [1] |
李丹丹, 史云, 李会宾, 等. 农业机器人研究进展评述[J]. 中国农业信息, 2018, 30(6): 1-17. Li D D, Shi Y, Li H B, et al. Review on the progress of agricultural robot research[J]. China Agricultural Informatics, 2018, 30(6): 1-17. (in Chinese) |
| [2] |
姬长英, 周俊. 农业机械导航技术发展分析[J]. 农业机械学报, 2014, 45(9): 44-54. Ji C Y, Zhou J. Current situation of navigation technologies for agricultural machinery[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(9): 44-54. (in Chinese) |
| [3] |
胡静涛, 高雷, 白晓平, 等. 农业机械自动导航技术研究进展[J]. 农业工程学报, 2015, 31(10): 1-10. Hu J T, Gao L, Bai X P, et al. Review of research on automatic guidance of agricultural vehicles[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(10): 1-10. (in Chinese) DOI:10.11975/j.issn.1002-6819.2015.10.001 |
| [4] |
Gan-Mor S, Clark R L, Upchurch B L. Implement lateral position accuracy under RTK-GPS tractor guidance[J]. Computers and Electronics in Agriculture, 2007, 59(1/2): 31-38. |
| [5] |
Kaivosoja J, Linkolehto R. GNSS error simulator for farm machinery navigation development[J]. Computers and Electronics in Agriculture, 2015, 119: 166-177. DOI:10.1016/j.compag.2015.10.021 |
| [6] |
兰玉彬, 王林琳, 张亚莉. 农用无人机避障技术的应用现状及展望[J]. 农业工程学报, 2018, 34(9): 104-113. Lan Y B, Wang L L, Zhang Y L. Application and prospect on obstacle avoidance technology for agricultural UAV[J]. Transactions of the Chinese Society of Agricultural Engineering, 2018, 34(9): 104-113. (in Chinese) |
| [7] |
Eltner A, Schneider D. Analysis of different methods for 3D reconstruction of natural surfaces from parallel-axes UAV images[J]. The Photogrammetric Record, 2015, 30(151): 279-299. DOI:10.1111/phor.12115 |
| [8] |
韩冰, 陈军. 拖拉机行驶路径的多项式设计[J]. 农机化研究, 2006, 28(10): 98-99, 106. Han B, Chen J. Autonomous tractor trajectory design using polynomial function[J]. Journal of Agricultural Mechanization Research, 2006, 28(10): 98-99, 106. (in Chinese) DOI:10.3969/j.issn.1003-188X.2006.10.034 |
| [9] |
霍迎辉, 张连明, 杨宜民. 移动机器人路径规划的最短切线路径算法[J]. 广东自动化与信息工程, 2003, 24(1): 10-12. Huo Y H, Zhang L M, Yang Y M. The shortest tangent path planning for mobile robot[J]. Guangdong Automation & Information Engineering, 2003, 24(1): 10-12. (in Chinese) |
| [10] |
刘向锋. 面向GPS导航拖拉机的最优全局覆盖路径规划研究[D]. 阜新: 辽宁工程技术大学, 2011. Liu X F. Research on optimal global path planning for complete coverage with GPS guidance on tractor[D]. Fuxin: Liaoning Technical University, 2011. (in Chinese) |
| [11] |
奚小波, 史扬杰, 单翔, 等. 基于Bezier曲线优化的农机自动驾驶避障控制方法[J]. 农业工程学报, 2019, 35(19): 82-88. Xi X B, Shi Y J, Shan X, et al. Obstacle avoidance path control method for agricultural machinery automatic driving based on optimized Bezier[J]. Transactions of the Chinese Society of Agricultural Engineering, 2019, 35(19): 82-88. (in Chinese) DOI:10.11975/j.issn.1002-6819.2019.19.010 |
| [12] |
郭成洋, 刘美辰, 高泽宁, 等. 基于改进人工势场法的农机避障方法研究[J]. 中国农机化学报, 2020, 41(3): 152-157. Guo C Y, Liu M C, Gao Z N, et al. Research on agricultural machinery obstacle avoidance method based on improved artificial potential field method[J]. Journal of Chinese Agricultural Mechanization, 2020, 41(3): 152-157. (in Chinese) |
| [13] |
Yao J F, Lin C, Xie X B, et al. Path planning for virtual human motion using improved A* star algorithm[C]//2010 Seventh International Conference on Information Technology: New Generations, April 12-14, 2010, Las Vegas, NV, USA. IEEE, 2010: 1154-1158.
|
| [14] |
Ge C J, Kasabov N, Liu Z, et al. A spiking neural network model for obstacle avoidance in simulated prosthetic vision[J]. Information Sciences, 2017, 399: 30-42. DOI:10.1016/j.ins.2017.03.006 |
| [15] |
Wang M, Liu. Fuzzy logic based robot path planning in unknown environment[C]//2005 International Conference on Machine Learning and Cybernetics, August 18-21, 2005, Guangzhou, China. IEEE, 2005: 813-818.
|
| [16] |
Oksanen T, Visala A. Coverage path planning algorithms for agricultural field machines[J]. Journal of Field Robotics, 2009, 26(8): 651-668. DOI:10.1002/rob.20300 |
| [17] |
孟志军, 刘卉, 王华, 等. 农田作业机械路径优化方法[J]. 农业机械学报, 2012, 43(6): 147-152. Meng Z J, Liu H, Wang H, et al. Optimal path planning for agricultural machinery[J]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(6): 147-152. (in Chinese) DOI:10.6041/j.issn.1000-1298.2012.06.027 |
| [18] |
Ball D, Upcroft B, Wyeth G, et al. Vision-based obstacle detection and navigation for an agricultural robot[J]. Journal of Field Robotics, 2016, 33(8): 1107-1130. DOI:10.1002/rob.21644 |
| [19] |
贾春雪, 罗琦, 龚杨杨. 不规则障碍物的避障路径规划[J]. 计算机科学, 2017, 44(9): 290-295. Jia C X, Luo Q, Gong Y Y. Obstacle avoidance path planning for irregular obstacles[J]. Computer Science, 2017, 44(9): 290-295. (in Chinese) |
| [20] |
刘宇峰, 姬长英, 田光兆, 等. 自主导航农业机械避障路径规划[J]. 华南农业大学学报, 2020, 41(2): 117-125. Liu Y F, Ji C Y, Tian G Z, et al. Obstacle avoidance path planning for autonomous navigation agricultural machinery[J]. Journal of South China Agricultural University, 2020, 41(2): 117-125. (in Chinese) |
| [21] |
严国军, 贲能军, 顾建华, 等. 基于MPC的无人驾驶拖拉机轨迹跟踪控制[J]. 重庆交通大学学报(自然科学版), 2019, 38(9): 1-6. Yan G J, Ben N J, Gu J H, et al. Trajectory tracking control of intelligent tractor based on MPC algorithm[J]. Journal of Chongqing Jiaotong University (Natural Science), 2019, 38(9): 1-6. (in Chinese) DOI:10.3969/j.issn.1674-0696.2019.09.01 |
| [22] |
白国星, 刘立, 孟宇, 等. 基于非线性模型预测控制的农用拖挂车避障控制器研究[J]. 农业机械学报, 2019, 50(4): 356-362. Bai G X, Liu L, Meng Y, et al. Study of obstacle avoidance controller of agricultural tractor-trailers based on predictive control of nonlinear model[J]. Transactions of the Chinese Society for Agricultural Machinery, 2019, 50(4): 356-362. (in Chinese) |
| [23] |
龚建伟, 刘凯, 齐建永. 无人驾驶车辆模型预测控制[M]. 2版. 北京: 北京理工大学出版社, 2020. Gong J W, Liu K, Qi J Y. Model predictive control for self-driving vehicles[M]. 2nd ed. Beijing: Beijing Insititute of Technology Press, 2020. (in Chinese) |
| [24] |
Borrelli F, Falcone P, Keviczky T, et al. MPC-based approach to active steering for autonomous vehicle systems[J]. Int J of Vehicle Autonomous Systems, 2005, 3(2/3/4): 265-291. DOI:10.1504/IJVAS.2005.008237 |
| [25] |
李升波, 王建强, 李克强. 软约束线性模型预测控制系统的稳定性方法[J]. 清华大学学报(自然科学版), 2010, 50(11): 1848-1852. Li S B, Wang J Q, Li K Q. Stabilization of linear predictive control systems with softening constraints[J]. Journal of Tsinghua University (Science and Technology), 2010, 50(11): 1848-1852. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45


