1b. 武汉大学 水射流理论与新技术湖北省重点实验室, 湖北 武汉 430072;
2. 炼焦煤资源开发及综合利用国家重点实验室, 河南 平顶山 467000;
3. 中国平煤神马能源化工集团有限责任公司, 河南 平顶山 467000
1b. Hubei Key Laboratory of Waterjet Theory and New Technology, Wuhan University, Wuhan 430072, P. R. China;
2. State Key Laboratory of Coking Coal Exploitation and Comprehensive Utilization, Pingdingshan 467000, Henan, P. R. China;
3. China PingMei ShenMa Group, Pingdingshan 467000, Henan, P. R. China
管道作为一种重要的工业物料传输工具,承担着能源输送、动力传输、物质循环的重大任务, 在国民生产中发挥着重要作用,被誉为工业生产的动脉。柔性压力管道作为一种重要的流体输送工具,以适用性强、安装快捷等特点广泛应用于临时或机动工程中,如工程机械、煤矿工业、冶金锻压、各种机床以及各工业部门机械化、自动化液压系统中输送具有一定压力和温度的石油基液体、气体等。当柔性压力管道脱扣断裂时,管内高压流体喷射而出,管道受到流体的喷射力作用发生变形,管道的变形也引起流场变化,这种流体和固体间的耦合作用,使管道持续发生甩动,对周围人或物的安全造成极大的威胁。柔性压力管道工作压力高,甩击事故时常发生。当应用于高压射流技术时,其工作压力普遍在20 MPa以上,在采矿、非常规油气开采等特定领域中,超高压水射流工作压力已达400 MPa以上。由于管道自身韧性小,管道振甩波及范围大,在同一尺度下的甩击破坏性强,防控难度更大。柔性压力管道在管道破断泄漏过程中涉及的耦合参数较多,加上柔性压力管道在铺设过程中比较随意,延伸过程中管道起伏不定情况更为复杂。目前有关柔性压力管道甩击运动的特点和防护理论成果较少,随着柔性压力管道的应用范围加大及工作压力等级的提高,这项工作变得尤为迫切,特别是矿业和石油行业临时性使用的柔性压力管道数量极多,因此很有必要对柔性压力管道的甩击运动特性进行系统研究,提高我国的压力管道安全管理水平。
柔性压力管道的甩击运动是一种高度非线性化的运动,本质上是一个大变形瞬态动力学过程。几何非线性、材料非线性和接触非线性都对管道的甩击运动有非常显著的影响,在分析管道甩击运动的过程中,很多理论都难以同时考虑到以上几种情况。随着计算机技术的飞速发展,利用数值模拟的方法对柔性管道的甩击行为研究得以实现,给该问题带来了新的突破方向。在20世纪70年代和80年代,意大利Dini、Lazzeri等先后发展了FRUSTRA、PAULA82等有限元软件,美国通用电气也开发了三维非线性动力分析程序COMET以及ADINA、ABAQUS等大型通用有限元分析软件,这些软件对简化过后的数值模型进行分析求解。该阶段主要采用梁单元模拟管道,用弹簧单元模拟限制件,在理论上尚存在诸多不完善的地方。Dini和Lazzeri[1-3]随后改进了梁单元模型,通过建立管道扁平化下“弯矩-曲率”的非线性关系,使其更符合管道甩击过程中的变形。Ueda等[4]则在对管道弯头碰撞区进行静力弹塑性分析尝试使用壳单元模型,取得了不错的效果。Ma等[5]使用ADINA分析程序对管道与限制件之间碰撞接触进行了数值模拟计算。1997年,Olson等[6]对直管与管内流体的耦合振动变形的有限元法进行了综述,系统地总结了计算压力管道流固耦合问题的基本思想。Potapov等[7]利用一维、三维混合管道模型对甩击运动的变形和断裂情况进行了模拟计算,取得了比简化的管道模型更好的结果。刘德辅等[8]利用有限单元法推导在外界环境载荷条件下管道的侧向振动微分方程,研究随机波浪对管道振动的影响。张艳萍等[9]采用结构有限元方法和CFD方法实现管道与流体间的双向耦合,重点研究了变化流速下管道结构和流体的瞬态响应。Reid等[10]利用小直径悬臂管的甩击过程来模拟研究管道的甩击行为,得到了管道甩击运动的影响范围,并进行了甩击测试实验对结果进行验证。Vongmongkol等[11]和Pieters等[12]研究了管道与防甩击限制件的碰撞问题,初步得到了冲击力和管道变形等参数的简化计算方法。Zhao等[13]采用有限元法,结合RANS方程研究了在横向流作用下管道排列方式对甩击振动的影响。王春霖等[14]利用有限元分析软件LS-DYNA模拟了管道在环向断裂条件下的甩击运动行为,但他的分析没有考虑管道的大变形效应,其结果可靠性较差。He等[15]基于流体弹性模型,建立了管道非线性方程,推动了管道振动锁定区域研究计算方法发展。Li等[16]采用变分迭代法开展了对两端弹性支承限制下输流管道的流固耦合振动理论研究,并进行了实验加以验证。刘锋等[17]采用不同工况下的弯矩-曲率关系对管道瞬态甩击运动进行了数值模拟分析。
通过以上分析,发现目前学者对流体喷射力影响下管道的甩击运动和变形特性进行的数值模拟研究取得了一系列较好的研究成果,但总的来说仍存在不少问题。其中,最关键的是大多数的研究都以悬臂直管作为研究对象,研究思路都是着眼于固体,流体冲击力的计算过于简化,多数情况下只是简单将其作为变化荷载加载在固体上,同时对弯管这一类更复杂的情景考虑较少。然而,正如前文所言,管道的甩击运动是一种典型的流固耦合问题,流体的各项参数会受到管道变形的影响,仅从固体出发无法真正得到关于整个管道的运动,流体对柔性压力管道的作用不能简单地简化为动荷载或冲击荷载。柔性压力管道由于弹性较大,受流固耦合的影响更加明显。因此,需要进一步从整体出发,将流体和固体统一考虑,求解整个流固耦合方程,得到柔性压力管道甩击运动的特点,并对影响因素进行分析。笔者拟在现有刚性管道失稳振动分析基础上针对柔性管道运行过程中发生的脱扣断裂大变形振甩行为进行数值模拟研究,系统分析柔性管道流固耦合作用下断裂失稳运动规律及影响因素,为柔性压力管道安全运行及管理提供理论支撑。
1 柔性压力管道有限元计算模型流固耦合计算涉及到流体域和固体结构的数值计算,柔性压力管道弹性大,在流体的作用下会发生大变形运动,因此不能忽略管道的形变,必须进行双向流固耦合计算。ANSYS Workbench平台可以很好地解决不同求解器之间的数据传递,并在耦合求解器中进行数据交换,对流固交界面进行求解计算,实现双向流固耦合。这里拟采用ANSYS Workbench平台进行柔性压力管道甩击运动的模拟计算。
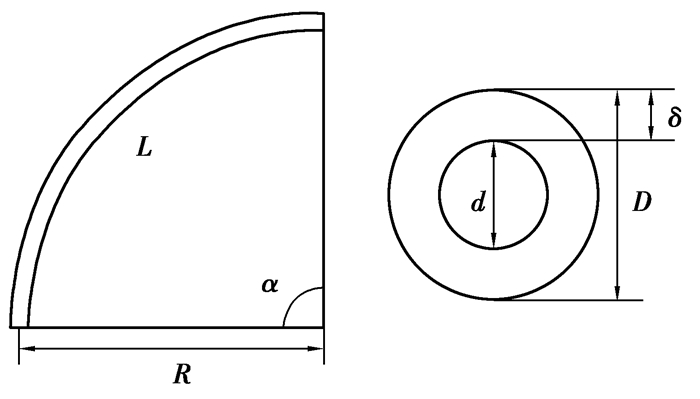
1.1 建立几何模型柔性管道由于结构刚度低、可变性强、自由度高等特点多数应用在临时工程中,在延展过程中铺设比较随意,管道起伏不定,存在许多弯曲段,管道的流固耦合失稳表现得非常强烈。直角弯是柔性管道布设中常见的一种弯曲类型,选取这种弯曲形状的柔性压力管道作为研究对象,分析甩击过程中的形变、应力分布和能量分布等问题。图 1中管道内部为流体域。几何尺寸参数如表 1所示,包括管道长度L,管道弯曲半径R,管道弯曲角度α,管道外径D,管道内径d以及管壁厚度δ。
|
图 1 柔性压力管道模型 Fig. 1 Geometric model of flexible pressure pipeline |
| 表 1 管道几何参数 Table 1 Pipe geometry parameters |
关于柔性压力管道材料物理参数,采用的柔性压力管道由两层钢丝包裹复合而成,其壁面能承受的最大工作压力为25 MPa。管道内流体为水。具体参数见表 2。
| 表 2 材料物理参数 Table 2 Material parameters |
管道的流固耦合计算流体域时需抑制固体管道的几何体,计算固体域时也同样如此,考虑到柔性压力管道甩击运动幅度大,本次计算采用适应性更好的四面体网格。
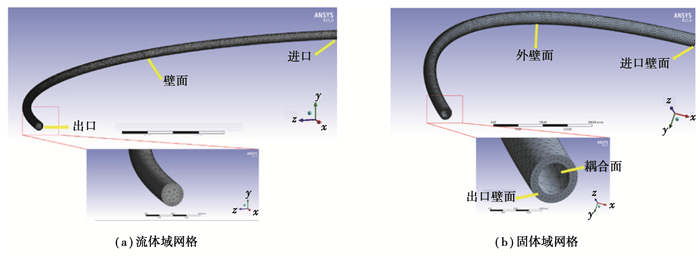
计算中流体域使用映射面网格方式进行划分,并在流体边界处进行加密,边界层网格共5层,增长率为1.3;固体域使用sweep方式进行网格划分。为了提高计算效率获得可靠的模拟结果,计算过程中对网格数量进行无关性验证,最终确定流体域和固体域网格尺寸均为3 mm,网格数分别为112 860和17 930。流体域和固体域网格划分如图 2所示。
|
图 2 网格划分示意图 Fig. 2 Schematic diagram of meshing |
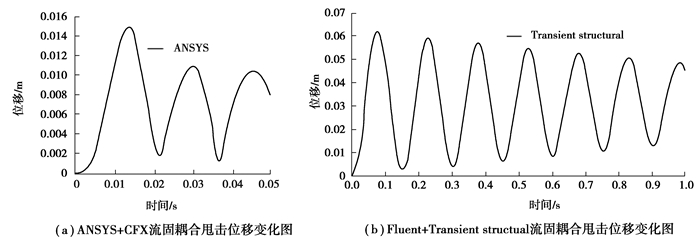
管道甩击是典型的流固耦合问题,实际上也可以看成管道的一种振动行为,当振动幅度达到一定程度时,管道振动发展成为甩击。因此,在研究管道甩击特性的数值模拟研究过程中,可以参考输流管道流固耦合有限元模型,利用Workbench实现双向流固耦合仿真分析。陈雄[18]研究90°柔性液压弯管振动特性时发现,随着流速的增加,管道最大位移和最大幅值增加,且在恒定流速、脉动流速和脉动压力下,管道速度和位移的变化趋势大体相同。刘发明等[19]通过Workbench中的ANSYS+CFX建立流固耦合模型,研究了脉动入口压力下管道的自由甩动情况。如图 3所示,(a)图为刘发明等[19]所绘管道自由端位移变化图,(b)图为本文仿真时所绘位移变化图。将两者位移变化情况进行对比,可以发现具有相同的变化趋势,位移呈现周期性波动,且位移峰值随着时间增加逐渐减小。因此,通过Workbench进行双向流固耦合仿真计算能较好地对管道甩击特性进行研究。
|
图 3 管道甩击位移对比图 Fig. 3 Comparison of pipe displacement |
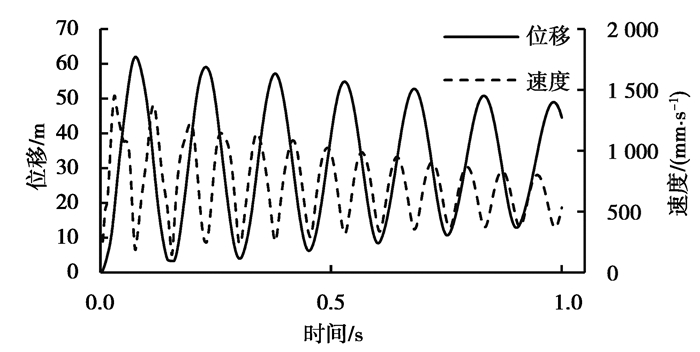
管道的最大位移和最大速度可衡量管道甩击的剧烈程度,在本次计算中流体流速为v=20 m/s,管道弯曲半径为1 200 mm,弯曲角度为90°,图 4是管道发生甩击的整个过程中管道最大总位移和最大总速度变化图像。从图 4中可以看出在柔性压力管道发生甩击运动时,管道的最大位移和速度呈周期性变化。当流体的流速为20 m/s,管道内流体为水的条件下,整个甩击过程中最大变形位移达到62.0 mm,最大甩击速度则达到了1 452.4 mm/s。
|
图 4 柔性压力管道甩击变形位移和速度变化曲线 Fig. 4 Deformation displacement and velocity change curves of flexible pressure pipeline |
随着时间的推移,最大位移和最大甩击速度的峰值都在逐渐衰减。从能量转化的角度来看,柔性压力管道发生变形时,部分能量被管道材料吸收,如果材料发生了塑性变形,则这部分能量将会损失,导致管道变形的位移和速度降低。因此,经过一段时间后,管道的状态可能会到达稳定的变化趋势。管道变形位移波动的平衡点约为25 mm,表明管道始终存在变形,最终在新的位置重新建立了平衡。但在实际工程中,这种平衡是很不稳定的,一旦流体、管道等任何状态发生变化,管道会马上发生二次甩击。图 5是管道总体最大变形位移和各个坐标轴方向上位移分量随时间的变化情况。由图 5可知,在y轴方向,管道的正向位移始终为0,管道在y轴方向上没有发生扭曲。相反,x轴方向和z轴方向上同时存在正负2个方向上的位移,即管道在这2个方向上发生了扭曲。
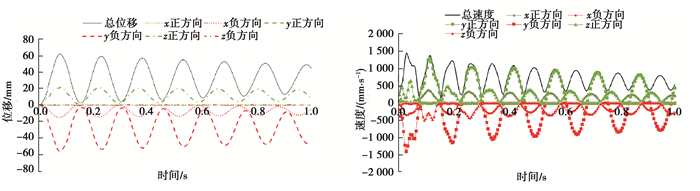
|
图 5 柔性压力管道总变形位移、甩击速度和各分量变化曲线 Fig. 5 Total deformation displacement, slamming speed and various components change curve |
对图 4中的柔性管道甩击变形位移变化曲线做快速傅里叶变换,得到甩击过程中振动信号的幅频曲线如图 6所示。从图 6中可以看出,在甩击过程中振动信号主要分布在低频段,主导频率为6.65 Hz。对该系统进行模态分析,得到其前六阶固有频率如表 3所示。由此可见,在柔性管道甩击过程中,被激发的主要是第二阶模态。
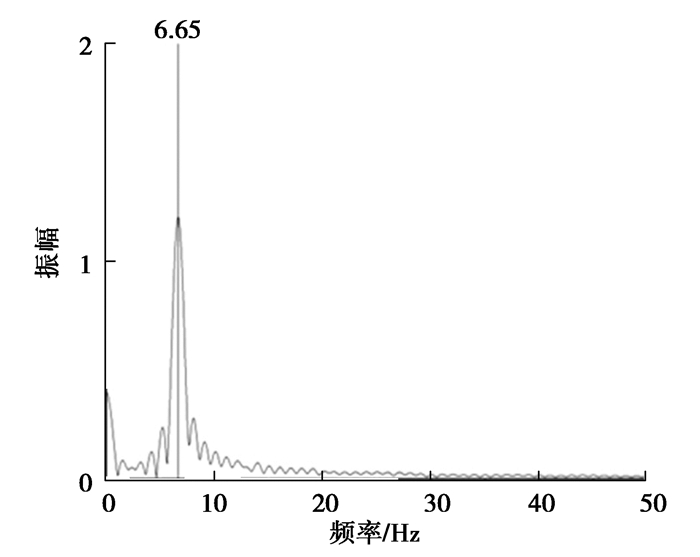
|
图 6 柔性压力管道甩击振动幅频曲线 Fig. 6 Amplitude-frequency curve of flexible pressure pipeline |
| 表 3 系统前六阶固有频率 Table 3 System natural frequencies |
等效应力是材料力学理论中将主应力的某一综合值与材料单向拉伸轴向拉压许用应力比较综合值。等效应力越大,管道离发生失效断裂就越近。柔性压力管道的等效应力分布情况如图 7所示,管道在y轴负方向上变形位移最大,在相反的方向上发生了拉伸变形,等效应力分布集中且数值非常大,由图 8可知在管道内水的流速为20 m/s时,等效应力最大可达50.4 MPa,而在管道受到压缩变形的一侧,等效应力值很小。
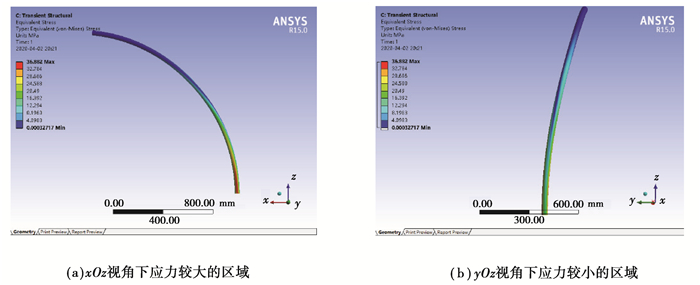
|
图 7 柔性压力管道等效应力分布图 Fig. 7 Equivalent stress distribution |
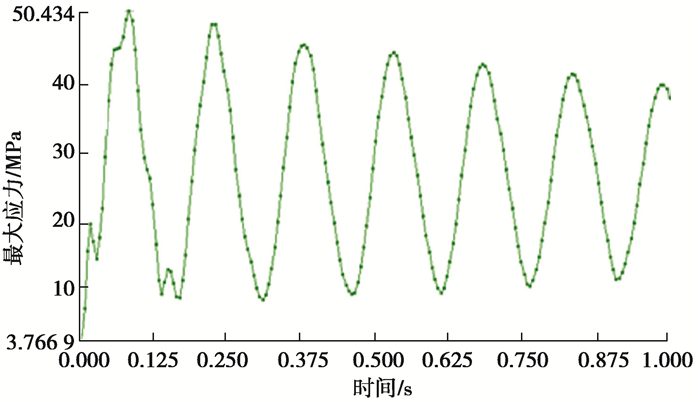
|
图 8 柔性压力管道甩击过程最大应力变化曲线 Fig. 8 Maximum stress curve |
管道受到的压缩变形可以用应变能来描述,应变能越大,材料就越容易达到屈服极限。图 9是柔性压力管道处于最大变形位移时的应变能分布情况,除了前面发生拉伸变形的部分,管道靠近变形方向的内侧的应变能也非常明显。这表明尽管柔性压力管道靠近固定约束这一侧变形位移较小,但管道材料内部反而受到了强烈的拉伸和压缩作用。如果管道的变形足够大,柔性压力管道的这些位置可能因应力过大发生二次断裂,造成更大的人员和财产损失。
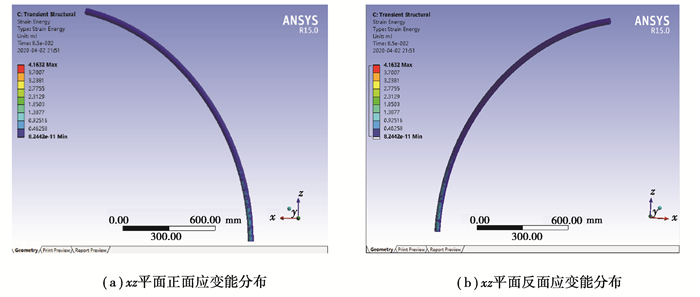
|
图 9 柔性压力管道甩击运动应变能分布 Fig. 9 Strain energy distribution |
管道中流体流速由实际应用中所需的工况决定,其大小对柔性压力管道的甩击行为具有明显影响。为了研究不同流速下管道的甩击行为,分别对流体流速为20,30,40 m/s时柔性压力管道甩击运动进行计算分析。从图 10、11可以发现,柔性压力管道的最大变形位移、甩击速度、等效应力都随时间不断衰减,衰减速度基本相同。当v=20 m/s时第七个变形位移峰值约为第一个峰值的78.9%,而当v=40 m/s时,这个比例为78.1%,说明流速增大,管道吸收的能量增加,管道的失效速度加快。
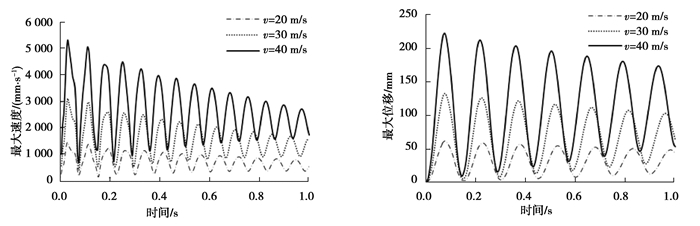
|
图 10 不同速度下的最大变形位移和甩击速度变化曲线 Fig. 10 Curves of maximum deformation displacement and slamming speed at different speeds |
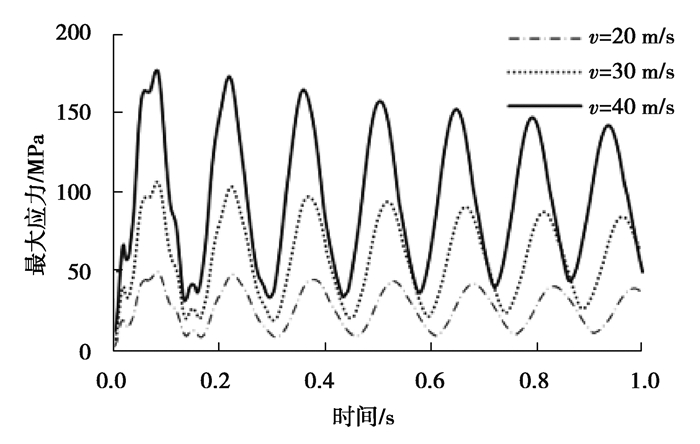
|
图 11 不同流速下的最大应力变化曲线 Fig. 11 Variation curve of maximum stress at different flow rates |
表 4是在不同的流体流速下,柔性压力管道的甩击运动各项参数。从表 4中可以看到,随着流体速度的增加,甩击变形位移、甩击速度、等效应力急剧增加,应变能的增加速度甚至呈现高次方变化。
| 表 4 柔性压力管道甩击运动各项参数最大值 Table 4 Maximum sports parameters |
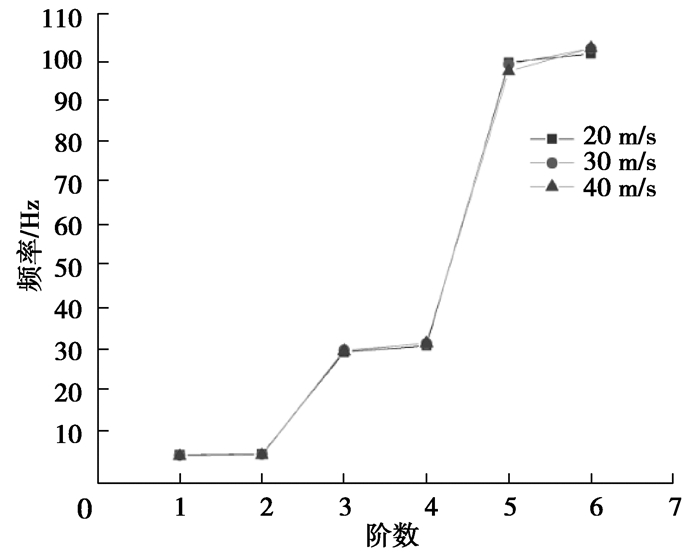
对不同流速下管道最大变形位移变化曲线做快速傅里叶变换,得到不同流速下甩击过程中振动信号的幅频曲线如图 12所示。随着流速的增加,振动信号的幅值明显增加,但振动信号的频率分布及主导频率的变化则相对较小。对不同流速下的该系统进行模态分析,得到不同流速下的前六阶固有频率如图 13所示。从图 13中可以看出随着流速的增大,系统前六阶固有频率变化较小,在一定情况下可以忽略不考虑。在流速为30 m/s和40 m/s时,柔性压力管道甩击振动的主导频率均靠近系统第二阶固有频率。可见,管道甩击过程中被激发的仍为第二阶模态。
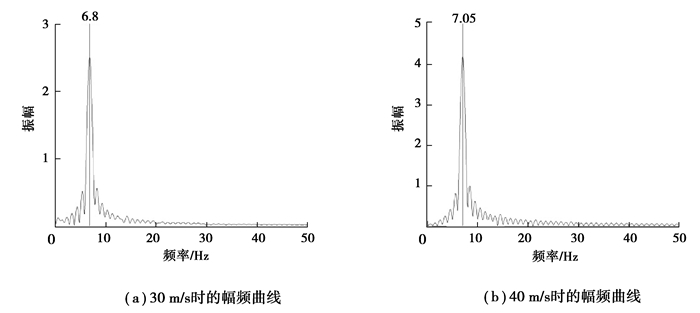
|
图 12 不同流速下柔性压力管道甩击振动幅频曲线 Fig. 12 Amplitude-frequency curve of flexible pressure pipeline under different flow velocities |
|
图 13 不同流速系统前六阶固有频率 Fig. 13 Natural frequencies of system under different flow velocities |
柔性压力管道广泛应用于工程实践中,输送介质也是多种多样,如液压管道中流体介质是液压油,矿井中的管道很多是水和磨料的混合物。这些流体性质差异较大,为了研究不同流体的性质对管道甩击的影响,对液压油、水和含磨料的混合水3种流体进行柔性压力管道的甩击特性分析。其中混合水由体积分数为8%的石榴石作为磨料混合而成。在计算中,不考虑管道在径向发生的变形,即不改变流体域的体积大小,所以不用考虑流体的压缩性。3种流体的主要性质如表 5所示。
| 表 5 3种流体的基本性质 Table 5 Basic properties of the three fluids |
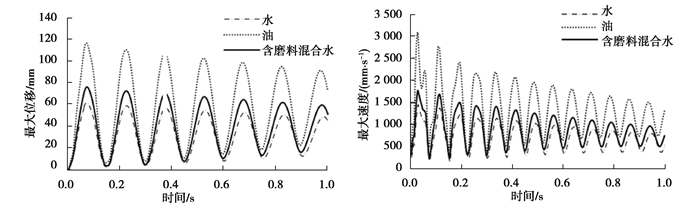
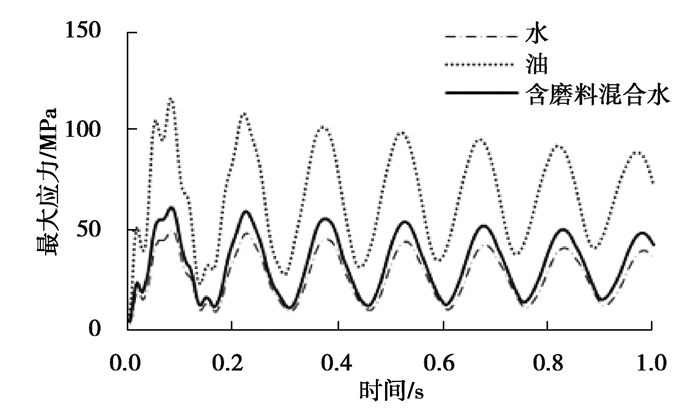
图 14、15分别是流体为油和含磨料水时,流速v=20 m/s的条件下柔性压力管道甩击过程中的变形位移、甩击速度、等效应力的变化曲线。流体的性质变化对柔性压力管道甩击运动的总体趋势没有影响,整体来看都是随着时间的增加甩击的强度在逐渐减弱。
|
图 14 不同流体作用下的最大变形位移和甩击速度变化曲线 Fig. 14 Variation curve of maximum deformation displacement and slamming velocity under different fluids |
|
图 15 不同流体作用下的最大应力变化曲线 Fig. 15 Variation curve of maximum stress under different fluids |
表 6分别是3种不同流体下柔性压力管道甩击运动各项参数的最大值。含磨料的水和纯水相比,密度更大,能量更高,因此在各项甩击运动参数上都相对较大,二者的数值与流体的密度大致成正比。即流体密度越大,则柔性压力管道的甩击运动越剧烈,管道材料承受的应力等也越大,危险性也越高。
| 表 6 不同流体下柔性压力管道甩击运动各项参数的最大值 Table 6 Maximum values of parameters of flicking motion of flexible pressure pipes under different fluids |
液压油和水相比,密度更小,但黏度系数更大,从而导致结果上的差异。根据水和含磨料水的比较结果可知,如果液压油的黏度系数和水一样,那么柔性压力管道的甩击应该更轻微。由于液压油具有较大的黏度系数,使其在密度更小的条件下,柔性压力管道的甩击剧烈程度远超流体为水时的情况。流体黏度越大,其和柔性压力管道的耦合效应就越强烈,可以将更多的能量传递到管道,引起更加剧烈的甩击运动。
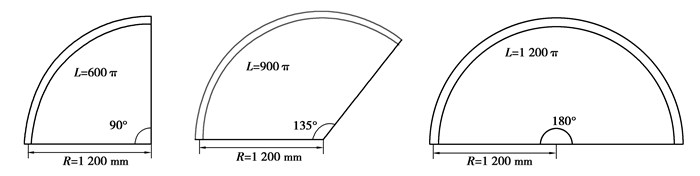
3.3 管道弯曲长度柔性压力管道的在铺设过程中,弯曲半径会随实际情况而改变。为了研究不同的弯曲长度对柔性压力管道甩击运动的影响,建立了3种不同长度的管道模型,长度分别为600π、900π和1 200π,如图 16所示。
|
图 16 3种不同弯曲长度管道模型 Fig. 16 Three kinds of pipe models with different bending lengths |
图 17和图 18是管道长度为900π和1 200π时管道甩击的各项参数变化曲线。在相同的流速下,管道越长,甩击运动的变化周期也就长,管道甩击的频率越慢。长度为1 200π时,其周期约为0.45 s,长度为600π时,周期只有约0.14 s。
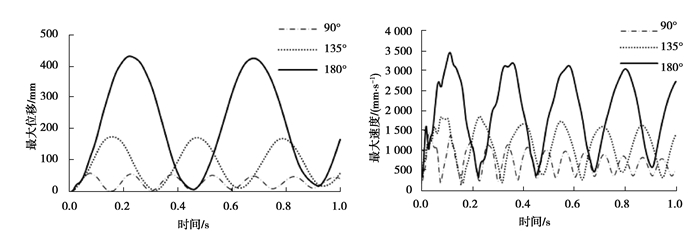
|
图 17 不同弯曲长度下的最大变形位移和甩击速度变化曲线 Fig. 17 Variation curve of maximum deformation displacement and flicking speed under different bending lengths |
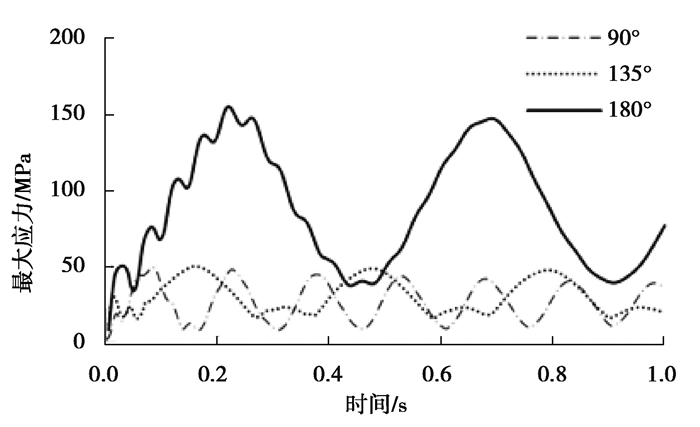
|
图 18 不同弯曲长度下的最大应力变化曲线 Fig. 18 Maximum stress variation curve under different bending lengths |
图 19是由模态分析得到的不同弯曲长度系统的前六阶固有频率,从中可以发现,随着弯曲长度的增大,系统前六阶固有频率均显著减小;阶数越高,固有频率减小幅度越大。因此,弯曲长度对系统固有频率的显著影响导致了柔性压力管道振幅的显著增大与其变化周期的显著延长。同时,对不同弯曲长度的管道最大变形位移变化曲线做快速傅里叶变换,得到不同弯曲长度管道甩击过程中振动信号的幅频曲线如图 20所示。随着弯曲长度的增加,振动信号的幅值显著增加,振动信号的频率分布及主导频率的变化也发生显著变化。此时,起主导作用的仍为二阶模态。
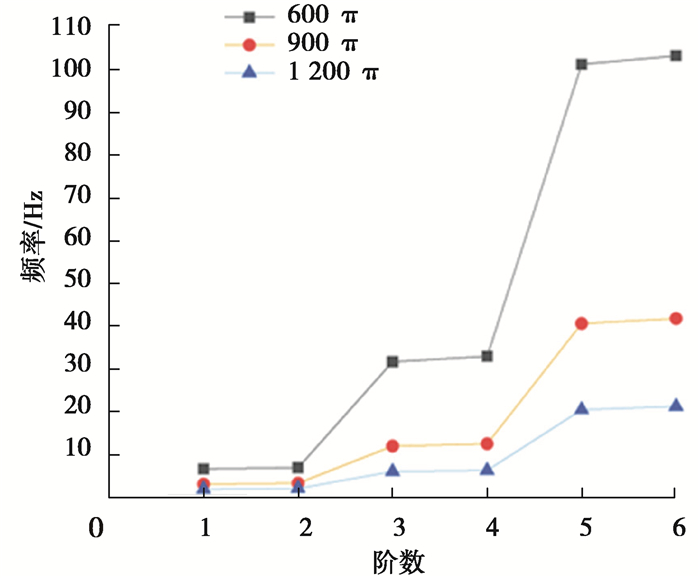
|
图 19 不同弯曲长度系统前六阶固有频率 Fig. 19 Natural frequencies of system of different lengths |
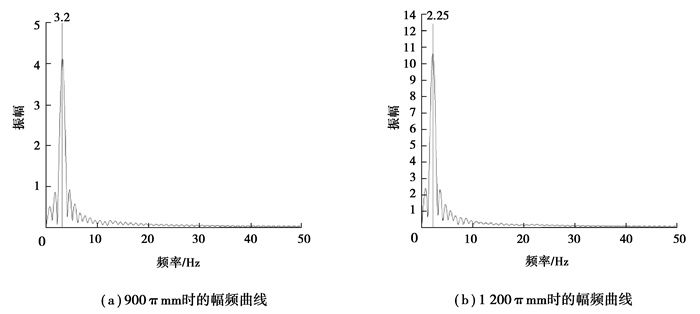
|
图 20 不同弯曲长度柔性压力管道甩击振动幅频曲线 Fig. 20 Amplitude-frequency curve of flexible pressure pipeline of different lengths |
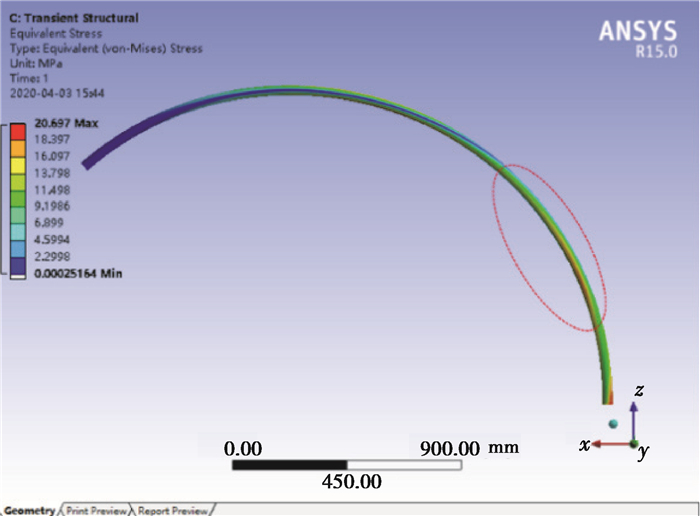
表 7是3种不同弯曲长度下甩击行为参数的最大值。从表 7中可以看出,随着柔性压力管道弯曲段长度的增加,其甩击行为变得更加剧烈。管道的弯曲长度增加1倍,管道的变形位移增加了6倍,甩击速度则增加了1.5倍。弯曲长度从600π增加到900π的过程中,柔性压力管道上的等效应力几乎保持不变,应变能略有增加。当管道弯曲长度从900π增加到1 200π的时候,管道的等效应力和应变能出现了剧烈的变化,分别为原来的3倍和6倍。等效应力在弯曲长度为900π时,管道的变形位移图像出现了次峰,图 21是t=1 s时的等效应力分布情况。
| 表 7 不同弯曲长度下,柔性压力管道甩击运动各项参数的最大值 Table 7 The maximum value of various parameters of flicking motion of flexible pressure pipes under different bending lengths |
|
图 21 t=1 s,管道弯曲段长900π时,管道等效应力分布 Fig. 21 t=1 s, the equivalent stress distribution of the pipeline when the bending section of the pipeline is 900π long |
图 21中红色圆圈出的应力集中是导致弯曲长度为900π时管道等效应力曲线出现次峰的原因。也因此,管道发生次级变形,吸收了流体的能量,管道的最大等效应力变化也较小。这种现象可能与流体初始速度的方向和约束面存在夹角有关。
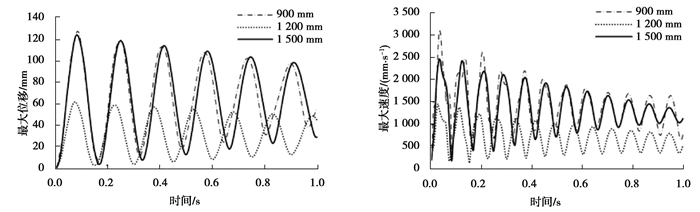
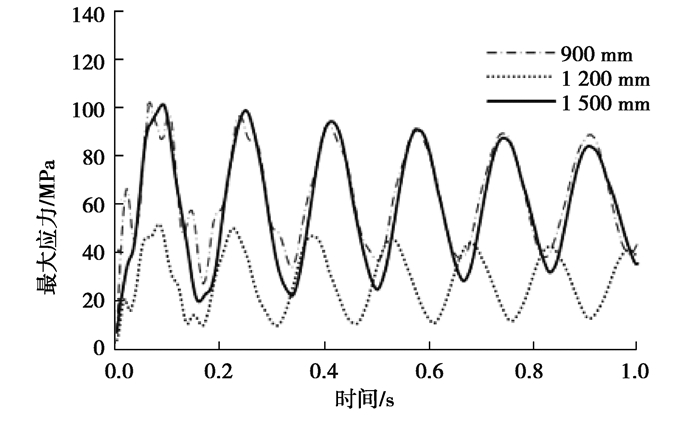
3.4 管道弯曲半径柔性压力管道的在铺设过程中,障碍物不同,弯曲半径也不同。对弯曲半径分别为900,1 200,1 500 mm,总长均为2 000 mm的管道进行分析,图 22和图 23是不同弯曲半径的柔性压力管道甩击运动参数时间变化曲线,,随着曲率半径的增大,柔性压力管道的最大变形位移和最大甩击速度都逐渐减小,等效应力也随曲率半径的增大而减小,但减小的幅度相比之下要小得多。表 8是不同弯曲半径下管道甩击运动各项参数的最大值,随着曲率半径增大,柔性压力管道的位移、速度、等效应力和应变能的最大值都减小。
|
图 22 不同弯曲半径下的最大变形位移和甩击速度变化曲线 Fig. 22 Variation curve of maximum deformation displacement and flicking speed under different bending radii |
|
图 23 不同弯曲半径下的最大应力变化曲线 Fig. 23 Maximum stress variation curve under different bending radii |
| 表 8 不同弯曲半径下,柔性压力管道甩击运动各项参数的最大值 Table 8 The maximum value of various parameters of flicking motion of flexible pressure pipes under different bending radii |
管道的弯曲半径增大减小了管道的甩击变形位移和甩击速度,减小的幅度较为明显。同时,增大管道的弯曲半径还可以减小管道固定端受到的等效应力,降低管道的应变能,增强管道在甩击运动过程中的安全性。
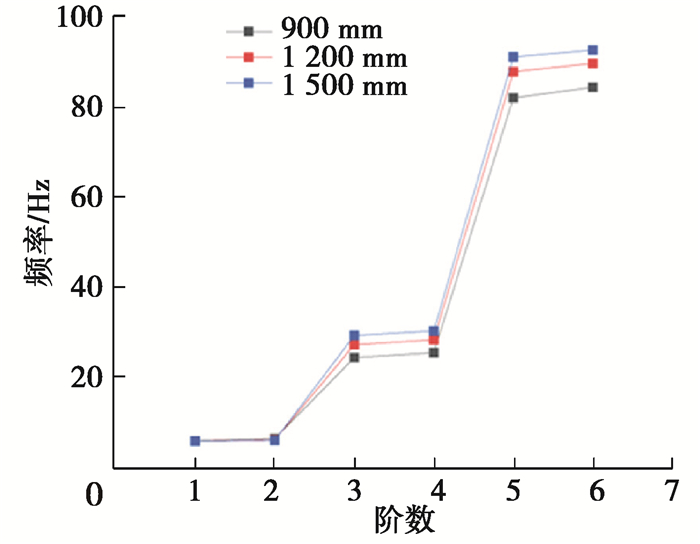
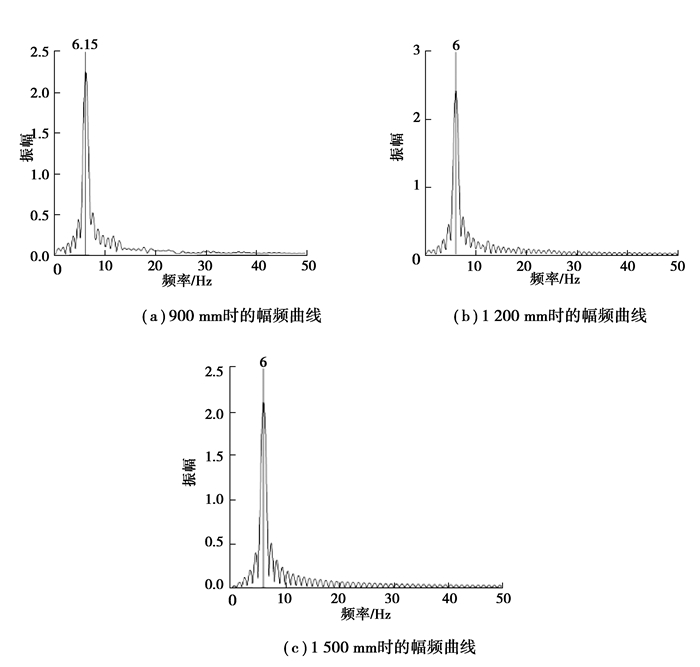
图 24是由模态分析得到的不同弯曲长度系统的前六阶固有频率,从中可以发现,随着弯曲半径的增大,系统前两阶固有频率减小,三到六阶固有频率显著增大;阶数越高,固有频率变化幅度越大。同时,对不同弯曲半径的管道最大变形位移变化曲线做快速傅里叶变换,得到不同弯曲半径管道甩击过程中振动信号的幅频曲线如图 25所示。随着弯曲半径的增加,振动信号的幅值与主导频率发生变化。此时,起主导作用的仍为二阶模态。
|
图 24 不同弯曲半径系统前六阶固有频率 Fig. 24 Natural frequencies of system of different curvature radiuses |
|
图 25 不同弯曲半径柔性压力管道甩击振动幅频曲线 Fig. 25 Amplitude-frequency curve of flexible pressure pipeline of different curvature radiuses |
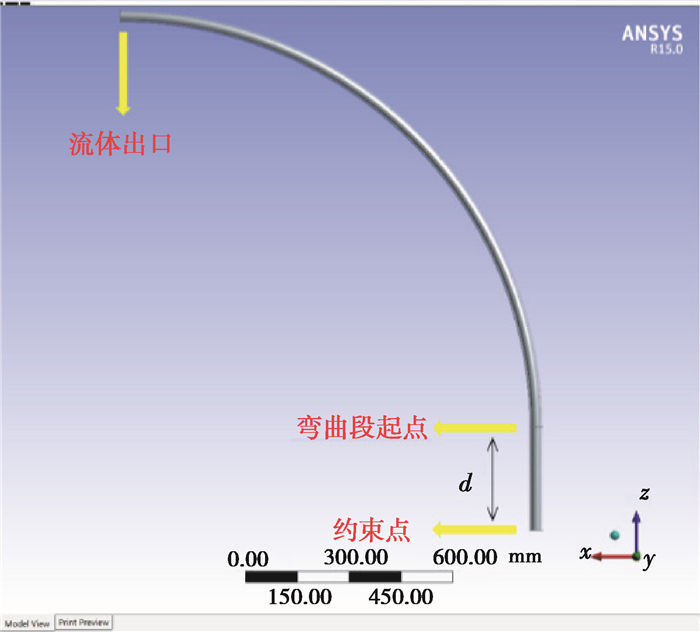
柔性压力管道在工作时,一般每隔一段距离就设置一个安全扣进行约束,安全扣和弯曲管道的位置关系对管道另一端脱扣后的甩击行为有很大的影响。管道的几何模型如图 26所示,对d=0,300,600 mm的情况进行管道甩击分析。图 27和28是不同约束位置下管道的甩击运动参数变化曲线。
|
图 26 不同约束位置几何模型 Fig. 26 Geometric models with different constrained positions |
|
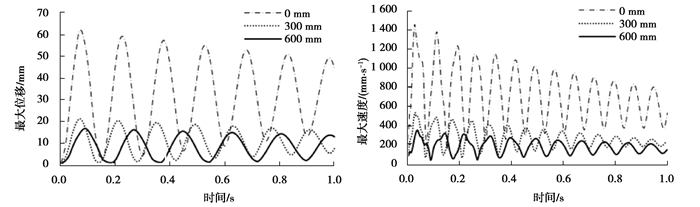
图 27 不同约束位置下变形位移和甩击速度变化曲线 Fig. 27 Curves of deformation displacement and slamming speed under different constrained positions |
|
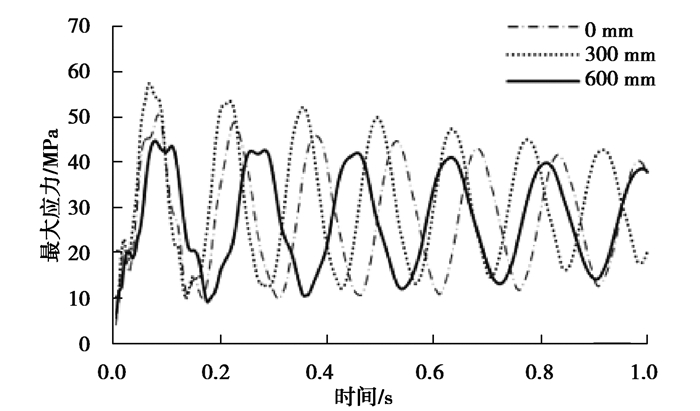
图 28 不同约束位置下的最大应力变化曲线 Fig. 28 Maximum stress change curve under different constrained positions |
随着约束点离弯曲段的距离不断增大,管道甩击的整体最大位移不断减小,最大甩击速度也不断减小,但管道靠近固定端的等效应力变化不大。从表 9可以看出,随着约束点离弯曲段的距离不断增大,柔性压力管道的位移、速度和应变能的最大值都减小。从图 29、30可以发现,随着约束点距离管道弯曲段越来越远,弯曲段的变形由于没有约束的存在会继续向直管段传递,能量也传递到直管部分,使得更多的管道变形,每个单位的应力能反而下降。约束点距离管道弯曲段越远,这种效应越显著,对防止管道发生二次断裂更有利。但约束点越远,则管道甩击运动的范围会越大,对人员和设备的危险性反而提升。因此,需要综合考虑对管道的约束。
| 表 9 不同约束点下柔性压力管道甩击运动各项参数的最大值 Table 9 The maximum value of parameters of flicking motion of flexible pressure pipes under different constraints |
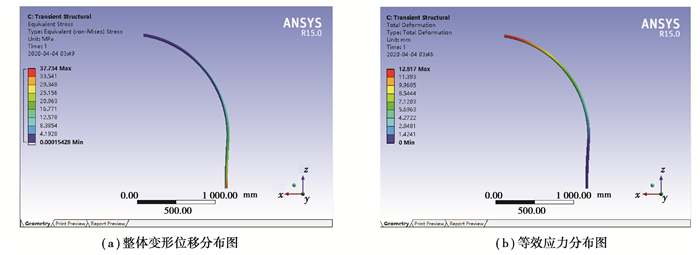
|
图 29 d=300 mm,t=1 s时,管道变形位移和等效应力分布图 Fig. 29 d= 300 mm, t = 1 s, the distribution of deformation and equivalent stress of pipeline |
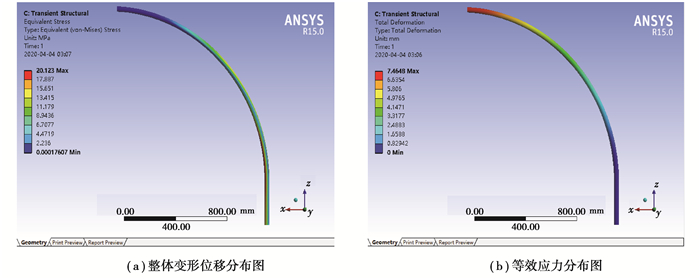
|
图 30 d=600 mm,t=1 s时,管道变形位移和等效应力分布图 Fig. 30 d= 600 mm, t = 1s, the distribution of deformation and equivalent stress of pipeline |
1) 管道发生脱扣甩击时,运动具有很强的非线性特征,最大变形位移和甩击速度的空间分布没有明显规律。管道靠近自由端的变形位移和甩击速度最大,对人员和设备危险性高,而固定端的等效应力最大,容易产生疲劳破坏造成二次危害。
2) 流体流速增加,柔性压力管道甩击变形位移、甩击速度、等效应力也迅速增大,应变能受流速的影响更大,与流速呈高次方增加的关系。
3) 流体对柔性压力管道甩击行为的影响主要体现在流体的密度和黏度系数两个方面。随着流体密度增加,柔性压力管道甩击运动的主要参数都线性增加。而流体黏度对柔性压力管道的甩击影响较为复杂,它会影响管道和流体的耦合效应,进而影响管道的甩击行为。随着流体黏度的增加,管道的甩击行为更加剧烈。
4) 柔性压力管道的长度越长,甩击就越剧烈,管道的疲劳损坏风险大大增加,其运动周期也延长。
5) 管道的弯曲半径增大,管道的甩击变形位移和甩击速度明显减小。增大弯曲半径,还可减小管道固定端的等效应力,降低管道的应变能,改善柔性压力管道的受力情况,延长管道使用寿命;此外,利于延长甩击运动的周期,极大地提高柔性压力管道的总体安全性。
6) 改变管道安全扣的约束位置的本质是在调节管道运行的长度和弯曲半径两个参数,它们的变化规律共同影响了约束点对甩击运动的影响。
7) 通过频谱分析和模态分析发现,管道振动都是由二阶模态主导。
| [1] |
Dini D, Lazzeri L. Modelling techniques for pipe whip analysis[J]. Nuclear Engineering and Design, 1976, 37(3): 361-371. DOI:10.1016/0029-5493(76)90066-2 |
| [2] |
Lazzeri L. Application of plastic analysis to the pipe whip problem[J]. International Journal of Pressure Vessels and Piping, 1979, 7(3): 183-197. DOI:10.1016/0308-0161(79)90017-6 |
| [3] |
Lazzeri L. On the influence of multiple loadings to plastic pipe elements: application to the pipe whip problem[C/OL]//SMiRT 4, 1977, San Francisco. IASMiRT, 1977[2021-01-05]. http://www.lib.ncsu.edu/resolver/1840.20/27634.
|
| [4] |
Ueda S, Kurihara R, Miyazaki N, et al. Analytical studies of four-inch pipe whip tests under BWR LOCA conditions[J]. International Journal of Pressure Vessels and Piping, 1985, 18(3): 161-176. DOI:10.1016/0308-0161(85)90009-2 |
| [5] |
Ma S M, Bathe K J. On finite element analysis of pipe whip problems[J]. Nuclear Engineering and Design, 1976, 37(3): 413-429. DOI:10.1016/0029-5493(76)90069-8 |
| [6] |
Olson L G, Jamison D. Application of a general purpose finite element method to elastic pipes conveying fluid[J]. Journal of Fluids and Structures, 1997, 11(2): 207-222. DOI:10.1006/jfls.1996.0073 |
| [7] |
Potapov S, Galon P. Modelling of Aquitaine Ⅱ pipe whipping test with the EUROPLEXUS fast dynamics code[J]. Nuclear Engineering and Design, 2005, 235(17/18/19): 2045-2054. |
| [8] |
刘德辅, 王树青, 郭海燕. 海洋立管综合环境条件设计标准研究[J]. 海洋工程, 2001, 19(2): 13-17. Liu D F, Wang S Q, Guo H Y. Study on combined design criteria for marine risers conveying flowing fluid[J]. The Ocean Engineering, 2001, 19(2): 13-17. (in Chinese) DOI:10.3969/j.issn.1005-9865.2001.02.003 |
| [9] |
张艳萍, 徐治萍, 刘土光, 等. 输液管道流固耦合的响应分析[J]. 中国舰船研究, 2006, 1(3): 66-69. Zhang Y P, Xu Z P, Liu T G, et al. Response analysis of fluid-structure interaction in pipelines transporting fluids[J]. Chinese Journal of Ship Research, 2006, 1(3): 66-69. (in Chinese) DOI:10.3969/j.issn.1673-3185.2006.03.016 |
| [10] |
Reid S R, Wang B, Aleyaasin M. Structural modelling and testing of failed high energy pipe runs: 2D and 3D pipe whip[J]. International Journal of Pressure Vessels and Piping, 2011, 88(5/6/7): 189-197. |
| [11] |
Vongmongkol S, Faal-Amiri A, Srivastava H M. Simplified approach to design of crushable material due to dynamic load[C]// Proceedings of 2012 20th International Conference on Nuclear Engineering and the ASME 2012 Power Conference, July 30-August 3, 2012, Anaheim, California, USA. ASME, 2013: 139-147.
|
| [12] |
Pieters A C. Whip restraint for a steam pipe rupture event on a nuclear power plant[D]. Potchefstroom, South Africa: North-West University, 2013.
|
| [13] |
Zhao W S, Xue F, Shu G G, et al. Analysis of flow-induced vibration of steam generator tubes subjected to cross flow[J]. Nuclear Engineering and Design, 2014, 275: 375-381. DOI:10.1016/j.nucengdes.2014.05.029 |
| [14] |
王春霖, 佘靖策, 褚金华. 基于LS-DYNA的主蒸汽管道甩动仿真分析[J]. 核动力工程, 2011, 32(S1): 93-97. Wang C L, She J C, Chu J H. Simulation and analysis of main steam pipe whip based on LS-DYNA[J]. Nuclear Power Engineering, 2011, 32(S1): 93-97. (in Chinese) |
| [15] |
He F, Dai H L, Huang Z H, et al. Nonlinear dynamics of a fluid-conveying pipe under the combined action of cross-flow and top-end excitations[J]. Applied Ocean Research, 2017, 62: 199-209. DOI:10.1016/j.apor.2016.12.007 |
| [16] |
Li Y D, Yang Y R. Vibration analysis of conveying fluid pipe via He's variational iteration method[J]. Applied Mathematical Modelling, 2017, 43: 409-420. DOI:10.1016/j.apm.2016.11.029 |
| [17] |
刘锋, 吴月磊, 张航, 等. 端部撞击下内充压力介质悬臂管道瞬态动力响应研究[J]. 山东科技大学学报(自然科学版), 2017, 36(3): 50-56. Liu F, Wu Y L, Zhang H, et al. Transient response of pressurized cantilever pipe subjected to transverse impact at its tip[J]. Journal of Shangdong University of Science and Technology(Natural Science), 2017, 36(3): 50-56. (in Chinese) |
| [18] |
陈雄. 基于液压柔性管道流固耦合振动特性的研究[D]. 湖南湘潭: 湖南科技大学, 2015. Chen X. Study on the dynamic characteristics of hydraulic flexible pipe fluid-structure coupling vibration[D]. Xiangtan, Hunan: Hunan University of Science and Technology, 2015. (in Chinese) |
| [19] |
刘发明, 晏石林. 基于ANSYS Workbench的输液管道断裂甩动分析[J]. 固体力学学报, 2014, 35(S1): 256-260. Liu F M, Yan S L. The rupture shaking analysis of pipeline based on ansys workbench[J]. Chinese Journal of Solid Mechanics, 2014, 35(S1): 256-260. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45

