为了应对日益严重的世界能源危机,风能作为一种最具发展潜力的绿色可再生能源,引起了世界各国广泛关注。风电齿轮箱是支撑风电机组高效开发风能资源的关键传动部件,但在时变风速作用下,百米级大尺寸、大柔性叶片与塔筒的耦合变形会使风电齿轮箱的输入载荷产生明显的随机特性,容易恶化齿轮箱行星级均载性能[1-2],增大故障失效率[3],因此开展多工况下风电齿轮箱行星级均载性能优化研究对提高风电机组运行安全具有重要的意义。
近年来,大量学者针对齿轮箱行星级均载特性分析开展了深入研究。Mo等[4]建立了考虑齿轮平移和扭转振动的行星级系统动力学模型,研究了面齿轮行星级传动的均载特性。Mo等[5]采用集中参数法和拉格朗日方程,建立了人字齿行星级系统动力学模型,研究了太阳轮浮动支撑和固定2种情况下人字齿轮行星级传动系统的均载特性。Gonzalez-Perez等[6]通过建立行星级传动系统有限元模型,分析了行星级传动系统的均载特性。董惠敏等[7]提出了一种差动轮系与定轴轮系复合的功率分流新构型,建立了齿轮箱系统动力学模型,分析了齿轮箱行星级的均载特性。Park等[8]考虑了箱体柔性与非线性时变啮合刚度,建立了1.5 MW风电齿轮箱系统动力学模型,分析了齿轮副齿向修形对行星级均载特性的影响规律。周璐等[9]建立了行星级非线性平移—扭转系统动力学模型,分析了误差及其相位角对系统均载特性的影响规律。朱增宝等[10]考虑了行星架位移、时变啮合刚度、旋转阻尼和构件重量,建立了行星传动系统动力学模型,分析了轴承支撑刚度对行星级均载特性的作用规律。徐向阳等[11]通过建立多浮动构件的柔性销轴式风电齿轮箱行星级系统动力学模型,研究了柔性销轴刚度和误差对系统均载特性的影响。彭则明等[12]在ADAMS中建立了复合行星级动力学模型,分析了齿轮偏心误差、负载及转速对行星级均载特性的影响。Guo等[13]指出齿轮箱输入端的轴向推力、水平剪力以及倾覆力矩等非扭载荷会恶化行星级均载性能。综上所述,现有研究重点关注纯扭矩作用下不同结构参数对行星级动态特性的作用规律,忽略了因运行工况改变造成的转矩及非扭载荷变化对齿轮箱行星级均载性能的影响,加之复杂的齿轮箱结构变形,造成现有基于单工况的齿轮箱行星级均载性能优化方法难以满足风电机组多工况运行需求。
因此,笔者综合考虑时变的齿轮副啮合刚度和传动误差以及传动轴和箱体的柔性,建立了某型5 MW海上风电齿轮箱系统动力学模型,分析了不同风速工况下齿轮副修形参数对行星级内部激励和均载特性的影响规律;采用支持向量回归方法,重构风速工况—齿轮修形参数—均载系数之间的映射关系,建立多风速工况下齿轮箱行星级均载系数优化模型,并利用遗传算法求解最优齿轮修形参数;最后,对比分析了优化前后齿轮箱行星级内部激励、齿面载荷、轴承力以及均载性能。
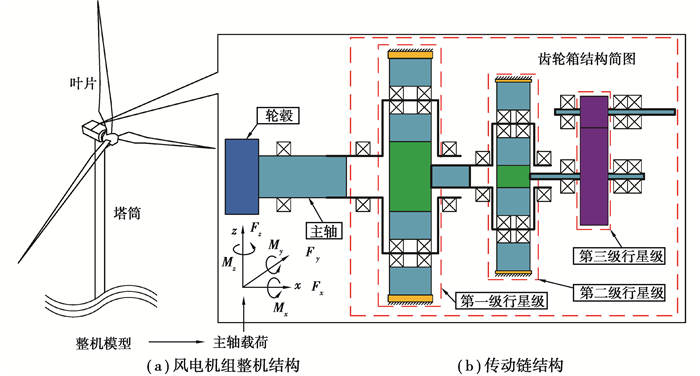
1 风电齿轮箱系统动力学建模 1.1 风电齿轮箱结构及传动原理图 1给出了某型5 MW海上风电机组的结构简图。其中,齿轮箱传动系统包括两级行星级和一级平行级。在两级行星级中,内齿圈固定,扭矩经主轴传递到第一级行星架上,随后经过行星轮功率分流和太阳轮功率汇流,输出传递到第二级行星架,并由第二级太阳轮将转矩传递至第三级平行级。风电齿轮箱传动结构参数如表 1所示[14]。采用解耦分析方法,首先在指定运行工况下通过求解整机模型(齿轮箱简化为传动比)[15],得到主轴与轮毂连接处六自由度载荷(轴向推力Fx,水平剪力Fy,垂直剪力Fz,主轴转矩Mx,水平弯矩My,垂直弯矩Mz),并将其作为主轴—齿轮箱系统动力学模型的载荷输入。
|
图 1 风电机组结构图 Fig. 1 Structure of wind turbine |
| 表 1 风电齿轮箱传动结构参数 Table 1 Structure parameters of wind turbine gearbox |
风速频率表示在风电机组20年运行期间内,相同平均风速总时长与测量时长的百分比值,是反映风场平均风速统计特性的重要参数。根据某风场风速统计数据[15],采用双参数威布尔分布对风速频率进行拟合,其概率密度函数为
| $ f(u)=\frac{k}{c}\left(\frac{u}{c}\right)^{k-1} e-\left(\frac{u}{c}\right)^k, $ | (1) |
式中,k=8.426,c=1.708。
对应的分布函数为
| $ F(u)=1-e^{-\left(\frac{u}{c}\right)^k}, $ | (2) |
式中:u为风速;k为形状参数;c为尺度参数。
考虑风切变效应,轮毂高度处的风速
| $ u_{\mathrm{hub}}=u\left(\frac{z_{\mathrm{hub}}}{z}\right)^{0.2}, $ | (3) |
式中:zhub为轮毂处高度;uhub为轮毂处风速;z为欲求的风速离地面高度。
采用Kaimal模型计算湍流风,湍流风在空间3个分量的谱为
| $ S_k(f)=\frac{\frac{4 \sigma_k^2 L_k}{\bar{u}_{\mathrm{hub}}}}{\left(1+\frac{6 f L_k}{\bar{u}_{\mathrm{hub}}}\right)^{\frac{5}{3}}}, $ | (4) |
式中:k=u, v, w为风的3个方向;uhub为轮毂处平均风速;f为循环频率;Lk为积分尺度参数。根据IEC 61 400-1[16]标准,可得
| $ L_k=\left\{\begin{array}{l} 8.10 \Lambda_u, K=u, \\ 2.70 \Lambda_u, K=v \;, \\ 0.66 \Lambda_u, K=w, \end{array}\right. $ | (5) |
式中,Λu为湍流尺度系数。
空间中k, h 2点处风速相关模型表示为
| $ S_{k, h}(f)=P_{\mathrm{Coh}}(f) \sqrt{S_{k, k}(f) \cdot S_{h, h}(f)}, $ | (6) |
式中:PCoh(f)为空间相干度;Sk, k(f)和Sh, h(f)分别为k和h处的功率谱;Sk, h(f)为空间k和h处的互功率谱;f为频率。
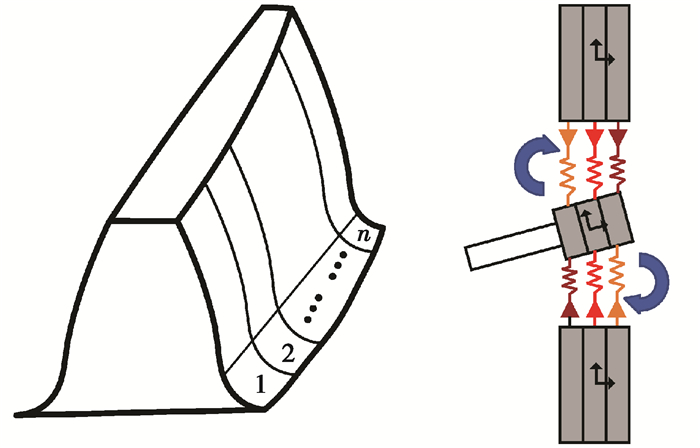
1.2.2 内部激励齿轮啮合是齿轮箱内部激励的主要来源之一。如图 2所示,笔者采用齿轮分片法,将齿轮沿齿宽方向划分为若干薄片,用弹簧单元表示一对薄片齿的啮合,其啮合刚度通过ISO 6336标准[17]计算。齿轮副法向啮合刚度函数为抛物线模型,最大值在节点处,计算公式为
| $ c_{\max }=c^{\prime} C_R, $ | (7) |
|
图 2 轮齿分片示意图 Fig. 2 Schematic diagram of gear slicing |
式中:c′为单齿啮合刚度;CR为轮齿结构系数。
单齿啮合刚度的计算公式为
| $ c^{\prime}=c_{\mathrm{th}} C_M C_B \cos \beta \text {, } $ | (8) |
式中:cth为理论单齿啮合刚度;CM为理论修正系数;CB为基本齿条系数;β为螺旋角。
理论单齿啮合刚度cth定义为
| $ c_{\mathrm{th}}=\frac{1}{q}, $ | (9) |
| $ \begin{aligned} q=& 0.047\;23+\frac{0.155\;51}{z_{n 1}}+\frac{0.257\;91}{z_{n 2}}-0.006\;35 x_1-\frac{0.116\;54}{z_{n 1}}-\\ & 0.001\;93 x_2-\frac{0.241\;88 x_2}{z_{n 2}}+0.005\;29 x_1^2+0.001\;82 x_2^2, \end{aligned} $ | (10) |
式中:zn1和zn2分别为主动轮和从动轮的当量齿数;x1和x2分别为主动轮和从动轮的变位系数。
齿轮时变啮合刚度函数可以表示为
| $ c(\varphi)=c_{\max }\left[1-\left(1-S_R\right)\left(\frac{s(\varphi)}{\max \left(s_{1 c}, s_{2 c}\right)}\right)^2\right], $ | (11) |
式中:
传动误差计算公式为
| $ e_L=\varphi_2-\left[\left(\varphi_1-\varphi_{10}\right) \frac{N_1}{N_2}+\varphi_{20}\right], $ | (12) |
式中:φ10和φ20分别为主动轮和从动轮进入啮合时刻的初始转角;φ1和φ2分别为主动轮和从动轮转动的位移角;N1和N2分别为主动轮和从动轮的齿数。
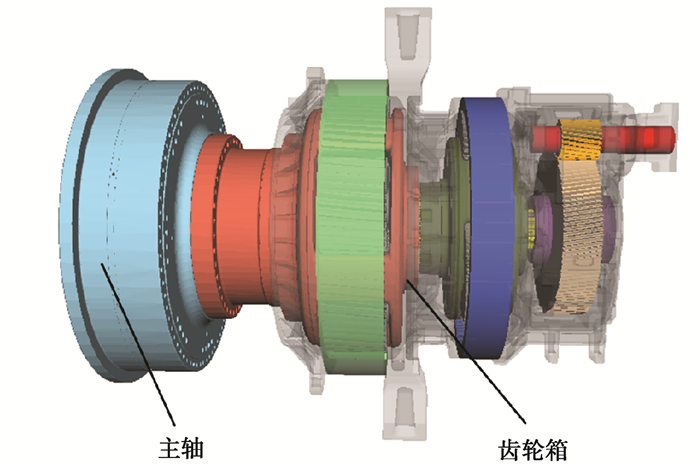
1.2.3 齿轮箱系统动力学模型采用SIMPACK建立风电齿轮箱系统动力学模型如图 3所示。采用模态缩减法计算部件柔性变形[18-19],其中,柔性体节点平移速度为
| $ \boldsymbol{v}=\frac{\mathrm{d} \boldsymbol{r}}{\mathrm{d} t}=\left(\boldsymbol{I}^G \boldsymbol{A}^B(s+\boldsymbol{u}) \boldsymbol{B}^G \boldsymbol{A}^B \mathit{\pmb{\Phi}}\right) \dot{\xi}, $ | (13) |
|
图 3 SIMPACK齿轮箱系统动力学模型 Fig. 3 Gearbox dynamic model of SIMPACK |
式中:r为柔性体节点位移;GAB为局部参考到惯性参考的转换矩阵;s和u分别为柔性体变形前和变形后的节点位移;I为节点惯性张量;Φ为节点模态矩阵;ξ为节点广义坐标矩阵。
柔性体节点角速度为
| $ { }^{\mathrm{G}} \boldsymbol{\omega}^{\mathrm{J}}=\boldsymbol{}^{\mathrm{G}} \boldsymbol{\omega}^B+{ }^{\mathrm{G}} \boldsymbol{\omega}^{\mathrm{P}}, $ | (14) |
式中:GωB为物体的角速度;GωP为由于物体变形引起的角速度。
基于公式(13)和式(14),可得柔性体动能表达式为
| $ E_{\mathrm{k}}=\frac{1}{2} \int\limits_V \rho \boldsymbol{v}^{\mathrm{T}} v \mathrm{d} V \approx \frac{1}{2} \sum m \boldsymbol{v}^{\mathrm{T}} \boldsymbol{v}+{ }^{\mathrm{G}} \boldsymbol{\omega}^{\mathrm{BT}} \boldsymbol{I}^{\mathrm{G}} \omega^{\mathrm{B}}=\frac{1}{2} \dot{\boldsymbol{\xi}}^{\mathrm{T}} \boldsymbol{m} \dot{\xi}, $ | (15) |
式中,ρ, V, m和m分别为部件的密度、体积、节点质量和质量矩阵。
柔性体势能包括重力和弹性势能,其表达式为
| $ E_p=\int \rho\left[\boldsymbol{x}+\boldsymbol{A}\left(\boldsymbol{s}+\mathit{\pmb{\Phi}}_q\right)\right]^{\mathrm{T}} g \mathrm{d} v+\frac{1}{2} \boldsymbol{\xi}^{\mathrm{T}} \boldsymbol{K} \boldsymbol{\xi}, $ | (16) |
式中:x为部件参考系相对于惯性参考系的位移;A为转换矩阵;g为重力加速度;q为模态坐标系;K为广义刚度矩阵。
基于式(15)和式(16),可得风电机组齿轮箱系统动力学方程为
| $ \boldsymbol{m} \;\boldsymbol{\xi}+\boldsymbol{m}\; \dot{\boldsymbol{\xi}}+\frac{1}{2}\left(\frac{\partial \boldsymbol{m}}{\partial \xi} \boldsymbol{\xi}\right)^{\mathrm{T}} \dot{\xi}+\boldsymbol{K} \boldsymbol{\xi}+f_{\mathrm{g}}+\boldsymbol{D}\; \dot{\boldsymbol{\xi}}+\left(\frac{\partial \boldsymbol{\psi}}{\partial \boldsymbol{\xi}}\right)^{\mathrm{T}} \lambda=\boldsymbol{Q}, $ | (17) |
式中:D为模态阻尼矩阵;fg为广义重力;ψ为代数约束方程;λ为拉格朗日算子;Q为广义力。
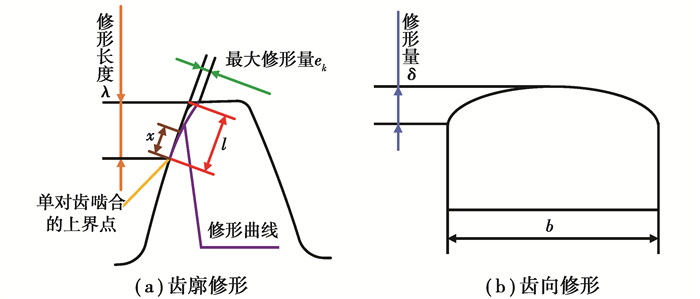
2 风电齿轮箱均载优化 2.1 设计变量齿轮修形一般包括齿廓修形和齿向修形。如图 4(a)所示,针对齿廓修形,采用齿顶修缘,包括最大修形量e、修形长度λ和修形曲线3个要素。其中,修形曲线采用抛物线。如图 4(b)所示,齿向修形则采用修鼓形方式。由于风电齿轮箱第一级行星级容易受到非扭载荷的作用,造成其动态性能较差[20],因此重点优化第一级行星级齿轮修形参数,共计9个优化变量,如表 2所示。
|
图 4 齿轮修形示意图 Fig. 4 Schematic diagram of gear modification |
| 表 2 优化变量参数表 Table 2 Optimization variable parameters |
基于式(18)~式(19)计算齿廓修形参数[21]
| $ e=e_k\left(\frac{x}{l}\right)^b, $ | (18) |
式中:最大修形量ek=fKT+fm;fKT为弹性变形,加工误差fm=fpb+1/3ff,fpb为基节误差,ff为齿形误差。l为沿单对齿啮合的上界点至啮合始点长度。x为啮合位置坐标(原点在界点处)。
| $ \lambda=P_b\left(\varepsilon_\alpha-1\right), $ | (19) |
式中:λ为修形长度;Pb为齿轮基节;εα为齿轮端面重合度。
基于式(20)计算齿向修形参数[21]
| $ \delta=7 \times 10^{-3} \frac{F_t}{b}, $ | (20) |
式中:δ为鼓形量;Ft为啮合圆周力;b为齿宽。
分别选取式(18)~式(20)计算值的70%和130%作为表 2中修形参数的最小值和最大值。
2.3 优化目标如式(21)所示,对n种风速工况下行星级均载系数求和,并将其最小值作为优化目标。
| $ \min f_{\Sigma}=k_1 f_1+k_2 f_2+\cdots+k_n f_n, $ | (21) |
式中,ki(i∈[1, n])为第i种工况对应的权重值,基于式(22)计算得到。fi(i∈[1, n])为第i种工况下行星级均载系数。
| $ k_i=\int_{a i}^{b_i} f(u)=F\left(b_i\right)-F\left(a_i\right), $ | (22) |
式中,f(u)为风速概率密度函数,可由公式(1)计算得到。ai和bi分别为该风速工况下的风速区间的下界和上界。
采用拉丁超立方抽样方法,对表 2中9个优化变量进行抽样组合,然后将每一种抽样组合作为齿轮箱系统动力学模型(式(17))中第一级行星级齿轮修形参数的输入,并计算行星级均载系数[22-23]。最后,采用支持向量机回归(SVR)[24]重构第i种风速工况下齿轮修形参数与均载系数之间的映射函数,即可得式(21)中fi,其中fi(i∈[1, n])。
假设x是第i种风速工况下的9个齿轮修形参数,f(x)则是对应的均载系数,利用SVR可以构建x和f(x)之间的非线性关系为
| $ f(x)=w^{\mathrm{T}} \varphi(x)+b, $ | (23) |
式中:f(x)表示预测值;φ(x)表示非线性映射函数;w和b是系数[25]。
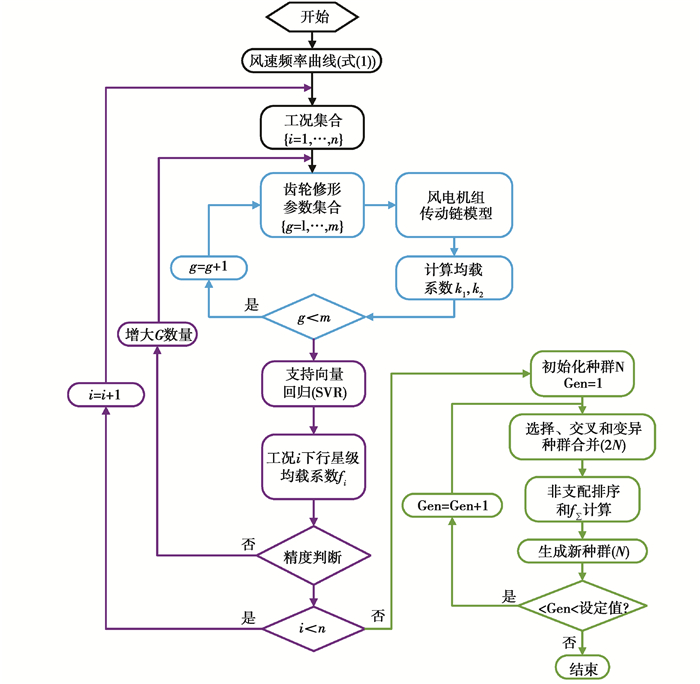
图 5所示为在多风速工况下风电齿轮箱行星级均载特性优化流程。
|
图 5 风电机组多工况优化流程 Fig. 5 Flow chart of multi-operating condition optimization of wind turbine |
首先,根据风速频率曲线(式(1))生成具有n种风速工况,并作为风电机组整机模型的外部激励,进而计算主轴与轮毂连接处六自由度载荷(Fx,Fy,Fz,Mx,My,Mz);然后,将每一种风速工况下计算得到的主轴与轮毂连接处六自由度载荷作为齿轮箱系统动力学模型的载荷输入,计算不同齿轮修形参数组合(表 2)下的行星级均载系数,并利用SVR构建修形参数与均载系数之间的映射关系;最后,将n种风速工况下行星级均载系数进行加权求和,以其最小值作为优化目标,采用遗传算法求解最优的齿轮修形参数。
在一台CPU主频为2.9G Hz的计算机上使用SVR进行齿轮修形参数寻优所需要的计算时间约10 min。而采用SIMPACK动力学模型进行一次计算需耗时20 min。由此可见,文中提出的优化方法可以大幅提高优化效率。
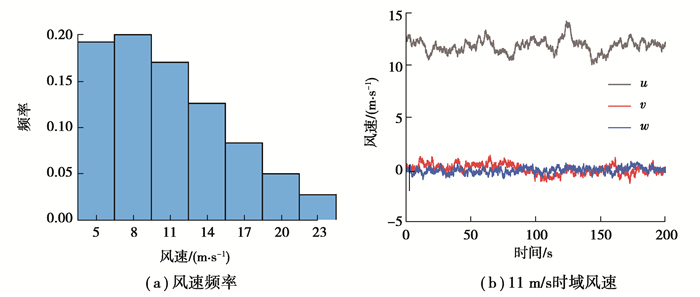
3 结果与讨论 3.1 外部激励分析如图 6(a)所示,从风电机组切入至切出风速区间5~23 m/s,间隔3 m/s,共计取n=7组风速工况,并利用式(22)计算对应的风速频率,作为式(21)中工况的权重值。参照IEC 61400-1标准,湍流强度设置为0.14[16],可得额定风速(11 m/s)下u、v和w 3个方向的湍流风速,如图 6(b)所示。
|
图 6 风速频率及时域风速 Fig. 6 Wind speed frequency and time domain wind speed |
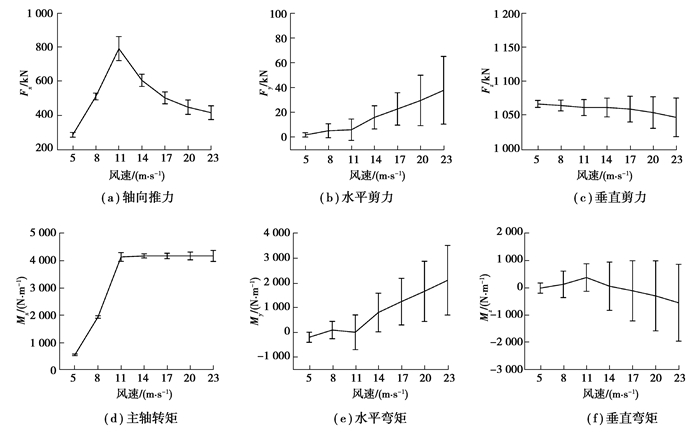
图 7所示为7种风速工况下主轴与轮毂连接处的六自由度载荷。从图中可以看出,在额定风速以下,随着风速的增加,气动转矩也逐渐增大,但非扭载荷与气动转矩的比值显著下降;在额定风速以上时,由于变桨系统开始运行,此时主轴处气动转矩近似恒定,而非扭载荷与气动转矩的比值逐渐增大。
|
图 7 不同风速下主轴载荷 Fig. 7 Mainshaft load under different wind speeds |
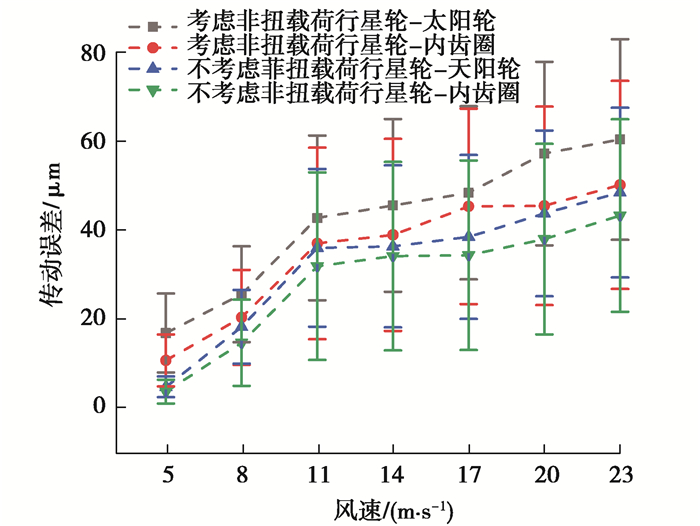
笔者仅针对第一级行星级齿轮开展修形优化设计,图 8所示为非扭载荷对齿轮箱行星级齿轮副传动误差的影响。从图中可以看出,随着风速的增加,传动误差幅值也逐渐增大;当考虑非扭载荷时,传动误差幅值略有增大。
|
图 8 非扭载荷对传动误差影响 Fig. 8 Influence of non-torque load on transmission error |
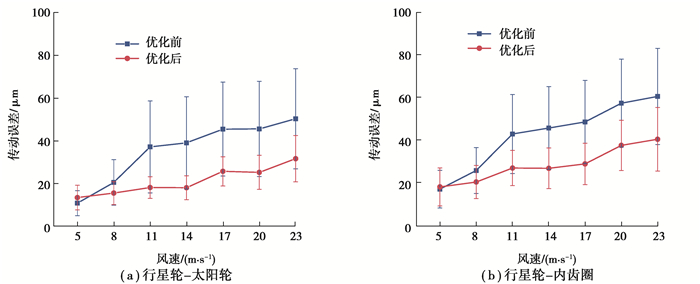
图 9(a)所示为优化前后行星轮—太阳轮传动误差对比。从图中可以看出,优化后各风速工况下的齿轮副传动误差显著减小,在额定风速工况下行星轮—太阳轮传动误差均值由40 μm下降到了18 μm,减小了55%。图 9(b)所示为优化前后行星轮—内齿圈传动误差的对比,其随风速工况的变化趋势与行星轮—太阳轮相同,在额定风速工况下行星轮—内齿圈传动误差均值由42 μm下降到了22 μm,减小了48%。
|
图 9 不同风速下优化前后行星级传动误差 Fig. 9 Planetary gear transmission error before and after optimization under different wind speeds |
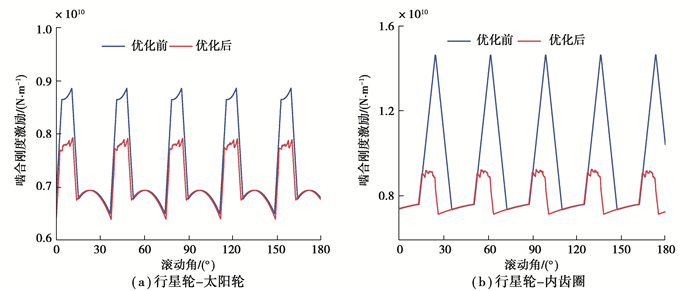
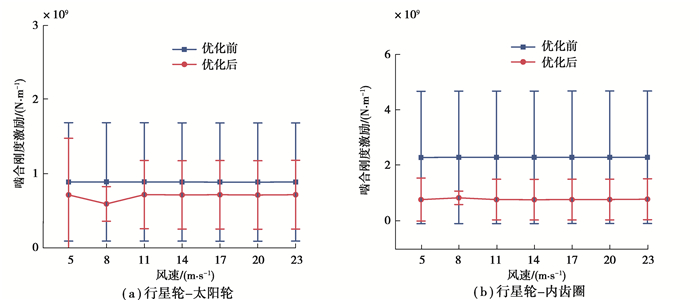
图 10所示为额定风速工况下行星级齿轮副时变啮合刚度优化前后对比。从图中可以看出,优化后的齿轮副啮合刚度激励(波动)显著减小。图 11所示为不同风速工况下行星级齿轮副啮合刚度激励优化前后对比。从图中可以看出,齿轮副啮合刚度激励受风速工况的影响不大,整体变化较为平缓。但优化后的行星级啮合刚度激励显著降低。
|
图 10 行星级优化前后齿轮副时变啮合刚度对比 Fig. 10 Comparison of time-varying meshing stiffness of planetary gears before and after optimization |
|
图 11 不同风速下行星级齿轮副啮合刚度激励 Fig. 11 Meshing stiffness of planetary gears under different wind speeds |
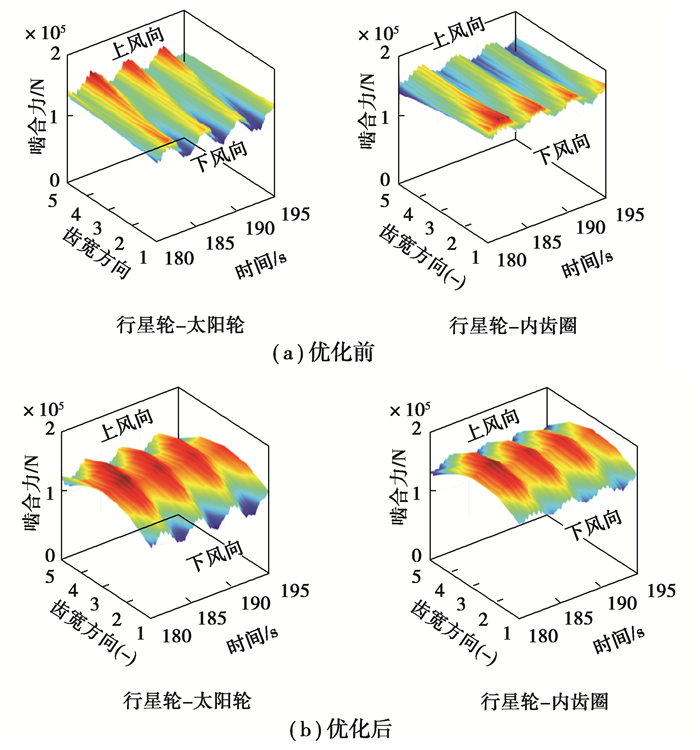
图 12(a)所示为额定风速工况下行星轮—太阳轮和行星轮—内齿圈动态啮合力在优化前沿齿宽方向的分布情况。从图中可以看出,优化前的行星轮—太阳轮齿轮副动态啮合力主要集中在上风向侧,而行星轮—内齿圈则相反,表明行星级齿面载荷存在明显偏载现象。图 12(b)所示为额定风速工况下行星轮—太阳轮和行星轮—内齿圈动态啮合力在优化后沿齿宽方向的分布情况。从图中可以看出,优化后的行星级齿面载荷分布均匀,偏载现象得到有效改善。
|
图 12 额定风速下优化前后齿面载荷分布 Fig. 12 Load distribution of tooth surface before and after optimization under rated wind speed |
通过行星轮和内齿圈动态啮合力计算均载系数k1,同时利用行星轮轴承力计算均载系数k2[24-25],分别如式(24)和式(25)所示。
| $ k_1=\max \left(\frac{\left.\max \left\{f_p^j(t)\right\}\right|_j}{\operatorname{mean}\left\{\sum\limits_j f_p^j(t)\right\}}\right), j=1 \cdots l, $ | (24) |
| $ k_2=\max \left(\frac{\left.\max \left\{f_b^j(t)\right\}\right|_j}{\operatorname{mean}\left\{\sum\limits_j f_b^j(t)\right\}}\right), j=1, \cdots, l, $ | (25) |
式中:fpj(t)为第j对行星轮和内齿圈的动态啮合力;fbj(t)为第j个行星轮轴承力;l为行星轮个数。
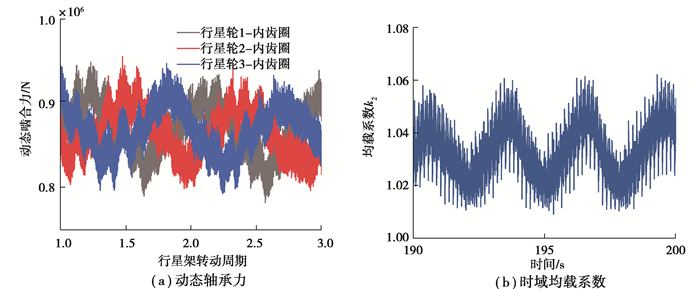
图 13所示为额定风速工况下行星轮—内齿圈动态啮合力和均载系数k1,图 14所示为额定风速工况下行星轮轴承力和均载系数k2。从图 13和图 14中可以看出,行星轮—内齿圈动态啮合力和行星轮轴承力变化趋势相同,均载系数k1和k2的最大值出现位置也相同,表明2种均载系数计算结果具有一定的等效性。
|
图 13 额定风速下行星轮-内齿圈动态啮合力及均载系数k1 Fig. 13 Dynamic meshing force and load sharing coefficient of planet-ring gear under rated wind speed |

|
图 14 额定风速下行星轮轴承力及均载系数k2 Fig. 14 Dynamic bearing force and load sharing coefficient of planet gear under rated wind speed |
利用式(26)计算行星轮上、下风向轴承力差值与轴承力额定值的百分比p。
| $ p=\frac{F_{\text {upwind }}-F_{\text {downwind }}}{F_{\text {rated }}} \times 100 \%, $ | (26) |
式中:Fupwind和Fdownwind分别为行星轮上、下风向轴承力;Frated为额定的行星轮轴承力。
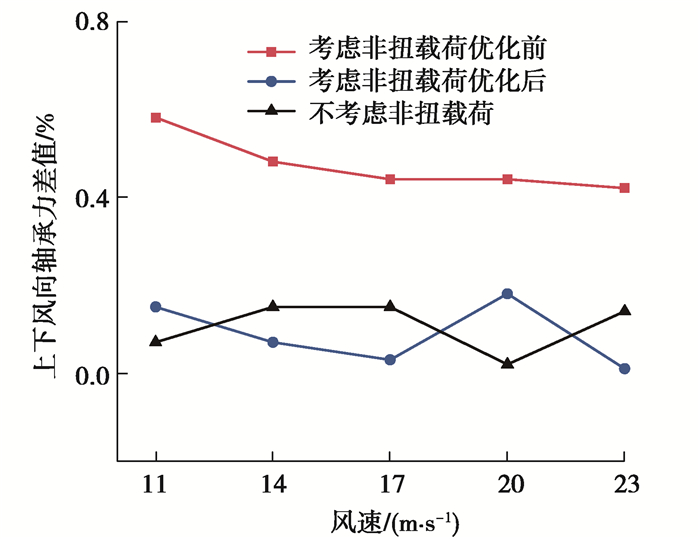
图 15所示为第1个行星轮上、下风向轴承力差值。从图中可以看出,当不考虑非扭载荷时,行星轮1上、下风向轴承力差值较小,而考虑非扭载荷后,行星轮1上、下风向轴承力差值显著增大,但随着风速的增加,其差值又逐渐减小。其主要原因是在低风速工况时,气动转矩较小,行星轮轴承力也较小,此时行星轮轴承力易受到非扭载荷的影响[2, 19],而在额定风速及以上时,气动转矩为额定值,此时行星轮轴承以承担扭矩载荷为主。优化后的行星轮上、下风向轴承力差值明显减小,偏载现象得到明显改善,与图 12结果相符。
|
图 15 优化前后行星轮1上下风向轴承力 Fig. 15 Upwind and downwind bearing force of planet gear 1 before and after optimization |
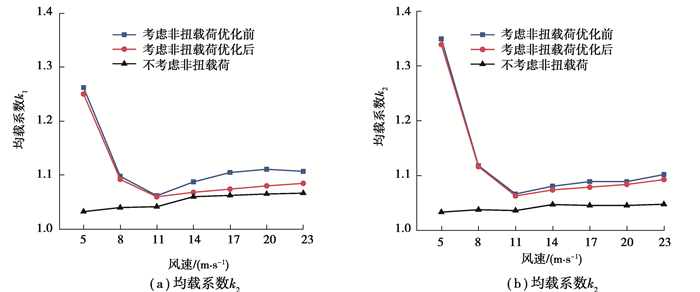
图 16所示为优化前后的行星级均载系数k1和k2对比。从图中可以看出,不考虑非扭载荷时,行星级均载系数随着风速的增加而增大,在达到额定风速后保持不变,但考虑非扭载荷后,随着风速的增大,行星级均载系数先减小再增大。结合图 7可知,在额定风速工况以下时,随着风速的增加,气动转矩也逐渐增大,但非扭载荷与气动转矩的比值显著下降,因此行星级均载系数逐渐减小,均载性能提高。当达到额定风速后,主轴处气动转矩近似恒定,但非扭载荷与气动转矩的比值逐渐增大,导致行星级均载系数增大,均载性能降低。优化后的行星级均载性能在不同风速工况下均有所提升,在额定风速及以上时均载优化效果较好。
|
图 16 优化前后行星级均载系数对比 Fig. 16 Comparison of load sharing coefficient of planetary stage before and after optimization |
该文考虑不同风速工况下风电齿轮箱时变输入载荷的影响,结合风电齿轮箱系统动力学模型,构建了多风速工况下风电齿轮箱行星级均载性能优化模型,以齿轮箱行星级均载系数综合最小为优化目标对行星级齿轮副进行修形优化设计,对比了不同风速工况下优化前后风电齿轮箱运行性能,得出以下结论:
1) 在额定风速以下时,随着风速的增加,非扭载荷与气动转矩比值显著减小,而在额定风速及以上时,在变桨控制作用下其比值逐渐增大。较大的非扭载荷占比会造成行星级齿轮和轴承产生明显的偏载。
2) 不同风速工况下,优化后的行星级齿轮副传动误差和啮合刚度波动幅值均显著降低,并且齿面载荷分布均匀,行星轮上、下风向轴承的偏载现象得到有效改善。
3) 随着风速的增加,非扭载荷占比变化会使行星级均载系数先减小再增大,并且优化后的行星级均载性能在不同风速工况下均有所提升,在额定风速及以上时均载优化效果较好。
| [1] |
Munch K, McDade M. Gearbox reliability collaborative: gearbox inspection metadata[R]. National Renewable Energy Lab. 2010.
|
| [2] |
Guo Y, Keller J, LaCava W. Planetary gear load sharing of wind turbine drivetrains subjected to non-torque loads[J]. Wind Energy, 2015, 18(4): 757-768. DOI:10.1002/we.1731 |
| [3] |
Hossain M L, Abu-Siada A, Muyeen S M. Methods for advanced wind turbine condition monitoring and early diagnosis: A literature review[J]. Energies, 2018, 11(5): 1309-1322. DOI:10.3390/en11051309 |
| [4] |
Mo S, Yue Z X, Feng Z Y, et al. Analytical investigation on load-sharing characteristics for multi-power face gear split flow system[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2020, 234(2): 676-692. DOI:10.1177/0954406219876954 |
| [5] |
Mo S, Zhang T, Jin G G, et al. Analytical investigation on load sharing characteristics of herringbone planetary gear train with flexible support and floating Sun gear[J]. Mechanism and Machine Theory, 2020, 144: 103670-103696. DOI:10.1016/j.mechmachtheory.2019.103670 |
| [6] |
Gonzalez-Perez I, Fuentes A, Hayasaka K. An enhanced finite element model for determination of load capacity in planetary gear trains[C]//Proceedings of the FISITA 2012 World Automotive Congress. Springer, Berlin, Heidelberg, 2013: 119-129.
|
| [7] |
董惠敏, 夏永, 李亚美, 等. 基于ADAMS仿真驱动的8MW风电齿轮箱均载设计[J]. 机械传动, 2015, 39(7): 53-58. Dong H M, Xia Y, Li Y M, et al. Load sharing design of 8 MW wind power gearbox based on ADAMS simulation driving[J]. Journal of Mechanical Transmission, 2015, 39(7): 53-58. (in Chinese) |
| [8] |
Park Y J, Kim J G, Lee G H, et al. Load sharing and distributed on the gear flank of wind turbine planetary gearbox[J]. Journal of Mechanical Science and Technology, 2015, 29(1): 309-316. DOI:10.1007/s12206-014-1237-5 |
| [9] |
周璐, 巫世晶, 李景, 等. 误差对行星传动系统均载特性影响分析[J]. 机械传动, 2017, 41(6): 1-8. Zhou L, Wu S J, Li J, et al. Analysis of the influence of error on load sharing characteristic of planetary transmission system[J]. Journal of Mechanical Transmission, 2017, 41(6): 1-8. (in Chinese) |
| [10] |
朱增宝, 江志祥, 尹敏. 支撑刚度对行星传动系统动态均载特性的影响[J]. 航空动力学报, 2016, 31(4): 986-992. Zhu Z B, Jiang Z X, Yin M. Impact of support stiffness on dynamic load sharing characteristics of planetary train system[J]. Journal of Aerospace Power, 2016, 31(4): 986-992. (in Chinese) DOI:10.13224/j.cnki.jasp.2016.04.027 |
| [11] |
徐向阳, 朱才朝, 刘怀举, 等. 柔性销轴式风电齿轮箱行星传动均载研究[J]. 机械工程学报, 2014, 50(11): 43-49. Xu X Y, Zhu C C, Liu H J, et al. Load sharing research of planetary gear transmission system of wind turbine gearbox with flexible pins[J]. Journal of Mechanical Engineering, 2014, 50(11): 43-49. (in Chinese) |
| [12] |
彭则明, 巫世晶, 王晓笋, 等. 复合行星轮系均载特性仿真研究[J]. 机电工程, 2015, 32(2): 157-162, 174. Peng Z M, Wu S J, Wang X S, et al. Virtual prototype simulation of load sharing characteristics of compound planetary gear sets[J]. Journal of Mechanical & Electrical Engineering, 2015, 32(2): 157-162, 174. (in Chinese) |
| [13] |
Guo Y, Keller J, Lacava W. Combined effects of input torque, non-torque load, gravity, and bearing clearance on planetary gear load share in wind turbine drivetrains[C]//AGMA fall technical meeting. 2012.
|
| [14] |
Nejad A R, Guo Y, Gao Z, et al. Development of a 5 MW reference gearbox for offshore wind turbines[J]. Wind Energy, 2016, 19(6): 1089-1106. DOI:10.1002/we.1884 |
| [15] |
Nejad A R, Gao Z, Moan T. On long-term fatigue damage and reliability analysis of gears under wind loads in offshore wind turbine drivetrains[J]. International Journal of Fatigue, 2014, 61: 116-128. DOI:10.1016/j.ijfatigue.2013.11.023 |
| [16] |
Madsen P H, RISØ D T U. Introduction to the IEC 61400-1 standard[S]. Risø National Laboratory, Technical University of Denmark, 2008.
|
| [17] |
ISO 6336-6-2006, Calculation of service life under variable load[S]. 2006.
|
| [18] |
Tan J J, Zhu C C, Song C S, et al. Dynamic modeling and analysis of wind turbine drivetrain considering platform motion[J]. Mechanism and Machine Theory, 2019, 140: 781-808. |
| [19] |
Tan J J, Zhu C C, Song C S, et al. Effects of flexibility and suspension configuration of main shaft on dynamic characteristics of wind turbine drivetrain[J]. Chinese Journal of Mechanical Engineering, 2019, 32(1): 1-15. |
| [20] |
沈意平, 李斌, 李学军, 等. 非扭矩载荷下风电齿轮传动系统动力学响应特性分析[J]. 湖南科技大学学报(自然科学版), 2018, 33(4): 49-55. Shen Y P, Li B, Li X J, et al. Dynamic response analysis of wind turbine gear transmission system subjected to non-torque loads[J]. Journal of Hunan University of Science & Technology (Natural Science Edition), 2018, 33(4): 49-55. (in Chinese) |
| [21] |
朱才朝, 陈爽, 马飞, 等. 轮齿修形对兆瓦级风电齿轮箱动态特性影响[J]. 振动与冲击, 2013, 32(7): 123-128. Zhu C C, Chen S, Ma F, et al. Effect of gear teeth modification on dynamic characteristics of a megawatt level wind turbine gearbox[J]. Journal of Vibration and Shock, 2013, 32(7): 123-128. (in Chinese) |
| [22] |
胡升阳, 方宗德. 行星传动均载及动载系数定义改进与分析[J]. 西安交通大学学报, 2019, 53(8): 40-46, 113. Hu S Y, Fang Z D. Improvement and analysis of the definitions of load sharing and dynamic load factors of planetary transmission[J]. Journal of Xi'an Jiaotong University, 2019, 53(8): 40-46, 113. (in Chinese) |
| [23] |
Standard A. Design manual for enclosed epicyclic gear drives[J]. Alexandria, VA: American Gear Manufacturers Association, 2006, 1-104. |
| [24] |
Xiang H Y, Li Y L, Liao H L, et al. An adaptive surrogate model based on support vector regression and its application to the optimization of railway wind barriers[J]. Structural and Multidisciplinary Optimization, 2017, 55(2): 701-713. |
| [25] |
Schölkopf B, Smola A J, Williamson R C, et al. New support vector algorithms[J]. Neural Computation, 2000, 12(5): 1207-1245. |
 2022, Vol. 45
2022, Vol. 45


