道路压实工作是筑路、筑坝工程建设中的关键环节,主要依靠人工操作振动碾压机完成。该过程存在作业时间长、振动强度大的问题,严重危害操作人员的身心健康且无法长时间保证作业精度。无人驾驶碾压机具备高精度作业能力,能有效降低操作人员的劳动强度、大幅度提高施工质量和效率、降低运行成本[1-2],应用前景十分广阔。
对于无人驾驶系统而言,由传感器、控制器、执行器构成的硬件系统是其精准、安全运行的基础[3]。而各类硬件受到自身特性、运行环境、运行时长等因素的影响,在车辆运行过程中可能发生故障,影响整个系统的稳定性与安全性。国内外学者针对硬件故障问题提出了容错控制理论。
在容错控制领域,早期的解决方案主要基于硬件冗余技术,并行安装多个具有相同功能的组件以完成相同的任务,实现系统在部分组件故障后的正常运行。但该方案极大地增加了系统结构的复杂度和成本,因此基于解析冗余的容错控制方案被提出和广泛使用。解析冗余的容错控制主要分为主动与被动容错技术,其核心思想是在系统存在一定的硬件冗余基础上辅以软件冗余技术,在不过分增加系统复杂度的情况下实现容错控制[4]。Gadda等[5-6]基于传统的卡尔曼滤波对汽车线控转向系统进行了容错控制研究。Chamseddine等[7]基于滑模控制技术对汽车液压主动悬架传感器故障展开了容错控制研究。Fekih等[8]提出一种基于观测器的故障检测方案和线性二次调整器优化设计相结合的容错控制方法,实现地面车辆的转向容错控制。田承伟[9]基于自适应渐消卡尔曼滤波构建了四倍冗余体系来实现汽车线控转向系统传感器的容错控制。何磊等[10]基于多维高斯隐式马尔可夫模型展开了线控转向汽车转向盘转角传感器的容错控制策略研究。在车辆的容错控制方面,国内外研究的焦点多为乘用车或商用车,而对碾压机这类具有特殊车体结构与复杂运动规律的工程车辆却鲜有研究。
笔者搭建的无人驾驶碾压机平台主要依靠全球定位系统(GPS,global positioning system)进行车体定位,但GPS存在信号易丢失、不稳定等缺点[11],极有可能导致车辆失控进而发生难以挽回的安全事故,如图 1所示。针对该问题,若仅采取常规的紧急停车手段势必会降低工程施工效率,增加车辆磨损与油耗,而相应的容错机制设计有望改善这一问题。

|
图 1 无人驾驶碾压机事故现场 Fig. 1 The accident caused by unmanned roller |
笔者主要从信号代偿角度对无人驾驶碾压机的容错控制展开研究,其中代偿即代替、补偿的简称。基于无人驾驶碾压机运行特性构造了带流量损耗参数的线性转向模型,并结合带遗忘因子的最小二乘自学习方法揭示了碾压机方向盘与铰接角的实时对应关系。当单组GPS设备发生故障时利用自学习模型与冗余硬件信息协同重构无人驾驶碾压机位置与航向,实现车辆在传感器短时失效场景下的容错控制。
1 无人驾驶碾压机平台描述无人驾驶碾压机平台主要由单钢轮振动碾压机改装而成,其核心硬件布置方案如下:前、后车体分别横向布置2个定位天线构成4天线GPS测量系统,用于准确测量前、后车体的位置与航向信息;前、后车体分别安装一个航姿参考系统(AHRS,attitude and heading reference system)以测量车体姿态信息;平台主要依靠自主研发设计的域控制器进行信号处理与控制输出,借助自主改造的转向与速度控制机构实现车辆行驶控制。笔者所设计的转向控制机构主要包含转向电机、角度传感器、电机控制器与连接支撑部件,通过硬连接方式植入原车转向柱中。在无人驾驶碾压机自动化作业过程中,转向电机带动原车转向柱转动进而控制全液压转向器的流量输出,角度传感器会实时记录电机转角作为方向盘转动反馈。由于该转向控制机构安装在驾驶室内,能有效减少因振动、扬尘等情况引起的传感器失效故障,与直接改造液压转向系统的方案相比,改装、维护更简单,可靠性更强。整车硬件布置示意图如图 2所示。
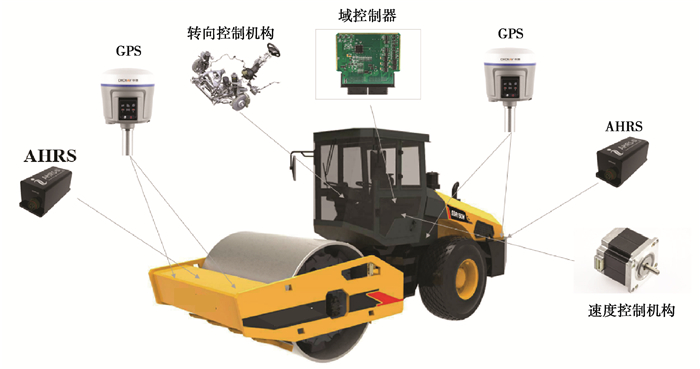
|
图 2 无人驾驶碾压机硬件布置 Fig. 2 Hardware layout of unmanned roller |
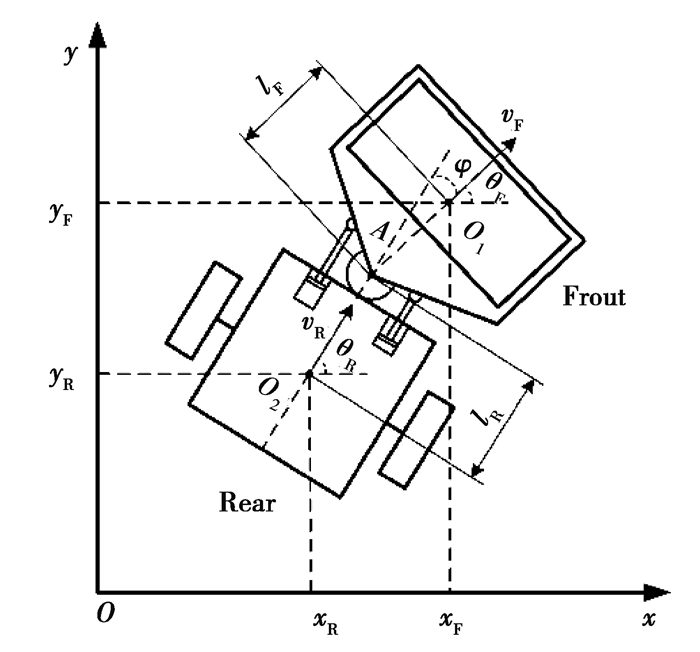
作为铰接式车辆,碾压机具有特殊的车体结构与运动规律,而信号重构策略与路径跟踪控制器的设计依赖于其几何结构关系与运动学特性,因此构建碾压机的运动学模型[12],如图 3所示。
|
图 3 碾压机运动学模型 Fig. 3 Kinematic model of unmanned roller |
定义大地东向为x方向,大地北向为y方向;前车身中心位置为O1(xF, yF),距离铰接点A的距离为lF,前车身运行速度为vF,航向角θF;后车身中心位置为O2(xR, yR),距离铰接点A的距离为lR,后车身运行速度为vR,航向角θR;前后车身的航向偏差为φ,将其定义为铰接角。下面给出碾压机在运动过程中的相关运动学方程。
前车位置、航向、速度之间的关系表达为
| {˙xF=vF⋅cosθF,˙yF=vF⋅sinθF。 | (1) |
前、后车身中心位置坐标以及两者航向之间的关系表达为
| {xR=xF−lF⋅cosθF−lR⋅cosθR,yR=yF−lF⋅sinθF−lR⋅sinθR,θR=θF+φ。 | (2) |
由式(1)和式(2)可以得出前车的航向变化率,表达为
| ˙θF=vFsinφ+lR˙φlFcosφ+lR。 | (3) |
无人驾驶碾压机转向系统采用全液压转向结构[13-14],通过方向盘带动全液压转向器转动,进而使油泵供出的液压油进入到转向油缸中推动活塞伸缩,最终实现前、后车体的相对偏转。碾压机液压转向系统零件众多、结构复杂,难以建立精确的数学模型。构建的碾压机液压转向系统模型主要考虑液压油在转向器、油管、转向油缸、活塞等核心元件中的传输过程。转向器的线性化流量方程表达为
| QL=Kq˙xi−KJpJ, | (4) |
式中:Kq为转向器流量放大系数;KJ为转向器流量压力系数;xi为阀芯和阀套相对转角在阀套内圆上所对应的弧长;pJ为液压缸高压腔与低压腔压力差。
方向盘与转向器运动的对应关系表达为
| ˙xi=dq2˙θsteer , | (5) |
式中:dq为转向器阀套的内圆直径;θsteer为方向盘反馈角度。
液压转向过程中,存在相对运动的零部件主要为液压油缸与活塞。长期的相对运动过程会导致两者之间的密封性由于摩擦而发生改变,进而产生内泄漏。泄漏原理如图 4所示。
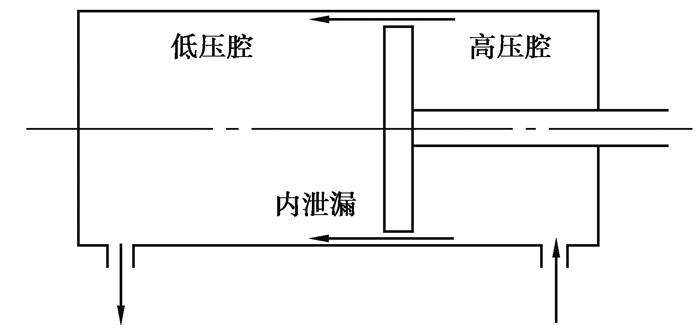
|
图 4 液压缸内泄漏示意图 Fig. 4 Schematic diagram of leakage in hydraulic cylinder |
泄漏量表示为
| QLeak =πdh3(1+1.5ε2)12ηlpJ, | (6) |
式中:d为活塞外径,h为缝隙高度,η为液压油动力粘度,l为缝隙高度,ε为相对偏心率。根据液压缸流量连续方程可得活塞位移量,为
| ˙xp=QL−QL.eak −Vt4β˙PfA, | (7) |
式中:xp为液压缸活塞的移动量,Vt为液压缸有效容积,β为油液的体积弹性模量。将铰接角φ与液压缸活塞移动量xp的关系以线性方式表达为
| φ=Kφxp, | (8) |
式中:Kφ为铰接角与油缸活塞移动量的比例系数。
对式(4)~式(8)进行整理可得铰接角与方向盘转角的动态关系为
| ˙φ=dqKq2AKφ˙θsteer −[KJKφA+πdh3(1+1.5ε2)12AKφηl]PJ−Vt4βA˙PJ。 | (9) |
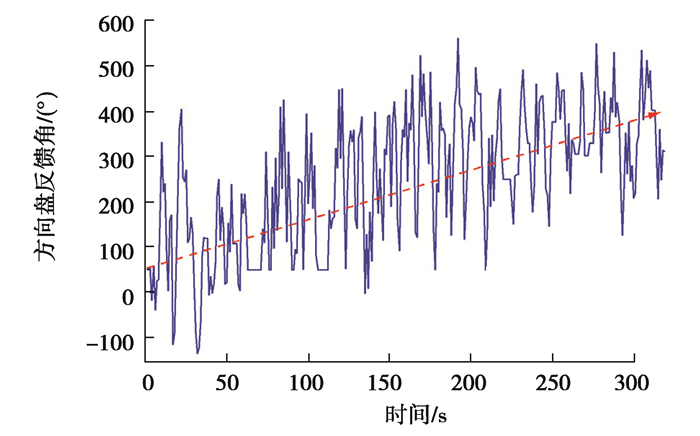
无人驾驶碾压机的作业是一个长时间、高强度、多变化的过程,需要长时间以强振动模式工作在非结构化道路上,在这个过程中无人驾驶系统以及车辆自身的特性都有可能发生显著的变化。通过对无人驾驶碾压机的运行数据分析可以发现其转向系统的变化,如图 5所示。
|
图 5 方向盘反馈角度曲线 Fig. 5 Feedback angle of steering wheel |
图 5是转向控制机构角度传感器在车辆自动化运行过程中测量的方向盘反馈角。无人驾驶碾压机的作业主要是一种直线往复运行的过程,其方向盘反馈角理论上应该在定值附近上下波动,但从图 5可以看出,随着时间的推移,转向系统中位呈现出不断漂移的现象,在300 s的时间内漂移量达到了约300°。由此可以看出,中位漂移是无人驾驶碾压机转向系统的重要特性,是传感器失效后的信号代偿所要考虑的关键要素。从式(9)可以发现,漂移产生的内在原因主要是液压系统的油液在输送过程中存在流量损失。因此,作为代偿容错控制的核心信息来源,液压转向系统模型应具备反映与预测油液流量损耗的能力。但转向系统模型存在参数众多且难以直接获取的问题,因此按照下述流程对模型进行了简化。
由于信号的微分会引入大量噪声,对式(9)进行积分,并对部分复杂参数进行简化处理得到铰接角与方向盘转角的最终关系式为
| φ=K⋅θsteer +b+∫c dt, | (10) |
式中:
所设计的无人驾驶碾压机容错控制框架如图 6所示。信号代偿模块主要包含液压系统自学习与信号决策模块,其中液压系统自学习模块主要用于学习转向系统特性,信号决策模块主要进行信号筛选与输出;车辆控制主要由串联抗扰控制器完成。
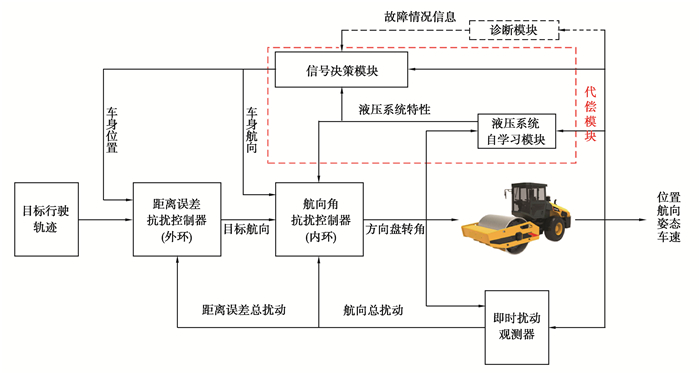
|
图 6 无人驾驶碾压机代偿容错控制架构 Fig. 6 Frame work of fault-tolerant control of unmanned roller |
无人驾驶碾压机的信号代偿主要依据式(2),即当单组GPS设备失效后利用另外一组GPS设备提供的航向与定位信息,结合转向模型估计的铰接角重构出控制器所需要的车体位置与航向信息。
3.1 自学习转向模型递推最小二乘(RLS,recursive least squares)是系统参数学习常用的方法[15],其主要利用实时运行系统所提供的数据来对参数进行估计,估计的核心思想是使误差的平方和最小来获得数据的最佳匹配参数。但针对于慢时变参数系统,RLS存在“数据饱和”现象,即随着数据量的增长,新采集数据对于估计参数的更新作用将越来越弱,导致系统无法准确跟踪参数的变化。笔者采用带遗忘因子的递推最小二乘算法(FFRLS,forgetting factor recursive least squares)来克服这种现象,设计的转向模型参数迭代公式如式(11)所示。待辨识参数包含方向盘与铰接角的比例系数K,参数b,流量损耗参数c,辨识输入包含方向盘转角θsteer,辨识输出为铰接角φ:
| {P(k)=1λ[I−Z(k)⋅[θsteer(k)1t(k)]T]⋅P(k−1),Z(k)=P(k−1)⋅[θsteer(k)1t(k)]1+[θsteer(k)1t(k)]T⋅P(k−1)⋅[θsteer(k)1t(k)],[ˆK(k)ˆb(k)ˆc(k)]=[ˆK(k−1)ˆb(k−1)ˆc(k−1)]+Z(k)⋅[φ(k)−[θsteer(k)1t(k)]⋅[ˆK(k−1)ˆb(k−1)ˆc(k−1)]T], | (11) |
式中:k为迭代次数;P为协方差矩阵;Z为误差修正增益;λ为遗忘因子(0 < λ < 1)。
3.2 串联抗扰控制器笔者利用串联结构的抗扰控制器实现对无人驾驶碾压机的路径跟踪控制[16],结构中包含的2个控制器分别用于控制系统的横向偏差和航向偏差,利用图 7描述2种偏差的表现形式。其中eD为实际距离偏差,θpathref为目标轨迹航向。
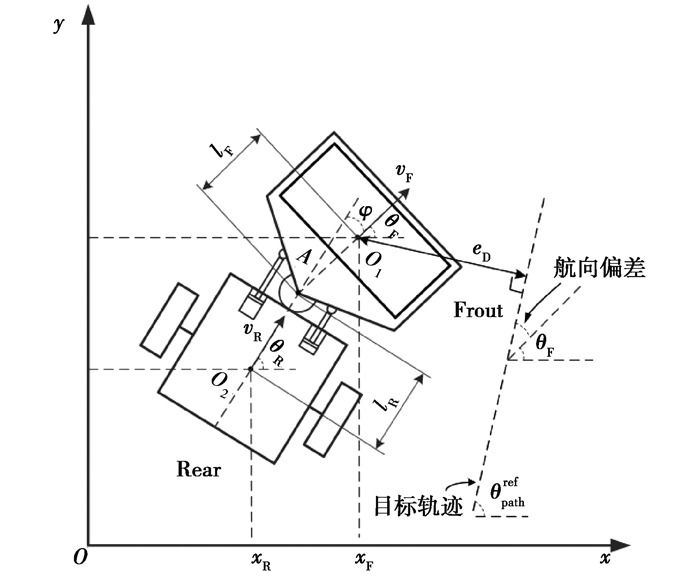
|
图 7 横向和航向偏差示意图 Fig. 7 Horizontal and heading error |
无人驾驶碾压机的控制需要考虑系统的动态过程,因此针对液压转向系统引入时间常数将转向模型转化为一阶惯性环节为
| ˙φ=−1τ⋅φ−Kτ⋅θstcer +zτ, | (12) |
式中:τ为转向系统在动态过程中的时间常数,z=b+∫c dt。
将式(12)代入到式(3)中,得到航向角对时间的导数
| ˙θF=vFsinφ−lR⋅φτ+z⋅φ⋅lRτlFcosφ+lR−K⋅lRτlFcosφ+lR⋅θstert =f0+b0⋅θster +f, | (13) |
式中:
| u0=KLL(θdesF−θF), | (14) |
式中: KLL为比例增益,θFdes为目标航向。
上述控制器即为航向偏差控制器(定义为内环控制器)。其中目标航向θFdes由横向偏差控制器(定义为外环控制器)提供。下面介绍外环控制器设计思路。
前车体距离目标轨迹的距离误差为
| ˙eD=vF⋅sin(θref path −θF)+W, | (15) |
式中:θpathref为目标轨迹的参考航向角;W为外部扰动。目标轨迹的参考航向角为
| θrefpath=tan−1(x1−x0y1−y0), | (16) |
式中(x0, y0)和(x1, y1)分别为目标轨迹的起点和终点坐标。定义uHL=sin(θpathref-θF),式(15)可以转化为
| ˙eD=vmeas F⋅uHL+(vF−vmeas F)⋅uHL+W=bHL⋅uHL+fHL , | (17) |
式中:vFmeas为传感器测量车速;bHL=vFmeas;fHL= vF-vFmeas ·uHL+W。实际距离误差为
| eD=(xF−x0)⋅(y0−y1)−(x0−x1)⋅(yF−y0)√(x0−x1)2+(y0−y1)2。 | (18) |
针对式(17),利用内环控制器的控制率求解方法,可以得到外环控制器的控制率为
| uHL=KHL(edes D−eD)−ˆfHLbHL, | (19) |
式中:eDdes为与目标轨迹之间理想的横向偏差;KHL为比例控制器增益。所需的目标航向角θFdes为
| θdes F=θref path −sin−1(uHL)。 | (20) |
笔者利用33 t无人驾驶碾压机实车运行数据,在Matlab/Simulink仿真软件中对线性液压转向模型参数进行离线辨识,效果如图 8所示。
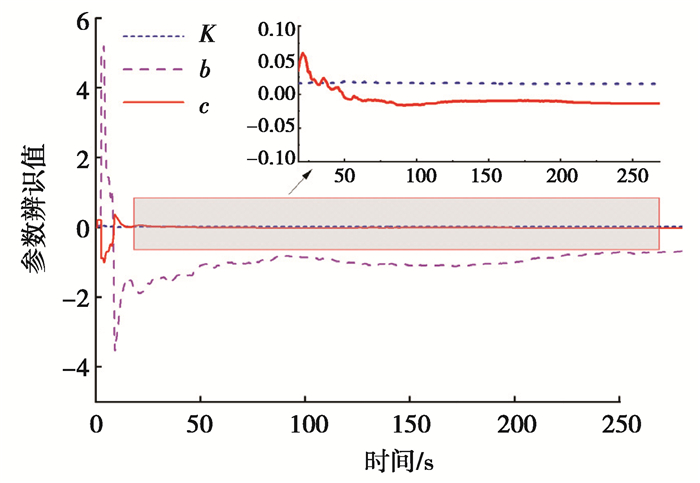
|
图 8 模型参数离线辨识效果 Fig. 8 Off-line identification of model parameters |
如图 8所示,参数K、b、c的辨识值在约30 s趋于相对稳定的状态,在后续辨识中仅存在小幅度波动。将辨识出的参数与系统输入相结合对铰接角进行估计并与实际测量铰接角进行对比,效果如图 9所示。
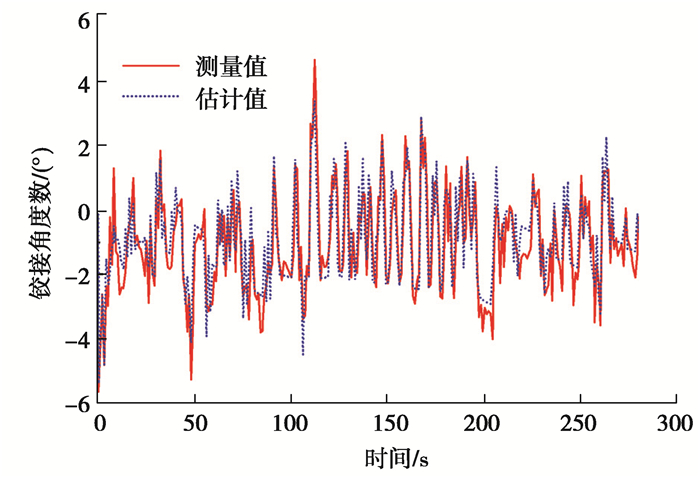
|
图 9 铰接角拟合效果 Fig. 9 Result of joint angle fitting |
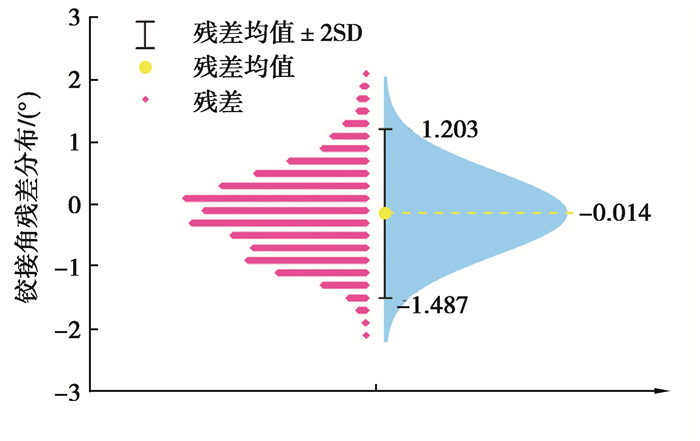
从图 9中可以看出,在参数辨识作用下模型可以有效估计出实际铰接角,其残差分布如图 10所示。根据分布统计可以看出拟合残差均值为-0.014°,以正态分布拟合残差曲线则有95.5%的残差分布在[-1.487, 1.203]范围内,其中大部分残差分布在±1°以内。从离线辨识结果看,带流量损耗参数的线性液压转向模型能够有效表达无人驾驶碾压机的转向系统特性。
|
图 10 模型离线辨识下铰接角估计残差分布 Fig. 10 Residual distribution of joint angle estimation |
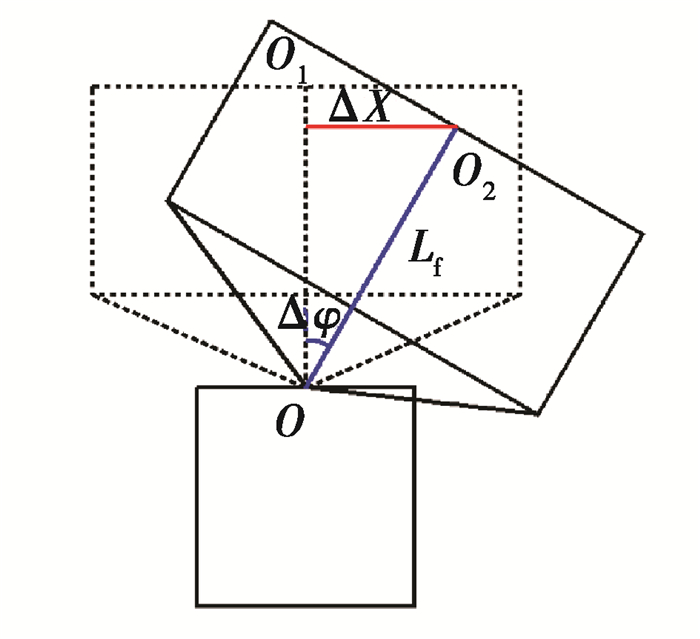
在系统运行过程中若停止模型的参数学习过程势必会产生估计偏差,为探究该偏差分别对车辆前进、后退过程的定位代偿产生的影响,现利用图 11所示的几何原理图展开分析。
|
图 11 铰接角偏差对横向定位的影响 Fig. 11 Effect of joint angle bias on horizontal location |
图 11描述的是铰接角偏差对车辆横向定位的影响,其对应关系为
| Δx=Lfsin(Δφ), | (21) |
式中:Δx为产生的横向定位偏差;Δφ为铰接角偏差;Lf为定位点与铰接点之间的距离。根据式(21)可以看出,横向定位偏差的大小不仅仅取决于铰接角偏差,还受到定位点与铰接角之间距离的影响。通常情况下,碾压机后车体长于前车体,因此在铰接角存在相同偏差的情况下后退过程的代偿受到该偏差的影响更大。所以文中主要针对无人驾驶碾压机后退过程展开实车代偿效果验证。
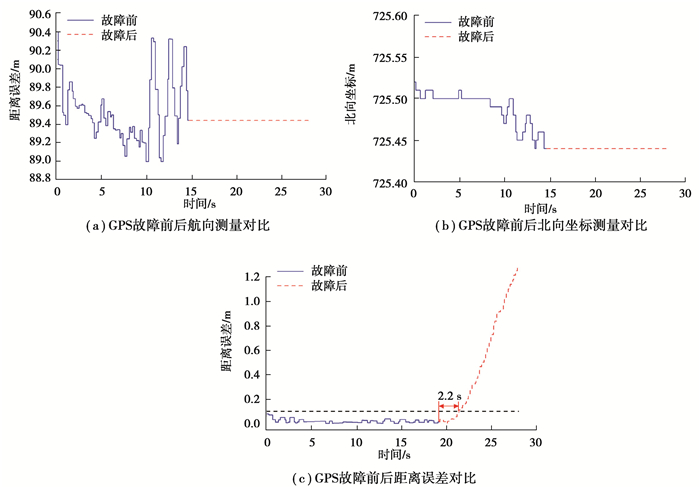
4.2 实车验证 4.2.1 无代偿情况下的失效控制分析为了充分验证文中所设计代偿方法的有效性,无人驾驶碾压机在GPS设备典型故障下的路径跟踪控制效果如图 12所示。
|
图 12 GPS信号不更新情况下的路径跟踪控制效果 Fig. 12 Path tracking control effect without GPS's updating |
图 12为GPS设备信号不更新情况下的路径跟踪控制效果图。从图 12中可以看出,在GPS设备出现故障后,若以0.1 m作为高精度运行失效阈值车辆仅能正常运行约2.2 s,即系统在无代偿情况下无法应对GPS设备的失效。
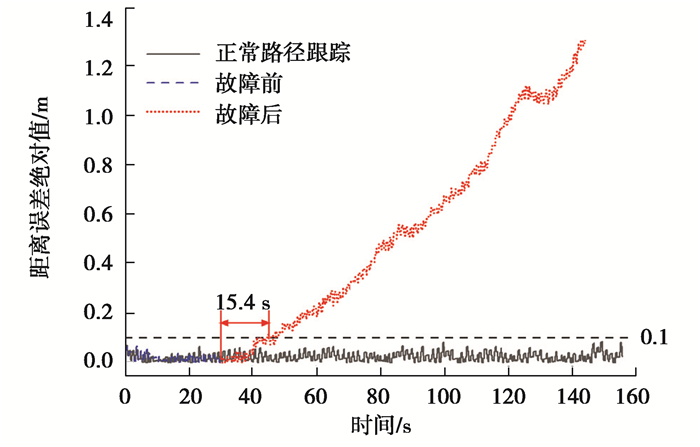
4.2.2 模型无学习情况下的代偿效果验证为了验证模型自学习的必要性,现做如下实验:使无人驾驶碾压机分别进行正常作业与代偿作业,记录二者的路径跟踪效果。代偿过程采用的模型参数均使用经验估值,转向系统比例系数K设定为0.025,参数b设定为0,系统流量损耗参数c设定为-0.025,并且在开始运行约30 s后进行代偿。效果如图 13所示:黑线代表正常路径跟踪控制效果;蓝线代表模型无学习情况下,GPS故障前的路径跟踪控制效果;红线代表模型无学习情况下,GPS故障后的路径跟踪控制效果。
|
图 13 正常路径跟踪控制与模型无自学习代偿情况下的距离误差对比 Fig. 13 Comparison of horizontal error between normal and fault-tolerant control without self-learning |
从图 13可以看出,若以0.1 m作为高精度运行失效阈值系统能够稳定运行约15.4 s,具备一定的定位失效容错能力。
4.2.3 不同仓面下的代偿效果验证文中基于4个平整度相近但位于不同位置的仓面进行代偿实验,构成4组实验案例来验证代偿效果。实验过程如下:在后退开始运行约20~30 s时停止对模型参数的学习,之后的模型参数均保持学习最后时刻的值,如表 1所示。
| 表 1 模型参数辨识值 Table 1 Model parameter identification value |
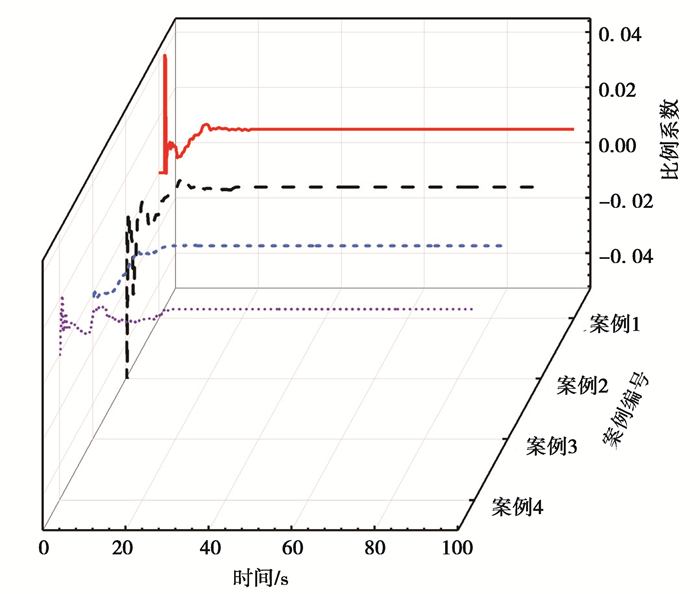
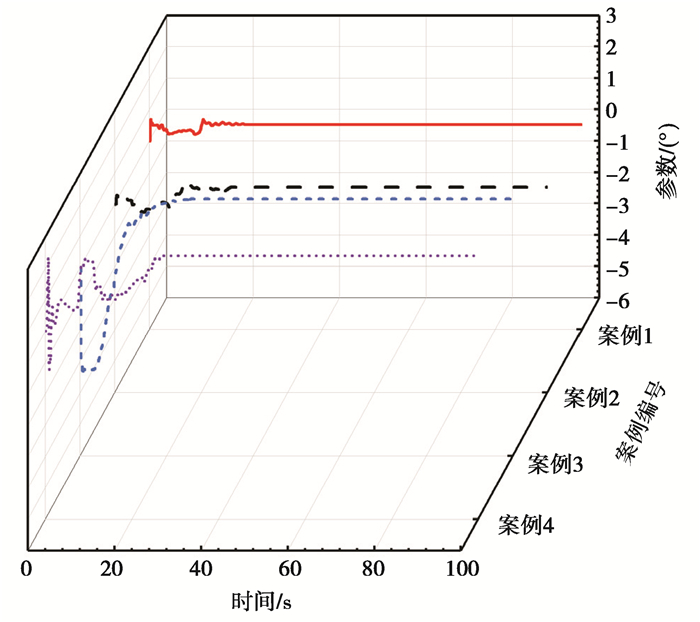
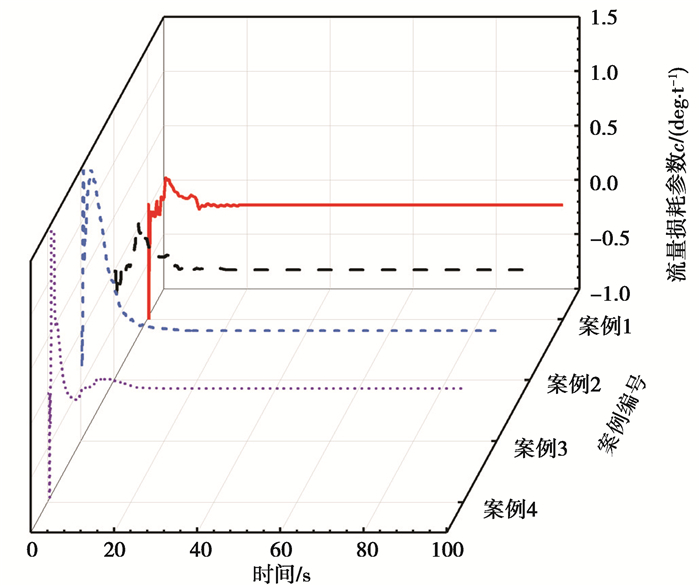
4组案例的参数辨识过程如图 14~图 16所示,分别给出了方向盘与铰接角的比例系数K,参数b,流量损耗参数c的辨识情况。
|
图 14 转向系统比例系数K辨识 Fig. 14 Identification of steering system's proportionality coefficient |
|
图 15 参数b辨识 Fig. 15 Identification of steering system's initial-value |
|
图 16 转向系统流量损耗参数c辨识 Fig. 16 Identification of steering system's flow loss |
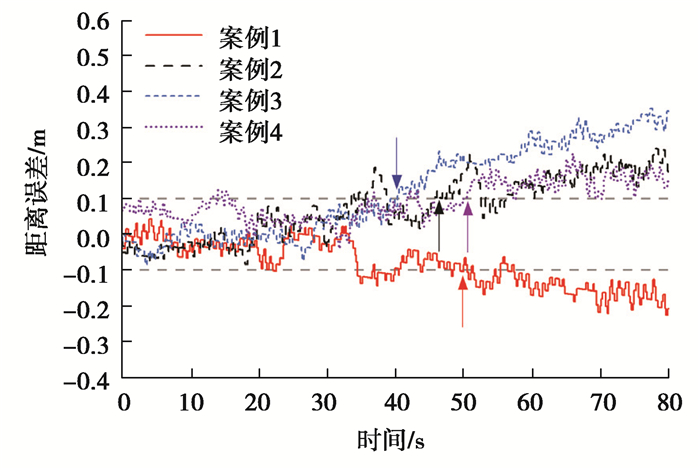
车辆控制效果对比如图 17和图 18所示,图 17为4组案例故障后的代偿距离误差时域图,图 18表达的是以10 s作为统计间隔对比4组案例的代偿距离误差绝对值均值变化情况。
|
图 17 各仓面代偿运行距离误差 Fig. 17 Distance error of fault-tolerance control on different roads |
|
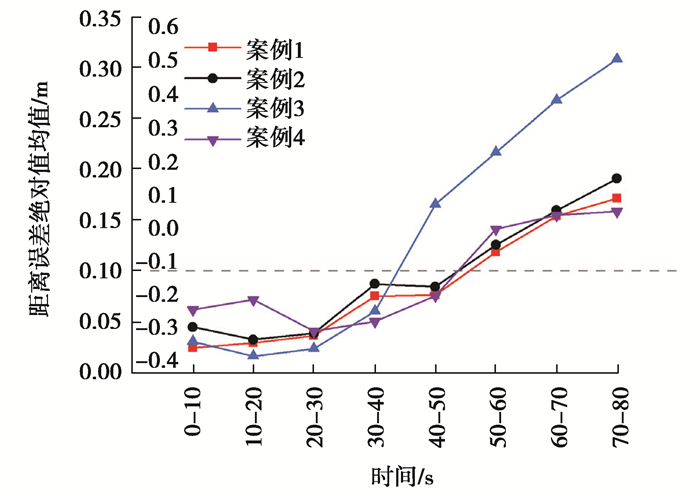
图 18 各仓面代偿运行距离误差绝对值均值 Fig. 18 Mean absolute value of distance error of faulttolerance control on different roads |
从图 17可以看出,若以0.1 m作为高精度运行失效阈值,4组案例的高精度运行时间基本分布在40~50 s区间。从图 18可以更直观地看出,4组案例的距离误差均值在40 s的时间内均可以维持在0.1 m以内,因此将完整代偿场景下的有效运行时长定义为40 s。
将无代偿、代偿无学习、完整代偿3种场景下,车辆故障后高精度运行时长进行汇总,如图 19所示:红色扇形为无代偿场景的运行时长,黄色扇形为代偿无学习场景的运行时长,蓝色扇形为完整代偿场景的运行时长。
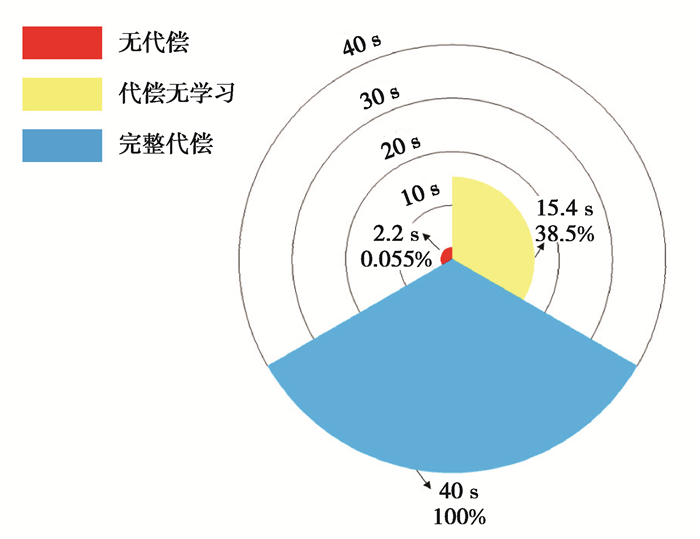
|
图 19 3种场景故障后高精度运行时长对比 Fig. 19 Comparison of high-precision running time after failure in three scenarios |
图 19以40 s作为标准,呈现了3种运行时长的相对大小关系。从图 19中的扇形大小可以直观地看出:代偿无学习、完整代偿相对于无代偿场景,运行时长均有大幅度提升。从量化的角度分析:以40 s作为标准的情况下,无代偿情况的运行时长2.2 s仅能达到0.055%,代偿无学习情况的运行时长15.4 s仅能达到38.5%。完整代偿情况的40 s运行时长相较于前二者分别提高了18.7倍和2.7倍,极大地提高了系统运行的安全性、稳定性,提升了系统运行效率。
5 总结笔者针对无人驾驶碾压机在恶劣工况下的定位失准问题,提出了将自学习模型与冗余硬件信息相结合的信号代偿容错控制方法。基于大坝填筑现场的车辆运行数据对模型进行了仿真分析,并利用现场车辆进行了代偿策略的实车试验。研究方法与验证效果如下:
1) 基于无人驾驶碾压机在实际运行过程中呈现的转向系统中位漂移现象,构建了带流量损耗参数的线性液压转向模型以充分体现转向系统特性,结合铰接式车辆的运动规律与几何特性设计了基于模型信息与冗余硬件的信号代偿策略。
2) 基于带遗忘因子的最小二乘方法,在Matlab/Simulink仿真软件中利用实车运行数据对模型进行了辨识,结果表明:95.5%的铰接角估计残差能够分布在±1.5°以内。
3) 利用4组案例对比验证了33 t无人驾驶碾压机的实车代偿效果,并且对比了无代偿、代偿无学习、完整代偿3种场景的故障运行情况。结果表明:完整代偿情况下,车辆能够在传感器失效后约40 s的时间内继续进行高精度作业,相较于无代偿情况延长了近18.7倍的运行时间,相较于代偿无学习情况延长了近2.7倍的运行时间,有效避免系统在单组GPS设备短时失效后的控制失控,提高了无人驾驶碾压机系统运行的稳定性和系统作业的安全性与效率。
| [1] |
Yongming B, Meng Y, Xiaojun F, et al. Kinematics and path following control of an articulated drum roller[J]. Chinese Journal of Mechanical Engineering, 2017, 30(4): 888-899. DOI:10.1007/s10033-017-0102-8 |
| [2] |
Yao D C, Xie H, Qiang W, et al. Accurate trajectory tracking with disturbance-resistant and heading estimation method for self-driving vibratory roller[J]. IFAC-PapersOnLine, 2018, 51(31): 754-758. DOI:10.1016/j.ifacol.2018.10.135 |
| [3] |
兰京. 无人驾驶汽车发展现状及关键技术分析[J]. 内燃机与配件, 2019(15): 209-210. Lan J. The development status and key technology analysis of unmanned vehicles[J]. Internal Combustion Engine & Parts, 2019(15): 209-210. (in Chinese) DOI:10.3969/j.issn.1674-957X.2019.15.111 |
| [4] |
孙成功. 线控转向叉车传感器故障诊断及容错控制[D]. 合肥: 合肥工业大学, 2019. Sun C G. Sensor fault diagnosis and fault tolerance control of steer-by-wire system for forklift[D]. Hefei: Hefei University of Technology, 2019. (in Chinese) |
| [5] |
Gadda C D. Incorporating a model of vehicle dynamics in a diagnostic system for steer-by-wire vehicles[C]//Proceedings of Avec International Workshop. 2004.
|
| [6] |
Gadda C D, Laws S M, Gerdes J C. Generating diagnostic residuals for steer-by-wire vehicles[J]. IEEE Transactions on Control Systems Technology, 2007, 15(3): 529-540. DOI:10.1109/TCST.2007.894650 |
| [7] |
Chamseddine A, Noura H. Control and sensor fault tolerance of vehicle active suspension[J]. IEEE Transactions on Control Systems Technology, 2008, 16(3): 416-433. DOI:10.1109/TCST.2007.908191 |
| [8] |
Fekih A, Seelem S R. A fault tolerant control design for automatic steering control of ground vehicles[C]//IEEE International Conference on Control Applications. IEEE, 2013: 1491-1496.
|
| [9] |
田承伟. 线控转向汽车容错控制方法研究[D]. 长春: 吉林大学, 2010. Tian C W. Research on fault tolerant control method for steer-by-wire automobile[D]. Changchun: Jilin University, 2010. (in Chinese) |
| [10] |
何磊, 马伯祥, 宗长富. 线控转向汽车转向盘转角传感器的容错控制策略[J]. 汽车工程, 2015, 37(3): 327-330, 345. He L, Ma B X, Zong C F. Fault-tolerance control strategy for the steering wheel angle sensor of a steer-by-wire vehicle[J]. Automotive Engineering, 2015, 37(3): 327-330, 345. (in Chinese) |
| [11] |
王晓伟. 基于GPS/INS组合定位系统的滤波算法的研究与仿真[D]. 成都: 西南交通大学, 2013. Wang X W. Research and simulation of the filtering algorithm in GPS/INS[D]. Chengdu: Southwest Jiaotong University, 2013. |
| [12] |
Scheding S, Dissanayake G, Nebot E M, et al. An experiment in autonomous navigation of an underground mining vehicle[J]. IEEE Transactions on Robotics and Automation, 1999, 15(1): 85-95. DOI:10.1109/70.744605 |
| [13] |
乔伊娜. 关于铰接车辆铰接机构的研究[D]. 大庆: 东北石油大学, 2015. Qiao Y N. Research on the articulated mechanism of articulated vehicles[D]. Daqing, China: Northeast Petroleum University, 2015. (in Chinese) |
| [14] |
牛平杰. 工程车辆铰接桥式转向系统动态特性研究[D]. 长春: 吉林大学, 2016. Niu P J. Dynamic characteristics research on articulated axle steering system of construction vehicle[D]. Changchun: Jilin University, 2016. (in Chinese) |
| [15] |
吴敏, 俞烨隆. 基于FFRLS与转速扰动注入法的永磁同步电机在线参数辨识[J]. 电机与控制应用, 2020, 47(4): 44-48. Wu M, Yu Y L. Online parameters identification for PMSM based on FFRLS and speed disturbance injection[J]. Electric Machines & Control Application, 2020, 47(4): 44-48. (in Chinese) |
| [16] |
Song K, Xie H. Path-following control for unmanned rollers: a composite disturbance rejection-based framework[C]//2020 IEEE 9th Data Driven Control and Learning Systems Conference (DDCLS). Liuzhou, China. IEEE, 2020: 432-437.
|
| [17] |
韩京清. 从PID技术到"自抗扰控制"技术[J]. 控制工程, 2002, 9(3): 13-18. Han J Q. From PID technique to active disturbances rejection control technique[J]. Basic Automation, 2002, 9(3): 13-18. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45



