2. 国网河南省电力公司, 郑州 450001;
3. 重庆大学 自动化学院, 重庆 400044
2. State Grid Henan Electric Power Company, Zhengzhou 450001, P. R. China;
3. School of Automation, Chongqing University, Chongqing 400044, P. R. China
安全、可靠、优质、经济是电力系统运行的基本要求。电力线路的安全可靠运行关乎国民生产、人民生活的各个方面。在中国6~66 kV的中低压配电网中广泛采用了小电流接地系统,又称中性点不直接接地系统(NUGS)[1]。
单相接地指的是小电流接地系统单相接地,单相接地故障是配电网系统中最常见的故障,约占配电网故障总数的80%。当小电流接地系统发生单相接地故障时不形成低阻抗的短路回路,而是由线路对地电容形成高阻抗回路,短路电流非常小,同时线电压依然保持对称,短时间内不会对负荷的连续供电造成一定的影响,可以带故障运行1~2 h。但是若发生单相接地故障时电网仍长期运行,可能引起绝缘的薄弱环节被击穿,发展成为相间短路,使事故扩大,影响用户的正常用电。同时弧光接地还会引起全系统过电压,进而损坏设备,破坏系统安全运行,甚至将会进一步带来巨大的经济损失和恶劣的社会影响。所以需要在故障后第一时间内准确识别故障类型,为后续制定有针对性的故障处理措施提供可靠依据。
目前针对小电流系统的单相接地故障类型辨识的研究较多,根据特征量应用途径的不同,现有的识别方法可分为2类:一类是特征分析法,如:文献[2]提出一种配电网高阻接地故障在线监测与辨识方法,利用高阻接地故障时产生的高次谐波,作为高阻接地故障的判别依据;文献[3]提出一种配电网单相电弧接地故障的辨识方法,认为单相电弧接地故障相较金属接地故障,其暂态过程持续存在,并提取高频信号切片图来识别单相电弧性故障;文献[4]提出了高阻故障模型,并通过故障零序量的小波特征值识别高阻接地故障;文献[5]结合零序等值网络分析了配网高阻故障产生高频分量的原因以及正常状态对高频分量的影响,提出了一种基于零序电压小波包能量比的配电网单相高阻接地故障辨识方法;文献[6]在分析小电阻接地系统发生接地故障时故障线路、非故障线路零序电流与中性点电流关系的基础上,提出了一种基于中性点电流与线路零序电流投影量差动的高阻接地故障判断方法。
另一类识别方法是结合时频分解与机器学习的智能方法,如:文献[7]提出了离散小波变换和k近邻机器学习算法的组合模型,以检测和分类高阻单相接地故障;文献[8]将人工智能技术运用于故障类型识别中,提出了一种小电阻接地系统间歇性弧光过电压分析方法,利用HHT算法,提取零序电压的IMF分量,并采用支持向量机对间歇性弧光故障进行识别;文献[9]利用小波分析的方法从相电压和电流数据中提取特征,并基于XGBoost模型对中性点不接地系统的3种状态进行辨识,分别是:无故障、接地故障和零线故障。文献[10]首先根据各节点LOF值的大小实现智能配电网的故障检测与定位,然后对故障处的三相电压进行小波变换,以三相电压的小波奇异熵值建立SVM故障类型判别预测模型。
现有的研究成果在单相接地故障检测中取得了一定效果,但大多只选取了配电网的部分特征,即某类故障的特有属性来进行分析,造成了对故障整体信息描述不充分,只能针对某一特定的故障类型进行识别,并未对单相接地故障类型进行全面综合划分,算法的通用性不足,不利于运维人员制定有针对性的故障处理措施。
笔者考虑要对包括高阻接地故障与间歇弧光接地故障在内的共7种类型的单相接地故障进行综合辨识,对此需要提取更加全面的故障特征。由于现场采集到的故障录波数据特征维度高,采样点数量较多,其中蕴含了丰富的与故障类型强相关的复杂非线性特性,有利于故障类型辨识。而深度学习十分擅长从高维数据集中自动学习复杂且有用的特征,相比于过去出现的很多优秀的手动特征提取器,比如:尺度不变特征变换(SIFT),Gabor滤波器和定向梯度直方图(HOG)等,深度学习模型可以通过搭建不同的结构、调整隐藏层的数量来学习得到不同性质、不同层次的特征,可实现端到端的任务学习或者提取抽象特征用于下游任务的学习。
综上所述,提出一种融合特征分解和深度学习思想的单相接地故障类型辨识方法。首先采用希尔伯特黄变换(HHT, hilbert-huang transform)对配电网特征进行初步处理,突出不同故障类型的特点;其次设计深度学习模型ResNet18学习故障事件的复杂非线性特征,从而辨识出故障类型结果。通过国内某真型试验场采集到的录波数据进行验证,证明了提出的方法具有较高的辨识精度和较强的鲁棒性,通用性好。
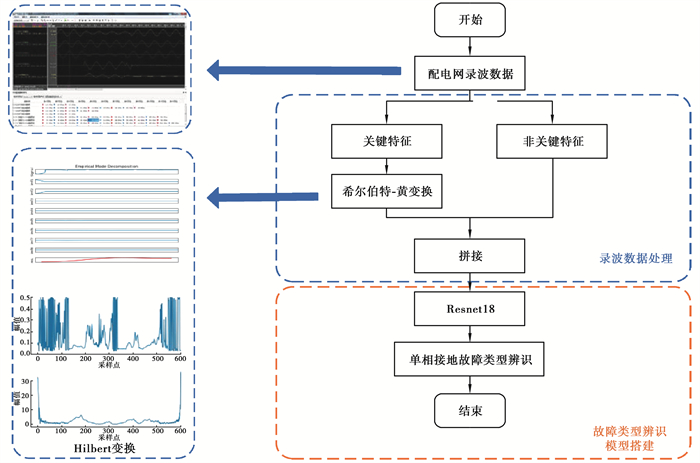
1 单相接地故障类型辨识方法总体流程笔者提出的基于特征分解和深度学习的单相接地故障类型辨识方法的总体流程如图 1所示。配电网现场采集到的录波数据是配电网实时状态、运行情况的“心电图”,能为单相接地故障的类型辨识提供最直接、最准确的依据。所以,考虑将配电网的故障录波数据作为原始数据集。首先将其划分为关键特征部分和非关键特征部分,并对关键特征部分进行HHT变换,将重点关注的和故障类型强相关的特征从复杂信号中分离出来生成新的特征变量;同时为保证故障信息的完整性,并未将非关键特征部分直接舍弃,而是将其与关键特征部分的HHT变换结果进行拼接;其次设计深度学习模型ResNet18对经特征处理后的数据集进行学习,辨识出具体的单相接地故障类型。
|
图 1 单相接地故障类型辨识方法总体流程 Fig. 1 The overall process of single-phase grounding fault type identification method |
HHT是一种具有自适应的时频分析方法,结果反映信号的频域特征随时间变化的规律。作为时频域分析的重要手段,HHT既吸取了小波变换的多分辨率的优势,又克服了小波变换中选择小波基困难的问题,可以对局部特征进行反映,有利于提取复杂故障信号中的重要特征[11]。
HHT具体包括2个过程:经验模态分解(EMD)和Hilbert变换。EMD是依据信号特点自适应地把任意一个复杂信号分解为一系列本征模态函数(IMF, intrinsic mode function)。经验模态分解后, 再对每一个IMF作Hilbert变换,继而可求取每一个IMF的瞬时频率和瞬时幅值。
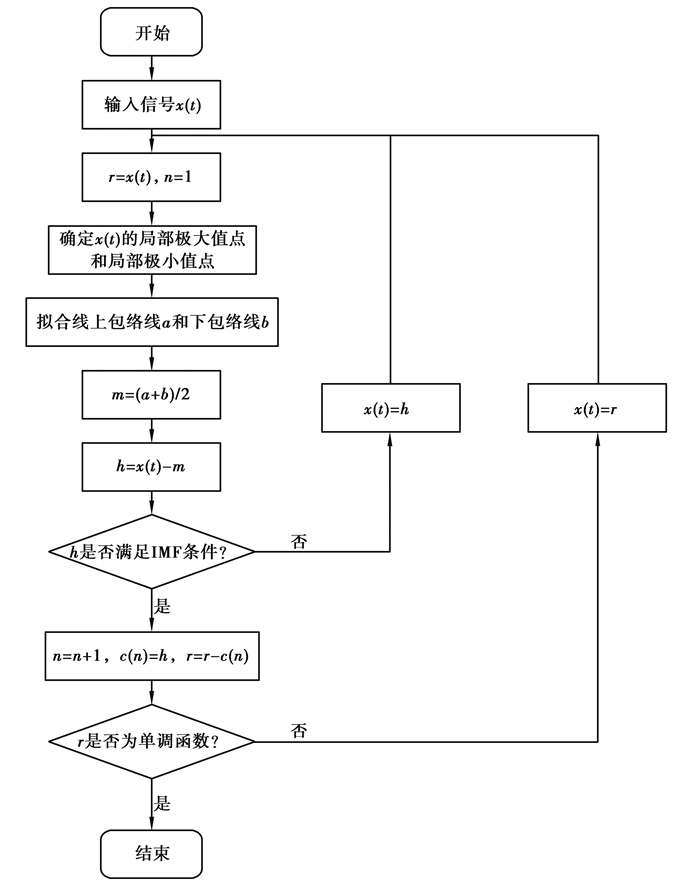
EMD分解出的IMF分量需要满足2个条件,分别是:在整个信号长度上,极值点的个数和过零点的个数相同或相差至多一个;在任意时刻,由极大值点形成的上包络线和由极小值点形成的下包络线的平均值为零,即上、下包络线对称于时间轴[12]。EMD的分解过程如图 2所示。
|
图 2 EMD的分解过程 Fig. 2 Decomposition process of EMD |
再对EMD分解出的IMF分量ci(t)依次进行Hilbert变换,公式为
| $ \widehat{c_i}(t)=\frac{1}{{\rm{ \mathsf{π} }}} \int_{-\infty}^{\infty} \frac{c_i(\tau)}{t-\tau} \mathrm{d} \tau, $ | (1) |
由原始的IMF分量和其对应的Hilbert变换结果构成的解析信号zi(t)为
| $ z_i(t)=c_i(t)+j \widehat{c_i}(t)=A_i(t) e j \theta_i(t), $ | (2) |
其中,瞬时幅值表示为
| $ A_i(t)=\sqrt{c_i^2(t)+\widehat{c_i}^2(t)} \text { 。} $ | (3) |
θi(t)可根据下式求得
| $ \tan \theta_i(t)=\frac{\widehat{c_i}(t)}{c_i(t)} \text { 。} $ | (4) |
瞬时频率表示为
| $ \omega_i(t)=\frac{\mathrm{d} \theta_i(t)}{\mathrm{d} t} 。$ | (5) |
特征x(t)的Hilbert谱表示为
| $ H(\omega, t)={Re}\left[\sum\limits_{i=1}^q A_i(t) e^{j \int{\omega i}(t) \mathrm{d} t}\right] 。$ | (6) |
式中,q表示分解出的IMF分量的个数。通过对故障录波数据的关键特征进行HHT变换,提取出其中隐藏的局部暂态特征:瞬时频率、瞬时幅值、Hilbert谱。
3 ResNet18深度学习模型深度学习通过构建具有很多隐藏层的神经网络模型来学习更有用的特征,从而最终提升分类或回归的准确性。深度学习模型提取特征的能力主要是通过卷积层、激活操作、池化层等来实现的,其中起主要作用的是卷积层,卷积层中的卷积核等价于很多不同的滤波器,通过卷积层来对原始特征进行“滤波”处理,从而实现数据集中特征的提取。
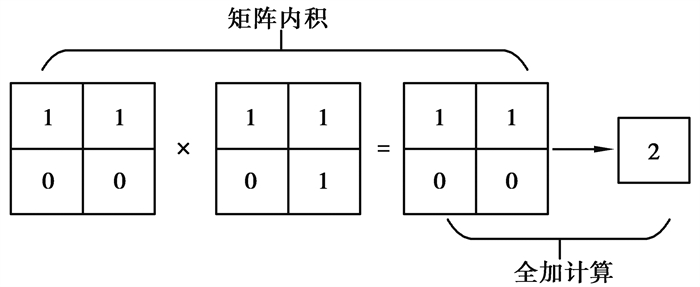
卷积层中涉及的卷积运算由矩阵内积和全加计算组成,如图 3所示。卷积计算的本质是内积运算[13]。对于一维向量的卷积运算,2个向量的内积越大,则2个向量的相似度越高。而卷积计算实际上是将一维的内积运算推广至二维平面,卷积核在滑移卷积时,其实就是提取和它相似的特征。卷积核的参数是根据数据集的标签来不断地进行修正。通过逐层地卷积运算,不断组合和抽象,就可以提取到一系列代表单相接地故障类型的复杂非线性特征。
|
图 3 卷积计算过程 Fig. 3 Convolution calculation process |
由前述理论可简单推知深度学习网络模型的层数越多,模型可以从数据中提取到更加抽象的特征,更有利于提高模型的准确度。但根据研究学者的实验结果表明,当网络层数超出了一定范围内,随着其的增加,梯度弥散问题严重制约了深度学习的性能,浅层网络几乎学不到任何知识。并且因为卷积核参数的盲目性、激活函数的抑制作用等,造成每做一次卷积运算和对应的激活操作都会在原始特征或上一步提取到的特征结果的基础上浪费掉一些信息。
Resnet网络巧妙地利用了残差连接的方式,很好地解决了深度网络中模型退化的问题[14]。Resnet网络中的残差连接,在反向传播时,每2个残差块之间不仅传递了梯度,还加上了求导之前的梯度,从而减小梯度弥散的可能性[15]。同时将上一步的处理结果直接拿到当前时刻一并处理,减少了信息损失。
为此,笔者设计使用深度学习模型ResNet来学习经特征变换后的数据集与故障类型之间的复杂抽象映射。
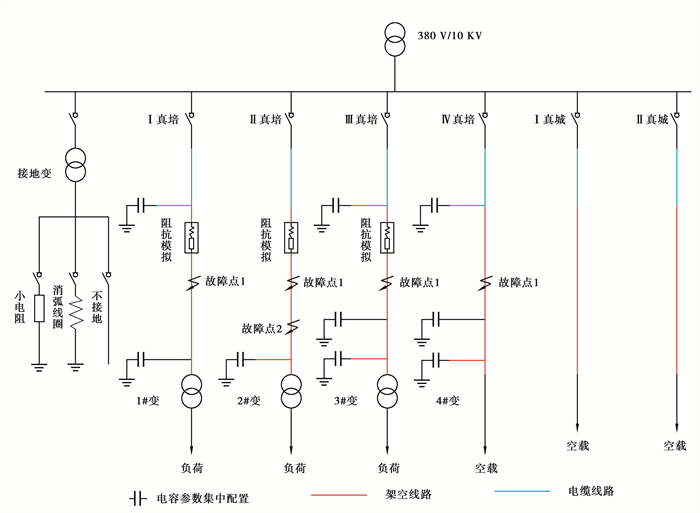
4 实验分析 4.1 训练集和测试集的建立本研究使用的录波数据来自国内某真型试验场,其拓扑结构如图 4所示。试验时通过改变中性点的接地运行方式、接地介质种类、接地电阻大小等,得到不同类型的单相接地故障录波数据。其中,中性点接地方式覆盖不接地、经消弧线圈接地和经小电阻接地等主流形式;接地介质包括经间歇性弧光接地、经稳定弧光接地、经泥土地接地、经电阻接地等常见故障类型;接地电阻阻值选取了250、1 000、2 000、5 000 Ω等典型值。试验在3种接地运行方式下各自产生420、600、240条故障录波数据;录波装置的采样频率为10 kHz,采样周期包含12 014个采样点,每段录波数据包含291个电气量;数据分析时以8:2的比例划分训练集和测试集。
|
图 4 配电网拓扑图 Fig. 4 Distribution network topology diagram |
所用实验环境平台条件为Windows10 X64操作系统、Inter i5-7200,使用Python编程语言实现,ResNet18采用pytorch框架实现。
4.2 录波数据的处理由于每个完整的单相接地故障录波数据样本,并非在整个采样阶段都是处于故障状态,还包含发生故障前的正常状态,非永久性故障还包括故障发生后恢复正常的过渡状态。为了使观察对象更加明确并且减少分析的数据量,对处于故障状态的录波数据进行截取。通过对录波数据的观察,截取的时间周期包含600个采样点。
对于录波数据中包含的291个电气量,由于其中的许多特征在整个时间周期内都保持一个常数,或者呈现周期性的规律变化,所以对单相接地故障类型辨识的意义不大。根据配电网运维工程人员的经验,将录波数据中包含的所有电气量特征分为2个部分:关键特征部分和非关键特征部分,其中关键特征部分包含:母线零序电流3I0、母线零序电压3U0、Ⅰ真培1三相电流3I0Ⅰ、Ⅱ真培1三相电流3I0Ⅱ、Ⅲ真培1三相电流3I0Ⅲ,其余电气量特征则属于非关键特征。为了进一步分析这5个关键特征,对其进行HHT变换得到对应的时频信息,这些分解得到的局部暂态特征使不同故障类型之间的特征区分度更高[16-18]。
对几种不同故障类型线路的母线零序电流3I0进行EMD分解,并对比分解结果。
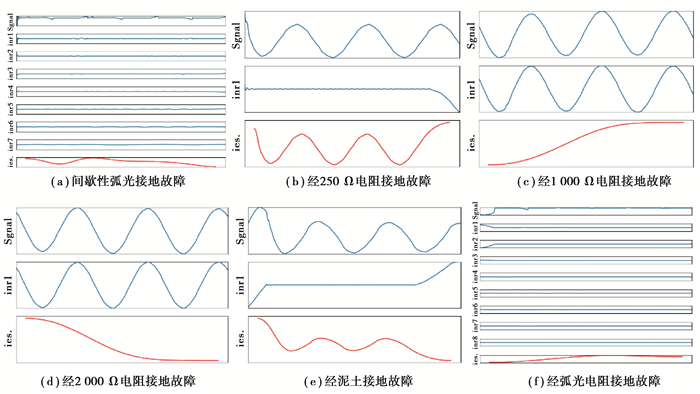
图 5中的(a)为间歇性弧光接地故障、(b)为经250 Ω电阻接地故障、(c)为经1 000 Ω电阻接地故障、(d)为经2 000 Ω电阻接地故障、(e)为经泥土接地故障、(f)为经弧光电阻接地故障。通过对图 5观察得出:不同故障类型线路的母线零序电流3I0的EMD分解结果存在着明显的区别,具体表现在IMF分量的个数、波形以及残差的波形都不尽相同,可作为后续故障类型辨识研究的故障特征之一。
|
图 5 EMD分解结果对比 Fig. 5 Comparison of EMD decomposition results |
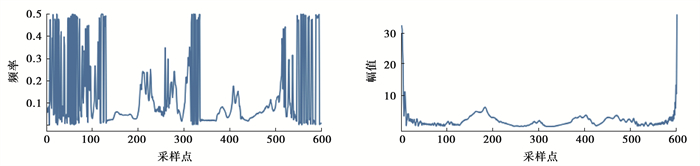
对图 5中的间歇弧光接地故障线路(a)的IMF1分量进行Hilbert变换,得到对应的瞬时幅值和瞬时频率曲线,如图 6所示。
|
图 6 IMF1的瞬时频率和瞬时幅值 Fig. 6 Instantaneous frequency and instantaneous amplitude of IMF1 |
通过上述实验结果表明,使用HHT有利于提取录波数据的局部暂态特征,使得不同类型的单相接地故障之间的特征区分度更高。因此,对所有故障样本的关键特征部分进行HHT操作,由于EMD分解出的IMF分量个数不完全相等,为了保证特征数量的一致性,便于后续建模训练,对分解出的IMF分量个数少于设定阈值的用零来进行填充,超出阈值部分的IMF分量则舍弃。其次再对IMF分量依次进行Hilbert变换。经过HHT变换后,5个关键特征的维度由(5,600)变换为(185,600)。
尽管非关键特征与单相接地故障类型间的关联性很弱,但其仍包含了一些有用信息。对此,将关键特征部分经过HHT变换后的结果与原始的非关键特征部分进行拼接,拼接后的特征维度为(471,600),使特征维度处于可接受范围内的同时也保证了故障信息的完整度。
为了使经过特征处理后的数据样本变成传统意义上的“图像样本集”,便于后续使用卷积操作来提取特征,还需要将特征归一化至(0,255)区间,并转换为灰度图。特征归一化的公式为
| $ x^{\prime}=255 \cdot \frac{x-x_{\min }}{x_{\max }-x_{\min }}, $ | (7) |
式中,xmin表示该特征中的最小值,xmax表示该特征中的最大值。
4.3 ResNet18模型的参数设置配电网采集得到的录波数据经过特征处理后,采用深度学习模型ResNet来对单相接地故障类型进行辨识。根据特征数据集的特征数量和硬件环境情况,设置ResNet结构为ResNet18,如图 7所示。

|
图 7 ResNet18的基本结构 Fig. 7 Basic structure of ResNet18 |
结合故障录波数据的特性,在原始结构的基础上对其进行了局部改动,具体如下:1)为了与故障录波数据的维度匹配,将第一层conv的卷积核修改为3×3;2)根据预期辨识的单相接地故障类别数量,调整模型最后一层(全连接层)的输出维度。修改后的具体网络参数如表 1所示。
| 表 1 ResNet18的模型参数 Table 1 Model parameters of ResNet18 |
模型训练时,使用的损失函数为交叉熵损失函数。假设概率分布p为期望输出,概率分布q为实际输出,H(p, q)为交叉熵,其表达式为
| $ H(p, q)=-\sum\limits_x p(x) \log q(x)。$ | (8) |
录波数据的处理阶段相当于对样本数据进行特征工程操作。原始特征经特征工程处理后表征能力变强,通过其训练得到的模型在未知数据上的性能表现可以达到更优。
本实验对故障录波数据的关键特征部分进行HHT变换,通过实验结果验证了特征变换对于提高辨识模型的最终分类精度是有效的。基于表 2中的3种录波数据处理方式得到的样本数据,分别运用本文设计的深度学习模型ResNet18进行训练和分类,对比分类精确度如图 8所示。
| 表 2 3种录波数据的处理方式 Table 2 Three kinds of recording data processing methods |
|
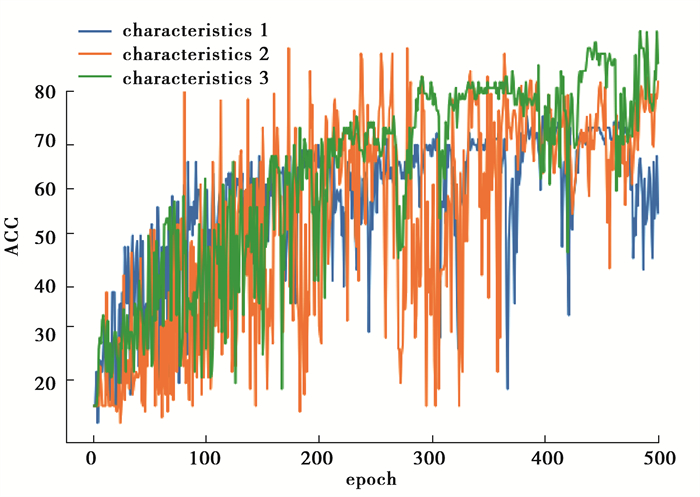
图 8 3种录波数据处理方式的分类效果对比 Fig. 8 Comparison of the classification effects of the three recording data processing methods |
对比得出:不预先对特征进行任何处理操作得到的特征1的分类精确度最低,为67.9%;将剩余的286个原始的电气量直接舍去,仅对关键特征部分进行了HHT变换得到的特征2,损失部分故障相关信息,但由于其将关键特征通过分解和变换提取出更有利于故障类型辨识的新特征,所以模型收敛后分类的精度优于特征1,为83.1%。然而不同故障样本的特征经过EMD分解得到的IMF分量的个数不一致,对于分解个数低于设定阈值的采用补零方法进行填充,由此造成特征矩阵稀疏,模型的精确度波动比较大;而采用提出的特征处理方式得到的特征3结合前2种方式的优势,既提取了更有利于故障类型辨识的新特征,使特征维度处于可接受的范围内的同时也保证了故障信息的完整度,故障类型辨识的精度也是最优的,模型收敛后的精确度为92.8%。
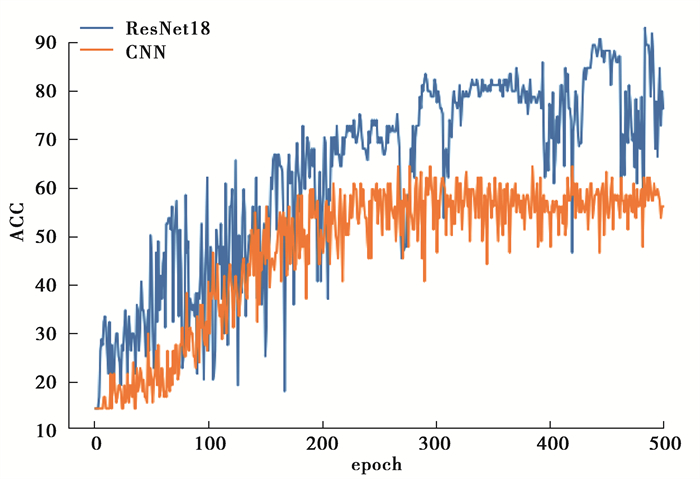
4.4.2 实验二本实验对比分析了使用设计的ResNet18模型和使用传统的深度CNN模型的预测分类效果。同样以测试集的最终分类精确度Acc作为评价指标,设置训练的epoch为500。使用本文设计的ResNet18模型和传统的CNN模型的分类效果对比如图 9所示。由图可以看出,ResNet18模型的精确度整体上都明显优于CNN模型。CNN模型从200个epoch之后没有明显的增长,保持在60%左右,当epoch=283时,模型的精确度最高,为61.9%。CNN模型从训练初期到模型收敛,精确度变化曲线的波动幅度较小。ResNet18模型在模型训练前期的精确度变化曲线的波动较大,但随着训练轮数的增加,波动幅度逐渐减小。ResNet18模型和CNN模型因神经网络的深度和庞大的参数量,具有强大的拟合输入与输出之间复杂非线性关系的能力,区别在于ResNet18模型克服了CNN模型随着模型深度增加,造成因梯度消失而导致的深度学习模型效果退化的问题。所以ResNet18模型的分类效果明显优于CNN模型,当ResNet18模型收敛后,精确度保持在90%附近波动,epoch=484时,模型的精确度最高,为92.8%。通过本实验验证了使用设计的ResNet18模型对于单相接地故障类型辨识的有效性。
|
图 9 ResNet18和CNN的分类效果对比 Fig. 9 Comparison of classification effects between ResNet18 model and CNN model |
本实验基于相同的样本集,对比了文献[10]中提出的方法:结合小波变换和SVM模型对多种单相接地故障类型进行辨识,以及对比了单独使用SVM模型和结合HHT和SVM模型对单相接地故障类型进行综合辨识的效果。其中SVM模型基于网格搜索法设定超参数,小波变换选择的小波基函数是Daubechies(db5)小波。同样以测试集的最终分类精确度Acc作为评价指标,各种方法的辨识效果对比如表 3所示。
| 表 3 综合辨识方法效果对比 Table 3 Comparison of comprehensive identification methods |
对比得出:单独使用SVM模型的辨识效果最差,精确度为79.5%。SVM模型利用核函数将特征映射到高维空间,并基于样本与决策面间的距离最大化来进行分类,但其难以挖掘样本中的复杂非线性特征,并且其性能易受缺失数据影响,对参数和核函数的选择也比较敏感,最终造成其辨识效果不佳。而将SVM模型与小波变换结合,利用小波变换的时频多分辨率的特点,可以捕捉到更多关于单相接地故障类型的细节信息,相比于单独使用SVM模型,辨识效果有明显地提升,精确度为86.0%。但小波变换的性能也和所选择的小波基函数直接关联,不同的信号可能需要选择不同的小波基函数,自适应性能略显不足。使用HHT替代小波变换与SVM模型结合,其辨识效果又在前一基础上有一定提升,精确度为87.4%。而使用提出的辨识方法,结合了HHT的自适应时频分析能力和ResNet18模型提取抽象特征的能力,相比于其他辨识方法,辨识精确度最高,为92.8%。
5 总结笔者提出了一种融合特征分解和深度学习思想的单相接地故障类型辨识方法。首先采用希尔伯特-黄变换对配电网特征进行初步处理,突出不同故障类型的特点;其次设计深度学习模型ResNet18学习故障事件的复杂非线性特征,最终辨识出故障类型结果。通过国内某真型试验场采集到的录波数据进行验证,证明了本文提出的模型能准确识别出多种单相接地故障的类型,具有较高的辨识精度和较强的鲁棒性,通用性好,可为后续制定有针对性的故障处理措施提供可靠依据。
| [1] |
张志霞. 小电流接地系统单相接地故障选线理论研究[M]. 辽宁: 辽宁科学技术出版社, 2014. Zhang Z X. Theoretical research on single-phase grounding fault line selection in small current grounding system[M]. Liaoning: Liaoning Science and Technology Press, 2014. (in Chinese) |
| [2] |
周封, 朱瑞, 王晨光, 等. 一种配电网高阻接地故障在线监测与辨识方法[J]. 仪器仪表学报, 2015, 36(3): 685-693. Zhou F, Zhu R, Wang C Q, et al. Online criterion and identification of single-phase ground fault with high resistence in distribution network[J]. Chinese Journal of Scientific Instrument, 2015, 36(3): 685-693. (in Chinese) |
| [3] |
沈煜, 阮羚, 戴兵, 等. 配电网单相电弧接地故障的辨识方法[J]. 武汉大学学报(工学版), 2018, 51(12): 1098-1104. Shen Y, Ruan L, Dai B, et al. Identification of single-phase arc grounding fault in power distribution network[J]. Journal of Wuhan University (Engineering Edition), 2018, 51(12): 1098-1104. (in Chinese) |
| [4] |
陈民铀, 黄永, 瞿进乾. 配电网线路高阻故障识别方法[J]. 重庆大学学报, 2013, 36(09): 83-88. Chen M Z, Huang Y, Zhai J Q. High impedance fault identification method of distribution network[J]. Journal of Chongqing University, 2013, 36(09): 83-88. (in Chinese) |
| [5] |
陈振宁, 李勇汇, 彭辉, 等. 基于零序电压小波包能量比的配网单相高阻接地故障辨识分析[J]. 科学技术与工程, 2020, 20(20): 8202-8209. Chen Z N, Li Y H, Peng H, et al. Identification of Single-phase high resistance earth fault in distribution network based on wavelet packet energy ratio of zero sequence voltage[J]. Science Technology and Engineering, 2020, 20(20): 8202-8209. (in Chinese) |
| [6] |
盛亚如, 丛伟, 卜祥海, 等. 基于中性点电流与零序电流投影量差动的小电阻接地系统高阻接地故障判断方法[J]. 电力自动化设备, 2019, 39(3): 17-22. Sheng Y R, Cong W, Bu X H, et al. Detection method of high impedance grounding fault based on differential current of zero-sequence current projection and neutral point current in low-resistance grounding system[J]. Electric Power Automation Equipment, 2019, 39(3): 17-22. (in Chinese) |
| [7] |
Nakho A, Hamam Y. Detection and classification of single phase to ground faults under high resistance ground paths in power systems using machine learning[C]// 2021 Southern African Universities Power Engineering Conference/Robotics and Mechatronics/Pattern Recognition Association of South Africa (SAUPEC/RobMech/PRASA). doi: 10.1109/SAUPEC/RobMech/PRASA52254.2021.
|
| [8] |
童奕宾, 尤智文, 李姝. 小电阻接地系统间歇性弧光过电压分析[J]. 电力系统及其自动化学报, 2012, 24(3): 116-120. Tong Y B, You Z W, Li S. Analysis of intermittent arc overvoltage in low resistance grounding system[J]. Power system and its automatic chemistry report, 2012, 24(3): 116-120. (in Chinese) |
| [9] |
Zhang J Y, Li Z, Zhang Z, et al. XGBoost classifier for fault identification in low voltage neutral point ungrounded system[C]// 2019 IEEE Sustainable Power and Energy Conference (iSPEC). Beijing, China: IEEE, 2019, 1767-1771.
|
| [10] |
胡伟, 李勇, 曹一家, 等. 基于LOF和SVM的智能配电网故障辨识方法[J]. 电力自动化备, 2016, 36(6): 7-12. Hu W, Li Y, Cao Y J, et al. Fault identification based on LOF and SVM for smart distribution network[J]. Electric Power Automation Equipment, 2016, 36(6): 7-12. (in Chinese) |
| [11] |
Liu Z L, et al. Improved Hilbert-Huang transform with soft sifting stopping criterion and its application to fault diagnosis of wheelset bearings[J]. ISA transactions, 2021. |
| [12] |
王艳松, 徐海亮, 衣京波, 等. 基于Hilbert-Huang变换的配电馈线接地故障测距[J]. 电气工程学报, 2020, 15(4): 18-26. Wang Y S, Xu H L, Yi J B, et al. Distribution feeder ground fault location based on hilbert-huang transform[J]. Journal of Electrical Engineering, 2020, 15(4): 18-26. (in Chinese) |
| [13] |
Zhang R C, El-Gohary Nora. A deep neural network-based method for deep information extraction using transfer learning strategies to support automated compliance checking[J]. Automation in Construction, 2021, 132. |
| [14] |
Yu X, Wang S H, Skarbek Wladyslaw, et al. Abnormality diagnosis in mammograms by transfer learning based on resNet18[J]. Fundamenta Informaticae, 2019, 168(2-4): 89-92. |
| [15] |
Zagoruyko S, Komodakis N. Wide residual networks[C]// proceedings of the British Machine Vision Conference. York, UK: BMVA Press, 2016: 87.
|
| [16] |
邵庆祝, 郭霖徽, 刘亚东, 等. 基于LSTM模型的配电网单相接地故障辨识方法[J]. 广东电力, 2019, 32(9): 100-106. Shao Q Z, Guo L H, Liu Y D, et al. Identification method for single-phase ground fault of distribution network based on LSTM model[J]. Guangdong Electric Power, 2019, 32(9): 100-106. (in Chinese) |
| [17] |
杨凤生, 熊波, 蔡广林, 等. 基于数据分析的配电网故障数据特征变量提取[J]. 电力大数据, 2018, 21(3): 22-26. Yang F S, Xiong B, Cai G L, et al. Feature variable extraction of fault data in distribution network based on data analysis[J]. Power big data, 2018, 21(3): 22-26. (in Chinese) |
| [18] |
王友明. 基于故障录波数据和气象信息的架空输电线路故障类型辨识方法研究[D]. 山东: 山东大学, 2020. Wang Y M. Research on identification method of overhead transmission line fault type based on fault recording data and meteorological information[D]. Shandong: Shandong University, 2020. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45


