2. 重庆科技学院 建筑工程学院, 重庆 401331
2. School of Building engineering, Chongqing University of Science and Technology, Chongqing 401331, P. R. China
涡激共振是流体力学中一个典型工程问题,相关研究主要围绕雷诺数影响[1]、约束影响[2]、粗糙度影响[3]、自由度影响[4]以及质量比影响[5]等方面。相比单圆柱涡激共振,由于圆柱之间以及圆柱与流体之间的相互干扰,双圆柱流致振动是一个更为复杂的流固耦合过程,除了涡激共振模式,还存在一种振幅随风速接近线性增加的振动模式。Assi等[6-8]把这种振动定义为尾流致振并且对这种振动模式进行了大量的实验研究。文献[6]对固定圆柱后弹性支撑的下游圆柱(只允许横向振动)进行实验,揭示了尾流致振的机理,表明下游圆柱和尾流之间不稳定的涡结构相互作用是导致尾流致振的主要因素。文献[7]保持模型不变,将下游圆柱的弹性支撑撤除进行了实验,提出了尾流刚度的概念。文献[8]随后又对下游圆柱进行了两自由度实验,再一次观察到振幅随折减风速单调递增的现象,实验结果与单自由度的结果相差不大。
除了定义为尾流致振,也有学者将上述振动定义为尾流驰振。Brika等[9]对固定的上游圆柱和自由运动的下游圆柱进行实验(雷诺数Re=5 000~27 000,两圆柱流向间距比L/D=7~25,折减风速Vr=4~11),在L/D=7.5和8时,发现下游圆柱经历涡激共振与尾流驰振的组合振动现象。King等[10]通过对2个自由振动的串列圆柱进行实验,在流向间距L/D=2.5,Vr>11时,观察到尾流驰振现象。Hover等[11]对处于固定圆柱后的弹性支撑的下游圆柱(仅允许横向振动)进行风洞实验,在串联距离L/D=4.75时,观察到高振幅的尾流驰振现象,且该振幅随折减风速不断增加,在实验的折减风速范围不出现峰值。Tokoroa等[12]利用风洞对串列布置(L/D=4.3~8.7,Vr=0~25)的双圆柱进行全尺度实验,在L/D=4.3时,观察到下游圆柱的尾流驰振现象,对应振幅随着折减风速无限制增大,该现象于L/D=6.5时消失。
上述研究中,虽然对双圆柱尾流驰振振动响应展开了实验,但是并未获得尾流驰振发生时的气动荷载,数值模拟可以方便地得到尾流驰振全过程的气动荷载并加以分析。根据Zdravkovich等[13]的研究,两圆柱流向间距比L/D=2和横流向间距比T/D=1时,处于尾流干扰的区域,文中采用基于RANS的SST k-ω湍流模型,假定上游圆柱固定,对弹性支撑两自由度的下游圆柱振动特性和气动荷载进行研究。利用ICEM对流域进行结构化网格划分,结合动网格、滑移网格技术以及用户自定义接口编程,将计算结构响应的Newmar k-β代码嵌入Fluent软件进行数值模拟,折减风速范围为Vr=5~60,观察下游圆柱的尾流驰振特性,并将对应的气动荷载模拟结果与准定常数值计算结果进行对比分析。
1 控制方程 1.1 流体控制方程二维不可压缩均匀粘性牛顿流体运动的基本控制方程为连续性方程和Navier-Stokes方程,密度为ρ、动力粘度为μ的流体域的控制方程为
| $ \nabla \boldsymbol{u}=0, $ | (1) |
| $ \frac{\partial \boldsymbol{u}}{\partial t}+\boldsymbol{u} \cdot \nabla \boldsymbol{u}=-\frac{1}{\rho} \nabla p+\frac{\mu}{\rho} \nabla^2 \boldsymbol{u}, $ | (2) |
式中:p为压力;u为流速矢量,包括流向x方向与横向y方向的流速分量;ρ表示空气的密度;μ表示空气的动力粘度。
1.2 结构控制方程上游圆柱固定不动,尾流下运动圆柱不考虑扭转自由度时,圆柱在2个方向的运动为往复运动,接近简谐振动,在其运动过程中会受到阻尼力与弹性恢复力,可将其简化成双自由度的弹簧振子模型,该模型在运动时,除了要满足上述的流体控制方程外,还需满足如下运动方程:
| $ m_x \ddot{x}(t)+c_x \dot{x}(t)+k_x x(t)=F_D(t), $ | (3) |
| $ m_y \ddot{y}(t)+c_y \dot{y}(t)+k_y y(t)=F_L(t), $ | (4) |
| $ F_D(t)=\frac{1}{2} C_D(t) \rho V^2 D l, $ | (5) |
| $ F_L(t)=\frac{1}{2} C_L(t) \rho V^2 D l, $ | (6) |
式中:由于是二维圆柱,圆柱长度l为单位长度;V为来流速度;ρ为流体密度;mx, cx和kx为圆柱流向单位长度的质量、阻尼和刚度;my, cy和ky为圆柱横流向单位长度的质量、阻尼和刚度;D为圆柱的直径;x(t)和y(t)为圆柱顺流向与横流向在t时刻的位移;V为来流速度;FD(t)和FL(t)为圆柱在t时刻受到的阻力和升力;CD(t)和CL(t)为在t时刻对应的阻力系数与升力系数。
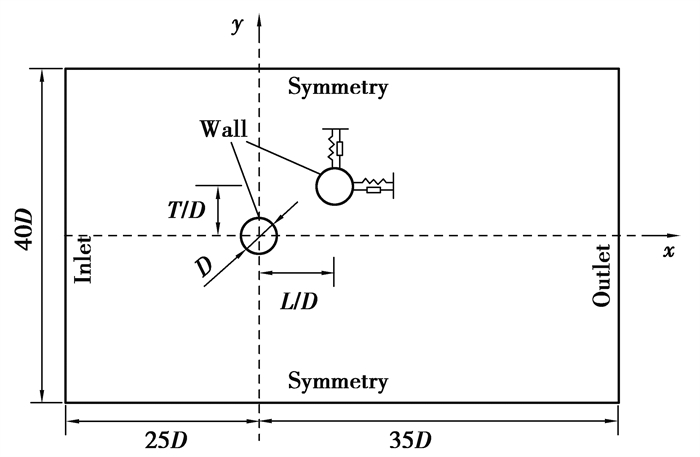
2 计算模型及设定 2.1 模型计算域以及边界条件计算域阻塞率是设计流域计算范围的主要参数,其定义为结构总迎风面积与计算域风场宽度的比值,圆柱绕流主要以侧面绕流为主,阻塞率过大会对圆柱侧面的流场湍流度以及圆柱表面风压产生不利影响,导致计算结果不精确,根据方平治等[14]研究的阻塞率对风场数值模拟的影响结果,阻塞率取值2.5%~7%的计算域在计算风工程中有重要参考意义。文中选定的阻塞率为5%,考虑到湍流的充分发展,采用的计算域为60D×40D,如图 1所示,上游圆柱中心距离入口边界为25D,下游圆柱中心距离出口边界为33D。计算域的边界条件设为:流域入口边界设为速度入口边界条件(velocity-inlet),流域出口边界设为压力出口边界条件(pressure-outlet),上下边界定义为对称边界条件(symmetry),圆柱周围采用无滑移壁面(wall)。
|
图 1 计算域和边界条件 Fig. 1 Computational domain and boundary conditions |
文中利用ICEM CFD对计算域进行网格划分,如图 2所示。网格为非均匀四边形结构化网格,由于导线附近的流场变化剧烈,对圆柱近壁面的网格进行加密处理,通过控制壁面网格高度减小网格对数值计算的影响,第1层网格高度通过y+=1计算。

|
图 2 计算域网格和圆柱壁面网格 Fig. 2 Global mesh and grid near the rigid wall |
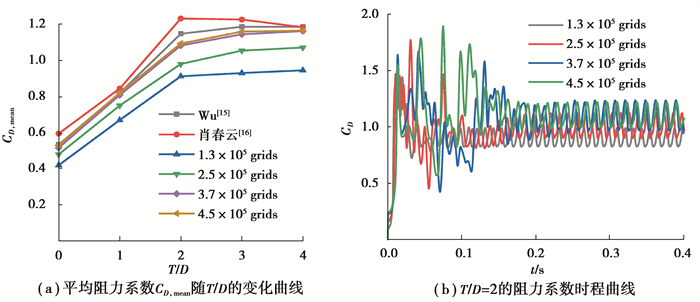
为了验证文中数值模拟方法的可行性与最优的网格划分策略,需要对不同网格数下圆柱的气动特性进行模拟,模拟的圆柱间距选为L/D=6,T/D=0~4,雷诺数Re=3.48×104,处于亚临界范围,湍流度为1%,通过y+计算得到的壁面第一层网格厚度为0.013 mm,选用了4种不同数量的网格进行计算,并将模拟的平均升阻力系数与Wu等[15]的实验结果以及肖春云[16]的数值计算结果进行对比。结果表明,随着流域的网格数量从1.3×105增加到3.7×105时,图 3(a)的平均阻力系数曲线表现为不断接近肖春云和Wu的曲线结果,图 3(b)的阻力系数时程曲线表现为上升,但是当网格数量由3.7×105增加至4.5×105时,图 3(a)的2种网格对应的平均阻力系数曲线非常接近,图 3(b)的阻力系数时程曲线在稳定段几乎重合,由此可见,继续加密网格已经对结果的精确度无明显提升,后续动态圆柱的模拟选用与370 000网格数相似的网格划分策略可达到精度要求,即圆柱壁面第一层网格利用y+=1计算,圆柱壁面的网格增长率为1.05,除了壁面以外的网格增长率为1.08,结构化长方形网格的长边尺寸与短边尺寸最大比例控制在5以内,相邻block之间的网格尺寸应尽量保持一致。
|
图 3 网格依赖性研究 Fig. 3 Grid sensitivity research |
文中模拟的流场与圆柱参数为:空气密度ρ=1.225 kg/m3,导线直径D=30 mm,质量比m*=m/(1/4πρD2L)=2.18,导线自振频率为fn=9.33 Hz,阻尼比ξ=0.964%。整个数值模拟的雷诺数范围为2 400≤Re≤28 200,始终处于亚临界范围,折减风速Vr=V/fnD=5~60,湍流度为1%,时间步Δt=0.000 4 s。
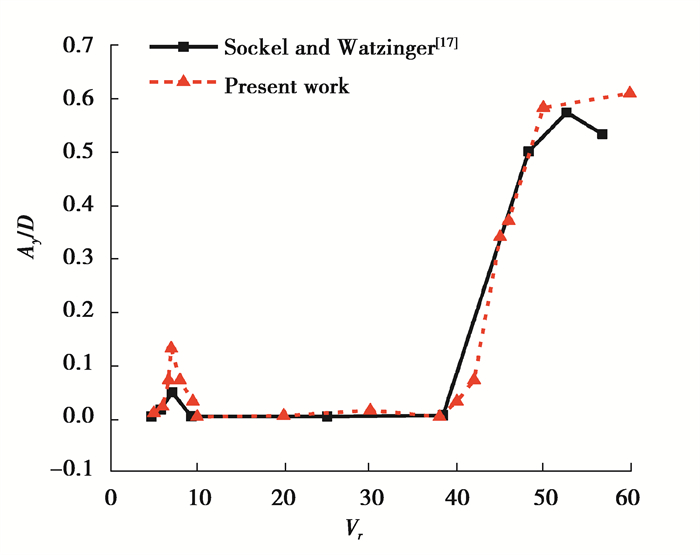
3.2 尾流下下游圆柱的驰振特性分析图 4给出了下游圆柱的横向无量纲振幅随折减风速的变化曲线,在尾流驰振发生之前,最大无量纲振幅发生在Vr=7.5时,振幅值可达到0.13D,再结合图 5所示,Vr=7~9时,涡脱频率与自然频率比值fs/fn=0.97~0.99,可认为下游圆柱发生了涡激共振。本节模拟的Re与Socker等[17]的实验保持一致,保证了流体的运动相似,为了更好地观察到错列布置下游圆柱的涡激振动特性,文中选用的圆柱质量与Socker不同,所以在Vr=7~9时,Socker的涡激共振振幅较小,而文中涡激共振现象较为明显。由图 4可以看出,在折减风速Vr为38时,横向的无量纲振幅突然以接近直线趋势上升,说明在该折减风速下游圆柱受上游圆柱的尾流影响开始发生尾流驰振,直到折减风速Vr达到50时,直线上升斜率开始减小,本节的模拟结果与Socker的实验结果吻合较好,验证了所采用的数值模拟方法在研究尾流驰振响应上的可行性。
|
图 4 下游圆柱横向振幅随Vr变化曲线 Fig. 4 Variation of the dimensionless amplitude Ay/D with the reduced velocity Vr |
|
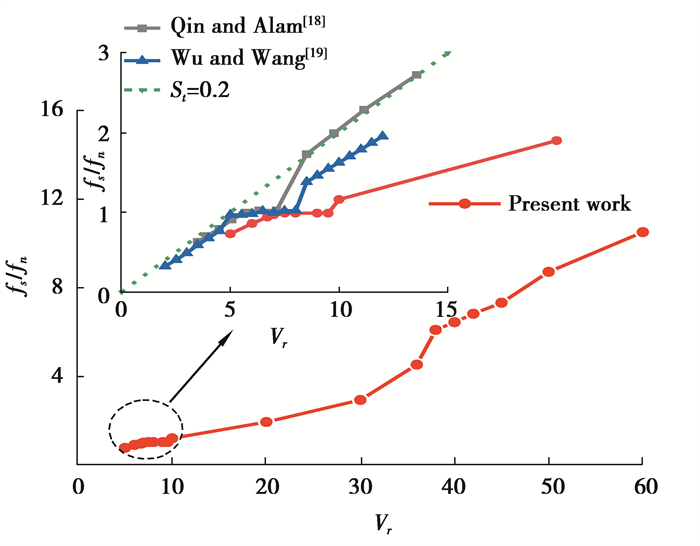
图 5 无量纲频率随Vr变化曲线 Fig. 5 Variation of the frequency ratio fs/fn with the reduced velocity Vr |
此外,Qin等[18]和Wu等[19]的单圆柱涡激振动和文中模拟的下游圆柱振动的无量纲频率随折减风速的变化曲如图 5所示,由于St=fsD/V, Vr=V/(fnD),fs为涡脱主频,D为圆柱直径,V为来流风速,Vr为折减风速,fn为自然频率。将两式相乘可得St=fs/(fnVr),曲线斜率的变化表示为斯托罗哈数的变化,由图 5可知,单圆柱的St几乎为一个定常数0.2,而下游圆柱的St小于0.2,并且在涡激共振之后与尾流驰振起振之前的区域有较大变化,而文献[18-19]中在涡激共振之后无明显变化,St的值与圆柱的涡脱频率息息相关,表明上游圆柱的尾流在下游圆柱产生的随机涡脱弱于来流直接在单圆柱产生的涡脱,即在涡激共振区尾流抑制了下游圆柱表面的随机涡脱。
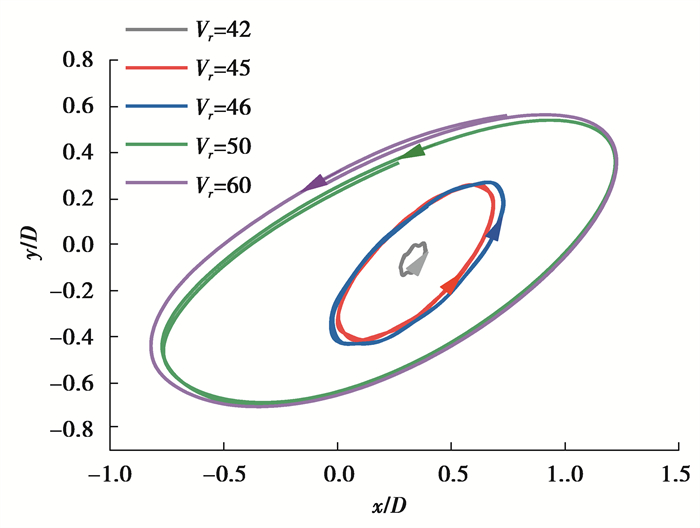
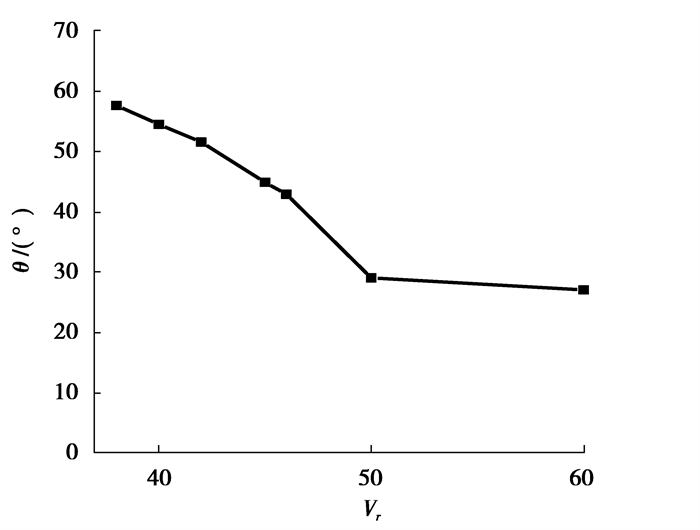
为了更清楚地获得尾流驰振的振动特性,将Vr为42、45、46、50和60对应下游圆柱的运动轨迹绘制在图 6中,可以明显发现,椭圆长轴随折减风速的增加会朝流向倾斜再逐渐趋于稳定,值得注意的是,所有的运动轨迹都为逆时针,说明尾流驰振具有明确方向性和自限性的风致响应的振动;定义θ为椭圆长轴与流向的夹角,图 7表明在发生尾流驰振后,θ随折减风速的增加一直在减小,当Vr到达60时,θ为27°,与两圆柱圆心连线与流向的夹角26.5°几乎相等,这些现象表明,下游圆柱尾流驰振的最终椭圆运动轨迹长轴会与两圆柱圆心连线重合。
|
图 6 尾流驰振风速范围下游圆柱运动轨迹 Fig. 6 Trajectory of the downstream cylinder under wake galloping region |
|
图 7 θ随折减风速的变化曲线 Fig. 7 Variation of θ with Vr under wake galloping region |
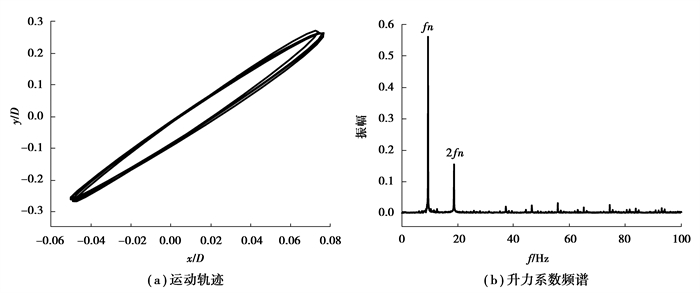
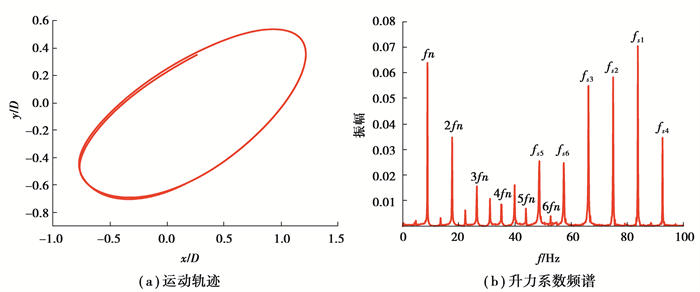
图 8和图 9为涡激共振区Vr=7.5与尾流驰振区Vr=50所对应的运动轨迹和升力频谱结果。图 8(a)表明,受上游圆柱的涡脱和自身的涡脱影响,下游圆柱在“锁定区”的振动轨迹呈现为椭圆环的形式,已有研究对二维单圆柱两自由度的涡激共振进行模拟,发现单圆柱的涡激共振响应轨迹为8字形的Lissajou图,说明尾流会改变下游圆柱的运动轨迹。由图 9(a)可知,发生尾流驰振后,下游圆柱的运动轨迹仍然保持着椭圆环的形式,说明下游圆柱从流体中吸取的能量与自身耗散的能量最终会达到一个动态平衡的过程,尾流驰振同涡激共振一样是一种具有自限性的风致响应。图 8(b)和9(b)表明,在涡激共振区,漩涡脱落主频除了有接近于自振频率的一阶频率9.3 Hz,还有一个二阶频率18.6 Hz,是非线性振动产生的倍频,频率成分较为单一;而在尾流驰振区,除了漩涡脱落主频还有大量的其他频率成分,包括自振频率的倍频和其他涡脱频率,说明尾流驰振是一种涡脱模式复杂并且带有强非线性的振动响应。所有发生了尾流驰振的其他风速也都有着类似的频谱成分,由图 5可知,这些涡脱频率值的大小随折减风速的增加呈线性增加,说明尾流驰振区域圆柱的St为一个定值。值得注意的是,尾流驰振高频成分占比高于低频成分,这些频率会对运动响应造成影响。
|
图 8 Vr=7.5下游圆柱运动轨迹和升力系数频谱 Fig. 8 Trajectory and frequency spectrum of CL at vortex-induced vibration reduced velocity Vr=7.5 |
|
图 9 Vr=50下游圆柱运动轨迹和升力系数频谱 Fig. 9 Trajectory and frequency spectrum of CL at wake galloping oscillation reduced velocity Vr=50 |
准定常数值计算方法是求解尾流驰振振动响应的传统方法,准定常理论是将流经微振动细结构的气流假设为定常流,依据相对运动原理,视物体为静止状态,在建立尾流驰振力学模型时忽略了流体与结构运动的相互反馈作用。利用准定常方法求解下游圆柱的动力响应时,先拟合得到下游圆柱静态的气动力系数CD, CL与位置的分布函数,如式(7)所示,是x和y的多项式函数,根据文献[15]以及考虑到拟合曲面的整体光顺性要求,文中选用拟合的最高次数为6,代入式(8)求解获得圆柱的运动位移x(t)和y(t),再将x(t)和y(t)重新代回式(7),最终得到圆柱运动过程中气动力系数CD, CL随时间的变化曲线。以上过程求解式(8)时气动力系数CD, CL是圆柱处于静态时(其周围的流场为定常流)得到的,故称之为准定常方法。
| $ \left.\begin{array}{l} C_D=\sum\limits_{i=0}^n a_i x^i \sum\limits_{j=0}^m b_j y^j \\ C_L=\sum\limits_{i=0}^p c_i x^i \sum\limits_{j=0}^q d_j y^j \end{array}\right\}, $ | (7) |
| $ \left.\begin{array}{l} m_x \ddot{x}+c_x \dot{x}+k_x x=\frac{1}{2 \alpha^2} \rho D \sqrt{(\alpha V-\dot{x})^2+\dot{y}^2}\left(C_D(\alpha V-\dot{x})+C_L \dot{y}\right) \\ m_y \ddot{y}+c_y \dot{y}+k_y y=\frac{1}{2 \alpha^2} \rho D \sqrt{(\alpha V-\dot{x})^2+\dot{y}^2}\left(C_L(\alpha V-\dot{x})-C_D \dot{y}\right) \end{array}\right\}, $ | (8) |
式中:
图 10给出了使用2种方法得到的下游圆柱的升力系数时程和阻力系数时程。由图可见,2种方法的气动力周期都几乎相同,在一个特定周期t=10.20~10.31 s里,2种方法的阻力系数在10.20~10.22 s以及10.28~10.31 s很接近,而2种方法的升力系数在整个周期具有明显的差异。对气动力进行FFT傅里叶变换,如图 11所示,由频谱可知,2种方法都存在较为明显的自然频率的倍频2fn-4fn,气动力的差异主要表现在准定常数值计算方法对较高次倍频和涡脱频率的贡献考虑不足。
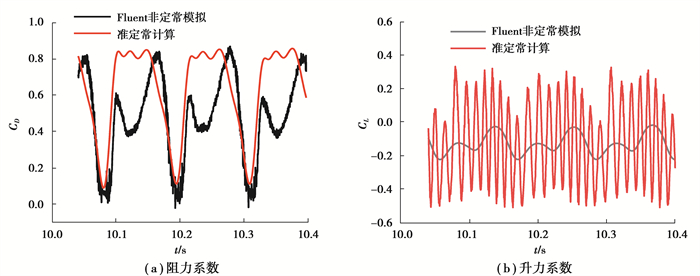
|
图 10 两种方法得到的气动力时程曲线 Fig. 10 Time history of the aerodynamic coefficients obtained by the two methods |
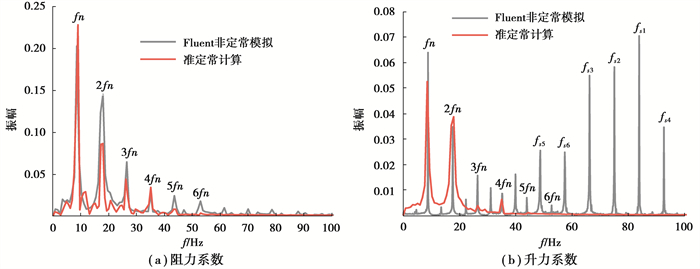
|
图 11 气动力时程曲线傅里叶变换 Fig. 11 Frequency of the aerodynamic coefficients obtained by the two methods |
图 12为2种求解方法顺流向与横流向的位移时程,可以知道,准定常数值计算结果与文中模拟结果在波峰处达到最大误差,x方向位移相对误差为2%,y方向位移相对误差为6%,其余部分曲线几乎完全重合。因此,即使气动力在较高次倍频和涡脱频率有非常大的差别时,运动响应也保持着较高的吻合性,说明高倍频的自激力和涡激力对运动响应的贡献非常小,这些力在下游圆柱的整个运动过程中做的总功非常小,自振频率的前四阶倍频的自激力对尾流驰振的位移和速度起主要控制作用,在一定程度上说明尾流驰振是一种自激振动,高倍频的自激力占比较小,所以影响较小,而涡激力占比较大,但是由于力与位移的相位关系,只在尾流驰振起振阶段提供初始动力,在整个驰振过程对圆柱做的总功非常小,存在气动力差异较大但是运动响应结果相差不大的现象。如果需要准确得到下游圆柱的气动力,文中的流固耦合模拟方法可以提供较好的途径。
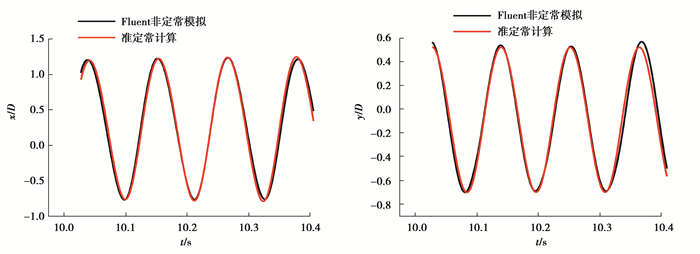
|
图 12 2种方法得到下游圆柱的位移时程曲线 Fig. 12 Displacement-time curves of the downstream obtained by the two methods |
文中利用ICEM对流域进行结构化网格划分,结合动网格及滑移网格技术以及用户自定义接口编程,将计算结构响应的Newmar k-β代码嵌入Fluent软件,利用流固耦合方法对双圆柱间距L/D=2、T/D=1,在折减风速Vr=5~60的范围内模拟研究了圆柱尾流振动特性,并将准定常数值方法的结果与模拟结果进行对比,可以得到主要结论:
1) 文中的流固耦合数值模拟结果与Socker的实验结果有着较高的吻合度,验证了文中采用的数值模拟方法在研究尾流驰振响应上的可行性。尾流驰振阶段对应的下游圆柱自振频率与涡脱主频相差较大,与已有结论一致。相比于单圆柱,尾流扩大了斯托罗哈数的不稳定风速区域,在涡激共振区尾流抑制了下游圆柱表面的随机涡脱。
2) 尾流驰振发生后,下游圆柱的横向振幅随折减风速的增大以接近直线上升,并且都呈现为椭圆形的逆时针运动轨迹,椭圆长轴与流向的夹角会先减小再稳定,稳定角θ与两圆柱圆心连线与流向的夹角几乎相等,说明尾流驰振是一种有自限性和明确方向性的风致失稳响应。
3) 2种方法得到气动力系数的周期几乎相同,都存在较为明显的自然频率的倍频2fn-4fn,气动力的差异主要表现在准定常数值计算方法对较高次倍频和涡脱频率的贡献考虑不足。高倍频的自激力和涡激力对运动响应做的贡献非常小,自振频率的前四阶倍频的自激力对尾流驰振的位移和速度起主要控制作用,在一定程度上说明尾流驰振是一种自激振动。
| [1] |
康庄, 张橙. 雷诺数对圆柱体涡激振动特性影响研究[J]. 华中科技大学学报(自然科学版), 2017, 45(11): 74-79. Kang Z, Zhang C. Impact of Reynolds number on vortex-induced vibration performance of cylinder[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2017, 45(11): 74-79. (in Chinese) |
| [2] |
Morse T L, Govardhan R N, Williamson C H K. The effect of end conditions on the vortex-induced vibration of cylinders[J]. Journal of Fluids and Structures, 2008, 24(8): 1227-1239. DOI:10.1016/j.jfluidstructs.2008.06.004 |
| [3] |
晏致涛, 王灵芝, 刘军, 等. 表面粗糙度对导线风荷载及涡激振动的影响[J]. 振动与冲击, 2018, 37(7): 146-151. Yan Z T, Wang L Z, Liu J, et al. Effects of surface roughness of conductors on their wind loads and vortex-induced vibration[J]. Journal of Vibration and Shock, 2018, 37(7): 146-151. (in Chinese) |
| [4] |
方平治, 顾明. 圆柱两自由度涡激振动的数值模拟研究[J]. 同济大学学报(自然科学版), 2008, 36(3): 295-298. Fang P Z, Gu M. Numerical simulation for vortex-induced vibration of circular cylinder with two degree of feedoms[J]. Journal of Tongji University (Natural Science), 2008, 36(3): 295-298. (in Chinese) DOI:10.3321/j.issn:0253-374X.2008.03.003 |
| [5] |
Khalak A, Williamson C H K. Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping[J]. Journal of Fluids and Structures, 1999, 13(7/8): 813-851. |
| [6] |
Assi G R S, Bearman P W, Meneghini J R. On the wake-induced vibration of tandem circular cylinders: the vortex interaction excitation mechanism[J]. Journal of Fluid Mechanics, 2010, 661: 365-401. DOI:10.1017/S0022112010003095 |
| [7] |
Assi G R S, Bearman P W, Carmo B S, et al. The role of wake stiffness on the wake-induced vibration of the downstream cylinder of a tandem pair[J]. Journal of Fluid Mechanics, 2013, 718: 210-245. DOI:10.1017/jfm.2012.606 |
| [8] |
Assi G R S. Wake-induced vibration of tandem and staggered cylinders with two degrees of freedom[J]. Journal of Fluids and Structures, 2014, 50: 340-357. DOI:10.1016/j.jfluidstructs.2014.07.002 |
| [9] |
Brika D, Laneville A. The flow interaction between a stationary cylinder and a downstream flexible cylinder[J]. Journal of Fluids and Structures, 1999, 13(5): 579-606. DOI:10.1006/jfls.1999.0220 |
| [10] |
King R, Johns D J. Wake interaction experiments with two flexible circular cylinders in flowing water[J]. Journal of Sound and Vibration, 1976, 45(2): 259-283. DOI:10.1016/0022-460X(76)90601-5 |
| [11] |
Hover F S, Triantafyllou M S. Galloping response of a cylinder with upstream wake interference[J]. Journal of Fluids and Structures, 2001, 15(3/4): 503-512. |
| [12] |
Tokoro S, Komatsu H, Nakasu M, et al. A study on wake-galloping employing full aeroelastic twin cable model[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000, 88(2/3): 247-261. |
| [13] |
Zdravkovich M M. Review of interference-induced oscillations in flow past two parallel circular cylinders in various arrangements[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1988, 28(1/2/3): 183-199. |
| [14] |
方平治, 顾明, 谈建国, 等. 阻塞率对表面风压系数影响的数值模拟[J]. 建筑科学与工程学报, 2013, 30(3): 101-106. Fang P Z, Gu M, Tan J G, et al. Numerical simulation of effect of blockage ratio on facade pressure coefficient[J]. Journal of Architecture and Civil Engineering, 2013, 30(3): 101-106. (in Chinese) |
| [15] |
Wu W S, Huang S, Barltrop N. Current induced instability of two circular cylinders[J]. Applied Ocean Research, 2002, 24(5): 287-297. DOI:10.1016/S0141-1187(03)00003-8 |
| [16] |
肖春云. 大跨度柔性桥梁双索股尾流驰振机理研究[D]. 长沙: 湖南大学, 2016. Xiao C Y. The research on mechanism of double strands wake galloping of the long-span flexible bridge[D]. Changsha: Hunan University, 2016. (in Chinese) |
| [17] |
Sockel H, Watzinger J. Vibrations of two circular cylinders due to wind-excited interference effects[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 74/75/76: 1029-1036. |
| [18] |
Qin B, Alam M M, Zhou Y. Free vibrations of two tandem elastically mounted cylinders in crossflow[J]. Journal of Fluid Mechanics, 2019, 861: 349-381. |
| [19] |
Wu W B, Wang J S. Numerical simulation of VIV for a circular cylinder with a downstream control rod at low Reynolds number[J]. European Journal of Mechanics - B/Fluids, 2018, 68: 153-166. |
 2022, Vol. 45
2022, Vol. 45


