随着社会经济不断发展,城市机动车数量日益增多,停车困难与城市发展之间的矛盾日益突出。为有效缓解城市停车困难的问题,平面移动式立体车库以其占地面积小,车库容量大,自动化程度高等优点得到了广泛的认可和应用。
平面移动式立体车库在建设过程中可以有效地提高城市空间利用率,但本身也存在顾客等待时间过长,车辆出入库效率低下的局限性。为解决此类问题江代君[1]根据车辆到达率的变化,提出将调度堆垛机数量和运行速度相结合的调度策略,但研究过程中未考虑车辆停留时间的状态因素;王小农[2]等人提出了基于神经网络和果蝇算法相结合的立体车库车位分配决策模型,但单一神经网络对车辆停留时间预测准确率较低,进而影响车库车位分配效率;张海飞[3]等人则以排队论为理论基础,分析了单服务台系统车库的布局方案,以提高立体车库服务效率;文献[4-5]分别通过遗传算法[4],改进遗传[5],模拟退火[5]对立体车库车位分配过程进行优化研究。
目前对立体车库效率研究大多集中于堆垛机的调度策略[6]、车库布局方式[7]以及智能算法与调度策略[8]的结合,未考虑车辆停留时间以及车位分配过程中库位变化状态对立体车库服务效率的影响[9-10]。
笔者提出一种立体车库动态库位分配策略:首先以蜻蜓算法优化的BP神经网络为理论依据,提高对车辆在库内停留时间的预测准确性;其次通过车库车辆的停留时间,选择车库内较大概率进行出车任务的车位区域;最后利用禁忌搜索算法较强的全局寻优能力搜索出此区域内最适宜的车位位置。同时,将此组合方案与遗传算法和模拟退火算法的优化效果进行对比分析,用以说明该策略的可行性和有效性,为立体车库的建设提供参考依据。
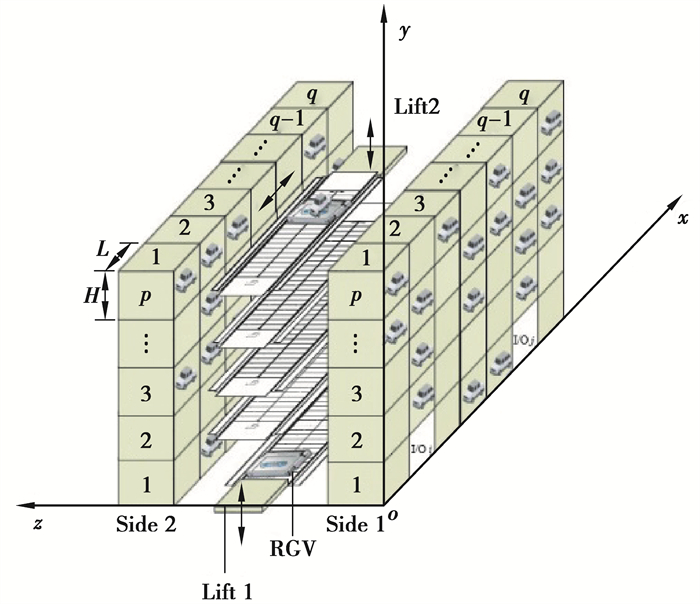
1 立体车库的数学模型平面移动式立体车库的立体模型如图 1所示,车库结构为p层q列,车厅(I/O)负责车辆的进出,调度设备是搬运器(RGV, rail-guided vehicle)和升降机(Lift),其中RGV负责车辆在x轴方向的水平横移运动,lift负责车辆在y轴方向的垂直升降运动。
|
图 1 平面移动式车库的立体模型 Fig. 1 Stereo model of plane mobile garage |
由于车辆的存取调度操作需要RGV与Lift协同完成,当立体车库进行多个调度任务时,RGV与Lift存在同层与跨层2种复合工作方式。选取双车厅平面移动式立体车库为研究对象,在车库中配置有2台RGV与Lift。设双车厅立体车库I/Oi的位置坐标为(ai, bi), I/Oj的位置坐标为(aj, bj);调度设备需要在(xa, yb)处存车,在(xc, yd)处取车;RGV的水平运行功率为Px,运行速度为Vx,Lift的垂直运行功率为Py,运行速度为Vy;车位的宽为L,高为H。以顾客的等待队长,等待时间,服务时间和车库运行能耗作为立体车库服务效率评价指标,则评价指标的数学表达式如下所示
1.1 顾客的等待队长L| $ L = m + n, $ | (1) |
式中:m,n分别表示排队队列中存车和取车的顾客数量。
1.2 单次存车或取车作业的服务时间Tserve0| $ {T_{{\rm{server0 }}}} = 2*\left( {L*\frac{{{a_i} + {x_a}}}{{{V_x}}} + H*\frac{{\left| {{y_b} - {b_i}} \right|}}{{{V_y}}}} \right)。$ | (2) |
1) 单次同层复合作业的服务时间Tserve1
| $ {T_{{\rm{server}}1}} = L*\frac{{{a_i} + {a_j} + {x_a} + {x_c} + \left| {{x_c} - {x_a}} \right|}}{{{V_x}}} + H*\frac{{\left| {{y_b} - {b_i}} \right| + \left| {{y_d} - {b_j}} \right|}}{{{V_y}}}。$ | (3) |
2) 单次跨层复合作业的服务时间Tserve2
| $ {T_{{\rm{server}}2}} = L*\frac{{2{x_a} + 2{x_c} + {a_i} + {a_j}}}{{{V_x}}} + H*\frac{{\left| {{y_b} - {b_i}} \right| + \left| {{y_d} - {y_b}} \right| + \left| {{y_d} - {b_j}} \right|}}{{{V_y}}}。$ | (4) |
顾客的等待时间为多次复合作业服务时间的总和,假设顾客到达时,需要等待A次存车任务,B+C+D次取车任务(其中B次为同层复合取车任务,C次为跨层复合取车任务,D次为单次取车任务),才能接受服务,则顾客的等待时间Twait
| $ {T_{{\rm{wait }}}} = B*{T_{{\rm{server1 }}}} + C*{T_{{\rm{server2 }}}} + [(A + D) - (B + C)]*{T_{{\rm{server0}}}}。$ | (5) |
| $ {W_{{\rm{energy0 }}}} = 2*\left( {{p_x}*L*\frac{{{a_i} + {x_a}}}{{{V_x}}} + {p_y}*H*\frac{{\left| {{y_b} - {b_i}} \right|}}{{{V_y}}}} \right)。$ | (6) |
1) 同层复合作业的运行能耗Wenergy1
| $ {W_{{\rm{energyl }}}} = {p_x}*L*\frac{{{a_i} + {a_j} + {x_a} + {x_c} + \left| {{x_c} - {x_a}} \right|}}{{{V_x}}} + {p_y}*H*\frac{{\left| {{y_b} - {b_i}} \right| + \left| {{y_d} - {b_j}} \right|}}{{{V_y}}}。$ | (7) |
2) 跨层复合作业的运行能耗Wenergy2
| $ {W_{{\rm{energy2 }}}} = {p_x}*L*\frac{{2*\left( {{x_a} + {x_c}} \right) + {a_i} + {a_j}}}{{{V_x}}} + {p_y}*H*\frac{{\left| {{y_b} - {b_i}} \right| + \left| {{y_d} - {y_b}} \right| + \left| {{y_d} - {b_j}} \right|}}{{{V_y}}}。$ | (8) |
蜻蜓算法(DA, dragonfly algorithm)是通过对蜻蜓种群避撞,结队,聚集,捕食以及避敌5种行为模式进行数学建模的群智能优化算法[11]。
蜻蜓个体的避撞行为位移公式
| $ {S_i} = - \sum\limits_{j = 1}^N {{X_i}} - {X_j}。$ | (9) |
结队行为位移公式
| $ {A_i} = \frac{{\sum_{j = 1}^N {{X_j}} }}{N}。$ | (10) |
聚集行为位移公式
| $ {C_i} = \frac{{\sum_{j = 1}^N {{X_j}} }}{N} - {X_i}。$ | (11) |
捕食行为位移公式
| $ {F_i} = X + - {X_i}。$ | (12) |
避敌行为位移公式
| $ {E_i} = X - 1{X_i}。$ | (13) |
综合上述5种蜻蜓群体行为,蜻蜓个体的步长向量更新策略公式
| $ {\rm{\Delta }}{X^{t + 1}} = \left( {s{S_i} + a{A_i} + c{C_i} + f{F_i} + e{E_i}} \right) + w{\rm{\Delta }}{X^t}。$ | (14) |
蜻蜓种群位置更新策略公式为
| $ {X^{t + 1}} = {X^t} + {\rm{\Delta }}{X^{t + 1}}。$ | (15) |
式中:Si,Ai,Ci,Fi,Ei分别表示第i个蜻蜓个体在种群行为中产生的位移;Xi表示第i个蜻蜓个体位置;Xj表示第j个蜻蜓个体位置;N表示与第i个蜻蜓个体相邻的蜻蜓数量;X+表示食物所在位置,X-表示天敌所在位置;s,a,c,f,e分别为5种蜻蜓群体行为权重;w表示惯性权重;t为当前迭代次数;ΔXt+1表示在t+1代种群更新步长,Xt+1表示第t+1代种群位置。
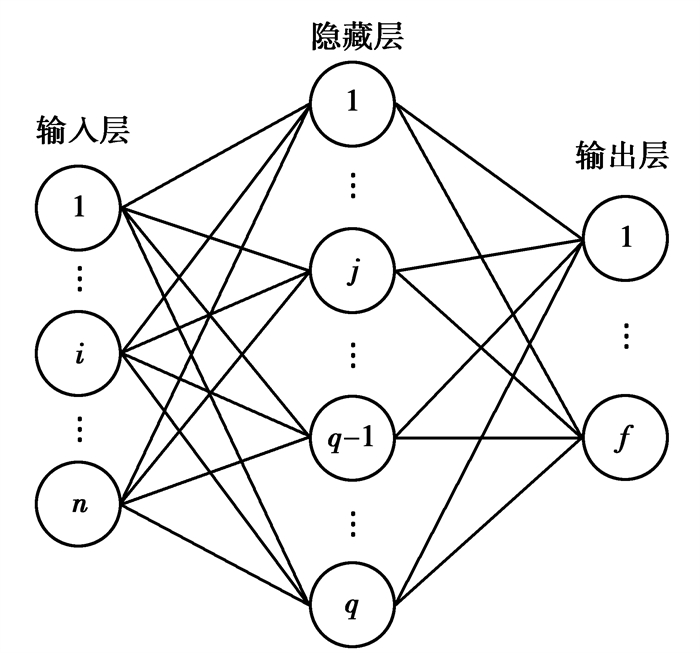
2.2 蜻蜓算法优化BP神经网络BP(back propagation)神经网络是一种多层前馈网络[12],通常为输入层,隐藏层,输出层3层网络结构,神经网络模型如图 2所示。BP神经网络算法通过信号正向传播和误差信号反向传播来动态迭代修正网络的权值和阈值,使误差函数达到期望要求。
|
图 2 BP神经网络模型 Fig. 2 BP neural network model |
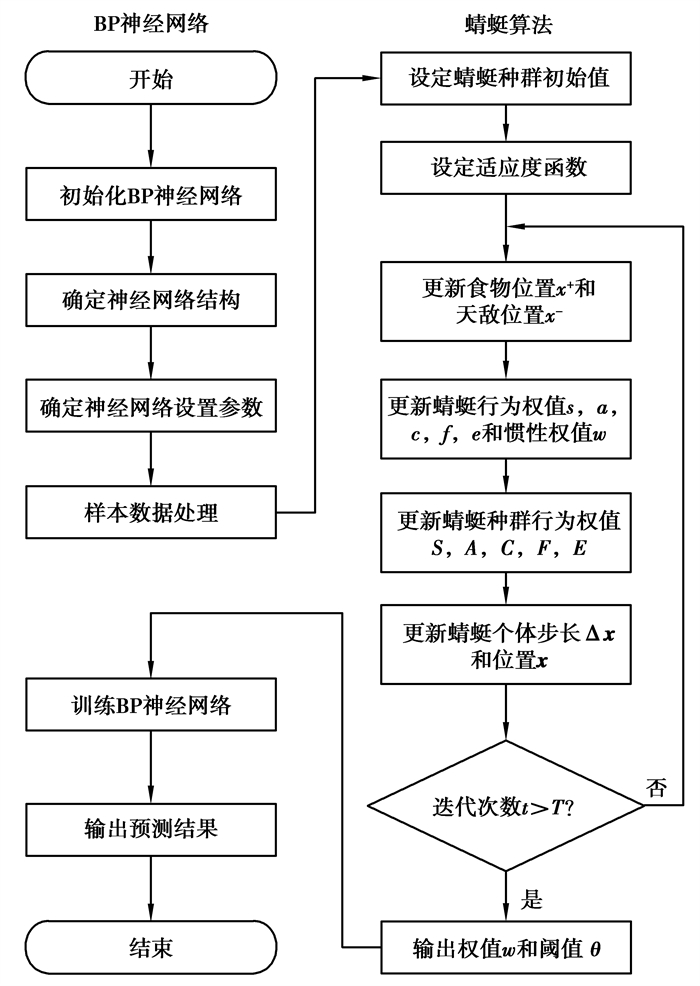
由于神经网络权值和阈值的初始选择值对最终训练结果影响较大,且存在收敛速度较慢,训练结果易陷入局部最优解的局限性,整体预测精度不高[13]。而蜻蜓算法具有良好的全局寻优能力,通过蜻蜓算法来优化神经网络的权值与阈值,可以提高神经网络的预测精度。蜻蜓算法优化BP神经网络的实验步骤:
Step1:初始化BP神经网络模型,确定神经网络的层数,权值w以及阈值θ,传递函数,训练函数,以及各层的节点数;
Step2:样本数据处理,设置训练样本集和测试样本集,并对数据进行归一化处理;
Step3:DA算法初始化,确定蜻蜓种群规模N和迭代次数T,将神经网络的权值w和阈值θ有序排列组成(w, θ)行向量,作为蜻蜓个体位置x,根据权值和阈值范围随机初始化蜻蜓个体位置;
Step4:将训练样本数据输入BP神经网络,根据适应度函数计算蜻蜓个体的适应度值,并记录当前最优解;
选择均方误差为适应度函数,其数学表达式为
| $ {\rm{ fitness }} = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{y_i} - \bar y} \right)}^2}} , $ | (16) |
式中,n为样本数量,yi,y分别表示第i个样本的实际输出和期望输出;
Step5:更新食物位置x+(当前最优解)和天敌位置x-(当前最差解),更新蜻蜓种群的行为权重s,a,c,f,e和惯性权重w;
Step6:根据蜻蜓种群行为公式9~13,更新S,A,C,E和F;
Step7:根据公式14~15,更新蜻蜓步长向量Δx和位置向量x;
Step8:若迭代次数t>T, 则保留连接权值w和阈值θ,否则t=t+1,返回步骤4;
Step9:将最优解对应的权值w和阈值θ,作为BP神经网络初始连接值,再按BP神经网络算法进行训练。
通过蜻蜓种群的5种行为模式,使蜻蜓个体不断搜索,最终寻找到最优解位置。将蜻蜓算法搜索到的最优解作为BP神经网络权值和阈值的初始选择值,可以缩短神经网络训练时间,提高预测结果的准确性。蜻蜓算法优化BP神经网络的实验流程图如图 3所示。
|
图 3 蜻蜓算法优化神经网络 Fig. 3 Dragonfly algorithm optimizes the neural network |
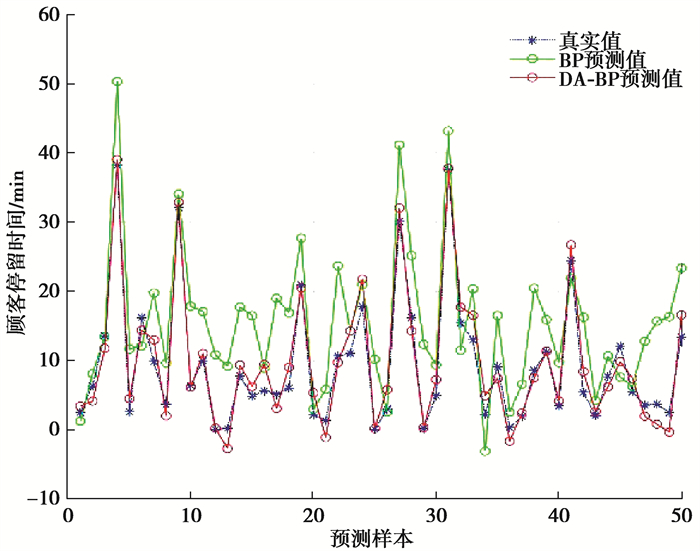
神经网络的具体设置参数:输入层,隐藏层,输出层的节点数分别为1,6,1;隐藏层的传递函数选取为logsig函数,输出层的传递函数为purelin函数,学习率为0.01;以车辆到达时间作为输入量,停留时间作为输出量。通过对平面移动式立体车库实际运行数据进行统计分析,选取500组车辆到达和停留时间数据作为实验数据,其中450组数据作为训练集,50组数据作为测试集,采用监督学习算法对神经网络进行训练,训练次数为2 000次;蜻蜓算法的种群规模设置为200,迭代次数为400次,实验仿真结果如图 4所示。
|
图 4 车辆停留时间预测图 Fig. 4 Prediction of vehicle stay time |
从仿真结果中可知初始BP神经网络模型预测精度不高,误差较大,预测结果的整体准确率为63.2%;而DA-BP组合模型,由于优化了神经网络的阈值与权值,减少了神经网络训练误差,提高了预测精度,预测结果的整体准确率为90.4%,比单一BP神经网络的预测精度提高了27.2%,整体预测性较好。
3 车位分配三维图形的建立立体车库车位分配三维图形在建立过程中,以DA-BP组合模型获得的车辆停留时间和车位位置坐标为轴线建立三维立体图形,通过其在平面坐标上的投影图形来选择车位。由于存在多个车辆停留时间相同或相近的情况,并且在车库作业过程中库位状态是动态变化的过程,所以以区域选择的方式来动态选择车位。
图 5为实验仿真过程中车位分配的三维立体图形(a)和其俯视图(b),(c,d,e)分别为每间隔30 min后车库车位动态变化的状态图,其中X轴,Y轴分别表示车库的层和列,即库位的位置坐标,Z轴则表示车辆在库内停留时间。在俯视图(b)中,车辆在库内停留时间长短用不同颜色的深浅来区分表示,停留时间较长的车位区域用黄色区域表示,停留时间较短车位区域用蓝色区域表示,且停留时间越短颜色越深,则这一区域的车辆有较大的概率进行出车作业(图中红色方框区域)。在进行存车任务时则优先考虑蓝色较深区域的车位,以适应系统可能发生的出车请求任务,达到存车与取车兼顾,减少调度设备空载运行距离,缩短顾客等待时间的目的。
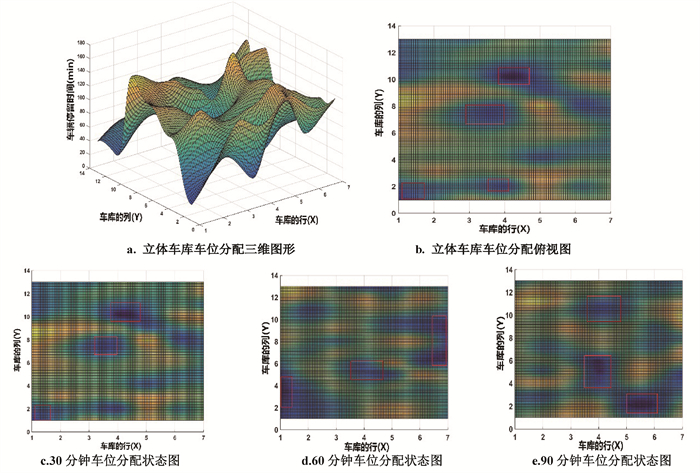
|
图 5 立体车库动态库位分配 Fig. 5 Dynamic location allocation of stereo garage |
禁忌搜索算法(TS, tabu search)是一种启发式随机搜索算法,它从一个初始可行解出发,通过引入灵活的存储结构和禁忌准则来避免迂回搜索,同时通过特赦准则来赦免一些被禁忌的优良状态,进而实现让目标函数值向全局最优解移动[14-16]。
通过车位分配图形的建立,选择出有较大概率进行出车作业的库位位置坐标区域,再用禁忌搜索算法进行寻优搜索,禁忌搜索算法的实验设计步骤如下所示:
Step1:选择俯视图深蓝色区域中的某一空闲车位作为初始解xnow,将初始车位周围邻近车位作为候选解,确定禁忌对象与禁忌长度,并令禁忌表为空;
Step2:选择特定方向进行禁忌移动,选取公式(16)作为适应度函数,找出候选解中的最优解xbest,并令xnow=xbest,记录最优解,同时更新禁忌表;
Step3:比较候选解中的xbest与禁忌表中的最优解xnow,若xbest>xnow,则忽视禁忌准则,更新最优值;若xbest<xnow,则进行禁忌释放,更新禁忌表;
Step4:判断当前最优值是否满足终止规则,若满足则执行步骤5,若不满足则返回步骤2;
Step5:输出最优解。
4.2 实验仿真与数据分析保持神经网络的实验设计参数不变,TS算法中禁忌对象为车位位置,禁忌长度为3,车库系统服务规则为先到先服务原则,RGV待命位策略为存车优先策略,顾客的客源数为500,车辆到达率为15.7辆/min,采用MATLAB2014进行仿真实验,立体车库评价指标数据的实验仿真结果如图 6所示。
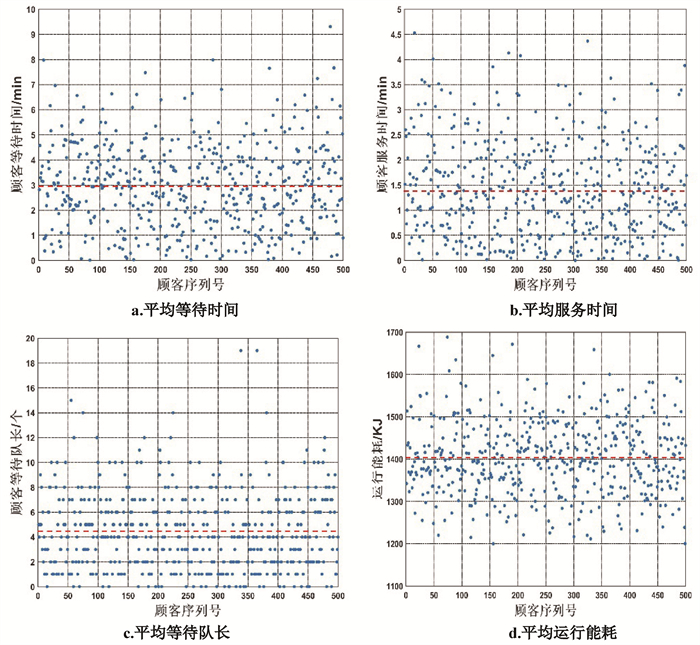
|
图 6 立体车库评价指标数据 Fig. 6 Evaluation index data of stereo garage |
从实验仿真结果中可知顾客平均等待时间为2.94 min,平均服务时间1.38 min,平均等待队长为4.5个,立体车库平均运行能耗为1 403 KJ。多次进行仿真实验,实验结果取平均值,将DA-BP模型与禁忌搜索算法的动态组合方案与遗传算法(GA, genetic algorithm),模拟退火算法(SA, simulated annealing)优化效果进行对比分析,实验仿真结果如表 1所示。
| 表 1 不同优化算法下立体车库的评价指标数据 Table 1 Evaluation index data of stereo garage under different optimization algorithms |
从表 1中可知,组合方案优化下的评价指标数据均为最小值,同比于遗传算法与模拟退火算法优化,顾客的平均等待时间,平均服务时间,平均等待队长和立体车库运行能耗优化效率分别提高了39.6%和32.5%,33.3%和22.2%,13.2%和9.8%,18.5%和13.3%,具有更好的优化效果。
5 结论以平面移动式立体车库的车位分配策略为研究对象,建立了立体车库数学模型,提出DA-BP预测模型与禁忌搜索算法的动态车位分配方案,并将此方案与现有库位分配优化方式进行了对比分析,研究结果表明:
1) 动态库位分配策略在预测车辆停留时间的基础上,根据库位变化状态来动态选择分配车位,可以达到存车任务与出车请求兼顾,减少调度设备空载运行距离,提升立体车库整体作业效率的目的。
2) 采用此组合方案可以更为有效地减少顾客等待队长,缩短顾客等待时间和车辆服务时间,降低立体车库运行能耗,提高顾客的满意程度。
但是在动态库位分配策略研究中车辆停留时间预测存在误差,在今后的研究中需要进一步研究车辆停留时间预测出现偏差时对立体车库作业效率的影响。
| [1] |
江代君. 巷道堆垛式立体车库排队及库位优化研究[D]. 重庆:重庆大学, 2014. Jiang D J. The queuing and scheduling optimization research for laneway-stow-typed 3D-park[D]. Chongqing:Chongqing University, 2014. (in Chinese) |
| [2] |
王小农, 李建国, 张海飞. 两阶段混合算法的立体车库车位分配建模与仿真[J]. 重庆邮电大学学报(自然科学版), 2018, 30(5): 724-730. Wang X N, Li J G, Zhang H F. Two stage hybrid algorithm modeling and simulation of stereo garage parking location[J]. Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition), 2018, 30(5): 724-730. (in Chinese) |
| [3] |
张海飞, 李建国, 王小农. 巷道堆垛式自动化立体车库库位布局方案的优化[J]. 厦门大学学报(自然科学版), 2019, 58(3): 436-441. Zhang H F, Li J G, Wang X N. Optimization on layout plan of automated stereoscopic garage space for stacking[J]. Journal of Xiamen University (Natural Science Edition), 2019, 58(3): 436-441. (in Chinese) |
| [4] |
陈桢, 杨旻. 基于遗传算法的自动化立体车库库位分配[J]. 制造业自动化, 2019, 41(11): 49-53. Chen Z, Yang M. Resource allocation based on genetic algorithm in automated stereo garage[J]. Manufacturing Automation, 2019, 41(11): 49-53. (in Chinese) DOI:10.3969/j.issn.1009-0134.2019.11.012 |
| [5] |
张健. 立体车库停车场动态规划算法研究及实现[D]. 北京:北京交通大学, 2019. Zhang J. Research and implementation of dynamic planning algorithms for stereo garage parking[D]. Beijing:Beijing Jiaotong University, 2019. (in Chinese) |
| [6] |
Zhong L, Lei M. Automated stereo-garage with multiple cache parking spaces-structure system and scheduling performance[J]. Automation in Construction, 2020, 119(4): 75-84. |
| [7] |
Debjit R, Ananth K, Sunderesh H, et al. Queuing models to analyze dwell-point and cross-aisle location in autonomous vehicle-based warehouse systems[J]. European Journal of Operational Research, 2015, 242(15): 72-87. |
| [8] |
Arjan S, Dijkstra, Kees J R. Exact route-length formulas and a storage location assignment heuristic for picker-to-parts warehouses[J]. Transportation Research Part E:Logistics and Transportation Review, 2017, 102(2): 38-59. |
| [9] |
赵齐辉, 杜兆宏, 刘升, 等. 差分进化的蜻蜓算法[J]. 微电子学与计算机, 2018, 35(7): 101-105. Zhao Q H, Du Z H, Liu S, et al. Dragonfly algorithm based on differential evolution[J]. Microelectronics and Computer, 2018, 35(7): 101-105. (in Chinese) DOI:10.19304/j.cnki.issn1000-7180.2018.07.021 |
| [10] |
张霄, 钱玉良, 邱正, 等. 基于蜻蜓算法优化BP神经网络的燃气轮机故障诊断[J]. 热能动力工程, 2019, 34(3): 26-32. Zhang X, Qian Y L, Qiu Z, et al. Gas turbine fault diagnosis based on BP neural network optimized by dragonfly algoritnm[J]. Thermal Energy and Power Engineering, 2019, 34(3): 26-32. (in Chinese) DOI:10.16146/j.cnki.rndlgc.2019.03.004 |
| [11] |
Li L L, Zhao X, Tseng M L, et al. Short-term wind power forecasting based on support vector machine with improved dragonfly algorithm[J]. Journal of Cleaner Production, 2020, 3(242): 54-62. |
| [12] |
刘瑜, 李秋莎. 基于BP神经网络的物流交通实载率监测仿真[J]. 计算机仿真, 2020, 37(6): 383-387. Liu Y, Li Q S. Real load rate monitoring simulation of logistics traffic based on BP neural network[J]. Computer Simulation, 2020, 37(6): 383-387. (in Chinese) DOI:10.3969/j.issn.1006-9348.2020.06.079 |
| [13] |
Loan N N D, Hai L V, Bao Q, et al. An effective spatial-temporal attention based neural network for traffic flow prediction[J]. Transportation Research Part C:Emerging Technologies, 2019, 6(128): 12-28. |
| [14] |
李国明, 李军华. 基于混合禁忌搜索算法的随机车辆路径问题研究[J]. 控制与决策, 2020, 29(5): 1-10. Li G M, Li J H. Research on stochastic vehicle routing problem based on hybrid tabu search algorithm[J]. Control and Decision, 2020, 29(5): 1-10. (in Chinese) |
| [15] |
郝群茹, 潘帅. 基于禁忌搜索算法的物流系统车辆路径优化[J]. 科学技术与工程, 2019, 9(34): 401-407. Hao Q R, Pan S. Vehicle routing optimization of logistics system based on tabu search algorithm[J]. Science Technology and Engineering, 2019, 9(34): 401-407. (in Chinese) DOI:10.3969/j.issn.1671-1815.2019.34.059 |
| [16] |
Kyoungsun L, Leyla O. Tabu search heuristic for the network design model with lead time and safety stock considerations[J]. Computers & Industrial Engineering, 2020, 6(148): 57-68. |
 2022, Vol. 45
2022, Vol. 45

