水平井在页岩气、煤层气开发及瓦斯探测等方面优势明显,在现今煤炭及石油开采领域得到迅速的发展与应用[1]。煤矿水平井钻进过程中,钻柱同时受到重力、轴向力、扭矩、井壁摩擦力等作用力,易诱发纵向、横向和扭转振动[2],钻柱的耦合振动是导致钻柱,特别是底部钻具失效、钻进效率低的主要原因之一[3-4]。钻柱的托压效应是指钻柱与井眼底边形成接触(或托底)而无法有效施加钻压的现象。与竖直井相比,随着钻进深度增加,水平井钻柱在重力作用下与井壁产生复杂的碰撞接触,由此产生的托压效应[5-6]更加显著,这对钻柱耦合振动特性影响明显。因此,研究水平井钻柱钻进过程中的振动特性具有重要的工程意义。
国内外学者围绕钻柱系统动力学开展了大量研究。Detournay等[7]建立了PDC钻头钻进响应模型,揭示了钻压、钻头扭矩、进给速度及角速度之间的关系;张强等[8]对液压凿岩机在回转-冲击载荷下连续破碎硬质岩层进行动力学仿真分析,结论表明破岩效率随钻头回转速度和冲击频率的增加先增加后趋于稳定;吴泽兵等[9]提出PDC钻头参数化布齿设计与破岩仿真方法,提高了破岩分析效率;崔新霞[10]、贾小龙[11]建立了岩石-钻头和钻柱-井壁动力学模型,将岩石-钻头模型中钻头获得的动载荷作为输入代入到钻柱-井壁模型中,进而获得钻柱的动力学规律;胡志强等[12]建立了钻柱-钻头-岩石系统动力学模型,采用有限元法模拟了三牙轮钻头破岩过程,结果表明钻头与岩石的相互作用及由此引起的底部钻具振动具有明显的非线性和随机性;Feng等[13]建立了六自由度有限元模型来表征钻柱力学特征,分析了钻压、转速等对底部钻具黏滑振动和涡动的影响,结果表明钻压与振动形式呈现严格的相关性,高钻压更易导致黏滑振动并加剧涡动,过度振动对钻头和底部钻具的磨损率影响更大。Zhang等[14]对比了钻柱振动的三种模式,即纵向、横向和扭转振动引起的钻柱跳钻、扰动、黏滑振动和涡动等现象对钻柱疲劳的影响,其中黏滑振动和涡动对钻柱疲劳寿命影响更大。
综上所述,早期钻柱动力学研究采用岩石-钻头和钻柱-井壁分别建模的方式,将岩石-钻头模型中钻头获得的动载荷代入到钻柱-井壁模型,这种方法忽略了钻柱扰动对钻头破岩的耦合作用,也未考虑托压效应产生的压力损失对钻进状态的影响。近年的研究多采用岩石-钻头-钻柱-井壁耦合分析模型,但在仿真分析时,一般是假定钻柱已钻进至某一深度,研究特定深度下钻柱的振动特性。然而钻进深度对水平井钻进过程中托压效应的影响更加明显,使得钻柱的纵向、横向和扭转特性随钻进深度增加而明显改变,进而影响钻柱的疲劳寿命。因此,笔者基于水平井岩石-钻头-钻柱-井壁耦合分析模型,研究了水平井钻柱在钻进至不同深度时的振动特性,研究结果可为水平井钻具的动态特性分析与优化、匹配现场钻进工艺参数、避免有害振动和提高钻具使用寿命提供有效帮助。
1 水平井钻柱系统耦合动力学模型对水平井钻柱系统钻进过程进行动力学分析十分复杂,将岩石、钻头、钻柱、井壁进行耦合分析难度巨大,需对井下环境适当简化后,采用子结构法建立钻柱系统动力学模型[15-17]。子结构法在现代工程结构的静、动力学分析中得到普遍应用。其基本思路是将结构划分为若干个子结构,先对子结构进行局部分析,然后综合组装再做整体分析。采用子结构法对复杂结构进行动力学分析,不仅能够大幅降低动力方程的阶数,而且能保证降阶后的精度。
1.1 基本假设为便于分析,对水平井钻柱系统进行适当简化:
1) 井眼水平,井眼截面为圆形。
2) 假设钻柱为均质圆环截面弹性梁。
3) 不考虑钻柱螺纹连接和局部的孔、槽。
4) PDC钻头和井壁为不可变形的刚体。
1.2 钻头-岩石互作用力模型水平井钻进过程中,岩石对钻头的作用力是钻柱在井眼内扰动的重要激励来源。在钻进至不同深度L(t)时,钻头均受来自钻柱的轴向压力和扭矩,同时受来自岩石的进给阻力及阻力矩。
根据力学平衡关系建立钻头-岩石纵向力学模型:
| $ {P_{\rm{z}}}(t) + {m_{\rm{z}}}a(t) + {F_{\rm{z}}}(t) = 0, $ | (1) |
| $ {P_{\rm{z}}}(t) = {\rm{WOB}} - {F_{{\rm{fz}}}}(L)。$ | (2) |
式中:Pz(t)为t时刻来自钻柱的钻压,kN;WOB为输入钻压,kN;Ffz(L)为托压效应造成的压降是钻进深度的函数,kN;mz为钻头质量,kg;a(t)为钻头t时刻纵向加速度,mm/s2;Fz(t)为t时刻岩石对钻头的纵向反力,kN。
钻头-岩石横向力学模型:
| $ \left\{\begin{array}{l} f_x(t)=\sum f_i(t) \cos \left(\pi+\alpha_i(t)\right), \\ f_y(t)=\sum f_i(t) \sin \left(\pi+\alpha_i(t)\right) 。\end{array}\right. $ | (3) |
式中:fx(t)和fy(t)为钻头所受横向力在X和Y两个方向的分量,kN;fi(t)为t时刻PDC钻头第i个复合片与岩石作用所受横向力,kN;αi(t)为t时刻第i个复合片与岩石作用的切削角度。
钻头所受岩石阻力矩与钻柱对其作用的扭矩相平衡,则钻头-岩石扭矩模型为:
| $ M(t)=\sum\limits_j l_{x j}(t) f_{x j}(t)+\sum\limits_j l_{y j}(t) f_{y j}(t) 。$ | (4) |
式中:lxj(t)、lyj(t)为t时刻钻头与岩石作用时第j个复合片与钻头坐标系X轴和Y轴距离,mm;fxj(t)和fyj(t)为t时刻钻头第j个复合片所受横向力在X和Y两个方向的分量,kN。
岩石材料具有非线性、弹塑性、黏弹性、剪胀性、各向异性等特点,一般的数学模型难以充分描述,Drucker-Prager强度准则是在Mohr-Coulomb准则和Von-Mises准则基础上扩展和推广而来,在岩石材料本构模型建立中应用广泛。Drucker-Prager模型具有以下特点:1)模拟岩石等摩擦材料,材料屈服与围压有关;2)模拟压缩屈服强度远大于拉伸屈服强度的材料;3)考虑材料的剪胀性;4)可模拟蠕变功能以描述材料的长期非弹性变形。以上特点均与岩石材料相一致。
岩石失效的塑性应变判据为:
| $ \varepsilon^{\mathrm{p}} \leqslant \bar{\varepsilon}_{\mathrm{f}}^{\mathrm{pl}}。$ | (5) |
式中:εp为岩石的等效塑性应变,εfpl为岩石完全失效时的等效塑性应变。
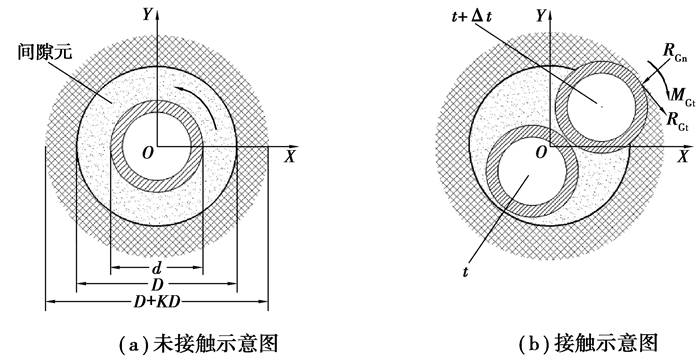
1.3 钻柱-井壁接触模型水平井钻进过程中,钻柱与井壁接触情况复杂,在重力作用下,钻柱与井壁接触面积更大。钻柱与井壁的复杂碰撞,可采用动力间隙元法来近似描述。动力间隙元具有随状态而改变的抗压刚度,动力间隙元的内边界和外边界分别与钻柱和井壁相连接。当钻柱与井壁分离时,动力间隙元不妨碍钻柱各方向的运动;但当钻柱与井壁碰撞接触时,动力间隙元的刚度会随接触状态发生改变,进而限制钻柱运动,如图 1所示。
|
图 1 动力间隙元模型 Fig. 1 Dynamic gap element model |
图 1中,d为钻柱直径,D为井壁直径,K为刚度系数,RGn为正压力,RGt为切向力,MGt为摩擦扭矩。
设ΔC为钻柱与井壁的初始间隙,mm;ΔC(t)为t时刻钻柱沿方向n向井壁的位移,mm;v(t)为钻柱与井壁接触时的周向速度,mm/s。则钻柱与井壁碰撞的判定条件如下。
未接触状态:
| $ \Delta C(t)<\Delta C 。$ | (6) |
接触状态:
| $ \Delta C(t) \geqslant \Delta C, v(t)=0 \text { 或 } v(t) \neq 0 \text { 。} $ | (7) |
式中:v(t)=0表示钻柱与井壁相对运动为滚动;v(t)≠0表示钻柱与井壁相对运动为滑动或滑滚结合。
1.4 岩石-钻头-钻柱-井壁耦合动力学模型由界面协调条件得到界面连续条件及对接条件,将1.2中的岩石-钻头子结构与1.3中的钻柱-井壁子结构组合成完整的钻柱系统耦合分析模型:
| $ \left\{\zeta_{\mathrm{B}}\right\}^{\mathrm{Sub} 1}=\left\{\zeta_{\mathrm{B}}\right\}^{\mathrm{Sub} 2}, $ | (8) |
| $ \left\{f_{\mathrm{B}}\right\}^{\mathrm{Sub} 1}=\left\{f_{\mathrm{B}}\right\}^{\mathrm{Sub} 2} \text { 。} $ | (9) |
式中:ζB为界面位移量,mm;fB为界面力,kN;Sub1为岩石-钻头子结构;Sub2为钻柱-井壁子结构。
2 水平井钻柱钻进过程动力学仿真本研究选用Abaqus/Explicit显示动力学模块建立岩石-钻头-钻柱-井壁耦合分析模型,对钻柱系统钻进过程进行动力学仿真。
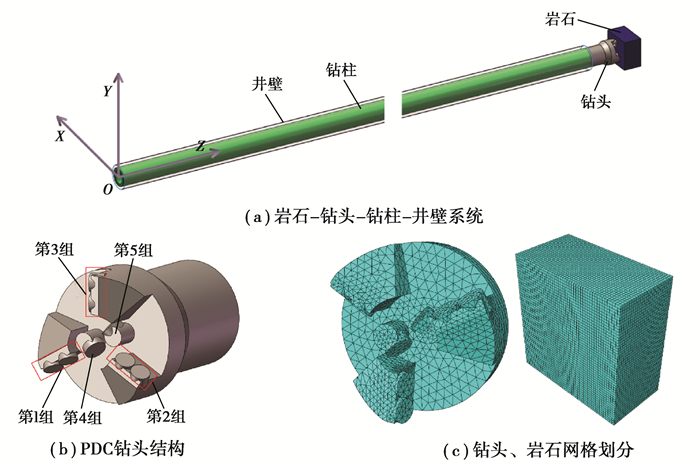
2.1 仿真模型的建立以煤矿旋转钻柱水平井为研究对象,井眼直径94 mm,钻柱外径73 mm。选取煤矿开采使用较多的三翼内凹PDC钻头,采用C3D10M四面体网格划分;岩石采用C3D8R六面体网格划分,并采用沙漏控制和单元删除功能来模拟岩石脱落;钻柱及井壁分别采用B31梁单元和SR4壳单元划分。所建仿真模型如图 2所示。
|
图 2 岩石-钻头-钻柱-井壁耦合分析模型 Fig. 2 Rock-bit-drill string-well wall coupling system model |
根据1.1节的假设,将钻头和井壁考虑为不可变形的刚体,钻柱为均匀截面弹性梁。煤矿水平井钻探过程中,当钻进岩层为硬质砂岩时钻进最为困难,钻柱扰动更为显著,因此选定岩石材料为硬质砂岩展开研究,采用施工中常见的硬质砂岩材料参数进行仿真[18]。材料参数如表 1所示。
| 表 1 仿真材料参数 Table 1 Parameters of simulation material |
设置边界条件时,井壁、岩石采用固定约束,钻柱与钻头耦合约束,钻柱输入端释放轴向位移及轴向转动自由度。考虑到目前工程中的井眼规格为94 mm的煤矿用旋转钻柱水平井钻进深度一般在300 m以内,故以50 m为间隔,对钻进深度50~300 m进行分析,输入钻压50 kN,转速30 rad/s。
2.2 仿真结果分析对钻进过程中的钻柱系统进行了动态仿真,限于篇幅,提取了钻进深度为100 m、200 m和300 m的结果进行对比分析。
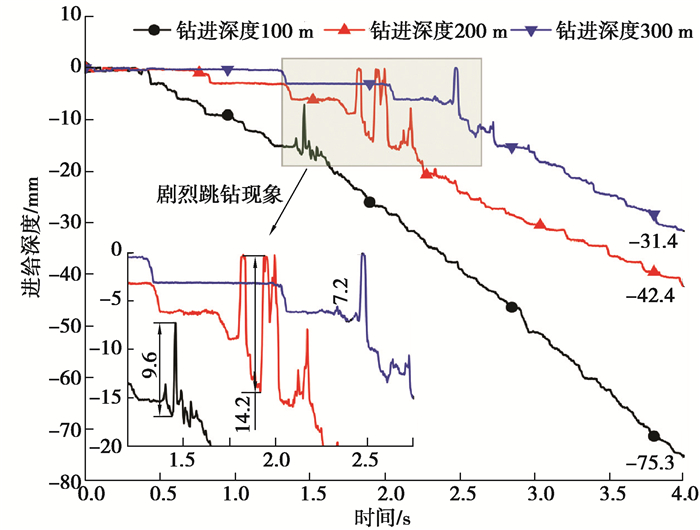
2.2.1 不同钻进深度下钻柱纵向振动特性图 3为不同钻进深度时钻头进给位移。随着钻进深度的增加,3种深度下钻头进给位移分别为75.3 mm、42.4 mm和31.4 mm,表明底部钻具钻压随钻进深度增加而减小。钻进深度为300 m时的进给位移为200 m时的74%,钻进深度为200 m时的进给位移为100 m时的56.3%,说明在相同的进给增量下,钻进深度较浅时托压效应变化更明显。
|
图 3 不同钻进深度时钻头进给位移 Fig. 3 Bit feed displacement at different drilling depths |
造成跳钻现象的原因有2个:1)钻进初期只有前3组复合片参与破岩,随着进给量增加,后2组复合片也参与到破岩过程,工作状态的改变使得进给加速度、速度发生跃变,钻头发生剧烈的跳钻现象;2)由现有研究[11, 19]可知,横向振动最易发生,横向振动发生阶段钻柱扰动最为剧烈,会损耗大量能量,导致底部钻具钻压失稳,进而形成纵向耦合振动,主要表现形式为钻头的剧烈跳钻现象。钻进深度200 m时,发生了3次剧烈跳钻,最大跳钻量为15 mm;100 m和300 m时均发生了1次剧烈跳钻,最大跳钻量为9.6 mm和7.2 mm。
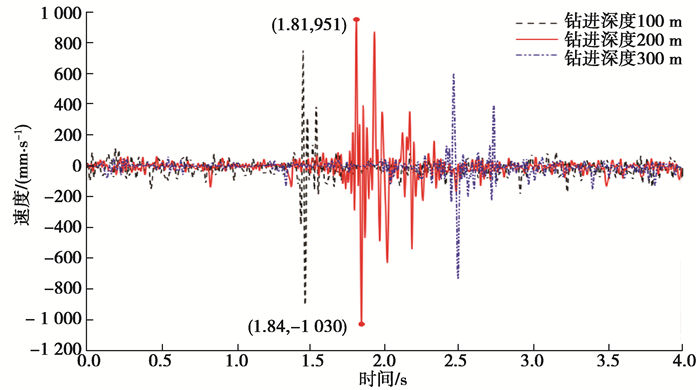
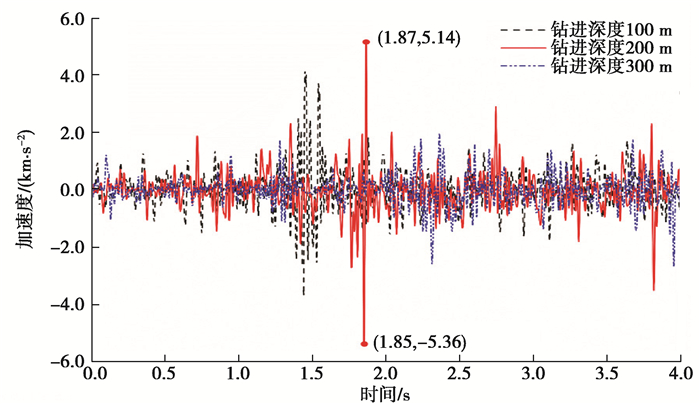
图 4、图 5为钻进至不同深度时钻头的进给速度、加速度曲线。由图可以看出,在跳钻阶段,钻进深度200 m时的进给速度、加速度跃变幅值最大,跃变持续时间最长。
|
图 4 不同钻进深度时钻头进给速度 Fig. 4 Bit feed rate at different drilling depths |
|
图 5 不同钻进深度时钻头进给加速度 Fig. 5 Bit feed acceleration at different drilling depths |
文献[1, 12, 17]研究了特定深度下钻柱系统的瞬态动力学特性,本研究中钻头处的进给位移、进给速度和进给加速度曲线变化范围及趋势规律都与上述文献研究结果一致,证明了本文中建立的瞬态动力学模型的正确性,进而表明了本文仿真结果的正确性。
由上可知,钻进深度的变化,显著影响了钻柱的纵向振动特性。在钻进深度200 m时,跳钻次数、最大跳钻量以及纵向速度、加速度跃变幅值、跃变持续时间均大于其余2个深度,纵向跳钻现象呈现出“平缓—剧烈—平缓”的趋势,钻柱纵向振动的剧烈程度与钻进深度呈非线性关系。
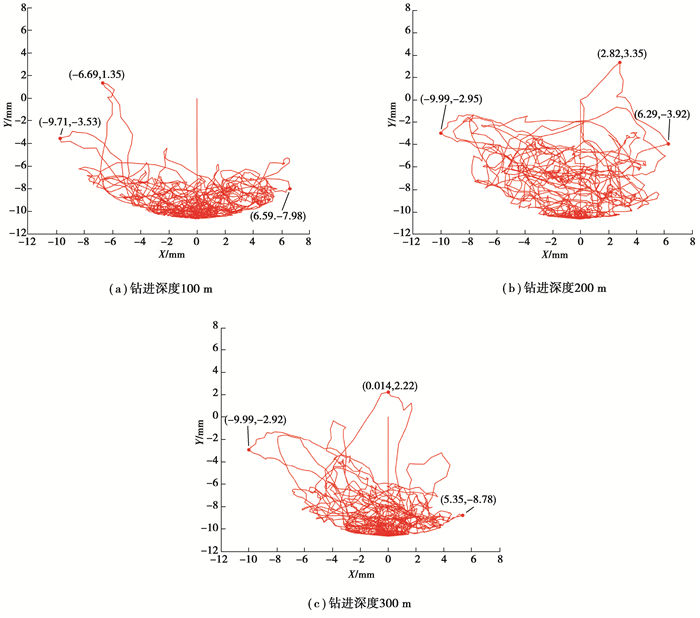
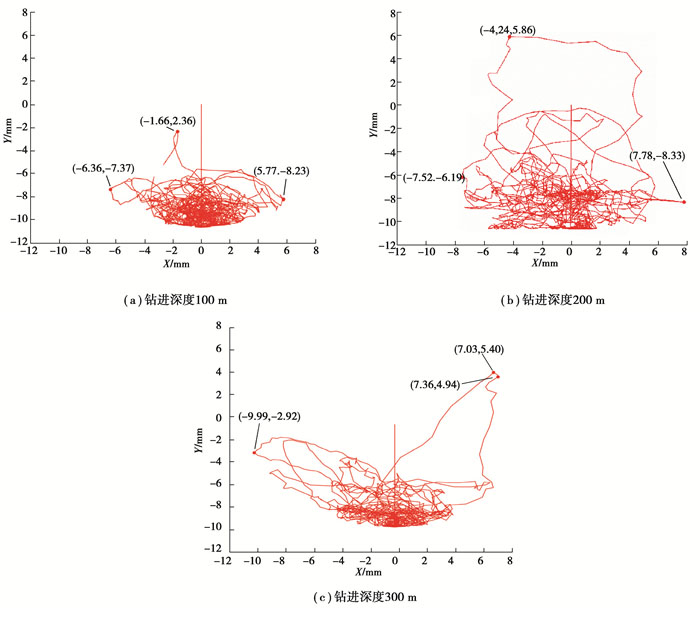
2.2.2 不同钻进深度下钻柱横向振动特性钻柱振动对底部钻具的磨损更为严重[3-4],故研究中提取了底部钻具节点进行分析。图 6、图 7为距钻头5 m、10 m处节点横向位移轨迹。3种深度下,钻柱X方向扰动范围变化不大,但在重力及井壁作用下,Y方向扰动变化明显。如图 6(a)、图 7(a),钻进深度100 m时,钻柱贴近下井壁蠕动,Y方向振动轻缓;图 6(b)、图 7(b),钻进深度200 m时,Y方向振动加剧,振动幅值变大且在高位置处扰动密度增大,下井壁处蠕动密度降低,钻柱发生大范围横向扰动;图 6(c)、图 7(c),钻进深度300 m时,Y方向振动减缓,钻柱再次表现为贴近下井壁蠕动,钻柱横向扰动随钻进深度增加呈现出“小范围蠕动—大范围扰动—小范围蠕动”的趋势。究其原因,钻柱扰动除与钻压、转速及井壁约束有关,还与钻进深度关系密切。钻进深度较浅时,钻柱刚度大,此时钻柱在载荷作用下变形小,扰动范围较小;当钻进深度增至200 m时,钻柱弯曲刚度降低,钻柱在载荷作用下更易发生变形,发生大范围扰动现象;当钻进深度增至300 m时,钻柱重力作用显现得更明显,转速及井壁对钻柱的碰撞作用难以使钻柱发生大范围扰动,表现为小范围蠕动现象。
|
图 6 不同钻进深度钻头5 m处钻柱横振轨迹 Fig. 6 Transverse vibration trajectory of drill string at different drilling depths 5 m away from the drill bit |
|
图 7 不同钻进深度钻头10 m处钻柱横振轨迹 Fig. 7 Transverse vibration trajectory of drill string at different drilling depths 10 m away from the drill bit |
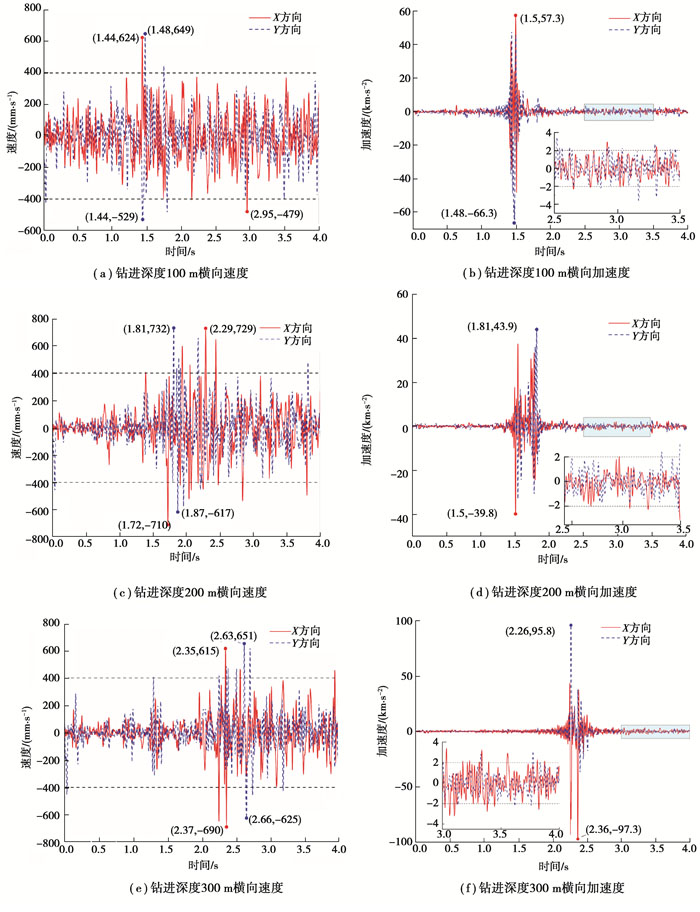
图 8为不同钻进深度距钻头5 m处横向速度和加速度曲线。由图可知,在稳定钻进阶段,3种钻进深度下横向速度及加速度分布较为一致,但当发生剧烈横向振动时,钻柱的横向速度、加速度跃变持续时间存在较大差异。钻进深度200 m时,横向速度、加速度跃变持续时间明显多于另2种深度。横向加速度、速度跃变导致横向振动加剧,增大钻柱与井壁的碰撞频率,产生较大接触应力,对钻具的疲劳强度产生较大影响。
|
图 8 不同钻进深度钻头5 m处横向速度及加速度 Fig. 8 Lateral velocity and acceleration at different drilling depths at a distance of 5 m from the drill bit |
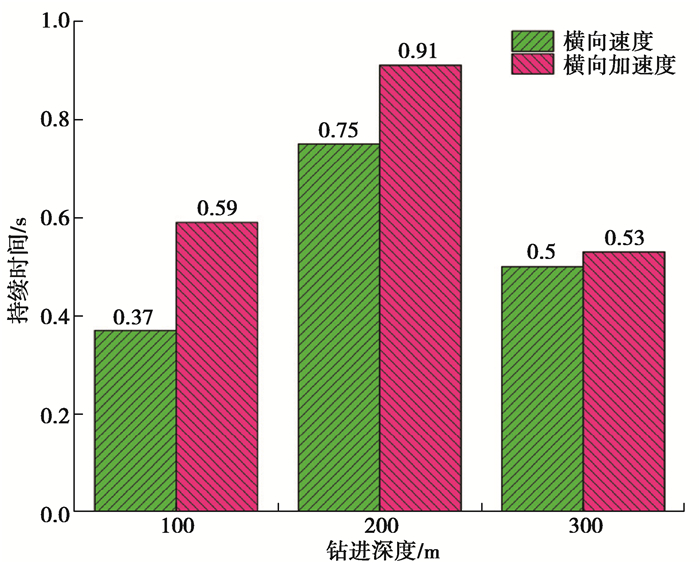
图 9提取了钻进过程中距钻头5 m处横向速度、加速度跃变持续时间。其中200 m时横向速度、加速度跃变持续时间为0.75 s和0.91 s,明显多于另2种深度,说明随着钻进深度增加,剧烈横向振动的持续时间呈现出先增加后减小的趋势。
|
图 9 不同钻进深度钻头5 m处横向速度及加速度跃变持续时间 Fig. 9 Transverse velocity and acceleration jump duration at 5 m from the drill bit at different drilling depths |
由上可知,不同钻进深度下钻柱横向扰动范围及剧烈横振持续时间等横向振动特性均发生显著变化。
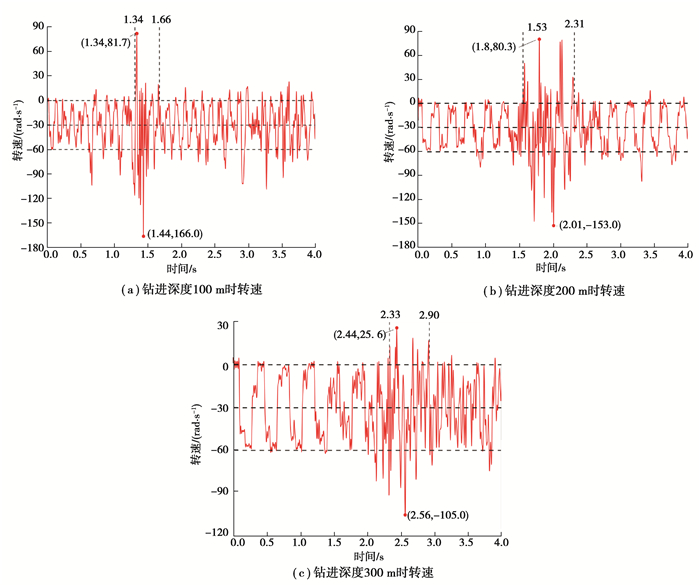
2.2.3 不同钻进深度下钻柱扭转振动特性图 10为钻进过程中不同钻进深度钻头处的转速曲线。可以看出,钻柱扭转振动形态主要表现为黏滑振动和涡动。所谓钻柱涡动,是指钻柱在绕自身轴线旋转的同时,也绕井眼轴线公转。在井壁摩擦力等因素的作用下,钻柱涡动表现为正反两个方向,其中反向涡动更易诱发钻柱疲劳破坏和钻头损坏[20],故将转速方向发生正反交替的涡动阶段称为剧烈涡动,在研究中重点关注。在钻柱发生剧烈纵向和横向振动的时段,钻柱转速也发生跃变,振动形式表现为剧烈涡动;其余时间段内钻柱转速相对稳定,振动形式表现为黏滑振动或轻微涡动。钻柱在黏滑振动状态时,滑移阶段最大转速为60 rad/s,为输入转速的2倍,这一规律与文献[13]描述相符,进一步验证了所建模型的正确性。在钻进深度200 m时,钻柱剧烈涡动持续时间最长,达0.78 s,明显多于其他2种深度。
|
图 10 不同钻进深度钻头处钻柱转速 Fig. 10 Rotation speed of drill string at different drilling depth |
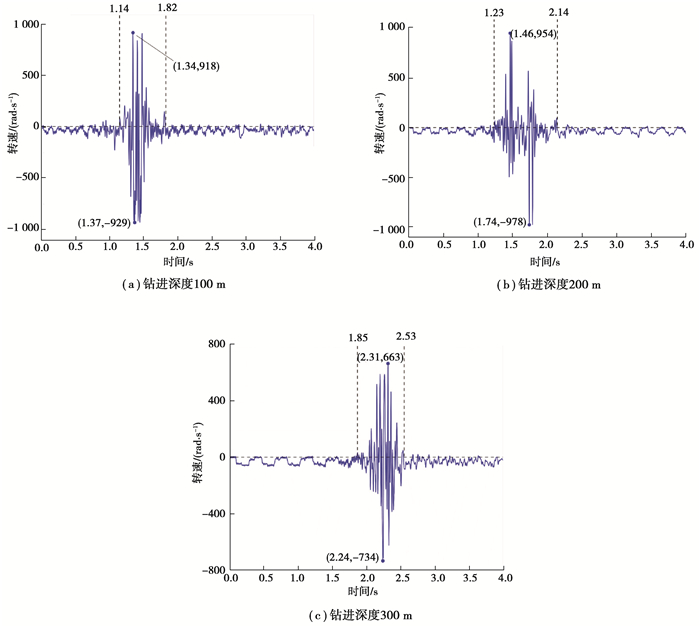
图 11为距钻头5 m处钻柱的转速曲线,可以看出,该处钻柱转速(尤其是剧烈涡动阶段)峰值高于钻头处,但两处变化规律一致,表明底部钻具与钻头处扭转振动形式呈现一致性。
|
图 11 不同钻进深度钻头5 m处钻柱转速 Fig. 11 Rotation speed of drill string at different drilling depth 5 m away from the drill bit |
现有研究表明钻柱黏滑振动时,黏滞阶段在钻柱内积聚扭矩,在滑移阶段释放扭矩产生冲击;剧烈涡动造成钻柱大范围、高频率扰动,加剧钻柱与井壁的撞击[13]。从图 11可以看出,钻柱涡动时转速变化频率及变化范围明显高于黏滑振动,3种钻进深度下底部钻具距钻头5 m处的最高瞬时转速分别达到输入转速的31倍、33倍和24倍,且发生明显的钻柱反转现象。钻柱转速的大幅跃变及连续反转对钻柱造成巨大冲击,可见涡动对钻柱疲劳寿命的影响更严重。
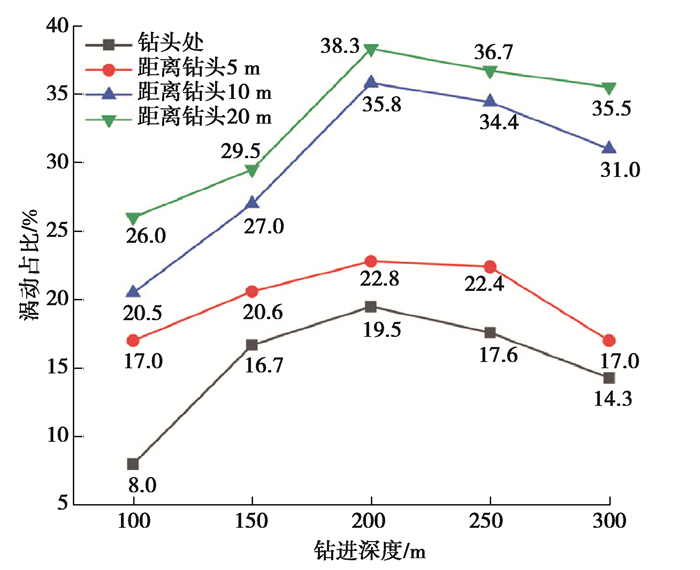
图 12为钻进过程中底部钻具剧烈涡动时间占比,当钻进深度200 m时,距钻头20 m处,剧烈涡动时间占比达38.3%,说明此处振动最为剧烈。此前的研究一般认为钻压与钻柱涡动、黏滑振动呈线性关系,降低钻压、提高转速能够减缓涡动及黏滑振动,但由图 12可知,底部钻具钻压随钻进深度增加逐渐减小,但剧烈涡动占比随钻井深度增加呈现出先增加后减小的趋势。
|
图 12 涡动占比 Fig. 12 Proportion of whirling |
从以上分析可以看出,对于某一结构的钻柱系统,在钻进至不同深度时,钻柱的纵向、横向和扭转振动规律发生明显变化,钻柱振动的剧烈程度与钻进深度呈非线性关系。因此,在对钻柱进行动态特性分析时,必须考虑钻进过程的影响。
3 结论1) 基于水平井岩石-钻头-钻柱-井壁耦合分析模型,对钻柱在钻进过程中的动态特性进行了分析,结果表明钻进深度会对钻柱的纵向、横向、扭转振动特性产生显著影响,因此在对钻柱系统进行动态分析及优化时,不能仅考虑特定深度,而应该包含整个钻进过程。
2) 讨论了在水平井托压效应下钻进深度对钻柱纵向跳钻、横向扰动、扭转黏滑振动和涡动等钻柱振动指标的影响规律,结果表明上述指标与钻进深度呈非线性关系。故在对钻柱系统进行动态性能分析和钻进工艺优化时,有必要探寻钻柱振动最为剧烈的钻进深度。
| [1] |
田家林, 杨应林, 杨琳, 等. 考虑井壁摩擦随机性的钻柱动力学模型[J]. 振动与冲击, 2018, 37(11): 252-258. Tian J L, Yang Y L, Yang L, et al. Dynamic model of drill strings considering stochastic frictional effects of well wall[J]. Journal of Vibration and Shock, 2018, 37(11): 252-258. (in Chinese) |
| [2] |
Qiu H Y, Yang J M, Butt S, et al. Investigation on random vibration of a drillstring[J]. Journal of Sound and Vibration, 2017, 406: 74-88. DOI:10.1016/j.jsv.2017.06.016 |
| [3] |
祝效华, 曾理, 李柯. 中浅层水平井钻柱振动分析及加压方案研究[J]. 振动与冲击, 2020, 39(23): 190-201. Zhu X H, Zeng L, Li K. Drill string vibration analysis and pressurization scheme for medium-shallow horizontal wells[J]. Journal of Vibration and Shock, 2020, 39(23): 190-201. (in Chinese) |
| [4] |
Sarker M, Rideout D G, Butt S D. Dynamic model for 3D motions of a horizontal oilwell BHA with wellbore stick-slip whirl interaction[J]. Journal of Petroleum Science and Engineering, 2017, 157: 482-506. DOI:10.1016/j.petrol.2017.07.025 |
| [5] |
易先中, 宋顺平, 陈霖, 等. 复杂结构井中钻柱托压效应的研究进展[J]. 石油机械, 2013, 41(5): 100-104, 110. Yi X Z, Song S P, Chen L, et al. Progress of research on drillstring backing pressure effect in complex structure well[J]. China Petroleum Machinery, 2013, 41(5): 100-104, 110. (in Chinese) |
| [6] |
豆旭谦, 王力, 王毅, 等. 张集煤矿灰岩顺层定向钻进托压效应及影响因素分析[J]. 煤矿安全, 2020, 51(3): 168-172, 177. Dou X Q, Wang L, Wang Y, et al. Back pressure effect of limestone consequent landslide directional drilling and analysis of influencing factors in Zhangji coal mine[J]. Safety in Coal Mines, 2020, 51(3): 168-172, 177. (in Chinese) |
| [7] |
Detournay E, Richard T, Shepherd M. Drilling response of drag bits: theory and experiment[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(8): 1347-1360. DOI:10.1016/j.ijrmms.2008.01.010 |
| [8] |
张强, 索江伟, 王海舰, 等. 基于ABAQUS的凿岩机钻头破岩数值模拟分析[J]. 振动与冲击, 2018, 37(1): 136-141. Zhang Q, Suo J W, Wang H J, et al. Numerical simulation analysis on the drill bit rock breaking process based on ABAQUS[J]. Journal of Vibration and Shock, 2018, 37(1): 136-141. (in Chinese) |
| [9] |
吴泽兵, 张帅, 王勇勇, 等. 基于ABAQUS的PDC钻头参数化布齿与破岩仿真[J]. 石油机械, 2020, 48(3): 30-36. Wu Z B, Zhang S, Wang Y Y, et al. ABAQUS-based parameterized cutter layout and rock breaking simulation of PDC bits[J]. China Petroleum Machinery, 2020, 48(3): 30-36. (in Chinese) |
| [10] |
崔新霞. 钻削式采煤机钻削系统振动特性研究[D]. 江苏徐州: 中国矿业大学, 2014. Cui X X. Research on vibration characteristics of auger drilling system[D]. Xuzhou, Jiangsu: China University of Mining and Technology, 2014. (in Chinese) |
| [11] |
贾小龙. 某型旋挖钻机钻杆振动及其控制仿真研究[D]. 西安: 长安大学, 2017. Jia X L. Simulation research on drill rod vibration and control of a rotary drilling rig[D]. Xi'an: Chang'an University, 2017. (in Chinese) |
| [12] |
胡志强, 祝效华, 郝军, 等. 钻柱-钻头-岩石系统动力学特性研究[J]. 石油机械, 2017, 45(12): 7-11. Hu Z Q, Zhu X H, Hao J, et al. Study on dynamic characteristics of drill string-drill bit-rock system[J]. China Petroleum Machinery, 2017, 45(12): 7-11. (in Chinese) |
| [13] |
Feng T H, Vadali M, Ma Z R, et al. A finite element method with full bit-force modeling to analyze drillstring vibration[J]. Journal of Dynamic Systems, Measurement, and Control, 2017, 139(9): 091016. |
| [14] |
Zhang H, Di Q F, Li N, et al. Measurement and simulation of nonlinear drillstring stick-slip and whirling vibrations[J]. International Journal of Non-Linear Mechanics, 2020, 125: 103528. |
| [15] |
朱才朝, 冯代辉, 陆波, 等. 钻柱结构与井壁岩石互作用下系统耦合非线性动力学研究[J]. 机械工程学报, 2007, 43(5): 145-149. Zhu C C, Feng D H, Lu B, et al. Nonlineaer study on dynamic action of integrated drill string-well rock system[J]. Chinese Journal of Mechanical Engineering, 2007, 43(5): 145-149. (in Chinese) |
| [16] |
崔新霞, 谭长均. 钻削机构与煤岩互作用系统耦合动力学研究[J]. 振动与冲击, 2014, 33(16): 97-104. Cui X X, Tan C J. Coupling vibration of a drilling system with interaction between drilling mechanism and coal rock[J]. Journal of Vibration and Shock, 2014, 33(16): 97-104. (in Chinese) |
| [17] |
宋朝省. 钻头-岩石-钻柱-井壁互作用下系统耦合非线性动力学研究[D]. 重庆: 重庆大学, 2007. Song C S. Study on nonlinear dynamics of system coupling under drillbit, rock, drillstring and shaft wall interaction[D]. Chongqing: Chongqing University, 2007. (in Chinese) |
| [18] |
谢志江, 常雪, 杨林等. 基于机械比能理论的煤岩可钻性分级方法[J/OL]. 煤田地质与勘探: 1-7[2021-01-18]. http://kns.cnki.net/kcms/detail/61.1155.P.20201215.1450.004.html Xie Z J, Chang X, Yang L, et al. Classification method of coal and rock drill ability based on mechanical specific energy theory[J/OL]. Coal Geology and Exploration: 1-7[2021-01-18]. http://kns.cnki.net/kcms/detail/61.1155.P.20201215.1450.004.html. (in Chinese) |
| [19] |
王宝金, 任福深, 朱安贺. 钻井液作用下水平井钻柱横向振动建模与分析[J]. 机械科学与技术, 2018, 37(11): 1670-1677. Wang B J, Ren F S, Zhu A H. Modeling and analysis of lateral vibration for horizontal drillstring under action of drilling mud[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(11): 1670-1677. (in Chinese) |
| [20] |
史玉才, 王军, 管志川. 下部钻柱涡动机理及规律研究[J]. 石油机械, 2007, 35(8): 1-3, 78. Shi Y C, Wang J, Guan Z C. Study of vortex mechanism and rule of bottom drill string[J]. China Petroleum Machinery, 2007, 35(8): 1-3, 78. (in Chinese) |
 2023, Vol. 46
2023, Vol. 46


