相比平腹板工字形梁,波纹腹板工字形梁(IG-CW)可在不使用加劲肋的情况下,以较小的腹板厚度获得较大的平面外刚度和较好的剪切性能,而钢管混凝土翼缘平腹板组合梁则在强度、刚度和稳定性方面都具有明显的优势[1-4]。国内学者[5-10]结合钢管混凝土翼缘与波纹腹板的优点,提出了矩形钢管混凝土翼缘波纹腹板组合梁(RCFTFG-CW)。试验结果表明,组合梁的平面外刚度、抗剪强度、抗弯强度和稳定性都有显著提高。文献[7]中RCFTFG-CW在集中荷载作用下,其波纹腹板并未发生预期的剪切破坏,而是荷载作用处附近波纹腹板发生了明显变形,导致不能继续承载。对于IG-CW,当集中荷载作用在无加劲肋位置时,波纹腹板容易发生局部受压破坏[11]。Elgaaly等[12]通过试验和有限元分析,提出了IG-CW波纹腹板局部破坏的2种模式:腹板折曲和腹板屈服,并建立了这2种破坏模式下承载力计算公式。Luo等[13]利用非线性有限元分析对IG-CW进行参数分析,结果表明,局部承压承载力与腹板和翼缘厚度成正比,荷载作用长度及位置(平板段、斜板段及其交接处)、波形及初始缺陷的选取也影响较大。郭彦林等[14]通过非线性有限元分析对波浪腹板工字形梁的翼缘和腹板的破坏机制及模式进行了研究,提出了波浪腹板局部承压承载力计算公式,建立了平面内弯矩与局部荷载共同作用下承载力计算公式。张哲等[15-16]研究了波纹腹板H形钢吊车梁的局部承压承载力。结果表明,相对于平腹板H形钢梁,相同腹板厚度的波纹腹板H形钢梁的局部承压承载力显著提高,承载力大小与腹板高度无关,文献还提出了波纹腹板H形钢梁的局部承压承载力计算公式。
IG-CW比平腹板工字形梁具有更高的局部承压承载力,但由于其翼缘和腹板的厚度较小,仍然容易发生局部受压破坏,波纹腹板的抗剪能力难以得到充分利用,承压承载力受荷载作用位置影响较大[13]。在局部荷载作用处焊接腹板加劲肋是提高局部承压强度的有效措施,但并不适用于承受移动荷载的结构(如,吊车梁)。由于RCFTFG-CW的钢管混凝土上翼缘具有一定厚度和较大刚度,使得更多的波纹腹板区域参与受力,所以具有更高的局部承压承载力。目前,国内外还没有关于RCFTFG-CW的局部承压承载力及其他方面的报道。因此,有必要研究RCFTFG-CW的局部承压承载力和应力发展,分析集中荷载作用位置对局部承压承载力的影响,对RCFTFG-CW进行参数分析并提出局部承压承载力计算公式,以便用于工程设计参考。
1 有限元模型及可靠性验证 1.1 有限元模型通过有限元软件ABAQUS对RCFTFG-CW和IG-CW进行建模分析。钢材的本构关系采用理想弹塑性模型。钢管内填混凝土应力应变关系采用韩林海[17]钢管混凝土本构模型。钢材弹性模量Es取206 GPa,屈服强度fy = 345 MPa,混凝土弹性模量
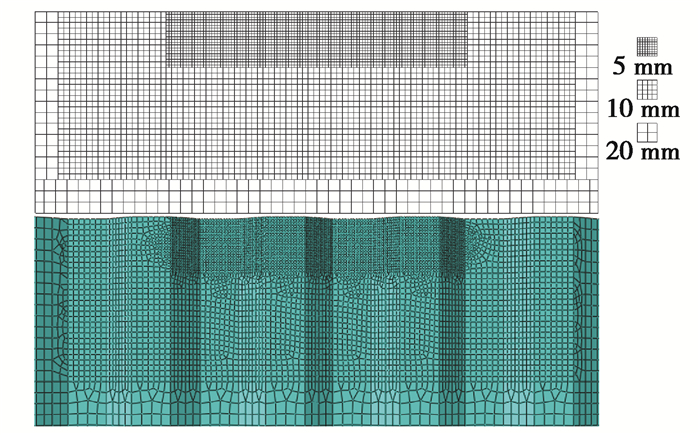
有限元模型中,RCFTFG-CW和IG-CW钢材的单元类型选用4节点减缩积分壳单元(S4R)模拟,沿厚度方向取5个积分点,采用八节点六面体减缩积分(C3D8R)单元模拟混凝土。梁端端板和跨中加载垫块均视为刚体,分别采用S4R和C3D8R单元模拟。钢梁的整体网格尺寸取20 mm[9]。因为是对集中荷载作用下波纹腹板局部承压破坏的研究,对腹板主要受力区域进行更详细的网格划分以保证分析结果更加精确[11, 13],详细划分尺寸如图 1所示。
|
图 1 波纹腹板局部网格划分 Fig. 1 Typical FE mesh for corrugated web |
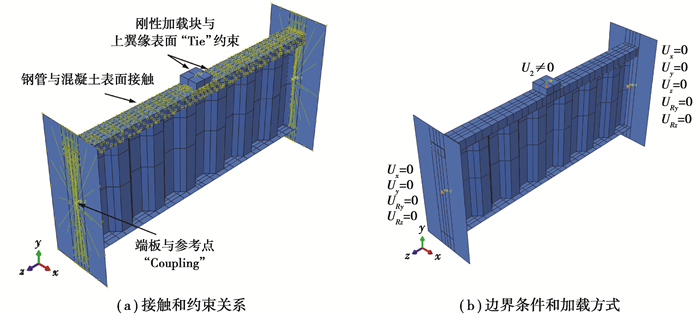
在有限元模型中,采用“Merge”命令来模拟钢梁上下翼缘与腹板的焊接。由图 2(a)可见,上翼缘钢管和混凝土的接触关系通过“Surface-to-surface contact”来实现,采用“硬”接触和“库伦摩擦模型”定义其法向接触行为和切向接触行为,摩擦因数取0.6[18]。钢梁的上翼缘表面(从面)和刚性加载块的下表面(主面)建立“Tie”约束。该约束将加载块和上翼缘绑定在一起,使它们之间不会产生相对滑动。边界条件如图 2(b)所示,将端板与端板中心的参考点建立耦合约束,端板的自由度则完全受到参考点的自由度约束,再将边界条件施加在参考点上。整个加载过程采用位移控制,荷载作用在刚性加载块上。
|
图 2 有限元模型接触方式和边界条件 Fig. 2 Interaction between components and boundary conditions of FE models |
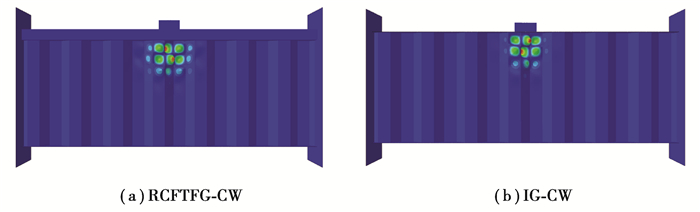
首先,通过Buckle线性特征值屈曲分析得到钢梁的第一阶屈曲模态,如图 3所示。RCFTFG-CW和IG-CW的第一阶屈曲模态均出现在局部荷载作用下方的波纹腹板上,将波纹腹板的平面外变形作为后续分析引入的初始缺陷,Tao等[19]也用类似的方法引入非线性分析的初始缺陷。将该模态作为静力分析的初始几何缺陷形状,其值取hw/500[14],再利用Riks非线性静力分析方法对RCFTFG-CW和IG-CW进行非线性求解,得到钢梁的极限荷载和荷载位移曲线。
|
图 3 RCFTFG-CW和IG-CW一阶屈曲模态 Fig. 3 First buckling modes of RCFTFG-CW and IG-CW |
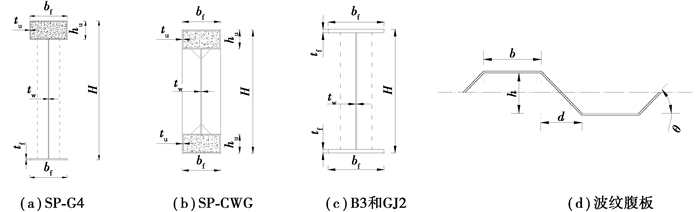
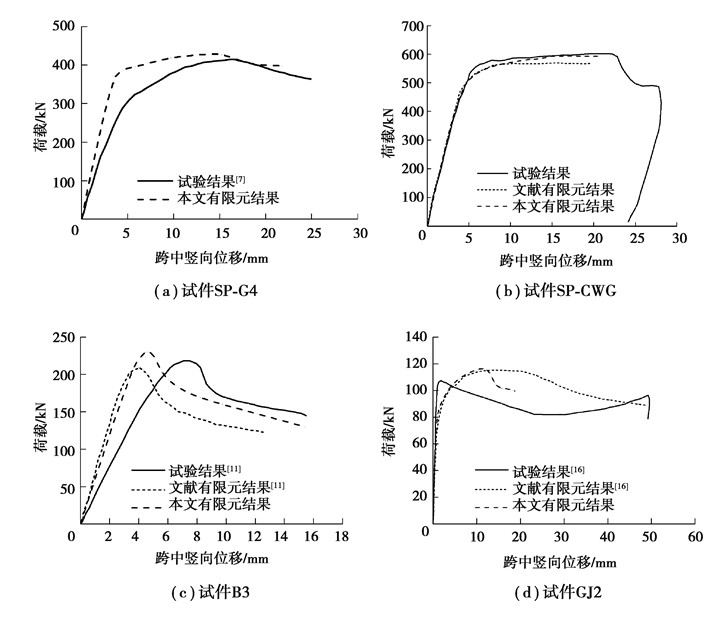
为了验证模型的可靠性,采用文中的建模方法分别对文献[7, 9, 11, 16]中的试验梁(SP-G4、SP-CWG、B3与GJ2)进行非线性有限元模拟。试件的截面特征,如图 4和表 1所示,模拟结果与试验结果的对比,如表 1、图 5和图 6所示。由表 1和图 5可见,有限元能够较好地模拟试件的极限承载力,与试验中试件的极限承载力相比,误差分别为3%、1%、6%和8%。由图 5可以看出,试验和有限元得到的荷载位移曲线存在一定偏差,主要由两个原因造成的:一是有限元模拟中没有考虑试件加工产生的残余应力,在一阶屈曲模态的基础上引入的初始缺陷并不能够代表整个试件的初始变形;二是试件和试验装置间也可能存在安装间隙。由图 6可知,有限元能够模拟出试件的失效模式。分析表明,建立的有限元模型能够准确模拟试件的承载力并且能够较好地预测试件的破坏模态。因此,文中的有限元建模方法得出的结果是可靠的。
|
图 4 SP-G4、SP-CWG、B3和GJ2几何尺寸 Fig. 4 Geometric notations of SP-G4、SP-CWG、B3 and GJ2 |
| 表 1 SP-G4、SP-CWG、B3和GJ2几何参数及结果对比 Table 1 Geometric parameters of SP-G4、SP-CWG、B3 and GJ2 and results |
|
图 5 有限元与试验荷载位移曲线比较 Fig. 5 Comparison of load-deformation curves between FE and test |

|
图 6 有限元与试验破坏模态结果对比 Fig. 6 Comparison of the failure modes between FE and test |
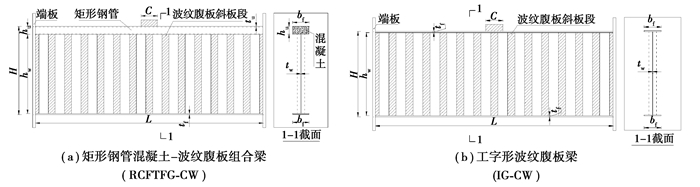
对集中荷载作用下用钢量基本相同、波纹腹板和下翼缘参数完全相同,但上翼缘形式不同的RCFTFG-CW和IG-CW(如图 7和表 2所示)进行非线性有限元分析,比较RCFTFG-CW和IG-CW的局部承压承载力大小以及加载过程中波纹腹板局部的应力发展,进一步比较不同加载位置对2种梁局部承压承载力的影响。
|
图 7 RCFTFG-CW和IG-CW几何尺寸 Fig. 7 Geometric notations of RCFTFG-CW and IG-CW |
| 表 2 模型几何参数 Table 2 Geometric parameters of models |
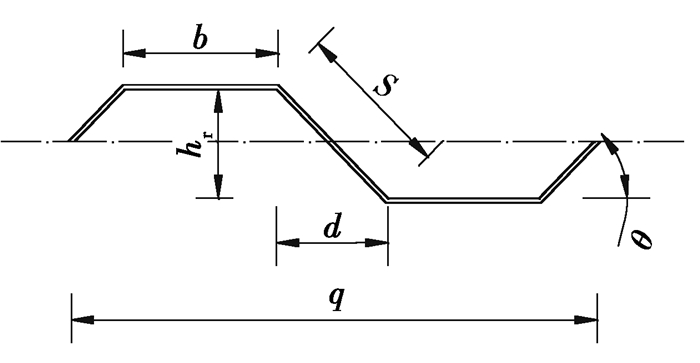
RCFTFG-CW上翼缘钢管内用混凝土灌实,下翼缘采用平钢板,IG-CW上下翼缘均是采用完全相同的平钢板。腹板波形及尺寸,如图 8和表 3所示,所有钢材型号采用Q345,上翼缘钢管内填混凝土强度等级为C40[6]。
|
图 8 波纹腹板 Fig. 8 Diagram of corrugated web |
| 表 3 波纹腹板几何参数 Table 3 Geometric parameters of corrugated web |
图 9是A、B、C 3组模型的荷载位移曲线。可以看出,RCFTFG-CW和IG-CW弹性段刚度基本相同,RCFTFG-CW的极限承载力大约是IG-CW的2~3倍。虽然,两者都是在弹性阶段结束后基本达到极限状态,但RCFTFG-CW在极限状态后曲线下降的趋势比IG-CW平缓,表现出更好的塑性性能。

|
图 9 RCFTFG-CW和IG-CW荷载位移曲线对比 Fig. 9 Comparison of load-deformation curves between RCFTFG-CW and IG-CW |
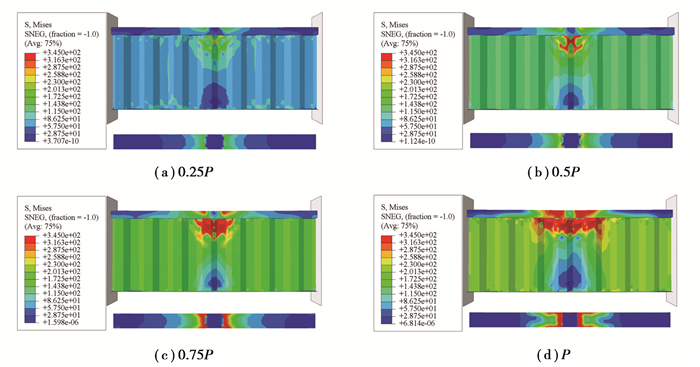
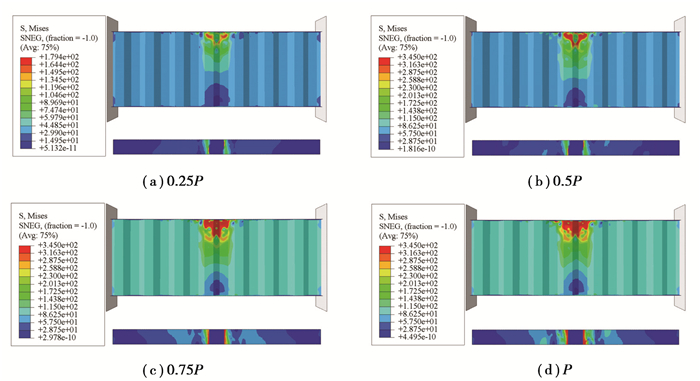
图 10和图 11为RCFTFG-CW-1和IG-CW-1加载过程中腹板和上翼缘的应力发展。由图可知,集中荷载作用下方两者波纹腹板的应力发展基本相似,应力在平板段和波折处发展较快。随着荷载增加,应力不断增大,并逐步向相邻的板带扩展,随后集中荷载下方的波纹腹板小部分区域先达到屈服,与之相邻的板带依次进入屈服状态。当波纹腹板局部受力区域内板带都屈服时,RCFTFG-CW-1和IG-CW-1丧失继续承载的能力,波纹腹板发生局部承压破坏,最终波纹腹板局部破坏处形成了一块弧形的塑性区域。RCFTFG-CW-1的塑性区域范围更大,这是因为钢管混凝土上翼缘增大了集中荷载在腹板计算高度边缘的分布宽度,使更多的波纹腹板板带参与受力。分析可知,钢管混凝土上翼缘提升了RCFTFG-CW对波纹腹板板带的利用率。
|
图 10 RCFTFG-CW-1应力发展过程(P=293 kN) Fig. 10 Stress development of RCFTFG-CW-1 (P=293 kN) |
|
图 11 IG-CW-1应力发展过程(P=139 kN) Fig. 11 Stress development of IG-CW-1 (P=139 kN) |
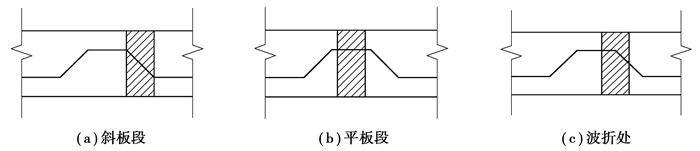
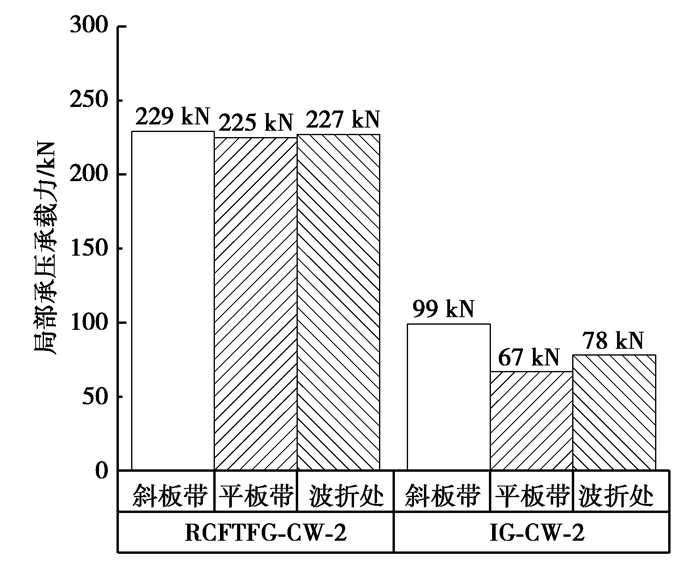
荷载作用位置(斜板段、平板段和波折处,如图 12所示)对IG-CW的局部承压承载力存在较大影响[12-13]。为分析荷载作用位置对RCFTFG-CW的影响,对表 3中B组模型进行有限元分析,加载长度(沿梁跨度方向)均为50 mm。图 13是RCFTFG-CW和IG-CW分别在3种作用位置的局部承压承载力。RCFTFG-CW-2在这3处的局部承压承载力大小相差在2%以内,而IG-CW-2在斜板段的承载力相较于平板段和波折处相差48%和16%。可以证明,RCFTFG-CW对荷载作用位置的适应性比IG-CW更好,更适用于移动集中荷载作用的情况。
|
图 12 荷载加载位置 Fig. 12 The positions of loading |
|
图 13 不同荷载作用位置对承载力的影响 Fig. 13 Influence of loading position on bearing capacity |
分析RCFTFG-CW各参数对局部承压承载力的影响,主要包括上翼缘矩形钢管混凝土等效惯转动惯量Ie[5]、腹板高度hw、腹板厚度tw、下翼缘厚度tf、荷载作用长度C、上翼缘钢管内填混凝土强度fc、腹板钢材强度fy以及波纹的展开长度与波长的比值γ。部分参数的变化范围参照《波纹腹板钢结构技术规程》(CECS 291 : 2011)[20],5种不同波形的具体几何尺寸,如表 3所示,参数分析中所有模型的破坏模式都是波纹腹板局部承压破坏。
3.1 上翼缘矩形钢管混凝土等效惯性矩Ie以下列模型(FE1-FE 16)为例,分析钢管混凝土上翼缘等效惯性矩Ie的影响:bf = 90~210 mm,hu = 40~90 mm,tu = 2~6 mm,hw = 600 mm,tw = 2 mm,tf = 6 mm,l = 1 680 mm,C = 120 mm,腹板选用波形1。
图 14为局部承压承载力Pu和等效惯性矩Ie的关系曲线。利用Matlab对其进行拟合,可以得到Pu和Ie的关系表达式(1)。从式(1)中可以看出,Pu与Ie的0.25次方成正比。
| $ P_{\mathrm{u}}=10 \times I_{\mathrm{e}}^{0.25}。$ | (1) |

|
图 14 上翼缘钢管混凝土等效惯性矩Ie的影响 Fig. 14 Influence of the equivalent moment of inertia Ie |
上翼缘钢管混凝土等效惯性矩Ie=It+ (Ec/Es)Ic[5];其中,It、Ic为上翼缘钢管的惯性矩和内填混凝土的惯性矩。
3.2 腹板高度hw和腹板厚度tw以下列模型(FE17-FE 37)为例,分析腹板高度hw和厚度tw的影响:bf = 120 mm,hu = 60 mm,tu = 3 mm,hw = 600~1 400 mm,tw = 2~4 mm,tf = 12 mm,l=1 680 mm,C=120 mm,腹板选用波形1。
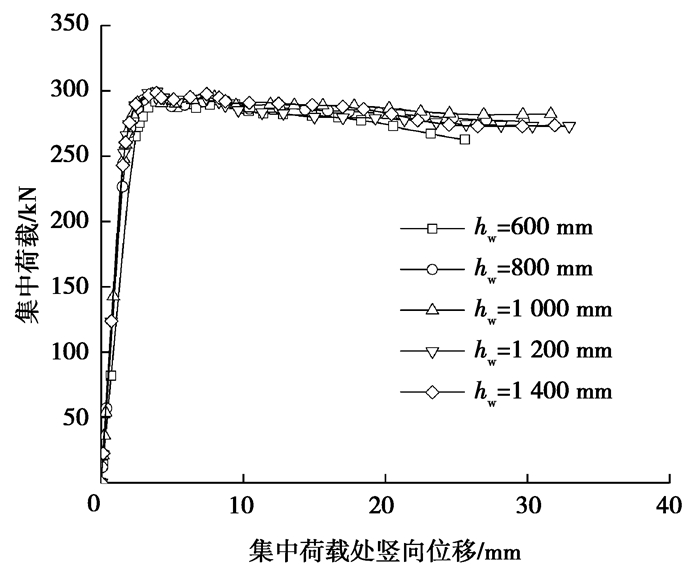
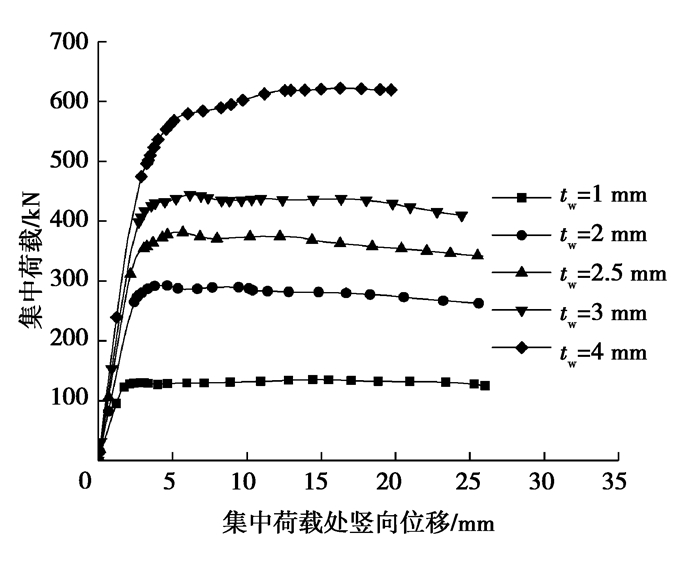
由图 15可知,腹板高度hw增大,承载力几乎没有变化。因此,对于波纹腹板出现局部承压的情况,腹板的高度hw变化对局部承压承载力Pu没有明显影响。这一结论与平翼缘波纹腹板梁类似[14-15]。由图 16可知,随着腹板厚度tw的增大,局部承压承载力Pu明显增大。此外,在不同腹板高度hw下,局部承压承载力Pu与腹板厚度tw之间的关系如图 17所示,发现两者近似成正比。
|
图 15 不同hw的荷载位移曲线(tw = 2 mm) Fig. 15 Load-deflection curves obtained with different web height hw |
|
图 16 不同tw的荷载位移曲线(hw = 600 mm) Fig. 16 Load-deflection curves obtained with different web thickness tw |

|
图 17 腹板厚度tw的影响 Fig. 17 Influence of the web thickness tw |
以下列模型(FE38-FE 42)为例,分析下翼缘厚度tf的影响:bf = 120 mm,hu = 60 mm,tu = 3 mm,hw = 600 mm,tw = 2 mm,tf = 5~12 mm,l = 1 680 mm,C = 120 mm,腹板选用波形1。
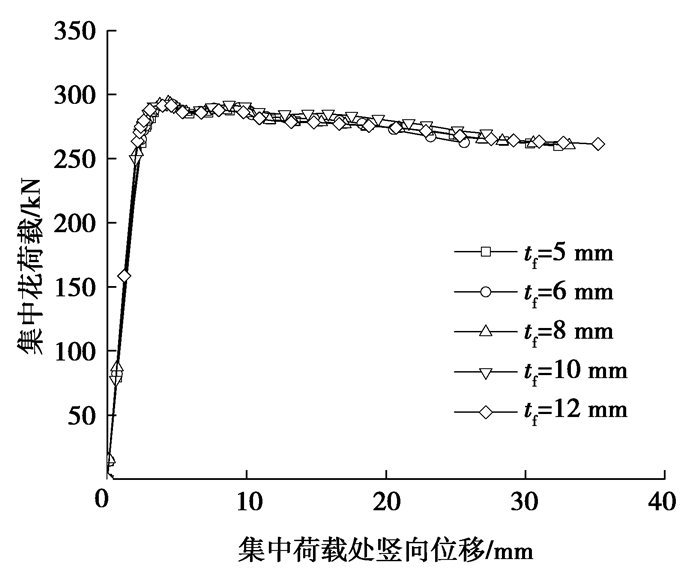
由图 18可知,下翼缘厚度tf在5~12 mm范围内变化,局部承压承载力Pu的大小几乎完全相同。尽管上述模型中最小下翼缘厚度tf只有5 mm,但是在腹板发生局部破坏时,下翼缘还没有达到其屈服应力。因此,在保证下翼缘受弯破坏不先于腹板局部承压破坏的前提下,下翼缘的厚度对局部承压承载力影响不大。
|
图 18 不同tf的荷载位移曲线 Fig. 18 Load-deflection curves obtained with different tf |
以下列模型(FE43-FE 53)为例,分析荷载作用长度C的影响:bf = 120 mm,hu = 60 mm,tu = 3 mm,hw = 600 mm,tw = 2 mm,tf = 6 mm,l = 1680 mm,C分别取0 mm,50 mm,80 mm,120 mm,160 mm,200 mm,240 mm,280 mm,320 mm,360 mm,400 mm,腹板选用波形1。C为刚性加载块长度,即荷载作用长度(沿梁跨度方向)。C = 0 mm表示在梁跨中施加线荷载。
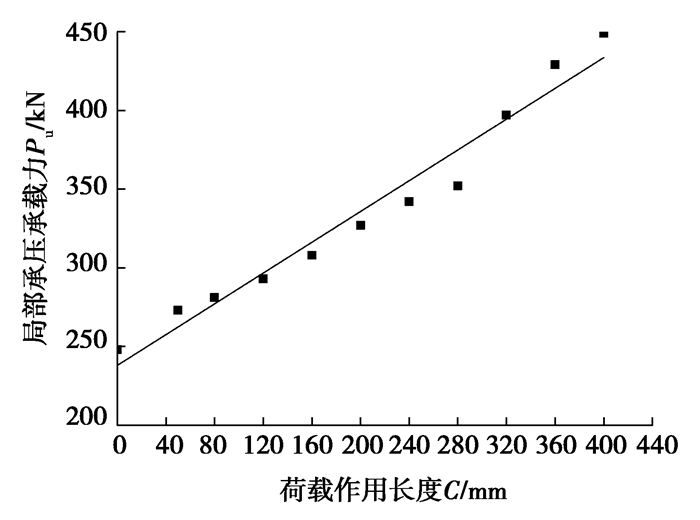
由图 19可知,局部承压承载力Pu与荷载作用长度C近似成线性关系,这与平翼缘波纹腹板梁结论类似[13, 15]。随着C的增大,更多的波纹腹板板带参与受力。
|
图 19 荷载作用长度C的影响 Fig. 19 Influence of the loading length C |
以下列模型(FE54- FE 65)为例,分析波纹的展开长度与波长的比值γ的影响:bf = 120 mm,hu = 60 mm,tu = 3 mm,hw = 600 mm,tw = 2~4 mm,tf = 12 mm,l = 1 680 mm,C = 120 mm,腹板选用波形1,2,3,4,5。
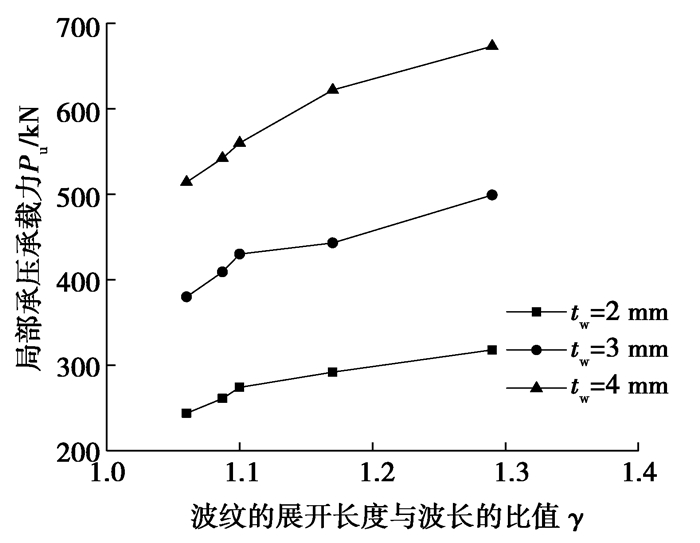
局部承压承载力Pu受腹板波纹的疏密影响较大[15],文中通过分析γ与Pu的关系来研究腹板波纹疏密对Pu影响。如图 20所示,在不同腹板厚度tw下,Pu与γ近似成直线关系。
|
图 20 波纹的展开长度与波长比值γ的影响 Fig. 20 Influence of the ratio of the stretched length of the wave to the wave length γ |
以下列模型(FE66-FE 75)为例,分析混凝土强度fc和腹板钢材强度fy的影响:bf = 120 mm,hu = 60 mm,tu = 3 mm,hw = 600 mm,tw = 2 mm,tf = 6 mm,l = 1680 mm,C = 120 mm,腹板选用波形1,fc分别取40、50、60、70、80 MPa;fy分别取235、295、345、390、420 MPa。上翼缘钢管内填混凝土的最低强度fc根据Wang等[6]提出的方法确定,可以保证混凝土强度fc满足上翼缘钢材强度fy对应的最低强度。
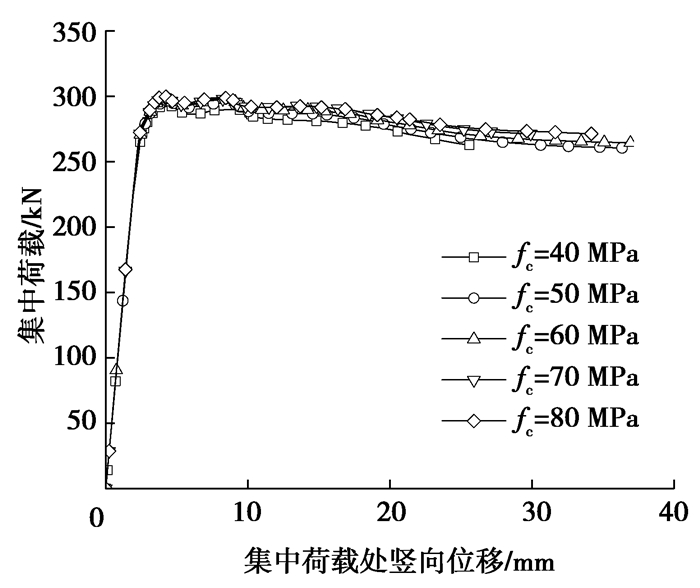
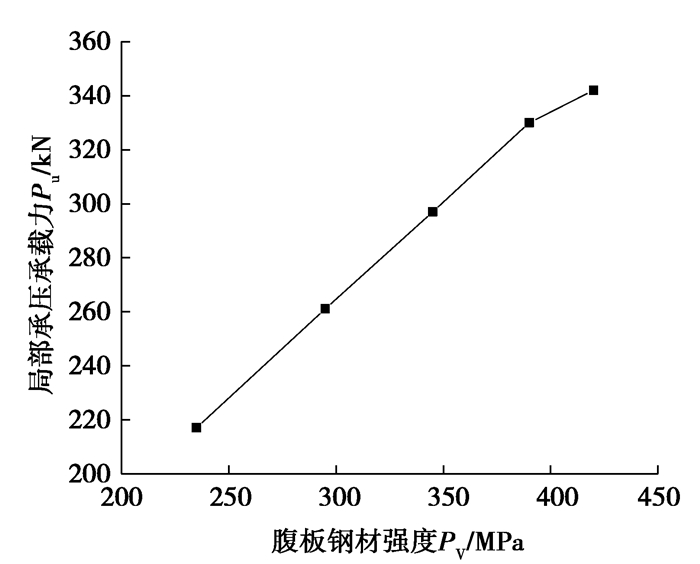
由图 21可知,凝土强度fc从40 MPa提升到80 MPa局部承压承载力几乎没有变化。因此,在满足上翼缘钢材对内填混凝土的最低强度要求的前提下,继续提高混凝土的强度对局部承压承载力几乎没有影响。由图 22可知,局部承压承载力Pu与腹板钢材强度fy近似成正比。
|
图 21 不同fc的荷载位移曲线(fy = 345 MPa) Fig. 21 Load-deflection curves obtained with different concrete strength fc |
|
图 22 腹板钢材强度fy的影响(fc = 50 MPa) Fig. 22 Influence of the web yielding stress fy |
表 4中模型FE1- FE 75分析了参数Ie、hw、tw、tf、C、γ、fc、fy对承载力的影响。分析结果可知,Ie对其局部承压承载力Pu影响较大,Pu与Ie的0.25次方成正比;Pu与tw、C、γ和fy均成线性关系;hw与tf对Pu影响很小;上翼缘钢管内填混凝土在满足上翼缘钢材强度对应最低强度的前提下,继续提高混凝土强度fc对局部承压承载力没有明显的影响。
| 表 4 RCFTFG-CW参数分析 Table 4 Information of RCFTFG-CW in parametric study |
钢结构设计标准[21]中推荐了工字形平腹板梁局部承压承载力的计算公式;Elgaaly[12]和张哲等[15]提出了IG-CW的局部承压承载力计算公式。但这些公式只适用于平钢板上翼缘工字形梁的局部承压承载力的计算。由参数分析的结果可知,RCFTFG-CW的钢管混凝土上翼缘对局部承压承载力的影响较大,因此,有必要对RCFTFG-CW局部承压承载力计算公式进行研究。RCFTFG-CW局部承压承载力计算公式的提出需要基于以下假定:
1) 集中荷载下方波纹腹板局部破坏区域应力都达到屈服应力;
2) 加载过程中RCFTFG-CW的截面满足平截面假定;
3) 钢材的应力应变关系为理想弹塑性模型。
由结果可知,局部承压承载力Pu与腹板厚度tw、腹板强度fy均成正比,这与Elgaaly[12]对IG-CW的分析结果一致。此外,由于波纹腹板疏密对局部承压承载力Pu存在影响,必须考虑Pu与参数γ的关系,Pu与是γ线性关系。结合RCFTFG-CW腹板局部破坏区域的应力发展和波纹腹板在有效承载宽度内的屈服理论,提出RCFTFG-CW的局部承压承载力计算公式:
| $ P_{\mathrm{u}}=\gamma l_0 t_{\mathrm{w}} f_{\mathrm{y}}, $ | (2) |
其中,l0是集中荷载在腹板计算高度边缘的假定分布宽度。
参照CIDECT设计指南3:矩形钢管(RHS)节点的静力强度设计指南[22],考虑方钢管混凝土T形节点中竖向腹杆的轴力在水平弦杆中的传力路径,可以得到集中荷载通过RCFTFG-CW钢管混凝土上翼缘扩散至腹板计算高度上边缘的假定分布长度l0的计算公式:
| $l_0=C+4 h_{\mathrm{u}}, $ | (3) |
结合式(1)中Pu与Ie的关系,对式(3)进行修正:
| $ l_0=\alpha I_{\mathrm{e}}^{0.25}+\beta\left(C+4 h_{\mathrm{u}}\right), $ | (4) |
其中,α和β是待定系数。
采用模型FE43-FE53的有限元计算结果对其进行拟合,求得α和β分别为5和0.6,得RCFTFG-CW局部承压承载力计算公式:
| $ P_{\mathrm{u}}=\gamma\left[5 I_{\mathrm{e}}^{0.25}+0.6\left(C+4 h_{\mathrm{u}}\right)\right] t_{\mathrm{w}} f_{\mathrm{y}}, $ | (5) |
| $\gamma=2(b+s) / q 。$ | (6) |
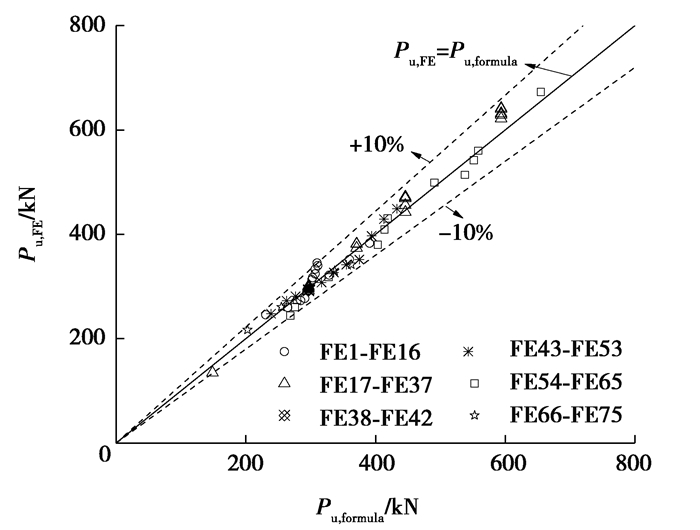
表 4中,Pu, formula为公式计算结果,Pu, FE为有限元计算结果。为了验证Pu, formula的准确性,将两者进行比较。计算结果的对比如图 23所示。由图中可知,式(5)计算结果与有限元计算结果吻合较好,所有模型Pu, formula与Pu, FE的误差均在±10%以内,满足实际工程中规定的误差范围,对误差结果进行分析,计算得到误差绝对值的平均值和均方差分别为0.032和0.026,表明式(5)能够较准确地计算RCFTFG-CW局部承压承载力。
|
图 23 公式(5)与有限元计算结果对比 Fig. 23 Comparison between analytical results from Eq.(5)and FE results |
1) 在RCFTFG-CW和IG-CW用钢量基本相同的情况下,RCFTFG-CW的承载力约为IG-CW的2~3倍,RCFTFG-CW具有更好的塑性性能。
2) RCFTFG-CW的上翼缘钢管混凝土使波纹腹板上的有效承载长度增加,集中荷载作用处下方形成更大范围的弧形塑性区域,有效提升了钢梁对波纹腹板板带的利用率。
3) 与IG-CW相比较,集中荷载作用位置对RCFTFG-CW的局部承压承载力几乎没有影响,RCFTFG-CW更适用于移动集中荷载作用的情况。
4) 上翼缘等效惯性矩Ie、腹板厚度tw、荷载作用长度C、波纹的展开长度与波长的比值γ及腹板强度fy对RCFTFG-CW的局部承压承载力Pu影响较大。对于波纹腹板发生局部承压破坏的情况,腹板高度hw、下翼缘厚度tf、混凝土强度fc对Pu的影响很小。
5) 提出了RCFTFG-CW波纹腹板的局部承载力计算公式,从有限元分析结果与公式计算结果比较来看,所提出的公式能够较准确地预测RCFTFG-CW的局部承压承载力。
| [1] |
Sause R, Kim B G, Wimer M R. Experimental study of tubular flange girders[J]. Journal of Structural Engineering, 2008, 134(3): 384-392. DOI:10.1061/(ASCE)0733-9445(2008)134:3(384) |
| [2] |
Gao F, Zhu H P, Zhang D H, et al. Experimental investigation on flexural behavior of concrete-filled pentagonal flange beam under concentrated loading[J]. Thin-Walled Structures, 2014, 84: 214-225. DOI:10.1016/j.tws.2014.06.008 |
| [3] |
Gao F, Zuo G J, Deng L X, et al. Flexural behaviour of horizontally curved Ⅰ-girders with round concrete-filled tubular flange[J]. Journal of Constructional Steel Research, 2020, 170: 106090. DOI:10.1016/j.jcsr.2020.106090 |
| [4] |
张文福, 任亚文. 矩形钢管混凝土翼缘组合梁的刚度与抗弯承载力[C]//第十五届全国现代结构工程学术研讨会论文集. 天津: 天津大学, 2015. Zhang W F, Ren Y W. Stiffness and flexural capacity of composite beams with rectangular concrete-filled steel tubular flanges[C]//Proceedings of the 15th National Symposium on Modern Structural Engineering. Tianjin: Tianjin University School of Civil Engineering, 2015: 1130-1147. (in Chinese) |
| [5] |
Shao Y B, Wang Y M. Experimental study on static behavior of Ⅰ-girder with concrete-filled rectangular flange and corrugated web under concentrated load at mid-span[J]. Engineering Structures, 2017, 130: 124-141. DOI:10.1016/j.engstruct.2016.10.002 |
| [6] |
Wang Y M, Shao Y B. Stress analysis of a new steel-concrete composite Ⅰ-girder[J]. Steel Composite Structures an International Journal, 2018, 28(1): 51-61. |
| [7] |
王亚敏. 矩形钢管混凝土翼缘-波纹腹板组合钢梁的性能研究[D]. 烟台: 烟台大学, 2015. Wang Y M. Study on the performance of composite steel beam with concrete-filled rectangular steel tube flange and corrugated web[D]. Yantai: Yantai University, 2015. (in Chinese) |
| [8] |
Wang Y M, Shao Y B, Chen C, et al. Prediction of flexural and shear yielding strength of short span Ⅰ-girders with concrete-filled tubular flanges and corrugated web-Ⅰ: Numerical simulation and theoretical analysis[J]. Thin-Walled Structures, 2020, 148: 106592. DOI:10.1016/j.tws.2019.106592 |
| [9] |
Wang Y M, Shao Y B, Chen C, et al. Prediction of flexural and shear yielding strength of short span Ⅰ-girders with concrete-filled tubular flanges and corrugated web- Ⅱ: Numerical simulation and theoretical analysis[J]. Thin-Walled Structures, 2020, 148: 106593. DOI:10.1016/j.tws.2019.106593 |
| [10] |
刘梓锋, 王志宇, 周夏芳. 波形钢腹板-钢管混凝土翼缘组合梁的受弯性能分析[J]. 建筑结构学报, 2019, 40(S1): 325-332. Liu Z F, Wang Z Y, Zhou X F. Bending behavior of composite girders with corrugated steel webs and concrete filled steel tube flanges[J]. Journal of Building Structures, 2019, 40(S1): 325-332. (in Chinese) |
| [11] |
Nikolaus L L, Olof K L. Girders with trapezoidally corrugated webs under patch loading[D]. Sweden: Chalmers University of Technology, 2010.
|
| [12] |
Elgaaly M, Seshadri A. Girders with corrugated webs under partial compressive edge loading[J]. Journal of Structural Engineering, 1997, 123(6): 783-791. DOI:10.1061/(ASCE)0733-9445(1997)123:6(783) |
| [13] |
Luo R, Edlund B. Ultimate strength of girders with trapezoidally corrugated webs under patch loading[J]. Thin-Walled Structures, 1996, 24(2): 135-156. DOI:10.1016/0263-8231(95)00029-1 |
| [14] |
郭彦林, 张博浩. 波浪腹板工形梁局部承压承载力设计方法研究[J]. 工业建筑, 2012, 42(7): 45-54. Guo Y L, Zhang B H. Strength of i-shaped girders with sinusoidal corrugated webs under patch loading[J]. Industrial Construction, 2012, 42(7): 45-54. (in Chinese) |
| [15] |
张哲, 李国强, 孙飞飞, 等. 波纹腹板H形钢吊车梁局部承压承载力[J]. 建筑钢结构进展, 2013, 15(6): 25-31, 41. Zhang Z, Li G Q, Sun F F, et al. Bearing capacity of H-shaped crane girder with corrugated webs under local compressive loading[J]. Progress in Steel Building Structures, 2013, 15(6): 25-31, 41. (in Chinese) DOI:10.3969/j.issn.1671-9379.2013.06.004 |
| [16] |
张哲. 波纹腹板H型钢及组合梁力学性能理论与试验研究[D]. 上海: 同济大学, 2009. Zhang Z. Theoretical and experimental study on mechanical properties of H-beam and composite beam with corrugated web[D]. Shanghai: Tongji University, 2009. (in Chinese) |
| [17] |
韩林海. 钢管混凝土结构: 理论与实践[M]. 2版. 北京: 科学出版社, 2016. Han L H. Concrete filled steel tubular structures: theory and practice[M]. The third edition. Beijing: Science Press, 2016. (in Chinese) |
| [18] |
Han L H, Yao G H, Tao Z. Performance of concrete-filled thin-walled steel tubes under pure torsion[J]. Thin-Walled Structures, 2007, 45(1): 24-36. DOI:10.1016/j.tws.2007.01.008 |
| [19] |
Tao Z, Uy B, Liao F Y, et al. Nonlinear analysis of concrete-filled square stainless steel stub columns under axial compression[J]. Journal of Constructional Steel Research, 2011, 67(11): 1719-1732. DOI:10.1016/j.jcsr.2011.04.012 |
| [20] |
中国工程建设标准化协会. 波纹腹板钢结构技术规程: CECS 291—2011[S]. 北京: 中国计划出版社, 2011. Construction Standard (Recommended) of the People's Republic of China. Technical specification for steel structures with corrugated webs: CECS 291—2011[S]. Beijing: China Planning Press, 2011. (in Chinese) |
| [21] |
中华人民共和国住房和城乡建设部. 钢结构设计标准: GB 50017—2017[S]. 北京: 中国建筑工业出版社, 2017. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Standard for design of steel structures: GB 50017—2017[S]. Beijing: China Architecture & Building Press, 2017. (in Chinese) |
| [22] |
Packer J A, Wardenier J, Zhao X L, et al. Design guide for rectangular hollow section (RHS) joints under predominatly static loading[M]//Construction with hollow steel sections, 2009.
|
 2023, Vol. 46
2023, Vol. 46


