1b. 广西电网有限责任公司 电力科学研究院, 南宁 530023;
2. 重庆大学 自动化学院, 重庆 400044
1b. Electric Power Research Institute, Guangxi Power Grid Co., Ltd., Nanning 530023, P. R. China;
2. College of Automation, Chongqing University, Chongqing 400044, P. R. China
当前电能的传输方式主要为有线输电,但其存在很多问题,如接触电火花、线路老化。且在一些特殊场合,如煤矿井下、水下等局限性很高。MC-WPT技术实现了电能从电源侧到用电设备端的无电气连接传输。由于电源端和负载端的电气隔离,该技术具有安全、可靠、灵活等优势,在电动汽车、医疗行业、家用电子产品等方面应用广泛。
MC-WPT系统输出功率受频率和传输距离影响很大,在SS补偿拓扑结构下,当系统耦合系数超过一个界限后会出现频率分裂现象,在原谐振频率点处的输出功率会随着传输距离减小急剧下降[1]。文献[2]把其分为过耦合、临界耦合、欠耦合3种情况。为了解决过耦合情况下频率分裂所导致输出功率降低问题,目前有使用频率跟踪[3-5]、减小耦合系数抑制过耦合发生[6-7]、增加阻抗匹配网络等方法[8-10]。改变耦合系数大小需要另外增加机械结构来调节耦合空间位置,不适用于位置不可移动情况;增加阻抗匹配网络需增加大量元件,带来额外的损耗。此外,改变耦合强度和增加阻抗匹配网络的实质都是调节系统参数使得系统不存在频率分裂现象。但目前没有相应的参数准则使得系统工作在临界耦合状态。在调节系统参数使得系统退出过耦合时,容易降低系统的最大能效。频率跟踪因为实现便捷,调整速度快,具有仅需调整系统工作频率而不改变系统结构参数的优势,成为目前最常用的一种方式。但现有的频率跟踪直接以检测发射和接收端的电流或功率对频率进行跟踪,此时逆变器输出的电压、电流存在较大相位差角,不能以软开关方式工作,开关损耗较大,难以兼顾输出功率和效率。
针对过耦合状态下磁耦合无线电能传输系统发生频率分裂导致原谐振点的能效降低,且目前频率跟踪无法实现电压电流同相位的问题,笔者提出一种可以在过耦合状态下以零相角状态工作并输出最大功率的方法。先通过实本征态计算系统的本征工作条件,后经过零相角计算出在耦合系数变化时谐振点的频率变化。再与实本征态得到的结果进行对比分析,证明了2种方法计算结果的一致性。并进行仿真验证分裂谐振点的系统性能优势,即在过耦合区通过分裂零相角点的跟踪可以保证稳定的效率和最大输出功率。
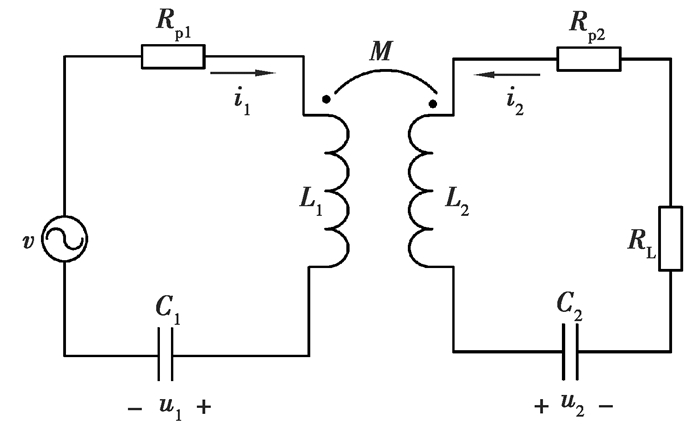
1 系统建模与理论分析 1.1 实本征态以串联串联(SS)型为例系统的等效电路模型如图 1所示,两线圈结构的MC-WPT系统由2个RLC回路组成。其中下标1和2分别表示发射回路和接收回路的相关参数。Rpj,Lj和Cj分别代表第j个线圈的等效串联电阻,自感以及补偿电容;ij和uj为第j个回路的电流和补偿电容Cj两端的电压(j=1, 2),v和RL为电源电压和负载电阻,M为2个线圈之间的互感。
|
图 1 两线圈结构MCR-WPT等效电路图 Fig. 1 Equivalent circuit diagram of MCR-WPT with two-coil structure |
根据基尔霍夫电压定律(KVL),该系统的数学模型可以表示为
| $ \left\{\begin{array}{l} L_1 C_1 \ddot{u}_1+M C_2 \ddot{u}_2+R_1 C_1 \dot{u}_1+u_1=\boldsymbol{v} ; \\ M C_1 \ddot{u}_1+L_2 C_2 \ddot{u}_2+R_2 C_2 \dot{u}_2+u_2=0, \end{array}\right. $ | (1) |
其中:R1=Rp1,R2=Rp2+RL。定义矢量v′= [v 0]T,i=[i1 i2]T,u=[u1 u2]T分别为系统的电源电压矢量,各回路电流矢量和电容电压矢量。定义矩阵L,C和R分别为系统的电感矩阵、电容矩阵和电阻矩阵,其相应表达式如式(2)所示
| $ \boldsymbol{L}=\left[\begin{array}{cc} L_1 & M \\ M & L_2 \end{array}\right], \boldsymbol{C}=\left[\begin{array}{cc} C_1 & 0 \\ 0 & C_2 \end{array}\right], \boldsymbol{R}=\left[\begin{array}{cc} R_1 & 0 \\ 0 & R_2 \end{array}\right], $ | (2) |
令x =[
| $ \boldsymbol{\dot{x}}=\boldsymbol{S} x+\boldsymbol{A}^{-1} \boldsymbol{v}_{\mathrm{in}} \text { 。} $ | (3) |
其中:S为系统的系统矩阵;In×m和0n×m分别表示n×m阶的单位矩阵和零矩阵。
| $ \boldsymbol{S}=\left[\begin{array}{cc} \mathit{\pmb{0}}_{2 \times 2} & \boldsymbol{I}_{2 \times 2} \\ -[\boldsymbol{L C}]^{-1} & -[\boldsymbol{L C}]^{-1} \boldsymbol{R C} \end{array}\right], \boldsymbol{A}=\left[\begin{array}{cc} \boldsymbol{R C} & \boldsymbol{L C} \\ \boldsymbol{L C} & \mathit{\pmb{0}}_{2 \times 2} \end{array}\right] \text {。} $ | (4) |
系统矩阵S的特征值为该系统的本征频率。可知求解矩阵特征值的公式为
| $ |\lambda \boldsymbol{I}-\boldsymbol{S}|=0 。$ | (5) |
将式(4)代入至式(5),可得
| $ \left|\boldsymbol{L} \boldsymbol{C} \lambda^2+\boldsymbol{R} \boldsymbol{C} \lambda+\boldsymbol{I}\right|=0 。$ | (6) |
将式(2)代入至式(6),可得系统的特征方程为
| $ \begin{aligned} & \left(L_1 C_1 L_2 C_2-M^2 C_1 C_2\right) \lambda^4+\left(L_1 C_1 R_2 C_2+L_2 C_2 R_1 C_1\right) \lambda^3+ \\ & \left(L_1 C_1+L_2 C_2+R_1 C_1 R_2 C_2\right) \lambda^2+\left(R_1 C_1+R_2 C_2\right) \lambda+1=0。\end{aligned} $ | (7) |
令ω1=
| $ \begin{gathered} \left(1-k^2\right) \omega^4-\left(r_1+r_2\right)\left(i \omega^3\right)-\left(\omega_1^2+\omega_2^2+r_1 r_2\right) \omega^2+ \\ \left(r_1 \omega_2^2+r_2 \omega_1^2\right)(i \omega)+\omega_1^2 \omega_2^2=0 。\end{gathered} $ | (8) |
把式(8)的实部和虚部分开,分别等于0可以得到
| $ \left(1-k^2\right) \omega^4-\left(\omega_1^2+\omega_2^2+r_1 r_2\right) \omega^2+\omega_1^2 \omega_2^2=0 $ | (9) |
| $ -\left(r_1+r_2\right) \omega^2+r_1 \omega_2^2+r_2 \omega_1^2=0 。$ | (10) |
此时可分情况讨论
1) 如果r1+r2=0,由式(10)可知必须满足ω1=ω2。此时物理结构上满足宇称对称。此时不妨令ω1=ω2=ω0。将r1+r2=0和ω1=ω2=ω0代入至式(9)可得
| $ \omega_{1, 2}^2=\frac{2 \omega_0^2-r_0^2 \pm \sqrt{r_0^4-4 \omega_0^2 r_0^2+4 k^2 \omega_0^4}}{2\left(1-k^2\right)} 。$ | (11) |
当(12)成立时,系统工作在实本征态。此时系统结构满足宇称对称,也就是所说的宇称时间对称态[11-14]。
| $ \left\{\begin{array}{l} r_1+r_2=0, \\ \omega_1=\omega_2=\omega_0, \\ \omega^2=\frac{2 \omega_0^2-r_0^2 \pm \sqrt{r_0^4-4 \omega_0^2 r_0^2+4 k^2 \omega_0^4}}{2\left(1-k^2\right)} 。\end{array}\right. $ | (12) |
2) 如果r1+r2≠0,不失一般性也可假设ω1=ω2=ω0。将r1+r2≠0和ω1=ω2=ω0代入至式(9)和式(10)可得
| $ \left\{\begin{array}{l} r_1=\frac{-k^2 \omega_0^2}{r_2}, \\ \omega=\omega_0 。\end{array}\right. $ | (13) |
当系统参数满足式(13),尽管系统结构参数并不满足宇称对称,但系统仍然工作在实本征态,该状态称之为实本征态破缺态。
1.2 零相角由电路方程可以计算出副边电路等效到原边后输入阻抗的实部为
| $ R_{\text {inre }}=R_{p 1}+\frac{(\omega M)^2\left(R_{p 2}+R_L\right)}{\left(\omega L_2-\frac{1}{\omega C_2}\right)^2+\left(R_{p 2}+R_L\right)^2} 。$ | (14) |
输入阻抗虚部为
| $ R_{i n\;\mathrm{im}}=j \cdot\left[\left(\omega L_1-\frac{1}{\omega C_1}\right)-\frac{(\omega M)^2\left(\omega L_2-\frac{1}{\omega C_2}\right)}{\left(\omega L_2-\frac{1}{\omega C_2}\right)^2+\left(R_{p 2}+R_L\right)^2}\right] 。$ | (15) |
为了保证系统谐振工作在零相角状态,需要使虚部为0。使虚部为0的条件有
1)
| $ \left(\omega L_1-\frac{1}{\omega C_1}\right)=\left(\omega L_2-\frac{1}{\omega C_2}\right)=0, $ | (16) |
此时实部为Rinre=Rp1+(ωM)2/Rp2+RL,系统工作在原谐振频率处,实部随k值增加单调递增。
2)
| $ \left\{\begin{array}{l} \left(\omega L_1-\frac{1}{\omega C_1}\right)=\left(\omega L_2-\frac{1}{\omega C_2}\right), \\ \frac{(\omega M)^2}{\left(\omega L_2-\frac{1}{\omega C_2}\right)^2+\left(R_{p 2}+R_L\right)^2}=1, \end{array}\right. $ | (17) |
此时实部为Rinre=R1+ Rp2+RL可以看到此时实部为定值不随k值变化而变化。而系统的工作频率需要随耦合系数的变化而变化。
通过计算可以得到1条件下即为设置的相同各回路谐振频率f,且在此频率下,k变化虚部始终为0。而2条件下k需要大于一定的值才有(ωM)2/[(ωL2-1/ωC2)2+(Rp2+RL)2]=1。
通过式(17)计算得到零相角频率为
| $ \omega_{1, 2}=\sqrt{-\frac{\left(C_2 R_{p 2}^2 \pm \sqrt{A}-2 L_2+C_2 R_L^2+2 C_2 R_{p 2} R_L\right)}{2\left(C_2 L_2^2-C_2 L_1 L_2 k^2\right)}}, $ | (18) |
式中:
| $ \begin{aligned} A & =C_2^2 R_{p 2}^4+4 C_2^2 R_{p 2}^3 R_L+6 C_2^2 R_{p 2}^2 R_L^2+4 C_2^2 R_{p 2} R_L^3 \\ +C_2^2 R_L^4 & -4 L_2 C_2 R_{p 2}^2-8 L_2 C_2 R_{p 2} R_L-4 L_2 C_2 R_L^2+4 L_1 L_2 k^2。\end{aligned} $ | (19) |
在本征态计算中得到式(11),通过把其中
| $ k_1 \geqslant \sqrt{\frac{4 \omega_0^2 r_0^2-r_0^4}{4 \omega_0^4}}。$ | (20) |
或者通过2条件计算可以得到
| $ k_1 \geqslant \sqrt{\frac{4 L_2^2-\left(\frac{2 L_2}{C_2}-\left(R_{p 2}+R_L\right)^2\right)^2 C_2^2}{4 L_1 L_2}}, $ | (21) |
2种方法得到的式子计算结果相同。
系统在耦合系数k<k1时只有一个零相角点,即原谐振频率点。当k=k1时有2个; k>k1时有3个或2个,此时还需要注意,通过(ω0M)≥(Rp2+RL),即
| $ k_2 \geqslant \frac{\left(R_{p 2}+R_L\right)}{\omega_0 \sqrt{L_1 L_2}} 。$ | (22) |
计算得到的虚部出现多个零相角点是不准确的,当k=k2时,新分裂出的2个零相角点中的1个与原零相角点ω0重合,当k>k2时新出现的另外2个点将分布在原零相角点的两边。k<k1时有1个零相角点,k=k1时有2个; k2>k>k1时有3个; k=k2时其中一个和原点重合变成2个,k>k2时还是3个(如表 1所示)。
| 表 1 耦合系数和零相角点关系 Table 1 Relationship between coupling coefficient and zero phase angle |
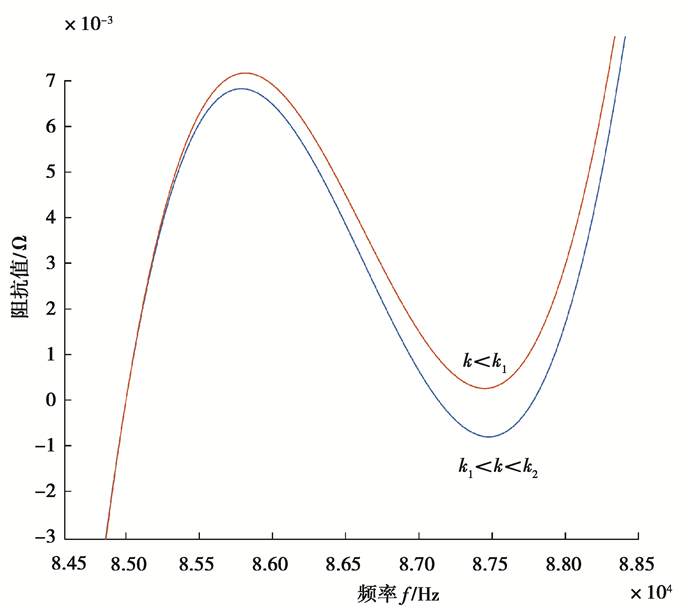
|
图 2 耦合系数小于k<k1和k<k1<k2虚部图 Fig. 2 Imaginary part diagram with k < k1 and k1 < k < k2 |
可以清楚看到零相角点位置的变化。在原边Rp1一定的情况下,输入阻抗实部越大,即副边反射到原边的阻抗实部越大,系统的效率就越高。对式(14)输入阻抗实部求导计算得到实部最大值点为
| $ \omega=-\frac{\sqrt{2\left(-C_2\left(C_2 R_{p 2}^2+2 C_2 R_{p 2} R_L+C_2 R_L^2-2 L_2\right)\right)}}{C_2^2 R_{p 2}^2+2 C_2^2 R_{p 2} R_L+C_2^2 R_L^2-2 L_2 C_2} 。$ | (23) |
通过式(23)发现电路参数固定后实部最大值点频率为固定值,不随k的变化而变化,且最大点频率和边界值k1点所对应的零相角频率相同,即把k=k1代入式(18)。
1.3 零相角频率和本征态频率的对比分析本征态计算得出的结果为虚部为0的ω,ω=ω0为一直的零相角点,当k>k1得到另外的零相角点即
| $ \omega^2=\frac{2 \omega_0^2-r_0^2 \pm \sqrt{r_0^4-4 \omega_0^2 r_0^2+4 k^2 \omega_0^4}}{2\left(1-k^2\right)} 。$ | (24) |
该式同零相角频率计算得到的结果式(18)相同。
| $ \omega_{1, 2}=\sqrt{-\frac{\left(C_2 R_{p 2}^2 \pm \sqrt{A}-2 L_2+C_2 R_L^2+2 C_2 R_{p 2} R_L\right)}{2\left(C_2 L_2^2-C_2 L_1 L_2 k^2\right)}} 。$ | (25) |
并且得到的边界耦合系数k1也是一样的。
| $ k_1=\sqrt{\frac{4 \omega_0^2 r_0^2-r_0^4}{4 \omega_0^4}}=\sqrt{\frac{4 L_2^2-\left(\frac{2 L_2}{C_2}-\left(R_{p 2}+R_L\right)^2\right)^2 C_2^2}{4 L_1 L_2}} 。$ | (26) |
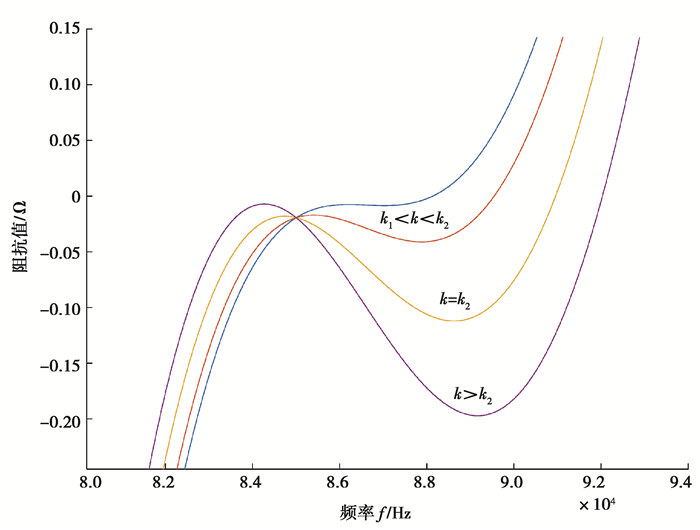
|
图 3 耦合系数k1<k2, k1=k2,k1>k2虚部图 Fig. 3 Imaginary part diagram with k1 < k < k2, k=k2 and k>k2 |
从而证明了实本征态和零相角点的相关性。
而另一个条件
| $ \left\{\begin{array}{l} r_1=\frac{-k^2 \omega_0^2}{r_2}, \\ \omega=\omega_0 \end{array}\right.。$ | (27) |
得到的|r|为原零相角点ω0处随k值变化的副边到原边的反射阻抗。由于出现的多个零相角点处副边反射到原边的阻抗恒为Rp2+RL,在特殊情况Rp1=Rp2+RL下,若由于耦合系数过大发生频率分裂即k>k1则可以通过调整工作频率保持式(11),系统工作在谐振点处并保证恒功率输出。
2 不同频率下的系统特性对比分析基于图 1所示的电路图,在MATLAB中的Simulink模块中搭建了相应的仿真模型,仿真参赛如表 2所示。基于所给电路参数,可知电路的原谐振频率为85 kHz。
| 表 2 仿真参数值 Table 2 Simulation parameter values |
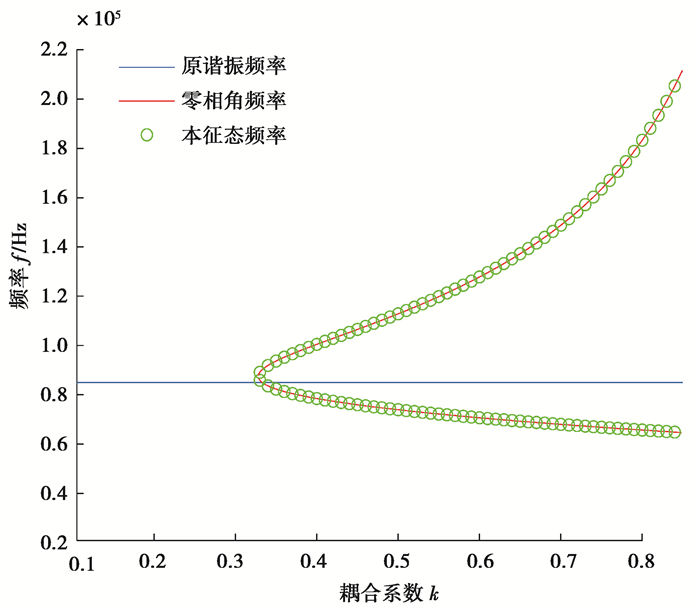
如图 4所示,蓝色是原谐振频率、绿色圈是本征频率、红色是零相角频率。可以看出,本征频率和零相角频率是一致的,且随着耦合系数增加,谐振频率个数变化和上面分析相同。
|
图 4 不同模式下谐振点频率随耦合系数的变化 Fig. 4 Variation of resonant frequency with coupling coefficient under different modes |
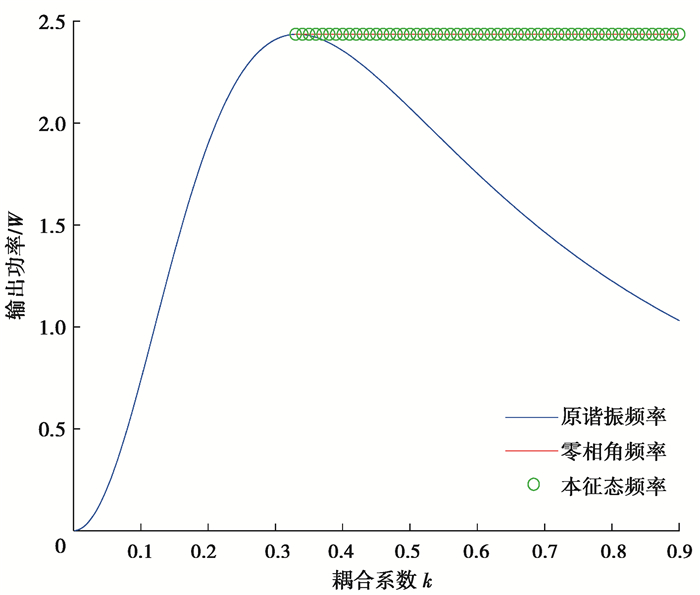
如果在耦合系数过边界点后,工作频率使用式(11)得到的频率进行跟踪,可以保证输出功率维持稳定。仿真结果如图 5所示。
|
图 5 不同模式下输出功率随耦合系数的变化 Fig. 5 Variation of output power with coupling coefficient under different modes |
不同互感下,原谐振频率处系统输出功率在出现多个零相角点前是逐渐增加的,但耦合系数k>k1后原谐振点处的功率反而会由于耦合系数增大而减小,但其实在其他零相角点处依然保持较大的输出功率。
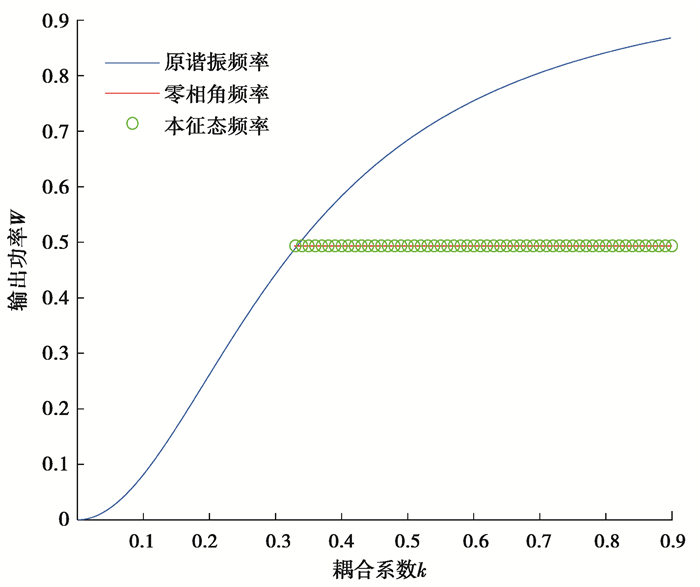
随着耦合系数增大如果系统工作在原谐振频率点处,效率会单调增加。但在过耦合情况下,多谐振点处的系统效率却维持一个定值,该定值的大小与原副边的阻抗有关。
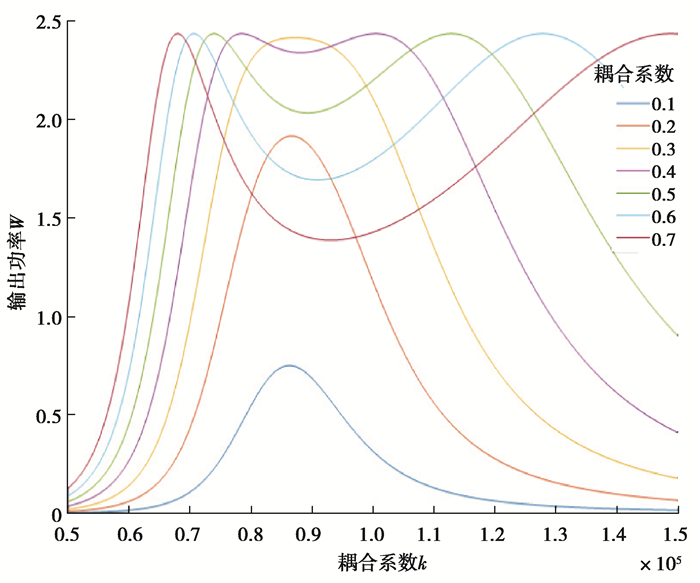
通过改变耦合系数k,观察在不同频率下系统的输出功率。可以看到在过边界点后最大输出功率不在原谐振点附近,出现明显的分裂。随着耦合系数的逐步增大,最大功率点向两边远离如图 6、图 7。
|
图 6 不同模式下效率随耦合系数的变化 Fig. 6 Variation of efficiency with coupling coefficient under different modes |
|
图 7 不同耦合系数下输出功率随工作频率变化 Fig. 7 Output power changes with operating frequency under different coupling coefficients |
基于实本征态理论和零相角点分析,得到SS结构磁耦合无线电能传输系统在过耦合情况下会分裂出多个零相角点。并且证实这2种方法所得到的计算结果的一致性。在过耦合区域通过跟踪非原谐振点的零相角频率,副边折射到原边的等效阻抗为恒定值,此时系统的输出功率也为恒定值,且在一定条件下可以解决频率分裂导致的输出功率急剧下降,保持输出功率在零相角点处为最大。从而实现系统保持恒功率和恒效率输出。
| [1] |
刘尚江, 沈艳霞. 磁耦合谐振式无线电能传输系统频率跟踪研究[J]. 电力电子技术, 2019, 53(2): 47-50. Liu S J, Shen Y X. Research on frequency tracking of magnetically coupled resonant wireless power transfer system[J]. Power Electronics Technology, 2019, 53(2): 47-50. (in Chinese) |
| [2] |
李阳, 张雅希, 杨庆新, 等. 磁耦合谐振式无线电能传输系统最大功率效率点分析与实验验证[J]. 电工技术学报, 2016, 31(2): 18-24. Li Y, Zhang Y X, Yang Q X, et al. Maximum power efficiency point analysis and experimental verification of magnetically coupled wireless power transfer system[J]. Journal of Electrical Technology, 2016, 31(2): 18-24. (in Chinese) DOI:10.3969/j.issn.1000-6753.2016.02.003 |
| [3] |
陈浩然. 磁耦合谐振式无线电能传输系统的最大功率跟踪[D]. 青岛: 青岛科技大学, 2019. Chen H R. Maximum power tracking of magnetically coupled resonant wireless power transfer system[D]. Qingdao: Qingdao University of Science and Technology, 2019. (in Chinese) |
| [4] |
邱毅. 无线电能传输系统的最大效率跟踪[D]. 青岛: 青岛科技大学, 2019. Qiu Y. Maximum efficiency tracking of wireless power transfer system[D]. Qingdao: Qingdao University of Science and Technology, 2019. (in Chinese) |
| [5] |
刘丽, 程本善, 杨凯宏, 等. 一种频率跟踪式无线电能传输装置设计[J]. 电子设计工程, 2017, 25(9): 132-136. Liu L, Cheng B S, Yang K H, et al. Design of a frequency tracking wireless power transfer device[J]. Electronic Design Engineering, 2017, 25(9): 132-136. (in Chinese) |
| [6] |
鲁扬. 抑制频率分裂的磁耦合无线能量传输系统研究[D]. 吉林: 东北电力大学, 2019. Lu Y. Research on magnetically coupled wireless power transfer system for suppressing frequency splitting[D]. Jilin: Northeast Electric Power University, 2019. (in Chinese) |
| [7] |
高伟康. WPT/MRC系统频率分裂抑制技术研究[D]. 新乡: 河南师范大学, 2017. Gao W K. Research on frequency splitting suppression technology of WPT/MRC system[D]. Xinxiang: Henan Normal University, 2017. (in Chinese) |
| [8] |
路倩云, 王文清, 翟志颖, 等. 三线圈无线输电系统的频率分裂特性和抑制方法[J]. 电气工程学报, 2018, 13(5): 27-32. Lu Q Y, Wang W Q, Zhai Z Y, et al. Frequency splitting characteristics and suppression methods of three-coil wireless power transfer system[J]. Journal of Electrical Engineering, 2018, 13(5): 27-32. (in Chinese) |
| [9] |
李中启, 黄守道, 易吉良, 李军军. 磁耦合谐振式无线电能传输系统频率分裂抑制方法[J]. 电力系统自动化, 2017, 41(2): 21-27. Li Z Q, Huang S D, Yi J L, et al. Frequency splitting suppression method for magnetically coupled resonant wireless power transfer system[J]. Power System Automation, 2017, 41(2): 21-27. (in Chinese) |
| [10] |
邱利莎. 磁耦合谐振式无线电能传输的阻抗匹配研究[D]. 长沙: 湖南大学, 2016. Qiu L S. Research on impedance matching of magnetically coupled resonant wireless power transfer system[D]. Changsha: Hunan University, 2016. (in Chinese) |
| [11] |
赵志友. 基于宇称时间对称的无线电能传输系统电路模型及分析[D]. 广州: 华南理工大学, 2018. Zhao Z Y. Circuit model and analysis of wireless power transfer system based on parity time symmetry[D]. Guangzhou: South China University of Technology, 2018. (in Chinese) |
| [12] |
Assawaworrarit S, Yu X, Fan S. Robust wireless power transfer using a nonlinear parity-time-symmetric circuit[J]. Nature, 2017, 546(7658): 387-390. DOI:10.1038/nature22404 |
| [13] |
Assawaworrarit S, Fan S. Robust and efficient wireless power transfer using a switch-mode implementation of a nonlinear parity-time symmetric circuit[J]. Nature Electronics, 2020(3): 273-279. |
| [14] |
Zeng C, Sun Y, Li G, et al. High-order parity-time symmetric model for stable three-coil wireless power transfer[J]. Physical Review Applied, 2020, 13(3). |
 2023, Vol. 46
2023, Vol. 46


