随着机器人和人类社会更加深入融合,机器人的种类和功能也越来越丰富。现阶段,传统刚性机器人执行器由刚性机械部件组成。因为其结构特性,容易建立动力学和运动学模型。文献[1]和[2]提出拟人化机械手,实现抓取功能。然而,这种刚性机械手在抓取物体时,不能调整变形来适应具有复杂几何形状的物体。鉴于传统机械手的局限性,人们从自然界中寻找灵感,模仿软体动物设计出了软体多自由度机器人,具有较高的自由度和灵活性。
国内外软体的研究成果较为丰富,根据软体驱动器发展可以分为以下类型:1)以介电弹性体(DEA)作为驱动器的研究,通过输入电压高低和频率控制驱动器,如,上海交通大学和麻省理工(MIT)研究的快速爬墙机器人[3]和浙江大学研究的DEA驱动的仿生鱼[4]等;2)以形状记忆材料(SMA、SMP)作为驱动,利用加热收缩的记忆效应特点,实现特定收缩变形,例如,首尔大学研究的软体抓手[5];3)以气压驱动的软体,利用气压使结构产生变形或者运动,从而实现驱动的一类软体机器人,如,纤维限制型软体驱动器[6]和多腔室气动网络驱动器[7-9],为了改善驱动器刚性不足的缺点,重庆大学和香港大学研究了变刚度软体驱动器[10-12],在多腔室的软体驱动器设计中,通过将腔室的横截面与驱动器轴向方向保持非垂直条件,实现驱动器的螺旋变形[13-15]。以上研究的变形方式中,驱动器末端轨迹只在直线或者二维平面上移动,驱动器灵活性不足;驱动器变形方式在结构设计时就已经确定,无法做到变形方式的动态调节。
综上所述,文中提出了一种低成本动态可控的新型螺旋扭转变形软体驱动器。利用拉线驱动产生变形,通过骨架层排列方向限制,实现对驱动器的螺旋扭转控制。建立了有效的运动学模型来展示驱动器空间位置姿态,将理论模型与实验数据进行比较,验证理论模型的有效性。
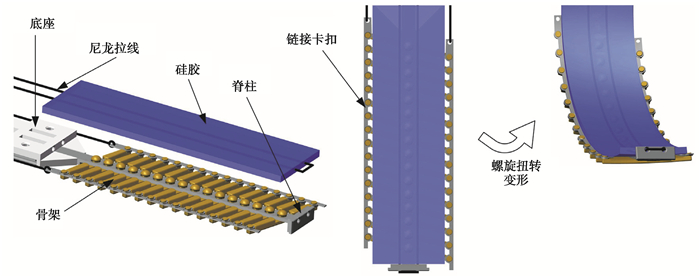
1 驱动器设计与建模 1.1 螺旋扭转变形驱动器设计与原理螺旋扭转变形软体驱动器由6部分构件组成,如图 1所示。驱动器部件分别有底座、硅胶、骨架、链接卡扣、TPU脊柱、尼龙拉线。每一个部件之间都紧密相连,构成一个紧凑的驱动器整体。底座用于固定驱动器和脊柱,并能够与其他通用夹具连接,拓展驱动器的应用场景;底座与硅胶粘在一起,在硅胶浇筑过程中,底座放置于模具之上,并在表面涂一层黏结剂(JUKAM 988强力接着剂),能让底座与硅胶连接紧密;脊柱与底座通过2颗螺钉连接,确保脊柱的稳固。硅胶作为驱动器的上表面——软体硅胶层,当驱动器与其他物体接触时,利用硅胶柔软特性,使得驱动器具有足够柔韧性,尤其是夹取易碎物体时,显得尤为重要。脊柱的作用是支撑和固定骨架,脊柱能够明显增大驱动器侧向刚度。骨架用于引导驱动器螺旋变形方向和角度。链接卡扣的作用是确保所有骨架方向一致,在弯曲时能够固定骨架的位置,确保骨架与脊柱之间的偏转角度不发生改变。通过外置驱动电机控制链接卡扣,带动所有骨架旋转改变骨架与脊柱的偏转角度,改变驱动器的扭转角度。尼龙拉线用于改变驱动器变形,通过拉线伸长量Δl来控制驱动器变形的情况。
|
图 1 螺旋变形软体驱动器设计结构 Fig. 1 Designing structure of the helix deformation soft actuator |
动态可控螺旋扭转变形软体驱动器划分为2层,第1层为硅胶柔性层,第2层骨架限制层。第1层由硅胶和尼龙拉线组成,刚度小,处于驱动器的上表面。第2层包括TPU脊柱、PLA骨架、链接卡扣。TPU材料和PLA材料刚度根据文献数据可以知道远大于硅胶刚度,所以骨架限制层在变形过程中会引导驱动器变形的方向和状态。其中,骨架的轴向方向总是与螺旋扭转驱动器的旋线径向方向垂直。
在初始状态时,尼龙拉线处于非张紧状态,驱动器硅胶两端不受作用力,保持平直初始状态。在驱动状态时,外部电机拉伸尼龙拉线,驱动器两端收到拉力影响。由于驱动器的中性层和拉力作用点的偏移距离为hc(hc≠0),长直梁结构的驱动器产生弯矩,使驱动器弯曲变形。同时,利用骨架限制层的导向作用,改变骨架与脊柱的偏转角度就能实现螺旋扭转变形的角度动态调节。
根据驱动器的设计和原理,提出一种适用于拉线驱动的螺旋扭转变形软体驱动器的运动学模型,通过拉线的伸缩量Δl和骨架偏转角φ来预测螺旋变形在全局坐标系下的末端坐标变化情况。
1.2 运动学建模对于弯曲变形和旋转的软体机器人,考虑驱动器是恒定曲率变形。参考Bernoulli-Euler横梁结构,在端点处施加恒定力矩,会产生一个恒定力矩结果。在大挠度平面连续介质机器人动力学与控制[16]中描述,根据驱动器设计结构推导出简化的运动学模型。在该模型中,驱动器受到施加的恒定力矩,产生近似常曲率变形。许多其他连续机器人也被验证近似为常曲率变形。
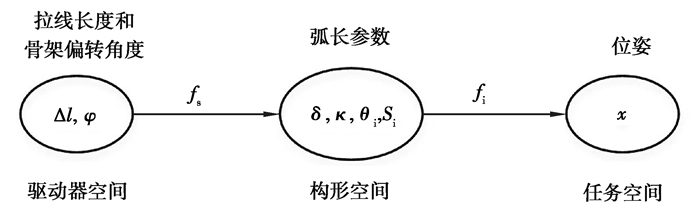
将螺旋变形驱动器的曲率近似为常量。利用几何关系提出了一种常曲率螺旋变形运动学模型预测和展示复杂螺旋扭转变形。在常曲率螺旋变形运动学模型中,将运动学模型分解为2个映射关系,如图 2所示。一方面,根据电机控制驱动绳和骨架,得到拉线的伸缩量Δl和骨架的偏转角度φ的2个已知量,通过基于几何关系的构造映射函数fs得到螺旋扭转变形下的驱动器的弧长参数等;另一方面,从驱动器螺旋变形的弧长参数通过弯曲旋转映射函数fi,得到驱动器末端的运动位姿和空间坐标。
|
图 2 常曲率螺旋变形运动学模型关系 Fig. 2 Dynamic relationship of the constant curvature helix deformation |
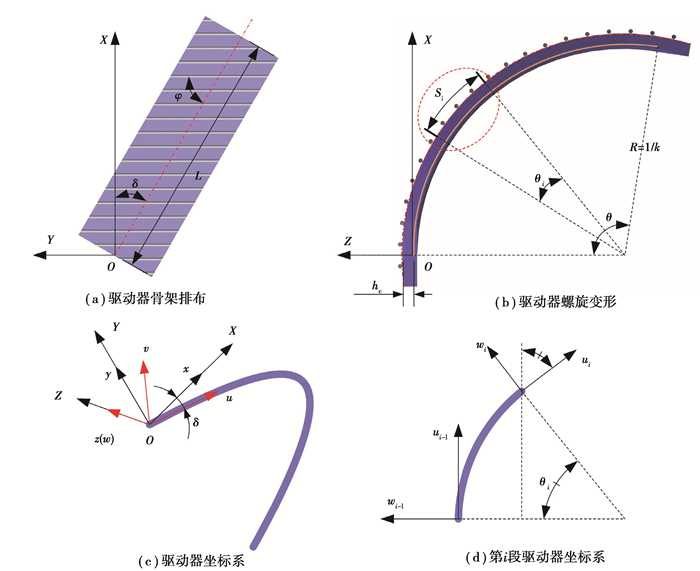
设定驱动器结构参数,如图 3所示。L为驱动器长度,Δl为拉线的伸缩量,φ骨架偏转角,κ为螺旋变形驱动器沿着中性层方向的曲率,θ为螺旋变形沿着驱动器方向的圆弧角,δ为驱动器螺旋升角。根据恒定曲率运动学建模方法[17],可以将螺旋扭转变形驱动器分为n(n≥1)段等长的圆弧,驱动器该段弧长为si,其中,si=sj(i, j∈(1, 2, …, n), i≠j)。根据几何关系可以得到驱动器长度L与弧si关系满足公式(1):
| $ L=\sum\limits_{i=1}^n s_i 。$ | (1) |
|
图 3 螺旋变形驱动器结构变形示意图 Fig. 3 Schematic diagram of helical deformed actuator structure |
同时,分段的驱动器圆弧角为θi,满足关系式θi=κ·si。为了简化模型,在推导运动学模型之前,做出如下设想:
1) 骨架偏转角φ和螺旋升角δ互余;
2) 螺旋变形驱动器是常曲率变形驱动器,各个部件之间紧密连接;
3) 将驱动器截取的弧长si认为是圆弧,扭转过程分为弯曲和旋转运动[18]。
螺旋扭转变形驱动器在变形过程中,链接卡扣可以固定所有骨架不发生偏转,骨架与脊柱的偏转角度一直不变。脊柱与骨架通过铰链连接,可以固定骨架位置不发生偏移。如图 3(a)(b)所示,脊柱与骨架的偏转角度φ与螺旋升角δ满足公式(2):
| $ \varphi+\delta=\frac{\pi}{2} \text { 。} $ | (2) |
为了方便建立运动学模型和进行数学运算,首先,建立一个全局坐标系{G},方向为X、Y、Z,原点位于驱动器底端端面的尼龙拉线处。在驱动器初始状态时,X轴方向指向驱动器轴向方向;Z轴方向为驱动器厚度方向,从硅胶层指向骨架限制层方向。在全局坐标原点处建立局部坐标系{A},在变形过程中原点O处局部坐标系方向x、y、z与全局坐标系方向重合,如图 3(c)所示。同时,在O处建立Frenet-SerretF-S相对坐标系{B},方向为u、v、w[19]。在Frenet-SerretF-S相对坐标系中,u方向为螺旋线的切线方向,v方向是螺旋线的副法线方向,w是螺旋线的主法线方向。w轴与局部坐标系z轴重合,其中u轴方向为局部坐标系x轴绕着z轴旋转角度-δ得到,如图 3(c)所示。
在变形过程中,螺旋变形驱动器的中性层长度为常值L,不发生变化;驱动器硅胶柔性层收缩,收缩变形程度由拉线伸缩量Δl决定。因此,驱动器产生螺旋扭转变形,中性层上圆弧曲率为κ。根据弧长公式和驱动器的几何关系可以知道,分为n段的驱动器每一段圆弧的圆弧角θi为
| $ \theta_i=\frac{L}{n} \cdot \kappa 。$ | (3) |
在驱动器变形过程中,拉线收缩引起驱动器变形。拉线与驱动器中性层的偏移距离为hc。在整个螺旋扭转变形过程中,根据拉线截面处的曲率和弧度角之间的几何关系,得到公式(4):
| $ \left(\frac{1}{\kappa}-h_{\mathrm{c}}\right) \cdot \theta_i=\frac{L-\Delta l}{n}, $ | (4) |
联合公式(3)和(4),推导出公式(5):
| $ \frac{L}{L-\Delta l}=\frac{1}{1-\kappa h_{\mathrm{c}}}, $ | (5) |
简化公式(5),得到螺旋形变的曲率κ和拉线伸缩量Δl的关系表达式
| $ \kappa=\frac{1}{L \cdot h_{\mathrm{c}}} \cdot \Delta l {\text {。}} $ | (6) |
在公式(6)中,驱动器长度L和拉线与中性层偏移距离hc都是常量。根据公式(3)的结论,联合曲率表达式(6),可以求解出驱动器第i段的弧度角θi的公式为
| $ \theta_i=\frac{1}{n \cdot h_{\mathrm{c}}} \cdot \Delta l 。$ | (7) |
观察曲率公式(6)和弧度角公式(7),发现2个变量都跟拉线伸缩量Δl为一阶线性关系。根据图 2所示模型,得到函数fs从参数(Δl, φ)到变量(δ, κ, θi, si)之间的映射关系。再根据驱动器的几何关系得到fi映射函数和驱动器的变换矩阵。
对于无扭转连续软体驱动器[20-21],通常用弯曲曲率、弯曲方向角和弧长定义的旋转和平移矩阵来描述各驱动段的变换方式。对于螺旋扭转连续软体驱动器,与局部坐标系{A}相关的相对坐标系{B}沿螺旋驱动器的厚度方向(z轴)旋转得到,如图 3(c)所示。考虑到在第i节驱动器局部坐标系的弯曲变形,如图 3(d)所示,将第i节驱动器弯曲变换矩阵Bi定义为2个独立的弯曲变换和位移变换。需要注意的是,弯曲方向的变化与扭转变形是不同的。对于具有弯曲和旋转变形的柔性驱动器结构,第i节驱动器相对坐标系i-1到第i节连杆的坐标系i映射需要2个独立的旋转和位移变形,外加1个扭转角参数δ来描述扭转。此外,由于弯曲变形和扭转变形的耦合,将扭转变形驱动器分节越多,建立的模型精度越高。
连续型软体驱动器的几何参数提供了一种定义其姿态的方法。在图 3(d)中,根据几何参数和全局坐标系下旋转偏移得到第si段末端处的位姿矩阵GTi,其中,驱动器在第si-1段末端处的位姿矩阵为GTi-1,满足公式(8):
| $ \begin{gathered} { }^{\boldsymbol{G}} \boldsymbol{T}_i={ }^{\boldsymbol{G}} \boldsymbol{T}_{i-1} B_i={ }^{\boldsymbol{G}} \boldsymbol{T}_{i-2}\left(B_{i-1} B_i\right)=\cdots={ }^{\boldsymbol{G}} \boldsymbol{T}_1\left(\prod\limits_{j=2}^i B_j\right) \\ ={ }^{\boldsymbol{G}} \boldsymbol{T}_{\boldsymbol{A}}\left(\prod\limits_{j=1}^i B_j\right) M, \end{gathered} $ | (8) |
其中,i=1, 2, …, n,GTA=I4×4。Bi是描述驱动器从第si-1段的末端坐标位姿变换到第si段的末端坐标位姿的变换过程。通过在相对坐标系{B}前i节驱动器的叠加变换,可以知道无扭转驱动器的最终坐标位姿矩阵和空间位置。所以,第i节驱动器弯曲变换矩阵Bi表示为
| $ \boldsymbol{B}_i=\operatorname{Rot}_{\mathrm{v}}\left(\theta_i\right) \cdot \operatorname{Trans}(p)=\left[\begin{array}{cc} R_{\mathrm{v}}\left(\theta_i\right) & 0 \\ 0 & 1 \end{array}\right]\left[\begin{array}{cc} I_{3 \times 3} & p \\ 0 & 1 \end{array}\right], $ | (9) |
式中,i=1, 2, …, n,Rotv(θi)为坐标系{i-1}绕着v轴旋转弧度角θi的旋转变换,Trans(p)为坐标系位移变换,位置变化向量为p=[(sinθi)/κ-sinδ·(1-cosθi)/κ-cosδ·(1-cosθi/κ]T。对于螺旋扭转驱动器,最终弯曲变换矩阵Bi由2个变换矩阵乘积得到。弯曲变换矩阵公式为
| $ \boldsymbol{B}_i=\left[\begin{array}{cccc} \cos \theta_i & 0 & \sin \theta_i & \sin \theta_i / \kappa \\ 0 & 1 & 0 & -\sin \delta\left(1-\cos \theta_i\right) / \kappa \\ -\sin \theta_i & 0 & \cos \theta_i & -\cos \delta\left(1-\cos \theta_{)_i} / \kappa\right. \\ 0 & 0 & 0 & 1 \end{array}\right], $ | (10) |
式中,i=1, 2, …, n。将驱动器均匀分为n(n≥1)段,每段的弯曲变换矩阵Bi都是相同的,Bi=Bji, j∈{1, 2, …, n}。对于螺旋扭转驱动器,在变形过程中螺旋升角δ始终保持恒定,变换矩阵T1需要分解为扭转变换矩阵M和弯曲变换矩阵B1的乘积。如图 3(c)所示,在螺旋扭转变形时,根据示意图坐标系旋转方向,得到扭转变换矩阵公式为
| $ \boldsymbol{M}=\operatorname{Rot}_z(-\delta)=\left[\begin{array}{cccc} \cos \delta & \sin \delta & 0 & 0 \\ -\sin \delta & \cos \delta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]。$ | (11) |
联合公式(8)~(11),在局部坐标系下的变换矩阵为
| $ { }^{\boldsymbol{G}} \boldsymbol{T}_{\boldsymbol{n}}=\boldsymbol{B}_i{ }^n \boldsymbol{M}=\left[\begin{array}{cccc} \mathrm{c} \theta_i & 0 & \mathrm{~s} \theta_i & \mathrm{~s} \theta_i / \kappa \\ 0 & 1 & 0 & -\mathrm{s} \delta\left(1-\mathrm{c} \theta_{\mathrm{i}}\right) / \kappa \\ -s \theta_{\mathrm{i}} & 0 & c \theta_{\mathrm{i}} & -c \delta\left(1-c \theta_{\mathrm{i}}\right) / \kappa \\ 0 & 0 & 0 & 1 \end{array}\right]^{\mathrm{n}}\left[\begin{array}{cccc} c \delta & s \delta & 0 & 0 \\ -s \delta & c \delta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right], $ | (12) |
式中:cθi=cosθi, sθi=sinθi, cδ=cosδ, sδ=sinδ。
由于螺旋变形软体驱动器为非对称驱动,驱动器产生螺旋扭转变形。根据上述模型特点,发现当n值越大,驱动器划分的节段越多,建立的模型越精确。
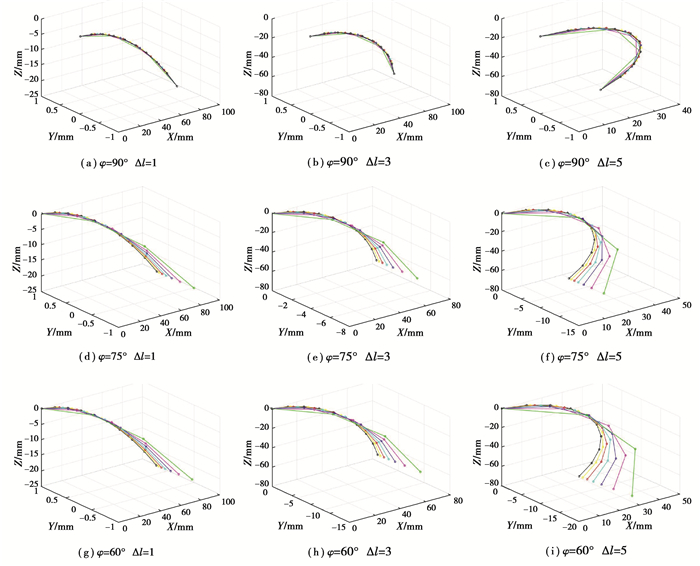
2 实验采用MATLAB软件仿真分析,通过实验进行理论模型的数据对比,验证所提出的螺旋扭转变形驱动器运动学模型的有效性,同时优化模型参数。在运动学模型中,将驱动器划分为n段,将每一节当作连杆来近似驱动器的螺旋扭转运动。采用MATLAB软件进行仿真,在空间绘制出驱动器的形变状态,如图 4所示。其中,每根线代表驱动器在骨架偏转角φ和拉线伸缩量Δl的情况下的形变情况。在每幅子图中,将驱动器分为不同数目的节段,用不同颜色的实线表示,其中,n=3, 4, …, 8。
|
图 4 不同分段数的螺旋驱动器仿真 Fig. 4 Simulation of helical actuator with different number of segments |
在图 4中,可以发现,当骨架偏转角度φ=90°时,拉线伸缩量增大过程中,驱动器的分段数n对运动学模型影响最小。骨架偏转角度φ=90°时,驱动器属于无扭转弯曲变形,只在二维平面内弯曲,不用考虑扭转对运动学模型影响,在该情况下驱动器的模型精度不会受到分节数n的影响。当骨架偏转角度φ≠90°时,需要考虑螺旋扭转条件下的驱动器变形。在所建立模型中,当骨架偏转角度恒定时,随着拉线伸缩量Δl的不断增大,相同分段数n条件下驱动器空间变形误差越大;在相同拉线伸缩量Δl和相同分节数n情况下,当骨架偏转角度减小时,驱动器仿真的偏差也会增大;当拉线伸缩量和骨架偏转角都恒定的情况下,分节数n越大,仿真驱动器的直线越趋近于一条螺旋线,模型精度越高。在建模过程中,只是将驱动器进行一次扭转坐标变换,在对驱动器分段的时候,如果分段数越多,驱动器越近似为一段常曲率的圆弧,在扭转变形时,能够近似表示出空间的螺旋线状态。如果n越小,驱动器更类似于长连杆,无法近似为空间螺旋扭转变形。因此,分节数n越大,模型越精确。模型计算过程中,坐标变换矩阵与n呈指数关系,n越大,坐标变换矩阵计算难度越大。
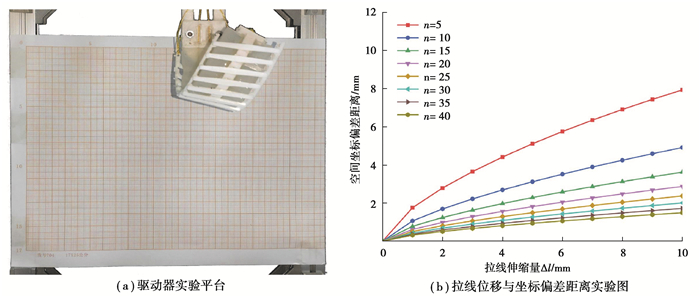
图 5为驱动器手指的螺旋扭转弯曲变形实验。实验和模型验证时,驱动器骨架偏转角φ为75°,图 5(a)为驱动器试验平台,从不同角度观测驱动器变形,利用坐标纸标记驱动器在空间的位置。得到实际螺旋扭转驱动器变形的坐标和模型求解的驱动器空间位置坐标比较,对实验模型进行验证。图 5(b)为驱动器理论模型坐标与实验所测得坐标在空间中的距离偏差。通过尼龙拉线伸缩量Δl的变化,观察驱动器不同分段数n的条件下理论模型与实验数据的距离偏差。分段数n越大,理论运动学模型的精度越高。驱动器长度L=100,在Δl=0时,驱动器处于初始状态,认为螺旋扭转运动学模型的精度为100%。可以发现,距离偏差变化随着拉线伸缩量Δl增加,曲线斜率越来越小。在驱动器长度L=100,Δl=10,n≥30时,模型精度达到98%以上。在实验中,拉线长度参数保证Δl≤10,将模型中驱动器分段数设置为n=30,能够确保计算复杂程度不高,同时使得模型精度在可接受的范围以内。
|
图 5 驱动器弯曲变形试验 Fig. 5 Helical deformation experiment of actuator |
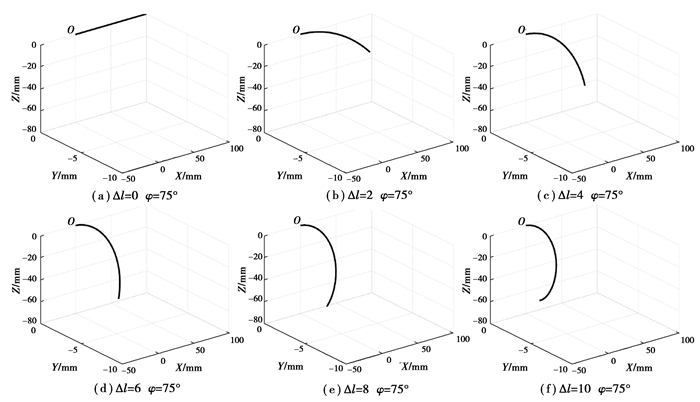
如图 6所示,通过拉伸尼龙拉线观察螺旋扭转驱动器的变形情况。驱动器分段数n对驱动器运动学建模具有较大影响。为了优化模型,节约计算资源,实验仿真驱动器的分段数n设置为30。仿真实验的骨架偏转角φ=75°。在图 6中,可以发现,随着Δl增大,驱动器的形变越明显。同时,在Y轴方向上,驱动器螺旋扭转变形沿着负方向。随着Δl增大,驱动器末端位置在Y轴方向减小。在XOZ平面上,驱动器在变形过程中弯曲半径逐渐减小。Δl与驱动器弯曲半径呈反比关系。
|
图 6 螺旋扭转驱动器变形仿真图 Fig. 6 Deformation simulation of helical actuator |
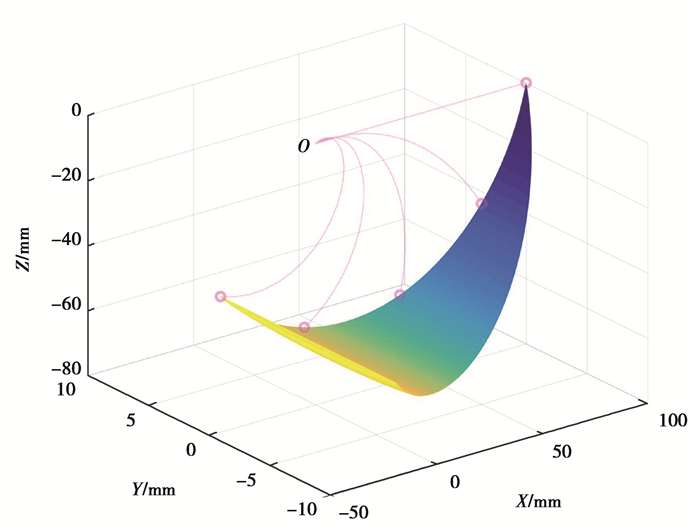
图 7中描述了螺旋扭转驱动器的工作空间,驱动器参数设置为:骨架偏转角φ∈[30°, 150°],Δl∈[0, 10],拉线伸缩量单位为mm。驱动器底端原点O在坐标系点(0, 0, 0)处,驱动器末端的运动空间为图中的曲面。当驱动器的变形越大,曲面颜色越深。驱动器末端的运动空间呈扇形分布。当驱动器处于初始状态时,驱动器受到骨架偏转角度影响较小,曲面面积小;当驱动器拉线伸缩量增大时,驱动器骨架的偏转角度对螺旋扭转变形影响越显著,驱动器末端运动空间越大。
|
图 7 螺旋扭转驱动器末端坐标空间 Fig. 7 Coordinate space of helical actuator end |
为了提高驱动器变形灵活性和达到变形动态可调节目的,提出了一种基于拉线驱动动态可调螺旋扭转变形驱动器的新设计。驱动拉线和骨架的球关节嵌入在硅胶层中,使用3D打印和模具浇筑方法制作。同时,针对该驱动器变形机理,提出了一种适用于拉线手指的螺旋扭转变形运动学模型,模型根据拉线伸缩量的大小、骨架偏转角度来预测螺旋变形时驱动器末端在空间的坐标位置和姿态。最后,通过MTLAB仿真和实验结果对比分析,验证了该驱动器的运动学模型合理性和有效性。基于所提出驱动器设计和理论模型,得出以下结论:
1) 驱动器在变形过程中,骨架与脊柱之间的偏转角度可以顺畅调节,产生理想的空间螺旋变形结果,驱动器的工作稳定性和精度良好,变形曲率均匀。
2) 提出的驱动器运动学模型中,驱动器分段数n大小会影响模型精度。仿真中分段数n设置为30,模型数据与实验测量偏差较小,可以很好预测驱动器在驱动过程中的螺旋变形情况。
3) 在基于拉线驱动动态可调螺旋扭转变形驱动器中,许多参数可能会影响它的性能,包括硅胶层厚度与材料、拉线与驱动器中性层偏移距离、TPU脊柱厚度、骨架间隔距离、TPU卡片的厚度等。在未来的工作中,可以进一步优化理论模型,考虑驱动器变形过程中硅胶和骨架的微小变形量等,让模型更加精确地预测驱动器变形。
4) 思考驱动器的应用方向和环境,提出更加具体的应用方案。
| [1] |
Butterfass J, Grebenstein M, Liu H, et al. DLR-Hand Ⅱ: next generation of a dextrous robot hand[C]//Proceedings 2001 ICRA. IEEE International Conference on Robotics and Automation, May 21-26, 2001, Seoul, Korea (South). IEEE, 2006: 109-114.
|
| [2] |
Kawasaki H, Komatsu T, Uchiyama K. Dexterous anthropomorphic robot hand with distributed tactile sensor: Gifu hand Ⅱ[J]. IEEE/ASME Transactions on Mechatronics, 2002, 7(3): 296-303. DOI:10.1109/TMECH.2002.802720 |
| [3] |
Gu G Y, Zou J, Zhao R K, et al. Soft wall-climbing robots[J]. Science Robotics, 2018, 3(25): eaat2874. DOI:10.1126/scirobotics.aat2874 |
| [4] |
Li T F, Li G R, Liang Y M, et al. Fast-moving soft electronic fish[J]. Science Advances, 2017, 3(4): e1602045. DOI:10.1126/sciadv.1602045 |
| [5] |
Rodrigue H, Wang W, Kim D R, et al. Curved shape memory alloy-based soft actuators and application to soft gripper[J]. Composite Structures, 2017, 176: 398-406. DOI:10.1016/j.compstruct.2017.05.056 |
| [6] |
Polygerinos P, Wang Z, Overvelde J T B, et al. Modeling of soft fiber-reinforced bending actuators[J]. IEEE Transactions on Robotics, 2015, 31(3): 778-789. DOI:10.1109/TRO.2015.2428504 |
| [7] |
Fei Y Q, Wang J B, Pang W. A novel fabric-based versatile and stiffness-tunable soft gripper integrating soft pneumatic fingers and wrist[J]. Soft Robotics, 2019, 6(1): 1-20. DOI:10.1089/soro.2018.0015 |
| [8] |
Mosadegh B, Polygerinos P, Keplinger C, et al. Pneumatic networks for soft robotics that actuate rapidly[J]. Advanced Functional Materials, 2014, 24(15): 2163-2170. DOI:10.1002/adfm.201303288 |
| [9] |
Xu Q P, Liu J Y. Effective enhanced model for a large deformable soft pneumatic actuator[J]. Acta Mechanica Sinica, 2020, 36(1): 245-255. DOI:10.1007/s10409-019-00903-9 |
| [10] |
Li Y Q, Chen Y H, Ren T, et al. Passive and active particle damping in soft robotic actuators[C]//2018 IEEE International Conference on Robotics and Automation (ICRA), May 21-25, 2018, Brisbane, QLD, Australia. IEEE, 2018: 1547-1552.
|
| [11] |
Jiang P, Yang Y D, Chen M Z Q, et al. A variable stiffness gripper based on differential drive particle jamming[J]. Bioinspiration & Biomimetics, 2019, 14(3): 036009. |
| [12] |
Li Y T, Chen Y H, Yang Y, et al. Passive particle jamming and its stiffening of soft robotic grippers[J]. IEEE Transactions on Robotics, 2017, 33(2): 446-455. DOI:10.1109/TRO.2016.2636899 |
| [13] |
Chandler J H, Chauhan M, Garbin N, et al. Parallel helix actuators for soft robotic applications[J]. Frontiers in Robotics and AI, 2020, 7: 119. DOI:10.3389/frobt.2020.00119 |
| [14] |
Ge L S, Wang T Y, Zhang N B, et al. Fabrication of soft pneumatic network actuators with oblique chambers[J]. Journal of Visualized Experiments: JoVE, 2018(138): 58277. |
| [15] |
Realmuto J, Sanger T. A robotic forearm orthosis using soft fabric-based helical actuators[C]//2019 2nd IEEE International Conference on Soft Robotics (RoboSoft), April 14-18, 2019, Seoul, Korea (South). IEEE, 2019: 591-596.
|
| [16] |
Gravagne I A, Rahn C D, Walker I D. Large deflection dynamics and control for planar continuum robots[J]. IEEE/ASME Transactions on Mechatronics, 2003, 8(2): 299-307. DOI:10.1109/TMECH.2003.812829 |
| [17] |
Simaan N, Xu K, Kapoor A, et al. Design and integration of a telerobotic system for minimally invasive surgery of the throat[J]. The International Journal of Robotics Research, 2009, 28(9): 1134-1153. DOI:10.1177/0278364908104278 |
| [18] |
Guan Q H, Sun J, Liu Y J, et al. Novel bending and helical extensile/contractile pneumatic artificial muscles inspired by elephant trunk[J]. Soft Robotics, 2020, 7(5): 597-614. DOI:10.1089/soro.2019.0079 |
| [19] |
Webster R J, Jones B A. Design and kinematic modeling of constant curvature continuum robots: a review[J]. International Journal of Robotics Research, 2010, 29(13): 1661-1683. DOI:10.1177/0278364910368147 |
| [20] |
Hannan M W, Walker I D. Kinematics and the implementation of an elephant's trunk manipulator and other continuum style robots[J]. Journal of Robotic Systems, 2003, 20(2): 45-63. DOI:10.1002/rob.10070 |
| [21] |
Neppalli S, Jones B A. Design, construction, and analysis of a continuum robot[C]//2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, October 29 - November 2, 2007, San Diego, CA, USA. IEEE, 2007: 1503-1507.
|
 2023, Vol. 46
2023, Vol. 46


