随着全球化石燃料日渐枯竭和污染排放问题日益严重,世界各国都将全面推行电动汽车排上日程[1]。然而,电动汽车充电过程缓慢且对电网负荷影响较大,阻碍了电动汽车大面积推广应用[2-3]。为提高液压驱动移动机器人的能量利用效率,对液压关节进行优化设计,提出了一摆盘式液压关节,提高了液压系统的能量利用效率。Vladimir等[4]提出了一种以最小能耗和最小质量为目标,通过遗传算法优化各机械臂杆长的节能方法。Yu等[5]提出一种基于弹性弯曲梁和驱动重物旋转的跳跃机器人,建立能够描述机器人基本运动原理的最小能耗模型,通过优化重物质量和弹性弯曲梁的结构参数,使机器人在跳跃过程中能耗最低。Seok等[6]介绍了高效腿式机器人的设计原理,分析了3种主要能量损失机制,通过采用高转矩密度电机,降低机械传输阻抗和机械腿的转动惯量,可以最大限度地减少损耗。
另一部分学者从优化控制参数方面,对提高机器人能量利用率展开了研究。Norsahperi等[7]提出了一种改进的最优积分滑模控制方法,通过仿真验证了该方法能够在保证机器人性能的情况下,显著降低机器人的抖振和能耗。Koivumki等[8]提出一种高能效、高精度的非线性液压机器人闭环控制器,为系统执行器设计了一种基于子系统动力学的模块化控制器,实验证明与采用传统运动跟踪控制器相比能够显著降低能耗。Zhang等[9]提出了一种基于数据驱动的能耗优化方法,利用遗传算法对可调参数进行优化,使机器人能耗最小化。Meike等[10]提出了一种以最小机器人空载时间和电机制动时间为优化目标的能耗优化方法,对机器人空载运动轨迹和电机制动控制程序进行修改来降低能耗。
综上所述,不难看出结构参数和控制参数对机器人能耗均有影响,但现有研究都是对结构参数和控制参数单独进行设计优化。单独结构参数优化时,在机器人结构尺寸确定后,并没有对同样会影响机器人能耗的控制参数进行优化。单独控制参数优化时,提高了机器人能效,但并不能保证原有的结构使机器人能量效率达到最高。由此可见,为使换电机器人举升系统节能设计达到最优,应将结构与控制参数集成优化。因此,笔者以换电机器人举升过程能耗和控制精度为优化目标,建立了换电机器人举升系统结构参数与控制参数的集成优化模型,并通过样机实验验证了优化结果的可靠性。
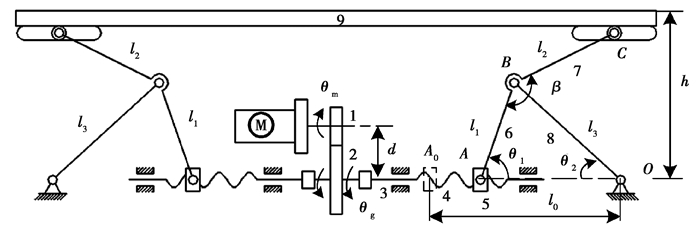
1 结构设计及参数初步匹配 1.1 举升系统结构设计换电机器人举升系统如图 1所示,由交流伺服电机、减速齿轮、丝杠螺母机构、摇杆滑块机构及电池托盘组成。举升过程如下,交流伺服电机通过1对齿轮(1,2)和联轴器3带动丝杠4旋转,进而驱动滑块5沿导轨作直线运动,滑块带动连杆(6,7,8)作平面运动,连杆7末端限制在电池托盘9的水平槽孔内,连杆7末端的竖直分运动完成电池托盘的举升。图 1以A0为原点,A0-O为x轴正方向,垂直于A0-O向上为y轴正方向建立坐标系。
|
注:1.齿轮1 2.齿轮2 3.联轴器 4.丝杠 5.滑块 6.连杆 7.连杆 8.摇杆 9.电池托盘 图 1 换电机器人举升系统结构简图 Fig. 1 Structure diagram of the lifting system of the battery swapping robot |
换电机器人举升系统需要符合电动汽车换电模式需求,部分设计参数如表 1所示。
| 表 1 换电机器人举升系统设计参数 Table 1 Design parameters of the battery swap robot lifting system |
换电机器人举升系统需要举升的电池包质量为80 kg,选用一款400 W~24 V的永磁交流伺服电机。根据举升时间、电机转速、负载质量,选用公称直径12 mm,导程10 mm的丝杠,齿轮减速比定为1.2∶1.0。根据设计举升高度h≥220 mm,连杆l1,l2,l3尺寸分别定为110、180、130 mm。综上所述,换电机器人举升系统参数初步匹配结果如表 2所示。
| 表 2 举升系统初步匹配参数 Table 2 Preliminary matching parameters of the lifting system |
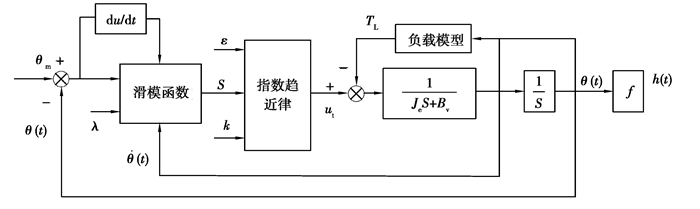
伺服控制系统直接影响换电机器人举升系统的动态特性、举升精度和响应性能。笔者设计了一种伺服控制系统位置滑模控制器如图 2所示,输入为期望角位移与实际角位移之差,控制电池托盘向着消除偏差的方向运动,保障系统的动态性能和跟踪精度。伺服系统中滑模控制器的参数对控制性能有着重要影响,如果控制器参数改变,伺服系统的响应特性和跟踪精度会随之改变,影响到换电机器人举升系统的能耗。
|
图 2 举升系统角位移控制结构框图 Fig. 2 Block diagram of the angular displacement control structure of the lifting system |
不考虑电机、丝杠、滑块、连杆等机械部件的弹性变形,举升系统的状态方程为
| $ J_{\mathrm{e}} \ddot{\theta}_{\mathrm{m}}(t)+B_{\mathrm{v}} \dot{\theta}_{\mathrm{m}}(t)=u(t)-T_{\mathrm{L}} \text {, } $ | (1) |
式中:Je为举升系统各部分等效到电机轴的转动惯量;Bv为等效阻尼系数;
系统在转动惯量等效前后的总动能相等,因此,
| $ J_{\mathrm{e}}=\sum m_i\left(\frac{v_i}{\omega_{\mathrm{e}}}\right)^2+\sum J_j\left(\frac{\omega_j}{\omega_{\mathrm{e}}}\right)^2, $ | (2) |
式中:i=5,9;j=1,2,3,4,6,7,8;vi为移动部件的速度;ωj为转动部件的角速度;ωe为电机的输出转速;Ji为举升系统各部件的转动惯量;具体参数如表 3所示。
| 表 3 举升机构中各组成部分的质量、质心参数、转动惯量 Table 3 Parameters of each component in the lifting mechanism |
该举升系统为单自由度系统,定义伺服电机输出角位移θm和负载扭矩TL为系统中的广义坐标和广义力,忽略摩擦损耗,根据拉格朗日方程建立不含电机部分的动力学方程为
| $ \frac{\mathrm{d}}{\mathrm{d} t}\left(\frac{\partial(T-V)}{\partial \dot{\theta}_{\mathrm{m}}}\right)-\frac{\partial(T-V)}{\partial \theta_{\mathrm{m}}}=T_{\mathrm{L}}, $ | (3) |
式中:T为系统动能;V为势函数。
图 2中齿轮1、齿轮2、联轴器、丝杠和滑块均只有动能做功,系统中动能T为
| $ T=\sum\limits_{i=1}^9 \frac{1}{2}\left[m_i v_i^2+J_i\left(\dot{\theta}_i\right)^2\right]+\sum\limits_{i=3}^9 \frac{1}{2}\left[m_i v_i^2+J_i\left(\dot{\theta}_i\right)^2\right] 。$ | (4) |
以O点为重力势零势位,系统中势函数V为
| $ V=\sum\limits_{i=6}^9 m_i g y_i。$ | (5) |
分析可得,负载力矩TL为
| $ \begin{gathered} T_L=\frac{\mathrm{d}}{\mathrm{d} t}\left(\frac{\partial(T-V)}{\partial \dot{\theta}_{\mathrm{m}}}\right)-\frac{\partial(T-V)}{\partial \theta_{\mathrm{m}}}= \\ \sum\limits_{i=3}^9 \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial}{\partial \dot{\theta}_{\mathrm{m}}} 2\left(\frac{1}{2} m_i v_i^2+\frac{1}{2} J_i\left(\dot{\theta}_i\right)^2-m_i g y_i\right)-\sum\limits_{i=3}^9 \frac{\partial}{\partial \theta_{\mathrm{m}}} 2\left(\frac{1}{2} m_i v_i^2+\frac{1}{2} J_i\left(\dot{\theta}_i\right)^2-m_i g y_i\right)+ \\ \sum\limits_{i=1}^2 \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial}{\partial \dot{\theta}_{\mathrm{m}}}\left(\frac{1}{2} m_i v_i^2+\frac{1}{2} J_i\left(\dot{\theta}_i\right)^2\right)-\sum\limits_{i=1}^2 \frac{\partial}{\partial \theta_{\mathrm{m}}}\left(\frac{1}{2} m_i v_i^2+\frac{1}{2} J_i\left(\dot{\theta}_i\right)^2\right), \end{gathered} $ | (6) |
式中:mi,vi,Ji,yi分别为举升系统各组成部分的质量、质心速度、转动惯量、质心y坐标;其表达式如表 3所示。
表中:b1和b2为齿轮1、2的齿宽;mn为齿轮1、2的模数;ds为丝杠直径;ρ为各部件的密度;l为各部件的长度;s为各部件的横截面积,且s1=s2=s3=300 mm2。根据加工经验,β取120°。ABC段连杆的参数由AB段、BC段连杆计算得出,其质量、质心坐标、质心速度、转动惯量分别计算如下:
| $ m_{67}=\rho_3 l_1 s_1+\rho_3 l_2 s_2, $ | (7) |
| $ x_{67}=\frac{x_6 m_6+x_7 m_7}{m_6+m_7}=\frac{\left(x_5+\frac{1}{2} l_1 \cos \theta_1\right) \rho_3 l_1 s_1+\left(x_5+l_1 \cos \theta_1+\frac{1}{2} l_2 \cos \left(\beta+\theta_1-\pi\right)\right) \rho_3 l_2 s_2}{\rho_3 l_1 s_1+\rho_3 l_2 s_2}, $ | (8) |
| $ y_{67}=\frac{y_6 m_6+y_7 m_7}{m_6+m_7}=\frac{\left(\frac{l_1 \sin \theta_1}{2}\right) \rho_3 l_1 s_1+\left(l_1 \sin \theta_1+\frac{l_2 \sin \left(\beta+\theta_1-\pi\right)}{2}\right) \rho_3 l_2 s_2}{\rho_3 l_1 s_1+\rho_3 l_2 s_2}, $ | (9) |
| $ v_{67}=\sqrt{\dot{x}_6^2+\dot{y}_6^2+\dot{x}_7^2+\dot{y}_7^2+2 \sqrt{\dot{x}_6^2+\dot{y}_6^2} \sqrt{\dot{x}_7^2+\dot{y}_7^2} \cos (\pi-\beta)}, $ | (10) |
| $ J_{67}=\frac{m_6 l_1^2}{12}+m_6\left(\sqrt{\left(x_{67}-x_6\right)^2+\left(y_{67}-y_6\right)^2}\right)^2+\frac{m_7 l_2^2}{12}+m_7\left(\sqrt{\left(x_{67}-x_7\right)^2+\left(y_{67}-y_7\right)^2}\right)^2 。$ | (11) |
通过式(1)可得到伺服电机轴的角加速度:
| $ \ddot{\theta}_{\mathrm{m}}(t)=\frac{1}{J_{\mathrm{e}}}\left(u(t)-B_{\mathrm{v}} \dot{\theta}_{\mathrm{m}}(t)-T_L\right)。$ | (12) |
根据系统结构分析,取目标值和实际反馈值的偏差量为控制变量[11],定义举升系统的位置跟踪误差及其导数为
| $ \left\{\begin{array}{l} e=\theta_{\mathrm{r}}(t)-\theta_{\mathrm{m}}(t), \\ \dot{e}=\dot{\theta}_{\mathrm{r}}(t)-\dot{\theta}_{\mathrm{m}}(t) 。\end{array}\right. $ | (13) |
式中:θr为交流伺服电机期望角位移;θm为交流伺服电机实际角位移。
线性滑模面对系统稳定性强,定义滑模变结构中滑模面[12]为
| $ S(t)=\lambda e+\dot{e}, $ | (14) |
式中:λ为控制参数。
对式(14)进行求导,得到其和指数趋近律之间的关联关系为
| $ \dot{S}(t)=\lambda \dot{e}+\ddot{e}=-\lambda \dot{\theta}_{\mathrm{m}}(t)-\ddot{\theta}_{\mathrm{m}}(t)=-\lambda \dot{\theta}_{\mathrm{m}}(t)-\left(u(t)-B_{\mathrm{v}} \dot{\theta}_{\mathrm{m}}(t)-T_{\mathrm{L}}\right) /J_{\mathrm{e}} \text { 。} $ | (15) |
采用指数趋近律进行滑模控制器的设计,其表达式为
| $ \dot{S}(t)=-\varepsilon \operatorname{sgn}(S(t))-k S(t), $ | (16) |
式中:ε和k均为控制参数。
结合式(15)和式(16),得到滑模控制器的控制律表达式为
| $ u(t)=J_{\mathrm{e}}\left(\varepsilon \operatorname{sgn}(S(t))+k S(t)-\lambda \dot{\theta}_{\mathrm{m}}(t)\right)+B_{\mathrm{v}} \dot{\theta}_{\mathrm{m}}(t)+T_L \text { 。} $ | (17) |
滑模控制器的符号函数会造成系统抖动问题,利用饱和函数sat(S(t))代替符号函数sgn(S(t)),能够有效降低控制律的抖动现象,饱和函数的表达式[13]为
| $ \operatorname{sat}(S(t))=\left\{\begin{array}{l} \operatorname{sgn}(S(t))|S(t)| \geqslant \varphi, \\ \frac{S(t)}{\varphi}|S(t)|<\varphi, \end{array}\right. $ | (18) |
式中, φ为正常数。
用式(18)代替式(17)中的符号函数,可得电机角位移滑模控制律的表达式为
| $ u(t)=J_{\mathrm{e}}(\lambda \dot{e}+\varepsilon \operatorname{sat}(S(t))+k S(t))-B_{\mathrm{v}} \dot{e}+T_L \text { 。} $ | (19) |
将角位移稳态误差ess作为评价电机角位移响应性能优劣的指标,稳态误差表达式为
| $ e_{\mathrm{ss}}=\frac{\left|\theta_{r 1}-\theta_1\right|+\left|\theta_{r i}-\theta_i\right|+\cdots+\left|\theta_{r n}-\theta_n\right|}{n}, $ | (20) |
式中:ess为伺服电机角位移稳态误差;θi为第i个采样时刻的伺服电机角位移值;θri为i个采样时刻点期望的伺服电机角位移值;n为采样时刻点的总数量。
2.2 举升系统能耗建模换电机器人举升系统主要通过丝杠螺母机构和摇杆滑块机构将电机的旋转运动转换为电池在竖直方向的升降,其结构参数对系统的能耗以及举升过程的动力学和运动学性能影响较大,控制参数直接影响举升时间和速度。建立举升系统的功率流方程为
| $ P_{\text {m-in }}=P_{\text {m-out }}+P_{\text {loss }}=\frac{P_{\text {m-out }}}{\eta}, $ | (21) |
式中:Pm-out为举升伺服电机的输出功率;Ploss为电机的损耗功率;η为伺服电机效率。
伺服电机输出功率与其输出轴角速度和转矩密切相关。伺服电机系统状态方程为[14]:
| $ J_{\mathrm{e}} \ddot{\theta}_{\mathrm{m}}+B_{\mathrm{v}} \dot{\theta}_{\mathrm{m}}=T_{\mathrm{m}}-T_L \text {, } $ | (22) |
式中:Je为举升系统各部分等效转动惯量;Bv表示为等效阻尼系数;Tm为伺服电机轴的输出转矩;
根据式(12)与式(22),可得到伺服电机输出功率为
| $ \begin{gathered} P_{\mathrm{m}-\mathrm{out}}=T_{\mathrm{m}} \dot{\theta}_{\mathrm{m}}=J_{\mathrm{e}} \ddot{\theta}_{\mathrm{m}}+\left(\sum\limits_{i=3}^9 \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial}{\partial \dot{\theta}_{\mathrm{m}}}\left(m_i v_i^2+J_i\left(\dot{\theta}_i\right)^2-2 m_i g y_i\right)-\sum\limits_{i=1}^2 \frac{\partial}{\partial \theta_{\mathrm{m}}}\left(\frac{1}{2} m_i v_i^2+\frac{1}{2} J_i\left(\dot{\theta}_i\right)^2\right)+\right. \\ \left.B_{\mathrm{v}} \dot{\theta}_{\mathrm{m}}+\sum\limits_{i=1}^2 \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial}{\partial \dot{\theta}_{\mathrm{m}}}\left(\frac{1}{2} m_i v_i^2+\frac{1}{2} J_i\left(\dot{\theta}_i\right)^2\right)-\sum\limits_{i=3}^9 \frac{\partial}{\partial \theta_{\mathrm{m}}} 2\left(\frac{1}{2} m_i v_i^2+\frac{1}{2} J_i\left(\dot{\theta}_i\right)^2-m_i g y_i\right)\right) \dot{\theta}_{\mathrm{m}}。\end{gathered} $ | (23) |
换电机器人举升系统举升过程的能耗可以表示为举升电机输入功率对时间的积分,举升电机输入功率表示为举升电机输出功率与主轴电机效率的比值,可得举升过程能耗为
| $ E=\int_0^t P_{\mathrm{m} \text {-in }} \mathrm{d} t=\int_0^t \frac{P_{\mathrm{m} \text {-out }}}{\eta} \mathrm{d} t 。$ | (24) |
举升系统中齿轮减速比i,丝杠导程Ph,连杆长度l1,l2,l3等结构参数的变化会影响举升系统的动力学关系和运动学关系,滑模控制参数ε,λ和k会影响举升系统角位移稳态误差和举升时间以及电机角速度,影响换电机器人能耗。优化变量X表示为
| $ X=\left[i, P_h, l_1, l_2, l_3, \varepsilon, \lambda, k\right] 。$ | (25) |
在提升换电机器人续航能力的同时须满足其举升系统控制精度,以举升系统举升电池过程中的能耗E和举升电机的角位移稳态误差ess为优化目标。
3.1.3 约束条件换电机器人举升系统参数选择,需要满足尺寸约束、控制约束和举升性能要求约束,优化变量必须满足以下约束条件。
1) 1 < i≤2, i∈34/21, 33/22, 32/23, 31/24, 30/25,换电机器人高度限制了1对减速齿轮的中心距,齿轮减速比取上述比值。
2) 5≤Ph≤12, Ph∈5, 6, 8, 10, 12,推荐导程范围,滚珠丝杠公称直径取12 mm。
3) 90≤l1≤130,180≤l2≤220,140≤l3≤170。
4) εmin≤ε≤εmax,λmin≤λ≤λmax,kmin≤k≤kmax。
5)
6) tr≤10,系统上升时间允许范围。
基于上述分析,电动汽车换电机器人举升系统节能性集成优化模型为
| $ \min f\left(i, P_{\mathrm{h}}, l_1, l_2, l_3, \varepsilon, \lambda, k\right)=\min \left(E, e_{\mathrm{ss}}\right), \\ \text { s.t. }\left\{\begin{array}{l} 1<i \leqslant 2, i \in\{34 /21, \ldots, 30 /25\}, \\ 5 \leqslant P_{\mathrm{h}} \leqslant 12, P_{\mathrm{h}} \in\{5, 6, 8, 10, 12\}, \\ 90 \leqslant l_1 \leqslant 130, \\ 180 \leqslant l_2 \leqslant 220, \\ 140 \leqslant l_3 \leqslant 180, \\ \varepsilon_{\min } \leqslant \varepsilon \leqslant \varepsilon_{\max }, \\ \lambda_{\min } \leqslant \lambda \leqslant k \leqslant \lambda_{\max }, \\ l_1+l_2 \sin \left(\beta-\frac{\pi}{2}\right) \geqslant 220, \\ t_{\mathrm{r}} \leqslant 10 。\end{array}\right. $ | (26) |
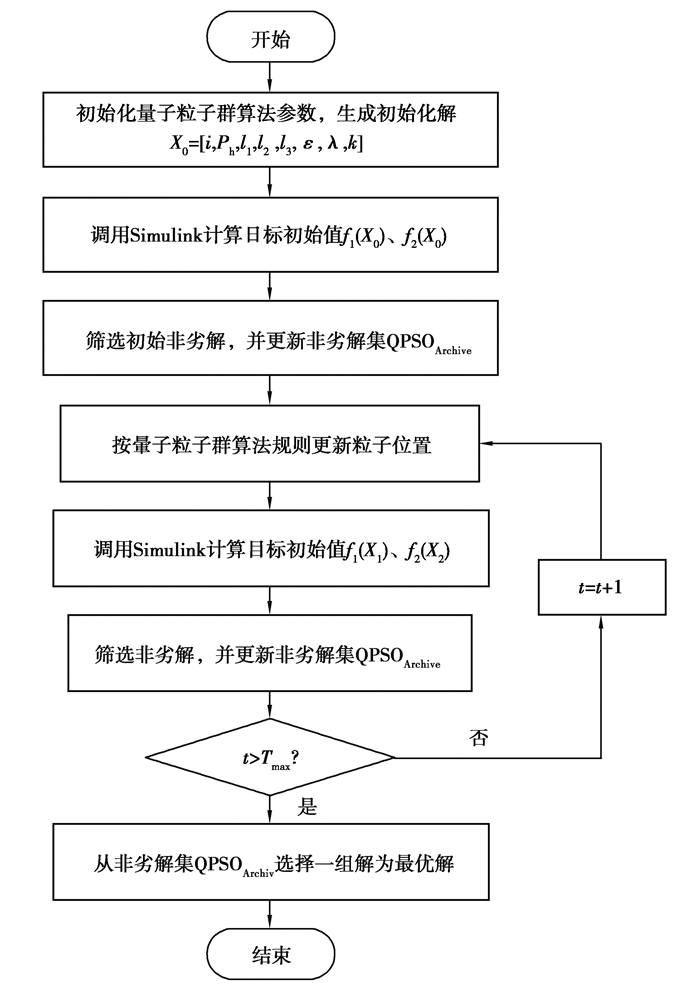
经典的粒子群算法[15](PSO)具有操作简单、容易实现、准确度高等优点,但容易陷入局部最优。受启发于量子行为与人类智能行为的相似性,Sun等[16-17]提出了量子粒子群算法(QPSO,quantum-behaved particle swarm optimization)以改善粒子群算法的不足。在量子粒子群算法中,用波函数来描述粒子搜索状态,粒子呈现一种类似于量子空间内的束缚状态,且能以一定概率出现在解空间的任意位置,以实现对整个解空间的搜索。其优化流程如图 3所示。
|
图 3 量子粒子群算法优化流程图 Fig. 3 Flow chart of quantum particle swarm optimization |
结合换电机器人举升系统参数匹配过程,QPSO算法的关键步骤如下:
1) 初始化算法参数设置及生成初始解。设置最大迭代次数为Tmax,粒子的个数为N,收缩-扩张系数β1,将初步匹配的举升系统参数作为初始解:X0=[i, Ph, l1, l2, l3, ε, λ, k], 根据X0随机生成N个粒子的种群。
2) 计算各粒子适应度值。调用Simulink仿真模型,将结构参数和控制参数带入角位移响应仿真模型,得到电机的角位移和角速度,再计算举升过程能耗E及角位移稳态误差ess。
3) 更新粒子位置。根据公式(39)对每组粒子进行更新:
| $ \left\{\begin{array}{l} X_i^{t+1}=P_i^t \pm \beta_1\left|m_{\text {best }}^t-X_i^t\right| \ln \frac{1}{u}, \\ P_i^t=\varphi_0 P_{\text {best }, i}^t+\left(1-\varphi_0\right) G_{\text {best } 。}^t \end{array}\right. $ | (27) |
式中:Xit,Xit+1为第t和t+1次迭代中的第i个粒子,Pit为第t次迭代中第i个粒子的势场位置吸引点;β1为收缩-扩张系数;mbestt为第t次迭代过程中所有粒子的局部最优位置的平均值;u为服从{0, 1}均匀分布的随机数;φ0为0~1之间的随机数; Pbest, it为第t次迭代中第i个粒子的局部最优位置; Gbestt为第t次迭代中所有粒子的全局最优位置。
4) 重新计算更新后的粒子适应度值,即计算举升过程能耗E及角位移稳态误差ess。
5) 算法终止。当迭代次数满足循环条件,输出Pareto解集,否则返回步骤3)。
4 优化结果分析与样机实验 4.1 优化结果与对比分析基于换电机器人举升系统初步匹配参数进行对比优化,采用Matlab编程,初始种群设置为50,最大迭代次数为200,收缩-扩张系数为
| 表 4 优化结果 Table 4 Optimization results |
可以看出,单独优化控制参数时,虽然能够大幅度降低角位移稳态误差,但是举升系统的能耗仅降低了1.60%。单独优化结构参数时,举升系统的能耗降低了7.77%,角位移稳态误差降低了50.62%。结构和控制参数集成优化时,能够在降低角位移稳态误差的同时,大幅度降低举升系统能耗,与单独进行结构参数相比,举升系统能耗降低了3.43%,角位移稳态误差降低了6.21%;与初步匹配参数相比,举升系统能耗降低了10.93%,角位移稳态误差降低了53.68%。综上所述,结构和控制参数集成优化相比于单独优化结构参数和控制参数,能够在保证机器人举升系统的动力学性能的前提下,使举升系统能耗最低。
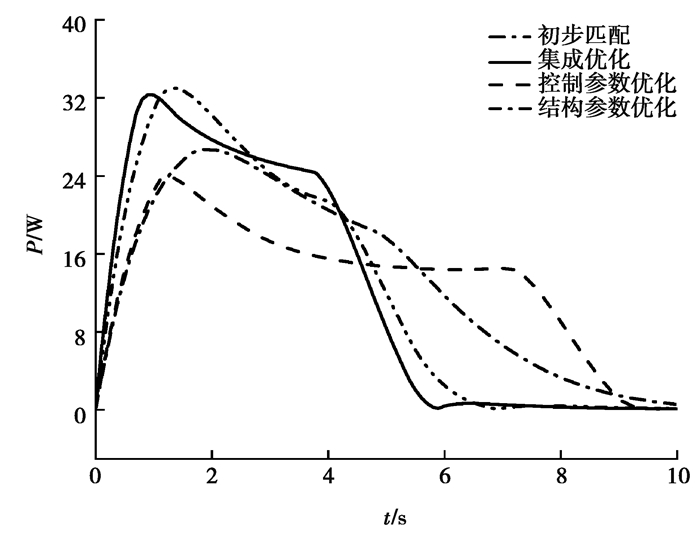
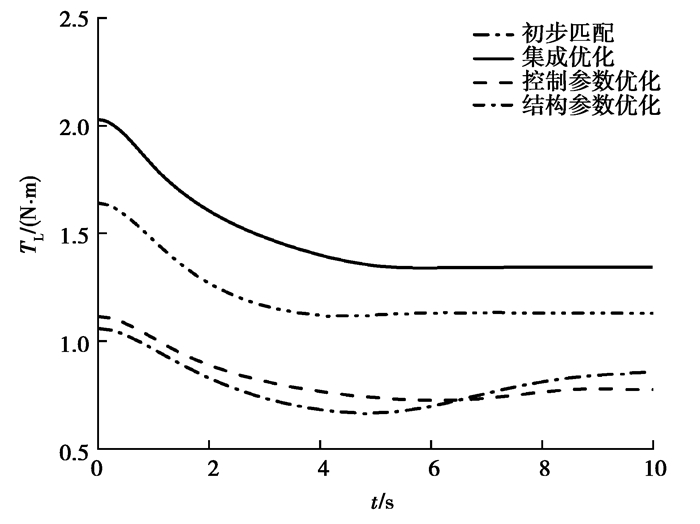
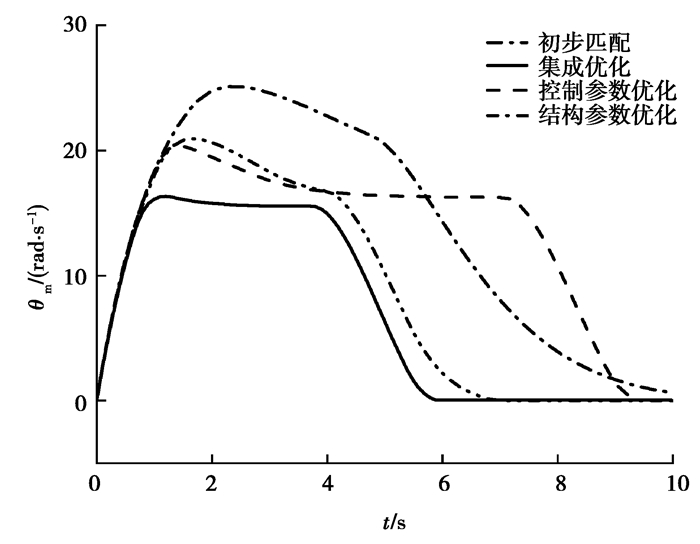
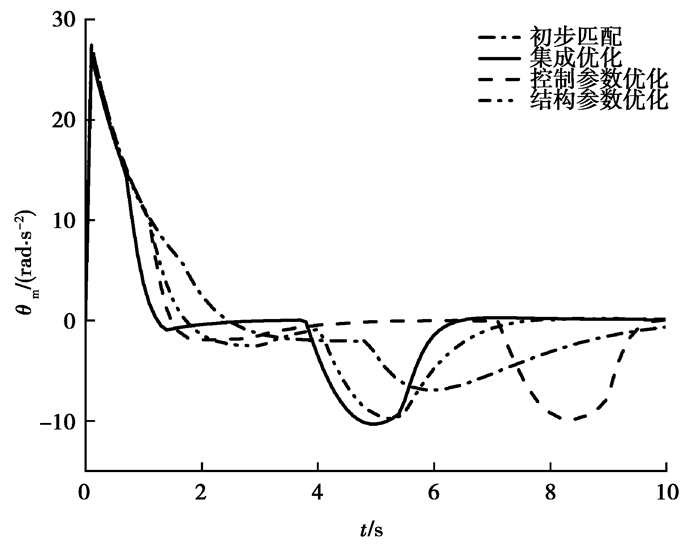
由图 4可知,结构和控制参数集成优化后的功率曲线上升更快,收敛最快。这是因为结构参数和控制参数会影响举升系统的期望角位移和负载力矩。由图 5~图 7和表 4可知,虽然集成优化后的负载力矩大于单独优化的负载力矩,但是集成优化后角速度和角加速度小于单独优化,且收敛最快,所以集成优化后的功率曲线上升更快,收敛最快,能耗最低。
|
图 4 四组参数下举升伺服电机功率图 Fig. 4 Lifting servo motor power diagram under four sets of parameters |
|
图 5 四组参数下举升系统负载力矩图 Fig. 5 Load torque diagram of lifting system under four sets of parameters |
|
图 6 四组参数下举升系统电机角速度图 Fig. 6 Angular velocity diagram of lifting system motor under four sets of parameters |
|
图 7 四组参数下举升系统电机角加速度图 Fig. 7 Angular acceleration diagram of lifting system motor under four sets of parameters |
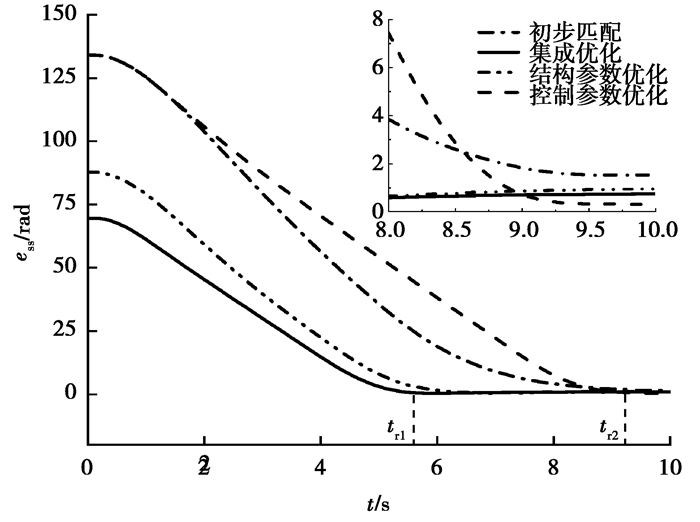
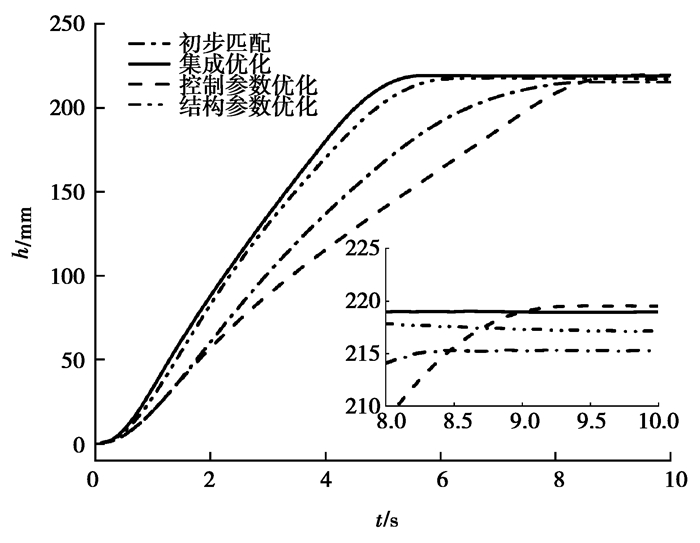
由图 8和图 9可知,结构和控制参数集成优化后的角位移稳态误差小于优化前,响应速度最快;单独优化控制参数的稳态误差最小。这是由于举升系统等效转动惯量与结构参数中的传动比i和连杆长度l1,l2,l3有关,系统等效转动惯量增大会导致换电机器人在举升电池时惯性增大产生颤动,在优化结构参数时会改变举升系统等效转动惯量,优化系统的稳态误差;而优化控制参数能够直接影响举升系统精度,对举升系统的稳态误差影响最大。
|
图 8 四组参数下角位移误差对比 Fig. 8 Comparison of angular displacement error under four sets of parameters |
|
图 9 四组参数下举升高度对比 Fig. 9 Comparison of lifting heights under four sets of parameters |
分析可知,结构参数对换电机器人举升系统能耗影响较大,控制参数对换电机器人举升系统稳态误差影响较大,结构参数与控制参数集成优化能够在保证机器人举升系统精度的前提下有效降低换电机器人举升能耗。
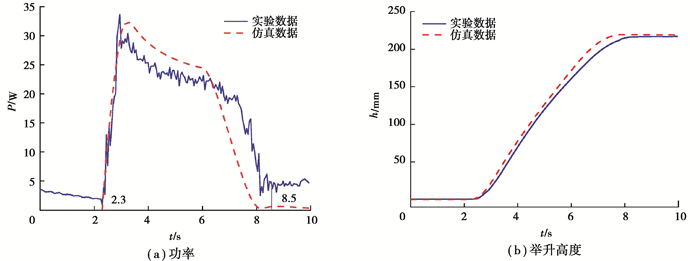
4.2 样机实验为验证优化结果的可靠性,根据集成优化的参数加工1台换电机器人,搭建实验平台,实验现场如图 10所示。实验中将80 kg的电动汽车动力锂电池包举升220 mm,测量举升过程的能耗和稳态误差。其中,功率信号采用HIOKI公司生产的日置功率测量仪进行采集,对时间积分得到换电机器人举升过程的能耗;另外,通过举升伺服电机的编码器测量得到举升过程的实际角位移,与期望角位移作差获得稳态误差。将实验测得的能耗和角位移稳态误差与仿真数据进行对比,结果如图 11和表 5所示。

|
图 10 换电机器人举升系统实验现场 Fig. 10 The experimental site of the battery-changing robot lifting system |
|
图 11 实验数据与仿真数据对比 Fig. 11 Comparison of experimental data and simulation data |
| 表 5 仿真与实验结果对比 Table 5 Comparison of simulation and experimental results |
由表 5可知,实验能耗为136.32 J,仿真偏差仅为7.78%;实验角位移稳态误差为0.598 4 rad,仿真值偏差仅为8.48%,说明笔者建立的能耗模型和仿真结果有较高的可靠性。
5 结论1) 基于电动汽车换电模式,设计了一种电动汽车动力锂电池举升系统,利用拉格朗日方程推导出换电机器人举升系统动力学方程,设计了滑模变结构控制器。构建举升系统举升过程的能耗模型,以举升系统能耗和系统角位移稳态误差为评价指标,建立了电机角位移响应性能仿真模型。
2) 建立了以举升系统能耗最小和角位移稳态误差最小为目标的优化模型,利用多目标量子粒子群优化算法求解,结果表明,结构与控制参数集成优化与单独进行结构参数优化和控制参数优化相比,能够在保证机器人举升系统动力学性能的同时,达到举升系统能耗最低。
3) 笔者在进行换电机器人节能优化时,仅对换电机器人的举升系统进行了节能优化设计,综合考虑换电机器人行走系统能耗开展节能优化设计,将是下一步的研究重点。
| [1] |
万钢. 新时代推进我国新能源汽车发展的新思考[J]. 汽车工程学报, 2018, 8(4): 235-238. Wan G. New thoughts on promoting the development of China's new energy vehicles in the new era[J]. Chinese Journal of Automotive Engineering, 2018, 8(4): 235-238. (in Chinese) |
| [2] |
Sun B, Sun X, Tsang D H K, et al. Optimal battery purchasing and charging strategy at electric vehicle battery swap stations[J]. European Journal of Operational Research, 2019, 279(2): 524-539. DOI:10.1016/j.ejor.2019.06.019 |
| [3] |
杨军宏, 冯勇, 尚建忠, 等. 摆盘式液压关节的结构设计与节能控制[J]. 机械工程学报, 2018, 54(20): 180-188. Yang J H, Feng Y, Shang J Z, et al. Structural design and energy saving control of wobble hydraulic joint[J]. Journal of Mechanical Engineering, 2018, 54(20): 180-188. (in Chinese) |
| [4] |
Mostyn V, Huczala D, Moczulski W, et al. Dimensional optimization of the robotic arm to reduce energy consumption[J]. MM Science Journal, 2020(1): 3745-3753. |
| [5] |
Yu X X, Iida F. Minimalistic models of an energy-efficient vertical-hopping robot[J]. IEEE Transactions on Industrial Electronics, 2014, 61(2): 1053-1062. DOI:10.1109/TIE.2013.2266080 |
| [6] |
Seok S, Wang A, Chuah M Y, et al. Design principles for energy-efficient legged locomotion and implementation on the MIT cheetah robot[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(3): 1117-1129. DOI:10.1109/TMECH.2014.2339013 |
| [7] |
Norsahperi N M H, Danapalasingam K A. An improved optimal integral sliding mode control for uncertain robotic manipulators with reduced tracking error, chattering, and energy consumption[J]. Mechanical Systems and Signal Processing, 2020, 142: 106747. DOI:10.1016/j.ymssp.2020.106747 |
| [8] |
Koivumäki J, Zhu W H, Mattila J. Energy-efficient and high-precision control of hydraulic robots[J]. Control Engineering Practice, 2019, 85: 176-193. DOI:10.1016/j.conengprac.2018.12.013 |
| [9] |
Zhang M Y, Yan J H. A data-driven method for optimizing the energy consumption of industrial robots[J]. Journal of Cleaner Production, 2021, 285: 124862. DOI:10.1016/j.jclepro.2020.124862 |
| [10] |
Meike D, Pellicciari M, Berselli G. Energy efficient use of multirobot production lines in the automotive industry: detailed system modeling and optimization[J]. IEEE Transactions on Automation Science and Engineering, 2014, 11(3): 798-809. DOI:10.1109/TASE.2013.2285813 |
| [11] |
韩俊庆, 吴爱国, 董娜. 基于滑模干扰观测器的机械臂终端滑模控制[J]. 中南大学学报(自然科学版), 2020, 51(10): 2749-2757. Han J Q, Wu A G, Dong N. Terminal sliding mode control for robotic manipulator based on sliding mode disturbance observer[J]. Journal of Central South University (Science and Technology), 2020, 51(10): 2749-2757. (in Chinese) |
| [12] |
吉鑫浩, 汪成文, 陈帅, 等. 阀控电液位置伺服系统滑模反步控制方法[J]. 中南大学学报(自然科学版), 2020, 51(6): 1518-1525. Ji X H, Wang C W, Chen S, et al. Sliding mode back-stepping control method for valve-controlled electro-hydraulic position servo system[J]. Journal of Central South University (Science and Technology), 2020, 51(6): 1518-1525. (in Chinese) |
| [13] |
陈松, 夏长高, 孙旭. 基于滑模变结构理论的车辆主动横向稳定杆控制[J]. 中国机械工程, 2016, 27(23): 3259-3265. Chen S, Xia C G, Sun X. Control on AARB of vehicle based on sliding mode variable structure theory[J]. China Mechanical Engineering, 2016, 27(23): 3259-3265. (in Chinese) |
| [14] |
Ji Q Q, Li C B, Zhu D G, et al. Structural design optimization of moving component in CNC machine tool for energy saving[J]. Journal of Cleaner Production, 2020, 246: 118976. DOI:10.1016/j.jclepro.2019.118976 |
| [15] |
牛江川, 韩利涛, 李素娟, 等. 基于PSO-BP神经网络的盾构刀具配置研究[J]. 机械工程学报, 2018, 54(10): 167-172. Niu J C, Han L T, Li S J, et al. Research on shield cutting tool configuration based on PSO-BP neural network[J]. Journal of Mechanical Engineering, 2018, 54(10): 167-172. (in Chinese) |
| [16] |
Sun J, Feng B, Xu W B. Particle swarm optimization with particles having quantum behavior[C]//Proceedings of the 2004 Congress on Evolutionary Computation (IEEE Cat. No. 04TH8753), June 19-23, 2004, Portland, OR, USA. IEEE, 2004: 325-331.
|
| [17] |
Sun J, Xu W B, Feng B. Adaptive parameter control for quantum-behaved particle swarm optimization on individual level[C]//2005 IEEE International Conference on Systems, Man and Cybernetics, October 12-12, 2005, Waikoloa, HI, USA. IEEE, 2006: 3049-3054.
|
 2023, Vol. 46
2023, Vol. 46

