2. 贵州群建精密机械有限公司, 贵州 遵义 563099
2. Guizhou Qunjian Precision Machinery Company, Zunyi, Guizhou 563099, P. R. China
行星滚柱丝杠副(planetary roller screw mechanism,PRSM)是一种通过内外螺纹啮合,实现旋转运动与直线运动相互转化的新型机械装置,具有高承载、高精度、高刚度、耐冲击、长寿命、小尺寸等优点。PRSM可广泛应用于航空、航天、武器以及机器人等军民领域智能化、全电化、低碳化机械装备中,是装备制造业和国防工业极其重要的关键功能部件。随着武器装备、飞行器、高档机床对直线传动装置服役性能要求的日益需求,行星滚柱丝杠副成为国内外研究的热点。
目前,国内外针对PRSM研究主要集中在载荷分布、动力学分析、力学行为与承载特性以及摩擦力矩及传动精度计算等方面。Zhang等[1]建立了PRSM螺纹载荷分布模型,研究了安装配置、荷载条件和螺纹形参数对荷载分布的影响。Fu等[2]提出了一种确定PRSM啮合螺纹面接触位置和间隙的综合接触分析模型,计算了任意一对配合面沿各方向和接触位置的间隙。Fu等[3]建立了PRSM的动力学模型,有效确定PRSM的运动和内力。Ma等[4-5]开发了考虑误差和间隙的自由载荷下的PRSM传动误差计算模型,开展了PRSM原型在自由载荷和不同工作载荷下的传动误差实验。付永领等[6]利用理论力学解析解与有限元仿真对PRSM寿命对比分析,发现随着丝杠螺纹升角增大和滚柱根数增多,丝杠副寿命逐渐增大。Abevi等[7]提出一种计算PRSM静载荷分布和轴向刚度的方法,发现在螺母的法兰与接触螺纹相互作用下螺母的形状对载荷分布有显著影响。Velinsky等[8]分析了PRSM的空间运动与传动特性,推导了响应面法的承载能力和效率。Jones等[9]推导了带有黏性摩擦的拉格朗日方法推导了PRSM运动方程,得到了验算滚柱和丝杠的稳态角速度、滑移速度的相关理论。Aurégan等[10]通过对PRSM滚动滑动接触试验仿真,结果表明在没有润滑的情况下,曲率引起的滚动微滑移足以产生磨损。已有相关研究为PRSM主动设计与加工制造奠定了较好的理论基础。
然而,小螺距PRSM螺纹因自身性能要求,具有小而精密的结构特点,这对PRSM螺纹加工质量精密检测和牙型偏差精准评价造成了极大困难。根据国标GB/T 028703—2012圆柱螺纹检测方法[11]所述的螺纹牙型测量方法,工程实际中一般都是通过测量PRSM螺距、中径、牙型角偏差等单项参数偏差作为螺纹牙型精度评定指标,其检测精度难以保证。已有的常规螺纹检测方式包括传统量具检测法、CCD视觉检测技术法[12-13]、激光三角法[14]等。实现了对螺纹中径、螺距、牙型角3个重要参数的在线测量和自动测量,能满足在速度、精度和整体测量能力等方面的要求。Feng等[15]将角点检测原理应用于螺纹视觉测量,提出了Harris算法重新寻找角点,验证了Harris算法在角点检测中的可靠性。
综上可知,目前国内外对小螺距PRSM滚柱牙型检测方式比较传统,螺纹牙型形状、位置精度评价研究不足,导致PRSM螺纹牙型偏差检测标准缺失、牙型评价理论匮乏、工程中检测困难等现状。针对上述问题,开展了对小螺距PRSM滚柱牙型非接触式检测与偏差评价方法研究,提出了基于非线性内点算法的小螺距PRSM滚柱牙型曲线高精度拟合方法,建立了PRSM滚柱牙型偏差模型和偏差评价方法,对5种牙型偏差进行评价,并结合0.8 mm螺距PRSM滚柱牙型测量和偏差评价案例分析,验证了文中所提出的检测评价方法具有可行性与精确性。滚柱牙型检测与偏差评价研究对改善PRSM滚柱加工、装配工艺、提升滚柱丝杠副的综合性能有重要意义。
1 PRSM滚柱螺纹牙非接触式检测 1.1 检测样件PRSM的运动传递,以丝杆、滚柱和螺母螺纹牙相互旋合而成,包括单丝杠多滚柱啮合与多滚柱单螺母啮合2种运动形式。滚柱短圆弧牙型形状在整个空间旋合运动中至关重要,直接决定其传动精度和承载性能,故实际工程中滚柱牙型加工的质量对指导加工生产工艺、提高PRSM综合性能有重要意义,研究中取PRSM 0.8 mm螺距滚柱为检测对象,如图 1所示。

|
图 1 0.8 mm螺距滚柱 Fig. 1 0.8 mm pitch roller |
图 1中,设计中径为5.100 mm,螺距为0.800 mm,牙型圆弧半径为3.606 mm。
1.2 检测设备如图 2所示,利用PMM-C高精度三坐标测量机对PRSM滚柱样件进行检测,该测量机主要包括气控动力源、夹具转台、测头、操作面板以及Quindos操作系统等模块,可以实现接触式检测(红宝石测头)和非接触式检测(红外线测头)2种检测方式。由于检测滚柱样件尺寸较小,为保证能够精准检测样件表面最小尺寸,采用非接触式检测方式,其测量距离为6 mm,最高测量精度可达到0.5 μm,可以满足检测需要。检测滚柱样件时,应注意严格控制检测环境:1)环境温度保持20±1°;2)环境湿度保持50%等。

|
图 2 PMM-C高精度三坐标测量机 Fig. 2 PMM-C high precision coordinate measuring machine |
根据PMM-C高精度三坐标测量机非接触式检测原理,制定滚柱非接触式检测流程,如图 3所示,主要测试流程包括检测前样件表面反光处理(如样件发黑、涂层等),防止出现过多坏点影响测量精度;检测中依据样件设计基准建立测量的工件坐标系,从而确定测头扫描路径;检测后可视化扫描的数据点集,并判断点集是否合格。此外,为保证测量结果的准确性,校验红外线测头时,必须使用灰色标准球防止散光。

|
图 3 三坐标测量机非接触式检测流程 Fig. 3 CMM non-contact testing process |
对0.8 mm螺距PRSM滚柱进行三坐标测量机非接触式检测,得到滚柱牙型轴向二维轮廓单牙左侧扫描数据点集(zi,xi),共36个测点,如图 4和表 1所示。其中,zi为轴向二维轮廓横坐标(轴线方向),xi为轴向二维轮廓纵坐标(垂直于轴线方向)。

|
图 4 滚柱单牙左侧扫描数据点集 Fig. 4 Data point set of scanning on the left side of roller single tooth |
| 表 1 滚柱牙型轴向二维轮廓扫描数据 Table 1 Axial two-dimensional profile scanning data of roller tooth profile |
根据罗智孙等[16]的研究,非完整小圆弧的圆弧半径大小和圆弧中心角大小会对拟合精度产生一定程度的影响。在拟合牙型测量点集时,为避免上述因素对牙型偏差评价带来不稳定的结果,并满足滚柱加工原理限制滚柱牙型圆弧圆心坐标在中心轴线上的特点,提出一种非线性内点算法对牙型圆弧测量数据进行处理,并与经典最小二乘法拟合[17-18]对比分析,发现在拟合精度上切实可行。
2.1 非线性内点算法优化模型为了精确拟合滚柱牙型齿廓,采用非线性内点算法对滚柱牙型齿廓进行拟合,具有较高拟合精度,能使滚柱牙型齿廓半径残差平方和minS达到最小值[19],其实质是一个求解非线性最小优化解的问题。如图 5所示,利用常规的非线性内点优化算法(不约束圆心x0坐标)和考虑滚柱加工限制牙型圆弧圆心坐标在中心轴线上的非线性内点优化算法(约束圆心x0坐标)分别对滚柱牙型点集进行拟合。其中,不约束圆心x0坐标的非线性内点优化算法的求解模型中优化变量包括圆心坐标(z0,x0)及牙型半径R 3个参数,在满足边界条件R>0的条件下,寻求非线性最小优化解;而约束圆心x0坐标的非线性内点算法的求解模型中,考虑到滚柱理论设计时滚柱牙型圆心坐标在滚柱中心轴线上,加工时加工基准也在滚柱中心轴线上,同时检测基准与加工基准重合,最终导致滚柱的牙型圆心坐标限定在滚柱中心轴线上,即x0为零,此时优化变量变为牙型圆心横坐标z0和牙型半径R 2个参数,再迭代出最优解。

|
图 5 圆心坐标x0约束前后非线性内点算法牙型拟合对比示意图 Fig. 5 Comparison diagram of tooth shape fitting of nonlinear interior point algorithm before and after center x0 constraint |
滚柱牙型圆心x0坐标不受约束的非线性内点算法模型的目标函数和边界条件:
| $ \left\{ {\begin{array}{*{20}{l}} {\min S = \min \sum\limits_{i = 1}^n {{{\left[ {{r_i} - R} \right]}^2}} = \min \sum\limits_{i = 1}^n {{{\left[ {\sqrt {{{\left( {{z_i} - {z_0}} \right)}^2} + {{\left( {{x_i} - {x_0}} \right)}^2}} - R} \right]}^2}} , }\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;R > 0。} \end{array}} \right. $ | (1) |
滚柱牙型圆心x0坐标受约束的非线性内点算法模型的目标函数和边界条件:
| $ \left\{ {\begin{array}{*{20}{l}} {\min S = \min \sum\limits_{i = 1}^n {{{\left[ {{r_i} - R} \right]}^2}} = \min \sum\limits_{i = 1}^n {{{\left[ {\sqrt {{{\left( {{z_i} - {z_0}} \right)}^2} + x_i^2} - R} \right]}^2}} , }\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;R > 0。} \end{array}} \right. $ | (2) |
式中:(z0,x0)为拟合牙型圆心坐标;R为拟合牙型半径;(zi,xi)为牙型测量数据点集坐标;n为数据坐标点的个数。在优化目标函数中,含有z0,x0,R 3个待优化自变量和minS一个目标优化解。
根据上述目标函数和边界条件,综合考虑求解时间和目标函数收敛性,采用Matlab优化工具箱中fmincon非线性多元函数最小值求解器对非线性内点算法进行求解[20],如图 6所示。内点法是利用Hessian矩阵迭代,在求解过程中构造了卡罗需库恩塔克(Karush-Kuhn Tucker)条件的拉格朗日辅助函数[21],通过对修正方程组中的矩阵进行变换和LDL分解,可以实现回代修正求解。迭代流程中T为当前迭代与上次迭代计算的解差值,ε为迭代终止差值限,k为当前迭代次数,Km为最大迭代次数。

|
图 6 非线性内点算法迭代流程 Fig. 6 Iterative flow of nonlinear interior point algorithm |
因此使用Hessian矩阵迭代的内点法对滚柱牙型拟合问题求解如下:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\min f(x), \\ {\rm{s}}{\rm{.t}}{\rm{. }}\left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{c}}(x) \le 0, }\\ {{\mathit{\boldsymbol{c}}_{{\rm{eq}}}}(x) = 0, }\\ {\mathit{\boldsymbol{A}}x \le \mathit{\boldsymbol{b}}, }\\ {{\mathit{\boldsymbol{A}}_{{\rm{eq}}}}x = {\mathit{\boldsymbol{b}}_{{\rm{eq}}}}, }\\ {{\mathit{\boldsymbol{l}}_b} \le x \le {\mathit{\boldsymbol{u}}_b}{\rm{。}}} \end{array}} \right. \end{array} $ | (3) |
式中:f(x)为优化目标函数;c(x)为优化变量满足的非线性不等式;ceq(x)为优化变量满足的非线性等式约束;A、b为优化变量满足的线性不等式约束的系数矩阵;Aeq、beq为优化变量满足的线性等式约束的系数矩阵;lb和ub分别为优化变量x的下限和上限。
这里以滚柱牙型圆心x0坐标受约束的非线性内点算法模型为例,其中优化变量x包括牙型圆弧圆心z0坐标值、牙型半径R值,由于边界条件只有R>0一个线性不等式约束,故c(x)、ceq(x)、Aeq、beq、lb和ub全取空矩阵,A =[0, 1],b =[0]。滚柱牙型拟合非线性内点算法迭代优化结果,如图 7所示,经过非线性内点算法迭代49次后,得到目标函数半径残差平方和minS的最佳优化值,为1.5×10-4 mm2,此时牙型圆心z0坐标为-24.161 mm,牙型半径R值为3.600 mm,较理论设计值相差0.006 mm。

|
图 7 非线性内点算法迭代优化结果 Fig. 7 Iterative optimization results of nonlinear interior point algorithm |
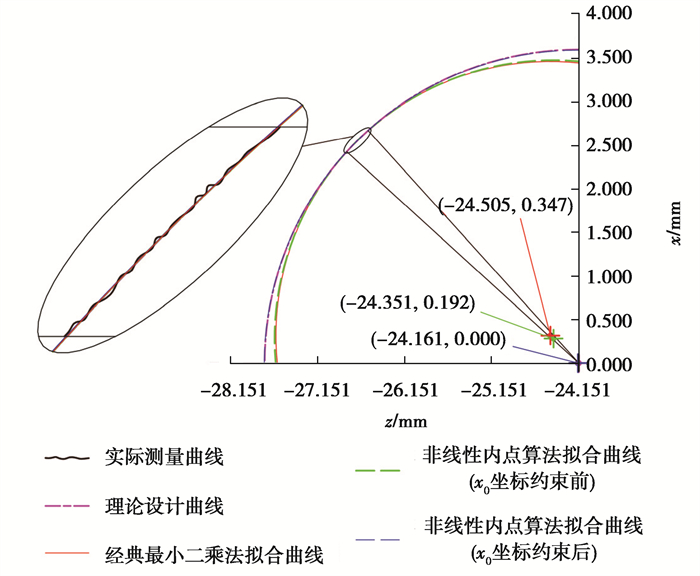
基于2.1节所述非线性内点算法的原理和表 2滚柱牙型轴向二维轮廓扫描数据,对比分析经典最小二乘法、非线性内点算法约束圆心x0坐标前和约束圆心x0坐标后的拟合效果,如图 8所示。可以看出,在滚柱牙型理论设计圆心(-24.151,0.000)与滚柱中心轴z所建立滚柱牙型离散点拟合坐标系中,粉色曲线表示滚柱牙型理论设计值,实际测量牙型点集(zi,xi)。滚柱牙型测量点集均匀分布在拟合曲线两侧,3种方法的拟合半径依次增大,并逐渐接近理论设计值,拟合圆心位置逐步靠近理论设计圆心。
| 表 2 拟合效果对比数据 Table 2 Comparison of fitting effect of different algorithms |
|
图 8 滚柱牙型拟合效果对比 Fig. 8 Comparison of roller tooth shape fitting effect |
如表 2所示,3种拟合算法得到的牙型圆心坐标(z0,x0)、牙型半径R和半径残差平方和minS结果与理论设计值对比发现:3种拟合方法残差平方和均在1.5×10-4数级;牙型拟合半径值较理论设计值误差而言,经典最小二乘法拟合为494.0 μm,x0坐标约束前非线性内点算法为276.0 μm,x0坐标约束后非线性内点算法为6.0 μm;滚柱牙型圆心z0坐标较理论设计值误差,第一种方法为353.8 μm、第二种方法为199.8 μm、第三种方法为9.8 μm;滚柱牙型圆心x0坐标较理论设计值依次相差347.0 μm,192.0 μm,0.0 μm;由此可见,第三种拟合方法更能反映实测滚柱牙型,更适用于滚柱牙型偏差的评价。
3 PRSM滚柱牙型偏差评价牙型偏差指在牙型计算范围内,实际牙型与设计牙型的偏离量,该量在轴向截面内且垂直于圆弧牙型的方向计值。此外评价模型中定义牙型总偏差、牙型形状偏差、牙型倾斜偏差、牙型圆弧半径偏差和牙型圆心轴向偏差5个参数对PRSM滚柱牙型偏差进行评价。
滚柱圆弧牙型偏差示意图,如图 9所示。其中,牙型计算范围Lα为整个滚柱牙型长度中的一部分,其长度可等于靠近牙顶的第一个测量点开始到牙根圆弧半径切点前1~2个测量点之间的距离;理论设计牙型即为符合设计规定的牙型,当无其他限定时,应为滚柱轴向截面内牙型的设计迹线;平均牙型为设计牙型迹线的纵坐标与一条斜直线的相应纵坐标之差得到的一条迹线,使之在计算范围内,实际牙型迹线偏离平均牙型迹线之偏差的平方和最小,平均牙型迹线的位置和倾斜度利用3.2节中x0坐标约束后非线性内点算法拟合的牙型曲线确定。

|
图 9 滚柱牙型偏差示意 Fig. 9 Roller tooth profile deviation |
牙型总偏差Fα,即在计算范围内包容实际牙型迹线的2条设计牙型迹线间的距离,如图 9(a)所示。在牙型计算范围内,可以用式(4)表示滚柱牙型总偏差的大小。
| $ {F_\alpha } = {F_{\alpha \max }} - {F_{\alpha \min }}, $ | (4) |
式中:Fαmax为实际测量牙型上相对理论设计牙型外凸最高点;Fαmin为实际测量牙型上相对理论设计牙型内凹最低点;Fα表示理论设计牙型的2条偏置曲线通过实际测量牙型外凸最高点与内凹最低点之间的距离。
牙型形状偏差ff,即在计算范围内包容实际牙型迹线的,与平均牙型迹线完全相同的2条迹线间的距离,如图 9(b)所示。在牙型计算范围内,可以用式(5)表示滚柱牙型形状偏差的大小。
| $ {f_{\rm{f}}} = {f_{{\rm{fmax}}}} - {f_{{\rm{f}}\min }}, $ | (5) |
式中:ffmax为实际测量牙型上相对平均牙型外凸最高点;ffmin为实际测量牙型上相对平均牙型内凹最低点;ff表示平均牙型的2条偏置曲线通过实际测量牙型外凸最高点与内凹最低点之间的距离。
牙型倾斜偏差fH,即在计算范围内两端与平均牙型迹线相交的2条设计牙型迹线间的距离,如图 9(c)所示。在牙型计算范围内,可以用式(6)表示滚柱牙型倾斜偏差的大小。
| $ {f_{\rm{H}}} = {f_{{\rm{H}}\max }} - {f_{{\rm{H}}\min }}, $ | (6) |
式中:fHmax为平均牙型上最高点;fHmin为平均牙型上最低点;fH表示理论设计牙型的2条偏置曲线通过平均牙型上最高点与最低点之间的距离。
牙型圆心轴向偏差δZ,即在滚柱中心轴线上平均牙型圆心与理论设计牙型圆心之间的距离,如图 9(d)所示。在牙型计算范围内,可以用式(7)表示滚柱牙型圆心轴向偏差的大小。
| $ {\delta _Z} = {z_i} - {z_0}, $ | (7) |
式中:zi为平均牙型圆心在滚柱中心轴线上的位置;z0为理论设计牙型圆心在滚柱中心轴线上的位置;δZ表示在滚柱中心轴线上平均牙型圆心与理论设计牙型圆心之间的距离。
此外,在牙型计算范围内,可以用式(8)表示滚柱牙型半径偏差的大小。
| $ {\delta _R} = {R_i} - R, $ | (8) |
式中:Ri为平均牙型半径;R为理论设计牙型半径;δR表示平均牙型半径与理论设计牙型半径之间的差值。
实际测量牙型相对理论设计牙型、平均牙型外凸用“+”表示,实际测量牙型相对理论设计牙型、平均牙型内凹用“-”表示。
4 滚柱牙型检测与偏差评价实例 4.1 牙型实际测量曲线根据轴向剖面二维轮廓扫描法的基本原理,利用高精度三坐标测量机对1.1节所示的0.8 mm螺距PRSM滚柱进行非接触式扫描,得到15颗连续螺纹牙左侧牙型测量曲线,其沿着平行于滚柱中心轴平行线从左往右(图中依次为1,2,…,15)扫描,如图 10所示。

|
图 10 牙型偏差 Fig. 10 Tooth profile deviation |
基于4.1节扫描得到的牙型曲线和第3节牙型偏差数学模型,评价得到牙型总偏差、牙型形状偏差、牙型倾斜偏差数据,如表 3所示。
| 表 3 牙型总偏差、牙型形状偏差和牙型倾斜偏差评价数据 Table 3 Evaluation data of total deviation, deviation of tooth shape and deviation of tooth tilt |
根据表 3牙型总偏差、牙型形状偏差、牙型倾斜偏差的评价数据,绘制3种偏差的评价图,如图 11所示。可以看出,滚柱牙型总偏差与牙型形状偏差变化趋势一致,且偏差极值点出现在同一处。评价所得牙型总偏差最大值为15.9 μm、最小值为6.7 μm,牙型形状偏差最大值为16.3 μm、最小值为8.0 μm,变化趋势出现较大波动,主要原因在于滚柱表面的缺陷(反光、毛刺)引起的。牙型倾斜偏差变化趋势相对比较平缓,变化范围在3.2 μm以内,其值仅为牙型总偏差和牙型形状偏差的1/5,故对于小螺距螺纹的滚柱,在工程上评价牙型的形状精度应重点考虑牙型总偏差和牙型形状偏差,若研究对象螺纹几何形状变化较大,应该考虑牙型倾斜偏差对螺纹牙型的形状精度影响。

|
图 11 牙型偏差评价图 Fig. 11 Evaluation chart of tooth profile deviation |
同理,基于4.1节扫描得到的牙型曲线和第3节牙型偏差数学模型,检测后评价得到牙型圆心轴向偏差、牙型半径偏差数据,如表 4所示。
| 表 4 牙型圆心轴向偏差评价数据 Table 4 Evaluation data of axial deviation of tooth profile center |
据表 4的牙型圆心轴向偏差评价数据,绘制出牙型半径偏差的评价图,如图 12所示。可以看出,所测滚柱牙型圆心轴向偏差最大值为25.8 μm、最小值为-32.8 μm,变化趋势出现较大波动,主要原因可能在于滚柱磨削加工过程中砂轮轴向窜动引起的,故实际加工中可以通过改善砂轮轴向限位结构减小牙型圆心轴向偏差,并利用牙型圆心轴向偏差间接评价螺纹牙的位置精度,若想要直观地评价螺纹的位置精度可采用螺距误差或螺距累积误差描述。

|
图 12 牙型圆心轴向偏差评价图 Fig. 12 Evaluation chart of axial deviation of tooth profile center |
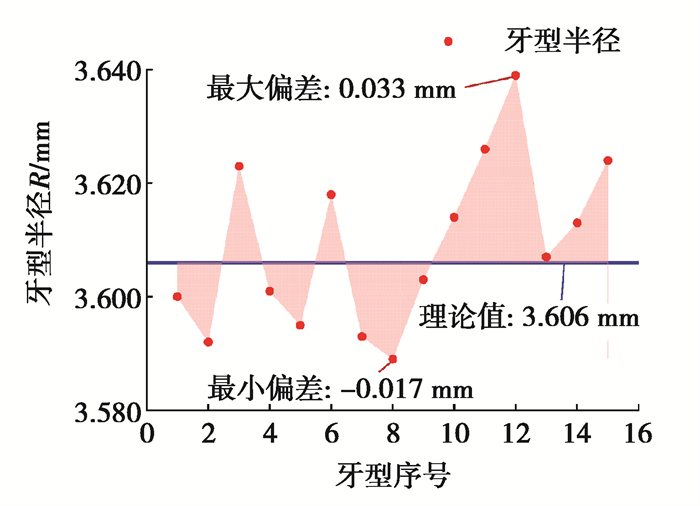
根据表 5牙型半径及牙型半径偏差的评价数据,绘制出牙型半径偏差的评价图,如图 13所示。可以看出,所测滚柱牙型半径最大值为3.639 mm、最小值为3.589 mm,牙型半径偏差最大值为33 μm、最小值为-17 μm,变化趋势出现较大波动,其主要原因可能是滚柱磨削加工过程中砂轮磨损引起的,故在实际加工中可以通过修整砂轮、优化磨削工艺参数等方式减小滚柱牙型半径偏差;同时滚柱牙型半径偏差作为尺寸精度指标,在一定程度上受到牙型形状、位置误差共同影响,综合反映滚柱牙型的形状、位置精度,能直接反映滚柱螺纹齿廓圆弧半径是否正确,具有一定的工程意义。
| 表 5 牙型半径及牙型半径偏差评价数据 Table 5 Evaluation data of tooth radius and tooth radius deviation |
|
图 13 牙型半径偏差评价图 Fig. 13 Evaluation chart of tooth profile radius deviation |
基于提出的小螺距滚柱牙型非接触式检测与偏差评价方法研究,可得到如下结论:
1) 利用高精度三坐标测量机与螺纹轴向剖面二维扫描法结合,实现PRSM滚柱螺纹牙型的非接触式检测,提出了基于非线性内点算法的小螺距PRSM滚柱牙型曲线高精度拟合方法,拟合残差平方和可达到1.5×10-4数级,将牙型半径拟合精度提高至6 μm,牙型圆心z0坐标拟合精度提高至9.8 μm。
2) 首次建立了滚柱螺纹牙型偏差评价模型和偏差评价方法,利用牙型总偏差、形状偏差、倾斜偏差、圆弧半径偏差和圆心轴向偏差对PRSM滚柱牙型形状、位置精度进行评价,绘制了基于本偏差模型的牙型偏差评价图,为精确确定滚柱牙型形状精度提供一种新的参考方法。
3) 研究发现,PRSM滚柱牙型总偏差与牙型形状偏差变化趋势、幅值一致,其值比牙倾斜偏差值大了近5倍,故在工程应用中评价滚柱牙型的形状精度应首先考虑用牙型总偏差和牙型形状偏差评价滚柱牙型形状精度。
此外,文中研究内容存在一些不足之处,没有对滚柱牙型位置精度更深入研究,后续的研究可以围绕滚柱牙型位置精度进行展开,精确确定滚柱牙型形状和位置精度,建立小螺距滚柱牙型精度评价体系,为提高PRSM制造、装配精度提供理论支撑。
| [1] |
Zhang W J, Liu G, Tong R T, et al. Load distribution of planetary roller screw mechanism and its improvement approach[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2016, 230(18): 3304-3318. DOI:10.1177/0954406215610361 |
| [2] |
Fu X J, Liu G, Ma S J, et al. A comprehensive contact analysis of planetary roller screw mechanism[J]. Journal of Mechanical Design, 2017, 139(1): 012302. DOI:10.1115/1.4034580 |
| [3] |
Fu X J, Liu G, Ma S J, et al. An efficient method for the dynamic analysis of planetary roller screw mechanism[J]. Mechanism and Machine Theory, 2020, 150: 103851. DOI:10.1016/j.mechmachtheory.2020.103851 |
| [4] |
Ma S J, Liu G, Zhou J X, et al. Optimal design and contact analysis for planetary roller screw[J]. Applied Mechanics and Materials, 2011, 86: 361-364. DOI:10.4028/www.scientific.net/AMM.86.361 |
| [5] |
Ma S J, Cai W, Wu L P, et al. Modelling of transmission accuracy of a planetary roller screw mechanism considering errors and elastic deformations[J]. Mechanism and Machine Theory, 2019, 134: 151-168. DOI:10.1016/j.mechmachtheory.2018.12.025 |
| [6] |
付永领, 郑世成, 甘发金. 基于结构参数的标准式行星滚柱丝杠副寿命分析[J]. 机械传动, 2018, 42(11): 117-122. Fu Y L, Zheng S C, Gan F J. Life analysis of standard planetary roller screw mechanism based on structural parameter[J]. Journal of Mechanical Transmission, 2018, 42(11): 117-122. (in Chinese) |
| [7] |
Abevi F, Daidie A, Chaussumier M, et al. Static load distribution and axial stiffness in a planetary roller screw mechanism[J]. Journal of Mechanical Design, 2016, 138(1): 012301. DOI:10.1115/1.4031859 |
| [8] |
Velinsky S A, Chu B, Lasky T A. Kinematics and efficiency analysis of the planetary roller screw mechanism[J]. Journal of Mechanical Design, 2009, 131(1): 011016. DOI:10.1115/1.3042158 |
| [9] |
Jones M H, Velinsky S A, Lasky T A. Dynamics of the planetary roller screw mechanism[J]. Journal of Mechanisms and Robotics, 2016, 8(1): 014503. DOI:10.1115/1.4030082 |
| [10] |
Aurégan G, Fridrici V, Kapsa P, et al. Experimental simulation of rolling-sliding contact for application to planetary roller screw mechanism[J]. Wear, 2015, 332/333: 1176-1184. DOI:10.1016/j.wear.2015.01.047 |
| [11] |
国家质量监督检验检疫总局, 中国国家标准化管理委员会. 圆柱螺纹检测方法: GB/T 28703-2012[S]. 北京: 中国标准出版社, 2013. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China. Test methods for parallel screw threads: GB/T 28703-2012[S]. Beijing: Standards Press of China, 2013. (in Chinese) |
| [12] |
雷吉平, 颜树华, 沈少伟. 螺纹参数CCD视觉检测系统的研究[J]. 制造技术与机床, 2010(4): 96-99. Lei J P, Yan S H, Shen S W. Research on measuring system of thread parameters by CCD vision[J]. Manufacturing Technology & Machine Tool, 2010(4): 96-99. (in Chinese) DOI:10.3969/j.issn.1005-2402.2010.04.032 |
| [13] |
左建中, 刘峰, 张定昭. 机器视觉技术在螺纹检测中的应用[J]. 机械设计与制造, 2006(4): 113-114. Zuo J Z, Liu F, Zhang D Z. The application of machine vision technology in measuring screw thread[J]. Machinery Design & Manufacture, 2006(4): 113-114. (in Chinese) DOI:10.3969/j.issn.1001-3997.2006.04.053 |
| [14] |
Vitecek A, Sioma A, Suliga P, et al. Automatization of screw thread profile measurement using a 3D vision system[J]. Journal of Machine Construction and Maintenance-Problemy Eksploatacji, 2018(3): 15-22. |
| [15] |
Feng Z B, You F C, He J W. Research on application of corner detection in thread vision measurement[J]. Journal of Physics: Conference Series, 2021, 1812(1): 012020. DOI:10.1088/1742-6596/1812/1/012020 |
| [16] |
罗智孙, 吴国新, 何小妹. 一种非完整小圆弧曲率半径参数的评价方法[J]. 中国测试, 2021, 47(4): 7-13. Luo Z S, Wu G X, He X M. An evaluation method for the radius of curvature parameters of non-holonomic small arcs[J]. China Measurement & Test, 2021, 47(4): 7-13. (in Chinese) |
| [17] |
Gander W, Golub G H, Strebel R. Least-squares fitting of circles and ellipses[J]. BIT Numerical Mathematics, 1994, 34(4): 558-578. DOI:10.1007/BF01934268 |
| [18] |
黄力峰, 汪伟, 吴南星. 基于最小二乘原理的圆拟合及误差评定算法研究[J]. 机械工程与自动化, 2020(2): 4-6. Huang L F, Wang W, Wu N X. Research of circle fitting and error evaluation algorithm based on least square principle[J]. Mechanical Engineering & Automation, 2020(2): 4-6. (in Chinese) |
| [19] |
Morgan J A, Tatar J F. Calculation of the residual sum of squares for all possible regressions[J]. Technometrics, 1972, 14(2): 317-325. DOI:10.1080/00401706.1972.10488918 |
| [20] |
Capitanescu F, Wehenkel L. Experiments with the interior-point method for solving large scale optimal power flow problems[J]. Electric Power Systems Research, 2013, 95: 276-283. |
| [21] |
徐青山, 曾艾东, 王凯, 等. 基于Hessian内点法的微型能源网日前冷热电联供经济优化调度[J]. 电网技术, 2016, 40(6): 1657-1665. Xu Q S, Zeng A D, Wang K, et al. Day-ahead optimized economic dispatching for combined cooling, heating and power in micro energy-grid based on hessian interior point method[J]. Power System Technology, 2016, 40(6): 1657-1665. (in Chinese) |
 2023, Vol. 46
2023, Vol. 46


