2. 重庆大学 航空航天学院, 重庆 40044;
3. 北京航空航天大学 航空科学与工程学院, 北京 100191
2. College of Aerospace and Astronautics, Chongqing University, Chongqing 400044, P. R. China;
3. Institute of Solid Mechanics, School of Aeronautic Science and Engineering, Beihang University(BUAA), Beijing 100191, P. R. China
在工程实际中,许多结构的危险部位都承受着多轴疲劳载荷的作用[1-2],如飞机蒙皮、起落架主起梁、航空发动机中的叶片和轮盘结构等。不同于单轴疲劳问题,多轴疲劳的影响因素包含多个,已有研究表明对于不同的材料,应力幅比、相位差、平均应力等因素对疲劳寿命的影响也不相同[3-6]。
多轴高周疲劳寿命预测准则主要分为4类[7-10]:等效应力准则、应力不变量准则、细观积分准则和临界面准则。等效应力准则[11]在静强度理论的基础上根据试验数据得出,形式简单,但缺乏合理的物理背景;应力不变量准则[12]一般以应力偏量第二不变量和静水压力为参量,计算方便,但是其对多轴疲劳失效机理解释的有效性还有待验证,尤其在非比例加载时需要进行修正;细观积分准则最早由Dang等[13, 14]基于应力微元的概念提出,之后Papadopoulos[15-17]和Morel等[18, 19]都基于该原理提出了相应的积分准则;临界面准则[20-22]建立在裂纹萌生和扩展的基础上,认为在疲劳载荷下,裂纹萌生于一个特定的平面上,该平面上的切应力和正应力都会影响疲劳裂纹的萌生与扩展。无论是哪种准则,其对于多轴疲劳寿命的预测均为采用一个等效的应力参量与单轴拉压或纯扭S-N曲线相结合的方式,等效应力参量的计算往往涉及复杂的过程,且需要进行大量的多轴疲劳试验进行修正,不方便工程应用[23-25]。
笔者基于加载参量对30CrMnSiA钢多轴疲劳寿命影响的研究,首先提出了等效S-N曲线的概念;然后,基于等效S-N曲线建立了一种快速预测硬质金属材料多轴疲劳寿命的经验公式;最后,为验证该经验公式的适用性,选取文献中多种材料的多轴疲劳试验结果,采用所提出的经验公式对试验寿命进行了预测。
1 多轴疲劳寿命快速预测方法 1.1 多轴疲劳应力分析对于恒幅拉扭复合加载,通常包含5个加载参量,其形式如式(1)(2)所示。
| σx(t)=σx,asinωt+σx, m, | (1) |
| τxy(t)=τxy,asin(ωt−δ)+τxy, m, | (2) |
式中:σx(t)和τxy(t)分别为随时间变化的正应力和切应力,σx, a和τxy, a分别为正应力幅值和切应力幅值,δ为正应力和切应力之间的相位差,σx, m和τxy, m分别为平均正应力和平均切应力。
定义应力幅比为切应力幅值与正应力幅值的比值,如式(3)所示。
| λ=τxy,aσx,a。 | (3) |
经过推导可以知道,拉扭复合加载下的应力加载路径是以平均应力为中心的椭圆,椭圆的中心为(σx, m,τxy, m),椭圆的长短半轴分别为
| la,lb=1√2√(σ2x,a+τ2xy,a)±√(σ2x,a+τ2xy,a)2−4σ2x,aτ2xy,asin2δ。 | (4) |
由此可知,3种相位差δ=0°(比例加载)、δ=45°和δ=90°(非比例加载)下的拉扭复合加载路径如图 1所示。
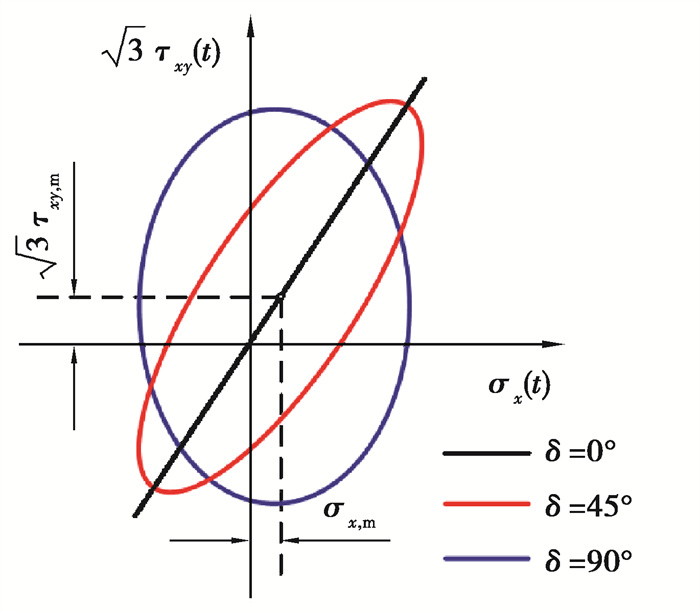
|
图 1 拉扭复合加载下von Mises应力路径 Fig. 1 Loading paths under combined tension and torsion |
在研究加载参量对多轴疲劳寿命的影响规律时,通常试验会采用相同的von Mises等效应力作为参量,该应力的幅值可采用“最小外接椭圆[26]”法计算,定义von Mises等效应力的幅值为加载路径最小外接椭圆长短半轴平方和的根。多轴疲劳载荷下的von Mises等效应力可以表示为
| σeq(t)=√σ2x(t)+3τ2xy(t), | (5) |
式(5)在数学上表示点(
| laeq,lbeq=1√2√(σ2x,a+3τ2xy,a)±√(σ2x,a+3τ2xy,a)2−12σ2x,aτ2xy,asin2δ。 | (6) |
因此,根据“最小外接椭圆”法,von Mises等效应力幅值如下所示:
| σeq,a=√l2aeq+l2beq=√σ2x,a+3τ2xy,a 。 | (7) |
对于单轴拉压,则有σeq, a=σx, a;对于纯扭,则有
在参考文献[26][27]中,根据30CrMnSiA钢的单轴、多轴疲劳试验过程和结果,在研究应力幅比对多轴疲劳寿命的影响时,采用了相同的等效von Mises应力幅值。试验结果表明:不同相位差下的疲劳寿命随应力幅比增大而增大。因此,考虑将单轴拉压疲劳试验的应力幅值与纯扭疲劳试验的应力幅值分别用von Mises等效应力幅值表示,将单轴拉压和纯扭的S-N曲线转变为等效von Mises应力幅值寿命曲线,单轴拉压等效S-N曲线如式(8)所示:
| logNf=6.9577−1.2294log(σx,a−565.25)。 | (8) |
纯扭载荷下的等效S-N曲线如(9)所示:
| logNf=39.041−11.659log(√3τxy,a)。 | (9) |
式(8)和式(9)中,σx, a和τxy, a的单位均为兆帕(MPa)。对于不同应力幅比及相位差下的多轴疲劳试验,多轴疲劳寿命分布在2条等效S-N曲线之间,如图 2所示。由此可以知道,随着应力幅比的增大,疲劳寿命的变化规律取决于单轴拉压与纯扭的等效von Mises S-N曲线。
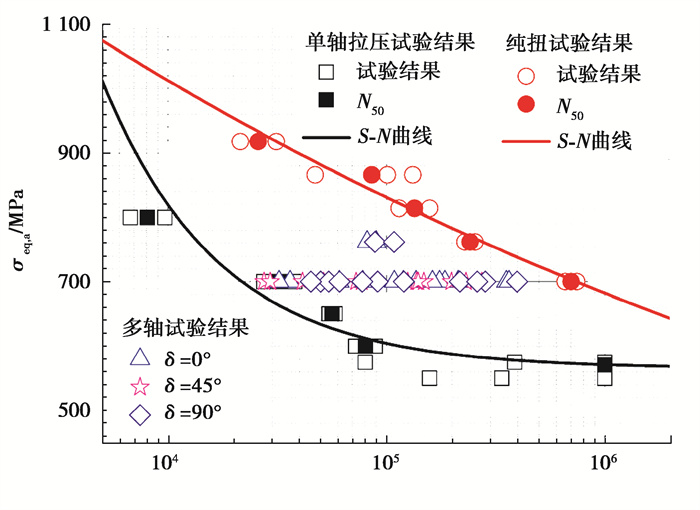
|
图 2 等效S-N曲线及多轴疲劳试验寿命分布[26] Fig. 2 Equivalent S-N curves and the distribution of multi-axial fatigue life[26] |
Papadopoulos[15-17]认为对于硬金属(纯扭疲劳极限与单拉疲劳极限的比值处于
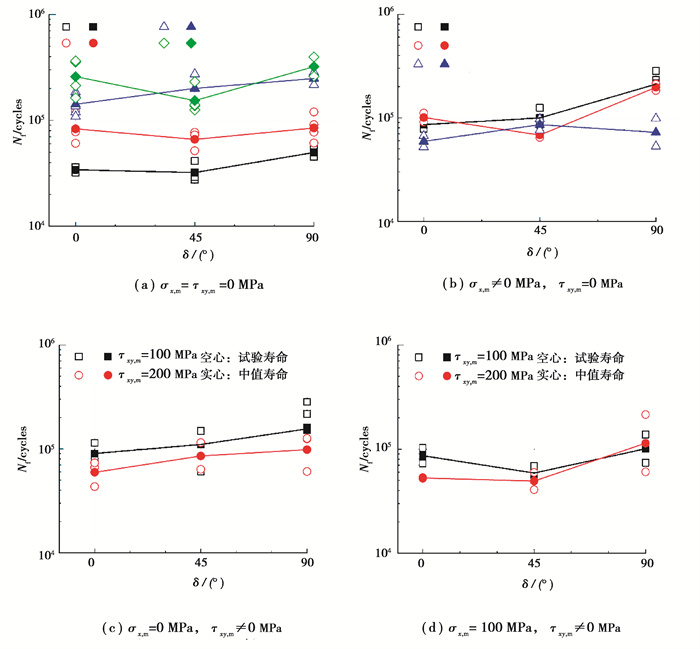
|
图 3 相位差对30CrMnSiA钢多轴疲劳寿命的影响[26, 27] Fig. 3 Effect of phase angles on multiaxial fatigue life[26, 27] |
在相等的等效von Mises应力幅值下,分别定义单轴拉压和纯扭的疲劳寿命为NT和NS,采用式(10)估算不同应力幅比下的多轴疲劳寿命。
| logNλ=λ1+λ(logNS−logNT)+logNT。 | (10) |
当存在平均应力时,采用Goodman准则将正应力或切应力等效为应力比为-1时的应力幅值,定义等效应力幅比为
| λ∗=τ∗xy,aσ∗x,a=(τxy,a1−τxy, mτu)/(σx,a1−σx, mσu)。 | (11) |
存在平均应力时,等效应力幅值表示为
| σ∗eq,a=√(σ∗x,a)2+3(τ∗xy,a)2 。 | (12) |
采用等效S-N曲线进行多轴疲劳寿命预估步骤如下:
1) 采用von Mises应力幅值拟合单轴拉压和纯扭S-N曲线;
2) 根据式(12)计算得到等效应力幅值,并分别计算该等效应力幅值下单轴拉压和纯扭的疲劳寿命;
3) 根据式(11)计算得到等效应力幅比,代入式(10)计算多轴疲劳寿命。
对于存在相位差的情况,采用该方法进行寿命预估时,其预测结果与相位差δ=0°时的情况相同。
2 预测方法验证使用30CrMnSiA钢多轴疲劳试验结果,同时选取文献中共8种金属材料共计318个数据点验证本研究所提出的快速寿命预测方法,8种材料的单轴拉压及纯扭S-N曲线拟合结果及拟合优度见表 1。
| 表 1 单轴拉压及纯扭载荷下等效S-N曲线拟合结果 Table 1 The equivalent S-N curve fitting formula under axial tension-compression and pure torsional |
9种金属材料的预测结果与试验结果的对比如图 4所示,经过数据统计表明,超过94.0%的数据点都处于±3倍疲劳寿命分散带之内,大约81.8%的数据点都处于±2倍疲劳寿命分散带之内,本文所提出的快速寿命预测方法具有一定的适用性。
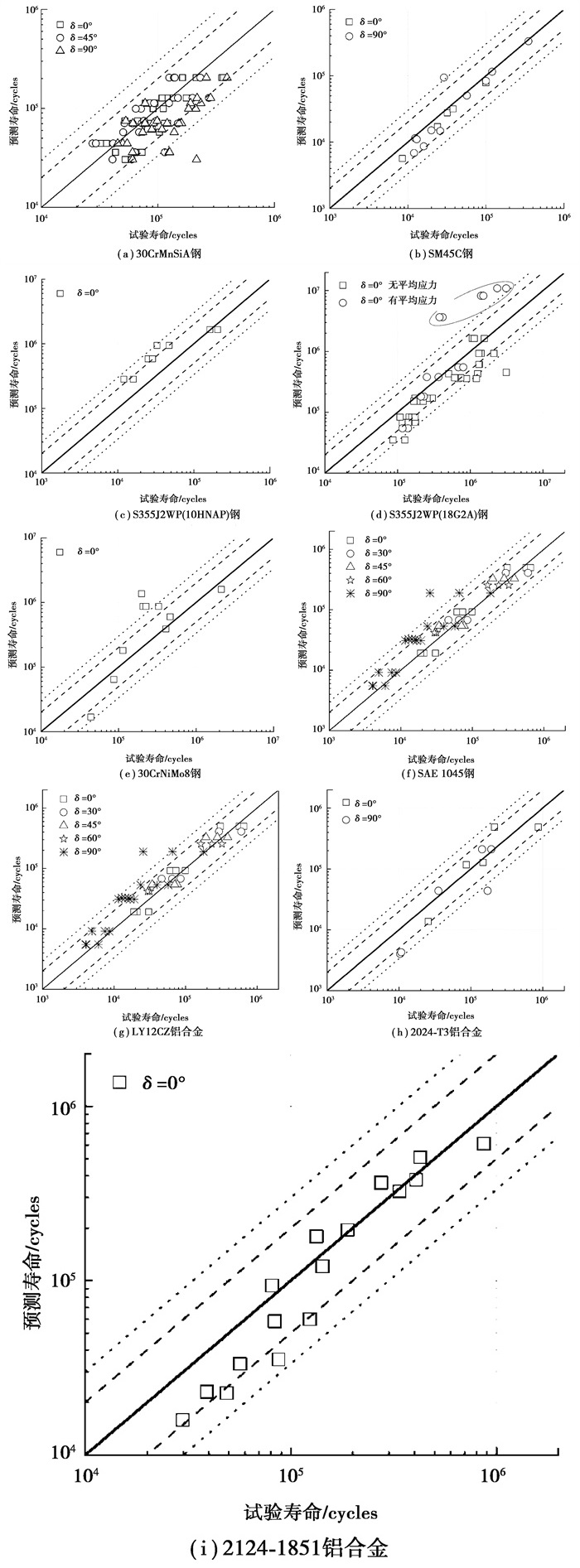
|
图 4 快速预测方法对不同材料疲劳寿命的预测结果 Fig. 4 Predicted results versus test results for different materials |
基于加载参量对30CrMnSiA钢多轴疲劳寿命的影响规律,考虑多轴疲劳加载路径的特点,提出了等效S-N曲线的概念,在此基础上建立了一种多轴高周疲劳寿命快速预测方法。为了验证该方法的适用性,对文献中多种材料的试验结果进行了预测。通过本研究,可以得到如下结论:
1) 在相同的等效von Mises应力幅值下,多轴加载疲劳寿命通常分布于单轴拉压和纯扭S-N曲线之间;
2) 建立的多轴高周疲劳寿命快速预测方法对于多种材料预测结果显示超过94.0%的数据点均处于±3倍疲劳寿命分散带之内,81.8%以上的数据点处于±2倍疲劳寿命分散带之内;
3) 建立的多轴高周疲劳寿命快速预测方法参数获取简单,便于工程应用,并具备较强的适用性。
| [1] |
Wang C, Shang D G, Wang X W. A new multiaxial high-cycle fatigue criterion based on the critical plane for ductile and brittle materials[J]. Journal of Materials Engineering and Performance, 2015, 24(2): 816-824. DOI:10.1007/s11665-014-1335-7 |
| [2] |
亚伯·斯海维. 结构与材料的疲劳[M]. 吴学仁, 等, 译. 北京: 航空工业出版社, 2014. Schijve J. Fatigue of structures and materials[M]. Wu X R, et al, trans. Beijing: Aviation Industry Press, 2014. (in Chinese) |
| [3] |
Socie D, Marquis G. Multiaxial fatigue[M]. Warrendale, Pennsylvania: SAE, 2000.
|
| [4] |
Zhu S P, Yu Z Y, Correia J, et al. Evaluation and comparison of critical plane criteria for multiaxial fatigue analysis of ductile and brittle materials[J]. International Journal of Fatigue, 2018, 112: 279-288. DOI:10.1016/j.ijfatigue.2018.03.028 |
| [5] |
Montalvão D, Qiu S W, Freitas M. A study on the influence of Ni-Ti M-Wire in the flexural fatigue life of endodontic rotary files by using Finite Element Analysis[J]. Materials Science and Engineering: C, 2014, 40: 172-179. DOI:10.1016/j.msec.2014.03.061 |
| [6] |
Reis L, Li B, de Freitas M. A multiaxial fatigue approach to rolling contact fatigue in railways[J]. International Journal of Fatigue, 2014, 67: 191-202. DOI:10.1016/j.ijfatigue.2014.02.001 |
| [7] |
时新红, 鲍蕊, 张建宇, 等. 多轴高周疲劳失效准则的对比分析[J]. 航空动力学报, 2008, 23(11): 2007-2015. Shi X H, Bao R, Zhang J Y, et al. Comparative study of multiaxial high-cycle fatigue-prediction criteria[J]. Journal of Aerospace Power, 2008, 23(11): 2007-2015. (in Chinese) DOI:10.13224/j.cnki.jasp.2008.11.003 |
| [8] |
时新红, 张建宇, 鲍蕊, 等. 材料多轴高低周疲劳失效准则的研究进展[J]. 机械强度, 2008, 30(3): 515-521. Shi X H, Zhang J Y, Bao R, et al. Development of failure criterion on high-cycle and low-cycle multiaxial fatigue[J]. Journal of Mechanical Strength, 2008, 30(3): 515-521. (in Chinese) DOI:10.3321/j.issn:1001-9669.2008.03.034 |
| [9] |
Qi X X, Liu T Q, Shi X H, et al. A sectional critical plane model for multiaxial high-cycle fatigue life prediction[J]. Fatigue & Fracture of Engineering Materials & Structures, 2021, 44(3): 689-704. |
| [10] |
Fatemi A, Shamsaei N. Multiaxial fatigue: an overview and some approximation models for life estimation[J]. International Journal of Fatigue, 2011, 33(8): 948-958. DOI:10.1016/j.ijfatigue.2011.01.003 |
| [11] |
Gough H J. Engineering steels under combined cyclic and static stresses[J]. Journal of Applied Mechanics, 1950, 17(2): 113-125. DOI:10.1115/1.4010088 |
| [12] |
Wang Y Y, Yao W X. Evaluation and comparison of several multiaxial fatigue criteria[J]. International Journal of Fatigue, 2004, 26(1): 17-25. DOI:10.1016/S0142-1123(03)00110-5 |
| [13] |
Dang Van K, Griveau B, Message O. On a new multiaxial fatigue limit criterion: theory and application[C]//Biaxial and Multiaxial Fatigue. London: Mechanical Engineering Publications, 1989: 479-496.
|
| [14] |
Dang van K, Cailletaud G, Flavenot J F, et al. Criterion for high-cycle fatigue failure under multiaxial loading[C]//Biaxial and Multiaxial Fatigue. London: Mechanical Engineering Publications, 1989: 459-478.
|
| [15] |
Papadopoulos I V. A new criterion of fatigue strength for out-of-phase bending and torsion of hard metals[J]. International Journal of Fatigue, 1994, 16(6): 377-384. DOI:10.1016/0142-1123(94)90449-9 |
| [16] |
Papadopoulos I V. A high-cycle fatigue criterion applied in biaxial and triaxial out-of-phase stress conditions[J]. Fatigue & Fracture of Engineering Materials & Structures, 1995, 18(1): 79-91. |
| [17] |
Papadopoulos I V. Long life fatigue under multiaxial loading[J]. International Journal of Fatigue, 2001, 23(10): 839-849. DOI:10.1016/S0142-1123(01)00059-7 |
| [18] |
Morel F. A fatigue life prediction method based on a mesoscopic approach in constant amplitude multiaxial loading[J]. Fatigue & Fracture of Engineering Materials & Structures, 1998, 21(3): 241-256. |
| [19] |
Morel F, Palin-Luc T, Froustey C. Comparative study and link between mesoscopic and energetic approaches in high cycle multiaxial fatigue[J]. International Journal of Fatigue, 2001, 23(4): 317-327. DOI:10.1016/S0142-1123(00)00100-6 |
| [20] |
Kluger K, Karolczuk A, Robak G. Validation of multiaxial fatigue criteria application to lifetime calculation of S355 steel under cyclic bending-torsion loading[J]. Procedia Structural Integrity, 2019, 23: 89-94. DOI:10.1016/j.prostr.2020.01.068 |
| [21] |
Xu S, Zhu S P, Hao Y Z, et al. A new critical plane-energy model for multiaxial fatigue life prediction of turbine disc alloys[J]. Engineering Failure Analysis, 2018, 93: 55-63. DOI:10.1016/j.engfailanal.2018.07.001 |
| [22] |
de Freitas M, Reis L, Meggiolaro M A, et al. Stress scale factor and critical plane models under multiaxial proportional loading histories[J]. Engineering Fracture Mechanics, 2017, 174: 104-116. DOI:10.1016/j.engfracmech.2016.12.016 |
| [23] |
Matsubara G, Nishio K. Multiaxial high-cycle fatigue criterion considering crack initiation and non-propagation[J]. International Journal of Fatigue, 2013, 47: 222-231. DOI:10.1016/j.ijfatigue.2012.09.004 |
| [24] |
Papuga J. Improvements of two criteria for multiaxial fatigue limit evaluation[J]. Bulletin of Applied Mechanics, 2010, 5(20): 80-86. |
| [25] |
Carpinteri A, Boaretto J, Fortese G, et al. Fatigue life estimation of fillet-welded tubular T-joints subjected to multiaxial loading[J]. International Journal of Fatigue, 2017, 101: 263-270. DOI:10.1016/j.ijfatigue.2016.10.012 |
| [26] |
Liu T Q, Shi X H, Zhang J Y, et al. Crack initiation and propagation of 30CrMnSiA steel under uniaxial and multiaxial cyclic loading[J]. International Journal of Fatigue, 2019, 122: 240-255. DOI:10.1016/j.ijfatigue.2019.02.001 |
| [27] |
Liu T Q, Shi X H, Zhang J Y, et al. Multiaxial high-cycle fatigue failure of 30CrMnSiA steel with mean tension stress and mean shear stress[J]. International Journal of Fatigue, 2019, 129: 105219. DOI:10.1016/j.ijfatigue.2019.105219 |
| [28] |
Lee S B. A criterion for fully reversed out-of-phase torsion and bending[M]//Miller K J, Brown M W. Multiaxial fatigue. Philadelphia: ASTM International, 1982: 553-568.
|
| [29] |
Papuga J, Vízková I, Nesládek M, et al. Validation data set for testing the criteria for multiaxial fatigue strength estimation[J]. Fatigue & Fracture of Engineering Materials & Structures, 2018, 41(11): 2259-2271. |
| [30] |
Gasiak G, Pawliczek R. Application of an energy model for fatigue life prediction of construction steels under bending, torsion and synchronous bending and torsion[J]. International Journal of Fatigue, 2003, 25(12): 1339-1346. DOI:10.1016/S0142-1123(03)00055-0 |
| [31] |
Karolczuk A, Kluger K. Analysis of the coefficient of normal stress effect in chosen multiaxial fatigue criteria[J]. Theoretical and Applied Fracture Mechanics, 2014, 73: 39-47. DOI:10.1016/j.tafmec.2014.07.015 |
| [32] |
Karolczuk A, Kluger K, Łagoda T. A correction in the algorithm of fatigue life calculation based on the critical plane approach[J]. International Journal of Fatigue, 2016, 83: 174-183. DOI:10.1016/j.ijfatigue.2015.10.011 |
| [33] |
Yip M C, Jen Y M. Biaxial fatigue crack initiation life prediction of solid cylindrical specimens with transverse circular holes[J]. International Journal of Fatigue, 1996, 18(2): 111-117. DOI:10.1016/0142-1123(95)00057-7 |
| [34] |
Wang Y Y, Yao W X. A multiaxial fatigue criterion for various metallic materials under proportional and nonproportional loading[J]. International Journal of Fatigue, 2006, 28(4): 401-408. DOI:10.1016/j.ijfatigue.2005.07.007 |
| [35] |
Luo P, Yao W X, Susmel L, et al. A survey on multiaxial fatigue damage parameters under non-proportional loadings[J]. Fatigue & Fracture of Engineering Materials & Structures, 2017, 40(9): 1323-1342. |
| [36] |
张成成. 复杂应力场下结构高周疲劳寿命分析[D]. 南京: 南京航空航天大学, 2010. Zhang C C. Fatigue life prediction of structures in HCF region under complex stress field[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010. (in Chinese) |
| [37] |
Gates N R, Fatemi A. On the consideration of normal and shear stress interaction in multiaxial fatigue damage analysis[J]. International Journal of Fatigue, 2017, 100: 322-336. DOI:10.1016/j.ijfatigue.2017.03.042 |
| [38] |
Karolczuk A, Papuga J, Palin-Luc T. Progress in fatigue life calculation by implementing life-dependent material parameters in multiaxial fatigue criteria[J]. International Journal of Fatigue, 2020, 134: 105509. DOI:10.1016/j.ijfatigue.2020.105509 |
 2023, Vol. 46
2023, Vol. 46



