随着社会经济发展、汽车技术进步和汽车制造成本降低，汽车成为生活中不可或缺的交通工具^[1]。车辆数量剧增造成了交通和汽车安全问题。根据世界卫生组织统计，2015年全球约130万人死于交通事故，交通事故成为引起人员死亡的第一原因^[2]。驾驶员误操纵造成的交通事故占总交通事故比例较高^[3]。智能汽车能够减轻驾驶员的负担和压力，较驾驶员控制快且准，成为降低交通事故的有效途径。鉴于此，越来越多的高校、企业和研究院积极开展此技术研究。

智能汽车避障，尤其侧向避障容易造成交通事故且影响交通系统中其他车辆运行成为智能汽车控制的重要研究问题^[4]。针对此问题，国内外学者采用各种方式进行了深入研究。He等^[5]综合考虑避障安全性和车辆稳定性，基于前轮转向系统，采用运动学和动力学相结合的分层控制策略方式，提出了危险工况的避障控制策略。Gao等^[6]针对湿滑路面，采用分层控制方式，上层基于简化模型实时规划避障轨迹，下层基于模型预测控制算法跟踪上层规划轨迹。Shim等^[7]基于主动转向和差动制动集成，采用6次多项式进行避障轨迹规划，并应用模型预测控制算法对规划的轨迹进行跟踪控制，实现了自动驾驶车辆避障控制。Shah等^[8]采用电子助力转向系统，基于最大加速度和需求侧向位移设计变道通道，提出了后部防碰撞控制策略。Cui等^[9]基于转向系统和差动制动集成，提出了防后端碰撞控制策略。以上研究只针对了静止和匀速障碍物，未对障碍物速度和加速度动态变化进行研究。Erlien等^[10]通过设置极限操纵和障碍物2个安全区，提出了人车共驾的半主动驾驶车辆避障控制策略。Ji等^[11]基于路径规划和路径跟踪的架构，基于车辆与障碍物即将碰撞来规划期望避障轨迹，并采用多约束的模型预测算法实现期望轨迹跟踪控制。Anderson等^[12]针对紧急的避障工况，通过评估危险程度来规划最优避障轨迹，进而实现紧急情况的避障控制。但研究未考虑避障过程中智能汽车车速动态变化，并且未考虑传感器信号噪声干扰。Gao等^[13]针对附着极限工况，基于改进哈密顿算法，采用转向和制动结合方法，提出了避障自动驾驶车辆的避障控制策略。任玥等^[14]基于分层控制方式，利用模型预测控制算法，进行避障轨迹规划和轨迹跟踪控制，实现车辆主动避障控制。王其东等^[15]基于转向和制动相结合，考虑路面附着条件限制，实现了紧急情况的车辆避障控制。但上述研究未考虑汽车质量和转动惯量的参数摄动。Lian等^[16]针对四轮独立电动汽车，基于鲁棒控制方法，提出了侧向避障控制策略，实现了电动汽车良好避障；但未考虑随车辆状态实时变化的前后侧偏刚度参数摄动和障碍物汽车加速度动态变化。Hajiloo等^[17]针对静止障碍物，采用MPC控制算法，进行了智能车辆的避障控制。但此研究只针对静止障碍物且MPC算法存在计算量较大问题。Yang等^[18]考虑周围汽车车速动态变化，通过监测周围汽车速度等信息，提出了自动驾驶汽车变道动态轨迹规划算法。但未考虑动态轨迹规划与轨迹跟踪动态相互影响，即轨迹跟踪效果会影响实时轨迹规划。

很多研究针对避障的障碍物为静止物体或车辆，而实际交通环境下，速度较慢的汽车也是障碍物；同时，有些学者研究了动态障碍物，但障碍物速度匀速即速度不发生变化，而实际交通环境下障碍物汽车速度是动态变化的，即可能存在加减速。因此，侧向避障控制应该实时感知障碍物汽车加速度和速度等变化，实时动态规划避障安全轨迹。由于汽车载货或载客量等变化，将造成质量和转动惯量等参数摄动，从而影响避障控制系统最优控制；同时，汽车状态实时变化造成前后侧偏刚度参数动态摄动。而以往避障研究较少考虑参数摄动，尤其是前后侧偏刚度参数动态摄动，传感器信号可能存在信号干扰。针对智能汽车避障控制研究的不足，研究提出了考虑参数摄动的智能汽车动态侧向避障鲁棒控制策略。此控制策略针对障碍物汽车加速度和速度动态变化信息，实时动态规划避障轨迹，从而获得实际交通环境安全的动态避障参考轨迹。同时，为实现智能汽车动态侧向避障鲁棒精准控制，控制策略不仅考虑了汽车质量和转动惯量参数摄动，也考虑了随车辆状态变化而变化的前后侧偏刚度动态参数摄动，以及传感器信号噪声干扰；并且，采用增益调度方式应对动态避障过程中的智能汽车车速变化。最终，利用MATLAB/Simulink和Trucksim联合仿真，验证所提控制策略控制效果。

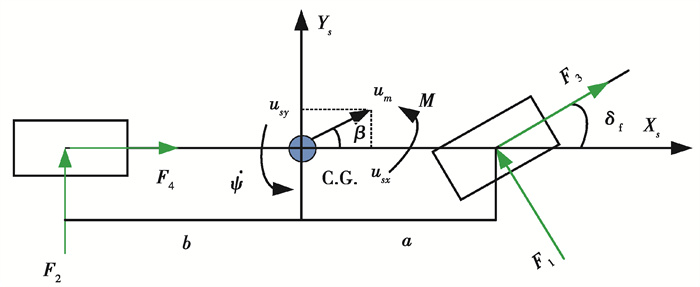
1 简化模型

根据考虑参数摄动的智能汽车动态侧向避障鲁棒控制策略的需求，建立汽车简化模型，如图 1所示。

动力学方程

$ m\left(\dot{u}_{s x}-\dot{\psi} u_{s x} \beta\right)=F_3 \cos \delta_{\mathrm{f}}+F_4-F_1 \sin \delta_{\mathrm{f}}, $

(1)

$ m u_{s x}(\dot{\beta}+\dot{\psi})=F_1 \cos \delta_{\mathrm{f}}+F_2+F_3 \sin \delta_{\mathrm{f}}, $

(2)

$ I_{z z} \ddot{\psi}=\left(F_1 \cos \delta_{\mathrm{f}}+F_3 \sin \delta_{\mathrm{f}}\right) a-F_2 b+\Delta \boldsymbol{M}。$

(3)

其中：m为车辆质量；u_sx, $\dot{u}_{s x}$分别为车辆坐标系纵向速度和加速度；u_m为车辆速度；$\psi, \dot{\psi}, \ddot{\psi}$分别为航向角、角速度和角加速度；$\beta, \dot{\beta}$分别为质心侧偏角和角速度；F₁, F₂为前后轴侧向力；F₃, F₄为前后轴纵向力；δ_f为前轴转角；X_s, Y_s分别为车辆坐标系X和Y轴；a为质心到前轴距离；β为质心侧偏角；I_zz为横摆转动惯量；b为质心到后轴距离；ΔM为附加力矩。

侧向避障控制主要关注的是车辆侧向运动和位姿；并且每一个采样时刻，可以认为车辆纵向速度一定。因此，上面模型可以简化为二自由度侧向简化模型。在文献[19-21]采用此简化模型进行智能车辆路径跟随控制。此二自由度分别为表征侧向避障位移的侧向运动以及侧向避障车辆的横摆运动，为智能汽车动态侧向避障鲁棒控制策略奠定了必要基础^[22]。同时，假设车轮转角等角度较小，模型进行简化处理。

轮胎模型

$ F_1=k_{\mathrm{f}}\left(\beta+\frac{a}{u_{s x}} \dot{\psi}-\delta_{\mathrm{f}}\right), $

(4)

$ F_2=k_{\mathrm{r}}\left(\beta-\frac{b}{u_{s x}} \dot{\psi}\right) \text { 。} $

(5)

式中：k_f, k_r分别为前后轴侧偏刚度。

研究针对四轮独立驱动客车进行研究。在动态避障过程中，智能汽车根据外部环境变化设置目标车速。根据目标车速，智能汽车决策出每个车轮的驱动力。所提控制策略在保证总驱动力不变的情况下，通过调整每个车轮驱动力增减量来实现控制策略决策的附加力矩。如果控制策略决策的附加力矩为零，则各轮驱动力不变。假设前后轴长度相等。

$ \Delta \boldsymbol{M}=\left(\Delta F_{x 2} \cos \delta_{\mathrm{f}}+\Delta F_{x 4}\right) l_w-\left(\Delta F_{x 1} \cos \delta_{\mathrm{f}}+\Delta F_{x 3}\right) l_{w}。$

(6)

式中：l_w为前后轴半轴长；ΔF_x1…ΔF_x4为各车轮纵向力增量。

简化模型状态空间

$ \left\{\begin{array}{l} \dot{x}=\boldsymbol{A} \boldsymbol{x}+\boldsymbol{Bu} \boldsymbol{}, \\ y=\boldsymbol{C} \boldsymbol{x}, \end{array}\right. $

(7)

式中：$\boldsymbol{u}=\left[\delta_{\mathrm{f}} \Delta \boldsymbol{M}\right]^{\mathrm{T}}, \boldsymbol{M}=\left[\begin{array}{cc} m u_{s x} & 0 \\ 0 & I_{z z} \end{array}\right]$，$\boldsymbol{x}=\left(\begin{array}{ll} \beta & \dot{\psi} \end{array}\right)^{\mathrm{T}}, \boldsymbol{G}=\left[\begin{array}{cc} k_{\mathrm{f}}+k_r & -m u_{s x}+a k_{\mathrm{f}} / u_{s x}-b k_r / u_{s x} \\ a k_{\mathrm{f}}-b k_r & \left(a^2 k_{\mathrm{f}}+b^2 k_r\right) / u_{s x} \end{array}\right]$，$\boldsymbol{S}=\left[\begin{array}{cc} -k_{\mathrm{f}} & 0 \\ -k_{\mathrm{f}} a & 1 \end{array}\right], \boldsymbol{A}=\boldsymbol{M}^{-1} \boldsymbol{G}, \boldsymbol{B}=\boldsymbol{M}^{-1} \boldsymbol{S}$，$\boldsymbol{y}=\left[\begin{array}{ll} \beta & \dot{\psi} \end{array}\right]^{\mathrm{T}} \quad \boldsymbol{C}=\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]$；u为控制向量；B为控制量输入矩阵；y为输出状态；A为状态矩阵；M, S, G都为转换矩阵；C为输出状态矩阵；x为状态向量。

2 动态侧向避障鲁棒控制策略

基于参数摄动的智能汽车动态侧向避障鲁棒控制策略分为2层，上层动态轨迹规划层，即实时感知障碍物汽车加速度和速度变化，以智能汽车与障碍物汽车避障极限位置为边界，实时动态规划侧向避障安全参考轨迹，并基于动态参考轨迹获得实时的航向角速度和质心侧偏角期望值；下层动态轨迹跟踪层，即考虑质量和转动惯量参数和随车辆状态变化而动态变化的前后侧偏刚度参数摄动，设计基于参数摄动的鲁棒控制器，实现动态轨迹鲁棒跟踪控制；并且考虑避障过程智能汽车速度变化，采用增益调度方法实现变速避障精准控制。

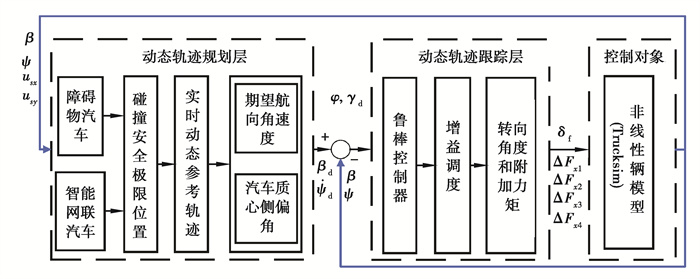
通过上层轨迹实时规划和下层实时跟踪此刻轨迹，并根据障碍物汽车和智能汽车状态实时动态变化，整个避障过程实时调整轨迹，从而实现智能汽车实际交通环境的安全动态侧向避障控制，具体控制策略控制框如图 2所示。采用转向与附加力矩相结合的方式，有利于提高动态侧向避障过程的车辆稳定性。

2.1 侧向避障动态轨迹规划 2.1.1 实时参考轨迹

动态轨迹规划首先需要选择基本轨迹线型。多种线型用于侧向避障轨迹规划，例如，B样条曲线、螺旋曲线、多项式曲线、正余弦曲线、梯形曲线和圆形曲线等。各种曲线都有各自优点和缺点，为了能够根据外界环境变化，快速简单高效地规划出智能汽车侧向避障实时安全最优轨迹且保证在轨迹完成后无侧向速度，采用文献[23-24]所采用的余弦曲线作为侧向避障轨迹动态规划曲线，并假设智能汽车避障初始位置和终止位置都为相应车道中心线位置，即车辆在车道中央行驶。初始位置之前和终止位置之后的调整曲线为相应车道中心线。避障规划曲线函数为

$ Y_{\mathrm{r}}=\frac{R_{\mathrm{e}} X_{\mathrm{r}}}{D}-\frac{R_{\mathrm{e}}}{2 \pi} \sin \left(\frac{2 \pi X_{\mathrm{r}}}{D}\right), $

(8)

式中：D为避障轨迹曲线的纵向长度；Y_r为曲线侧向位移；X_r为曲线纵向位移；R_e为车道宽度。

由公式(8)可知，曲线参数为车道宽度和侧向避障轨迹的纵向长度，而车道宽度一般为固定的，因此轨迹纵向长度决定轨迹曲线变化，即通过改变轨迹纵向长度就能够实时规划动态侧向避障的参考轨迹。

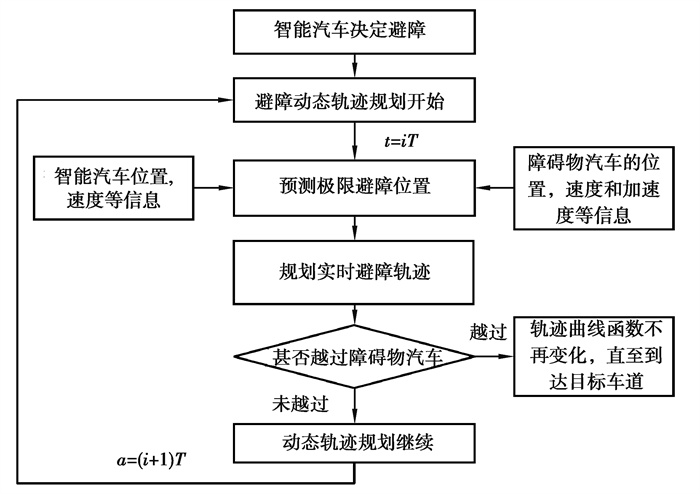
避障轨迹动态规划流程图如图 3所示。当智能汽车决定避障，即开始启动动态避障轨迹规划。首先，根据自车位置，速度等信息，结合障碍物汽车的位置，速度和加速度等信息，基于极限位置假设，预测极限避障位置；其次，根据预测避障位置，规划实时避障轨迹。同时，如果智能汽车侧向位移已经超过障碍物汽车的最外点，智能汽车将不会与障碍物汽车发生避障，实际上智能汽车已经完成了避障。因此，需要判断智能汽车是否越过障碍物汽车，如果越过了，避障轨迹形状将不发生变化，并利用此形状不变的轨迹，控制智能汽车变道到目标车道；如果没有越过，动态轨迹规划继续，根据障碍物汽车状态变化，实时调整避障轨迹形状。

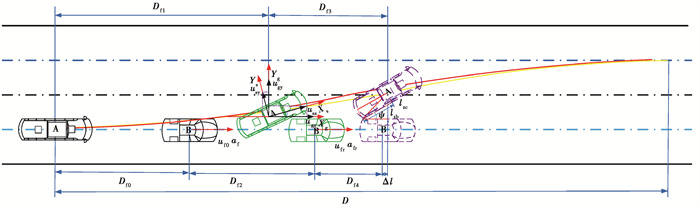
图 4显示了智能汽车侧向避障动态轨迹过程，车辆A为智能汽车，车辆B为障碍物汽车。假设智能车辆行驶在平直道路上，不考虑道路的弯道和坡度。黑实线车辆、绿实线车辆和紫虚线车辆分别为决定开始避障的初始位置、实时位置以及实时位置预测的车辆避障极限位置。红线为实时位置前一时刻规划的避障轨迹，智能汽车以此参考轨迹由实时位置前一时刻运行到实时位置；黄线为实时位置动态规划的实时时刻运行到下一时刻的侧向避障实时参考轨迹。以实时位置为例，介绍智能汽车侧向避障动态轨迹规划。基于实时的障碍物汽车车速和加速度以及智能车辆车速和航向角等状态，在每一个采样时刻，假设预测时间内，智能汽车大地坐标系下的纵向车速和航向角不变，进而预测智能汽车和障碍物汽车形成极限避障位置，如图 4所示。

通过相关计算，获得预测避障极限位置的纵向距离和横向距离；因预测避障极限位置为侧向避障参考轨迹上的点，进而代入公式(8)，求解出公式中曲线的纵向位移，从而规划出此时刻侧向避障参考轨迹。整个侧向避障过程中，通过滚动方式反复上述过程，实时获得动态的智能汽车避障参考轨迹。为了保证避障控制冗余，对障碍物汽车进行蓬松化处理，即将障碍物汽车进行等比例放大，使规划的避障参考轨迹更为保守，以保证避障控制过程中以智能汽车后部动态规划的避障轨迹能够保证包括前部在内的智能汽车整车避障安全性。并且，在实际应用中，蓬松化因子能够根据前后车辆速度加速度，障碍物前车宽度和智能汽车状态等进行调整。

智能汽车车速为车辆坐标系下的车速，为了满足轨迹跟踪的需要，将智能汽车车速从车辆坐标系转换到大地坐标系。

智能汽车大地坐标系下纵侧向速度

$ u_{\mathrm{g} x}=u_{\mathrm{s} x} \cos \psi-u_{\mathrm{s} y} \sin \psi, $

(9)

$ u_{\mathrm{g} y}=u_{\mathrm{s} x} \sin \psi+u_{\mathrm{s} y} \cos \psi \text { 。} $

(10)

式中：u_gx，u_gy为大地坐标系下的智能汽车纵向和侧向速度。

智能汽车从初始位置到实时位置的纵向行驶距离

$ D_{\mathrm{f} 1}=\int u_{\mathrm{g} x} \mathrm{d} t 。$

(11)

障碍物汽车从初始位置到实时位置的纵向行驶距离

$ D_{\mathrm{f} 2}=\int u_{f 0}+a_{\mathrm{f}} t \mathrm{d} t , $

(12)

式中：u_f0为障碍物汽车初始位置的速度；a_f为实时时刻之前的智能汽车加速度。

智能汽车在实时位置到预测极限避障位置的运行距离见公式(13)。假设从实时位置到预测位置，智能汽车的大地坐标系下纵向车速和航向角不变。不考虑在预测时间内，由于障碍物汽车制动而智能汽车采取制动；并且，此算法为动态过程，下一刻的智能汽车速度将会进行更新。

$ D_{\mathrm{f} 3}=u_{\mathrm{g} x} t_p, $

(13)

式中：D_f3为智能汽车从实时位置到预测避障极限位置的纵向距离。

障碍物汽车从实时位置到预测极限安全避障位置运行距离见公式(14)，假设障碍物汽车从实时位置到预测极限位置，障碍物汽车加速度不变。

$ D_{\mathrm{f} 4}=u_{\mathrm{fr}} t_{\mathrm{p}}+\frac{1}{2} a_{\mathrm{fr}}\left(t_{\mathrm{p}}\right)^2 。$

(14)

式中：D_f4为障碍物汽车从实时位置到预测避障极限位置的距离；u_fr、a_fr分别为障碍物汽车实时位置的速度和加速度；t_p为实时位置到预测避障极限位置的预测时间。

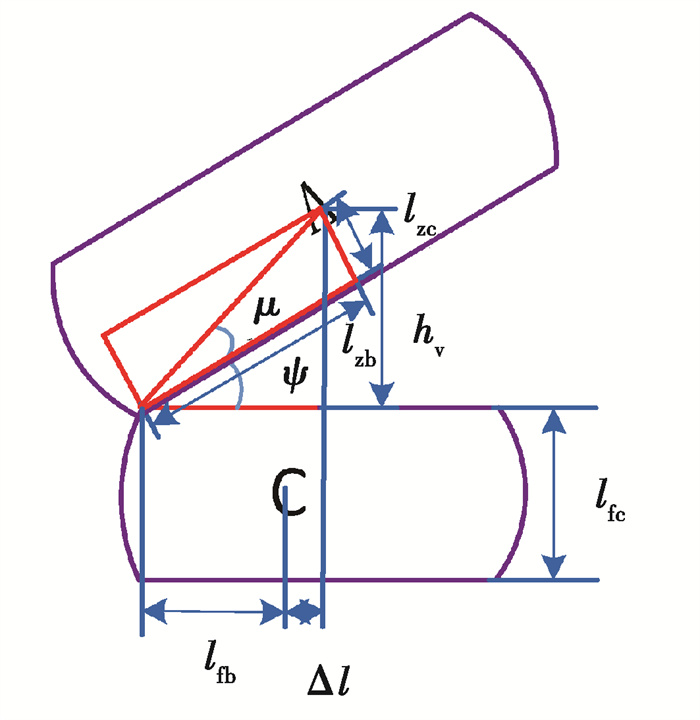
为能够将预测避障极限位置描述更为详细清晰，将预测避障极限位置两车状态从图 4独立出形成图 5。同时，障碍物汽车的信息，例如质心位置等，可以通过车车通讯，传递到智能汽车。

智能汽车极限避障点与质心形成的夹角。

$ \mu=\operatorname{atan}\left(\frac{l_{\mathrm{zc}}}{l_{\mathrm{zb}}}\right), $

(15)

智能汽车与障碍物汽车边缘侧向距离。

$ h_{\mathrm{v}}=\sqrt{\left(l_{\mathrm{zc}}\right)^2+\left(l_{\mathrm{zb}}\right)^2} \sin (\mu+\psi), $

(16)

式中：l_zc、l_zb分别为智能汽车半车宽和质心位置到极限位置车辆坐标系的纵向距离。

智能汽车质心位置与障碍物汽车质心位置的纵向距离差值。

$ \Delta l=\sqrt{\left(l_{\mathrm{zc}}\right)^2+\left(l_{\mathrm{zb}}\right)^2} \cos (\mu+\psi)-l_{\mathrm{fb}}, $

(17)

式中：l_fb为质心位置到避障极限位置的纵向距离；μ为智能汽车极限避障点到质心位置的夹角。

由图 4位置几何关系可获得公式(18)。

$ D_{\mathrm{f} 0}+D_{\mathrm{f} 2}+D_{\mathrm{f} 4}=D_{\mathrm{f} 1}+D_{\mathrm{f} 3}-\Delta l \text { 。} $

(18)

式中：Δl为避障极限位置智能汽车和障碍物汽车大地坐标系下质心位置的纵向距离差值。

借助公式(18)，并将相应公式代入，即可获得智能汽车从实时位置到预测的侧向避障极限位置的运行时间t_p，并将时间t_p代入相应公式中可获得相应距离。

侧向避障极限位置的纵向和侧向距离。

$ X_{\mathrm{p}}=D_{\mathrm{f} 1}+D_{\mathrm{f} 3}, $

(19)

$ Y_{\mathrm{p}}=\frac{l_{\mathrm{fc}}}{2}+h_{\mathrm{v} 。} $

(20)

式中：l_fc为障碍物汽车的车宽到避障极限位置的纵向距离；X_p、Y_p为侧向避障极限位置的纵向和侧向距离。

避障安全极限位置为实时时刻规划的侧向避障轨迹上一点，因此，将相应坐标代入公式(8)，能够反求轨迹曲线长度D，从而获得此时刻侧向避障实时安全参考避障轨迹曲线。同时，一旦智能汽车实现了避障后，轨迹曲线函数的纵向长度参数不再调整，即变道正弦曲线线型不再变化，沿着原来的正弦曲线继续变道，直到成功变道到目标车道。若智能汽车到达目标车道后，智能汽车继续运行的参考目标轨迹为目标车道中心线。

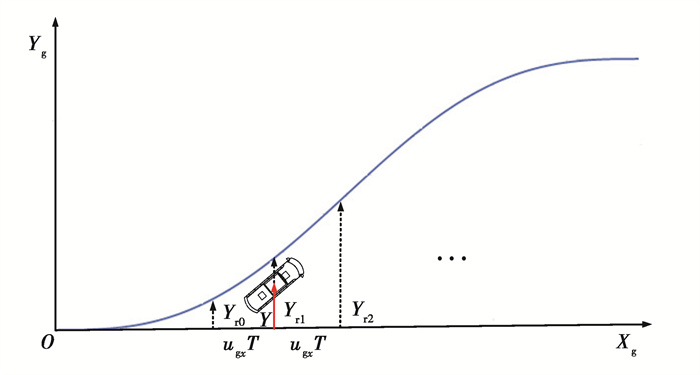
2.1.2 实时轨迹期望值

为了实现智能汽车顺利安全避障，就需要对侧向避障实时动态轨迹进行跟踪。轨迹跟踪涉及到侧向位移和航向角跟踪。航向角跟踪通过航向角速度来跟踪；侧向位移可以通过跟踪侧向速度，也可以通过跟踪质心侧偏角，本质上等效。并且，质心侧偏角能够通过估算算法估计获得。鉴于此，所提侧向避障鲁棒控制策略跟踪实时参考轨迹的航向角速度和质心侧偏角。通过预瞄实时变道轨迹曲线，获得实时航向角和质心侧偏角期望值，如图 6所示。

航向角参考值^[25]

$ \psi_{\mathrm{d}} \approx \frac{\Delta y_{\mathrm{r}}}{\Delta x_{\mathrm{r}}}=\frac{y_{\mathrm{r} 2}-y_{\mathrm{r} 1}}{u_{\mathrm{g} x} T}, $

(21)

式中：y_r1为实时时刻轨迹侧向位置值；y_r2为实时时刻下一时刻轨迹侧向位置值；T为采用时间。

航向角速度期望值

$ \dot{\psi}_{\mathrm{d}} \approx \frac{\Delta \psi_{\mathrm{d}}}{T}=\left(\frac{y_{\mathrm{r} 2}-y_{\mathrm{r} 1}}{u_{\mathrm{g} x} T}-\frac{y_{\mathrm{r} 1}-y_{\mathrm{r} 0}}{u_{\mathrm{g} x} T}\right) / T=\frac{y_{\mathrm{r} 2}-2 y_{\mathrm{r} 1}+y_{\mathrm{r} 0}}{u_{\mathrm{g} x} T^2} 。$

(22)

式中：y_r0为实时时刻上一时刻轨迹侧向位置值

质心侧偏角期望值^[25]

$ \beta_{\mathrm{d}} \approx \operatorname{atan}\left(\frac{u_{\mathrm{g} y}}{u_{\mathrm{g} x}}\right)-\psi_{\mathrm{d} 。} $

(23)

2.2 动态避障轨迹跟踪鲁棒控制

由于汽车侧向避障较为危险，因此控制系统需要保证侧向避障动态轨迹精准跟踪，进而实现智能汽车安全侧向避障。但智能汽车质量和转动惯量以及前后侧偏刚度参数会发生摄动，并且智能汽车速度动态变化以及传感器信号干扰，从而影响控制器参考轨迹精准控制跟踪。鉴于此，针对参数摄动和智能汽车速度变化，设计了基于增益调度的鲁棒控制策略，以实现侧向避障动态参考轨迹良好跟踪。

2.2.1 线性分式变换

车辆载荷等发生变化，造成质量和转动惯量参数摄动；同时，前后侧偏刚度随着车辆实时状态变化而实时变化，从而形成了动态参数摄动。虽然这些参数不确定，但其在一定范围内变化。因此，选取这些参数的平均值作为名义值，并选择变化比例，实现这些参数变化值全覆盖，如公式(24)。

$ \left\{\begin{array}{l} m=\bar{m}\left(1+p_{\mathrm{m}} \sigma_{\mathrm{m}}\right), \\ I_{z z}=\bar{I}_{z z}\left(1+p_{{I}} \sigma_I\right), \\ \bar{k}_{\mathrm{f}}=\bar{k}_{\mathrm{f}}\left(1+p_{\mathrm{f}} \sigma_{\mathrm{f}}\right), \\ k_{\mathrm{r}}=\bar{k}_{\mathrm{r}}\left(1+p_{\mathrm{r}} \sigma_{\mathrm{r}}\right) 。\end{array}\right. $

(24)

基于公式(24)，获得这4个参数的线性分式形式公式(25)；注意在模型中质量存在倒数形式，所以需要将其倒数作为另外一个变量^[26]。

$ \left\{\begin{array}{l} \frac{1}{m}=\frac{1}{\bar{m}}-\frac{p_{\mathrm{m}}}{\bar{m}} \sigma_{\mathrm{m}}\left(1+p_{\mathrm{m}} \delta_{\mathrm{m}}\right)^{-1}=F_u\left(\boldsymbol{M}_{\mathrm{m} 1}, \sigma_{\mathrm{m}}\right), \\ m=\bar{m}\left(1+p_{\mathrm{m}} \sigma_{\mathrm{m}}\right)=F_u\left(\boldsymbol{M}_{m 2}, \sigma_{\mathrm{m}}\right), \\ \frac{1}{I_{z z}}=\frac{1}{\bar{I}_{z z}}-\frac{p_I}{\bar{I}_{z z}} \sigma_I\left(1+p_I \sigma_I\right)^{-1}=F_u\left(\boldsymbol{M}_{\mathrm{I}}, \sigma_I\right), \\ k_{\mathrm{f}}=\bar{k}_{\mathrm{f}}\left(1+p_{\mathrm{f}} \sigma_{\mathrm{f}}\right)=F_u\left(\boldsymbol{M}_{\mathrm{f}}, \sigma_{\mathrm{f}}\right), \\ k_{\mathrm{r}}=\bar{k}_{\mathrm{r}}\left(1+p_{\mathrm{r}} \sigma_{\mathrm{r}}\right)=F_u\left(\boldsymbol{M}_{\mathrm{r}}, \sigma_{\mathrm{r}}\right) 。\end{array}\right. $

(25)

式中：$\boldsymbol{M}_{\mathrm{m} 1}=\left[\begin{array}{cc} -p_{\mathrm{m}} & \frac{-p_{\mathrm{m}}}{\bar{m}} \\ 1 & \frac{1}{\bar{m}} \end{array}\right], \boldsymbol{M}_{\mathrm{m} 2}=\left[\begin{array}{cc} 0 & p_{\mathrm{m}} \bar{m} \\ 1 & \bar{m} \end{array}\right]$，$\boldsymbol{M}_{\mathrm{I}}=\left[\begin{array}{cc} -p_{{I}} & \frac{-p_{{I}}}{I_{z z}} \\ 1 & \frac{1}{I_{z z}} \end{array}\right], \boldsymbol{M}_{\mathrm{f}}=\left[\begin{array}{cc} 0 & p_{\mathrm{f}} \bar{k}_{\mathrm{f}} \\ 1 & \bar{k}_{\mathrm{f}} \end{array}\right], \boldsymbol{M}_{\mathrm{r}}=\left[\begin{array}{cc} 0 & p_{\mathrm{m}} \bar{k}_{\mathrm{r}} \\ 1 & \bar{k}_{\mathrm{r}} \end{array}\right]$。

2.2.2 参数不确定性车辆简化

将公式(7)结合参数摄动线性分式公式(25)形成参数不确定车辆简化模型式(26), 为考虑参数摄动的智能汽车动态避障鲁棒控制策略奠定必要基础。模型状态空间输入输出分别为${\left[ {\begin{array}{*{20}{l}} \beta &{\dot \psi }&{{\mu _{{\rm{m}}1}}}&{{\mu _{{\rm{m}}2}}}&{{\mu _{\rm{I}}}}&{{\mu _{\rm{f}}}}&{{\mu _{\rm{f}}}}&{{\mu _{\rm{r}}}}&{{\mu _{\rm{r}}}}&{{\delta _{\rm{f}}}}&{\Delta M} \end{array}} \right]^{\rm{T}}}, {\left[ {\begin{array}{*{20}{l}} {\dot \beta }&{\dot \psi }&{{y_{{\rm{m}}1}}}&{{y_{{\rm{m}}2}}}&{{y_{{\rm{m}}3}}}&{{y_{{\rm{m}}4}}}&{{y_{{\rm{m}}5}}}&{{y_{{\rm{m}}6}}}&{{y_{{\rm{m}}7}}}&\beta &{\dot \psi } \end{array}} \right]^{\rm{T}}}$。μ_m1…μ_r和y_m1…y_m7分别为鲁棒控制器小增益推导过程量。参数不确定车辆简化模型具体推导过程可详细参考文献[26-27]。

$ \boldsymbol{G}_{\mathrm{m}}=\left[\begin{array}{lll} \boldsymbol{A}_{\mathrm{m}} & \boldsymbol{B}_{\mathrm{m} 1} & \boldsymbol{B}_{\mathrm{m} 2} \\ \boldsymbol{C}_{\mathrm{m} 1} & \boldsymbol{D}_{\mathrm{m} 11} & \boldsymbol{D}_{\mathrm{m} 12} \\ \boldsymbol{C}_{\mathrm{m} 2} & \boldsymbol{D}_{\mathrm{m} 21} & \boldsymbol{D}_{\mathrm{m} 22} \end{array}\right], $

(26)

式中：$\boldsymbol{A}_m=\left[\begin{array}{cc} \frac{\left(\bar{k}_{\mathrm{f}}+\bar{k}_{\mathrm{r}}\right)}{\bar{m} u_{s x}} & \frac{\left(a \bar{k}_{\mathrm{f}}-b \bar{k}_{\mathrm{r}}\right)}{\bar{m}\left(u_{s x}\right)^2}-1 \\ \frac{a \bar{k}_{\mathrm{f}}-b \bar{k}_{\mathrm{r}}}{\bar{I}_{z z}} & \frac{a^2 \bar{k}_{\mathrm{f}}+b^2 \bar{k}_{\mathrm{r}}}{\bar{m} u_{s x}} \end{array}\right] ;\boldsymbol{B}_{m 1}\left[\begin{array}{c} 1 & -\frac{1}{\bar{m}} & 0 & \frac{p_{\mathrm{f}}}{\bar{m} u_{s x}} & 0 & \frac{p_{\mathrm{r}}}{\bar{m} u_{s x}} & 0 \\ 0 & 0 & 1 & 0 & \frac{p_{\mathrm{f}}}{\bar{I}_{z z}} & 0 & \frac{p_{\mathrm{r}}}{\bar{I}_{z z}} \end{array}\right], \boldsymbol{B}_{m 2}=\left[\begin{array}{ccc} \bar{k}_{\mathrm{f}} & 0 \\ \bar{m} u_{s x} & 0 \\ -\frac{a \bar{k}_{\mathrm{fr}}}{\bar{I}_{z z}} & \frac{1}{\bar{I}_{z z}} \end{array}\right]$；${{\boldsymbol{C}}_{{\rm{m1}}}} = \left[ {\begin{array}{*{20}{c}} { - \frac{{{p_m}\left( {{{\bar k}_{\rm{f}}} + {{\bar k}_{\rm{r}}}} \right)}}{{{{\bar m}_{{\rm{s}}x}}}}}&{ - \frac{{{p_m}\left( {a{{\bar k}_{\rm{f}}} - b{{\bar k}_{\rm{r}}}} \right)}}{{\bar m{{\left( {{u_{{\rm{s}}x}}} \right)}^2}}} + {p_m}}\\ 0&{{p_m}m - }\\ { - \frac{{{p_I}\left( {a{{\bar k}_{\rm{f}}} - b{{\bar k}_{\rm{r}}}} \right)}}{{{{\bar I}_{zz}}}}}&{ - \frac{{{p_I}\left( {{a^2}{{\bar k}_{\rm{f}}} + {b^2}{{\bar k}_{\rm{r}}}} \right)}}{{{{\bar I}_{zz}}{u_{sx}}}}}\\ {{{\bar k}_{\rm{f}}}}&{\frac{{a{{\bar k}_{\rm{f}}}}}{{{u_{{\rm{s}}x}}}}}\\ {a{{\bar k}_{\rm{f}}}}&{\frac{{{a^2}{{\bar k}_{\rm{f}}}}}{{{u_{sx}}}}}\\ {{{\bar k}_{\rm{r}}}}&{ - \frac{{b{{\bar k}_{\rm{r}}}}}{{{u_{sx}}}}}\\ { - b\bar k}&{\frac{{{b^2}\bar k}}{{{u_{{\rm{s}}x}}}}} \end{array}} \right]$；$\boldsymbol{D}_{\mathrm{m11}}=\left[\begin{array}{ccccccc} -p_{\mathrm{m}} & \frac{p_{\mathrm{m}}}{\bar{m}} & 0 & -\frac{p_{\mathrm{f}} p_{\mathrm{m}}}{\bar{m} u_{s x}} & 0 & -\frac{p_{\mathrm{m}} p_{\mathrm{r}}}{\bar{m} u_{s x}} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & -p_I & 0 & -\frac{p_{\mathrm{f}} p_I}{\bar{I}_{z z}} & 0 & -\frac{p_I p_{\mathrm{r}}}{\bar{I}_{z z}} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right]$；$\boldsymbol{D}_{\mathrm{m} 12}=\left[\begin{array}{ccccccc} \frac{p_{\mathrm{m}} \bar{k}_{\mathrm{f}}}{\bar{m} u_{s x}} & 0 & \frac{p_I a \bar{k}_{\mathrm{f}}}{\bar{I}_{z z}} & -\bar{k}_{\mathrm{f}} & -a \bar{k}_{\mathrm{f}} & 0 & 0 \\ 0 & 0 & -\frac{p_I}{\bar{I}_{z z}} & 0 & 0 & 0 & 0 \end{array}\right]^{\mathrm{T}}$；$\boldsymbol{C}_{\mathrm{m} 2}=\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right] ; \quad \boldsymbol{C}_{\mathrm{m} 21}=\left[\begin{array}{lllllll} 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right] ; \quad \boldsymbol{C}_{\mathrm{m} 22}=\left[\begin{array}{ll} 0 & 0 \\ 0 & 0 \end{array}\right]$。

参数不确定性车辆模型的参数摄动部分可由不确定性对角矩阵表示，见公式(27)。

$ \Delta=\operatorname{diag}\left(\sigma_{\mathrm{m} 1}, \sigma_{\mathrm{m} 2}, \sigma_I, \sigma_{\mathrm{f}}, \sigma_{\mathrm{f}}, \sigma_{\mathrm{r}}, \sigma_{\mathrm{r}}\right), \|\Delta\|_{\infty} \leqslant 1 。$

(27)

最终原来系统不确定性可以通过一个线性分式来表示，并且控制系统输出见公式(28)。

$ \boldsymbol{y}=F_{\mathrm{u}}\left(\boldsymbol{G}_{\mathrm{m}}, \Delta\right) \boldsymbol{u}, $

(28)

式中：$\boldsymbol{y}=\left[\begin{array}{ll} \beta & \dot{\psi} \end{array}\right]^{\mathrm{T}} ; u=\left[\delta_{\mathrm{f}} \Delta M\right]^{\mathrm{T}}$。

2.2.3 控制器设计

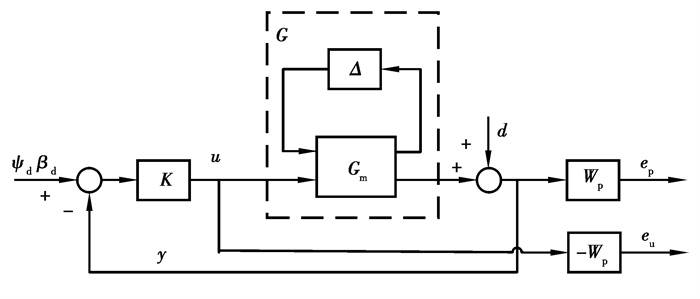
考虑参数摄动的智能汽车动态侧向避障鲁棒控制策略利用混合灵敏度函数(S/KS)来保证鲁棒控制器稳定性和跟踪性能，并抵抗模型参数摄动和外界干扰，实时决策转向角和附加力矩来控制智能汽车，从而实现侧向避障动态轨迹跟踪，其闭环控制框图见图 7。

为了保证系统的稳定性，鲁棒闭环控制系统的G=F_u(G_m, Δ)必须满足公式(29)的性能标准^[26]。

$ \left\| {\left[ {\begin{array}{*{20}{c}} {{W_{\rm{p}}}S}\\ {{W_{\rm{u}}}KS} \end{array}} \right]} \right\| = {\left\| {\left[ {\begin{array}{*{20}{c}} {{W_{\rm{p}}}{{(I + GK)}^{ - 1}}}\\ {{W_{\rm{u}}}K{{(I + GK)}^{ - 1}}} \end{array}} \right]} \right\|_\infty } < 1 。$

(29)

依据图 7，可获得闭环控制系统的输入输出广义控制系统式(30)。

$ \left[\begin{array}{c} e_{\mathrm{p}} \\ e_{\mathrm{u}} \\ y \end{array}\right]=\left[\begin{array}{cc} W_{\mathrm{p}} & -W_{\mathrm{p}} G \\ 0 & W_{\mathrm{u}} \\ I & -G \end{array}\right]\left[\begin{array}{l} d \\ u \end{array}\right]=\left[\begin{array}{ll} P_{11} & P_{12} \\ P_{21} & P_{22} \end{array}\right]\left[\begin{array}{l} d \\ u \end{array}\right], $

(30)

式中：$: \boldsymbol{P}_{11}=\left[\begin{array}{c} W_{\mathrm{p}} \\ 0 \end{array}\right] ; \boldsymbol{P}_{12}=\left[\begin{array}{c} -W_{\mathrm{p}} G \\ W_{\mathrm{u}} \end{array}\right] ; \boldsymbol{P}_{21}=\boldsymbol{I} ; \boldsymbol{P}_{22}=-\boldsymbol{G}$; $\boldsymbol{W}_{\mathrm{p}}=\left[\begin{array}{cc} W_{\mathrm{p} \beta} & 0 \\ 0 & W_{\mathrm{pr}} \end{array}\right] ; \boldsymbol{W}_{\mathrm{u}}=\left[\begin{array}{cc} W_{\mathrm{u} \delta} & 0 \\ 0 & W_{\mathrm{um}} \end{array}\right]$。

广义传递函数

$ F_l(\boldsymbol{P}, K)=\boldsymbol{P}_{11}+\boldsymbol{P}_{12} K\left(I-\boldsymbol{P}_{22} K\right)^{-1} \boldsymbol{P}_{21}=\left[\begin{array}{c} \boldsymbol{W}_p(\boldsymbol{I}+\boldsymbol{G} K)^{-1} \\ \boldsymbol{W}_{\mathrm{u}} K(\boldsymbol{I}+\boldsymbol{G} K)^{-1} \end{array}\right], $

(31)

通过广义传递函数变换，混合灵敏度问题式(29)转换为H_∞标准问题^[25]，即公式(32)

$ \left\|F_l(\boldsymbol{P}, K)\right\|_{\infty}<1 。$

(32)

2.2.4 增益调度

为了实现智能汽车不同速度或者避障过程中速度动态变化的动态避障精准控制，所提控制策略采用增益调度方式。具体为: 车速从15 km/h到95 km/h，每10 km/h设定一个基本控制点并求解此点控制增益函数。在实际控制过程中，通过线性插值方式获得对应速度的控制量。虽然线性插值相对曲线插值可能会存在细微偏差，但是鲁棒控制策略具备克服此干扰的能力。

3 结果验证

利用Matlab/Simulink和Trucksim软件进行联合仿真，对所提控制策略进行仿真验证。为了能够验证考虑参数摄动的智能汽车动态侧向避障鲁棒控制策略的控制效果，设计了二个测试工况。工况1：障碍物汽车速度固定，前后侧偏刚度摄动，避障过程中智能汽车车速动态变化，并且航向角速度测量信号加入白噪声。此工况验证控制策略变智能汽车车速和变侧偏刚度以及抗信号干扰的鲁棒控制能力；工况2：障碍物汽车变加速度和智能汽车变质量(转动惯量与质量相关)的工况。此工况为较少且极端工况，即智能汽车正在侧向避障过程中，障碍物汽车不仅车速变化且加速度动态变化，从而引起障碍物汽车速度激烈变化，进而造成智能汽车变道参考轨迹实时激烈变化；此工况验证控制策略应对突发情况和变质量鲁棒控制的能力。

此2个工况能够反映实际复杂交通环境下的侧向避障可能遇到障碍物汽车状态，即障碍物汽车定速(包括静止)、定加速度和变加速度。同时，既考虑了质量和转动惯量参数摄动，也考虑前后侧偏刚度动态参数摄动，以及外部传感器测量信号干扰。并且，考虑了智能汽车不同速度以及避障过程中的速度动态变化。因此，此两个工况能够较为全面测试所提控制策略实际交通环境下智能汽车动态侧向避障鲁棒控制能力。关于多障碍物汽车动态变化的工况，参考文献[28]，进行多车干扰下的轨迹规划限制设置。

研究的智能汽车采用一四轮独立驱动的客车，其主要参数如表 1所示，鲁棒控制器相关参数如表 2所示。

3.1 工况1

障碍物汽车车速为常值或者零的工况为侧向避障的常态工况。但是，在避障过程中，由于交通环境影响，智能汽车可能需要进行加减速，以保证智能汽车安全。为了验证更为危险的工况，智能汽车受到除障碍物汽车之外车辆的影响，动态侧向变道过程进行加速操作。并且，侧偏刚度增减30%和航向角速度信号加入白噪声来验证控制策略的动态参数摄动和抵抗外部干扰的鲁棒性。此工况设置为：障碍物汽车与智能汽车初始距离为35m, 障碍物汽车车速为8 km/h和加速度为0 m/s²；智能汽车目标车速由Trucksim软件进行设定；侧偏刚度的增减通过改变控制参考模型中的名义参数值来实现；为了体现鲁棒控制策略的控制优势，进行了LQR控制算法对比研究。此工况仿真控制结果如图 7所示。

一旦智能汽车实现了避障后，轨迹曲线函数的纵向长度参数不再调整，即变道正弦曲线线型不再变化，沿着原来的正弦曲线继续变道，直到成功变道到目标车道^[28]。若智能汽车到达目标车道，智能汽车运行目标为目标车道中心线，工况2同。

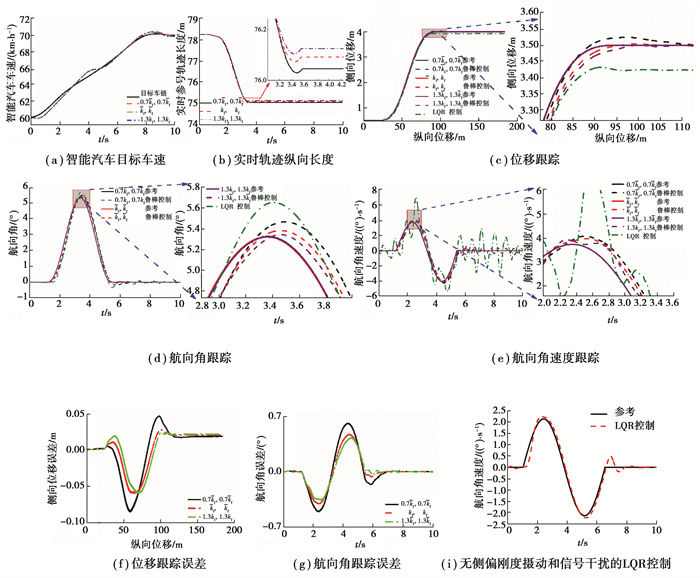
由图 8(a)可知，在动态侧向避障过程中，不同侧偏刚度下，智能车辆车速基本相同，并良好跟随动态目标车速。图 8(a)(b)可知，虽然避障过程中障碍物汽车车速不变，但智能汽车车速和位姿动态变化，造成在动态避障参考轨迹的纵向长度动态变化。基于实时动态参考轨迹纵向长度，能够获得侧向避障实时动态参考曲线。由图 8可知，侧向避障为一个动态过程，侧偏刚度发生变化后，整个避障过程会发生轻微变化，即参考曲线及状态将重新动态规划。因此，图 8中轨迹跟踪等呈现出与侧偏刚度变化相匹配的三组曲线。

由图 8(c)(f)可知，智能汽车能够良好地跟踪动态规划避障曲线位置，从而实现其安全侧向避障。通过分析数据可知：前后侧偏刚度减小30%时，不变时，增加30%时，轨迹位移误差量最大值和误差率分别为0.069 m，1.99%；0.061 m，1.75%；0.063 m，1.80%。由数据可知，所提控制策略克服了侧偏刚度摄动和信号噪声干扰，实现了避障动态轨迹位移跟踪且跟踪效果良好。同时，运用LQR算法对此相同动态轨迹跟踪，位移误差量最大值为0.089 m，误差率为2.54%。因此，在航向角速度信号干扰工况下，鲁棒控制器相对于LQR算法的实时动态轨迹的位移跟踪效果更好。

轨迹跟踪除下需要对路径进行跟踪，还是需要对轨迹航向角和角速度进行跟踪。若车辆位姿与参考曲线航向角存在很大误差或者波动较大，将影响智能汽车侧向避障和乘员舒适性。由图 8(d)(g)可知，所提控制策略控制智能汽车跟踪参考轨迹航向角有一定滞后，但跟踪效果良好。同时，控制的航向角幅度未发生激烈变化且变化平稳。通过数据分析可知，前后侧偏刚度减小30%时，不变时，增加30%时，参考峰值航向角，跟踪峰值航向角和误差率分别为5.33°，5.47°，2.66%；5.33°，5.39°，1.13%；5.32°，5.35°，0.43%。

由图 8(b)(c)(d)可知，车辆侧向位移和姿态能够良好跟踪实时规划的避障轨迹；同时，实时避障轨迹根据障碍物汽车状态实时调整。并且，算法对障碍物汽车进行蓬松化处理，能够提供一定范围的冗余。因此，轨迹跟踪算法良好地跟踪实时规划的避障轨迹，保证了智能汽车与障碍物汽车不发生碰撞。

由图 8(e)可知，航向角速度实现了良好跟踪。经过计算，前后侧偏刚度减小30%，不变和增加30%时，参考峰值航向角速度分别为4.04(°)/s，4.04(°)/s，4.04(°)/s；跟踪峰值航向角速度分别为4.23(°)/s，4.12(°)/s，4.11(°)/s，误差率4.74% 1.84%，1.93%。同时，控制后的航向角速度在±4.23(°)/s范围内，即控制策略保证动态侧向避障过程车辆横摆稳定性。

由图 8(d)(e)可知，LQR算法对信号干扰，实时动态轨迹和侧偏刚度摄动下的航向角和航向角速度跟踪效果较差，并且跟随过程呈现状态动态波动不稳定性现象。经过计算，参考峰值航向角为5.32°，跟踪峰值航向角为5.66(°), 误差率为5.92%。LQR算法参考峰值航向角速度为4.05(°)/s，跟踪峰值航向角速度为7.06(°)/s，误差为74.14%。相对于鲁棒控制器，LQR算法误差率更大，尤其是航向角速度波动不稳。由图 8(i)可知，采用LQR算法的控制策略，能够实现无侧偏刚度摄动和信号干扰工况下的良好轨迹跟踪。因此，LQR算法能够处理无侧偏刚度摄动和信号干扰的轨迹跟踪控制，而对有侧偏刚度摄动和信号干扰的轨迹跟踪控制效果很差，甚至发散。

综上所述，所提控制策略实现了前后侧偏刚度参数摄动和航向角速度信号干扰的动态参考轨迹跟踪鲁棒控制，克服了智能汽车车速动态变化，获得了良好智能汽车动态侧向避障控制，保证了侧向动态避障汽车横摆稳定性；并且，跟踪效果优于LQR控制效果。

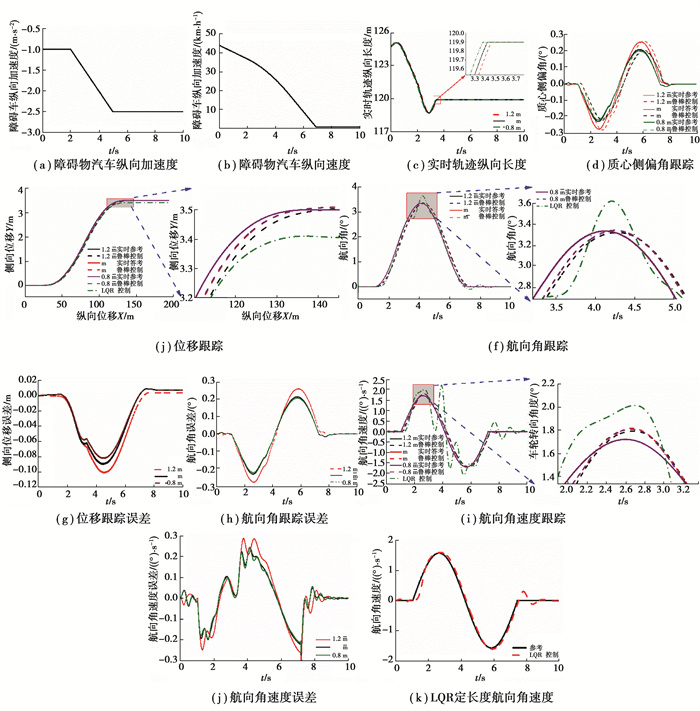
3.2 工况2

在实际交通环境下，前方障碍物汽车可能存在加速度；尤其特殊工况为当智能汽车正在侧向避障的时候，障碍物汽车变加速度，将造成障碍物车速激烈变化，从而智能汽车需要快速调整参考轨迹以保证侧向避障安全性。变质量变加速度工况将用于测试控制策略应对突发情况和变质量鲁棒控制的能力。此工况设置为：智能汽车与障碍物汽车初始距30 m，障碍物汽车初始车速为43 km/h，其加速度及速度变化如图 9(a)(b)，智能汽车目标车速通过Trucksim软件设定为70 km/h，其控制结果如图 9所示。

与前一工况所述类似，侧向避障为一个动态过程，质量(转动惯量)变化时，整个避障过程会发生轻微变化，即参考曲线及状态将重新动态规划。因此，图中轨迹跟踪等呈现出与质量(转动惯量)变化相匹配的三组曲线。

由图 9(a)(b)可知，障碍物汽车开始以-1 m/s²减速度进行减速，并且减速度强度一直增强至-2.5 m/s²；其速度从43 km/h减速到停止，即在障碍物汽车在整个侧向避障过程中加速度和速度动态变化，能够基本表征实际交通环境下侧向避障过程障碍物汽车速度变化过程。根据障碍物汽车速度和智能汽车状态等信息，通过侧向避障动态轨迹规划算法获得图 9(c)实时的轨迹曲线纵向长度，进而获得图 9(e)实时侧向避障参考轨迹。同时，车辆质量变化为正负20%，能够覆盖除载货汽车外的正常载荷变化范围。

由图 9(d)图可知，整个侧向避障过程中，质心侧偏角状态变化平稳，并且能够良好地跟踪参考质心侧偏角。由图 9(e)(g)可知，智能汽车能够良好地跟踪动态规划避障曲线位置，从而实现其安全侧向避障控制。通过分析仿真实验数据可知：质量增加20%，不变，减少20%时，轨迹位移误差量最大值为和误差率分别为0.091 m, 2.62%；0.089 m, 2.61%；0.082 m, 2.32%。由数据可知，所提控制策略能够克服质量(转动惯量)参数摄动，实现了避障动态轨迹平滑稳定良好地跟踪。

由图 9(f)(h)可知，所提控制策略能够克服智能汽车质量(转动惯量)参数摄动，实现良好跟踪动态轨迹参考航向角且误差较小。经过计算，质量增加20%、不变和减小20%，峰值航向角误差量分别为0.015°、0.007°和0.007°，误差率为：0.44%、0.21%和0.21%。

由图 9(i)(j)可知，所提控制策略实现良好参考航向角速度跟随且误差较小。航向角速度能够平滑稳定地跟踪动态轨迹参考航向角速度且控制在±1.8°/s²范围内，即侧向避障过程中，所提控制策略能够控制航向角速度平稳变化且未出现过大超调和激烈波动，从而保证了避障过程中智能汽车横摆稳定性。经过计算：质量增加20%、不变和减小20%，峰值航向角速度误差量分别为0.070°/s²、0.095°/s²和0.086°/s²，误差率为：4.07%、5.49%和5.01%。

由图 9(e)(f)(i)可知，LQR算法对实时动态轨迹和质量摄动跟踪效果较差，并且跟踪过程呈现航向角速度动态波动不稳定性现象。经过计算，轨迹位移误差量最大值为0.099 m, 误差率为2.82%；峰值航向角误差量为0.284°，误差率为8.48%；峰值航向角速度误差量为0.493°/s，误差率为28.59%。图 9(k)为相同车速，但是轨迹长度为工况开始时的不变轨迹长度(124.7 m)变道轨迹，且智能汽车质量不变化的仿真结果图。由图 8(k)可知，LQR算法能够获得良好航向角速度跟随，并且不发生波动不稳定情况。因此，LQR算法对光滑轨迹和质量不变化的跟踪效果较好，而对于实时动态变化轨迹和质量摄动的控制效果较差，尤其是航向角速度。鉴于此，所提控制策略实现了变质量变加速度工况的动态侧向避障鲁棒控制，并保证了动态避障过程智能汽车横摆稳定性，且控制效果优于LQR控制算法。

综上所述，2个工况仿真控制结果表明，考虑参数摄动的智能汽车动态侧向避障控制策略能够根据障碍物汽车位置，加速度和速度以及智能汽车的速度、航向角速度等自身状态，动态规划侧向避障实时安全参考轨迹；同时鲁棒控制器能够克服质量、转动惯量、前后侧偏刚度参数摄动以及航向角速度信号干扰，并且通过增益调度方式适应智能汽车速度动态变化，实现对动态参考轨迹位置，航向角和航向角速度平滑稳定良好地跟踪，进而实现了动态侧向避障鲁棒精准控制；并且，保证了整个动态侧向避障过程智能汽车横摆稳定性。同时，所提控制策略优于LQR控制算法跟踪控制效果。

4 结语

1) 针对实际交通环境下障碍物汽车加速度和速度动态变化，利用障碍物汽车的车速、加速度、初始位置和智能汽车车速和航向角等自身状态等信息，提出了基于避障极限位置的侧向避障轨迹动态规划算法，获得了能够保证智能汽车侧向避障安全的实时避障参考轨迹，从而为考虑参数摄动的智能汽车动态侧向避障鲁棒控制策略提供了实时动态避障参考轨迹，奠定了所提控制策略实现实际交通环境下动态侧向避障控制的必要基础。

2) 针对智能汽车质量、转动惯量，尤其是随着汽车状态变化而变化的前后侧偏刚度参数摄动和测量信号干扰，以及实时参考轨迹不光滑动态变化，提出了基于参数摄动的智能汽车动态侧向避障鲁棒控制策略。所提控制策略克服了质量、转动惯量和前后侧偏刚度参数摄动和信号干扰，以及参考轨迹动态变化，并通过增益调度方法适应了智能汽车速度动态变化，实现了对实时参考轨迹位移、航向角、航向角速度和质心侧偏角的平滑稳定良好地跟踪，从而实现了智能汽车动态侧向避障，并保证了避障过程横摆稳定性。

3) 所提鲁棒控制策略与LQR控制算法对比研究表明，在参数摄动，信号干扰和动态参考轨迹影响下，所提控制策略轨迹跟踪效果优于LQR算法控制效果。

4) 后续研究将进行所控制策略硬件在环和实车实验，并考虑更为复杂路面状况。