2. 北京博电新力电气 股份有限公司, 北京 100089
2. PONOVO Power Co., Ltd., Beijing 100089, P. R. China
路面附着系数为车辆动力学控制的重要输入参数[1],许多汽车安全系统如车身电子稳定系统(electronic stability, ESP),防抱死系统(antilock braking system, ABS)等,其控制策略的直接或间接建立在路面附着系数已获取的基础上。因此,准确地获取路面附着系数是汽车主动安全系统的关键一环。目前,识别路面附着系数通常被分成Cause-based以及Effect-based两种识别方法[2]。
Cause-based识别方法是分析路面附着系数的物理因素,再运用经验模型对路面附着系数进行识别[3]。余卓平等[4]利用不同道路的材质不同,对激光雷达的反射也不同,构建了路面附着系数估计器,该估计器能实现5类典型路面的估计,该方法能实现对行驶车辆前方路面的估计。Leng等[5]首先基于修正的Burckhardt轮胎模型,设计了轮胎力和轮胎路面峰值附着系数的扰动观测器。其次采用颜色矩法和灰度共生矩阵法提取路面的颜色和纹理特征,并基于支持向量机对路面进行分类。最后基于增益调度法,设计了动态估计器和视觉估计器的融合策略。该方法充分利用多源传感器信息,并且具有更高估计精度。Song等[6]利用深度学习方法,提出了一种实用的路面附着系数估计器,该估计器由循环神经网络以及卷积神经网络所组成,且适用于各种行驶工况。王岩等[7]通过搭建智能轮胎,直接获取轮胎与路面作用信息,再采用支持向量机算法对路面附着系数进行估计。该方法具有稳定以及可靠等优势,并且不需要车辆进行加速、制动或转向就能够实现路面附着系数的估计,适用范围广。Dogan等[8-9]将麦克风装在汽车上,以监听车辆行驶时所产生的“胎噪”,从而识别路面附着系数。由于噪声信号复杂且难以解析,所以该方法的实现难度较大。
Effect-Based识别方法则根据不同路面条件车辆行驶产生的整车动力学响应不同,从而识别路面附着系数。Effect-Based识别方法通常不需要增添额外的传感器[10],并且抗干扰性较强,所以得到了许多关注。Chen等[11]提出了一种基于转向系统和轮上电机驱动系统固有频率的频域数据融合估计路面附着系数的方法。平先尧[12]、刘志强等[13]使用卡尔曼滤波估计汽车状态与路面附着系数。赵治国[14]等将传感器数据以及Burchhardt轮胎模型进行结合,提出了无迹卡尔曼滤波估计路面附着系数的方法,该方法对噪声进行了降噪。熊璐等[15]根据车轮的侧向力,提出了一种模糊自适应的路面附着系数估计方法,该方法是通过车辆的状态模糊推理出当前纵、侧向轮胎力所能达到的极限,从而设计融合观测器进行估计。该融合观测器在高低附路面以及不同轮胎力激励时,能够高精度地估计出路面附着系数,并且对轮胎力纵侧耦合的工况具有鲁棒性。Feng等[16]基于HSRI轮胎模型,设计了2种估计路面附着系数的方法。第一种方法是利用摩擦系数间接估计路面摩擦系数。第二种方法通过变换HSRI方程,将隐式形式转化为显式形式来进行估计。该方法能充分考虑实际物理条件下估计量的约束,不依赖于初始估计信息的选取。然后,结合这2种方法得优点,进行组合优化设计,得到更为准确的估计值。Gao等[17]利用实验数据对刷子轮胎模型进行修正,并基于车辆动力学以及运动学模型设计了非线性观测器,观测器利用车轮自调心力矩、横向加速度和车辆横向位移来估计转向过程中的路面附着系数,该方法在转向过程中性能良好,路面附着系数能够快速收敛于参考值。
由于识别路面附着系数的干扰因素较多,导致估计结果的准确率以及稳定性往往不够理想。人工神经网络通过模拟人脑思维方式,对问题进行处理,具有自学习、自适应、非线性映射以及联想记忆等特点。为获取更为准确地路面附着系数,基于Elman神经网络方法对路面附着系数进行识别,该方法显著具有准确率高、抗干扰能力强等优势。因此,笔者通过建立Carsim/Simulink联合仿真模型,获取了某车辆行驶过程中的动力学响应,从而建立了Elman神经网络方法的路面附着系数识别模型,并且通过实车实验对该方法进行了验证,证明该方法的有效性。
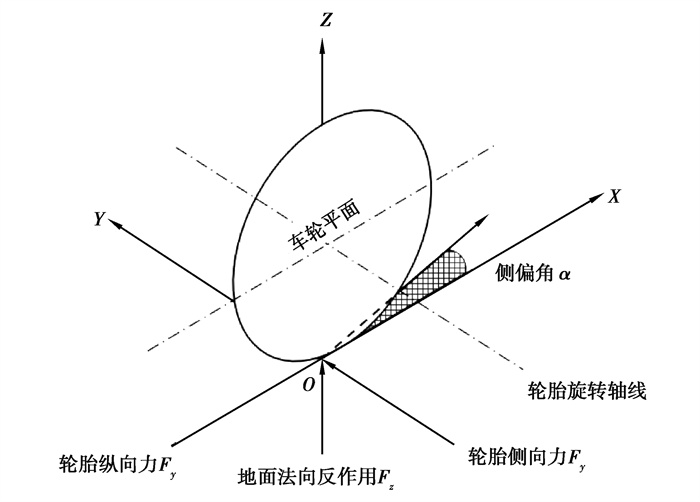
1 车辆动力学建模 1.1 轮胎模型建模由于所需动力学响应不涉及回正力矩,所以采用Dugoff轮胎模型。Dugoff轮胎模型所需参数相对于其他轮胎模型较少,并且能够较好地表现出其非线性特征[18]。图 1为Dugoff轮胎模型的力坐标系。通过Dugoff轮胎模型可得到Fx以及Fy[6]。
|
图 1 轮胎受力坐标系 Fig. 1 Tire force coordinate system |
通过Dugoff轮胎模型可得到Fx以及Fy,如下
| $ F_x=C_x \frac{S}{1+\mathrm{s}} \cdot f(P) \text {; } $ | (1) |
| $ F_y=C_y \frac{\tan \alpha}{1+\alpha} \cdot f(P) \text {; } $ | (2) |
| $ f(P)=\left\{\begin{array}{l} P(2-P), P \leqslant 1 , \\ 1, P>1 ; \end{array}\right. $ | (3) |
| $ P=\frac{\mu F_z(1+S)}{2 \sqrt{C_x^2 \cdot S^2+C_y^2 \cdot \tan ^2 \alpha}} 。$ | (4) |
式中:Cx是轮胎纵向刚度;Cy是轮胎侧向刚度;α是侧偏角;P是非线性特征参数;Fx与Fy分别是轮胎纵、侧向力;Fz为轮胎的法向载荷;f(P)是轮胎模型修正参数;S是滑移率。
联立(1)~(4)可得
| $ F_x=C_x \cdot \frac{S}{1+S} \cdot\left(\frac{4 \sqrt{C_x^2 \cdot S^2+C_y^2 \cdot \tan ^2 \alpha} \cdot \mu \cdot F_z \cdot(1+S)-\mu^2 \cdot F_Z^2 \cdot(1+S)^2}{4\left(C_x^2 \cdot S^2+C_y^2 \cdot \tan ^2 \alpha\right)}\right), $ | (5) |
| $ F_y=C_y \cdot \frac{\tan \alpha}{1+\alpha} \cdot\left(\frac{4 \sqrt{C_x^2 \cdot S^2+C_y^2 \cdot \tan ^2 \alpha} \cdot \mu \cdot F_z \cdot(1+S)-\mu^2 \cdot F_z^2 \cdot(1+S)^2}{4\left(C_x^2 \cdot S^2+C_y^2 \cdot \tan ^2 \alpha\right)}\right) 。$ | (6) |
由(5)(6)可得到μ与Fx, Fy, Fz, S, α构成函数关系,即
| $ \mu=f\left(F_{x i j}, F_{y i j}, F_{z i j}, S_{i j}, \alpha_{i j}\right) \text {, } $ | (7) |
其中:ij=左前轮fl,右前轮fr,左后轮rl,右后轮rr。
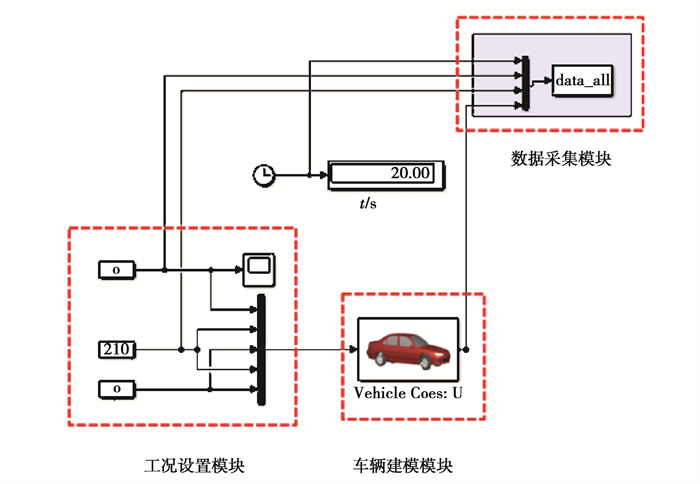
1.2 Carsim/Simulink联合仿真建模Carsim/Simulink联合仿真模型如图 2所示,由工况设置模块、车辆建模模块以及数据采集模块组成。工况设置模块上的个输入分别表示方向盘转角、前轮转矩以及后轮转矩。通过这个输入以及车辆建模模块中的初速度设置达到工况设置。车辆建模模块是由Carsim软件生成的一个S函数,从而实现Simulink与Carsim的联合仿真。
|
图 2 Carsim/Simulink联合仿真模型 Fig. 2 Carsim/Simulink co-simulation model |
在Carsim中选取B-Class Hatchback车辆作为研究对象,其车身尺寸等参数信息如表 1所示。
| 表 1 仿真车辆参数 Table 1 Simulation vehicle parameters |
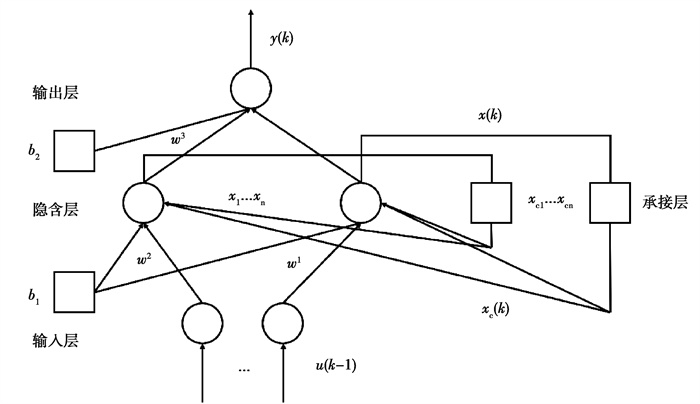
Elman神经网络的结构如图 3所示,其由输入层、隐含层、承接层、输出层所组成。其各层连接方式和前馈网络相似。输入层以及输出层节点作用分别是信号传递以及线性加权。隐含层节点的激活函数可以为线性或非线性函数。承接层作用为储存隐含层前一时刻的输出值,然后传达至网络输入,相当于延时算子,起到了记忆作用。承接层的存在增强了网络稳定性,且提升了系统对时变特性的适应性[19]。
|
图 3 Elman神经网络结构 Fig. 3 The structure of Elman neural network |
Elman神经网络的表达式为
| $ \boldsymbol{y}(k)=g\left(w^3 \boldsymbol{x}(k)\right) \text {, } $ | (8) |
| $ \boldsymbol{x}(k)=f\left(w^1 x_c(k)+\omega^2(\boldsymbol{u}(k-1))\right), $ | (9) |
| $ \boldsymbol{x}_c(k)=\boldsymbol{x}(k-1), $ | (10) |
式中: y是节点输出向量;u是输入向量;xc是反馈状态向量;w3是中间层到输出层连接权值;w2是输入层到中间层连接权值;w1为承接层到中间层的连接权值;x为n维中间层节点单元向量;输出节点的激励函数为g(*),中间层节点的激励函数为f(*),通常使用sigmoid函数。
其学习函数采用误差平方和函数。
| $ E(w)=\sum\limits_{k=1}^n\left(\boldsymbol{y}_k(w)-\tilde{\boldsymbol{y}}_k(w)\right)^2 \tilde{\boldsymbol{y}}_k, $ | (11) |
其中
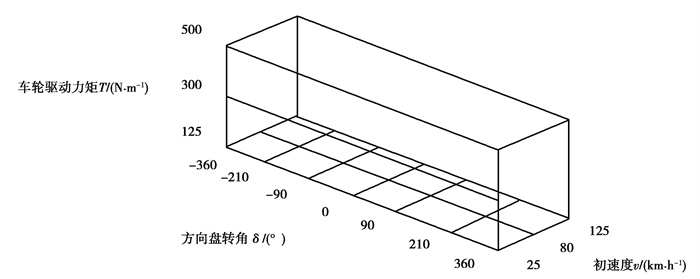
为了使得人工神经网络的预测性能达到最优,数据集也必须尽可能的覆盖实际的所有工况,以便增强神经网络的泛化性。为了使得采集的数据尽可能的覆盖所有的车辆行驶工况,仿真工况设计为下列参数的组合,路面附着系数μ∈(0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8),初始车速是v∈(25, 80, 125 km/h),方向盘转角δ∈(-360°, -210°, -90°, 0°, 90°, 210°, 360°),单个车轮驱动力矩T∈(150, 300, 500 N·m),仿真车辆为两驱驱动,共计504组仿真工况,每组工况仿真时间为20 s,采用频率为1 000 Hz。车辆建模模块具有20个输出变量,分别为Fxij(i=f, r; j=l, r), Fyij(i=f, r; j=l, r), Fzij(i=f, r; j=l, r), Sij(i=f, r; j=l, r), αij(i=f, r;j=l, r)。为了使得采集的数据更加全面,按照下表的工况进行数据采集,这不仅覆盖了车辆日常行驶的工况,还包括了一些较为极端的工况,一方面是为了获得一些出现大滑移率工况的训练数据,另一方面可以使得训练数据覆盖范围更广,提高神经网络的泛化性。采集数据的样本空间如图 4所示。
|
图 4 数据的样本空间 Fig. 4 Sample space of data |
由于采集到的动力学响应差异较大,输入值过大、过小都会使神经元输出处于饱和区。为防止数据中数值较低的特征被忽视,笔者将各其进行归一化处理。采用Matlab中mapminmax指令对数据做归一化处理,使输入量处于[-1, 1]区间,这样使得后续的数据处理更加方便,且提高了程序的收敛速度。
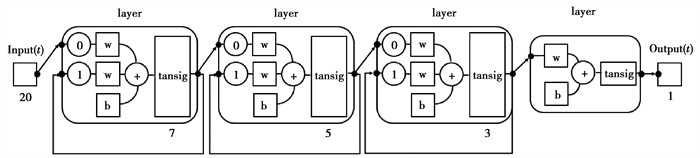
2.3 模型参数设置考虑到识别路面附着系数所需要的物理因素,笔者选取Fxij, Fyij, Fzij, Sij, aij,是Elman神经网络输入变量,即输入层节点数量是20。输出层设置成1个节点,对应Elman神经网络输出变量μ。隐含层一共有三层,第一层具有7个节点,第二层具有5个节点,第三层具有3个节点。Elman神经网络的拓扑结构如图 5所示。
|
图 5 Elman神经网络拓扑结构 Fig. 5 Elman neural network topology |
其中隐含层与输出层激励函数是tansig,网络训练算法选择Levenberg-Marquardt,对应训练函数trainglm,设定最大迭代次数epochs为1000,期望误差goal是1e-07,显示间隔show是10。
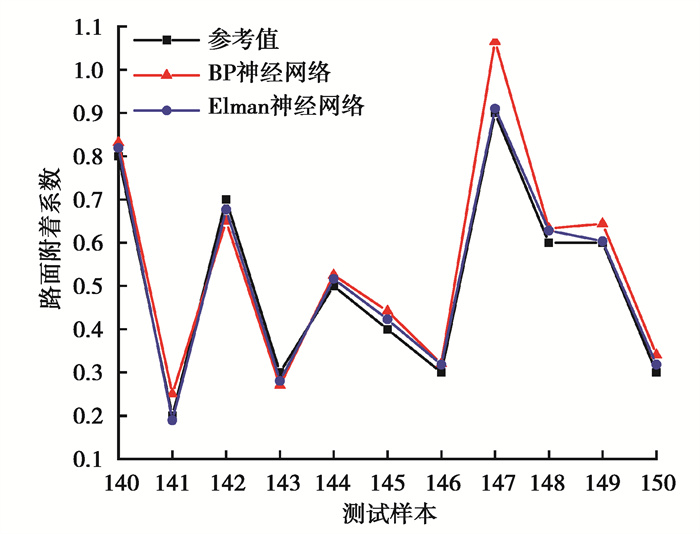
2.4 结果分析训练总共迭代了316次,耗时407 s。识别结果如图 6所示,黑色曲线为Carsim软件内设置的参考值,红色曲线为BP神经网络的识别值,蓝色曲线为Elman神经网络的识别值。尽管在第147个样本点时发生了振荡,BP神经网络的识别值与参考值偏离较远,但是Elman神经网络的识别值与参考值还是保持着较小的误差。总之,BP神经网络与Elman神经网络都可以实现对路面附着系数的识别,其中Elman神经网络识别结果相对BP神经网络识别结果更加逼近参考值。
|
图 6 模型的输出结果 Fig. 6 Model output |
为了能够更加充分的评价Elman神经网络的识别性能,笔者采用平均误差(eme)、平均绝对误差(emae)、均方根误差(ermse)、平均绝对百分比误差(emape)、均方误差(emse)和准确率六个评价指标来评价路面附着系数的识别精度。
eme定义如下
| $ e_{\mathrm{me}}=\frac{1}{N} \sum\limits_{j=1}^N\left(y_j-\hat{y}_j\right) 。$ | (12) |
emae定义如下
| $ e_{\text {mae }}=\frac{1}{N} \sum\limits_{j=1}^N\left|y_j-\hat{y}_j\right| \text { 。} $ | (13) |
ermse定义如下
| $ e_{\mathrm{rmse}}=\sqrt{\frac{1}{N} \sum\limits_{j=1}^N\left(y_j-\hat{y}_j\right)^2} 。$ | (14) |
emape定义如下
| $ e_{\text {mape }}=\frac{1}{N} \sum\limits_{j=1}^N \frac{\left|y_j-\hat{y}_j\right|}{y_j} \times 100 \% 。$ | (15) |
| $ e_{\text {mape }}=\frac{1}{N} \sum\limits_{j=1}^N \frac{\left|y_j-\hat{y}_j\right|}{y_j} \times 100 \% 。$ | (16) |
emse定义如下
| $ e_{\mathrm{mse}}=\frac{1}{N} \sum\limits_{j=1}^N\left|y_j-\hat{y}_j\right|^2 \text { 。} $ | (17) |
准确率定义如下
| $ \text { 准确率 }=\frac{Y}{N} \times 100 \% \text {, } $ | (18) |
式中:N是测试样本数量;yj是路面附着系数参考值;
各路面附着系数识别结果分析见表 2,由表得知Elman神经网络方法在5种方法中表现最佳。其中Elman神经网络的eme为-1E-04,低于BP神经网络的-1.2E-03,CKF的2.3E-02,以及DCKF的2.7E-03。Elman神经网络的emae为2.2E-02,也低于BP神经网络的3.1E-02,UKF的1.6E-01与STUKF的4.7E-02。在ermse中,Elman神经网络为5.5E-02,低于BP神经网络的7.3E-02。Elman神经网络识别路面附着系数的emape为4.92%,相比BP神经网络以及GABP神经网络分别降低了2.24%和1.08%。由于Elman神经网络能够适应时变特性,与BP神经网络相比,准确率由81.4%提升至91.22%,提高了9.82%。由此可见,Elman神经网络在识别路面附着系数中表现优越。
| 表 2 不同方法的性能比较 Table 2 Performance comparison of different methods |
为了验证Elman神经网络识别路面附着系数的可行性,采取实车实验。本实验车辆和数据采集装置如图 7所示。实验车辆长、宽、高分别是4.139 m、1.699 m、1.499 m,轴距是2.559 m,驱动方式为前置前驱, 最大功率为80 kW, 最大扭矩为140 N·m。车辆状态的采集对于实验至关重要,笔者选用IIMU57IMU惯性测量单元对车辆的纵向加速度、侧向加速度以及横摆角速度进行采集。图 7(b)为IMU570惯性传感器,该惯性传感器由陀螺仪、加速度计等组成,陀螺仪的测量范围是1 800°/s,零偏加速度敏感度是≤1°/h/g,加速度计测量范围是±38g,零偏误差为0.5 mg。

|
图 7 实验设备 Fig. 7 Experimental equipments |
实验道路如图 8所示,包括了干燥沥青路面以及潮湿沥青路面。

|
图 8 实验道路 Fig. 8 Experimental road |
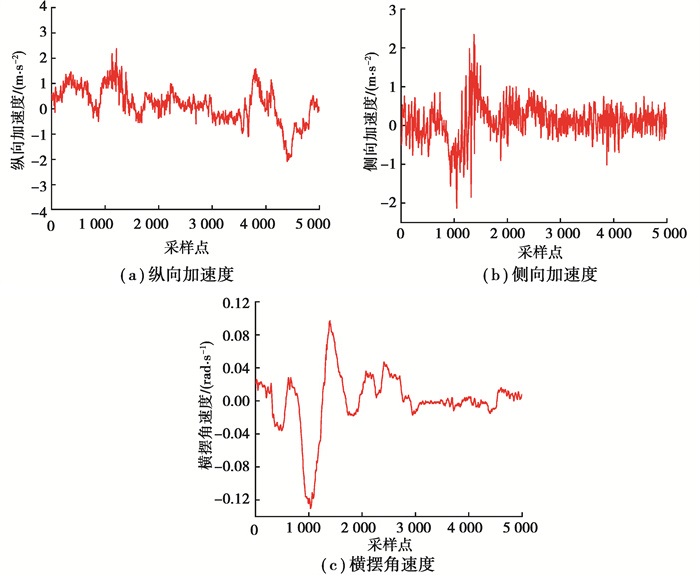
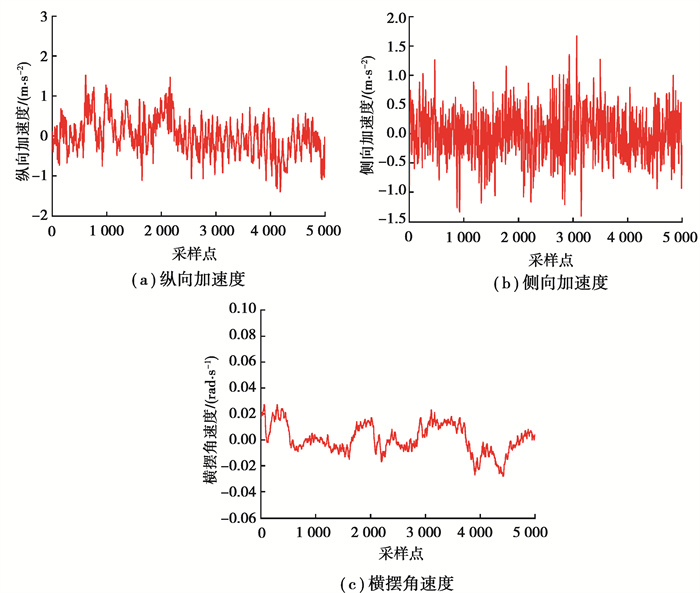
图 9、图 10为采集到数据实验数据,包含车辆的3个动力学响应,横向加速度、纵向加速度以及横摆角速度。图 9为干燥沥青路面的实验数据,图 10为潮湿沥青路面实验数据。
|
图 9 干燥沥青路面实验数据 Fig. 9 Experimental data of dry asphalt road |
|
图 10 潮湿沥青路面实验数据 Fig. 10 Experimental data of wet asphalt road |
误差分析如表 3所示,由实验结果可知,其中干燥沥青路面的误差在12.37%以内,emse为8.5E-03;潮湿沥青路面的识别结果相比干燥沥青路面稍逊,但是误差也控制在14.13%以内,emse为9.9E-03。由于实验车辆的参数与仿真车辆无法保持完全一致,所以实验结果未能与仿真结果保持一致;实验过程中的道路存在着坡度、不平度等外在因素影响,以及无法获知实验道路的真实路面附着系数,只能得到一个参考值,导致了实验误差相比仿真误差更大。尽管存在着诸多不定因素的干扰,基于Elman神经网络识别路面附着系数在干燥沥青路面以及潮湿沥青路面都能够有效的识别,表现出其良好的抗干扰性以及有效性。
| 表 3 实验误差 Table 3 Test error |
笔者构建了Carsim/Simulink仿真模型,并建立了覆盖典型工况的仿真样本空间,分别采用仿真和实验的数据,采用Elman神经网络方法对路面附着系数进行了识别,主要成果如下:
1) 首次构建了Elman神经网络路面附着系数识别模型,并使其和BP神经网络等方法进行对比,结果显示Elman神经网络相比BP神经网络的准确率提升了9.82%,emape降低了2.24%。
2) 通过实车实验对干燥沥青路面与潮湿沥青路面进行了验证。结果表明Elman神经网络识别路面附着系数具有较强的自适应能力以及抗干扰能力,能够有效地识别出路面附着系数。
| [1] |
付翔, 孙威, 黄斌, 等. 基于指数加权衰减记忆无迹卡尔曼滤波的路面附着系数估计[J]. 汽车技术, 2018(1): 31-37. Fu X, Sun W, Huang B, et al. Estimation of road adhesion coefficient based on fading memory unscented Kalman filtering with exponential weighting[J]. Automobile Technology, 2018(1): 31-37. (in Chinese) |
| [2] |
Liu Y H, Li T, Yang Y Y, et al. Estimation of tire-road friction coefficient based on combined APF-IEKF and iteration algorithm[J]. Mechanical Systems and Signal Processing, 2017, 88: 25-35. DOI:10.1016/j.ymssp.2016.07.024 |
| [3] |
Zhang X D, Göhlich D. A hierarchical estimator development for estimation of tire-road friction coefficient[J]. PLoS One, 2017, 12(2): e0171085. DOI:10.1371/journal.pone.0171085 |
| [4] |
余卓平, 曾德全, 熊璐, 等. 基于激光雷达的无人车路面附着系数估计[J]. 华中科技大学学报(自然科学版), 2019, 47(7): 124-127. Yu Z P, Zeng D Q, Xiong L, et al. Road adhesion coefficient estimation for unmanned vehicle based on lidar[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2019, 47(7): 124-127. (in Chinese) |
| [5] |
Leng B, Jin D, Xiong L, et al. Estimation of tire-road peak adhesion coefficient for intelligent electric vehicles based on camera and tire dynamics information fusion[J]. Mechanical Systems and Signal Processing, 2021, 150: 107275. DOI:10.1016/j.ymssp.2020.107275 |
| [6] |
Song S, Min K, Park J, et al. Estimating the maximum road friction coefficient with uncertainty using deep learning[C]//2018 21st International Conference on Intelligent Transportation Systems (ITSC). New York: ACM, 2018: 3156-3161.
|
| [7] |
王岩, 梁冠群, 危银涛. 基于支持向量机的智能轮胎路面辨识算法[J]. 汽车工程, 2020, 42(12): 1671-1678, 1717. Wang Y, Liang G Q, Wei Y T. Road identification algorithm of intelligent tire based on support vector machine[J]. Automotive Engineering, 2020, 42(12): 1671-1678, 1717. (in Chinese) |
| [8] |
Dogˇan D. Road-types classification using audio signal processing and SVM method[C]//2017 25th Signal Processing and Communications Applications Conference (SIU), May 15-18, 2017, Antalya, Turkey. IEEE, 2017: 1-4.
|
| [9] |
Alonso J, López J M, Pavón I, et al. On-board wet road surface identification using tyre/road noise and Support Vector Machines[J]. Applied Acoustics, 2014, 76: 407-415. DOI:10.1016/j.apacoust.2013.09.011 |
| [10] |
Shao L, Jin C, Lex C, et al. Robust Road friction estimation during vehicle steering[J]. Vehicle System Dynamics, 2019, 57(4): 493-519. DOI:10.1080/00423114.2018.1475678 |
| [11] |
Chen L, Luo Y G, Bian M Y, et al. Estimation of tire-road friction coefficient based on frequency domain data fusion[J]. Mechanical Systems and Signal Processing, 2017, 85: 177-192. DOI:10.1016/j.ymssp.2016.08.006 |
| [12] |
平先尧, 李亮, 程硕, 等. 四轮独立驱动汽车多工况路面附着系数识别研究[J]. 机械工程学报, 2019, 55(22): 80-92. Ping X Y, Li L, Cheng S, et al. Tire-road friction coefficient estimators for 4WID electric vehicles on diverse road conditions[J]. Journal of Mechanical Engineering, 2019, 55(22): 80-92. (in Chinese) |
| [13] |
刘志强, 刘逸群. 路面附着系数的自适应衰减卡尔曼滤波估计[J]. 中国公路学报, 2020, 33(7): 176-185. Liu Z Q, Liu Y Q. Estimation algorithm for road adhesion coefficient using adaptive fading unscented Kalman filter[J]. China Journal of Highway and Transport, 2020, 33(7): 176-185. (in Chinese) DOI:10.3969/j.issn.1001-7372.2020.07.018 |
| [14] |
赵治国, 朱强, 周良杰, 等. 分布式驱动HEV自适应无迹卡尔曼车速估计[J]. 中国科学: 技术科学, 2016, 46(5): 481-492. Zhao Z G, Zhu Q, Zhou L J, et al. Vehicle speed estimation in driving case based on distributed self-adaptive unscented Kalman filter for 4WD hybrid electric car[J]. Scientia Sinica (Technologica), 2016, 46(5): 481-492. (in Chinese) |
| [15] |
熊璐, 金达, 冷搏, 等. 考虑复杂激励条件的分布式驱动电动汽车路面附着系数自适应估计方法[J]. 机械工程学报, 2020, 56(18): 123-133. Xiong L, Jin D, Leng B, et al. Adaptive tire-road friction estimation method for distributed drive electric vehicles considering multiple road excitations[J]. Journal of Mechanical Engineering, 2020, 56(18): 123-133. (in Chinese) |
| [16] |
Feng Y C, Chen H, Zhao H Y, et al. Road tire friction coefficient estimation for four wheel drive electric vehicle based on moving optimal estimation strategy[J]. Mechanical Systems and Signal Processing, 2020, 139: 106416. |
| [17] |
Gao L T, Xiong L, Lin X F, et al. Multi-sensor fusion road friction coefficient estimation during steering with Lyapunov method[J]. Sensors (Basel, Switzerland), 2019, 19(18): 3816. |
| [18] |
罗虹, 张立双, 来飞, 等. 采用横摆力矩优化分配方法的车辆稳定性控制系统[J]. 重庆大学学报, 2010, 33(10): 19-24. Luo H, Zhang L S, Lai F, et al. Vehicle stability control system design using optimal allocation of yaw moment[J]. Journal of Chongqing University, 2010, 33(10): 19-24. (in Chinese) |
| [19] |
汪涛. 面向商用车的路面附着系数估计研究[D]. 重庆: 重庆邮电大学, 2019. Wang T. Estimation of road adhesion coefficient for commercial vehicles[D]. Chongqing: Chongqing University of Posts and Telecommunications, 2019. (in Chinese) |
 2023, Vol. 46
2023, Vol. 46


