混凝土结构基本原理和混凝土结构设计是土木工程专业本科教学中最重要的专业基础课和专业课。这两门课程对学生在本科阶段打下良好的专业基础至关重要。然而,多年的教学实践表明:在混凝土结构基本原理课程的学习中,学生往往因锚固长度概念认识不足,而无法理解为保证钢筋混凝土梁抗弯承载力而规定的支座处钢筋的锚固要求以及梁负弯矩区钢筋的合理切断点位置。国内使用的教材中,对此也未作合理的描述。为此,有必要对这一问题加以讨论,澄清模糊认识,在教授知识的同时培养学生理解问题和解决问题的能力。
一、混凝土中受拉钢筋的锚固长度钢筋与混凝土之间良好的粘结性能是钢筋与混凝土两种不同材料共同工作的基础。当混凝土中的钢筋单独受力时,钢筋上的力必须通过一定长度上粘结力的累积方能传递到混凝土上,这个长度称为传递长度或称钢筋应力发展长度[1]。
以直径为2c′的圆形截面混凝土试件内配置直径为d的带肋钢筋拔出模型为例,图 1a、c所示,推算钢筋在混凝土中的传递长度ltr。当钢筋受到拉力T时,由于钢筋表面凸出的肋与混凝土间的机械咬合作用,钢筋的肋会对混凝土产生斜向挤压力(图 1a)。斜向挤压力的竖向分量合力就是钢筋与混凝土间的粘结力。斜向挤压力的水平分量使钢筋外围混凝土犹如受内压的管壁(图 1d)。假定:(1)粘结应力沿钢筋纵向均匀分布(图 1b);(2)内压p引起的混凝土中的拉应力按线性分布(图 1d);(3)当混凝土发生纵向劈裂破坏时粘结失效。

|
图 1 混凝土中钢筋的传递长度 |
由图 1d所示的截面受力平衡条件
| $ {l_{tr}}pd = \left( {2c'-d} \right)\frac{{{\sigma _t}}}{2}{l_{tr}} $ | (1) |
得
| $ p = \left( {\frac{{c'}}{d}-\frac{1}{2}} \right){\sigma _t} $ | (2) |
(为了便于理解对钢筋表面形状作了高度简化)
当σt=ft时,混凝土纵向劈裂,粘结失效。于是极限内压应力为
| $ {p_u} = \left( {\frac{{c'}}{d}-\frac{1}{2}} \right){f_t} $ | (3) |
取钢筋为隔离体由钢筋沿其纵向受力平衡(图 1b)得平均粘结应力为
| $ {\tau _u} = \frac{T}{{{\mu _s}{l_{tr}}}} = \frac{{{\rm{ \mathit{ π} }}{d^2}\frac{{{\sigma _s}}}{4}}}{{{\rm{ \mathit{ π} }}d{l_{tr}}}} = \frac{{d{\sigma _s}}}{{4{l_{tr}}}} $ | (4) |
式中,σs为拉力T在钢筋中产生的拉应力。
对于带肋钢筋,当肋的倾角为45°时,钢筋肋与混凝土间斜向挤压力的纵向分量和径向分量相等,故有
| $ {\tau _u} = {p_u} $ | (5) |
将式(3),(4)代入式(5),可得
| $ \frac{{{l_{tr}}}}{d} = \frac{{{\sigma _s}}}{{\left( {\frac{{4c'}}{d}-2} \right){f_t}}} $ | (6) |
若令c′=2d,则上式可以写成
| ${l_{tr}} = \frac{{{\sigma _s}}}{{6{f_t}}}d $ | (7) |
将式(7)写成一般形式,有
| $ {l_{tr}} = \alpha \frac{{{\sigma _s}}}{{{f_t}}}d $ | (8) |
式中,α为与钢筋截面形状等因素有关的常数。
由式(8)可知,钢筋要发挥多大的力就要求提供多长的传递长度或发展长度。特别地,若要保证钢筋受拉屈服,传递长度必须满足式(9)。
| $ {l_{tr}} \ge\alpha \frac{{{f_y}}}{{{f_t}}}d $ | (9) |
《混凝土结构设计规范》(GB50010-2010)(以下简称“规范”)推荐的充分利用钢筋抗拉强度时的钢筋锚固长度计算公式即是根据这一原理而建立的,如式(10)。
| $ {l_{tr}}{\rm{ = }}\alpha \frac{{{f_y}}}{{{f_t}}}d $ | (10) |
“规范”称la为基本锚固长度。
二、钢筋混凝土梁的抗弯承载力钢筋混凝土梁的正截面抗弯承载力取决于纵向受拉钢筋的应力σs。已知钢筋的应力σs及截面的内力臂γsh0,单筋矩形截面梁正截面抗弯承载力可由式(11)计算。
| $ {M_u} = {\sigma _s}{A_s}{\gamma _s}{h_0} $ | (11) |
式中,σs为钢筋应力,As为纵筋的面积,h0为截面有效高度。
由式(11)可知,当钢筋混凝土梁中的纵向受力钢筋的应力为0时,截面能抵抗的弯矩为0;当钢筋混凝土梁中的纵向受力钢筋的应力达屈服强度fy时,截面能抵抗的弯矩达最大值。
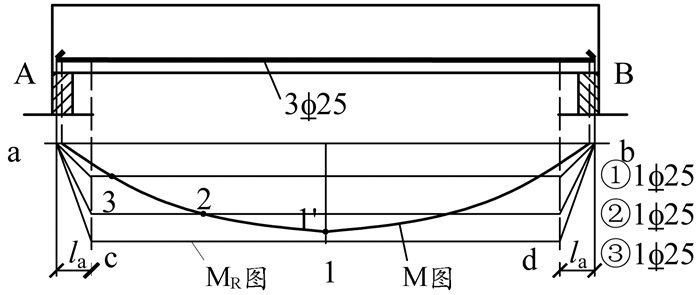
现有一钢筋混凝土简支梁如图 2所示,梁中配置3ϕ25的纵向受力钢筋,且为适筋梁。尽管此梁中的钢筋通长布置,但梁各截面的抗弯承载力却不相等。以支座A附近的各截面为例:钢筋端点处,由于传递长度或发展长度为0,由式(8)知钢筋中的应力只能为0,由式(11)知该处截面的抗弯承载力为0;由钢筋端点向右移动,钢筋的传递长度不断增加,钢筋中能达到的最大应力随之增加,截面的抗弯承载力相应增加;在距钢筋端点la处,极限状态下钢筋的应力可以达到fy,截面的抗弯承载力达最大值,如式(12)。
| $ {M_u} = {f_y}{A_s}{\gamma _s}{h_0} $ | (12) |
|
图 2 钢筋混凝土梁的抵抗弯矩图 |
B支座附近梁截面的抗弯承载力的变化情况和A支座类似。取截面的抵抗弯矩MR=Mu,并假定支座附近截面的抗弯承载力呈线性变化,则可绘出梁的抵抗弯矩图,如图 2中的梯形abcd。如再假定按钢筋的截面积确定每根钢筋对截面抵抗弯矩的贡献,亦可绘出每根钢筋的截面抵抗弯矩图(图 2)。显然,当梁的抵抗弯矩图(MR图)包住梁的弯矩图(M图)时,梁处于安全状态。
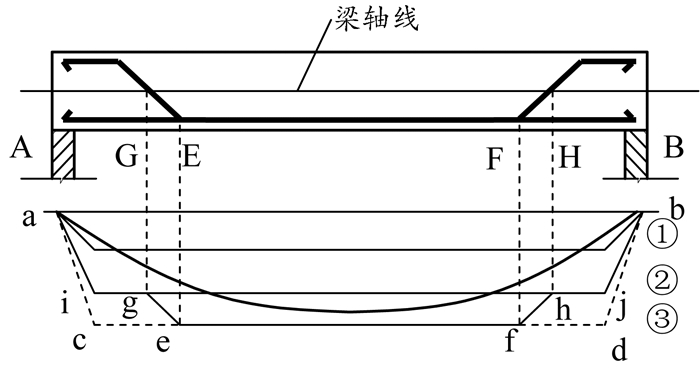
同理,当梁中有一根钢筋弯起时,可绘出梁的抵抗弯矩图(图 3)。
|
图 3 钢筋弯起后梁的抵抗弯矩图 |
值得一提的是,现有相关混凝土结构教材大都未对上述问题作清晰的描述,甚至错误地认为图 2所示梁各截面的抗弯承载力相等,而将梁的抵抗弯矩图绘成一水平线[3-7]。这不利于学生对基本概念的理解,不利于学生灵活应用已掌握的基本理论,也会使教师产生模糊的认识。
三、支座处纵向受力钢筋的锚固建立了正确的抵抗弯矩图就容易理解梁支座处纵向受力钢筋的锚固措施。
如图 4a所示,梁底部纵向受力钢筋伸入简支支座的锚固长度las,理论上只需要保证钢筋发挥到能够抵抗支座边缘设计弯矩值MA的应力即可。但是,若支座边缘截面处剪力过大,容易形成斜裂缝。斜裂缝出现后A点的钢筋却要参与抵抗B点的弯矩,纵向钢筋中的应力增大,由式(7)知,锚固长度应该加大。因此,“规范”对简支梁和连续梁简支端下部纵向受力钢筋伸入支座的长度las有如下要求:当剪力V≤0.7ftbh0时,las≥5d;当剪力V > 0.7ftbh0时,带肋钢筋las≥12d,光圆钢筋las≥15d。此处,d为纵向受力钢筋的直径。

|
图 4 纵筋在支座处锚固 |
一般认为,当V > 0.7ftbh0时,混凝土梁中将产生斜向裂缝,故相应的las应加大。
由图 4可以看出,尽管las < la,但抵抗弯矩图仍然能包住弯矩图。这是因为斜裂缝出现后,A点处钢筋的应力并没有达到其屈服应力。
对于框架梁,在水平风荷载或地震作用下,梁端支座处会产生较大的正弯矩。当水平风荷载或地震作用较大时,底部纵向受力钢筋也可能受拉屈服。故“规范”规定对梁底直锚入柱子的钢筋,锚固长度一般至少要达到la,如图 4b所示。对地震作用下还有相应更严格的构造措施,详见文献[8],此处不予赘述。
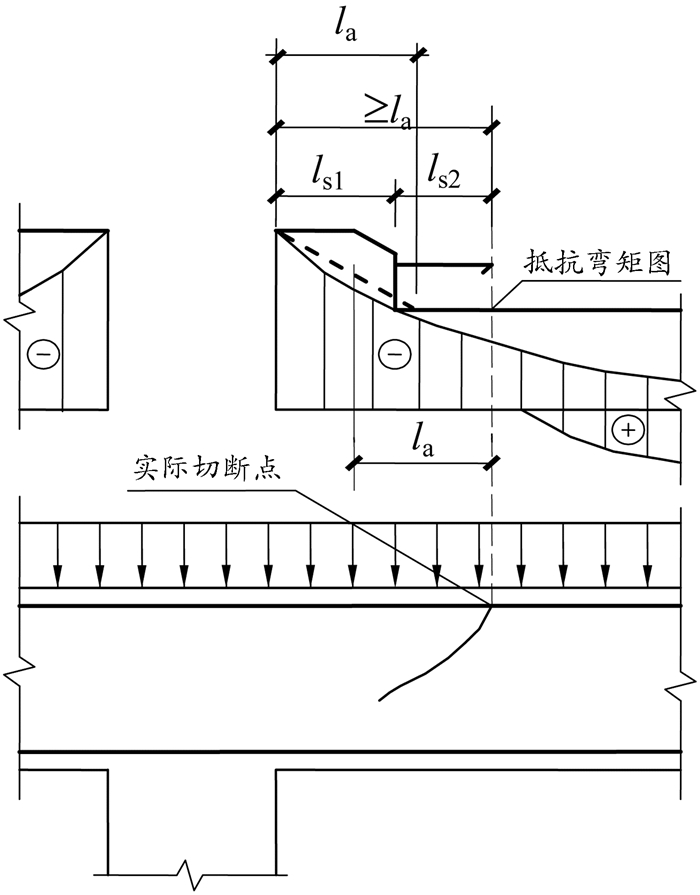
四、负弯矩区钢筋的切断点与上节分析类似,支座负弯矩区钢筋切断时,要同时保证正截面抗弯和斜截面抗弯承载力。在抵抗弯矩图中,钢筋的不需要点称为理论切断点。若在理论切断点处切断钢筋,就有可能使多个正截面的抗弯承载力不能满足要求,如图 5所示切断点左面的多个截面。由式(10)以及负弯矩区弯矩图的下凹特征可知,为避免纵筋切断点至支座处各截面发生正截面受弯破坏,纵筋至少应该在充分利用点外伸la处切断,此时的抵抗弯矩图如图 6中的虚线所示。然而,切断点处由于应力集中引起混凝土所承受的拉应力突增,往往会产生弯剪斜裂缝。斜裂缝出现后,钢筋切断点处的抵抗弯矩可能会小于裂缝尖端处的弯矩而发生斜截面受弯破坏。故为了避免发生沿斜截面的弯曲破坏,纵筋应从理论切断点外伸一定长度ls2后再切断,且应满足ls2+ ls2≥la,如图 6所示。这即是“规范”对梁负弯矩区纵向受力钢筋切断处有两个长度要求的原因。

|
图 5 在理论切断点处切断钢筋后的抵抗弯矩图 |
|
图 6 钢筋实际切断点的合理位置 |
如何在教学过程中调动学生的学习兴趣,培养学生理解知识、应用知识的能力,激发学生的创造性,值得广大高等教育工作者关注。讲清基本概念,注重知识体系的连贯性和完整性,引导学生用已掌握的理论方法去解决复杂问题是调动学生兴趣、培养学生能力、激发学生潜力的重要手段。文章从钢筋与混凝土之间的粘结与锚固出发,讨论了钢筋混凝土梁的抗弯承载力以及保证梁抗弯能力的一些构造措施,旨在使学生理解基本概念、灵活运用已掌握的基本理论和知识。
| [1] | 顾祥林. 混凝土结构基本原理[M]. 2版. 上海: 同济大学出版社, 2011. |
| [2] | GB50010-2010混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2011. http://www.bookask.com/book/63487.html |
| [3] | 东南大学, 同济大学, 天津大学. 混凝土结构(上册)[M]. 4版. 北京: 中国建筑工业出版社, 2010. |
| [4] | 沈蒲生, 梁兴文. 混凝土结构设计原理[M]. 北京: 高等教育出版社, 2007. |
| [5] | 梁兴文, 史庆轩. 混凝土结构设计原理[M]. 北京: 中国建筑工业出版社, 2008. |
| [6] | 刘文峰. 混凝土结构设计原理[M]. 北京: 高等教育出版社, 2004. |
| [7] | 杨政. 混凝土力学与构件设计原理[M]. 西安: 西安交通大学出版社, 2010. |
| [8] | GB50011-2010建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010. http://www.bookask.com/book/1575521.html |
 2013, Vol. 22
2013, Vol. 22

