在现行材料力学教材中,较少讲解逐段刚化法,只在用叠加法求解外伸梁变形时简单提及。逐段刚化法实质为材料力学常用方法——叠加法的一种特例,但在材料力学教材中,其原理及应用较少阐述,因此,对该问题进行深入研究,对于完善材料力学教学内容十分必要。
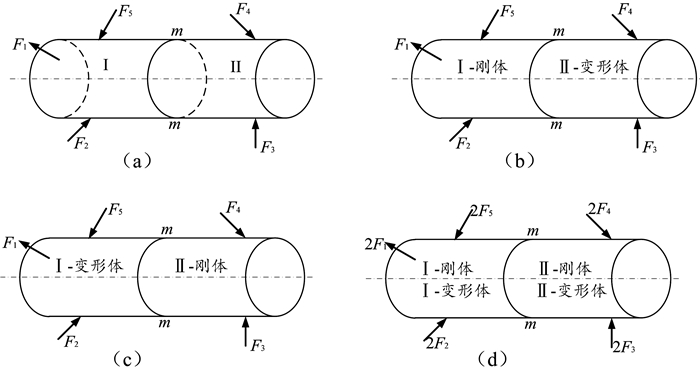
一、逐段刚化法的基本原理构件在受到外力作用下处于平衡状态,假想用m-m截面把构件分成Ⅰ、Ⅱ两部分(如图 1),则构件的变形由这两部分组成,即δsum=δⅠ+δⅡ,δ为广义变形。
|
图 1 |
将Ⅰ、Ⅱ段刚化得到图 1(b)、图 1(c)所示部分。将这两部分叠加,则得到图 1(d)所示构件。此时,构件相当于两个构件放在一起,载荷加倍。但由于两个构件中有一个为刚体,根据刚化原理:“如果变形体在某一力系作用下处于平衡,若将此变形体刚化为刚体,其平衡状态不变”,将原构件刚化后其平衡状态不变;再根据减平衡力系原理,减去作用在刚体上的一组平衡力,则变形体只受到一组平衡力作用,即得到初始变形体状态,如图 1(a)所示。通过逐段刚化法后,所求的变形与原始状态一致,从而说明了逐段刚化法具有可行性,其实质是叠加法的一种特例。传统的叠加法是构件不变,载荷叠加;而逐段刚化法,是载荷不变,构件叠加。
在应用逐段刚化法时要注意4点:(1)构件的变形为小变形,须满足虎克定律;(2)刚化部分的外力对变形体段的作用必须合成到变形段末端;(3)变形量为广义变形,可以为轴向变形、扭转角或梁弯曲时的转角和挠度;(4)由刚化所引起的刚体变形需考虑总变形,比如梁变形段末端转角会引起“刚化段”的刚体位移。
二、逐段刚化法应用逐段刚化法在材料力学中应用广泛,尤其是用来求解材料力学中较为复杂的问题比较简便,下面列举其应用。
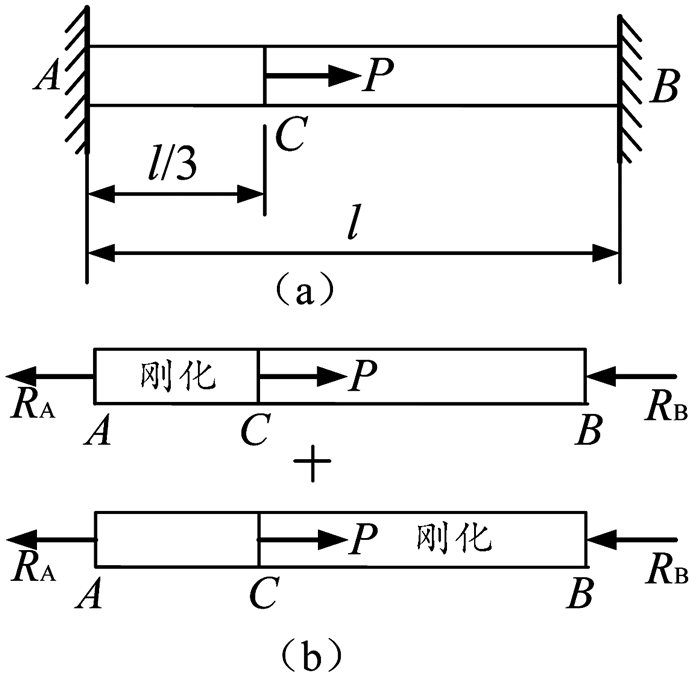
(一) 逐段刚化法在轴向拉压中的应用如图 2所示超静定杆AB,在1/3处受集中力P作用,求A、B两端约束反力,杆件抗拉刚度EA已知。
|
图 2 |
(1) 解题思路:此题可用变形协调条件补充一个几何学方程,再联立物理学方程和静力学平衡方程,求两端约束力,但此过程较为繁琐,如用逐段刚化法则较为简单。将杆件AB分为AC段和CB段进行刚化,如图 2(b)所示。AC段刚化后为刚体,无变形,CB段的变形由RB产生;而CB段刚化后,CB为刚体,无变形,AC段的变形由RA产生。由于杆件两端固定,所以它们的变形总和为零。
(2) 具体求解:AC段刚化,BC段变形:ΔlBC=(-RB)·
又根据静力学平衡方程:RA+RB=P,可得出RA=2P/3,RB=P/3。
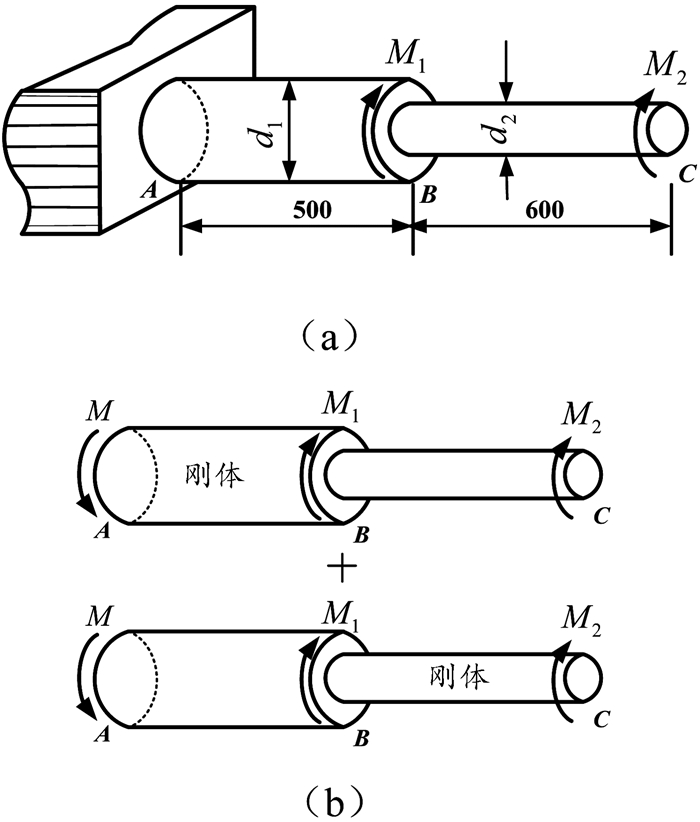
(二) 逐段刚化法在圆轴扭转中的应用变截面轴受力如图 2(a)所示,A端固定。M1=1 500 Nm,M2=1 000 Nm,d1=70 mm,d2=50 mm,材料的切变模量G=80.4 GPa。试求轴内最大相对扭转角。
(1) 解题思路:将变截面轴AC分为AB段和BC段进行刚化,如图 3(b)所示。AB段刚化后为刚体,无变形,CB段的扭转角由M2产生;而BC段刚化后为刚体,无变形,AB段的扭转角由M产生,从而求出AB段、BC段相对扭转角,也可确定最大相对扭转角。
|
图 3 |
(2) 具体求解:AB段刚化,BC段扭转角:
BC段刚化,AB段扭转角:
最大相对扭转角为AC段相对扭转角:φmax=φAC=φAB+φBC=0.018 8 rad。
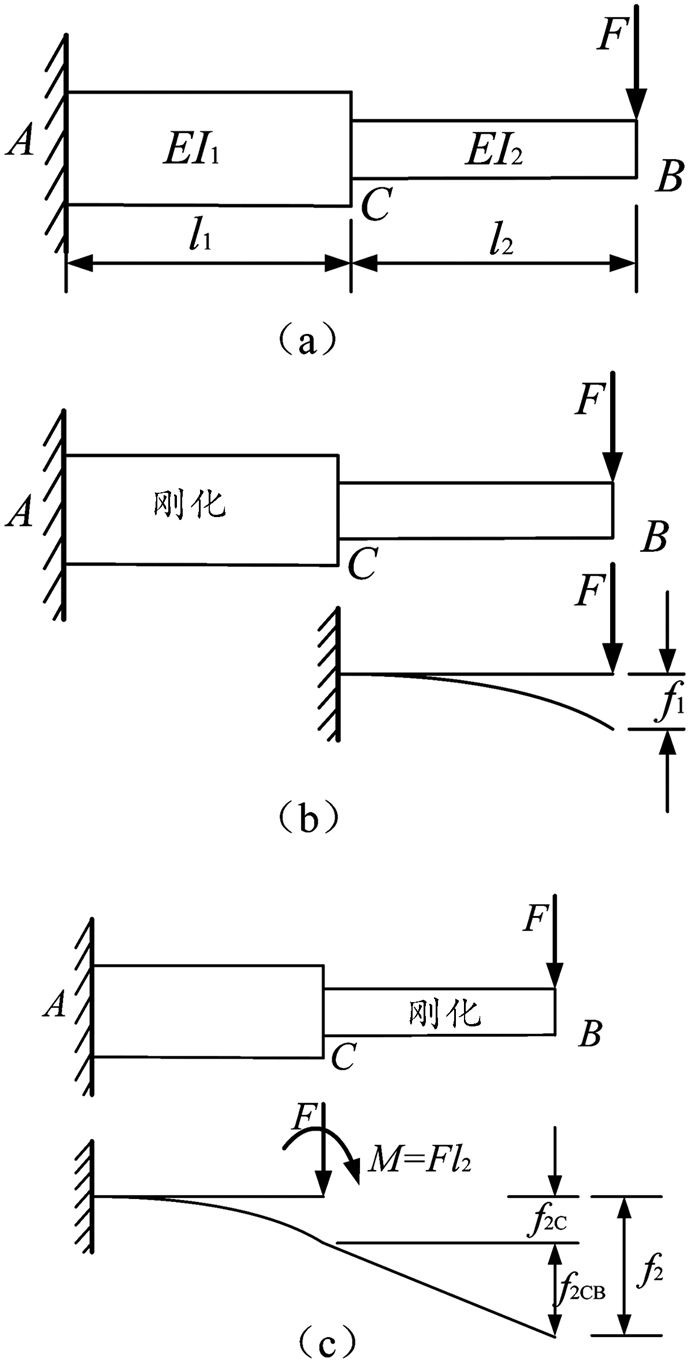
(三) 逐段刚化法在梁变形中的应用计算图 4(a)所示阶梯梁的最大挠度,已知EI1、EI2为常量。
|
图 4 |
(1) 解题思路:由图可知,最大挠度发生于B截面处。将变截面梁分为AC段和CB段进行刚化,如图 4(b)、(c)所示。AC段刚化后,则CB段相当于C截面固定的悬臂梁;而CB段刚化后,CB为刚体,AC段为悬臂梁,根据“静力等效原则”,C处受到的载荷为F和M,并且此时CB附在C截面上,B截面处的挠度由两部分组成:一为C点的挠度,二为由转角引起刚化段CB的刚性位移。
(2) 具体求解:
在图 4(b)中f1=
如图 5(a)所示刚架,试画出其内力图。其已知各段抗弯刚度均为EI,不计轴力和剪力的影响,试求A截面的垂直位移。
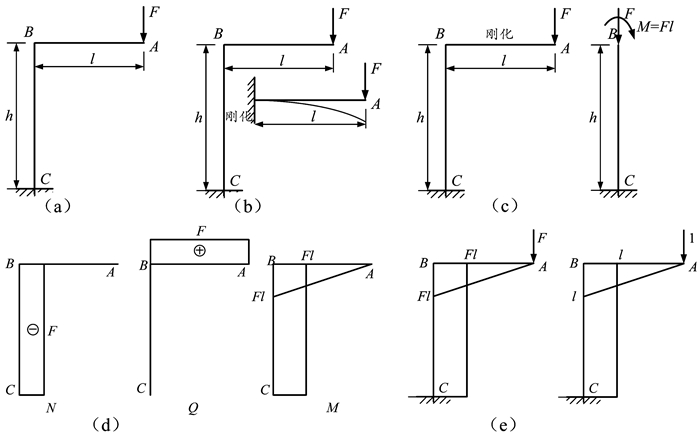
|
图 5 |
(1) 解题思路:将刚架分为CB段和BA段进行刚化,如图 5(b)、(c)所示。CB段刚化后,则BA段相当于B截面固定的悬臂梁,可在BA段画出内力图;而BA段刚化后,BA为刚体,根据“静力等效原则”,CB段B处受到的载荷为F和M,则CB段的内力图很容易画出。弯矩图得出后,用图乘法就可求出A点垂直位移。
(2) 具体求解:
CB段刚化,BA段为悬臂梁,其内力图如图 5(d)中BA段所示。BA段刚化,CB段受载荷为F和M作用,其内力图如图 5(d)中CB段所示。计算A点垂直位移采用图乘法,如果不计轴向拉压,在A点施加单位力,则刚架内力图和单位力图如图 5(e)所示。
| $ \begin{array}{l} \;\;\;\;\;\;EI{\mathit{\Delta} _A} = \frac{1}{2}Fl \cdot l \cdot \frac{2}{3}l + Fl \cdot h \cdot l = \frac{1}{3}F{l^3} + F{l^2}h,\\ {\mathit{\Delta} _A} = \frac{{F{l^2}\left( {l + 3h} \right)}}{{3EI}}。\end{array} $ |
对于材料力学中变截面梁问题和平面刚架等问题,一般叠加法难以求解,因为常用的叠加法都是载荷的叠加,不涉及变截面的问题。而通过上面的讨论可以看出,应用逐段刚化法求解超静定拉压杆、变截面梁、轴和平面刚架问题,其原理明了,易于理解,计算简单,是一种简单有效的方法。
| [1] | 刘鸿文. 材料力学[M]. 5版. 北京: 高等教育出版社, 2010. |
| [2] | 陈兰新. 逐段刚化法在材料力学中的应用[J]. 甘肃广播电视大学学报, 1998(3): 62–64. |
| [3] | 洪彩霞. 逐步刚化法的实质[J]. 电力学刊, 1991, 6(2): 41–43. |
 2013, Vol. 22
2013, Vol. 22


