由于公路工程技术的不断发展,交通部在1995年后陆续颁布了多个规范,如《公路沥青路面设计规范》(2006年版)和《水泥混凝土路面设计规范》(2011年版)等。但路基路面工程课程所用教材跟不上规范更新的步伐,这就给正常的授课带来困难。为此也有一些学者对这方面的教学内容进行了探讨和研究[1-2]。因此,文章针对新规范[3]和现有最新教材,结合学校及教育部专业建设要求[4-5],对路基路面工程中沥青路面结构设计章节的授课内容进行部分增补,便于学生在后续课程设计、毕业设计中进行手算分析。
一、详解沥青路面结构设计分析过程 (一) 沥青路面设计过程简介最新规范中沥青路面结构设计采用的方法是依据相应设计软件进行,即把待设计路面的交通量信息、道路信息、各层材料模量、除待定层以外其他层厚度,及设计限制(如最小设计厚度、防冻厚度等)输入程序中,程序将自动完成路面结构设计。
(二) 沥青路面结构设计步骤分析从软件设计过程可知,设计者应根据实际情况对设计结果进行适当调整,才可设计出比较符合实际的路面结构。近期出版的相关教材中[6-7],也全部采用了机算设计方法。但对初学者来说,由于对路面结构概念理解不够透彻,对软件设计结果的恰当与否也无从判断。因此,为了给学生讲清楚沥青路面结构设计的详细步骤,必须把软件中的设计过程展开来分步骤、分环节地讲解,否则学生无法透彻理解设计的内涵,也不能熟练掌握沥青路面结构设计过程。为此,文章根据最新规范,结合众多参考文献和相应规范,归纳总结出如下适用于授课内容的手算设计方法。
第一步:给出待设计道路等级、沥青路面类型、面层类型、设计年限t、车道系数η。进而确定道路等级系数Ac、面层类型系数As和基层类型系数Ab。
第二步:交通量和设计弯沉的计算。根据交通量调查结果给出交通量资料:(1) 道路上行驶车辆类型及其日交通量;(2) 设计年限内交通量平均增长率预测值γ。统计计算路面竣工后第一年平均日当量轴次N1(次/d),计算累计交通量
| $ {N_e} = \frac{{[{{(1 + \gamma )}^t}-1] \times 365}}{\gamma }{N_1}\eta $ | (1) |
依据规范,由Ne计算结果确定交通等级。
第三步:确定E0、σps,拟定路面结构组成方案。按照路基土类型与干湿类型,确定路基回弹模量E0。拟定路面结构组成层数,以及每层所用材料,实验测定或者查规范[3]确定各层材料在规定温度或龄期的劈裂强度σps(MPa),及抗压回弹模量Ei。选定待定设计层,除该层外确定其余所有层厚度。
对于二级及二级以上的公路,需要进行各整体结构层层底的弯拉应力验算,为此需要确定这些层的容许弯拉应力。计算各层对应容许拉应力
| $ {\sigma _R} = {\sigma _{sp}}/{K_s} $ | (2) |
式中,Ks—抗拉强度结构系数,可用下面公式求得。
对于沥青混凝土面层:
| $ {K_s} = 0.09N_e^{0.22}/{A_c} $ | (3a) |
对于无机结合料稳定集料类:
| $ {K_s} = 0.35N_e^{0.11}/{A_c} $ | (3b) |
对于无机结合料稳定细粒土类:
| $ {K_s} = 0.45N_e^{0.11}/{A_c} $ | (3c) |
第四步:计算沥青路面结构的设计弯沉ld。
| $ {l_d} = 600N_e^{ - 0.2}{A_c}{A_s}{A_b} $ | (4) |
第五步:给出限制条件并进行路面结构设计。
根据上述诸多条件,给出道路结构层最小设计厚度,以及总结构层的最小防冻厚度(对季冻区)。由设计弯沉ld通过机算或者查诺模图求解待设计层厚度hi。再对所有整体结构层层底拉应力进行计算。当所有层都满足要求,即说明拟定的路面结构合理。否则,调整设计层厚度后,重复上述步骤,直到满足要求为止。
二、详解沥青路面结构手算设计过程利用手算进行沥青路面结构设计时,在交通量统计和Ne已经获得的基础上,需按照下列步骤进行。
第一步:三层体系转化。
按照弯沉等效原则要求将多层体系转换成三层体系,如图 1所示。对应的具体换算公式为
| $ H = \sum\limits_{i = 2}^{n = 1} {{h_i}\sqrt[{^{2.4}}]{{{E_i}/{E_2}}}} $ | (5) |

|
图 1 路表弯沉等效的结构层换算图 |
第二步:综合修正系数F。
F是用来修正路表弯沉理论计算值ld的误差。规范中定义为[3]
| $ F = 1.63{(\frac{{{l_s}}}{{2\;000\delta }})^{0.38}}{(\frac{{{E_0}}}{p})^{0.36}} $ | (6) |
式中,ls为路面实际弯沉值(0.01 mm),当由弯沉来设计路面结构厚度时,取设计弯沉ld即可;p=0.7MPa为标准轴的轮胎接地压强;δ=10.65 cm为标准轴的当量圆半径。考虑F后弹性三层体系表面的回弹弯沉计算公式为:
| $ {l_s} = 1\;000 \cdot \frac{{2p\delta }}{{{E_1}}}{{\alpha '}_L}F $ | (7) |
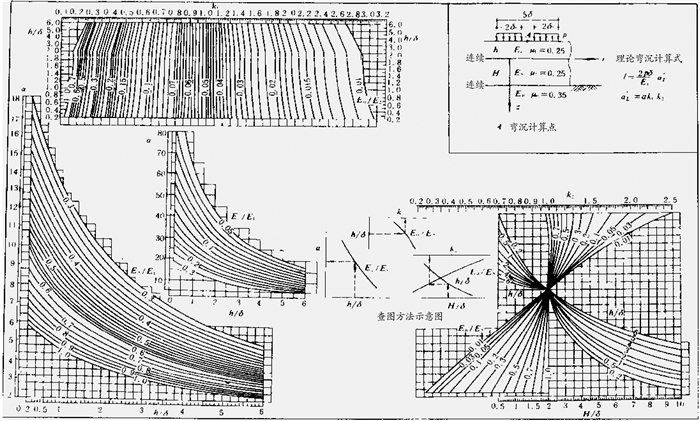
式中,E1(MPa)为三层体系中面层材料回弹模量;α′L为以E1表达时的理论弯沉系数,需通过软件程序或查表来计算。一般情况下,结构设计时上面层厚度为已知,其下某基层厚度为待定,故由上面公式转化后三层体系中层厚度H一般是未知量。故可根据三层体系弯沉系数诺模(图 2),并由ld反算三层体系中层厚度H,然后反求待定设计层厚度hi。图 2中理论弯沉计算式:
|
图 2 三层体系表面弯沉系数诺模图 |
第三步:按弯拉应力等效原则进行三层体系转化。
对需要进行层底拉应力验算的结构层,需将多层体系按照弯拉应力相等原则换算为三层体系,如图 3所示。

|
图 3 上层底面弯拉应力等效换算图 |
当计算第i层底面弯拉应力时,需利用公式(8) 将该层以上所有层换算为三层体系上层;用公式(9)=将i+1层至n-1层换算为三层体系中层
| $ h = \sum\limits_{k = 1}^i {{h_k}\sqrt[{^4}]{{{E_k}/{{E}_i}}}} $ | (8) |
| $ H = \sum\limits_{k = i + 1}^{n - 1} {{h_k}\sqrt[{^{0.9}}]{{{E_k}/{{E}_{i + 1}}}}} $ | (9) |
假设上层和中层间为连续接触,如为滑动接触,可查阅相关文献[6]计算,方法类似。上层和中层底面最大拉应力表达式分别为
| $ {\sigma _{{r_1}}} = p{{\bar \sigma }_{{r_1}}}, {\sigma _{{r_2}}} = p{{\bar \sigma }_{{r_2}}} $ | (10) |
其中,弯拉应力系数σr1和σr2可由软件电算直接得到,也可以查阅诺模图。
三、算例分析某一级公路宽15 m,取车道横向分布系数η=0.4,交通量平均增长率γ=4.5%,设计年限t=15 y。路线所经地区为Ⅱ2区,土质为粉质低液限粘土,根据相关规范和参考资料[3, 6],查得路基土回弹模量为31 MPa。通过分析得累计交通量为:Ne = 750(万次)。
初步拟定路面结构及力学计算参数如表 1所示。现利用手算计算确定待定层厚度h3(以下所有手算结果后括号内斜体数值为软件HPDS2011机算结果)。
| 表 1 路面结构材料及结构 |
| $ \begin{array}{*{20}{l}} {{l_d} = 600N_e^{ - 0.2}{A_c}{A_s}{A_b} = 600 \times 7\;500\;{{000}^{ - 0.2}} \times 1 \times }\\ {1 \times 1 = 600 \times 0.039\;83 = }\\ {25.5(0.01{\rm{mm}})(25.5)} \end{array} $ |
| $ \begin{array}{l} F = 1.63{\left( {\frac{{{l_s}}}{{2\;000\delta }}} \right)^{0.38}}{\left( {\frac{{{E_0}}}{p}} \right)^{0.36}} = \\ 1.63{\left( {\frac{{25.5}}{{2\;000 \times 10.65}}} \right)^{0.38}}{\left( {\frac{{31}}{{0.7}}} \right)^{0.36}} = 0.495 \end{array} $ |
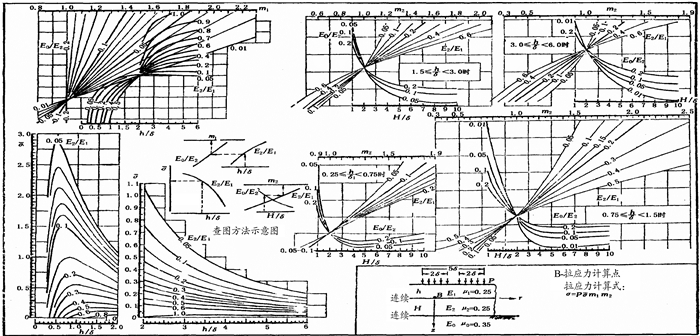
将5层体系简化成三层体系。由h1/δ=0.563 4,E2/E1=1 000/1 200=0.833,E0/E2=31/1 000=0.031,查图 4得α=6.3,k1=1.3。由系数α′L=αk1k2和式(7) 得
|
图 4 三层体系上层层底拉应力系数σr1诺模图 |
| $ \begin{array}{l} 61.8 = 8 + {h_3} \times \sqrt[{^{2.4}}]{{1\;300/1\;000}} + 20 \times \\ \sqrt[{^{2.4}}]{{180/1\;000}} \end{array} $ |
解得h3=39.3 cm(39.6),考虑实际施工采用水泥稳定砂砾层厚为40 cm,分两层施工。
(3) 验算中粒式沥青混凝土上面层层底拉应力三层体系为:下面为土基,上层为6 cm中粒式沥青混凝土,中层为由第2层到第4层组成的粗粒式沥青混凝土,厚度为
| $ \begin{array}{l} H = \sum\limits_{k = 2}^4 {{h_k}\sqrt[{^{0.9}}]{{{E_k}/{{E}_2}}}} = \\ 8 + 40 \times \sqrt[{^{0.9}}]{{3\;000/1\;600}} + 20 \times \\ \sqrt[{^{0.9}}]{{180/1\;600}} = 90.2({\rm{cm}}) \end{array} $ |
抗拉强度系数Ks=0.09Ne0.22/Ac=2.90。容许拉应力为:σR=σsp/Ks=1.0/2.9=0.344(MPa)。由h/δ =0.563 4,E2/E1=1 600/1 800=0.889,E0/E2=31/1 800=0.017。查图 4发现拉应力系数已不能从图中查到,表面层底将受压应力(或者拉应力很微小),应视为验算通过(机算结果:-0.128 MPa)。
(4) 验算粗粒式沥青混凝土下面层层底拉应力由上面两层作为上层,厚度为
| $ \begin{array}{l} h = \sum\limits_{k = 1}^i {{h_k}\sqrt[{^4}]{{{E_k}/{{E}_i}}} = 6 \times } \sqrt[{^4}]{{180/1\;600}} + 8 = \\ 14.2({\rm{cm}}); \end{array} $ |
由水泥稳定层和砂砾层组成中层,厚度为:
抗拉强度结构系数为Ks=0.09Ne0.22/Ac=2.9,σR=σsp/Ks=0.275(MPa)。由h/δ=1.33,E2/E1=1.875,E0/E2=0.01。查图 4发现拉应力系数已不能从图中查到,应视为拉应力验算通过(-0.093 MPa)。
(5) 验算水泥稳定砂砾半刚性基层层底拉应力三层体系为:天然砂砾为中层,上层厚度为
抗拉强度结构系数为:Ks=0.35Ne0.11/Ac=1.99,σR=σsp/Ks=0.251(MPa)。由h/δ=4.89,E2/E1=0.06,E0/E2=0.172,H/δ=1.88。查图 4得,σ =0.28,m1=1.08,m2=1.05,σr=0.22 (MPa) < σR,故水泥稳定砂砾基层层底拉应力验算通过(0.213 MPa)。
最后,由上述计算结果可知,此次拟定的沥青路面结构满足设计弯沉和整体结构层层底拉应力的要求,符合规范要求,可以作为最后设计结果。
四、结语文中介绍了沥青路面结构设计新规范中主要的修改内容,包括其中的设计理论和设计方法,以及根据这些改变,详细讲解现行沥青路面结构设计分析的计算过程。结合课程教学大纲要求,考虑学校目前的实际教学条件,针对沥青路面结构设计一章的授课内容要求,介绍了进行沥青路面结构设计的手算详细步骤,包括已知资料、计算公式、详细设计步骤,及对应设计结果。另外,以算例形式给出了结构手算设计过程,方便学生透彻掌握沥青路面结构设计的理论、依据方法、计算公式及设计结果等内容。通过手算计算结果和软件计算结果的对比分析发现,采用文中所提供的手算方法,沥青路面结构设计的结果和软件计算结果非常接近,证明手算计算方法的可行性,这也为多数学生和科研设计人员采用手算法提供了可靠保证。
| [1] | 宋高嵩, 张春萍, 王剑英. 《路基路面工程》课程教学改革探讨[J]. 哈尔滨学院学报, 2002, 23(8): 152–153. |
| [2] | 马培建, 朱亚光. 土木工程专业路基路面课程教学内容及方法探讨[J]. 高等建筑教育, 2003, 12(3): 41–43. |
| [3] | 中华人民共和国行业标准. JTG D50-2006沥青混凝土路面设计规范[S]. 北京: 人民交通出版社, 2006. |
| [4] | 内蒙古工业大学. 内蒙古工业大学理论课教学大纲[Z]. 2009. |
| [5] | 教育部高, 等. 普通高等学校本科专业目录和业介绍[M]. 北京: 高等教育出版社, 1998. |
| [6] | 邓学均. 路基路面工程[M]. 3版. 北京: 人民交通出版社, 2009. |
| [7] | 陆鼎中, 陈家驹. 路基路面工程[M]. 2版. 上海: 同济大学出版社, 2006. |
 2013, Vol. 22
2013, Vol. 22


