流体力学是研究流体在外力作用下平衡和运动规律的一门学科,是力学的一个分支。随着科学技术的日益发展和进步,流体力学课程不再仅仅是热能与动力工程专业的基础课,也逐渐成为机械、环境、石油、化工、土木等工程技术类专业的主要基础课,是连接基础课和专业课之间的重要桥梁和纽带[1-3]。同时,流体力学又是一门历史悠久而富有新生命力的学科,它综合了张量、场论、复变函数、数值方法以及计算机知识和光学测量技术等知识。随着新理论与新技术的不断涌现,如何提高流体力学课程的教学质量,推进课程教学与实验的改革是教育工作者面临的重要课题。
2008年笔者所在学校的流体力学课程被列为江苏省精品课程。在精品课程建设过程中,针对课堂教学与实践教学的不足,积极推进教学改革与实践创新。一是通过将新方法、新模式引入教学,积极探索新形势下传统流体力学课程教学模式与现代教育方式方法的融合[4-6]。二是针对不同层次学生对流体力学基础知识的不同需求,除按照学校各专业的总体培养计划进行教学之外,还在课堂教学与实践教学中推行分层次和分类别的教学模式,以达到教与学的统一,推进教与学的共同完善[7]。三是针对目前实验教学与课堂教学相互脱节的实际问题,推行任课教师指导实验教学的制度,将课堂教学与实验教学有机地结合在一起,将书本上的理论知识在实验中进行验证,实现课堂教学与实验教学的交融和互补,巩固学生对知识的理解,也调动学生的学习兴趣。此外,在实验教学中采用启发式教学模式,引导学生举一反三,培养学生的创新意识与能力[8]。四是积极推行计算流体力学(Computational Fluid Dynamics, CFD)教学,将科研工作引入对学生的培养之中[9-10]。五是注重启发式、互动式、质疑式等教学方法的应用,吸引学生的注意力,提高课堂教学效果。
一、多媒体教学方式与传统教学方式的互补积极推行多媒体教学方式与传统教学方式的有机结合。传统教学方法主要是教师利用板书进行教学,通过板书将理论分析、方程推导等演绎清楚,便于学生记好笔记,易于接受。教师与学生也能够实现良好的互动,教与学协调一致。但由于传统教学方式节奏较慢,在目前学时量减少的情况下难以完成繁重的教学任务,并且流体力学是一门理论与实践结合得十分紧密的学科,很多知识点可以通过影像和声音在多媒体上较好地展现出来,有助于加深学生对流体力学知识的认识和掌握。因此,多媒体课件在流体力学课程教学中发挥着重要的作用,它能将文本、图像、视频图像、动画与声音等信息集中展示,比传统的教学方法更为直观,更容易被学生理解和接受,并且能提供比传统教学方式大很多的信息量。因此,将多媒体教学与传统教学方式结合起来,达到优势互补是值得思考和研究的重大课题。需要明确的是,多媒体教学与传统教学方式处于同等重要的地位,二者不存在主次之分,只是互为补充。因此,将理论分析、方程推导等内容采用板书形式进行推导和分析,使学生能够了解基本方程的来龙去脉。对于推导过程繁琐且难于理解的部分,要将详细讲解和利用多媒体制作相应的图像、视频或动画说明结合起来,以强化学生的理解。比如流体微团的运动分析,通过对其平面的流动分析,可以知道流体微团平面运动时,其平动、线变形、转动、角变形可以表示为:
| $ \left\{ \begin{align} &{{u}_{x}}+\frac{\partial {{u}_{x}}}{\partial x}dx+\frac{1}{2}\left( \frac{\partial {{u}_{x}}}{\partial y}-\frac{\partial {{u}_{y}}}{\partial x} \right)dy+\frac{1}{2}\left( \frac{\partial {{u}_{x}}}{\partial y}+\frac{\partial {{u}_{y}}}{\partial x} \right)dy \\ &{{u}_{y}}+\frac{\partial {{u}_{y}}}{\partial y}dy+\frac{1}{2}\left( \frac{\partial {{u}_{y}}}{\partial x}-\frac{\partial {{u}_{x}}}{\partial y} \right)dx+\frac{1}{2}\left(\frac{\partial {{u}_{x}}}{\partial y}+\frac{\partial {{u}_{y}}}{\partial x}\right)dx~ \\ \end{align} \right. $ |
显然,采用方程形式表示的亥姆霍斯速度分解定理较难理解;而用多媒体教学中的动画来表示则能很好地解释这种现象的发生和演变过程。如果将两者有机地结合起来,使枯燥、呆板的公式与形象的视频动画演示相互融合补充,有助于学生对流体微团运动分解定理的理解和对亥姆霍斯定理的记忆[5]。因此,教学中将多媒体教学与传统教学结合起来,可以起到事半功倍的效果。
二、分层次与分类别教学方法的运用针对不同专业学生对流体力学知识的不同要求,在实际教学过程中采用分层次与分类别教学方法,将流体力学知识分为学术类与工程技术类。教学中以工程类教学作为主要模式,因为大多数学生面临就业,而只有少部分学生可能会继续深造。然而,在理论分析与方程推导中,应注重与高等数学、复变函数等知识的联系,以提高流体力学课程教学的学术性。比如对于连续性方程的推导,可以采用两种不同的方式进行推导。
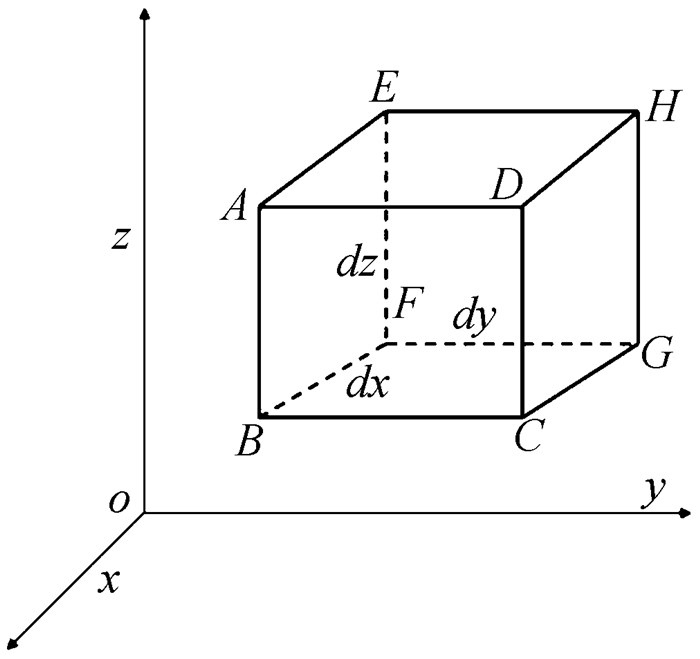
第一种方法。在直角坐标系中取一个由空间点作用的固定不动的平行六面体元素,其棱边dx, dy, dz分别平行于坐标轴(图 1所示)。
|
图 1 平行六面体元素 |
在x轴方向,单位时间内通过表面EFGH和ABCD的质量分别为[11],
| $ \rho udydz, \left[\rho u+\frac{\partial \left( \rho u \right)}{\partial x}dx \right]dydz $ |
在x轴方向,单位时间内通过表面EFGH和ABCD总的质量为,
| $ \frac{\partial \left( \rho u \right)}{\partial y}dxdydz $ |
同理,可得y方向和z方向上单位时间内通过表面的流体总质量分别为,
| $ \frac{\partial \left( \rho u \right)}{\partial y}dxdydz, \frac{\partial \left( \rho w \right)}{\partial z}dxdydz $ |
则,这三式相加的单位时间内通过六面体表面的总质量为,
| $ \left[\frac{\partial \left( \rho u \right)}{\partial x}+\frac{\partial \left( \rho v \right)}{\partial y}+\frac{\partial \left( \rho w \right)}{\partial z} \right]dxdydz $ | (1) |
由于密度的变化,六面体中单位时间内流体质量将减少
| $ -\frac{\partial \rho }{\partial t}dxdydz $ | (2) |
因此,根据质量守恒定律,流出六面体外的流体质量应该等于六面体内质量的减少
| $ \frac{\partial \rho }{\partial t}+\frac{\partial \left( \rho u \right)}{\partial x}+\frac{\partial \left( \rho v \right)}{\partial y}+\frac{\partial \left( \rho w \right)}{\partial z}=0 $ | (3) |
第二种方法主要针对学术类学生。在空间取以S面为界的有限体积τ,该体积由空间点组成,因此,它将固定在空间中不随时间改变。S即为控制面。取外法线方向为正,
一是通过表面S有流体的流入或者流出,单位时间内流出和流入的流体总和为[11],
| $ {{\int }_{S}}\rho {{v}_{n}}\delta S $ | (4) |
二是由于密度场的非定常性,单位时间内体积τ内的质量将减少,减少的数量为,
| $ -{{\int }_{\tau }}~\frac{\partial \rho }{\partial t}\delta \tau $ | (5) |
根据质量不灭定律,(4)等于(5)得
| $ {{\int }_{\tau }}~\frac{\partial \rho }{\partial t}\delta \tau +{{\int }_{S}}\rho {{v}_{n}}\delta S=0~ $ | (6) |
运用奥高公式,将上式中的面积分转换成体积分,即得
| $ {{\int }_{\tau }}~\left( \frac{\partial \rho }{\partial t}+div\rho \overrightarrow{v} \right)\delta \tau =0~ $ | (7) |
由于δτ是任意选取的,且被积函数连续,于是
| $ \frac{\partial \rho }{\partial t}+div\rho \overrightarrow{v}=0 $ | (8) |
以上即为两种不同的连续方程推导方式,此外还有其他方式。对学术性要求较高的学生,第二种方式既能使学生掌握较为深奥的流体力学知识,同时又将高等数学中的微积分、复变函数、线性代数等知识与流体力学紧密结合在一起,为学生在更高的平台进行学习和深造奠定了理论基础。
三、实验教学与课堂教学的统一实验教学是流体力学的重要教学手段,在流体力学课程教学中占有重要地位,是一个必不可少的教学环节。通过在实验中观察流动现象,能增强学生的感性认识,巩固已学过的基础理论知识;通过验证性实验能够验证所学过的流体力学原理,学会利用流体力学基本原理来分析和解释流体力学现象或者流体力学问题;通过实验学会利用各种仪器测量基本的流动参数,掌握一定的实验技能,有助于提高学生实际动手操作能力;通过实验获取相应的实验数据,通过对数据的整理、分析和撰写实验报告,能够培养学生在工程实际问题中的实验设计、数据整理与撰写报告的能力。因此,实际上可以将简单的流体力学实验看作是解决一个工程实践问题的全过程。
针对目前实验教学中存在的学生等、靠、要等较被动的问题,采取主要任课教师指导实验教学的方式。首先,通过课堂理论知识的讲解,帮助学生掌握理论分析的结果。然后,在审核通过学生的实验预习报告后再把学生带进实验室进行分组实验。在实验过程中注重学生动手能力的培养,一般3-4人为一组,测量—读数—数据计算调试设备等,做好分工协作,测量的数据须经教师审阅。在整理实验数据时,将实验结果与课堂教学得出的理论结果进行对比,分析二者之间存在的差距及误差的合理性。
此外,实验教学中应重视学生创新能力的培养。针对某一具体的实验,以课后作业的形式要求学生给出其具体实验的实现方式。学生给出的实验方式可能五花八门,有些甚至不切实际,但这种方法为他们提供了思考和创新的空间,培养了学生创新的思维与意识。有的学生提出的实验方式经过教师指导后,可借助学校的科研立项活动实现这种想法,或者以新型专利的形式申报课题。这既是对学生创新思维的一种鼓励,也能调动更多学生学习流体力学的积极性。例如,动量方程的验证实验,先让学生自己思考如何将动量方程的冲击力作用测量出来。有的学生提出采用弹簧称的办法,即将射流冲击一个带有弹簧秤的平板,这样就可以测量出射流的冲击力;还有的学生提出采用天平原理或杆秤测出射流的冲击力。在此基础上引导学生预习掌握动量方程验证性实验中冲击力的测量方法——活塞式动量方程实验装置[12]。学生在充分掌握动量方程的基本理论分析和实验测量的原理后,从实验中得到有关数据,最终分析计算出所对应的动量修正系数,从而加深对动量修正系数含义的理解。这是实验教学和课堂教学相互促进的典型事例。
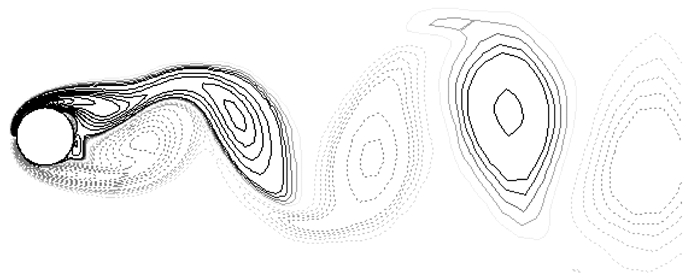
四、将CFD模拟技术引入教学过程在数学与计算机技术高速发展的今天,伴随着计算方法的不断扩展,不但解决了无法采用理论分析求解的复杂流动问题,而且通过数据处理还能得到整个流场的速度分布、压力分布以及其他物理量分布,并且可以通过图像甚至动画演示出来,达到在空间和时间上定量描述流场的目的。例如卡门涡街(如图 2所示),单独的一张图像难以说明卡门涡街的发生发展情况,而通过Fluent等计算流体力学软件模拟后作出的动画则能够形象地展示其流动形态,加深学生对卡门涡街形成和发展过程的理解。目前,商业化的计算软件已经日趋成熟,性能也在不断完善,已得到广大研究工作者和工业界的认同,CFD模拟技术的应用早已超越传统的流体力学和流体工程的范畴,成为工程设计中优化设计的重要技术手段[9]。
|
图 2 Re=150时对应的卡门涡街 |
在传统流体力学的教学过程中引入数值模拟的计算,旨在调动学生的学习兴趣,加深学生对流体力学基本方程的理解和应用。数值模拟教学主要针对以下几个方面:一是建立起反应流动问题的数学方程,确定数值模拟计算的边界条件;二是离散方程,这是课程的难点和核心内容,因为这部分内容在商业化的软件中无法体现出来,因此只能在课堂教学中阐述控制方程的离散方法,如有限元法、有限差分法和有限体积法等;三是程序的编写与调试以及网格的划分等,这部分内容同样已包含在软件中,教学中应主要用计算机语言C、Fortran等程序语言完成程序的编制;四是通用商业软件的具体操作,例如采用Gambit画网格,导入fluent后求解器的选择、模型选择等具体的步骤,可以通过教学和上机完成;五是计算结果的显示与处理[13]。
五、结语在教学过程中引入多媒体教学方法,实现传统教学方法与现代教学手段的有机结合,达到二种教学模式相互补充、相互促进的目的。分层次的教学方法,能实现因材施教,提高教学的针对性,使不同层次的学生学有所长,学有所用。在实验教学和课堂教学的统一中创新教学模式,充分调动学生学习的积极性和主动性,达到引导学生主动思考、创新思考的目的。将CFD模拟技术引入教学过程,能加深学生对流体力学理论和现象的理解。以上教学方法的改革与实践对提高流体力学课程教学质量和效果具有十分重要的作用。
| [1] | 王野, 李亚宁. 流体力学课程多视角教学方法的探索与实践[J]. 高等建筑教育, 2013, 22(4): 41–43. DOI:10.11835/j.issn.1005-2909.2013.04.011 |
| [2] | 王贞涛, 闻建龙, 王军锋, 等. 流体力学创新性教学初探[C]. 力学课程报告论坛论文集, 北京: 高等教育出版社, 2008: 313-315. |
| [3] | 杨小林, 杨开明, 严敬, 等. 流体力学课程教学改革探析[J]. 高等教育研究, 2006, 22(2): 47–48. |
| [4] | 谢振华, 宋洪庆. 多媒体在工程流体力学教学中的应用研究[J]. 教育教学论坛, 2013(13): 254–255. DOI:10.3969/j.issn.1674-9324.2013.13.176 |
| [5] | 毛欣炜, 毛根海. 数字流体力学教学系列——力学课程教学的改革[J]. 力学与实践, 2004, 26(6): 80–81. |
| [6] | 王军锋, 王贞涛, 王晓英, 等. 关于工科流体力学双语课程建设的思考[C]. 力学课程报告论坛论文集, 北京: 高等教育出版社, 2008: 310-312. |
| [7] | 张培红, 王晓华. 流体力学分层次教学模式研究[J]. 沈阳建筑大学学报:社会科学版, 2007, 9(2): 238–240. |
| [8] | 刘湘云, 刘良德. 流体力学泵与风机综合性实验教学实践[J]. 广东工业大学学报:社会科学版, 2010(10): 152–154. |
| [9] | 谢翠丽, 倪玲英. 《工程流体力学》本科课程引入CFD教学的探讨[J]. 力学与实践, 2013, 35(3): 91–93. DOI:10.6052/1000-0879-12-135 |
| [10] | 郑捷庆, 邹峰, 张军, 等. CFD软件在工程流体力学教学中的应用[J]. 中国现代教育装备, 2007(10): 119–121. DOI:10.3969/j.issn.1672-1438.2007.10.047 |
| [11] | 吴望一. 流体力学[M]. 北京: 北京大学出版社, 1982. |
| [12] | 闻建龙. 流体力学实验[M]. 镇江: 江苏大学出版社, 2010. |
| [13] | 韩占忠. FLUENT流体工程仿真计算实例与分析[M]. 北京: 北京理工大学出版社, 2009. |
 2014, Vol. 23
2014, Vol. 23


