Dirac函数是一个广义函数(或奇异函数),在近代物理学和工程技术中有着较广泛的应用[1-2]。通过引入Dirac函数,对许多集中于一点或一瞬时的物理量,如点质量、点电荷、点热源、集中力、集中力偶矩、瞬时脉冲力等,可以像处理连续分布的量那样,以统一的方式加以表达和解决,因而具有简便性,且物理意义明确。笔者尝试将Dirac函数引入到大学力学课程教学过程,以力学教学的开放性和多样性发掘力学课程的魅力。通过在材料力学、结构力学和弹性力学中的应用举例,说明Dirac函数在力学教学应用中的生命力。
一、Dirac函数的定义及基本性质如果函数f(x)满足如下条件[3]:
| $ f\left( x \right) = \left\{ \begin{array}{l} \infty ,\;\;\;\;for\;\;\;\;x = {x_0}\\ 0,\;\;\;\;\;otherwise \end{array} \right. $ | (1) |
| $ \int_{ - \infty }^\infty {f\left( x \right)dx} = 1 $ | (2) |
则称f(x)为Dirac函数。Dirac函数一般用δ(x-x0)表示,即
| $ f\left( x \right) = \delta \left( {x - {x_0}} \right) $ | (3) |
Dirac函数是一个广义函数,其图形如图 1所示。
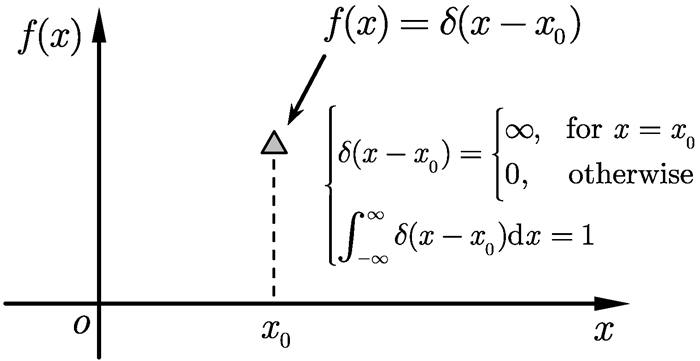
|
图 1 Dirac函数 |
Dirac函数也可以看作是单位阶跃函数的导数。事实上,根据单位阶跃函数(Heaviside函数)的定义[4]
| $ u\left( {x - {x_0}} \right) = \left\{ \begin{array}{l} 1,\;\;\;\;for\;\;\;\;x \ge {x_0}\\ 0,\;\;\;\;otherwise \end{array} \right. $ | (4) |
若定义
| $ \int_{ - \infty }^\infty {\dot u\left( {x - {x_0}} \right)dx} = u\left( \infty \right) - u\left( { - \infty } \right) = 1 $ | (5) |
| $ \dot u\left( {x - {x_0}} \right) = \left\{ \begin{array}{l} \infty ,\;\;\;\;for\;\;\;\;x = {x_0}\\ \;\;0,\;\;\;\;\;otherwise \end{array} \right. $ | (6) |
比较式(1)和式(2),显然有
| $ \dot u\left( {x - {x_0}} \right) = \delta \left( {x - {x_0}} \right) $ | (7) |
类似地,设D=(x, y, z),D0=(x0, y0, z0)为空间Ω内的两点,其中D0固定,则可定义三维Dirac函数为[5]:
| $ \begin{array}{l} \delta \left( {D - {D_0}} \right) = \delta \left( {x - {x_0},y - {y_0},z - {z_0}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left\{ \begin{array}{l} \infty ,\;\;\;\;for\;\;\;\;D = {D_0}\\ 0,\;\;\;\;\;otherwise \end{array} \right. \end{array} $ | (8) |
| $ \iiint\limits_\mathit{\Omega } {\delta \left( {x - {x_0},y - {y_0},z - {z_0}} \right)dxdydz} = 1 $ | (9) |
事实上,三维Dirac函数可以分为3个一维Dirac函数的乘积[5]:
| $ \begin{align} \delta \left( {D - {D_0}} \right)& = \delta \left( {x - {x_0},y - {y_0},z - {z_0}} \right) \\ & = \delta \left( {x - {x_0}} \right)\delta \left( {y - {y_0}} \right)\delta \left( {z - {z_0}} \right) \hfill \\ \end{align} $ | (10) |
下面,给出Dirac函数的基本性质——筛选性,对于一个连续函数g(x),则有
| $ \int_{ - \infty }^\infty {g\left( x \right)\delta \left( {x - {x_0}} \right)dx} = g\left( {{x_0}} \right) $ | (11) |
在实际应用中,通常考虑x≥0时才有意义,因此,上述筛选性质可以改写为
| $ \int_0^x {g\left( x \right)\delta \left( {x - {x_0}} \right)dx} = g\left( {{x_0}} \right) $ | (12) |
其中0≤x0≤x。
二、Dirac函数的物理背景 (一) 表示质点密度设有一质量为m的质点,置于空间Ω内的固定点D0=(x0, y0, z0),则质点在空间Ω内的分布密度可表示为
| $ {\rho _m} = m\delta \left( {D - {D_0}} \right) = m\delta \left( {x - {x_0},y - {y_0},z - {z_0}} \right) $ | (13) |
设有一细长直梁,在梁的A(x=a)和B(x=b)两点处分别作用有集中力P和集中力偶距M,则A点的分布力p(x)和B点的分布力偶矩m(x)可分别表示为
| $ p\left( x \right) = P\delta \left( {x - a} \right),m\left( x \right) = M\delta \left( {x - b} \right) $ | (14) |
当一个静止的质量m受到一个随时间变化的力f(t)作用,则力f(t)的冲量可表示为
| $ \kappa = \int_0^t {f\left( \tau \right)d\tau } = mv $ | (15) |
其中v是质量的速度。如果作用时间很短,那么获得同样速度v所需施加的力应该足够大。当t→0时,对于给定的速度v,有
| $ mv = \mathop {\lim }\limits_{t \to 0} \int_0^t {f\left( \tau \right)d\tau } = 常数 $ | (16) |
因此,可以得到
| $ f\left( t \right) = mv\delta \left( t \right) $ | (17) |
这表明δ(t)就是一个单位脉冲函数。因此,在工程中,将δ(t)函数用一个长度等于1的有向线段来表示,其中这个线段的长度表示δ(t)函数的积分值,称为δ(t)函数的强度[6]。
三、在力学教学中的应用 (一) 在材料力学中的应用图 2所示为一个等直简支梁问题。在梁AB上作用有竖向分布荷载p(x)和集中荷载P,以及集中力偶矩Me。
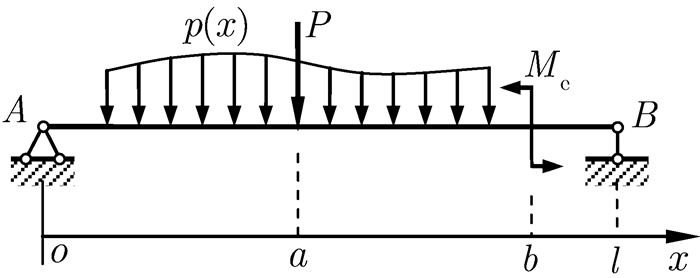
|
图 2 简支梁上的荷载 |
作用在梁AB上的荷载可以统一写成分布荷载的形式
| $ q\left( x \right) = - p\left( x \right) - P\delta \left( {x - a} \right) - {M_e}\delta '\left( {x - b} \right) $ | (20) |
容易求得支座A的反力RA,这时可得到梁任意截面的剪力和弯矩方程:
| $ \begin{align} Q\left( x \right) =& {R_A} - \int_0^x {p\left( \tau \right)d\tau - Pu\left( {x - a} \right) - {M_e}\delta } \hfill \\ &\left( {x - b} \right) \hfill \\ \end{align} $ | (21) |
| $ \begin{align} M\left( x \right) = &{R_A}x - \int_0^x {\left[ {\int_0^t {p\left( \tau \right)d\tau } } \right]dt} - P\left( {x - a} \right)u \hfill \\ &\left( {x - a} \right) - {M_e}u\left( {x - b} \right) \hfill \\ \end{align} $ | (22) |
不难验证,弯矩M(x)、剪力Q(x)与分布荷载q(x)满足如下的微分关系式:
| $ q\left( x \right) = \frac{{dQ\left( x \right)}}{{dx}},Q\left( x \right) = \frac{{dM\left( x \right)}}{{dx}} $ | (23) |
在实际应用中,可将剪力方程式(21)改写为
| $ Q\left( x \right) = {R_A} - \int_0^x {p\left( \tau \right)d\tau - Pu\left( {x - a} \right)} $ | (24) |
事实上,尽管剪力方程式(21)与式(24)在形式上所有不同,但其物理实质是相同的,即在截面x=b处的集中力偶矩Me投影到任意横截面上的剪力为零。因此,在式(21)中,多余项Meδ(x-b)仅仅表示了在截面x=b处作用着一集中力偶矩Me,而其值在剪力方程中为零。
顺便指出,若左端A为固定端,则初始截面上的剪力和弯矩分别等于固定端的支反力和支反力偶矩。此外,若竖向分布荷载p(x)沿梁长不连续时,则需分段积分,其积分下限作相应改动。
在本科材料力学的教材中,通常仅采用分布荷载来推导公式(23)中弯矩、剪力和荷载三者间的微分关系,然后再利用表格补充说明在有集中力与集中力偶矩时剪力图和弯矩图的特征。而在上述公式的推导中,荷载可以全面考虑分布荷载、集中力、集中力偶矩的情况,利用Dirac函数进行统一推导,具有合理性和简明性。
(二) 在结构力学中的应用在结构力学教材中,需要推导一般动力荷载P(t)作用下单自由度系统的位移动力反应,即Duhamel积分公式[3-4]。采用Dirac函数进行推导,系统的运动微分方程与零初始条件可合写为
| $ \left\{ \begin{array}{l} m\ddot Y\left( t \right) + c\dot Y\left( t \right) + kY\left( t \right) = P\left( t \right)\\ Y\left( 0 \right) = 0,\;\;\;\;\;\;\dot Y\left( 0 \right) = 0 \end{array} \right. $ | (25) |
根据Dirac函数的性质,任意的动力荷载P(t)可写为
| $ P\left( t \right) = \int_0^t {P\left( \tau \right)\delta \left( {t - \tau } \right)d\tau } $ | (26) |
相应地,系统的位移动力反应Y(t)可写为
| $ Y\left( t \right) = \int_0^t {y\left( {t - \tau } \right)d\tau } $ | (27) |
其中,y(t-τ)为脉冲力P(τ)δ(t-τ)作用在时刻t=τ的位移动力反应。事实上,当处于零初始条件的系统受到任意动力荷载P(t)作用时,可将动力荷载P(t)看作是一系列脉冲力的叠加,而系统的总位移反应Y(t)则为t时刻之前的各个脉冲反应的总和,如图 3所示。
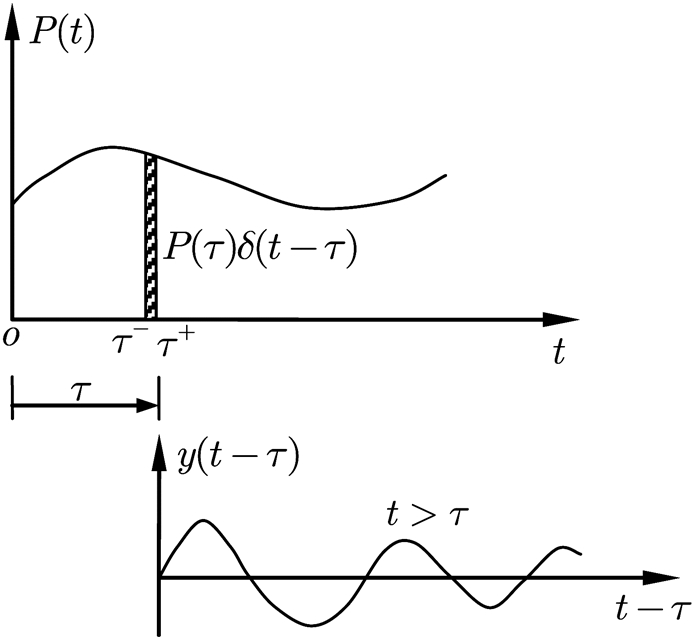
|
图 3 Duhamel积分的推导 |
现在,只需求出脉冲力P(τ)δ(t-τ)作用在时刻t=τ的位移动力反应y(t-τ)。记τ-和τ+分别为脉冲力作用瞬间的前后时刻,此时系统的运动微分方程与零初始条件合写为
| $ \begin{array}{l} \left\{ \begin{array}{l} m\ddot y\left( {t - \tau } \right) + c\dot y\left( {t - \tau } \right) + ky\left( {t - \tau } \right) = P\left( \tau \right)\delta \left( {t - \tau } \right)\\ y\left( {{\tau ^ - }} \right) = 0,\;\;\;\;\;\dot y\left( {{\tau ^ - }} \right) = 0 \end{array} \right.,\\ t > {\tau ^ - } \end{array} $ | (28) |
根据动量定理,有
| $ P\left( \tau \right)\delta \left( {t - \tau } \right)dt = md\dot y = m\ddot ydt $ | (29) |
将式(29)两边在区间τ-≤t≤τ+对时间积分,可得
| $ \int_{{\tau ^ - }}^{{\tau ^ + }} {P\left( \tau \right)\delta \left( {t - \tau } \right)dt} = m\int_{{\tau ^ - }}^{{\tau ^ + }} {\ddot y\left( t \right)dt} $ | (30) |
于是,有
| $ P\left( \tau \right) = m\left[ {\dot y\left( {{\tau ^ + }} \right) - \dot y\left( {{\tau ^ - }} \right)} \right] = m\dot y\left( {{\tau ^ + }} \right) $ | (31) |
可见,在脉冲力的作用下,系统的速度发生了突变,但在这一瞬间位移则来不及改变,即有y(τ+)=y(τ-)=0,而当t>τ+时,脉冲力的作用已结束。因此,当t>τ+时,
| $ \left\{ \begin{array}{l} m\ddot y\left( {t - \tau } \right) + c\dot y\left( {t - \tau } \right) + ky\left( {t - \tau } \right) = 0\\ y\left( {{\tau ^ + }} \right) = 0,\;\;\;\;\;\dot y\left( {{\tau ^ + }} \right) = P\left( \tau \right)/m \end{array} \right.,t > {\tau ^ + } $ | (32) |
由式(32)可得,在t=τ时刻脉冲力P(τ)δ(t-τ)所引起的系统脉冲反应:
| $ \begin{array}{l} y\left( {t - \tau } \right) = \frac{{P\left( \tau \right)}}{{m{\omega _D}}}\exp \left[ { - \xi \omega \left( {t - \tau } \right)} \right]\sin {\omega _D}\left( {t - \tau } \right),\\ t > \tau \end{array} $ | (33) |
其中,
于是,系统的总位移动力反应为
| $ Y\left( t \right) = \int_0^t {\frac{{P\left( \tau \right)}}{{m{\omega _D}}}\exp \left[ { - \xi \omega \left( {t - \tau } \right)} \right]\sin {\omega _D}\left( {t - \tau } \right)d\tau } $ | (34) |
采用Dirac函数来推导Duhamel积分公式,可充分体现数学推导过程的严谨性,同时又具有明确的物理意义,这对于进一步理解高等数学中微分方程的求解具有重要意义。
(三) 在弹性力学中的应用在弹性力学中,由于外力仅分为体力和面力,不包含集中力等概念,利用Dirac函数来将集中力直接推广到面力中去。比如,薄板弯曲问题中,若需考虑板面上受集中荷载的情况,此时薄板的弹性曲面微分方程可写为
| $ D{\nabla ^4}w\left( {x,y} \right) = q\left( {x,y} \right) $ | (35) |
其中,薄板的弯曲刚度D和单位面积内的横向荷载q(x, y)分别为:
| $ D = \frac{{E{h^3}}}{{12\left( {1 - {\mu ^2}} \right)}} $ | (36) |
| $ \begin{array}{l} q\left( {x,y} \right) = {\left( {{{\bar f}_z}} \right)_{z = - h/2}} + {\left( {{{\bar f}_z}} \right)_{z = h/2}} + \int_{ - h/2}^{h/2} {{f_z}dz} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; + \sum\limits_{j = 1}^N {{P_j}\delta \left( {x - {x_j},y - {y_j}} \right)} \end{array} $ | (37) |
在式(37)中,Pj(j=1, 2, …, N)为作用于板面上点(xj, yj)处的横向集中力。
算题:如图 4所示四边简支的矩形薄板,边长分别为a和b,在任意一点D(x0, y0)处受横向的集中力P作用,不考虑薄板的体力,试求薄板的挠度w(x, y)。
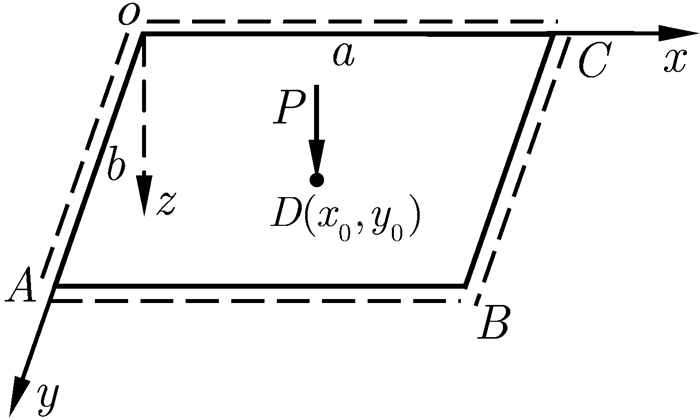
|
图 4 四边简支的矩形薄板问题 |
解:采用纳维解法,将挠度函数取为重三角级数。
| $ w = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{A_{mn}}\sin \frac{{m\pi x}}{a}\sin \frac{{n\pi y}}{b}} } $ | (38) |
由于不考虑体力的作用,此时横向荷载q(x, y)变为
| $ q\left( {x,y} \right) = P\delta \left( {x - {x_0}} \right)\delta \left( {y - {y_0}} \right) $ | (39) |
将q(x, y)代入纳维解法中的系数表达式
| $ \begin{array}{l} {A_{mn}} = \frac{{4\int_0^a {\int_0^b {q\left( {x,y} \right)\sin \frac{{m\pi x}}{a}\sin \frac{{n\pi y}}{b}dxdy} } }}{{{\pi ^4}abD\left( {\frac{{{m^2}}}{{{a^2}}} + \frac{{{n^2}}}{{{b^2}}}} \right)}}\\ \;\;\;\;\;\; = \frac{{4P\int_0^a {\delta \left( {x - {x_0}} \right)\sin \frac{{m\pi x}}{a}dx} \int_0^b {\delta \left( {y - {y_0}} \right)\sin \frac{{n\pi y}}{b}dy} }}{{{\pi ^4}abD\left( {\frac{{{m^2}}}{{{a^2}}} + \frac{{{n^2}}}{{{b^2}}}} \right)}}\\ \;\;\;\;\;\; = \frac{{4P\sin \frac{{m\pi {x_0}}}{a}\sin \frac{{n\pi {y_0}}}{b}}}{{{\pi ^4}abD\left( {\frac{{{m^2}}}{{{a^2}}} + \frac{{{n^2}}}{{{b^2}}}} \right)}} \end{array} $ | (40) |
于是,将式(40)代入薄板的挠度式(38)中,可得
| $ w = \frac{{4P}}{{{\pi ^4}abD}}\sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {\frac{{\sin \frac{{m\pi {x_0}}}{a}\sin \frac{{n\pi {y_0}}}{b}}}{{\left( {\frac{{{m^2}}}{{{a^2}}} + \frac{{{n^2}}}{{{b^2}}}} \right)}}\sin \frac{{m\pi x}}{a}\sin \frac{{n\pi y}}{b}} } $ |
利用Dirac函数来将集中力直接推广到面力中去,统一按面力来处理方便、合理,既体现了课程理论性强、逻辑严谨的特点,又便于学生加深对弹性力学知识点的理解。
四、结语在力学课程教学中,尝试引入Dirac函数,方便地将集中力、集中力偶矩以及瞬时脉冲力等物理量处理为连续分布的形式,以统一的方式加以表达和解决。通过在材料力学梁的剪力方程和弯矩方程的统一表达,结构力学Duhamel积分公式的推导,以及弹性力学薄板弯曲问题中的三处应用,可以看出Dirac函数在力学教学中的生命力。作为力学课程关联性教学的典型案例,将Dirac函数引入力学教学进行实例分析,可以加深学生对力学知识的理解,促进力学课程间的渗透与融合,激发学生学习兴趣,引导和培养学生的开放性和多元性思维,为力学专业教育和力学创新性人才培养提供借鉴。
| [1] | 卓士创, 李顺才. 广义函数及其在力学中的应用述评[J]. 甘肃科学学报, 2008, 20(1): 42–45. |
| [2] | 王燮山. 奇异函数及其在力学中的应用[M]. 北京: 科学出版社, 1993. |
| [3] | 倪振华. 振动力学[M]. 西安: 西安交通大学出版社, 1990. |
| [4] | 刘章军, 陈建兵. 结构动力学[M]. 北京: 中国水利水电出版社, 2012. |
| [5] | 柴伟文, 曹黎侠. 多维δ函数及其物理应用[J]. 西安工业学院学报, 2006, 26(2): 175–178. |
| [6] | 南京工学院数学教研组. 积分变换[M]. 2版. 北京: 高等教育出版社, 1982. |
 2014, Vol. 23
2014, Vol. 23

