2. 河北省土木工程技术研究中心, 天津 300401
2. Civil Engineering Technology Research Center of Hebei Province, Tianjin 300401, P. R. China
结构力学是土木工程专业一门非常重要的专业基础课,具有承前启后的作用,上承理论力学、材料力学等基础课程,下启混凝土结构设计、钢结构等专业课程,其重要性不言而喻。但是,结构力学课程往往又是土木工程专业学生最头疼的一门课程,主要原因在于:(1) 内容多。主要包括几何组成分析、静定结构(梁、刚架、桁架、拱和组合结构)内力计算、影响线、虚功原理和结构的位移计算、力法、位移法、矩阵位移法、力矩分配法以及结构动力计算等内容。(2) 课时少。由于大土木专业调整,该课课时由原来的128课时减少至96课时。(3) 理论性强。从结构内力计算到画出内力图,从内力图到位移计算,从静定结构到超静定结构,从结构静力计算到结构动力计算,环环相扣,逻辑推理严密。(4) 计算能力要求高。要求学生会计算内力,画出内力图,会计算位移,会求解超静定结构,会计算结构动力特性、动力反应等。那么,应如何学好结构力学课程呢?笔者在长期的结构力学教学过程中认识到,学生不会求解结构力学习题的关键问题是由于头脑中没有相应的力学概念,面对力学题目,不知道如何下笔。笔者认为,解决这一难题的方法就是在结构力学课程教学中重视力学概念的教学。本文结合结构力学中的虚功概念教学,探讨重视力学概念教学的重要性。
一、概念和力学概念现代汉语词典对概念的解释是:“思维的基本形式之一,反映客观事物的一般的、本质的特征。人类在认识过程中,把所感知的事物的共同特点抽出来,加以概括,就成为概念。比如从白雪、白马、白纸等事物里抽象出它们的共同特点,就得出‘白’的概念。”[1]毛泽东在《实践论》中说:“社会实践的继续,使人们在实践中引起感觉和印象的东西反复了多次,于是在人们的脑子里生起了一个认识过程中的突变(即飞跃),产生了概念。”可见,概念就是用一个词或词组定义这个事物是什么,以区别于其他事物。它是把这个事物的本质抽象出来,即概念本身就是对事物本质特征的一种把握。力学概念自然就是对各种力学现象抽象出来的概括其本质特征的一种认识。学生理解了结构力学概念,就等于在头脑中构建了一把钥匙,可以打开结构力学的大门。
二、结构力学课程应重视力学概念的教学力学概念是结构力学知识的根基和精髓。在教学中,第一节课的内容一般是新概念的引入。可教学中却常常发现学生在教师讲解新概念时并没有真正地去深刻理解,而是浮在表面上,对概念所表达的实质内容往往茫然而不知所言,更不可能在头脑中形成能动的概念体系。下面以虚功原理的讲解为例进行说明。
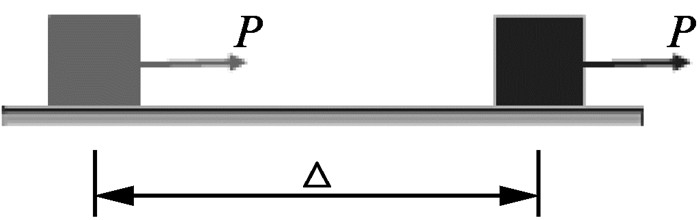
在讲解虚功原理时,虚功是首先必须学习的一个新的结构力学概念。结构力学课程教学中,概念可分为两类:一类是学生以前在其他课程中接触过的力学概念,一类是新的力学概念。教师在教学过程中,可通过学生已学习掌握了的概念引入新的概念。由熟悉到不熟悉,由旧知识到新知识,循序渐进,引导学生接受新知识。学生不熟悉虚功,但功这一概念,学生在高中物理学中学过。在讲解时可先引导学生回顾高中物理学中功的概念,高中物理学中功的定义是力在力方向上通过位移的乘积(如图 1)。功的计算公式如(1) 式。
|
图 1 功示意图 |
| $ T = P \cdot \mathit{\Delta } $ | (1) |
有了旧知识的铺垫,为便于学生理解虚功概念,教学过程中不妨引导学生在高中学过的功的前面加一个字,称作“实功”,即实功就是以前学生头脑中的原有功的概念,“虚”字与“实”字相对应,“虚功”与“实功”也相对应。教学中可以这样引导学生理解虚功,首先迁移实功内容至虚功内容,告诉学生虚功也是力和位移乘积,这样学生头脑中大体对虚功有了一个整体印象,再告诉学生其不同之处在于:实功中力与位移是在一个过程中发生的,有因果关系。而虚功中力与位移不是在一个过程中发生的,之间没有因果关系。虚功定义为力是在其它因素引起的位移上作的功,力与位移分别属于同一体系的两种彼此无关的状态。虚功的实质是借助与功的概念把毫无因果关联的两个量力与位移联系在一起。虚功计算公式如(2) 式。
| $ {T_{kj}} = {P_k} \cdot {\mathit{\Delta } _{kj}} $ | (2) |
再以图 2所示简支梁为例,具体进行解释说明。
|
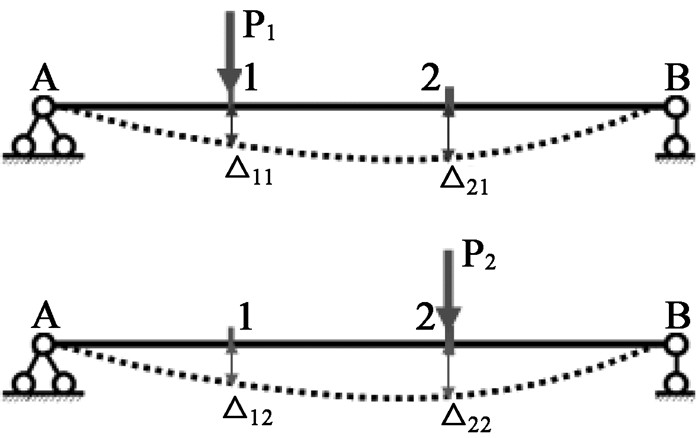
图 2 简支梁虚功实功示意图 |
该简支梁在P1作用下,产生挠曲线,在截面1和2位置上的位移记为:Δ11、Δ21;同理,在P2作用下,该简支梁产生另一个挠曲线,在截面1和2位置上的位移记为:Δ12、Δ22。根据以上功的概念讲解,可写出简支梁的实功为:T11=P1·Δ11;T22=P2·Δ22。虚功为:T12=P1·Δ12;T21=P2·Δ21。两个实功T11、T22和两个虚功T12、T21,其共同点为:力与位移乘积。不同点为:一个力与位移是同一个过程发生的,另一个不是同一个过程发生的。教师通过例子对比把虚功简明扼要地讲解清楚透彻。通过熟悉的功的概念,经对比引入虚功这一新概念,学生就非常容易接受和理解。
学生理解了虚功这一力学概念,以此作为一个基石,讲解虚功原理这一抽象深奥的基本规律,学生也就非常容易理解和掌握了。虚功原理的定义是“设变形体在力系作用下处于平衡状态,又设变形体由于其它原因产生符合约束条件的微小的连续变形,则外力在相应位移上所做的外力虚功T恒等于整个变形体各个微段内力在变形上所做的内力虚功U,即:外力虚功T=内力虚功U。”教学中可以引导学生这样理解虚功原理,简单地说,虚功原理就是外力虚功等于内外虚功,只不过一个是外力虚功,一个是内力虚功。如此简单明了,就可清楚地说明虚功原理的内容。再以刚架为例子具体说明虚功原理,如图 3所示。
|
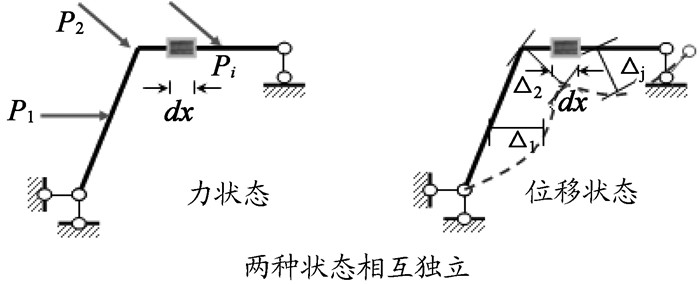
图 3 虚功原理两种状态示意图 |
先介绍外力虚功。一组外力P1、P2 …… Pi作用在该刚架上,使之处于静止状态,称为力状态。由于其他原因,这里是支座移动,刚架产生位移,称为位移状态。相应力截面对应的位移记:Δ1、Δ2 …… Δi。
按照虚功概念,外力虚功就可以表示出来。外力虚功都是宏观的,看的见摸得着的,比较直观。外力虚功为:
| $ T = {P_1} \cdot {\mathit{\Delta } _1} + {P_2} \cdot {\mathit{\Delta } _2} + \cdots \cdots + {P_i} \cdot {\mathit{\Delta } _i} = \sum {{P_j}} \cdot {\mathit{\Delta } _j} $ | (3) |
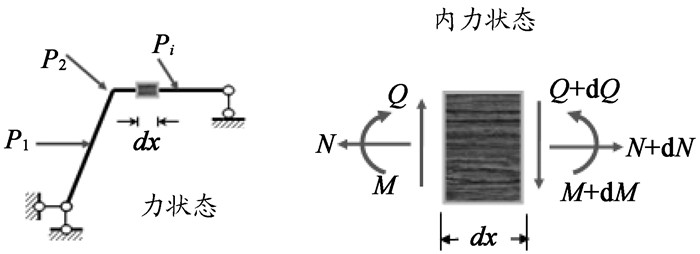
再介绍内力虚功。对于力状态,刚架作用一组外力P1、P2 …… Pi,必然会引起刚架内力。内力是看不见的,可取微段dx,截开截面,即可看到内力,如图 4所示。由于微段dx非常无限接近,微段左截面与右截面的内力增量可忽略不计,即整个微段内力认为相等:N、Q、M。
|
图 4 外力虚功示意图 |
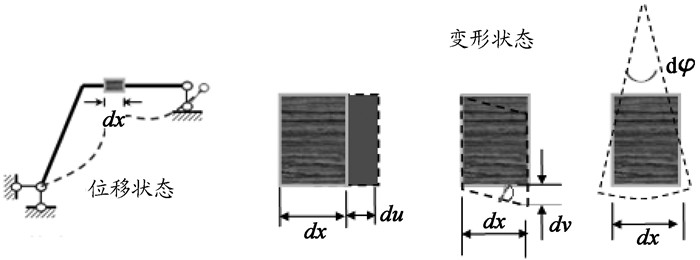
对于位移状态,刚架由于支座移动,产生宏观位移,相应的对于微段dx,会产生变形,如图 5所示。相应微段dx变形,将其分解为轴向变形、剪切变形和弯曲变形,即du、dv、dφ。
|
图 5 内力虚功示意图 |
同样按照虚功概念,可以写出微段内力虚功,虽然宏观上看不见内力虚功,但通过截开微段截面,就能看见内力虚功。微段dx上的内力虚功为:dU=Ndu+Qdv+Mdφ,其中,N、Q、M来自力状态;du、dv、dφ来自位移状态。这样整个刚架内力虚功为:
| $ U = \sum {\left( {\int {Ndu} + \int {Qdv} + \int {Md\varphi } } \right)} $ | (4) |
按照虚功原理,外力虚功T等于内力虚功U,对该刚架来说,它的虚功原理为:
| $ \sum {{P_j}} \cdot {\mathit{\Delta }_j} = \sum {\left( {\int {Ndu} + \int {Qdv} + \int {Md\varphi } } \right)} $ | (5) |
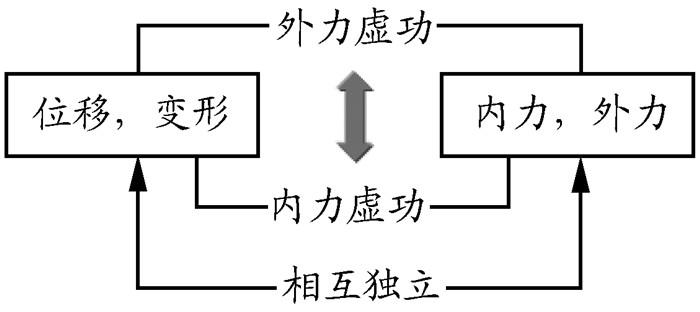
等式的左边是外力虚功,右边是内力虚功,其物理意义如图 6所示。
|
图 6 虚功原理力学意义示意图 |
由此可见,讲解整个虚功原理如围绕虚功这一核心概念,形成概念体系,反复运用,对虚功原理这一非常重要的基本理论,学生自然就能深刻理解了。
理解虚功这一核心概念,其意义远不止是有助于理解虚功原理,此后的结构力学内容几乎都可以由此串联起来,像滚雪球一样,越滚越大,形成连锁反应。如由虚功原理推导出的单位荷载法,即结构的位移计算,只不过是虚功原理在结构力学中的具体应用而已,它们是一般与特例的关系。至此,从功→虚功→虚功原理→单位荷载法→位移计算等这一连串的知识,学生都能轻松地理解。此外,理解了虚功原理,功的四个互等定理学生也容易接受。功的互等定理只不过是用了两次虚功原理,而其他三个互等定理:位移互等定理、反力互等定理、位移反力互等定理不过是功的互等定理的具体特例而已。这样讲解后,学生不仅对这一章的内容了然于心,而且也为后续内容的理解,奠定了扎实的基础。如力法无非是利用几何变形条件建立补充方程,求解赘余力,其实质就是位移的计算,只不过是多计算了几个位移而已。而位移法则是将超静定结构划分为单跨静定梁计算,其算法是以力法得到的单跨梁结论为基础的。力矩分配法则是位移法的一种适合于手算的变形方式。矩阵位移法更是以矩阵表达的转角位移方程,实质上就是位移法的另一种变形方式。由虚功引出的结构力学内容体系如图 7所示。可以看出,从理解虚功这一重要的力学概念出发,此后一连串的基本原理、基本方法都容易被学生理解和掌握。

|
图 7 结构力学体系 |
上述例子凸显出力学概念教学在结构力学课程中的重要性。只有理解了力学概念,才能理解原理,掌握计算方法。
力学概念是结构力学的根,只要学生理解了力学概念,才能把握结构力学的基本规律。清华大学袁驷教授倡导的定性结构力学[2],实质上就是要学生首先从概念上进行结构的分析、判断,并最终得出结论。没有力学概念支撑,就像人没有骨架一样,力学概念的把握本身就是一种对结构力学骨架的把握。因此,结构力学课程教学中,一定要重视力学概念的教学。
三、结语文章以虚功这一结构力学概念为例,揭示了力学概念教学在结构力学课程中的重要性。力学概念是对力学本质的一种认识,只有深刻理解了力学概念,才能以此为基石,构筑起结构力学的框架来。否则,结构力学的基本规律、计算公式、计算方法等内容就都没有依托的根。
| [1] | 中国社会科学院语言研究所词典编辑室编. 现代汉语词典[M]. 北京: 商务印书馆出版, 1998. http://ling.cass.cn/bsgk/bsgk_jgsz/bsgk_jgsz_cdbjs/201703/t20170322_3460684.html |
| [2] | 袁驷. 一个基础, 两座大厦——结构力学课程改革的思路与实践[J]. 力学与实践, 1998(4): 56–58. |
 2014, Vol. 23
2014, Vol. 23


